地球物理学报  2014, Vol. 57 Issue (4): 1284-1291   PDF    
引用本文
赵建国, 史瑞其, 陈竞一,等. 2014. 黏性声波方程数值正演中的匹配Z变换完全匹配层吸收边界. 地球物理学报, 57(4): 1284-1291, doi: 10.6038/cjg20140425   
ZHAO Jian-Guo, SHI Rui-Qi, CHEN Jing-Yi, et al. 2014. An matched Z-transform perfectly matched layer absorbing boundary in the numerical modeling of viscoacoustic wave equations. Chinese J. Geophys. (in Chinese), 57(4): 1284-1291, doi: 10.6038/cjg20140425   
黏性声波方程数值正演中的匹配Z变换完全匹配层吸收边界
赵建国1, 史瑞其2, 陈竞一3, 潘建国4, 王宏斌4    
1. 中国石油大学（北京）地球物理与信息工程学院;油气资源与 探测国家重点实验室;CNPC物探重点实验室, 北京 102249;
2. 中海油研究总院, 北京 100027;
3. Tulsa大学地球科学学院, Oklahoma, 74104 USA;
4. 中石油勘探开发研究院西北分院, 兰州 730000
投稿时间:2013-5-6    最后修改时间: 2014-1-18 .
基金项目：国家自然科学基金项目（41274138）及中国石油大学（北京）基础研究基金（KYJJ2012-05-25）资助.
第一作者简介：赵建国，男，1976年生，副教授，主要从事电磁勘探数据处理及岩石物理研究.E-mail：jgzhao761215@aliyun.com
通讯作者：史瑞其，男，1986年生，工程师，主要从事地震波传播及地震资料处理解释研究. E-mail：shiruiqi123@gmail.com
摘要：本文将非分裂场形式的匹配Z变换PML引入黏声波方程数值正演中，用时域有限差分模拟检验了其在黏声波方程模拟中的效果.数值正演结果表明，在大角度入射时匹配Z变换完全匹配层比传统PML表现更佳，消除了大角度入射产生的低频虚假反射.长时间能量衰减计算证明匹配Z变换完全匹配层在黏声波方程模拟中具有105时间步的稳定性.
关键词： 完全匹配层     匹配Z变换     吸收边界     黏声波方程     时域有限差分    
An matched Z-transform perfectly matched layer absorbing boundary in the numerical modeling of viscoacoustic wave equations
ZHAO Jian-Guo1, SHI Rui-Qi2, CHEN Jing-Yi3, PAN Jian-Guo4, WANG Hong-Bin4    
1. College of Geophysics and Information Engineering, China University of Petroleum (Beijing); State Key Lab of Petroleum Resource and Prospecting; CNPC Key Lab of China University of Petroleum (Beijing), Beijing 102249, China;
2. CNOOC Research Institute, Beijing 100027, China;
3. Department of Geoscience, University of Tulsa, Oklahoma 74104, U.S.A;
4. Northwest Institute of Oil Exploration and Development, CNPC, Lanzhou 730000, China
Abstract: An unsplit matched Z-transform PML (MZT-PML) is introduced in the modeling of viscoacoustic wave equations, and the performance of this technique is validated through time-domain finite-difference modeling. The numerical experiments demonstrate that MZT-PML performs better than the classical PML in high-angle incidence case and well eliminates the low-frequency spurious reflections in this case. Long-time calculation of energy decay shows that MZT-PML is stable up to 105 time steps in viscoacoustic wave modeling.
Key words: Perfectly matched layer     Matched Z-transform     Absorbing boundary     Viscoacoustic wave equation     Finite-difference in time-domain    
1 引言

地震波数值正演是研究地震波在地下介质传播规律的重要手段(金胜汶等，1994；刘礼农等，2004；谢桂生等，2005).在使用数值方法模拟无限或半无限大介质中的地震波传播会因计算机内存产生截断边界，从而产生虚假数值反射，吸收边界条件技术可以用于消除截断边界效应产生的虚假反射.经过三十多年的发展，在地震波数值领域中主要产生了两大类吸收边界技术：海绵边界条件(Cerjan et al., 1985；Sochacki et al., 1987)和旁轴近似边界条件(Clayton and Engquist， 1977；Stacey，1988；Higdon，1991；Quarteroni et al., 1988)，但是这些吸收边界技术在很多情况下表现不佳，比如对于大角度入射波和低频能量不能很好的吸收.Bérenger(1994)在Maxwell电磁波方程中提出了完全匹配层(Perfectly Matched Layer，PML)，用于消除时域有限差分法电磁波模拟中的虚假反射.PML对于较大范围入射角和频率成分的波具有高效的吸收作用，理论上对于入射波具有零反射系数，目前已经成为常用的吸收边界技术.之后，PML很快被证明在地震波场数值模拟同样高效(Chew and Liu， 1996；Hasting et al., 1996).

后来，PML从数学上证明可以同复拉伸坐标的 概念联系起来(Chew and Weedon， 1994).但Kuzuoglu和Mittra(1996)指出，使用传统复拉伸坐标算子的PML对于隐矢波和极低频波成分吸收效能会出现下降，并且在大角度特别是切入射情况下(如震源靠近PML吸收边界的情况下)会产生较大程度的虚假反射，因此为解决该问题，Kuzuoglu和Mittra(1996)在电磁波模拟中引入了复频移拉伸算子用于提高PML的吸收效能.在传统PML算法中，为在时间域中求解复拉伸坐标下的波动方程，需要对波场变量进行非物理分裂，但经典的分裂场形式的PML(Chew and Weedon， 1994)不能直接使用复频移拉伸算子.在PML实现形式上，一些非分裂场格 式被提出(Cheng and Zhao， 2011).Roden和Gedney(2000)在Maxwell方程模拟中提出了卷积PML来实施复频移拉伸算子，在PML方程中出现卷积项从 而得到非分裂场的形式.之后，使用复频移拉伸算子的卷积PML也被引入地震波模拟中(Drossaert and Giannopoulos， 2007；Komatitsch and Martin， 2007).

Li和Dai(2008)在电磁波模拟中提出了匹配Z 变换PML(Matched Z-transform PML，MZT-PML)，同卷积PML是基于Fourier变换理论导出不同，MZT-PML是基于匹配Z变换理论得到非分裂场PML格式，也避免了卷积PML中的片断常数近似(Roden and Gedney， 2000)，其推导过程也相对简单(Li and Dai， 2008).具有非分裂场格式的MZT-PML技术可以在地震波方程模拟中直接应用复频移拉伸算子(Shi et al., 2012)，本文推导了适用于速度-压力形式黏声波方程的MZT-PML吸收边界控制方程，并对相应的数值正演结果进行了吸收效果分析.

2 标准线性固体黏声波方程

在实际介质中，由于地层的吸收衰减作用引起的速度耗散，地震波频率会随着传播距离的增大而降低，因此近年来地震勘探研究越对黏弹性介质的 关注不断提高(Carcione et al., 1988；Liu and Chang， 1996). 常用的黏弹性介质模型有Kelvin-Voigt模型、Maxwell模型和标准线性固体(St and ard Linear Solid，SLS)模型，但Maxwell模型不能描述弹性蠕变，Kelvin-Voigt不能描述应力弛豫.SLS模型(Carcione，2007)可以同时描述上述两种现象，因此相对符合实际黏弹性介质中的地震波传播规律.本文主要目的在于说明PML吸收边界的应用，因此为简便起见使用基于单SLS模型的黏声波方程.在二维Cartesian直角坐标系中，速度-压力格式的SLS模型黏声波方程如下(Carcione，2007)：

其中，p为声压场；ρ为质量密度；体积模量K=ρc2p，cp为纵波速度；vx和vz分别为沿x和z方向的速度场分量.本文中带有下标t，x或z的算符∂表示对t，x或z求偏导数.R为记忆变量，τε和τσ分别为纵波应力和应变的弛豫时间常数.黏弹性介质常用品质因子Q值反映地下介质对于地震波能量衰减的吸收情况，与岩石物性、孔隙流体类型和流体饱和度等因素相关.根据Carcione等(1988)的推导，Q值与弛豫时间常数有如下关系：

其中，ω0为震源的中心角频率.由(1)式可见，当弛豫时间常数τε=τσ时，(1)式即退化为声波方程.

3 匹配Z变换完全匹配层

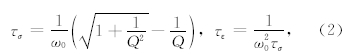
将(1)式变换到频率域，有

其中，i为虚数单位，ω为角频率，根据复拉伸坐标变换(Chew and Weedon， 1994)的概念，将空间偏导数∂η(η=x，z)替换为复拉伸坐标∂ =S－1η∂η.其中Sη为拉伸坐标算子，对PML的吸收特性有重要影响.传统拉伸坐标算子为

其中，实系数dη≥0，使波场振幅在PML内部呈指数级别衰减.使用传统拉伸算子(4)式的PML存在大角度入射波的吸收效能不足的问题，这是因为传统拉伸算子只对行波具有吸收作用，而对于沿求解区域和PML区域界面平行方向传播的隐矢波不起作用，另外对于极低频成分也存在奇异性因而也不能较好地消除极低频反射(Chew and Liu， 1996).为解决该问题，复频移拉伸坐标算子被提出：

式(5)中通过引入辅助衰减系数κη≥1和频移系数αη≥0，将复平面的极点从从实轴移动到负虚半平面上，以提高对隐矢波和低频波的吸收.易见(5)式比(4)式更具有一般性，令κη=1和αη=0即为传统拉伸算子(4)式.在复拉伸坐标下，(3)式改写为

因为拉伸坐标算子Sη为频率ω的函数，因此将(6)式变换回时间域会产生卷积项(Roden and Gedney， 2000).考虑到频率域的乘法运算和时间域的卷积运算都等价于Z域的乘法运算，因此将(6)式变换到Z域可以使推导过程相对简单.

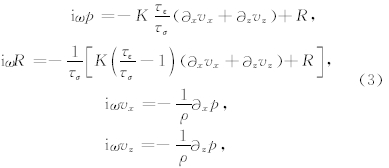
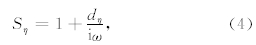
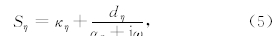
MZT-PML的主要思想在于将拉伸坐标算子(5)式的倒数分裂为两部分的乘积，且令iω仅存在于其中一项中：

利用对应关系iω↔s将(6)式变换到S域，有

对于任一变量A，满足该匹配Z变换映射关系:(s－A)↔(1－eAΔtz－1)可以得到1/Sη(s)的Z变换为

其中，算符ZT · 表示匹配Z变换运算，Δt表示时间采样间隔.为简短起见，这里只以式(6a)的MZT-PML格式为例进行说明；另外这里假设PML吸收边界由η=0(η = x，z)起始.将(6a)由频率域变换到Z域有：

其中，(1－z－1)/Δt是iω的Z变换，考虑映射关系iω↔∂t和∂t↔(1－z－1)/Δt，将(9)式代入(10)式可得

然后引入两个辅助变量Ψvx，x和Ψvz，z，分别对应速度场的空间偏导数∂xvx和∂zvz：

将(12)转化为

其中，bη=e－(αη+dη/κη)Δt，因此式(10)可以写作

其中，aη=e－αηΔt，考虑到z-1对应于在离散时间域中的Δt的单步时延：z－1u(z)↔u(n－1)Δt，这样可以直接得到方程(13)和(14)的时域有限差分更新格式:

式(15)即为关于声压场p连同辅助变量Ψvx，x和Ψvz，z的有限差分时间更新格式.Ψvx，x和Ψvz，z需要在更新速度场v和压力场p前计算，注意到式(15c)中同时含有不同离散时刻(n和n+1时间步)的Ψ，因此Ψn应当在更新前暂存于一个临时变量中.(6)式中关于速度场vx、vz和记忆变量R的MZT-PML格式可以同理导出.

4 数值正演

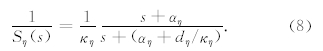
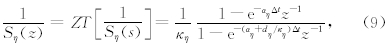
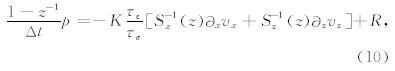
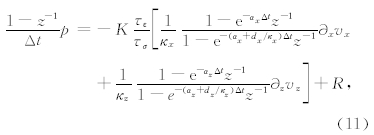
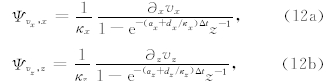
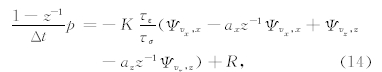
在数值模拟时，空间上采用八阶交错网格有限差分格式(Virieux，1986)，并采用比Taylor展开系数精度更高的Holberg差分系数(Holberg，1987)来计算所有空间导数.Holberg系数通过在给定阶数截断计算得到，降低了群速度产生的误差从而整体上减小了数值频散.例如，x方向空间偏导数在i+1/2网格点处的差分离散格式为

其中，八阶精度Holberg差分系数C1=1.231666，C2=-0.1041182，C3=0.02063707，C4=-0.003570998. 模型计算区域大小为5250 m × 1500 m的长方形区域，由701 × 201个网格点构成，有限差分元胞 边长为Δx=Δz=7.5 m.介质密度ρ=2000 kg·m-3，纵波速度cp = 3000 m/s，品质因子Q=30.时间上，采用二阶显式差分格式，因此时间更新步长Δt由需满足Courant稳定性条件：

取Δt=1.2 ms，模拟持续时长4.8 s，共计4000时间步.采用点声压震源激发，震源子波为一导数高斯函数f(t)=－2a(t－t0)e－a(t－t0)2，其中a= π2f20，震 源中心频率f0=20 Hz，子波时延t0=1.2/f0=0.06 s，激发点位于(517.5 m，180 m)处；这里设置2个检波点，检波点1和检波点2分别位于(742.5 m，1380 m)和(5017.5 m，142.5 m)处.计算区域四周由PML吸收边界包围，厚度为75 m，占10个有限差分元胞.故震源靠近顶部吸收边界，检波点1和2分别靠近底部和顶部吸收边界(图 1).一般在PML区域内，要将复频移算子(5)式中各参数设置为沿 PML区域和求解区域的交界面外法线方向渐进变化：

其中，η为PML内一点到与交界面的距离，L为 PML的厚度.各衰减参数取值如下(Li and Matar， 2010；Festa and Vilotte， 2005)：d0=-(Pd+1)cplog10(Rc)/2L，κ0=-(Pκ+1)blog10(Rc)/2L，α0=πf0；其中Rc=10-5，Pd=Pκ=2，Pα=1，b=10Δh，Rc为理论反射系数，Δh为空间元胞边长.这里也给出使用复拉伸坐标算子(3)式的传统分裂场PML吸收边界条件下的黏声波方程模拟(Liu and Tao， 1997)结果，用以分析对比.另外，为检验吸收边界效果需要同参考解对比，本文参考解是在不含吸收边界的足够大区域(模拟时间内边界反射不会到达检波器)使用相同的数值离散格式计算得到，震源和检波器相对位置不变.
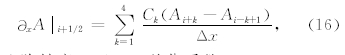
图 1 计算区域示意图 图中黑色内框线表示PML与求解区域的交界，圆圈表示震源位置，三角表示检波点位置Fig. 1 Diagrammatic figure of the computational model The inner black lines denote the interface between PML and solution domain，the circle denotes the source location and the triangles denote receiver locations

该算例中，由于震源靠近顶部吸收边界，形成了大角度入射PML的情况.从波场快照图 2可见，传统PML对大角度入射波吸收不完全，产生了低频 虚假反射，且虚假反射能量随着入射角度和传播距离的增大而增强.从1.68 s的波场可见，在远偏移距低频反射尤为明显.而图 3中MZT-PML边界由于使用复频移拉伸算子，对大角度入射波吸收很好，没有出现图 1中的低频反射；在图 3中1.68 s波场中，即使在远偏移距也没有可见的虚假反射.

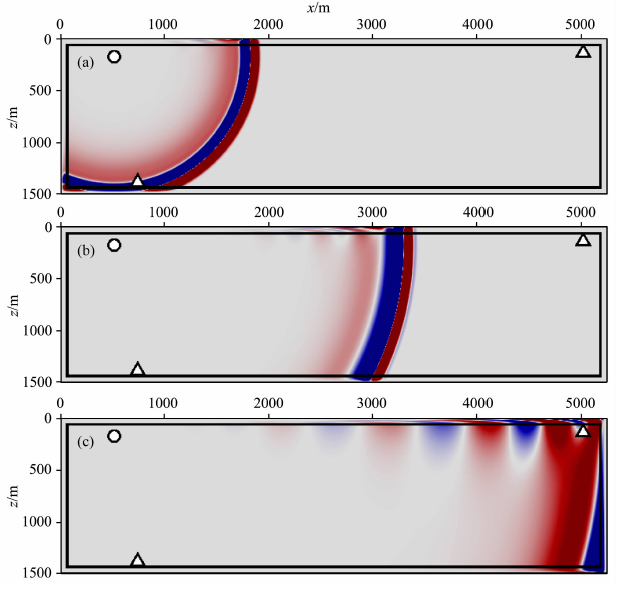图 2 传统PML边界条件下(a)0.48 s，(b)0.96 s和(c)1.68 s的黏声波声压场p的波场快照(振幅已加10倍增益)Fig. 2 Snapshots of the pressure field p of viscoacoustic wave at(a)0.48 s，(b)0.96 s and (c)1.68 s in the classical PML condition， and the amplitudes has been scaled by a factor of 10

图 3 MZT-PML边界条件下(a)0.48 s，(b)0.96 s和(c)1.68 s的黏声波声压场p的波场快照(振幅已加10倍增益)Fig. 3 Snapshots of the pressure field p of viscoacoustic wave at(a)0.48 s，(b)0.96 s and (c)1.68 s in the MZT-PML condition， and the amplitudes has been scaled by a factor of 10

从图 4a可见，在检波点1处无论是传统PML还是MZT-PML的计算结果都和参考解吻合良好，说明在小角度入射情况下，两种吸收边界都可以高效吸收外行波场能量.而从图 4b中检波点2的地震记录可见，PML情况下的地震记录上产生了明显的虚假反射抖动，与参考解吻合不佳，这是因为检波器2记录到了大角度入射波产生的低频虚假反射，这些虚假反射在远偏移距更强.而在检波器2处，MZT-PML情况下的记录与参考解吻合良好，说明MZT-PML相对于传统PML，对切入射波的吸收有明显改善.这里也给出完全弹性介质情况下(令弛豫时间常数τε=τσ)声波方程在MZT-PML边界条件下的模拟结果：图 5中，对比声波方程和黏声波方程的地震记录，由于介质的黏滞性，导致声波振幅衰减强烈(如图 5b).但MZT-PML边界条件下，无论是声波方程还是黏声波方程的计算结果都与各自参考解吻合良好.

图 4 传统PML和MZT-PML边界条件下得到的(a)检波点1和(b)检波点2的黏声波方程地震记录Fig. 4 Seismograms calculated in classical PML and MZT-PML conditions at(a)receiver 1 and (b)receiver 2

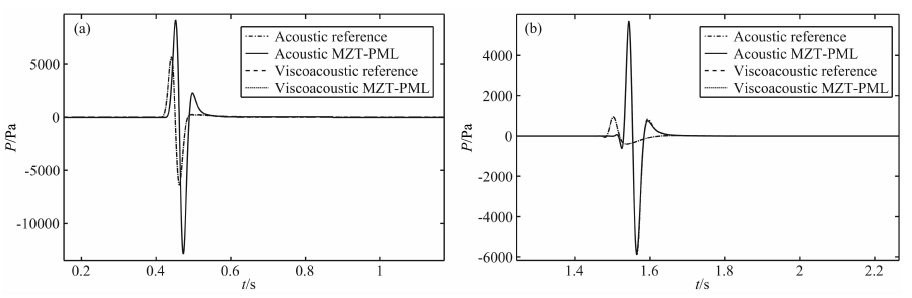图 5 MZT-PML边界条件下得到的(a)检波点1和(b)检波点2的声波、黏声波方程地震记录Fig. 5 Seismograms of acoustic and viscoacoustic wave calculated in MZT-PML condition at(a)receiver 1 and (b)receiver 2

另外，长时间数值正演中的稳定性也是吸收边界效能的一个重要指标(Komatitsch and Martin， 2007；Chen and Bording， 2010；Chen，2011)，本文将波场传播时间延长至120 s(共105时间步)，并记录求解区域Ω中(不包括PML吸收边界)的波场总能量E为

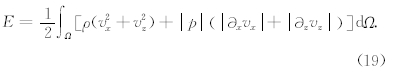
从图 6中展示了弹性和黏弹性介质中两种吸收边界条件下的波场总能量衰减情况.由图 6a可见，当数值正演开始时(约0.1 s左右)，震源将能量注入介质使得总能量急剧上升，之后由于黏弹性介质本身的衰减，使得黏声波情况下的总量明显低于弹性声波.由于PML吸收边界的作用，也导致两种介 质中的波场能量开始逐渐下降.在约1.7 s时能量出现一个陡降，因为这时直达波完全离开求解区域，理论上讲该时刻之后求解区域中的能量全部是虚假能量，这时的能量衰减情况可以较为准确地反映吸收边界的效能，从图 6a可见MZT-PML情况下波场剩余能量低于PML情况(红蓝色曲线之间，以及黑色实虚线之间的对比).由图 6b可见，在数值正演后期(6 s之后)，能量仍旧持续下降，说明MZT-PML在弹性声波、黏声波方程模拟中具有长时间数值稳定性.在黏声波介质中，MZT-PML情况下总能量持续下降至10-30 J数量级，低于PML情况下的10-13 J数量级.

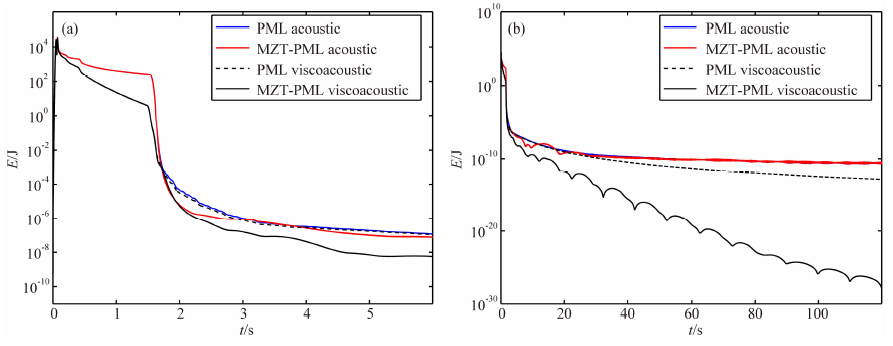图 6 吸收边界条件下黏声波场的总能量衰减(a)0~6 s(b)0~120 s，纵坐标轴为半对数坐标显示Fig. 6 Total energy decay of the viscoacoustic wave field on a semi-logarithmic scale for y-axis in the figure(a)0~6 s(b)0~120 s
5 讨论和结论

本文基于匹配Z变换的思想建立了用于黏声波方程正演的非分裂MZT-PML，这种非分裂PML技术可以直接使用复频移拉伸算子.在有限差分黏声波方程的数值正演实验中，同传统分裂场PML边界条件的应用效果进行了比较.数值实验结果说明，同传统PML相比，当震源靠近吸收边界时，MZT-PML可以明显改善对大角度入射波的吸收.另外，MZT-PML在完全弹性介质和黏弹性介质情况下均表现良好.从105时间步的能量衰减计算可见，MZT-PML边界条件下波场总能量在数值正演后期总体上呈持续下降趋势，说明MZT-PML在黏声波方程模拟中具有长时间稳定性.该方法具有比传统PML更好的吸收衰减效能.

参考文献
[1] Bérenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys., 114(2): 185-200.
[2] Carcione J M, Kosloff D, Kosloff R. 1988. Wave propagation simulation in a linear viscoelastic medium. Geophys. J. Int., 95(3): 597-611.
[3] Carcione J M. 2007. Wave Fields in Real Media: Theory and Numerical Simulation of Wave Propagation in Anisotropic, Anelastic, Porous and Electromagnetic Media. 2nd edn. Amsterdam, The Netherlands: Elsevier Science.
[4] Cerjan C, Kosloff D, Kosloff R, et al. 1985. A nonreflecting boundary condition for discrete acoustic and elastic wave equations. Geophysics, 50(4): 705-708.
[5] Chen J Y, Bording R P. 2010. Application of the nearly perfectly matched layer to the propagation of low-frequency acoustic waves. J. Geophys. Eng., 7(3): 277-283.
[6] Chen J Y. 2011. Application of the nearly perfectly matched layer for seismic wave propagation in 2D homogeneous isotropic media. Geophysical Prospecting, 59(4): 662-672.
[7] Cheng J Y, Zhao J G. 2011. Application of the nearly perfectly matched layer to seismic-wave propagation modeling in elastic anisotropic media. B. Seismol. Soc. Am., 101(6): 2866-2871.
[8] Chew W C, Liu Q H. 1996. Perfectly matched layers for elastodynamics: A new absorbing boundary condition. J. Comput. Acoust., 4(4), 341-359.
[9] Chew W C, Weedon W H. 1994. A 3D perfectly matched medium from modified Maxwell's equations with stretched coordinates. Microw. Opt. Tech. Lett., 7(13): 599-604.
[10] Clayton R, Engquist B. 1977. Absorbing boundary conditions for acoustic and elastic wave equations. B. Seismol. Soc. Am., 67(6): 1529-1540.
[11] Drossaert F H, Giannopoulos A. 2007. Complex frequency shifted convolution PML for FDTD modelling of elastic waves. Wave Motion, 44(7-8): 593-604.
[12] Engquist B, Majda A. 1977. Absorbing boundary conditions for the numerical simulation of waves. Mathematics of Computation, 31(139): 629-651.
[13] Festa G, Vilotte J P. 2005. The Newmark scheme as velocity–stress time-staggering: an efficient PML implementation for spectral element simulations of elastodynamics. Geophys. J. Int., 161(3): 789-812.
[14] Hasting F D, Schneider L B, Broschat S L. 1996. Application of the perfectly matched layer (PML) absorbing boundary condition to elastic wave propagation. J. Acoust. Soc. Am., 100(5): 3061-3069.
[15] Higdon R L. 1991. Absorbing boundary conditions for elastic waves. Geophysics, 56(2): 231-241.
[16] Holberg O. 1987. Computational aspects of the choice of operator and sampling interval for numerical differentiation in large-scale simulation of wave phenomena. Geophysical Prospecting, 35(6): 629-655.
[17] Jin S W, Chen B Y, Ma Z T. 1994. Three-dimensional wave equation forward modeling by the finite-difference methods. Acta Geophysica Sinica (in Chinese), 37(6): 804-810.
[18] Komatitsch D, Martin R. 2007. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics, 72(5): SM155-SM167.
[19] Kuzuoglu M, Mittra R. 1996. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers. IEEE Microwave Guided Wave Letters, 6(12): 447-449.
[20] Li J X, Dai J F. 2008. Modified Z-transform-based FDTD algorithm for the anisotropic perfectly matched layer. International Journal of Numerical Modelling: Electronic Networks, Devices and Fields, 21(5): 279-286.
[21] Li Y F, Matar O B. 2010. Convolutional perfectly matched layer for elastic second-order wave equation. J. Acoust. Soc. Am., 127(3): 1318-1327.
[22] Liu L N, Cui F L, Zhang J F. 2004. Seismic modeling with one-way wave equation in 3-D complex structures. Chinese J. Geophys. (in Chinese), 47(3): 514-520.
[23] Liu Q H, Chang C. 1996. Compressional head waves in attenuative formations: forward modeling and inversion. Geophysics, 61(6): 1908-1920.
[24] Liu Q H, Tao J P. 1997. The perfectly matched layer for acoustic waves in absorptive media. J. Acoust. Soc. Am., 102(4): 2072-2082.
[25] Quarteroni A, Tagliani A, Zampieri E. 1988. Generalized Galerkin approximations of elastic waves with absorbing boundary conditions. Comput. Method. Appl. M., 163(1-4): 323-341.
[26] Roden J A, Gedney S D. 2000. Convolution PML (CPML): An efficient FDTD implementation of the CFS-PML for arbitrary media. Microw. Opt. Tech. Lett., 27(5): 334-339.
[27] Shi RQ, Wang SX, Zhao JG. 2012. An unsplit complex-frequency-shifted PML based on matched Z-transform for FDTD modelling of seismic wave equations. J. Geophys. Eng., 9(2): 218-229.
[28] Sochacki J, Kubichek R, George J, et al. 1987. Absorbing boundary conditions and surface waves. Geophysics, 52(1): 60-71.
[29] Stacey R. 1988. Improved transparent boundary formulations for the elastic-wave equation. B. Seismol. Soc. Am., 78(6): 2089-2097.
[30] Virieux J. 1986. P-SV wave propagation in heterogeneous media: velocity-stress finite-difference method. Geophysics, 51(4): 889-901.
[31] Xie G S, Liu H, Li Y M, et al. 2005. Seismic modeling by reflection/transmission operator and one-way wave equation under the condition of fluctuating reflectors. Chinese J. Geophys. (in Chinese), 48(5): 1172-1178.
[32] 金胜汶, 陈必远, 马在田. 1994. 三维波动方程有限差分正演方法. 地球物理学报, 37(6): 804-810 .
[33] 刘礼农, 崔风林, 张剑锋. 2004. 三维复杂构造中地震波模拟的单程波方法. 地球物理学报, 47(3): 514-520 .
[34] 谢桂生, 刘洪, 李幼铭等. 2005. 界面起伏条件下反射／透射算子+单程波方程的地震波模拟方法. 地球物理学报, 48(5): 1172-1178.