地球物理学报  2014, Vol. 57 Issue (4): 1235-1240   PDF    
引用本文
李川, 王有学, 何晓玲,等. 2014. 基于二维三次卷积插值算法的辛几何射线追踪. 地球物理学报, 57(4): 1235-1240, doi: 10.6038/cjg20140420   
LI Chuan, WANG You-Xue, HE Xiao-Ling, et al. 2014. Symplectic ray-tracing based upon the bi-cubic convolution interpolation method. Chinese J. Geophys. (in Chinese), 57(4): 1235-1240, doi:10.6038/cjg20140420   
基于二维三次卷积插值算法的辛几何射线追踪
李川1, 王有学1,2, 何晓玲1, 刘荣平1, 贠鹏1, 熊彬1, 许继峰1,3    
1. 桂林理工大学地球科学学院, 桂林 541004;
2. 桂林理工大学广西矿冶与环境科学实验中心, 桂林 541004;
3. 中国科学院广州地球化学研究所, 广州 510640
投稿时间:2013-5-12    最后修改时间: 2014-1-23 .
基金项目：国家自然科学基金项目（41174077，41164004），广西壮族自治区“八桂学者”（2013），广西壮族自治区桂林市“漓江学者”（2013）专项经费联合资助.
第一作者简介：李川，男，1989年生，硕士研究生，研究方向为地震波理论及层析成像.E-mail：lichuan2015@gmail.com
通讯作者：王有学，男，博士，教授，主要从事勘探地球物理学研究.E-mail：uxue.wang@glut.edu.cn
摘要：射线追踪是地震波走时层析成像的基础，射线空间位置的准确性及射线走时的精度决定了层析成像的可靠性.本文根据哈密尔顿系统可以有效提高程函方程解稳定性的特性，采用辛几何算法（SAM-Symplectic Algorithm Method）及二维三次卷积插值技术进行地震波射线追踪.由于采用了SAM算法，保证了地震波波前精度，提高了射线空间位置的准确性.数值模拟结果表明SAM既能保证哈密尔顿系统的稳定性又具有运算速度快的特点，提高了射线追踪的计算精度.
关键词： 射线追踪     辛几何算法     二维三次卷积插值     数值模拟    
Symplectic ray-tracing based upon the bi-cubic convolution interpolation method
LI Chuan1, WANG You-Xue1,2, HE Xiao-Ling1, LIU Rong-Ping1, YUN Peng1, XIONG Bin1, XU Ji-Feng    
1. College of Earth Sciences, Guilin University of Technology, Guilin 541004, China;
2. Guangxi Scientific Experiment Center of Mining, Metallurgy and Environment, Guilin University of Technology, Guilin 541004, China;
3. Guangzhou Institute of Geochemistry, Chinese Academy of Sciences, Guangzhou 510640, China
Abstract: Ray tracing is the basic problem in seismic imaging, and the reliability of the imaging depends on the accuracies of both spatial trajectory and traveltime of the ray. Based upon the properties of Hamilton System that can keep the stability of the solution for the eikonal equation, the Sympletic algorithm method (SAM) and bi-cubic convolution algorithm are used in seismic ray tracing in this study. Due to the use of the Sympletic algorithm, the reliable seismic wavefront produces an accurate ray trajectory. Finally, the results from numerical modeling show that the use of SAM can not only keep the stability of the Hamilton System with a fast computation but also improve the accuracy of the seismic ray tracing.
Key words: Ray tracing     Symplectic algorithm     Bi-cubic convolution interpolation     Numerical modeling    
1 引言

射线追踪是地震学反演问题的基础，地震波的走时和射线路径广泛用于走时反演、层析成像、反射偏移及地震定位等领域中，而地震波射线追踪的速度及精度决定了反演的速度与质量.目前，广泛使用的射线追踪方法包括基于射线理论的打靶法(Julian and Gubbins， 1977；徐涛等，2004)、弯曲法(Moser et al., 1992)、高斯射线束算法(Červený and Pšenčík，1983；吴立明等，1995)等，基于网格单元扩展的有限差分解程函方程法(Vidale，1988； Cao Shun-hua et al., 1994；王秀明，2003)、最短路径算法(Moser，1991；张美根等，2006)，以及结合射线和网格单元扩展的波前构造法(Vinje et al., 1993；赵连锋等，2003)，求解程函方程的快速行进法(FMM- Fast Marching Method)(Sethian，1999；Rawlinson，2003)等. 在射线追踪的过程中，地震波的传播满足波动方程，我们在一般情况下很难得到精确解.最早针对波动方程求解的方法是一种高频近似法即几何光学法，几何光学法将波动现象转化成为射线理论，并用射线管的概念来解释射线的传播机制.但是，对于地下速度结构存在微小扰动的成像过程中，普通的射线理论会在焦散处出现奇点，这使得几何渐近 射线理论失效(Chapman and Drummond 1982，Chapman 1985). 前苏联学者Maslov根据方程变换和Fourier积分算子理论，引入具有相同维数的慢度向量空间，然后再利用Fourier逆变换回到原来的空间，并且引进正则(canonical)算子，在相空间中引入适当的辛内积后成为辛空间，从而可以得到焦散处附近有效地高频近似解(Maslov and Fedoriuk， 1981；李世雄，2001).

哈密尔顿(Hamiltonian)系统是描述各种守恒的物理和力学过程的三种基本形式(牛顿力学、拉格朗日力学及哈密尔顿力学)之一，而辛几何则是该系统的数学基础，并且哈密尔顿系统具有辛结构不变性和能量守恒性.作为弹性力学中的地震波射线追踪问题，当然也可以用哈密尔顿系统进行描述(罗明秋等，2001).早在1984年冯康先生首先提出了求解哈密尔顿动力学体系的辛几何算法(SAM-Symplectic Algorithm Method)(冯康和秦孟兆，2003)，并应用于哈密尔顿系统的求解(秦孟兆和陈景波，2000).陈景波与秦孟兆(2000，2001)在Maslov研究的基础上，采用辛几何算法这一专门针对Hamilton系统的数值方法，利用Maslov渐近理论对地震波波场进行了数值模拟，从SAM观点看来，射线是相空间中的特征线在物理空间上的投影，能有效地弥补传统方法上的不足(李世雄，2001).

本文利用SAM算法，结合二维三次卷积(韩复兴等，2008；Keys，1981)，对复杂速度介质模型的地震波射线追踪进行研究，并同龙格—库塔数值微分算法相比较，SAM可以保证哈密尔顿不变量守恒，具有不随运算时间增加而减弱的特点.

2 辛几何算法及二维三次卷积插值 2.1 射线追踪系统及其初始化

地震波在非均匀各向同性介质中传播满足如下的程函方程(Červený，2001；Comer，1984)：

程函方程(1)式也写成如下形式：

在笛卡尔坐标系中，我们用下标i=(1，2，3)分别表示(x，y，z).式(2)中t=t(xi)表示地震波走时(程函)，pi是介质的慢度向量， p = Δ t.

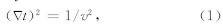
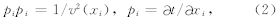
程函方程(2)是t(xi)的一阶非线性的偏微分方程，并且满足如下的哈密尔顿系统形式：

本文中哈密尔顿函数H选用可分系统哈密尔顿函数形式：

并且偏微分方程式(3)的在三维坐标系下的特征向量解形式为

其中，ζ=1/v，du为时间步长，dt为地震波走时，他们之间满足关系

将式(4)带入式(5)，并用变量τ代替时间步长变量u，便可得到需要求解的7个射线方程组：

在各向同性的三维介质中，地震波射线路径和它的走时都满足方程(7)，其初始条件的取值由震源S确定.设i0表示震源处射线与垂直方向之间的夹角，φ0为震源处射线在水平面投影与x1方向的夹角(图 1)，那么，由式(2)可得震源位置、变量处pi0及地震波走时的初始值为

其中p10=v－10sini0cosφ0，p20=v－10sini0sinφ0，p30=v－10cosi0，离源角的取值范围是0 ≤ i0≤ π，0 ≤φ0≤2π.

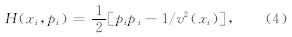
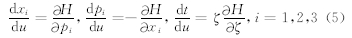
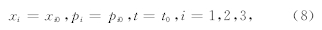
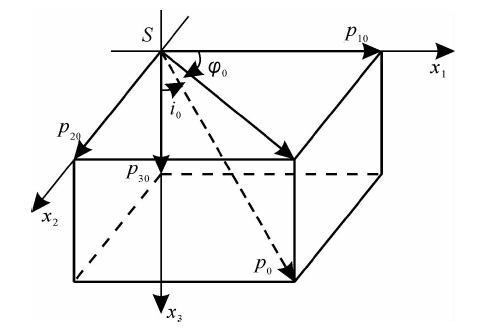图 1 震源S处射线参数示意图Fig. 1 The diagram of seismic ray parameters at source S
2.2 辛几何算法

为了求解哈密尔顿系统式(4)中射线的空间位置，我们采用辛几何数值积分方法(Feng and Qin， 2010；Thijssen，1999).

对于形如H=U(p)+W(x)形式的可分哈密尔顿系统，式(7)的k阶SAM下的解为

其中Wxi(xki)=Hxi(pki，xki)，Upi(pk+1i)=Hpi(pk+1i，xki)，τ 为时间步长，ak、bk是待定系数(Yoshida，1990)，并且ak、bk之间满足关系

待定系数ak、bk(k=1，2，3，…)的选取与射线追踪的精度有很大的关系，本文选取k=4(4阶)，其显式的辛格式系数为

此外，对于式(7)的第三项，我们用数值积分的方法，可以计算得到该地震波射线的走时.

2.3 二维三次卷积插值

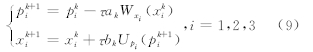
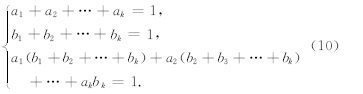
二维三次卷积插值是利用插值点g(x，z)周围16个节点进行加权求和(图 2)，该方法能够更好地描述介质模型中该点的速度值，并且可以用中心差分格式计算出插值点的一阶导数(韩复兴等，2008).

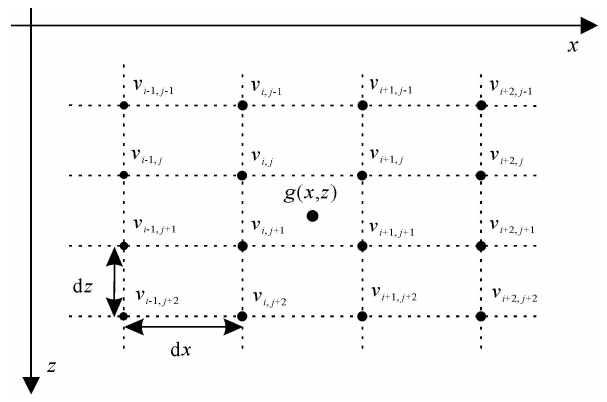图 2 二维三次卷积插值示意图Fig. 2 The diagram of bi-cubic interpolation

根据二维三次卷积插值方法，插值点g(x，z)处的值为

同时，利用中心差分方法可以计算得到插值点 g(x，z)的x、z方向的导数为 vx= 1 4dx CZ T VDX，

其中

3 数值计算与分析 3.1 SAM与FMM算法的走时误差分析

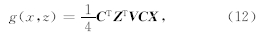
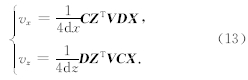
在速度为2 km/s 的均匀各向同性二维(x-z) 模型中，设震源S的坐标为(50，50)，分别用FMM和SAM进行地震波射线追踪，在SAM中，初始角i0=90°，并且φ0以步长为18°，时间步长τ=0.01 s，计算得到φ0=0°~360°的20条射线.然后，利用有限差分方法求解式(7)的第三项，计算各条地震波射线的走时，并将其与射线精确走时的差值取绝对值，即得到地震波射线走时的误差(Δt)，其结果如图 3所示.

图 3 射线追踪的走时误差分析.(a)FMM;(b)SAMFig. 3 The traveltimes error in raytracing.(a)FMM;(b)SAM

由图 3可知，用SAM得到的地震波射线走时最大误差为1.4×10-6 s，比FMM的精度要高出5个数量级.

如果将震源S置于点(50，0)，初始角i0=90°，并且φ0以步长20°、时间步长τ=0.01 s，用SAM计算得到φ0=10°~170°的地震波射线的空间误差(见图 4).

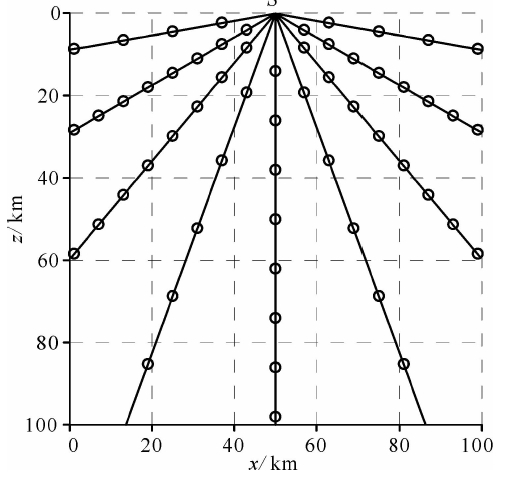图 4 SAM的地震波射线空间误差 小圆表示射线的实际空间位置，实线为SAM计算得到的射线位置.Fig. 4 The special error of seismic rays by using SAM Circles are the accurate rays，solid lines are the rays computed by SAM.
3.2 辛几何算法与龙格—库塔算法的射线路径分析

在速度随深度线性变化的各向同性介质中，设v=1.8+0.3 z，震源点S位于(0，4)，初始入射角i0=90°，时间步长τ=0.01 s，φ0以步长5°，分别用 SAM和龙格—库塔算法计算得到φ0=-60°~ -30° 的地震波射线路径，结果如图 5所示.

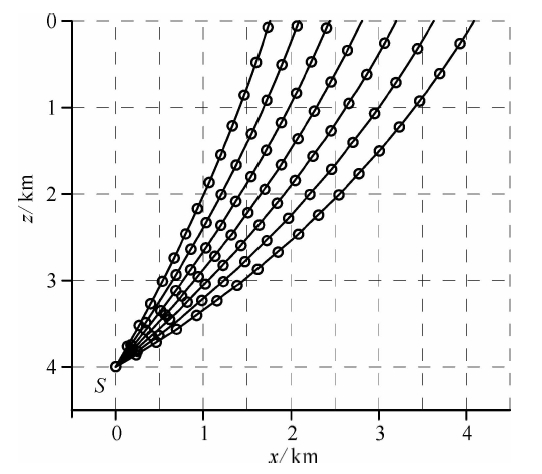图 5 SAM算法(小圆)与龙格—库塔算法(实线)计算得到的射线路径对比Fig. 5 The raypaths computed by SAM(circle) and Runge-Kutta algorithm(solid line)

从图 5中我们可以得出，SAM用于地震射线追踪是可行的，其中龙格—库塔算法CPU耗时1.2 s，而用SAM计算机只需0.0624 s，对于运算量巨大的地震层析成像，SAM会大幅度地减少计算时间.同时，图 5也说明在计算步数不太多的情况下，采用龙格—库塔算法求解哈密尔顿方程组(5)的初值问题，已可满足要求. 4 计算实例

对于图 6所示的二维Marmousi速度模型，设震源点S位于(250，0)，初始入射角i0=90°，时间步长τ=0.01 s，φ0以步长10°，将四阶(k=4)显式SAM与二维三次卷积插值算法相结合，对φ0=0°~ 180°之间的地震波进行射线追踪，其结果如图 6所示.

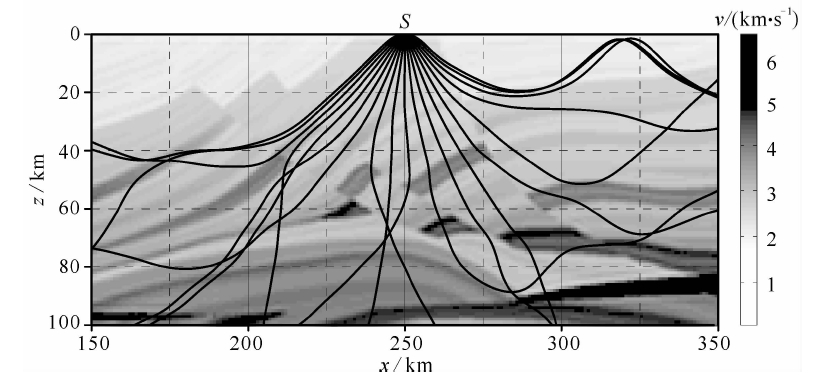图 6 二维Marmousi模型及射线路径Fig. 6 2-D Marmousi model and seismic raypaths

根据具有不同初始入射角(φ0)射线计算结果，其哈密尔顿系统函数值H的误差图如图 7所示.

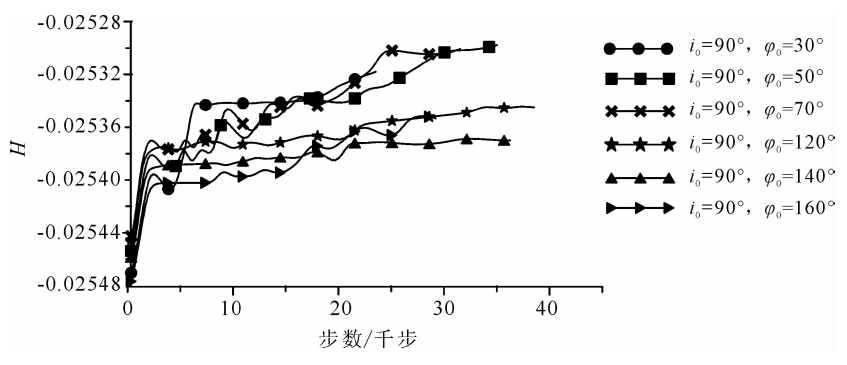图 7 四阶显式SAM计算的沿射线轨迹Hamilton函数值Fig. 7 The Hamiltonian(H)value along raypaths by 4-order explicit SAM

由图 7可知哈密尔顿系统函数的数值(H)保持在-0.0254左右，随着计算步数的增大没有大幅度的波动，比同阶的龙格—库塔算法效果更好.由此可见，SAM具有长时间运算保持哈密尔顿系统稳定性的特点.

5 结论

在利用SAM进行地震波射线追踪的过程中，由于采用了辛几何射线追踪算法和二维三次卷积插值，有效地保证了射线追踪的准确性和稳定性.根据数值计算及分析，可以得出如下结论：

(1)运用SAM进行地震波射线追踪，可以获得高精度的波前，进一步提高了射线空间位置的准确性；

(2)对于同样模型的计算结果，SAM的运算速度快，从而大幅度提高了射线追踪的效率；

(3)SAM能够保持哈密尔顿系统稳定性，同时也验证了SAM在射线追踪中的有效性和准确性.

参考文献
[1] Cao S H, Greenhalgh S. 1994. Finite-difference solution of the eikonal equation using an efficient, first-arrival, wavefront tracking scheme. Geophysics, 59(4): 632-643.
[2] Chapman C H, Drummond R. 1982. Body-wave seismograms in inhomogeneous media using Maslov asymptotic theory. Bull. Seism. Soc. Am., 72(6B): S277-S317.
[3] Chapman C. 1985. Ray theory and its extensions: WKBJ and Maslov seismograms. J. Geophys., 58(1): 27-43.
[4] Chen J B, Qing M Z. 2000. Ray tracing by symplectic algorithm. Journal On Numerical Methods And Computer Applications (in Chinese), 21(4): 255-265.
[5] Comer R P. 1984. Rapid seismic ray tracing in a spherically symmetric earth via interpolation of rays. Bull. seism. Soc. Am., 74(2): 479-492.
[6] Feng K, Qin M Z. 2003. Symplectic Geometric Algorithm for Hamiltonian Systems (in Chinese). Hangzhou: Zhejiang Science and Technology Press.
[7] Feng K, Qin M Z. 2010. Symplectic Geometric Algorithms for Hamiltonian Systems. New York: Springer.
[8] Gao L, Li Y M, Chen X R, et al. 2000. An attempt to seismic ray tracing with symplectic algorithm. Chinese Journal of Geophysics(in Chinese), 43(3): 402-410.
[9] Han F X, Sun J G, Yang H. 2008. Ray-tracing of wavefront construction by bicubic convolution interpolation. Journal of Jilin University: Earth Science Edition (in Chinese), 38(2): 336-340, 346.
[10] Yoshida H. 1990. Construction of higher order symplectic integrators. Physics Letters A, 150(5-7): 262-268.
[11] Julian B R, Gubbins D. 1977. Three-dimensional seismic ray tracing. J. Geophys., 43(1): 95-113.
[12] Li S X. 2001. High-frequency Approximation of Wave Equation and Symplectic Algorithm. Beijing: Science Press.
[13] Luo M Q, Liu H, Li Y M. 2001. Hamiltonian description and symplectic method of seismic wave propagation. Chinese J. Geophys. (in Chinese), 44(1): 120-128.
[14] Maslov V P, Fedoriuk M V. 1981. Semi-Classical Approximation in Quantum Mechanics. Hingham, Mass: D Reidel Publishing.
[15] Moser T J, Nolet G, Snieder R. 1992. Ray bending revisited. Bulletin of the Seismological Society of America, 82(1): 259-288.
[16] Moser T J. 1991. Shortest path calculation of seismic rays. Geophysics, 56(1): 59-67.
[17] Qing M Z, Chen J B. 2000. Maslov asymptotic theory and symplectic algorithm. Chinese J. Geophys. (in Chinese), 43(4), 522-533, doi: 10. 3321/j. issn: 0001-5733. 2000. 04. 013
[18] Rawlinson N. 2003. Seismic Ray Tracing and Wavefront Tracking in Laterally Heterogeneous Media. Canberra: Australian National University.
[19] Keys R G. 1981. Cubic convolution interpolation for digital image processing. IEEE Transaction on Acoustics, Speech, and Signal Processing, 29(6): 1153-1160.
[20] Sethian J A. 1999. Fast marching methods. SIAM Review, 41(2): 199-235.
[21] Thijssen J M. 1999. Computational Physics. Cambridge: Cambridge University Press.
[22] Červený, Pšenčík I. 1983. Gaussian beams and paraxial ray approximation in three dimensional elastic inhomogeneous media. J. Geophys., 53: 1-15.
[23] Červený. 2001. Seismic Ray Theory. Cambridge: Cambridge University Press.
[24] Vidale J E. 1988. Finite-difference calculations of traveltimes. Bull. Seism. Soc. Am., 78(6): 2062-2076.
[25] Vinje V, Iversen E, Gjystdal H. 1993. Traveltime and amplitude estimation using wavefront construction. Geophysics, 58(8): 1157-1166.
[26] Wang X M, Zhang H L, Wang D. 2003. Modelling of seismic wave propagation in heterogeneous poroelastic media using a high- order staggered finite-difference method. Chinese Journal of Geophysics (in Chinese), 46(6): 842-849.
[27] Wu L M. Xu Y, Wudabala. Applied study of Gaussian beam method in 2-D inhomogeneous media and laterally varying layered structures. Chinese J. Geophys. (in Chinese), 38(S1): 144-152.
[28] Xu T, Xu G M, Gao E G, et al. 2004. Block modeling and shooting ray tracing in complex 3-D media. Chinese J. Geophys. (in Chinese), 47(6): 1118-1126.
[29] Zhang L B, Rector J W, Michael Hoversten G. 2005. Eikonal solver in the celerity domain. Geophys. J. Int. (in Chinese), 162(1): 1-8.
[30] Zhang M G, Cheng B J, Li X F, et al. 2006. A fast algorithm of shortest path ray tracing. Chinese J. Geophys. (in Chinese), 49(5): 1467-1474.
[31] Zhao L F, Zhu J S, Cao J X, et al. 2003. Ray tracing using ordinal wave-front reconstruction method. Chinese J. Geophys. (in Chinese), 46(3): 415-420.
[32] 陈景波, 秦孟兆. 2000. 辛几何算法在射线追踪中的应用. 数值计算与计算机应用, 21(4), 255-265 .
[33] 冯康, 秦孟兆. 2003. 哈密顿系统的辛几何算法. 杭州: 浙江科学技术出版社.
[34] 高亮, 李幼铭, 陈旭荣等. 2000. 地震射线辛几何算法初探. 地球物理学报, 43(3): 402-410 .
[35] 韩复兴, 孙建国, 杨昊. 2008. 基于二维三次卷积插值算法的波前构建射线追踪. 吉林大学学报: 地球科学版, 38(2): 336-340, 346 .
[36] 李世雄. 2001. 波动方程的高频近似与辛几何. 北京: 科学出版社.
[37] 罗明秋, 刘洪, 李幼明. 2001. 地震波传播的哈密顿表述及辛几何算法. 地球物理学报, 44(1): 120-128 .
[38] 秦孟兆, 陈景波. 2000. Maslov渐近理论与辛几何算法. 地球物理学报, 43(4): 522-533, doi: 10. 3321/j. issn: 0001-5733. 2000. 04. 013.
[39] 王秀明, 张海澜, 王东. 2003. 利用高阶交错网格有限差分法模拟地震波在非均匀孔隙介质中的传播. 地球物理学报, 46(6): 842-849 .
[40] 吴立明, 许云, 乌达巴拉. 1995. 高斯束射线法在二维非均匀介质复杂构造中的应用. 地球物理学报, 38(S1): 144-152 .
[41] 徐涛, 徐果明, 高尔根等. 2004. 三维复杂介质的块状建模和试射射线追踪. 地球物理学报, 47(6): 1118-1126 .
[42] 张美根, 程冰洁, 李小凡等. 2006. 一种最短路径射线追踪的快速算法. 地球物理学报, 49(5): 1467-1474 .
[43] 赵连锋, 朱介寿, 曹俊兴等. 2003. 有序波前重建法的射线追踪. 地球物理学报, 46(3): 415-420.