2. 中国石化石油勘探开发研究院, 北京 100083
2. Petroleum Exploration and Production Research Institute, SINOPEC, Beijing 100083, China
1 引言
有限差分方法(FDM)和有限元方法(FEM)是地震正演模拟中非常重要的两种方法,其中有限差分方法因为其程序实现的便捷性和计算的高效性在生产上应用广泛,但是传统有限差分方法算子是基于均匀介质中规则网格条件下的泰勒展式推导,因而在模拟非规则的边界问题当中存在困难.此外,直接将差分算子应用于非均质问题中实际上也会引入相当的计算误差,这一现象在速度间断面上尤为明显,不少学者也对基于速度间断面的差分算子进行特殊处理(Kummer et al., 1987; Zahradnik et al., 1993; Lisitsa et al., 2010).相比而言,有限元方法因为其网格剖分的灵活性以及边界条件的适应性而日渐受工业生产的青睐,通过近几十年的发展,已经由最初的一维模型逐渐拓展到三维弹性波模拟(邓玉琼和张之力,1990; 张剑锋,1994;张美根等,2002;Zhang et al., 2002; Min et al., 2003;薛东川等,2007).然而有限元面临的一个主要问题还在于它的计算效率:在有限元计算过程当中涉及到对质量矩阵求逆计算.通常而言,有限元构架下的质量矩阵为一个对称的窄带宽的矩阵,使得质量矩阵的求逆非常耗费资源且复杂.为了解决这一问题,有些学者引入了集中质量矩阵技术将质量矩阵强行对角化以提高计算效率,但是在这一过程中会影响整体的计算精度(De Basabe,2009).
为了解决有限元的计算效率以及精度问题,谱 元法(SEM)被引入地震领域(Komatitsch and Vilotte, 1998; Komatitsch and Tromp, 1999; Komatitsch et al., 2001).谱元法的核心思想是:在单元内部求取质量矩阵过程中,通过引入一个高精度的积分公式,并将单元内节点配置于相应的积分点之上,结合Lagrange插值形函数计算,最终获得一个对角化的质量矩阵.这种方法和集中质量矩阵技术相比其优势在于,可以使得质量矩阵对角化并且具备更高的计算精度.谱元方法在计算效率上的改进,以及网格剖分中对于复杂结构描述的适应性,使得谱元法在短短的十几年间得到了迅猛的发展,并应用于正演模拟以及偏移成像当中.值得注意的是,大部分的谱元方法研究是基于四边形网格,其原因在于四边形网格中Lagrange形函数可以通过内积的方法求取(Cohen,2002),即可以方便地从一维Lagrange表达式直接推导.此外更重要的一点是,四边形网格中应用的GLL(Gauss-Lobatto-Legedre)积分公式被证明是具有很高的计算精度,并且随着积分点的增加其计算精度也在增加(Cohen,2002;De Basabe and Sen, 2007).
相比而言,使用三角单元的谱元方法研究和应用较少,因为在三角形网格当中,Lagrange形函数的构建比较复杂,不能直接通过内积的方式获得;更为关键的是,四边形网格中效果很好的GLL积分公式在三角网格中不再适用(Cohen,2002).然而这些问题的出现并不代表谱元法不能应用在三角形网格中,相反因为三角网格在模拟复杂的构造问题中具有更高的灵活性,一直以来也有不少学者致力于三角谱元法的研究,并提出了一系列新的积分点去替 代GLL积分公式(Blyth and Pozrikidis, 2006; Chen and Babuska, 1995; Hesthaven,1998; Taylor et al., 2000; Cohen et al., 2001).这当中最为常用的点包括Fekete点和Cohen点,其中Fekete点的位置是根据最优性插值而提出来的(Taylor et al., 2000),这类节点在三角网格的边界上,其配置方式与GLL点是一致的,因此可以很容易实现三角谱元法和四边谱元法的融合(Komatitsch et al., 2001).而Cohen点的配置是根据数值积分最优的原理进行求解.研究表明,对于N阶的Lagrange形函数,采用Cohen点进行积分计算具有2N-1阶的计算精度,已经基本接近于GLL点的计算精度(Liu et al., 2012).因此从计算质量矩阵的精度而言,Cohen积分点的方式将更为精确.Liu 等(2012)的文章中通过频散分析详细比较了基于Cohen点的和Fekete点的TSEM的精度,进一步论证了Cohen点在精度上的优越性.
本文主要研究采用2阶Cohen点的三角谱元方法(TSEM).首先是对三角谱元法的基本原理进行阐述,包括Cohen积分点的位置,Lagrange形函数的求取,以及质量矩阵的对角化处理.在这之后,本文将对2阶三角谱元法的计算精度和稳定性条件进行分析.为了进一步描述三角谱元法的计算特性,我们还将引入3阶精度下的三角有限元(TFEM)算子进行对比.分析表明,2阶TSEM方法相对于3阶TFEM方法具有更高的精度和稳定性条件,并且需要更少数目的节点进行刻画,而数值算例也进一步证明了分析结果的正确性.本文的最后部分将2阶TSEM方法应用于两个具有孔洞结构特征的地质模型正演当中,并探讨孔洞在地震波场当中的响应特征.其波场的计算结果展示了三角谱元方法在地震正演模拟计算中的有效性及其广阔的应用前景.
2 三角谱元法的基本原理
考虑二维(x-z)的声波方程,如果不考虑密度在空间上的变化,在进行有限元离散之后满足:
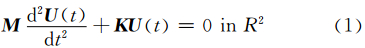
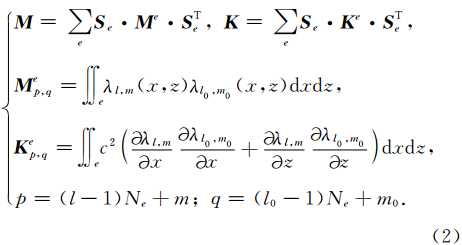
对于公式(1),在时间上采用2阶精度的有限差分格式求解,可以得到:
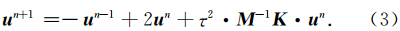

公式(4)的质量矩阵在积分过程中被求和替代,其中ω表示积分求和中的加权因子;同样的,p与(l,m)之间存在着线性映射关系.当插值形函数λ(x,z)为Lagrange函数时满足:
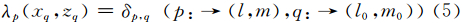
因此求和公式可以使得质量矩阵对角化,其对角元素的取值取决于加权因子ω.在四边形网格当中,加权因子由GLL积分公式确定.但是对于三角网格的情况,GLL的积分点配置情况和积分公式不再适用;此外,三角网格中Lagrange形函数不能简单地通过内积的方式进行求取,因而无法直接寻找到一个显式的表达式.为了解决以上问题,本文采用Cohen积分点对GLL积分点进行替代:研究表明使用N阶Cohen点计算质量矩阵具有2N-1阶的计算精度,保证了质量矩阵计算的精确性(Liu et al., 2012).
图 1展示了2阶Cohen积分点的配置方式:每个单元内部具有7个节点,其中6个节点是均匀配置在三角单元的边界之上,还有1个节点置于三角单元的中心.相比而言,传统的2阶TFEM使用的是6个节点离散,而3阶TFEM使用的是10个节点离散.传统有限元当中的节点都是均匀配置于三角单元中.对于高阶情况的Cohen积分点(如图 2所示),Cohen点不再均匀地配置在单元内部.
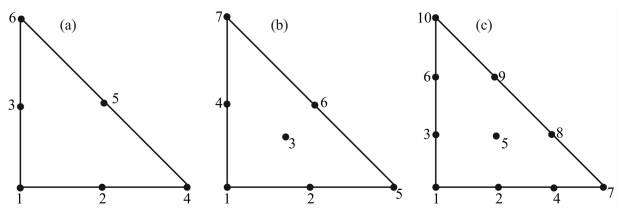 | 图 1 不同三角单元的节点配置方式(a)2阶三角有限元节点配置,1个单元内部配置6个节点,均匀分布;(b)2阶三角谱元法节点配置,单元内部具有7个节点;(c)3阶三角有限元节点配置,单元内共有10个节点信息.Fig. 1 The different node configurations in the triangular mesh(a)For the 2nd-order FEM scheme,there are 6 nodes placed at the vertices;(b)For the 2nd-order Cohen case,there are 7 nodes in the element;(c)For the 3rd-order FEM case,there are 10 nodes inside the element. |
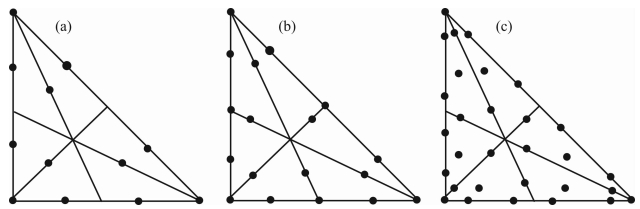 | 图 2 高阶Cohen积分点的配置情况(a)3阶Cohen点配置,单元内部一共有12个节点(Cohen et al., 1995);(b)4阶Cohen点配置,单元内一共有18个节点(Mulder,1996);(c)5阶Cohen点配置,单元内一共有30个节点(Chin-Joe-Kong et al., 1999).Fig. 2 The grid configuration for higher order Cohen nodes(a)The 3rd-order Cohen node,there are 12 nodes inside the element(Cohen et al., 1995);(b)The 4th-order Cohen nodes,there are 18 nodes for each element(Mulder,1996);(c)The 5th-order Cohen nodes(Chin-Joe-Kong et al., 1999),there are 30 nodes inside. |
三角单元中Lagrange形函数的求取可以通过基函数展开进行:
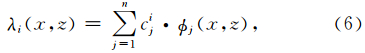
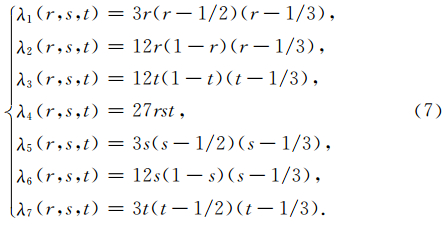
同样地,在构建过程中利用V and ermonde矩阵可以计算出权因子ω(Mercerat et al., 2006):
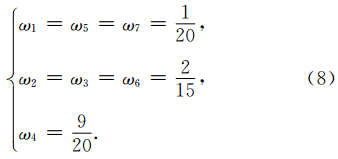
在获取三角网格中Lagrange插值形函数和相应的Cohen积分点和加权因子之后,可以根据公式(2)计算出相应的质量矩阵和刚度矩阵进行正演计算.
关于边界的实施,在实际模型的地震声波模拟中,最为常用的边界条件是吸收边界.其中,完全匹配层(PML)吸收边界在有限差分模拟当中应用最为广泛.尽管PML方法大部分情况下是基于有限差分法求解速度应力的一阶方程,同样的,该方法可以应用到二阶情况下的有限元和谱元法,只需在剖分网格完毕之后,对在边界上的单元进行PML的处理(Komatitsch and Tromp, 2003).
3 频散分析
有限元方法或者谱元方法作为一种数值模拟方法,在正演计算过程中存在着精度的问题.通常而言,对于固定的网格配置,地震频率越高的情况下计算误差也越大,这种误差也称为数值频散.常用的频散分析方法是通过一个平面波的近似解替换到控制方程中进行分析,这一方法在有限差分算子当中得 到了广泛的应用(Alford et al., 1974;Marfurt,1984; Moczo et al., 2000; 刘红伟等,2010).但是有限元算法的频散分析要复杂得多,考虑到有限元的求解算子在不同的网格点上是变化的,需要通过求解特征方程组的形式综合考虑不同算子的影响(Carcione et al., 2002).Mullen和Belytschko(1982)最早给出了一阶有限元的频散分析结果,他们考虑了矩形网格和不同形状的三角网格,最终的结论是矩形网格比三角网格具有更高的精度;之后Mulder(1999)分析了一维情况下谱元法的频散条件,得出在一维情况下谱元法的频散特性要优于常规有限元法;Cohen 等(2001)接着对低阶的四边形谱元法进行了频散分析,论证了谱元法在使用GLL积分点的高精度性.De Basabe和Sen(2007)通过数值求解的方法对高阶四边形谱元法进行了分析,并且证明高阶谱元法能够提高计算精度.Seriani和Oliveira(2008)在他们的研究中证明在弹性波问题中,高阶谱元法也将提高计算精度.在本节中,我们对2阶三角谱元法进行频散分析,并将分析结果和三角有限元方法进行对比.
为了分析方便,我们选择一种‘X’形状的三角网格,如图 3所示.2阶TSEM的单元内部一共有7个节点,但是组集到全空间之后,全局有12种计算算子(如图中所标注).对于3阶TFEM格式,单元内部一共有10个节点,相应的全局算子为18种.
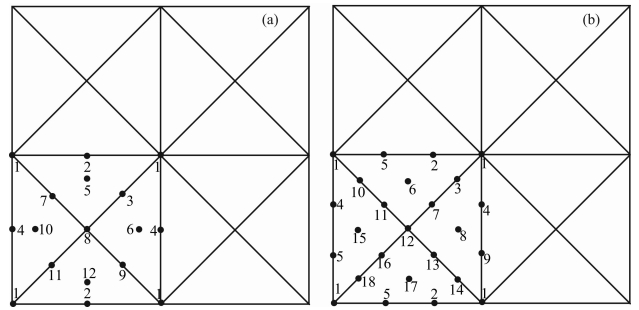 | 图 3 ‘X’形状TSEM和TFEM的计算节点配置情况(a)2阶TSEM方法,全局计算采用12个计算算子;(b)3阶TFEM方法,全局计算采用18个算子. Fig. 3 The grid configuration of the ‘X’ type triangular mesh(a)The grid configuration for the 2nd-order Cohen nodes. 12 classes of operators are considered in this case,which have been signed in the panel;(b)The grid configuration for the 3rd-order FEM,where 18 classes of operators are considered in this case. |
假设离散后的每个节点满足平面域解析解:
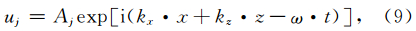
将公式(9)代入到求解方程(1)中,得到:
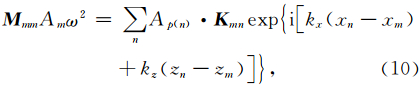
将公式(10)扩展成一个矩阵方程:

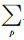 Kj,p×exp{i [kx(xp-xj)+kz(zp-zj)]},p对应着第j个计算点相邻的离散节点.假设求解公式(11)计算出的角频率可以表达成:
Kj,p×exp{i [kx(xp-xj)+kz(zp-zj)]},p对应着第j个计算点相邻的离散节点.假设求解公式(11)计算出的角频率可以表达成:
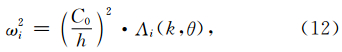
 .当算子足够精确的时候,我们认为计算出的相速度Cp应该接近于介质速度C0,因此Cp/C0可以用于判断数值频散的大小.
.当算子足够精确的时候,我们认为计算出的相速度Cp应该接近于介质速度C0,因此Cp/C0可以用于判断数值频散的大小.对于有限元类的方法,求解公式(12)将得到Nc个不同的角频率,每个计算出的角频率对应着一个频散因子,但只有一个频散因子具有物理意义.根据频散曲线的收敛性,我们可以确定相应的频散特性.图 4a为2阶TSEM的频散曲线,横轴对应着空间步长和波长的比值,纵轴为频散误差的大小,不同的曲线代表着不同的入射角度θ.分析结果表明,当入 射角度为30°时,频散误差最小.图 4b为3阶TFEM 的频散曲线,此处有限元采用的是集中质量矩阵进行处理,分析表明,当入射角为45°时,频散最小.当误差阀值设为0.1%时,频散曲线表明2阶TSEM需要空间采样率满足每个波长内平均有10个计算节点;而TFEM需要每个波长配置16个节点.结果显示,对于‘X’类型的网格,2阶TSEM相比于3阶TFEM具有更高的计算精度.
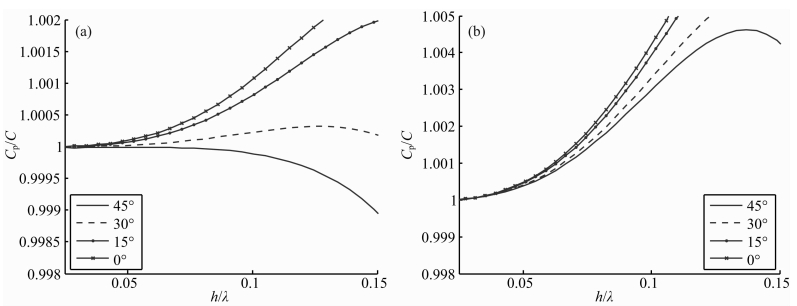 | 图 4 TSEM和TFEM的频散曲线(a)2阶TSEM频散曲线,横轴为空间采样率,纵轴为频散误差.可以看出,采样率越低,频散误差越小.当误差阀值取为0.1%时,对应着空间采样率应当大于每个波长10个采样点;(b)3阶TFEM频散曲线,当频散误差阀值为0.1%时要求空间采样率大于每个波长内配置16个计算节点. Fig. 4 Dispersion curves for TSEM and TFEM(a)The dispersive result for the 2nd-order Cohen nodes. It suggests that 10 nodes per wavelength are sufficient to constrain the dispersive error into 0.1%;(b)The dispersive curve for 3rd-order FEM in triangular mesh,where the curves indicate that 16 nodes per wavelength is sufficient for obtaining an accurate result. |
4 稳定性分析
在得到频散因子之后可以很容易分析其稳定性条件.假设求解波动方程时,时间因子通过2阶差分进行求解,则公式(11)变为:
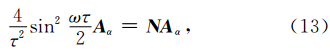
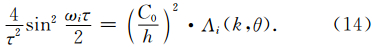
根据公式(14),可以得到以下关系式:
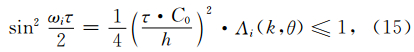
引入稳定因子:q= τ·C0 h,代入公式(14)可以得到:
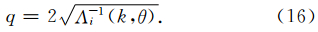
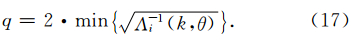
为了求取出Λ-1i(k,θ)的最小值,我们采用扫描的方式将所有的值画出来,如图 5所示,最终确定出稳定性条件.根据分析结果,2阶TSEM的稳定性因子为0.43,而3阶TFEM的稳定性因子为0.35.结果表明,2阶TSEM相对于3阶TFEM具有宽松的稳定性条件.
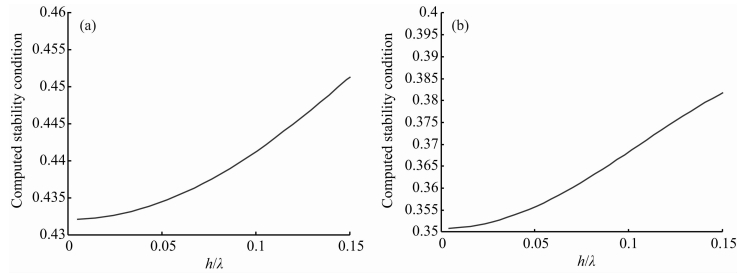 | 图 5 稳定性因子分析(a)2阶TSEM的稳定性条件;(b)3阶TFEM的稳定性条件.Fig. 5 The computed stability condition(a)The stability condition curve for the 2nd-order Cohen nodes,the minimum stability factor is 0.43; (b)The stability condition curve for 3rd-order FEM with triangular mesh,the minimum stability factor is 0.35. |
5 实例分析 5.1 数值算例
为了比较2阶TSEM和3阶TFEM的数值精度,考虑求解以下波动问题:
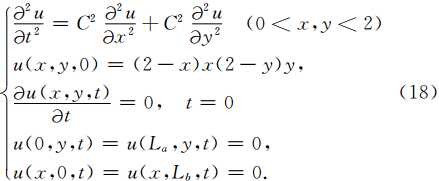
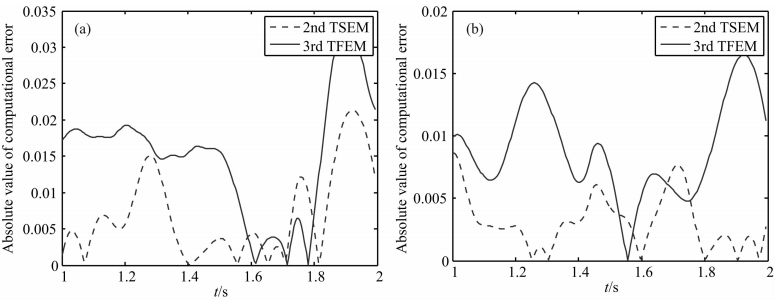 | 图 6 2阶TSEM(虚线)和3阶TFEM(实线)计算结果的误差绝对值对比(a)记录点放置于(1.0,1.0),其中2阶TSEM的误差绝对值要小于3阶TFEM;(b)记录点放置于(1.5,1.5),同样地,2阶TSEM的误差绝对值要小于3阶TFEM.对比显示,2阶TSEM精度要优于3阶TFEM. Fig. 6 The comparison of computational errors for TSEM and TFEM,where two mesh systems are employed to assure the same sampling ratio (a)The computed results recorded at the position of(1.0,1.0),which shows that the 2nd-order TSEM has less computational errors than the 3rd-order TFEM;(b)The comparison results recorded at the position of(1.5,1.5),the computational error also indicates that the 2nd-order TSEM scheme generates more accurate result than the 3rd-order TFEM. |
计算结果显示,波场的主频率大概在0.5 Hz,如果假设最高频率为主频的1.5倍,那么相当于最短波长约为1.5 m,即空间采样率为一个波长15个格点,属于高采样率范畴.从计算的误差绝对值对比上看,3阶TFEM的误差绝对值要大于2阶TSEM方法,即2阶TSEM法具有更高的计算精度,这也与我们之前的频散分析结果一致.
5.2 孔洞模型I
我们引入一个中国西部地区比较典型的孔洞模型,如图 7所示.这类孔洞介质经常在地震剖面上显示出一种串珠状的信号(图 8).模型设计的深度为1 km,宽2 km,并考虑几个不同大小形状各异的孔洞(尺寸大小约在20 m左右):其中第一个孔洞的横向宽度最大,第三个宽度最小,三种孔洞的速度都设置为1500 m·s-1.我们通过使用三角网格对孔洞进行刻画,使用2阶TSEM方法进行地震正演计算,并分析不同大小孔洞对应于地震波场的响应特征以及串珠状信号的形成机理.
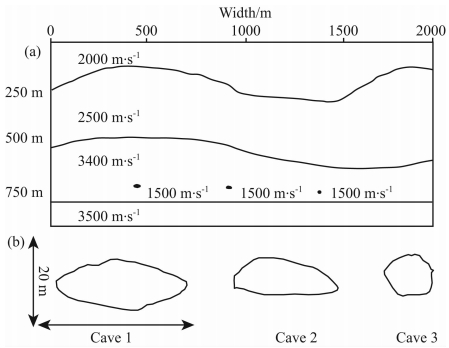 | 图 7 孔洞模型I示意图,空洞速度填充为1500 m·s-1(a)孔洞模型;(b)孔洞的具体形状. Fig. 7 The geological model with three caves of different shapes,where the velocity in the cave is set to be 1500 m·s-1(a)The geological model;(b)The details for the caves. |
 | 图 8 中国西部地区典型的串珠状现象 Fig. 8 One seismic section obtained from north-western China. Some typical phenomenal of “serials reflections” can be observed in the section after employing time migration,as signed in the graph |
在正演计算中,震源采用主频30 Hz的Ricker子波,置于模型地表中间.不同时刻的波场快照结果 如图 9所示:波场传播到第二个孔洞的时候(420 ms)产生了明显的绕射波场.这可以用惠更斯原理进行解释:波场传播到一个介质间断面之后,相当于在间断面产生了一个新的波源进行传播.波场在480 ms的时候,其他两个孔洞也发生了绕射,从绕射能量而言,第一个孔洞产生的绕射波场最强.到600 ms的时候,第一个孔洞又产生了一个绕射波,这说明在孔洞介质当中,一次绕射波产生之后,波场又传播到孔洞进行了二次绕射,我们解释这种现象为孔洞中产生的层间多次波.因为在孔洞中速度设置为水的速度,相对于围岩是一个低速带,这种情况很容易产生多次波.此外,在波场快照中其他几个孔洞也相应地产生了多次绕射波,但是能量相比于第一个孔洞,要小得多.地震正演模拟的结果展现出绕射波的能量与孔洞宽度相关.宽度最大的第一个孔洞产生的绕射能量最强,而宽度最小的第三个孔洞产生的绕射能量最弱.这里可以用横向分辨率去进行解释,在间断面小于横向分辨极限的情况下,所有在间断面上的绕射波场传播到检波器之后被当成一种信号接收.因此,当孔洞的宽度越大,同时被接收到的信号越多,相应的能量则越强.
 | 图 9 2阶TSEM正演模拟计算快照结果(a)360 ms波场快照;(b)420 ms波场快照;(c)480 ms波场快照;(d)600 ms波场快照. Fig. 9 The computed results generated by the second-order TSEM with Cohen nodes(a)The snapshot for 360 ms;(b)The snapshot for 420 ms;(c)The snapshot for 480 ms;(d)The snapshot for 600 ms. |
5.3 孔洞模型II
我们研究不同的孔洞 组合对于地震波场的响应特征.模型的大小为2 km×1 km,模型中考虑两种孔洞的组合模式,分别为平行式孔洞组合(图 10b)以及三角式孔洞组合(图 10c).同样地使用三角网格对孔洞进行刻画,网格大小大约为10 m,采用2阶TSEM方法进行正演模拟,地震主频取为40 Hz,位置放于模型地表中央.
 | 图 10 孔洞组合模型,其中孔洞大小约为50 m(a)孔洞模型II,考虑两种不同的孔洞组合模型;(b)平行排列孔洞组合模式;(c)三角排列孔洞组合模式.Fig. 10 The geological model with different types of caves(a)The velocity model,where two types of caves group are considered;(b)The triangular meshes characterizing the first group caves,where three caves are listed in a line;(c)The triangular mesh discretized for the second group of caves,where the caves are placed in a shape of triangle. |
正演计算之后得到的波场快照如图 11所示.250 ms的时候,如图 11a,来自于地下起伏界面的反射波可以清晰地观察到;当波场传播到270 ms的时候,第一组孔洞组分别所产生的绕射波已经出现在快照中;30 ms之后,第一组孔洞组分别产生的多次波可以被观察到,而此时第二组孔洞的绕射波已经形成,但是各溶洞产生的绕射波场叠合在一起,比较难区分;在320 ms的时候,第一组孔洞组中各孔洞产生的多次波场和绕射波场各自继续传播,并且具有较强的振幅;而第二组孔洞组合在波场上基本上体现为一个绕射波场和多次波场的传播形式,且能量较第一组孔洞组更弱一些.以上快照结果显示,平行式排布的孔洞组合在地震上具有更强的能量,而 且各孔洞产生的多次波场比较明显,在偏移结果上应该会出现多组串珠现象.而三角式排布的孔洞组合在地震上的绕射能量比较弱,且各个孔洞产生的 多次波场难以辨别,分析其原因是因为三角排布方式容易使得波场干涉,因此预测该类孔洞组合在偏移剖面上的串珠现象会比较模糊,加上横向分辨率的因素所产生的绕射波场不容易归位形成明显的串珠组现象.
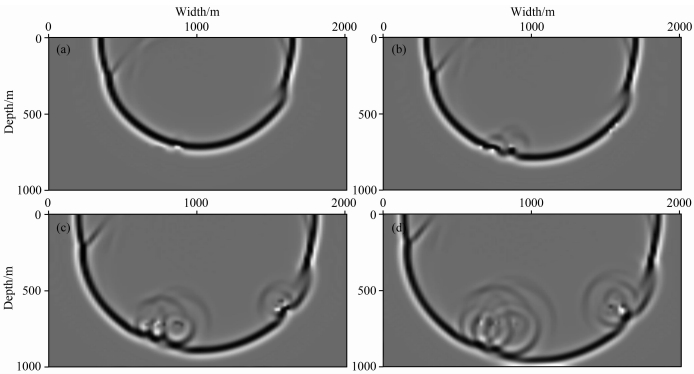 | 图 11 孔洞组合模型波场快照结果(a)250 ms波场快照;(b)270 ms波场快照;(c)300 ms波场快照;(d)320 ms波场快照.Fig. 11 The snapshot results for model with caves combination(a)The snapshot for 250 ms;(b)The snapshot for 270 ms; (c)The snapshot for 300 ms;(d)The snapshot for 320 ms. |
6 结论
谱元法通过将单元内部节点布置于特殊的积分点之上,并结合Lagrange形函数可以得到对角化的质量矩阵,从而在保证精度和网格灵活性的同时增加了其计算效率.常规的谱元法都是应用在四边形网格之上,而本文介绍了在三角网格中谱元法计算框架的构建,通过采用Cohen积分点去替代四边形网格中的GLL积分点,同样地可以保留质量矩阵对角化的优势.频散分析和稳定性分析表明,采用2阶Cohen积分点的三角谱元方法,相对于使用集中质量矩阵的3阶三角有限元方法具有更高的计算精度以及更宽松的稳定性条件.在本文的最后引入了两个中国西部地区典型的孔洞地质模型,并使用2阶 三角谱元法进行孔洞的刻画和正演模拟,其计算结果证明了该方法在模拟复杂构造情况下的有效性.
| [1] | Alford R M, Kelly K R, Boore D M. 1974. Accuracy of finite-difference modeling of the acoustic wave equation. Geophysics, 39(6): 834-842. |
| [2] | Blyth M G, Pozrikidis C. 2006. A Lobatto interpolation grid over the triangle. IMA J. Appl. Math, 71(1): 153-169. |
| [3] | Carcione J M, Herman G C, Ten Kroode A P E. 2002. Seismic modeling. Geophysics, 67(4): 1304-1325. |
| [4] | Chen Q, Babuska I. 1995. Approximate optimal points for polynomial interpolation of real functions in an interval and in a triangle. Comput. Methods Appl. Mech. Eng., 128(3-4): 405-417. |
| [5] | Chin-joe-kong M J S, Mulder W A, Van Veldhuizen M. 1999. Higher-order triangular and tetrahedral finite elements with mass lumping for solving the wave equation. J. Eng. Math., 35(4): 405-426. |
| [6] | Cohen G, Joly P, Tordjman N. 1995. Higher order triangular finite elements with mass lumping for the wave equation. // Third international conference on Mathematical and Numerical Aspects of wave propagation.Philadelphia,PA:SIAM,270-279. |
| [7] | Cohen G, Joly P, Roberts J E, et al. 2001. Higher order triangular finite elements with mass lumping for the wave equation. SIAM J. Numer. Anal., 38(6): 2047-2078. |
| [8] | Cohen G. 2002. Higher-Order Numerical Methods for Transient Wave Equations: Scientific Computation. New York: Springer-Verlag. |
| [9] | De Basabe J D. 2009. High-order finite element methods for seismic wave propagation . Texas, University of Texas at Austin. |
| [10] | De Basabe J D, Sen M K. 2007. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations. Geophysics, 72(6): 81-95. |
| [11] | Deng Y Q, Zhang Z L. 1990. Three-dimensional finite element modelling of elastic waves. Chinese J. Geophys. (in Chinese), 33(1): 41-53. |
| [12] | Gerald R. 1989. Applied Numerical Analysis. Addison-Wesley Publishing Co. |
| [13] | Hesthaven J S. 1998. From electrostatics to almost optimal nodal sets for polynomial interpolation in a simplex. SIAM J. Numer. Anal., 35(2): 655-676. |
| [14] | Kummer B, Behle A, Dorau F. 1987. Hybrid modeling of elastic wave propagation in two dimensional laterally inhomogeneous media. Geophysics, 52(6): 765-771. |
| [15] | Lisitsa V, Podgornova O, Tcheverda V. 2010. On the interface error analysis for finite difference wave simulation. Computational Geosciences, 14(4): 769-776. |
| [16] | Komatitsch D, Vilotte J P. 1998. The spectral-element method: an efficient tool to simulate the seismic response of 2D and 3D geological structures. Bull. Seism. Soc. Am., 88(2): 368-392. |
| [17] | Komatitsch D, Tromp J. 1999. Introduction to the spectral element method for three dimensional seismic wave propagation. Geophys. J. Int., 139(3): 806-822. |
| [18] | Komatitsch D, Martin R, Tromp J, et al. 2001. Wave propagation in 2-D elastic media using a spectral element method with triangles and quadrangles. J. Compu. Acoust., 9(2): 703-718. |
| [19] | Komatitsch D, Tromp J. 2003. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation. Geophys. J. Int., 154(1): 146-153. |
| [20] | Liu H W, Li B, Liu H, et al. 2010. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys. (in Chinese), 53(7): 1725-1733. |
| [21] | Liu T, Sen K M, Hu T Y, et al. 2012. Dispersion analysis of the spectral element method using a triangular mesh. Wave Motion, 49(4): 474-483. |
| [22] | Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics, 49(5): 533-549. |
| [23] | Mercerat E D, Vilotte J P, Sánchez-Sesma F J. 2006. Triangular spectral element simulation of two dimensional elastic wave propagation using unstructured triangular grids. Geophys. J. Int., 166(2): 679-698. |
| [24] | Min D, Shin C, Pratt R G, et al. 2003. Weighted-averaging Finite-element method for 2D Elastic wave equations in the frequency domain. Bull. Seism. Soc. Am., 93(2): 904-921. |
| [25] | Moczo P, Kristek J, Halada L. 2000. 3D fourth-order staggered grid finite difference schemes: stability and grid dispersion. Bull. Seism. Soc. Am., 90(3): 587-603. |
| [26] | Mulder W A. 1996. A comparison between higher-order finite elements and finite differences for solving the wave equation. Proceedings of the Second ECCOMAS Conference, 1-7. |
| [27] | Mulder W A. 1999. Spurious modes in finite-element discretizations of the wave equation may not be all that bad. Appl. Numer. Math., 30(4): 425-445. |
| [28] | Mullen R, Belytschko T. 1982. Dispersion analysis of finite element semidiscretizations of the two-dimensional wave equation. Int. J. Numer. Methods Eng., 18(1): 11-29. |
| [29] | Seriani G, Oliveira S P. 2008. Dispersion analysis of spectral element methods for elastic wave propagation. Wave Motion, 45(6): 729-744. |
| [30] | Taylor M A, Wingate B A, Vincent R E. 2000. An algorithm for computing Fekete points in the triangle. SIAM J. Numer. Anal., 38(5): 1708-1720. |
| [31] | Xue D C, Wang S X, Jiao S J. 2007. Wave equation finite-element modeling including rugged topography and complicated medium. Progress in Geophysics (in Chinese), 22(2): 522-529. |
| [32] | Zahradnik J, Moczo P, Horn F. 1993. Testing four elastic finite difference schemes for behavior at discontinuities. Bull. Seism. Soc. Am., 83(1): 107-129. |
| [33] | Zhang J, Verschuur D J. 2002. Elastic wave propagation in heterogeneous anisotropic media using the lumped finite-element method. Geophysics, 67(2): 625-638. |
| [34] | Zhang J F. 1994. An accurate method for finite-element elastic wave field modeling. Oil Geophysical Prospecting (in Chinese), 29(1): 29-36. |
| [35] | Zhang M G, Wang M Y, Li X F, et al. 2002. Finite element forward modeling of anisotropic elastic waves. Progress in Geophysics (in Chinese), 17(3): 384-389. |
| [36] | 邓玉琼, 张之力. 1990. 弹性波的三维有限元模拟. 地球物理学报, 33(1): 41-53. |
| [37] | 刘红伟, 李博, 刘洪等. 2010. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报, 53(7): 1725-1733. |
| [38] | 薛东川, 王尚旭, 焦淑静. 2007. 起伏地表复杂介质波动方程有限元数值模拟方法. 地球物理学进展, 22(2): 522-529. |
| [39] | 张剑锋. 1994. 一种高精度有限元弹性波场正演方法. 石油地球物理勘探, 29(1): 29-36. |
| [40] | 张美根, 王妙月, 李小凡等. 2002. 各向异性弹性波场的有限元数值模拟. 地球物理学进展, 17(3): 384-389. |
 2014, Vol. 57
2014, Vol. 57


