2. 中国石化地球物理重点实验室, 南京 210000
2. SINOPEC Key Laboratory of Geophysics, Nanjing 210000, China
1 引言
地表起伏是当今山前带地震勘探面临的一个难题,它除了引起观测系统设计、静校正、地震成像等方面的问题外,还会导致地震资料的低信噪比问题,成为制约目前山前带地震成像质量的主要瓶颈之一.通过起伏地表条件下地震波传播数值模拟,可以为山前带地震勘探的数据采集、资料处理和解释提供理论指导,这是目前解决山地地震勘探中的复杂观测系统设计、低信噪比、静校正以及地震成像等问题的有效途径.
目前,地震波传播数值模拟有多种方法,其中,高阶有限差分法因其高效便捷的优点应用最为广泛(董良国等, 2000a,2000b;Dablain,1986;Lev and er, 1988).但这些模拟方法多数所采用的规则网格在地下介质横向变速剧烈或地形起伏较大时,必然会导致模型的阶梯状离散,从而引起数值散射等问题.另外,在起伏地表条件下,这些方法(裴正林,2004;董良国,2005;Hestholm and Ruud, 1994;Tessmer et al., 1992)的自由边界条件的实现精度较低,地形起伏剧烈时,一些方法也极易产生数值计算的不稳定.而传统的有限元法和有限体法能够采用非结构网格对复杂模型进行贴体剖分,特别是采用三角形(或四面体)网格能够对任意复杂的起伏地表模型进行有效剖分.有限元法很早就被应用于地震波传播的数值模拟(Marfurt,1984;Serón et al., 1990;Padovani et al., 1994; 邵秀民等,1995;周辉等,1997;Zhang and Verschuur, 2002;杨顶辉,2002;黄自萍等,2004),但在地震勘探工业界并未得到广泛应用,主要是由于传统有限元法存在以下几方面的问题:(1)计算复杂,且需要对大型质量矩阵求逆,极大增加了计算量;(2)一般使用低阶空间离散格式,存在较强的数值频散;(3)使用高阶空间格式离散时容易产生伪波等.而传统的有限体法也因为精度不高,在地震波传播模拟中应用不多.谱元法(SEM)(Komatitsch and Vilotte, 1998)是一种高阶有限元法,但SEM一般使用四边形和六面体网格,而目前生成适应复杂介质分布的四边形和六面体网格的技术还不是很成熟,难以适应地表起伏剧烈、地下构造复杂情况下地震波数值模拟的需要.
间断Galerkin有限元法(DG-FEM)是近年来发展较快的一种改进有限元法,它最早应用于求解原子传输方程(Reed and Hill, 1973).Cockburn和Shu等(1989,2001)(Cockburn et al., 2004)将DG-FEM与Runge-Kutta时间离散格式结合,发展了RKDG方法,并对该方法的发展做出了很大贡献,之后,该方法被广泛地运用于电磁学(Cockburn et al., 2004)、气动声学(Toulopoulos and Ekaterinaris, 2004)等学科中.
基于数值流通量理论的DG-FEM本质上是有限元法和有限体法的结合,在单元内部使用有限元法处理,在单元边界上采用了有限体法中数值流通量的处理思想.DG-FEM继承了有限元法和有限体法的优点,同时也克服了这两个方法的一些缺陷,能够实现高精度、低频散、有效的数值模拟.它可以使用非结构网格单元(包括三角形或四面体网格),能够根据介质的分布特征设计出最优的网格,因此,能够适应起伏地表及复杂构造条件下地震波传播数值模拟.它继承了有限体法良好的局部特性,可以逐单元地求解弹性波方程,避免传统有限元法的大型矩阵求逆过程,且其局部特性也非常有利于算法的并行化.同时,该特性也允许DG-FEM在单元内部使 用高阶有限元,从而拥有高阶精度. Kaser和Dumbser(2006a)将任意高阶导数(ADEG)时间离散格式结合DG-FEM运用于求解弹性波动力学方程,ADEG格式采用空间导数替换时间导数的思想,因此该方法在时间和空间上均可以达到任意高阶精度.之后,他们又将该方法拓展到三维(Dumbser and Kser,2006)、黏弹(Kaser and Dumbser, 2006)、各向异性( De la Puente et al., 2007)等介质中弹性波传播数值模拟中,并发展了局部时间步长等(Dumbser et al., 2007;Hermann et al., 2011)求解策略.Etienne等(2010)基于中心数值流,采用低阶(≤2)的DG-FEM求解弹性波方程.因为该方法基于中心数值流,速度场的更新只与应力场有关,而应力场的更新只与速度场有关,所以非常适用于蛙跳(leap-frog)时间离散格式.
在本文的第2部分,介绍了利用任意高阶间断Galerkin有限元法模拟弹性波传播的基本原理,并在附录部分基于配点法对其完成细节作了详细推导.在时间离散方面,我们提出首先将空间离散后形成的非齐次线性常微分方程系统齐次化,然后再采用针对齐次问题的强稳定性保持龙格库塔(SSP Runge-kutta)时间格式,最终获得的算法在时间和空间上均可以达到任意高阶.在第3部分,基于近最佳匹配层(NPML)的思想和复频移(CFS)拉伸坐标 变换,我们推导了一种新的PML吸收边界条件 ——CFS-NPML,该技术能够有效地应用到DG-FEM中.通过第4部分的数值试验来说明发展的模拟方法的有效性.
另外,DG-FEM方法需要对介质模型进行贴体剖分,为此我们开发了一种模型的自适应三角剖分方法,该方法可以根据介质参数的变化程度进行自适应贴体剖分.这种自适应三角剖分方法我们将另文发表,这里不多赘述.
2 方法原理
二维速度-应力弹性波方程可以表示为下面的一阶变系数双曲型偏微分方程系统:
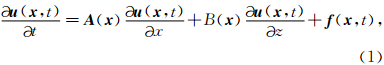
2.1 弹性波方程的DG-FEM公式
设计算区域为Ω,对其进行有限单元离散,划分为不重叠的子区域 {Ωi} .间断Galerkin有限元法采用分片(逐单元)光滑函数逼近波场,即不要求波场值在单元边界上保持连续.对方程(1)两边同时乘以标量试验函数φki(x),并在第k个单元Ωk上进行空间积分,有
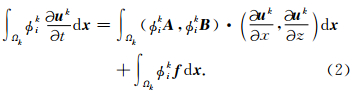
为了表示方便,设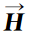 =(φkiA,φkiB),Δu k=(
=(φkiA,φkiB),Δu k=(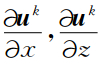 ),用高斯散度定理推论(附录A)处理上式右端第一项,得
),用高斯散度定理推论(附录A)处理上式右端第一项,得
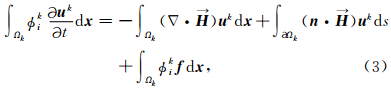
由于在单元边界上不要求波场连续,因此需要对单元边界上波场值给予定义,这里暂用 u k表示.对上式右端第一项可以再次使用高斯散度定理推论,得
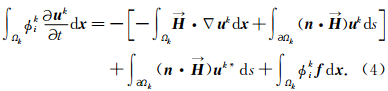
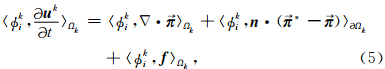
间断Galerkin有限元法通过使用有限体法中的数值流通量来定义单元边界上的波场值,这里,我们采用局部Lax-Friedrichs数值流通量.当采用高阶DG-FEM时,空间格式的精度主要由单元内部自由度驱动,使用局部Lax-Friedrichs数值流通量是比较合适的选择.下面给出局部Lax-Friedrichs数值流通量的定义:
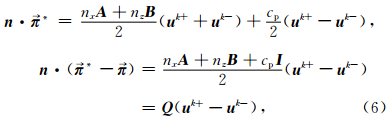
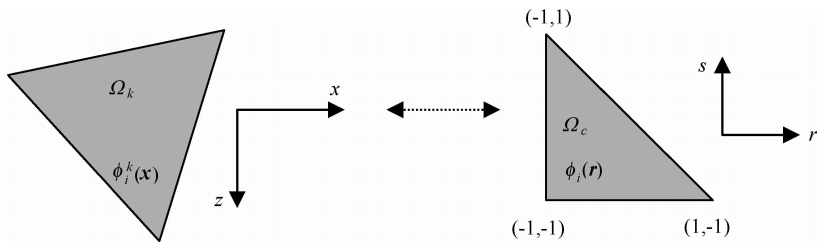 | 图 1 物理单元到参考单元映射示意图Fig. 1 Mapping between physical and canonical element |
为了计算方便,通过坐标变换将物理单元Ωk映射到标准单元Ωc上(图 1).当采用直边多边形网格单元时,物理单元Ωk与参考单元Ωc之间以及单元对应边之间的Jacobi映射关系为常数,则(5)式可进一步简化为
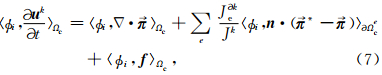
2.2 空间离散方程
上面推导中一阶双曲型系统方程是一般形式,声波方程、各向同性和各向异性弹性波方程、黏弹方程等均可以表达为一阶双曲方程系统,因此,它们都可以通过(5)式的DG-FEM求解.虽然DG-FEM并不限定网格单元类型,但这里我们主要考虑直边三角形网格单元.
按照有限元的思路,在每个单元内,用多项式基函数逼近波场,当采用的基函数与试验函数相同时,即为Galerkin方法.采用在三角网格单元上具有正交特性的Koornwinder-Dubiner多项式(附录C),波场分量ukm(x,t)展开表示为

假设单元Ωk内介质物性参数不变,即 A 、 B 为常系数矩阵.将(8)式代入(7)式,并选择合适的数值 流,经过数学推导,最终在单元Ωk上的半离散方程为
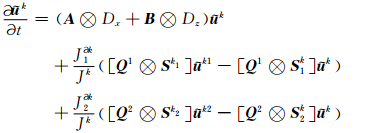
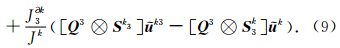
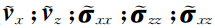 ]T(为5N×1的列向量),代表了每个单元上的全部自由度, k为第k个单元内波场展开系数,uki为相邻三个单元内的波场系数,D 为离散的空间微分算子,S 为单元边界积分相关的算子,它们都表示为N×N的矩阵形式,Q 为前文介绍的单元相应边上的流通量系数矩阵,为矩阵张量乘,(nx,nz)为单元边界上的法向量,cp为单元内介质的纵波速度.各算子的具体形式推导见附录B.
]T(为5N×1的列向量),代表了每个单元上的全部自由度, k为第k个单元内波场展开系数,uki为相邻三个单元内的波场系数,D 为离散的空间微分算子,S 为单元边界积分相关的算子,它们都表示为N×N的矩阵形式,Q 为前文介绍的单元相应边上的流通量系数矩阵,为矩阵张量乘,(nx,nz)为单元边界上的法向量,cp为单元内介质的纵波速度.各算子的具体形式推导见附录B.获得空间半离散方程后,再加上相应边界条件以及合适的时间离散格式,我们便可以对波场进行时间方向上的更新.从(9)式中可以看到,第k个单元上波场的更新只与本单元以及相邻三个单元有关,即该空间格式是紧致显式的,我们可以逐单元更新波场,而不需要形成整体的有限元方程.
2.3 时间积分格式
作为概念上的表示,我们也可以将(9)式的空间离散方程整合成下面形式的线性方程系统:
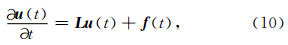
(10)式的解析解可以表示为
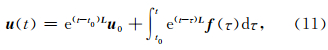
Al-Mohy和Higham(2011)通过对f(t)进行p阶Taylor级数展开,最终将(11)式的求解转化为一个扩展矩阵的指数函数的求解:
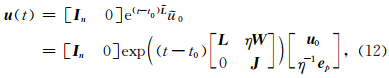
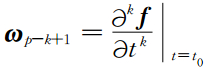 ,
,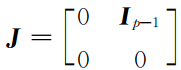 ,I n为(p-1)×(p-1)的单位矩阵,η=2-「log2(‖ W ‖1),η有利于数值计算稳定, e p为第p个元素不为零的单位向量.
,I n为(p-1)×(p-1)的单位矩阵,η=2-「log2(‖ W ‖1),η有利于数值计算稳定, e p为第p个元素不为零的单位向量.
利用(12)式的核心是计算指数矩阵-向量乘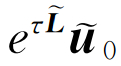 ,它等价于求解下面的齐次方程,
,它等价于求解下面的齐次方程,

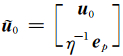 .
.Runge-Kutta方法是最早与DG-FEM结合使用的一种时间格式.目前,该方法从存储以及精度上都已获得了相当大发展.其中,强稳定保持Rugge-Kutta格式是一类具有较强稳定性的RK格式.尽管方法设计的出发点主要是针对非线性问题,但事实证明,它对于常系数的线性问题同样有效,且能达到高阶精度.对(13)式的齐次问题,Gottlieb(2005)给出了下面的m级m-1阶强稳定性保持Rugge-Kutta时间格式(SSP-RK(m,m-1)),其表达式为
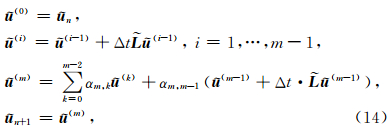
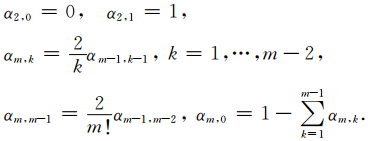
需要指出的是矩阵-向量乘的过程就是实施DG-FEM有限元空间离散的过程,因此并不需要显式的给出大型矩阵.
|
|
表 1 SSP-RK(m,m-1)系数表 Table 1 Coefficients αm,j of linear SSP-RK(m,m-1) |
3 震源及边界条件 3.1 震源
震源有不同的形式,一般需要模拟方向震源或爆炸震源的激发.这里讨论爆炸震源,设 x s为震源位置,且在单元Ωks内.施加爆炸震源时,将子波作用在正应力上比较方便,设正应力项上加载震源为f(x,t)=s(t)δ(x - x s),其中,s(t)为震动函数. 〈φksi,f(x,t)〉Ωks =s(t)〈φksi,δ(x - x s)〉Ωks =s(tφ)ksi(x s). 因此,在模拟过程中,只需要在震源所在单元的正应力对应项加上向量
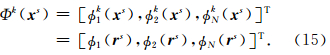
当采用低阶的DG法或者震源所在的网格单元较大时,这种施加方法产生的纵波源不纯,残留一些横波的痕迹.为了压制这种现象,可以在以震源为中心的高斯分布区域内施加.在物理空间完成方式中,可以在所有节点(附录B、C)上施加震源,具体可以直接将子波乘以节点对应高斯分布系数,然后加到相应正应力项上.
3.2 自由表面条件
自由边界条件要求作用在自由表面上的应力为零.在DG-FEM法中,数值流通量控制单元边界上的波场值,因此,可以通过设置(6)式中的数值流通量来实施自由边界条件.本文采用下面的方式来简化自由边界条件的实施:在自由表面处,采用中心数值流通量,然后采用镜像原理,将自由表面两侧应力分量设置为反对称,而速度分量设置对称即可.而在模型的内部单元边界上我们使用了更精确的Lax-Friedrichs数值流通量理论.
3.3 CFS-NPML吸收边界条件
地震波数值模拟一般计算有限区域内地震波的传播,因此需要引入人工吸收边界条件来处理人为边界反射问题.在DG-FEM中,单元边界处的数值流通量项包括两部分:流出单元部分和进入单元部分,进入单元部分由相邻单元控制.因此,在计算区域边界处可以通过将数值流通量的进入单元部分设置为零来控制边界反射.该吸收边界条件被称为开放边界条件.但开放边界条件对面波、倏逝波等的吸收效果并不理想,我们需要对吸收边界条件作进一步改善或采用最佳匹配层(PML)吸收边界条件.
对于PML技术,拉伸坐标变换是一个关键的手段,它通过一个拉伸函数将空间坐标系映射到复空间中去,然后对入射匹配层的平面波进行阻尼吸收.理论上,常规PML技术可以对进入匹配层的入射波完全吸收,但经过空间离散后,其对近平行入射到界面上的波以及低频波、倏逝波等吸收效果仍然欠佳.Kuzuoglu 等(1996)引入了复频移(CFS)拉伸函数,并采用了不分裂式PML.基于复频移拉伸函数的PML(一般简称为CFS-PML),对于近面波、倏逝波等都有良好的吸收效果.不分裂PML不需要分裂波场,但在时间域需要做大量褶积运算,计算量较大.Komatitsch和Martin(2007)发展了一种无需显式褶积计算、基于迭代格式的不分裂PML技术——卷积型完美匹配层CPML,大大降低了不分裂PML的时间域计算代价.
Cummer(2003)介绍了一种新的不分裂PML 技术——NPML(Nearly Perfectly Matched Layer). 该PML技术在推导过程中的一个假设前提是拉伸函数是空间不变的.事实上,从数学上也可以证明,在该假设条件下获得的吸收方程仍然是一种PML技术.本小节基于NPML的思想,同时采用复频移拉伸(CFS)函数,通过引入新的辅助变量推导了一种新的PML技术(简称为CFS-NPML).
定义复频移(CFS)拉伸函数:
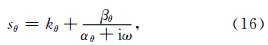
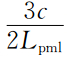 lgR,c为 纵波速度.参数αθ=παmax (1-δθ/Lpml ),其中,αmax=f0为子波的主频.(16)对应的空间导数变换关系为
lgR,c为 纵波速度.参数αθ=παmax (1-δθ/Lpml ),其中,αmax=f0为子波的主频.(16)对应的空间导数变换关系为

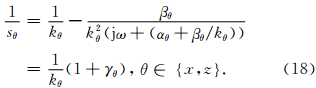
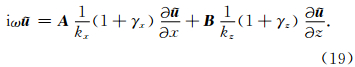
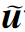 x、
x、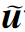 z,
z,
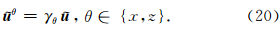
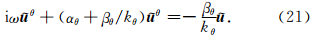
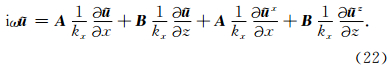
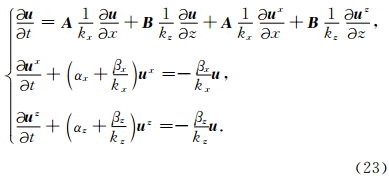
这里必须指出,表面上CFS-NPML需要10个辅助变量,但实际上σzxx和σxzz在计算过程中是不需要的,即辅助变量个数也为8个(与CPML相同).CFS-NPML可以写为下面的一阶双曲系统形式:

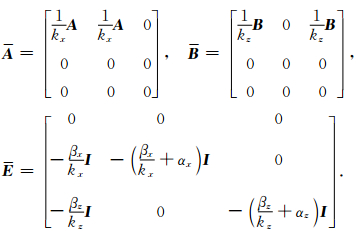
4 数值试验
下面,我们通过几个数值试验来验证发展的DG-FEM方法在复杂构造以及起伏地表情况下模拟弹性波传播的有效性. 4.1 Lamb问题
通过Lamb问题的求解,可以测试自由表面边界条件实施的有效性.图 2是一个自由地表倾角为10°的均匀介质模型,纵波速度为3200 m·s-1,横波速度为1847.5 m·s-1,密度为2200 kg·m-3.在自由表面(1720 m,401.72 m)处垂直地表施加震源(主频为14.5 Hz的雷克子波),在水平坐标为2694.95 m和3400.08 m的地表上设置两个检波 器.模拟采用空间3阶,时间3阶,时间步长为0.2 ms.
 | 图 2 倾斜地表模型Fig. 2 Geometry of the tilted surface model |
图 3为600 ms时的水平和垂直速度分量波场快照,图中P波、S波、Rayleigh面波以及Schmidt波等震相均清晰可见.为了验证模拟方法的有效性,我们将地表记录与解析解比较(图 4).从图中可以看到,无论是水平速度分量还是垂直速度分量,DG-FEM模拟结果和解析解都吻合得非常好,说明了DG-FEM方法可以获得高精度的弹性波模拟结果.
 | 图 3 600 ms时的波场快照(a)水平速度分量;(b)垂直速度分量. Fig. 3 Snapshots of velocity components at 600ms for Lamb′s problem(a)Horizontal velocity component;(b)Vertical velocity component. |
 | 图 4 DG-FEM(P3阶)模拟结果与解析解的对比第1道:第1个检波器接收记录;第2道:第2个检波器接收记录.(a)水平分量;(b)垂直分量. Fig. 4 Comparison between DG-FEM(P3)numerical results with analytical solution(a)Horizontal and (b)vertical components of the velocity. The 1st line seismogram at the first receiver,and the 2nd line at another receiver. |
4.2 CFS-NPML边界吸收效果验证
本试验主要目的是验证本文推导的CFS-NPML 技术对人为边界反射的吸收效果.鉴于CPML是近年来提出的边界吸收效果很好且得到广泛应用的吸收边界条件,下面将本文发展的CFS-NPML与CPML进行了对比分析.
试验模型为一个简单的水平自由表面均匀模型,纵波速度为3200 m·s-1,横波速度为1847.5 m·s-1,密度为2200 kg·m-3,大小为2000 m×2000 m.在自由表面(50 m,10 m)处施加爆炸震源(主频为25 Hz的雷克子波).采用P2阶空间离散.模拟的时间步长为0.25 ms.PML的宽度为160 m,7个单元的宽度.CPML和CFS-NPML的吸收参数相同,R=10-7.
图 5为采用上述两种不同PML吸收边界条件时1 s时刻速度水平分量的波场快照(左图为CFS-NPML,右图为CPML),为了显示效果,对快照作了适当增益.可以看到,不管是CPML,还是本文发展的CFS-PML,对面波等人为边界反射的吸收都非常干净.
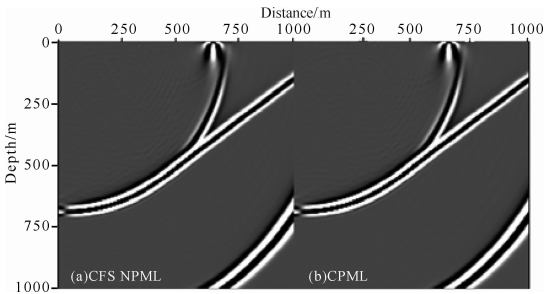 | 图 5 不同PML吸收边界条件下,1 s时刻水平速度分量波场快照,震源位置为(50 m,10 m)(a)CFS-NPML ;(b)CPML.Fig. 5 The snapshots of horizontal velocity component at 1 s computed by P2 DG-FEM with CFS-NPML(a) and CPML(b). The location of source is(50 m,10 m) |
为了进一步比较CFS-NPML和CPML的吸收效果,在地表(100 m,0 m)处设置检波器,图 6a为水平速度分量记录.直达波和面波的延续时间之后,记录上未看到任何边界反射,并且从图 6b的放大曲线可以看出,由于数值计算、边界反射等造成的曲线震荡峰值不到记录面波峰值的0.267%,而且CPML和CFS-NPML对应曲线吻合得很好,这进一步说明了CFS-NPML与CPML都具有非常理想的人为边界反射吸收效果.
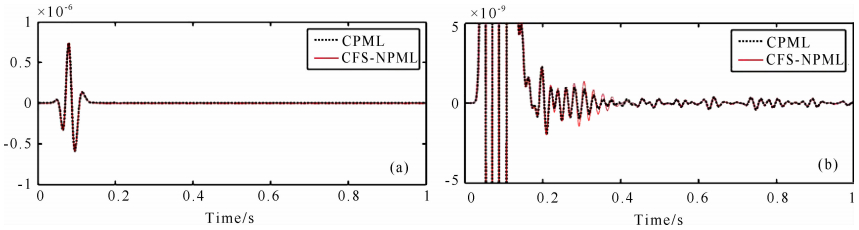 | 图 6 不同PML吸收边界条件下,地表(100 m,0 m)处检波器速度水平分量记录(a)及其放大图(b)对比 Fig. 6 Comparison of the horizontal velocity seismograms(a) and their local zoom(b)under CPML and CFS-NPML |
表 2列出了CFS-NPML与CPML计算效率对比.本实验的模拟总时长2 s,为了显示方便,上图只显示了0~1 s记录.从表中可以看到,CFS-NPML较CPML具有更大的计算效率,本次试验节约计算时间约27%.
|
|
表 2 CPML 与CFS-NPML计算效率对比 Table 2 The computational efficiency comparison of CPML and CFS-NPML |
利用常规的规则网格对复杂构造模型进行剖分时会形成边界的阶梯状离散,从而造成地震波传播 的数值散射问题.为了说明DG-FEM方法在模拟复杂构造模型中地震波传播时在剖分方面的优势,我们设计了一个含有高陡构造的模型(图 7),上层介质的纵横波速度及密度分别为3464 m·s-1、2000 m·s-1和2000 kg·m-3,下层介质的纵横波速度及密度 分别为4000 m·s-1、2300 m·s-1和2300 kg·m-3. 从图 8的网格剖分局部放大图中可以看到,DG-FEM可以沿着高陡构造的边界进行贴体的剖分,而有限差分法(FD)采用的矩形网格(dx=10 m)离散后高陡构造的边界呈现阶梯状.图 9对比了有限差分法(空间4阶,时间2阶)和DG-FEM(空间2阶,时间2阶)的地表速度分量记录,从地表记录中方框内可以看到FD模拟结果存在明显的数值散射.在图 10的地表 1500 m处的检波器记录上,FD模 拟方法因为阶梯离散造成的这种数值散射更为明显.
 | 图 7 高陡倾角模型 Fig. 7 Geometry of the high steeply-dipping model |
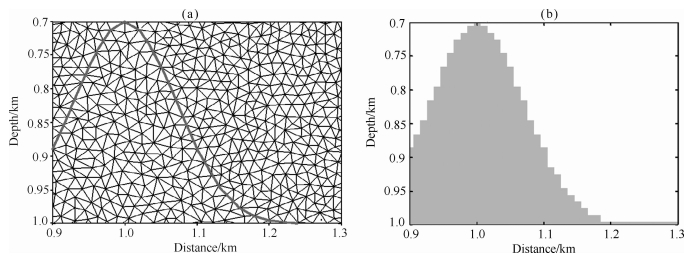 | 图 8 网格剖分局部放大图(a)DG-FEM三角网格剖分;(b)FD矩形网格剖分. Fig. 8 Local zoom of the discrete description for model(a)DG-FEM triangular mesh;(b)FD regular mesh. |
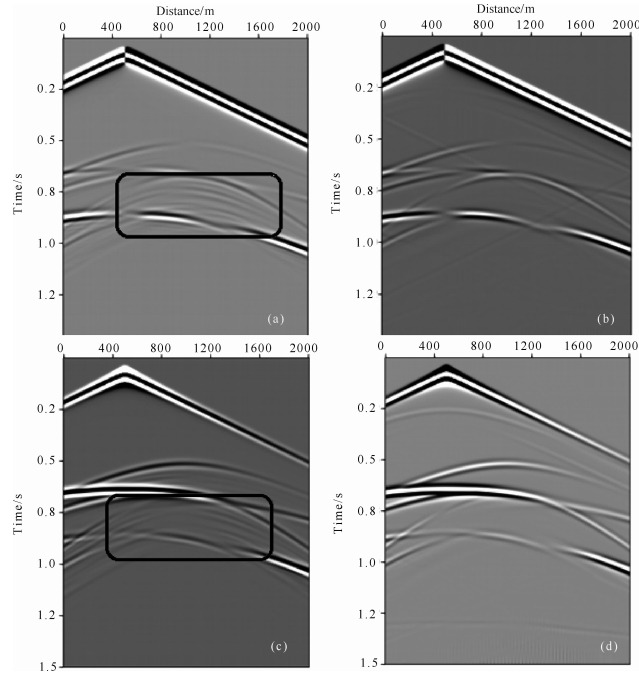 | 图 9 地表单炮记录(上:水平分量,下:垂直分量)(a,c)有限差分结果;(b,d)DG-FEM结果. Fig. 9 Surface single-shot records(above: horizontal components,below: vertical components)(a,c)FD results;(b,d)DG-FEM results. |
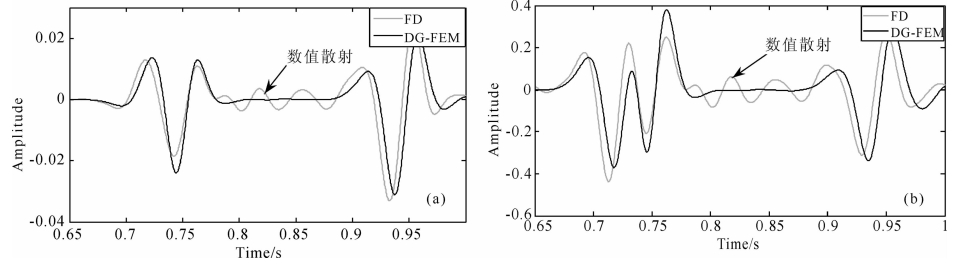 | 图 10 地表 1500 m处检波器记录(a)水平分量 ;(b)垂直分量. Fig. 10 Seismograms at surface location 1500 m(a)Horizontal component;(b)Vertical component. |
4.4 单峰模型
本模型(图 11)为一个单峰的单层均匀介质起伏地表模型,地表起伏呈高斯指数函数分布.模型横 向展布4500 m,单峰的中心轴大约在横向坐标2700 m 处,最高峰高程为400 m.纵波速度为3464 m·s-1,横波速度为2000 m·s-1,密度为2000 kg·m-3.在自由表面(2000 m,500 m)处施加爆炸震源(主频为 25 Hz的雷克子波).检波器排列在地表 1000~4000 m 范围内,151个检波器,相邻检波器横向间距20 m. 模拟采用空间2阶,时间2阶,时间步长为0.25 ms.
 | 图 11 单峰模型 Fig. 11 Geometry of the hill model |
图 12为用DG-FEM方法与基于纵向坐标变换有限差分方法分别模拟的地表速度垂直分量对比.可以发现,相比有限差分方法,DG-FEM方法能够更加精细地模拟地表起伏所引起的前向和后向散射波.
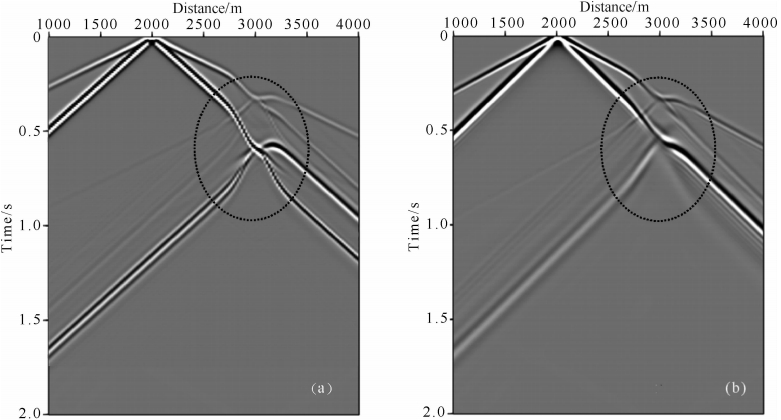 | 图 12 单峰模型地表垂直速度分量(a)DG-FEM结果;(b)FD结果. Fig. 12 Seismograms of vertical velocity component computed for the hill model(a)DG-FEM results;(b)FD results. |
图 13为单峰和凹陷模型下,DG-FEM模拟的地表速度垂直分量记录.我们可以清晰地看到,当地震波向右传播到地形起伏处时,会出现波场的分离和转换等现象,例如P波和Schmidt波的分离、P波和面波遇到界面时的转换及再发育,这些都导致了散射波发育丰富.从单峰和凹陷模型对比发现,地形隆起时,前、后向散射波发育都比较丰富,而地形凹陷时,前向散射更加丰富.
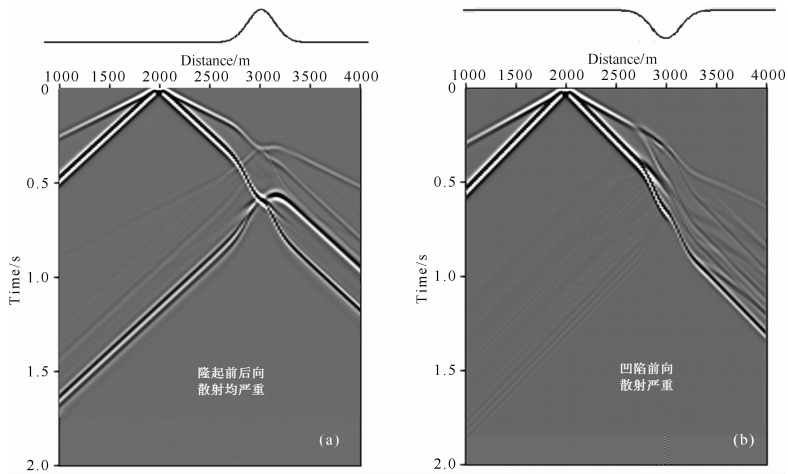 | 图 13 单峰和凹陷模型下,DG-FEM模拟的地表垂直速度分量记录(a)单峰模型;(b)凹陷模型. Fig. 13 Seismograms of vertical velocity components simulated by DG-FEM for(a)the hill model and (b)the sag model |
4.5 新疆模型
图 14是中石油东方地球物理公司根据准噶尔盆地一个工区的地表和地下构造特点设计的一个起伏地表模型(图中显示的是纵波速度),地下构造比较简单,但地形局部起伏比较剧烈,并且存在低速带(纵波 速度500 m·s-1)和降速带(纵波速度800 m·s-1). 在自由表面(X=4600 m)处施加爆炸震源(主频为 25 Hz的雷克子波),251个检波器排列在地表 1000~6000 m 范围内,相邻检波器间距20 m,模拟采用空 间2阶,时间2阶,时间步长为0.2 ms,模拟时长2 s.
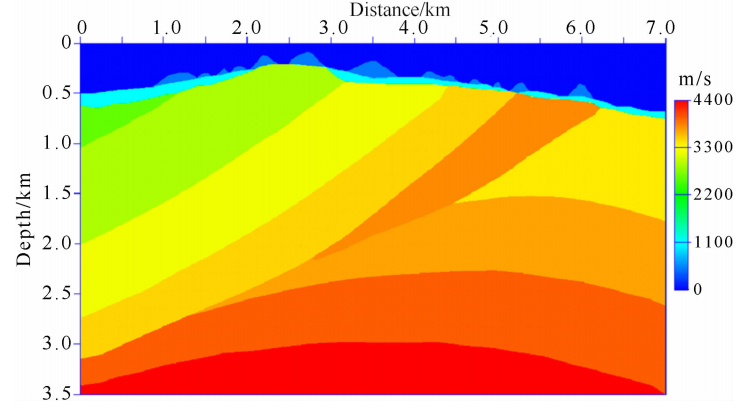 | 图 14 新疆模型(部分) Fig. 14 Geometry of the Xijiang model(partly) |
从图 15的模拟记录看出,由于地表起伏以及地表覆盖的低降速带的存在,近地表处地震波场的传播非常复杂,特别是面波散射十分严重,一次反射波信号被严重污染,大幅度降低了记录的信噪比.因此,起伏地表所引起的地震波场的散射是山地地震资料信噪比低的主要原因之一.
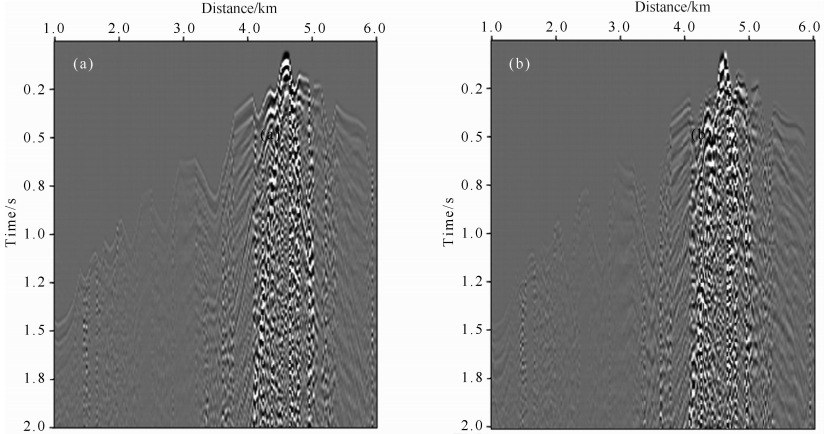 | 图 15 地表单炮记录(a)水平分量;(b)垂直分量. Fig. 15 Surface single-shot records(a)Horizontal component;(b)Vertical component. |
5 结论
本文结合针对齐次问题的强稳定性保持龙格库塔(SSP Runge-kutta)算法,将DG-FEM方法推广至时间任意高阶精度,用于求解弹性波方程.Lamb问题等一系列数值模拟计算实例表明,DG-FEM方法是一个高阶高精度的数值模拟方法.相比有限差分方法,DG-FEM方法能够高精度地实现起伏地表自由边界条件.同时,因为采用贴体的网格剖分,它能够避免有限差分等方法因阶梯状离散造成的数值 散射等问题,而三角形网格使DG-FEM方法能够有效模拟任意复杂起伏地表条件下弹性波的传播.
基于NPML的思想和复频移拉伸坐标变换,本文推导的CFS-NPML吸收边界条件能够与DG-FEM方法有效结合,并且对面波的人为边界反射也具有良好的吸收效果.通过数值试验对比CFS-NPML和CPML在DG-FEM模拟弹性波传播中的表现可以发现,二者都能有效吸收近平行边界入射的包括面波等震相的人为边界反射.在同样吸收参数条件下,两者吸收效果相当,但本文发展的CFS-NPML技术具有更高的计算效率.
本文发展的高精度的数值模拟方法可以为我们分析起伏地表条件下弹性波的传播规律以及波场响应特征提供一种有效的弹性波传播数值模拟工具.
附录A 高斯散度定理及其推论
高斯散度定理:
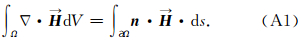
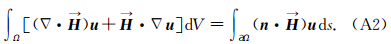
附录B DG-FEM空间离散算子推导
(1)模空间(Modal Space)
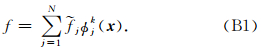
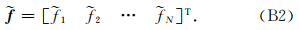
在单元Ωk上选一组离散节点 x = [x 1 x 2 … x N] (节点的选择见C部分),物理空间:

模空间和物理空间存在映射关系,定义广义范德蒙特矩阵:
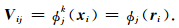

函数g(x)、f(x)定义在单元Ωk上,则它们之间的内积表示为
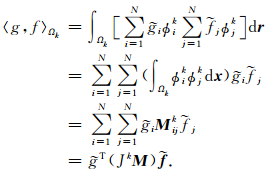

函数g(x)、f(x)定义在单元Ωk上,定义下面形式的内积:
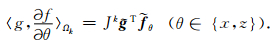
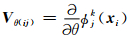 ,由(B1)有
,由(B1)有
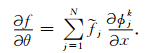

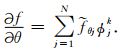

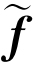 θ、
θ、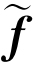 之间的关系:
之间的关系:

则偏导内积表示为
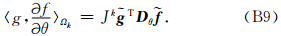
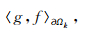
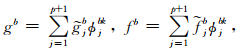
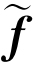 b.
b.在单元αΩek上选一组离散点 x b={ x b1 x b2 … x bp+1}, 我们选择边界上的节点与区域节点吻合,即 x b= x(ib),其中ib表示边界节点在区域节点中的索引编号(注意g,f所在单元不同,所以索引号不用).这里提醒,当我们采用所谓p自适应技术时,边界节点和区域节点不吻合,还需要采取其他处理手段.
由模空间和物理空间存在映射关系,有
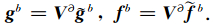
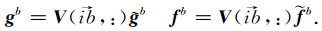
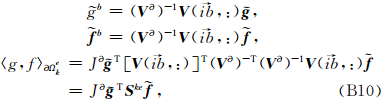
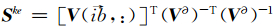

附录C 基函数和节点选择
我们一般先将物理单元映射到标准单元上,然后在参考单元上选择一组权函数用于上面的计算需求.在三角形单元上,我们一般采用Koornwinder-Dubiner 基函数:
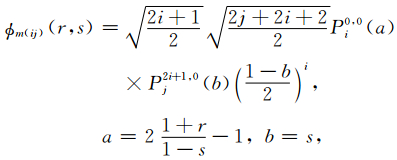
对于物理空间上的节点,我们选择使广义范德蒙特矩阵有更好求逆性质的Fekete点集(数据来至Alvise Sommariva的个人网站).
| [1] | Al-Mohy A H, Higham N J. 2011. Computing the Action of the Matrix Exponential, with an Application to Exponential Integrators. SIAM J. Sci. Comput., 33(2): 488-511. |
| [2] | Cockburn B, Li F Y, Shu C W. 2004. Locally divergence-free discontinuous Galerkin methods for the Maxwell equations. Journal of Computational Physics, 194(2): 588-610. |
| [3] | Cockburn B, Shu C W. 1989. Tvb Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws ii: general framework. Mathematics of Computation, 52(186): 411-435. |
| [4] | Cockburn B, Shu C W. 2001. Runge-Kutta discontinuous Galerkin methods for convection-dominated problems. Journal of Scientific Computing, 16(3): 173-261. |
| [5] | Cummer S A. 2003. A simple, nearly perfectly matched layer for gneral electromagnetic media. IEEE Microwave and Wireless Components Letters, 13(2): 128-130. |
| [6] | Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66. |
| [7] | De la Puente J, Köser M, Dumbser M, et al. 2007. An arbitrary high-order discontinuous galerkin method for elastic waves on unstructured meshes IV: anisotropy. Geophysical Journal International, 169(3): 1210-1228. |
| [8] | Dong L G, Ma Z T, Cao J Z, et al. 2000a. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese J. Geophys. (in Chinese), 43(3): 411-419. |
| [9] | Dong L G, Ma Z T, Cao J Z. 2000b. A study on stability of the staggered grid high order difference method of first order elastic wave equation. Chinese J. Geophys. (in Chinese), 43(6): 856-864. |
| [10] | Dong L G. 2005. Numerical simulation of seismic wave propagation under complex near surface conditions. Progress in Exploration Geophysics (in Chinese), 28(3): 187-194. |
| [11] | Dumbser M, Köser M. 2006. An arbitrary high order discontinuous galerkin method for elastic waves on unstructuredmeshes II: the three-dimensional isotropic case. Geophysical Journal International, 167(1): 319-336. |
| [12] | Dumbser M, Kaser M, Toro E. 2007. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes V: local time stepping and p-adaptivity. Geophysical Journal International, 171(2): 695-717. |
| [13] | Etienne V, Chaljub E, Virieux J, et al. 2010. An hp-adaptive discontinuous Galerkin finite-element method for 3D elastic wave modelling. Geophysical Journal International, 183(2): 941-962. |
| [14] | Gottlieb S. 2005. On high order strong stability preserving Runge-Kutta and multi step time discretizations. Journal of Scientific Computing, 25(1): 105-128. |
| [15] | Hermann V, Kaser M, Castro C E. 2011. Non-conforming hybrid meshes for efficient 2D wave propagation using the Discontinuous Galerkin method. Geophysical Journal International, 184(2): 746-758. |
| [16] | Hestholm S, Ruud B. 1994. 2D finite-difference elastic wave modelling including surface topography. Geophysical Prospecting, 42(5): 371-390. |
| [17] | Huang Z P, Zhang M, Wu W Q, et al. 2004. A domain decomposition method for numerical simulation of the elastic wave propagation. Chinese J. Geophys. (in Chinese), 47(6): 1094-1100. |
| [18] | Köser M, Dumbser M, de la Puente J, et al. 2007. An arbitrary high order Discontinuous Galerkin method for elastic waves on unstructured meshes III: Viscoelastic attenuation. Geophysical Journal International, 168(1): 224-242. |
| [19] | Kaser M, Dumbser M. 2006. An arbitrary high order discontinuous Galerkin method for elastic waves on unstructured meshes I: the two-dimensional isotropic case with external source terms. Geophysical Journal International, 166(2): 855-877. |
| [20] | Komatitsch D, Martin R. 2007. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics, 72(5): 155-167. |
| [21] | Komatitsch D, Vilotte J P. 1998. The spectral element method: an efficient tool to simulate the seismic response of 2D and 3D geological structures. Bull. seism. Soc. Am., 88(2): 368-392. |
| [22] | Kuzuoglu M, Mittra R. 1996. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers. IEEE Microwave and Guided Wave Letters, 6(12): 447-449. |
| [23] | Levander A R. 1988. Four-order finite-difference P-SV seismograms. Geophysics, 53(11): 1425-1436. |
| [24] | Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics, 49(5): 533-549. |
| [25] | Padovani E, Priolo E, Seriani G. 1994. Low-and high-order finite element method: experience in seismic modeling. J. Comp. Acous., 2(4): 371-422. |
| [26] | Reed W H, Hill T R. 1973. Triangular mesh methods for the neutron transport equation, Technical Report, LA-UR-73-479, Los Alamos Scientific Laboratory. |
| [27] | Serón F J, Sanz F J, Kindelán M, et al. 1990. Finite-element method for elastic wave propagation. Comm. Appl. Numerical Methods, 6(5): 359-368. |
| [28] | Shao X M, Lan Z L. 1995. Numerical simulation of the seismic wave propagation in inhomogeneous isotropic elastic media. Chinese J. Geophys. (in Chinese), 38(S1): 39-55. |
| [29] | Tessmer E, Kosloff D, Behle A. 1992. Elastic wave propagation simulation in the presence of surface topography. Geophys. J. Int., 108(2): 621-632. |
| [30] | Toulopoulos I, Ekaterinaris J A. 2004. High-order discontinuous Galerkin discretizations for computational aeroacoustics in complex domains. AIAA, 44(3): 502-511. |
| [31] | Yang D H. 2002. Finite element method of the elastic wave equation and wavefield simulation in two-phase anisotropic media. Chinese J. Geophys. (in Chinese), 45(4): 575-583. |
| [32] | Zhang J F, Verschuur D J. 2002. Elastic wave propagation in heterogeneous anisotropic media using the lumped finite-element method. Geophysics, 67(5): 625-638. |
| [33] | Zhou H, Xu S Z, Liu B, et al. 1997. Modeling of wave equations in anisotropic media using finite element method and its stability condition. Chinese J. Geophys. (in Chinese), 40(6): 833-841. |
| [34] | Pei Z L. 2004. Numerical modeling using staggered-grid high-order finite-difference of elastic wave equation on arbitrary relief surface. Oil Geophysical Prospecting (in Chinese), 39(6): 629-634. |
| [35] | 董良国, 马在田, 曹景忠等. 2000a. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报, 43(3): 411-419. |
| [36] | 董良国, 马在田, 曹景忠. 2000b. 一阶弹性波方程交错网格高阶差分解法稳定性研究. 地球物理学报, 43(6): 856-864. |
| [37] | 董良国. 2005. 复杂地表条件下地震波传播数值模拟. 勘探地球物理进展, 28(3): 187-194. |
| [38] | 黄自萍, 张铭, 吴文青等. 2004. 弹性波传播数值模拟的区域分裂法. 地球物理学报, 47(6): 1094-1100. |
| [39] | 邵秀民, 蓝志凌. 1995. 非均匀各向同性弹性介质中地震波传播的数值模拟. 地球物理学报, 38(S1): 39-55. |
| [40] | 杨顶辉. 2002. 双相各向异性介质中弹性波方程的有限元解法及波场模拟. 地球物理学报, 45(4): 575-583. |
| [41] | 周辉, 徐世浙, 刘斌等. 1997. 各向异性介质中波动方程有限元法模拟及其稳定性. 地球物理学报, 40(6): 833-841. |
| [42] | 裴正林. 2004. 任意起伏地表弹性波方程交错网格高阶有限差分法数值模拟. 石油地球物理勘探, 39(6): 629-634. |
 2014, Vol. 57
2014, Vol. 57


