2. 地下信息探测技术与仪器教育部重点实验室和地质过程与矿产资源国家重点实验室, 北京 100083
2. Key Laboratory of Geo-detection of Ministry of Education, Beijing 100083, China
大地电磁测深法(Magnetotelluric sounding, MT)是20世纪50年代初由A.N.Tikhonov和L. Cagnird分别提出的天然电磁场探测方法(Tikhonov,1950; Cagniard,1953),它以天然的平面电磁波为场源,通过在地表观测相互正交的电磁场分量来获取地下电性构造信息.由于天然场中含有从高频到低频丰富的频率成分,而不同频率成分的电磁波具有不同的穿透(趋肤)深度,因而大地电磁法能达到测深的目的(陈乐寿,王光鄂, 1990).由于它具有探测深度大、不受高阻屏蔽的影响、对低阻层反应灵敏等优点,该方法始终为人们所关注和研究.早在20世纪70年代,国内、外就开始了大地电磁测深正、反演的研究工作.近年来,随着计算机技术的迅速发展,大地电磁测深二维正、反演算法的研究已经趋于成熟;二维反演方法已成为大地电磁测深生产与科学研究中主要的反演计算方法.而水平地形条件下大地电磁测深三维正演算法研究的进展,也使三维反演算法日渐趋于实际应用(Avdeev, 2005; Börner, 2010);但是,要真正实现大地电磁测深三维反演的实用化,则必须解决复杂地形条件下大地电磁场的三维正演模拟和反演算法问题.
20世纪80年代以来,尽管国内、外许多学者在起伏地形条件下大地电磁场数值模拟问题上做了大量研究(Wannamaker et al., 1986; 徐世浙等, 1997; 陈伯舫等, 1998; Han et al., 2008),但对于带地形三维数值模拟,尤其是带地形三维反演方法的研究仍然很少,仅有的几种方法也未见公开代码(Ledo, 2005).由此可见,目前大地电磁场数值模拟领域一个亟待解决的问题是如何在大地电磁测深三维正演模拟和反演计算中有效加入复杂地形要素(Siripunvaraporn, 2011).我国地域辽阔,东、西部高程变化大,地形极为复杂,无论是大地电磁测深长剖面观测或是区域性阵列观测都难免跨越多个地形单元;因此,为了提高中国大陆大地电磁测深数据的解释精度,在进行大地电磁测深数据反演时,也同样需要考虑复杂地形的影响;为此,我们也迫切需要研究和发展一种高效的,能够进行带地形要素三维正、反演的大地电磁测深数值模拟软件.
在本项研究中,我们实现了基于交错网格剖分的有限差分算法的大地电磁测深带地形三维正演,以及基于非线性共轭梯度算法的带地形三维反演方法,本文将具体阐述所取得的研究成果.
众所周知,地球物理数值模拟的正演问题是反演方法的基础和前提,反演系统是否准确和有效很大程度上取决于正演方法的准确度和计算效率.对于大地电磁测深三维正演数值模拟算法,前人已经进行了大量的工作,常见的方法有积分方程法(IE)(Ting and Hohmann, 1981; Hohmann, 1983),有限差分法(FD) (Mackie et al., 1994; Smith 1996; Newman and Alumbaugh,1997;谭捍东等,2003), 有限单元法(FE)(Pridmore et al., 1981; Mitsuhata and Uchida, 2004; Nam et al., 2007),边界元法(BE)(徐世浙等, 1997; 阮百尧, 王友学, 2005)等.有限差分法因其具有计算精度和效率较高,不需要专门的网格离散化工具等优点,是目前大地电磁测深正、反演方法采用较多的数值模拟方法.
本研究中使用的正演方法为基于交错网格剖分的有限差分方法(谭捍东等, 2003).在大地电磁测深法研究的频率范围内,通常位移电流的作用可以被忽略.取电磁场的时谐因子为e-iωt,有麦克斯韦方程组的微分形式为
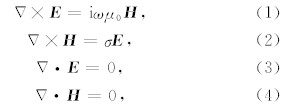
其中μ0是真空磁导率,σ是电导率,而ω为角频率,介质内没有电流源或磁场源.将方程组(2)式代入(1)式中,可以导出仅基于电场与仅基于磁场的麦克斯韦方程分别为
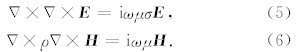
要计算出感兴趣的异常体中的电场 E 或磁场 H ,就需要将上述方程离散化;在有限差分法中,通常把求解模型域划分为若干长方体差分网格,用有 限个网格节点代替连续的模型域.在交错网格方法中,剖分单元中的电场和磁场并不取在网格单元的同一位置,而是取各网格单元边缘中点的电(或磁)场,与各网格面元中心的磁(或电)场相匹配,这样将可以最大限度的保证电磁场分布能够满足能量守恒定律(Mitsuhata and Uchida, 2004).

其中 C 为 E 或 H .假设模型域介质可以离散为 M =Nx×Ny×Nz个长方体网格单元,假设单元体中磁场为沿网格边元平均分布,而电场为沿网格面元均匀分布,如图1a所示,由平面波假设,大地电磁场的电磁波可以分解为相互垂直的线性偏振波的 组合的形式,设每一个网格有x,y,z三个方向的 电场/磁场物理量,单元体的长宽高分别为dx(i)(i=1,2,3,…,Nx),dy(j) (j=1,2,3,…,Ny)和dz(k)(k=1,2,3,…,Nz),单元体的电阻率为ρ=ρ(i,j,k). 对于感应磁场,(1)式的积分形式∮ E ·dl= ∫∫iωμ0 H ·d S 的x,y,z
三方向分量可以按照图1b离散为

 | 图1 交错网格有限差分单元网格离散化示意图 (a) 磁场沿网格边元平均分布,而电场沿网格面元均匀分布; (b) 感生磁场离散化示意图; (c) 感生电场离散化示意图. Fig.1 Discretion of stagger-grid finite element of a unit cell (a) Electric and magnetic field components are assumed to be edge-averaged and face-averaged, respectively; (b) Elementary loop of electrically induced magnetic field; (c) Elementary loop of magnetically induced electric field. |

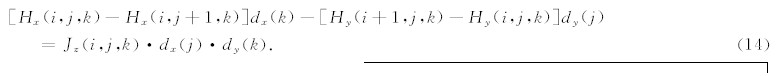
对于给定的频率,消去电场或磁场分量,这一问题就可以转换为求解线性方程组

其中, A 为3M×3M阶大型稀疏矩阵, x 为电/磁场的3M阶未知矢量,而 b 则为边界条件与场源的3M阶矢量;在这里,我们选择消去电场分量,求取磁场分量的线性方程组的解.与水平地面三维正演模拟相同,对于上边界的边界条件,其场值可以直接取采样点所在的源场值;而四个侧边界的边界条件则可以通过二维正演得到,在边界处取与三维介质边界层网格相同的电阻率和网格剖分建立二维模型,并针对不同的极化模式进行二维正演计算,即可得到四个侧边界上边界场值的分布;对于下边界的边界条件,一般可以设下边界以下半空间介质为均匀半空间或者层状介质,通过一维正演来进行计算(Mackie et al., 1994).由于正演问题中大型线性方程组的规模和复杂性,直接求解这一方程组几乎不可能,一般采用迭代计算的方法进行求解(Avdeev, 2005; Siripunvaraporn, 2011);为此,我们使用双共轭梯度(Bi-Conjugate Gradient) 最优化方法对其进行迭代求解(Smith, 1996).在已知磁场的分布后,就可以根据法拉第定律通过式(2)求得电场的分布.
在进行地形的数值模拟时,最重要的问题是如何处理空气与地下介质的关系.而在交错网格有限差分法中,由于要求满足介质渐变假设,空气电导率一般不能设置为零,而是设为一个很小的非零电导率(Nam, et al., 2007).而这样可能会使得系统方程组产生严重的病态(ill-conditioned)(Mackie, et al., 1994; Mitsuhata and Uchida, 2004).当ω→0时,由于方程组(5)或(6)的右侧趋于零,而左侧保持不变,因而这一点在计算低频响应时尤为严重.本研究中,我们采用了散度校正(divergence correction)(Mackie, et al., 1994; Smith, 1996)来对这一问题进行处理.根据库仑规范(Coulumb gauge),在地下介质中,显式地要求散度为零(即不存在场源),对于电势e或磁势h分别有:

而在空气中,由于要求不存在电荷的积累,可以将设电势设为

利用求解出的势场,对电场或磁场进行散度校正:
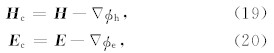
在求解(15)的迭代计算过程中,每隔若干次迭代 进行一次场的散度计算,当散度不能视为零时(>10-10),将使用(19)对磁场进行散度校正.由梯 度的旋度 Δ × Δφ=0,对于磁场的校正,有 Δ × H c= Δ ×( H - Δφ)= Δ × H =σ E ,这表明磁场的散度校正对于电场并无影响.类似的,对于电场我们有 Δ × E c= Δ ×( E - Δφ)= Δ × E =iωμ0 H ,表明电场的散度校正对于磁场同样无影响.
此外,由于大地电磁场源的平面波假设要求离散网格的面元要垂直于波阵面,当使用有限差分法模拟地形时,很难直接模拟倾斜的地形表面;因而,多采用“台阶状”网格逼近地形的起伏变化(如图4c所示).当在地形起伏界面(空气-地面界面)上加大剖分网度,使其剖分足够精细时,大地电磁场有限差分模拟响应将与理论场值相近,甚至趋于一致(陈伯舫等, 1998).
具体计算时,对于构筑起伏地形介面的“台阶状”网格单元顶面的大地电磁场值,假设有自顶部向下第k个网格为空气-地形介面,可以通过直接计算第k个网格的波场来确定;若网格剖分足够精细,可以认为“台阶状”网格单元顶面的大地电磁场值与空间位置的关系近似为线性关系.当测点在网格顶面正中心时,测点磁场值可以简单的取相邻网格磁场的平均值;而当测点不在网格顶面正中心时,可以通过线性插值的方法计算出测点位置的大地电磁场值.由于我们之前假设单元体中磁场为沿网格边元平均分布,而电场为沿网格面元均匀分布,设测点位置为x,y,z,测点所在单元为i,j,k,则对于Hy只需在x方向上进行线性插值:
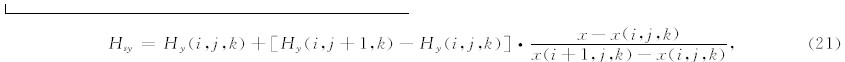
Hx则只需在y方向上进行线性插值:
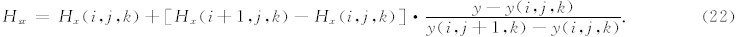
Hz则需要进行x和y方向的双线性插值(注意,这样Hz的变化将不是严格线性的),对于介面所在的第k个网格,有
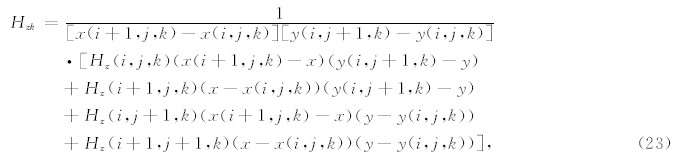
而对于与介面上方临接的网格(k-1),可以类似的得到
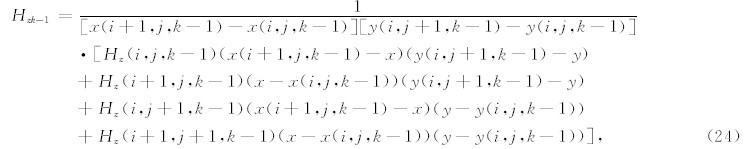
因此在第(i,j)个网格,空气-地下介面处(k和k-1之间)Hz可表示为
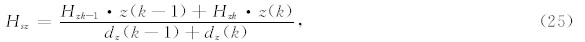
即可由磁场值计算电流密度水平x和y方向的电流为
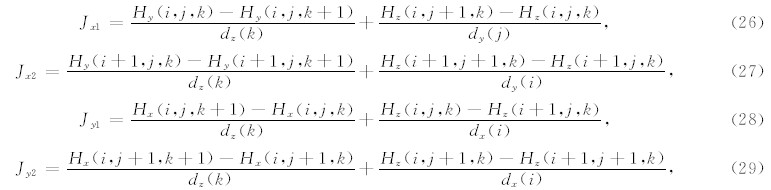
分别对于Jx和Jy做Y和X方向的线性插值,可以得到测点不在网格中心时的水平电流为

再由(12—13)式可得到空气-地下介面处水平方向电场为

对于水平地形的三维电磁数值模拟,由于空气与地下介质的电阻率间断面的存在,再考虑到大地电磁测深的频率范围,一般强制设置Ez=0.而若考虑垂直方向电场Ez对介面处电流密度的影响,不仅垂直方向的电场将不可被忽略,水平磁场也会受到当前网格(i,j)及周边四个网格(i-1,j),(i+1,j),(i,j-1),(i,j+1)的垂直电场的影响发生改变,从而进一步改变水平方向的电场,如图2所示.
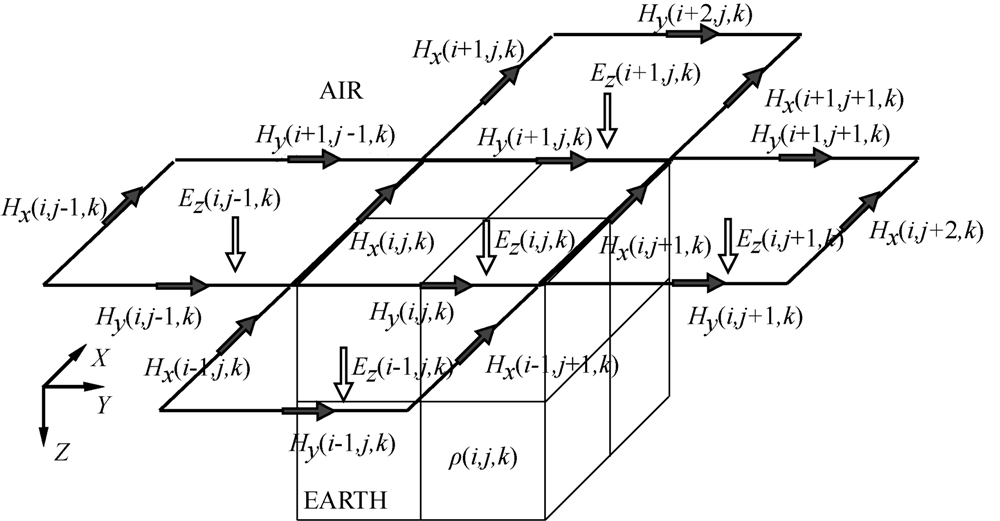 | 图2 交错网格有限差分法空气-地形介面电磁场离散化示意图 Fig.2 Discretionof electromagnetic fields at air-earth interface of stagger-grid finite difference method |
对于第(i,j)网格所在单元,垂直方向的电流密度和电场为
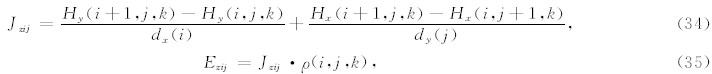
对于第(i-1,j)网格所在单元,有:
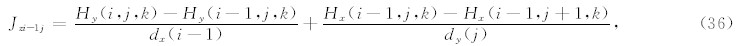

类似的可以求出第(i+1,j)网格,第(i,j-1)网格以及第(i,j+1)网格所在单元的电流密度和电场强度值,垂直电场对x方向磁场的贡献为
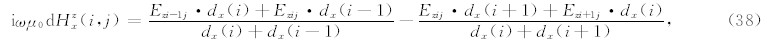
而垂直电场对y方向磁场的贡献为
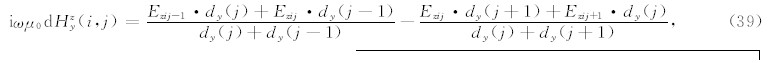
取之前得到的Esx和Hsy的值,有x方向水平电场可以写成
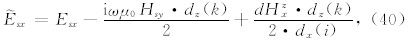
类似由Esy和Hsx的值的可以得到y方向水平电场为
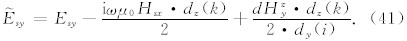
计算出电/磁场值之后,即可继而计算出大地电磁阻抗张量响应(Mackie et al., 1994; 谭捍东等, 2003).设大地电磁场的平面偏振波沿x方向的偏振分量为Hx1,Ex1,Hy1,Ey1,y方向的偏振分量分别为Hx2,Ex2,Hy2,Ey2,则阻抗张量可以由下式进行计算(Mackie et al., 1993):

总体而言,现有的多种反演方法都只是最优化方法的不同表述.水平地面三维大地电磁测深反演方法,包括高斯-牛顿法(GN)(Sasaki, 2001; Haber et al., 2004),共轭梯度高斯-牛顿法(GN-CG) (Mackie et al., 1993; 吴小平,徐果明, 2000; 林昌洪等, 2008), 拟牛顿法(QN)(Avdeev and Avdeeva, 2009),非线性共轭梯度法(NLCG)(Mackie et al., 2001; Newman and Alumbaugh, 2002; 林昌洪等, 2008)以及OCCAM法(Siripunvaraporn et al., 2005)等,其最终目标都是寻找一个“最优”模型,它既可以拟合观测数据,又在地质上最为“现实”.两者都通过寻求各自目标函数的最小化这一过程来实现.其中,NLCG方法因其不必对最优化问题进行线性化,在计算过程中也不需显式的计算与存储Jacobian矩阵,在反演时间和内存的耗费上相对较低,成为近年来大地电磁测深二维和三维反演的主流方法之一.
对于大地电磁测深反演而言,非线性最优化问题的表述可以简单地写为
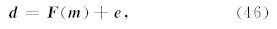
其中 d 表示数据向量,在这里即为实测阻抗张量(Z);而 m 表示模型向量,在这里即为电导率(log10σ); e 为观测误差向量; F 则表示上一节给出的带地形大地电磁场三维正演算子.对于非约束最优化数值模拟问题有目标函数为
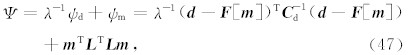
目标函数的第一部分ψd表征数据的拟合情况;第二部分ψm则为模型的一阶或二阶光滑度,其中 C d为控制数据误差的权重的协方差矩阵,λ则是平衡数据拟合和模型光滑度的正则化因子.而对于某个给定的模型 m ,目标函数的导数形式 Δ Ψ可以写为(Newman and Alumbaugh, 2002)
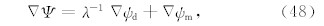
其中,第二部分ψm,即关于模型第k分量的偏导数则可以简单的写为
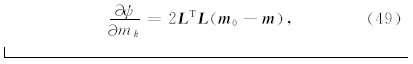
而第一部分ψd,即关于模型第k分量的偏导数为

注意这里计算目标函数的导数 g 不需要显式的计算和存储雅可比矩阵,而只需要其转秩和(加权的)误差分量的乘积 J ( m ) CT -1ed 即可(林昌洪等, 2008).其中 J 为雅可比矩阵,en=Zn- F ( m )为第n个数据误差, ε n为协方差矩阵 C d对于第n个数据的分量,*为复共轭.
对于 Z /mk,具体到 Z 的某个分量(Zxx,Zxy,Zyx,Zyy),根据式(42—45),我们可以得到其相对mk的导数,以Zxy为例,有
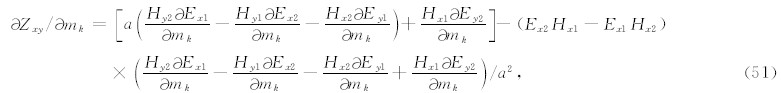
其中a=Hx1Hy2-Hx2Hy1(Newman and Alumbaugh, 2002).注意到式(51)中包含电磁场分量关于模型分量的偏导数,因此要计算 Z /mk还需得到这些偏导数的值.对于给定位置j的测站,有第i个分量的磁场/电场相对于第k个模型分量的偏导数为
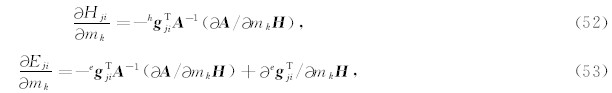
其中A即为式(15)中的线性关系,h g Tji为在给定测点j处的磁场的第i个分量(Hx,Hy)基于该给定磁场 H 的插值向量(interpolation vector),而e g Tji为在给定测点j处的电场的第i个分量(Ex,Ey)基于该给定磁场 H 的插值向量.将式(52—53)代入到式(51)中,可以得到(林昌洪等, 2008)
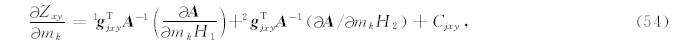
其中:

类似的可以求出 Z xx/mk, Z yx/mk, Z yy/mk的偏导数(Newman and Alumbaugh, 2002),由于篇幅所限,这里不再赘述.于是(50)式即可表示为

设
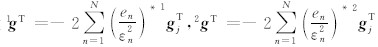
进而如果设

又由 A = A T,我们只需要求解如下线性方程,相当于两次正演计算:

就可以得到1 v 和2 v ,进而得到目标函数的导数 Δ Ψ(Newman and Alumbaugh, 2002).
若由任意给定的模型初始值 m 0开始,第k次迭代的模型的改变量可以由

进行迭代计算,其中 α k为第k次迭代的搜索步长,可以通过线搜索(line search)得到;而 d k为第k次迭代的搜索方向,可以递归的由
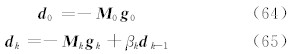
进行计算,其中 g k= Δ F( m k)T,即为函数 f 对于 x k的导数向量.观察 d 0可以发现,对于共轭梯度法,第一次进行最优化搜索的方向就是- g 0,即为函数值下降最快的方向,这一点和所谓最速下降法或梯度法是相同的.式中βk为共轭梯度方向更新因子;而由前人各自发展的不同的因子就确定了一系列不同的共轭梯度方法.在大地电磁数值模拟中,使用较多的是Hestenes and Stiefel(1952)的经典CG方法 βHSk= g Tk+1( g k+1- g k) d Tk( g k+1- g k) (Mackie et al., 1993),或者Polak and Ribiere(1969)的方法βPRk= g Tk M k( g k- g k-1) ( g Tk-1 M k-1- g k-1) (Mackie et al., 2001).在这里,经过对比试验,我们使用了Dai and Yuan的方法 βDYk= g Tk M k( g k) g Tk M k-1( g k- g k-1) 以提高全局收敛性(1999).
对于给定的搜索方向 d k, 我们可以通过线搜索来得到模型搜索步长 α k, 有最优化问题
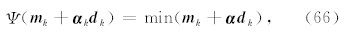
即寻找目标函数在 α k 所在的超平面上的最小值.实际上,这就变成了一个单分量 α k 函数的最优化问 题,对于函数 f ( x + αd ),将其进行泰勒级数分解,有

因此有
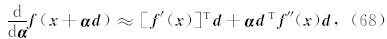
其中 f′ ( x )为梯度矩阵,而 f″ ( x )为海森矩阵(Hessian)(Ypma,1995).为了避免计算海森矩阵,我们将二次导数近似的表示为一次导数在给定的邻域 α =(0,σ)的微分,有
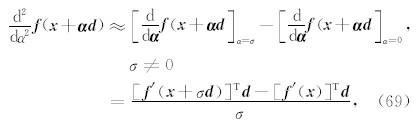
这样,利用泰勒级数展开,有
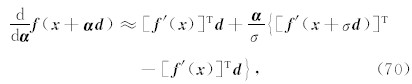
同样的当上式趋于零时, f ( x + αd )达到最小值(Press et al., 1992),这时有:
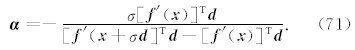
需要注意的是,以上的方法只能分辨出二阶导数为零的情况,而并不能分辨出最大值和最小值(Presset al., 1992).因此,在NLCG方法(或者任意一个依赖于线性搜索的方法)中,初值的选择有时可能会影响收敛速度,甚至出现不收敛(有可能收敛到局部最大而不是最小值)的情况;当搜索不到最小值时,我们将把线性搜索的方向设为- g k, 重置反演线性搜索方向.
一旦计算出了 α k和 d k,下个模型 m k+1 就可以不断的通过(63)式以迭代的方式计算出来,直到模型拟合差达到期望值或者迭代次数超出最大次数为止.对于带地形反演,我们不希望空气层的电阻率随 着反演的进行而发生变化,因此需要锁定地形中空气层所在的电阻率, 为此我们引入模型控制矩阵 C m为
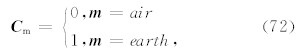
从而(40)式可表示为 m k+1= m k+ C m· α k d k,这样,模型改变量将不会应用到空气层当中.
由于地球物理问题中的线性系统常常是大型稀疏而病态的(Smith, 1996),为改善矩阵条件数(condition number),提高反演的收敛速度,我们引入预条件矩阵 M .对于线性问题 Ax = b ,我们可以通过解

间接的进行计算,如果有COND( M -1)≤COND( A ),我们就可以比原系统更快的收敛到所求解的邻域.对于第k次迭代,对于目标函数(47)式而言,效率最高的 M 自然应该是 A -1=[λ-1( d - F [ m k])]T C d( d - F [ m k])+ L T L ]-1,然而,这样将导致求解 M -1 Ax = M -1 b 和 Ax = b 完全一样而失去了 意义.在 M 的选择上,一种常见的做法是取目标函数的海森矩阵,即二次导数矩阵的近似.然而,由于海森矩阵的计算量过大,Newman等人(2002)提出了仅仅使用海森矩阵的对角元素作为预调节矩阵的方法,而其对角元素可以依靠目标函数的导数和上一次共轭梯度迭代的结果迭代地给出

反演的主要流程如图3所示.
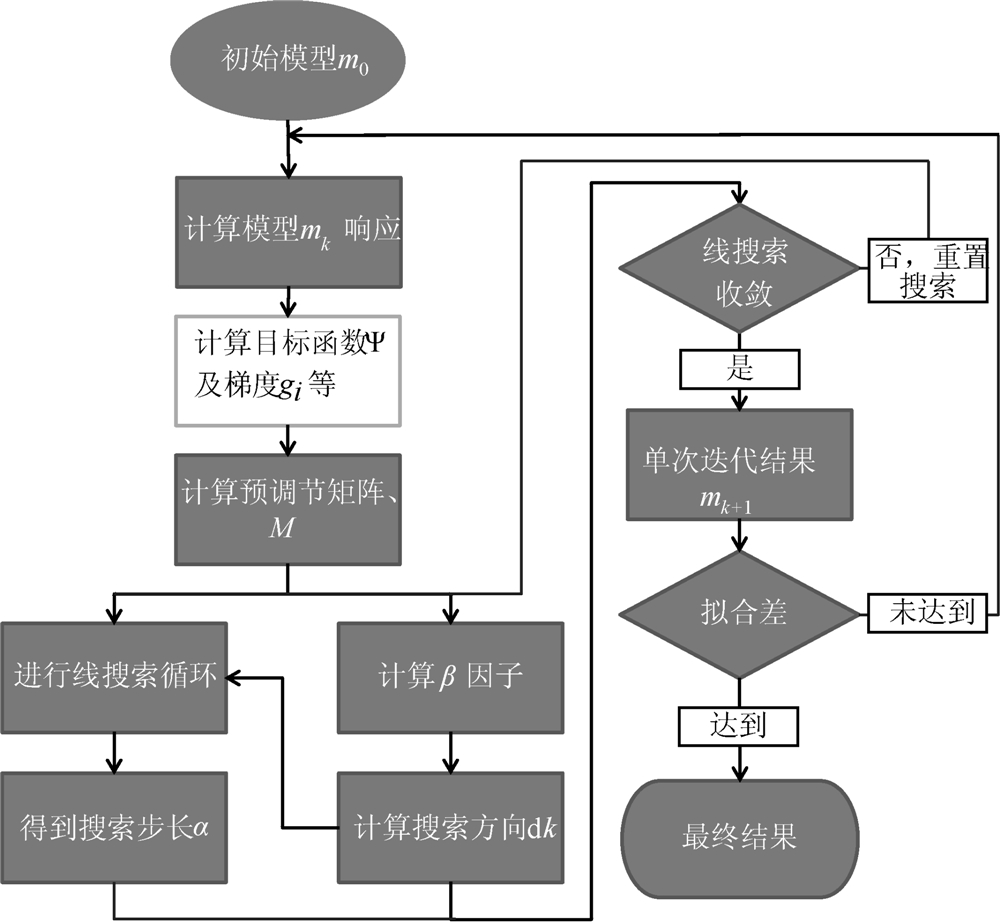 | 图3 非线性共轭梯度法反演流程示意图 Fig.3 Flow chart of NLCG inversion scheme |
为了测试正演代码的有效性与准确性,研究过程中我们把Wannamaker等提出的二维地形经典理论模型(Wannamaker et al., 1986)三维化,并用所开发的带地形有限差分大地电磁场三维正演代码进行纯地形响应的三维模拟计算.
图4所示为三维山峰模型及其有限差分网格离散化情况.模型中,正四棱台状山峰的高度相对于地面为450 m,其上底的边长为450 m,下底的边长为 2000 m.模型离散化为37m×37m×40m的网格.地下围岩的电阻率为100 Ωm,而空气的电阻率被固定为108 Ωm.
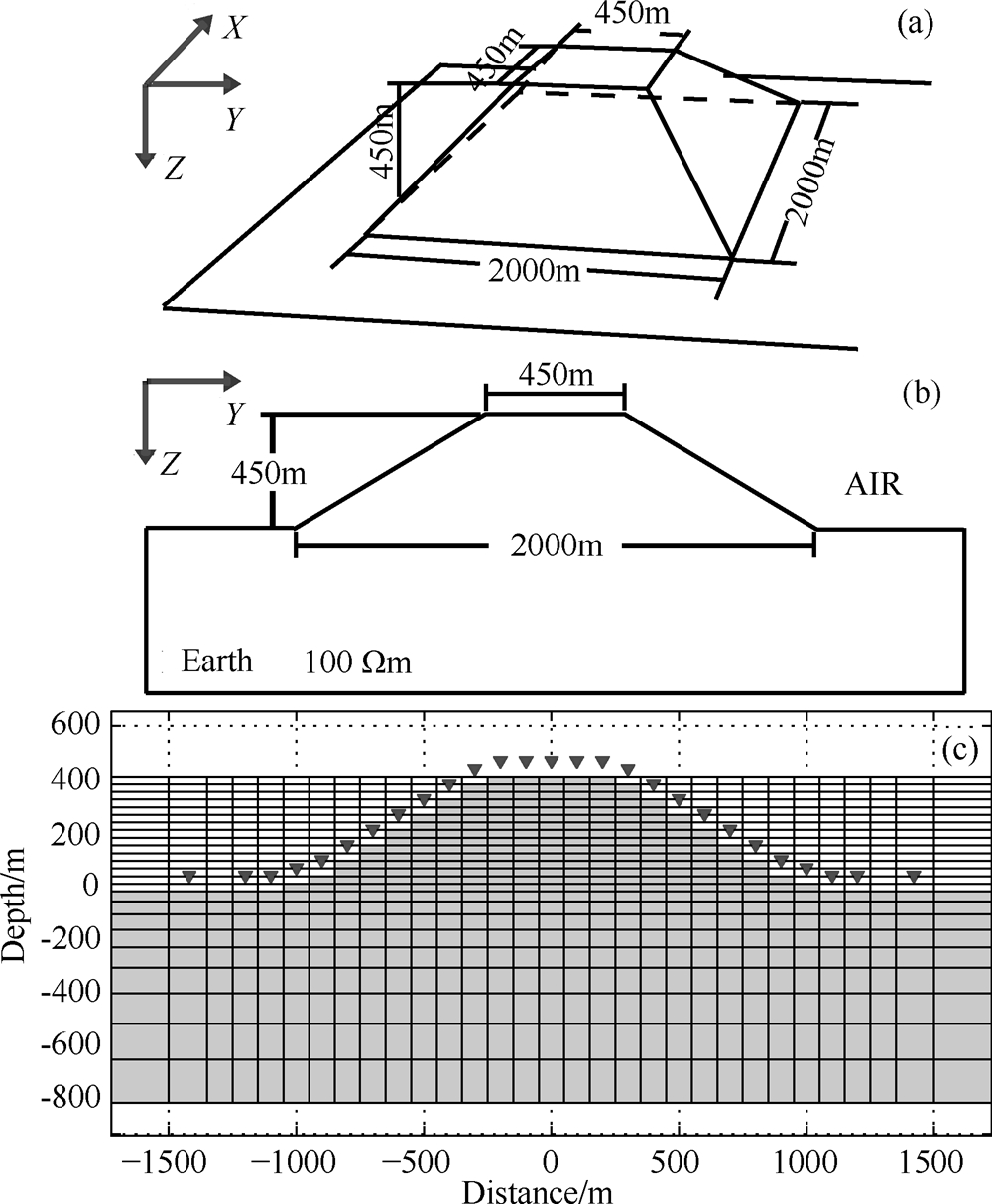 | 图4 四棱台形山峰地形正演模型 (a)正演模型的三维视图; (b)正演模型的 Y-Z方向视图; (c)网格离散化情况. Fig.4 Synthetic model of square frustum hill (a) 3D view of the synthetic model; (b) Y-Z plane view of the synthetic model; (c) Discretization of the synthetic model. |
由于有限单元法的网格剖分较为自由,可以使用不规则的三角/四面体网格模拟倾斜的地形界面,一般认为其对地形的模拟具有较高的计算精度.因此,我们将上述带地形三维有限差分法对纯地形模型的正演响应与前人使用三维有限元方法对同一模型得到的正演响应(Nam, et al., 2007)进行对比;图5所示即为频率为2 Hz时两种数值模拟方法的视电阻率与相位响应的对比图.对于YX极化模式而言,无论视电阻率还是相位的响应,有限差分的结果与有限元的结果几乎没有差别;而对于XY模式,除视电阻率在山峰的底缘有细微的差别之外,其余部分也都吻合的非常好.这表明三维有限差分法在网格剖分较为精细的情况下,其计算结果与有限单元法差别不大,计算结果是可靠的;同时,也证明了我们所开发的大地电磁场带地形三维有限差分法正演代码是正确可靠的.
 | 图5 三维有限元(FE)与三维有限差分(FD)的数值解的视电阻率 与相位对比,其中有限元方法的响应引自Nam等(2007) Fig.5 Comparison of apparent resistivity and phase from 3D Finite difference (FD) and 3D Finite element (FE) solutions at 2 Hz,The FE solutions are given by Nam et al (2007) |
为了测试反演代码的稳定性与有效性,在研究过程中设计了一系列带地形三维导电性结构模型进行正演计算,并在正演响应中加入噪声来模拟实测数据.在此,我们分别使用所开发的带地形三维反演方法和前人的水平地形三维反演方法进行反演,对 比、分析其反演模型.水平地形三维反演方法采用数据空间三维Occam法反演代码WSINV3DMT(Siripunvaraporn, et al., 2005). 一系列对比结果表明,所研发的大地电磁测深带地形三维反演模型能够更准确地反映地下真实的导电性结构特征.
图6a和4c所示为边坡对称的三维峰-谷组合地形下存在产状水平的长方体低阻异常的理论模型,其地形的峰高和谷深相对于地面均为2.5 km,山峰、山谷模型的宽度均为20 km,山峰和山谷地形的下方各设计了一个同样大小、产状水平的长方异常体,其x,y,z方向的尺度分别为10 km,10 km和2 km,异常体均为低阻,其电阻率为20 Ωm,围岩的电阻率为100 Ωm.设MN为横穿地形峰顶和谷底连线的测线,沿测线布设23个测点,在每个测点上 大地电磁测深观测信号的频率范围为100~0.01 Hz, 共截取21个频点.
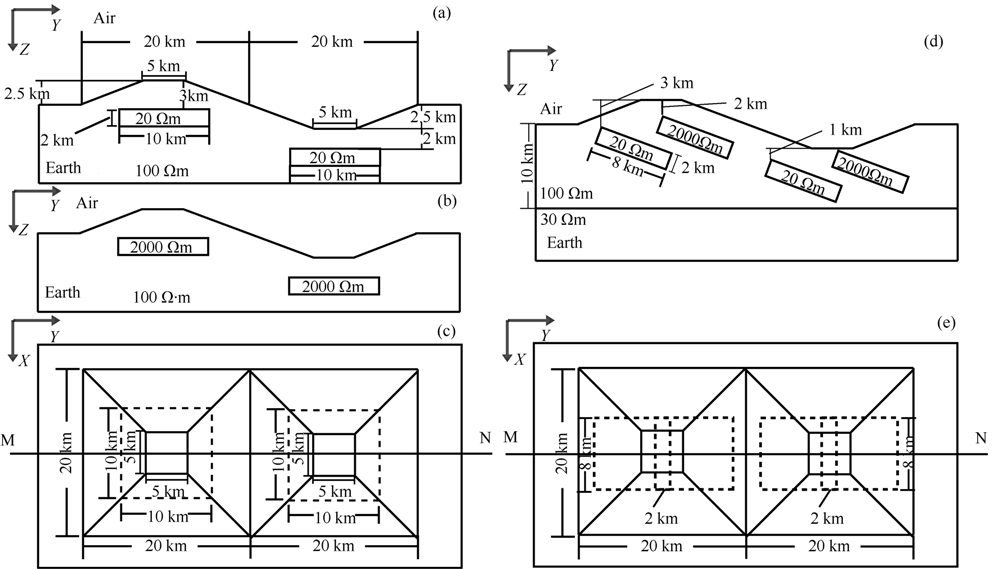 | 图6 边坡对称的三维峰-谷组合地形及异常体位置示意图 (a) 低阻异常模型的Y-Z方向剖面图; (b) 高阻异常模型的Y-Z方向剖面图; (c) 异常模型的X-Y方向的水平视图; (d)高阻-低阻组合异常体模型Y-Z方向剖面图; (e) 高阻-低阻组合异常体模型X-Y方向水平视图. Fig.6 Schematic illustrations of synthetic topography models (a) Y-Z section view of the conductive anomaly model; (b) Y-Z section view of the resistive anomaly model; (c) X-Y plane view of model; (d) Y-Z section view of the combined resistive-conductive model; (e) X-Y plane view of the combined resistive-conductive model. |
对该模型的正演响应数据迭加1%高斯噪声来模拟实测数据,进行反演理论研究.在进行反演时,模型网格的剖分方式、测点位置和频点设置均与正演计算的设计相同.反演运算使用装配2.4 GHz的Intel Core Duo处理器的PC机.计算过程经50次迭代后,反演模型的RMS均方根误差从初始的5.6下降到1.1,耗时为1907分.
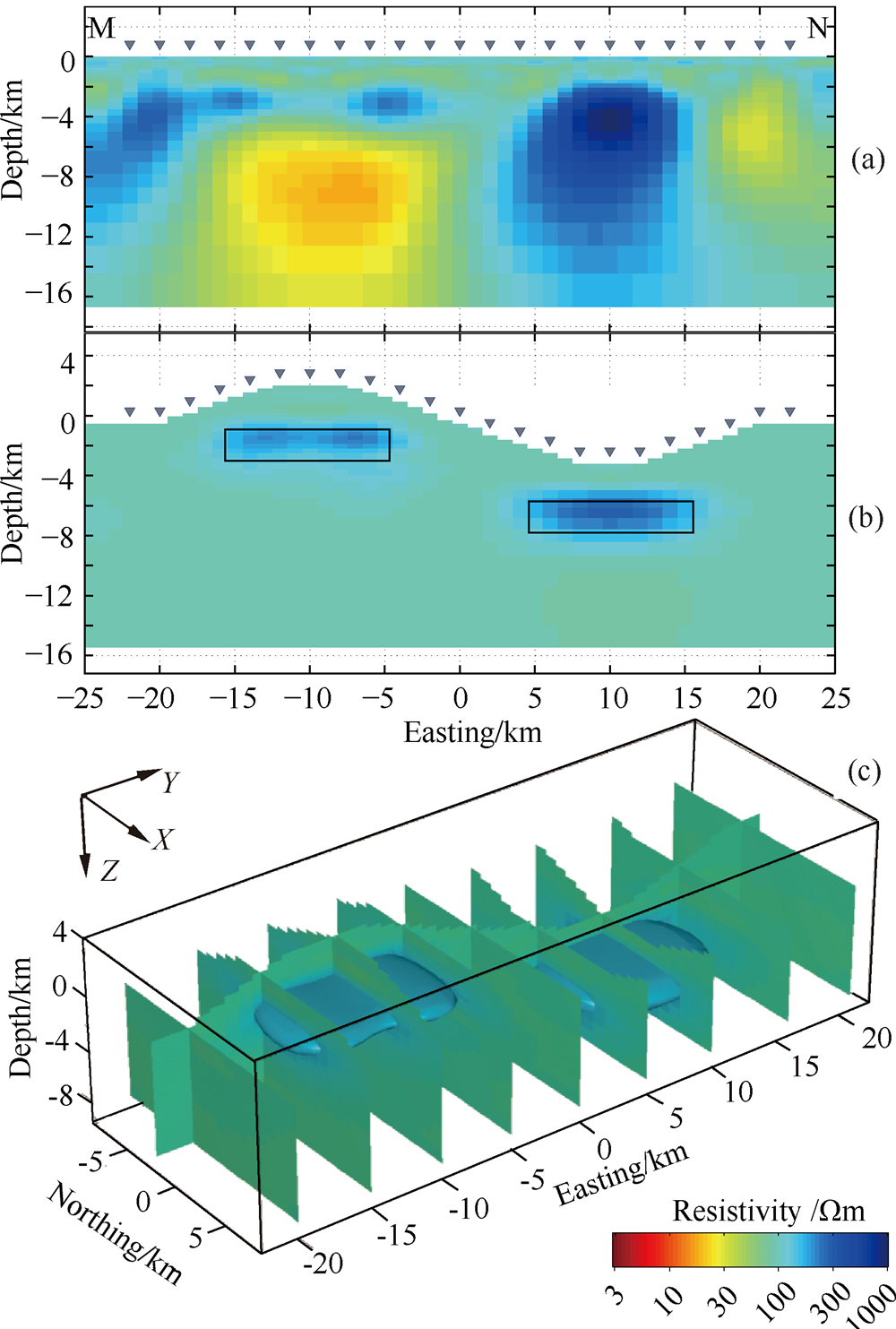
图7所示为边坡对称的三维峰-谷组合地形下低阻异常体三维反演模型沿MN测线的切片.不难看出,采用所研发的大地电磁测深带地形三维反演所获得的三维反演模型的导电性结构特征基本与理论模型结构吻合,异常体周围没有出现冗余的虚假异常(如图7b所示).而使用不带地形三维反演得到的结果,则不如带地形三维反演的结果好(如图7a所示),虽然,其反演模型也能大致反映低阻异常体的轮廓,异常体的埋深也相对准确;但其形状与产状等特征则与理论模型偏差较大.此外,在反演模型中还出现大范围的虚假异常,尤其位于山峰下方的低阻假异常和山谷下方的高阻假异常最为明显;这结果与起伏地形对电阻率法异常特征的畸变规律一致,很容易通过欧姆定律的微分公式对其进行定性分析.
 | 图7 边坡对称的三维峰-谷组合地形下低阻体模型三维反演结果 (a)水平地形三维反演结果沿MN测线的剖面; (b)带地形三维反演结果沿MN测线的剖面,黑色方框标示了异常体在正演模 型中的原始位置; (c)带地形三维反演结果的三维切片与等值面图,其中等值面的电阻率为30 Ωm. Fig.7 Sections of inversion results of synthetic topography data from conductive anomaly model (a) M-N section of result by WSINV3DMT; (b) M-N section of result by inversion with topography. The black box indicate the original location of the anomaly; (c) 3D slices of result by inversion with topography (with iso-surface of 30 Ωm). |
图6b和4c所示为边坡对称的三维峰-谷组合地形下存在产状水平的长方体高阻异常的理论模型,其地形与异常体的几何尺寸与上述低阻模型完全相同,仅仅是异常体的电阻率改为2000 Ωm的高阻.图8所示为边坡对称的三维峰-谷组合地形下高阻异常体反演模型沿MN测线的切片.与低阻体模型的反演结果相似的,对于带地形三维反演而言(如图8b所示),反演结果能较好地反映出高阻异常体模型的空间位置和形态,其周围也无冗余的虚假异常.但是,异常体的边界较为模糊,不如上述的低阻异常体的结果清晰;而且异常体的电阻率与围岩电阻率差异较小.而图8a为不带地形三维反演结果,由图可见,在反演模型中虚假异常的问题很严重,导致反演效果很差,很难反映出理论模型的真实结构.
 | 图8 边坡对称的三维峰-谷组合地形下高阻体模型三维反演结果 (a)水平地形三维反演结果沿MN测线的剖面; (b)带地形三维反演结果沿MN测线的剖面,黑色方框标示了异常体在正演模 型中的原始位置; (c)带地形三维反演结果的三维切片与等值面图,其中等值面的电阻率为200 Ωm. Fig.8 Section of inversion results of synthetic topography data from resistive anomaly model (a) M-N section of result by WSINV3DMT; (b) M-N section of result by inversion with topography. The black box indicate the original location of the anomaly; (c) 3D slices of result by inversion with topography (with iso-surface of 200 Ωm. |
图6d和4e所示边坡对称的三维峰-谷组合地形下存在产状倾斜的高-低阻体组合模型.其地形条件与以上两组模型完全相同.该模型的围岩导电性为两层结构,上层电阻率为100 Ωm,下层为30 Ωm的低阻基底.在上层介质中,山峰和山谷地形的下方各设置了两个相同大小的倾斜板状体,其x,y,z方向的尺度分别为8 km,8 km和2 km,其位置如图所示.图9所示为该模型三维反演结果沿MN测线的剖面结构.与上述模型的反演结果类似,对于带地形三维反演(见图9b所示),反演模型基本能反映出异常体的位置、产状和围岩的二层结构特征,低阻基底的深度也与模型基本吻合.而对于不带地形三维 反演结果(如图9a所示),不但在异常体周围出现了大量的虚假异常,目标体的产状和位置也与正演模型相差较大;低阻基底在山峰地形下方上隆,而在山谷地形下则出现了下凹的趋势.
 | 图9 边坡对称的三维峰-谷组合地形下高-低阻体 组合模型三维反演结果(沿MN测线的剖面) (a)水平地形三维反演结果沿MN测线的剖面; (b)带地形三维反演结果沿MN测线的剖面,黑色方框标示了异常体在正演模 型中的原始位置; (c)带地形三维反演结果的三维切片与等值面图,其中等值面的电阻率为30 Ωm与200 Ωm. Fig.9 Section of inversion results of synthetic topography data from combined resistive-conductive anomaly model (a) M-N section of result by WSINV3DMT; (b) M-N section of result by inversion with topography. The black box indicate the original location of the anomaly; (c) 3D slices of result by inversion with topography (with iso-surface of 30 Ωm and 200 Ωm). |
本项研究实现了基于有限差分法的带地形三维大地电磁测深反演算法,并使用一系列三维理论模型及由正演理论响应分别构筑的模拟实测数据,验证了所研发的带地形三维正、反演算法的准确性和有效性.
文中给出的正演模型中设计的地形条件虽然较为极端,但仍然可以有效的证明在地形起伏较大的情况下,普通水平地形的三维反演方法在处理带地形数据时,虽然也可以得到异常体的主要特征,但其形态与产状都受到了较强的畸变,可能是由于无法模拟地形产生的复杂电性畸变,反演程序对数据进行了过度拟合,从而产生了一系列明显的虚假异常;而带地形三维反演方法可以得到比较接近地下真实导电性结构的反演模型.因此,在地形起伏较大的情况下,应优先使用带地形方法进行大地电磁反演解释;当忽略地形进行反演时,需要依实际情况进行谨慎处理和分析,以免得出不当解释和推断.此外,由 于模型需要模拟地形起伏,而有限差分方法又要求在空气界面处剖分足够精细,这样不可避免的会造成模型网格数出现较大的增加,因此内存耗费以及反演CPU时间增长等问题难以避免,进一步的研 究将考虑采用并行算法以解决内存及计算效率问题.
致谢 笔者在此感谢Weerachai Siripunvaraporn教授提供其三维反演代码WSINV3DMT.并感谢匿名评审专家提出的宝贵意见和建议.| [1] | Avdeev D B. 2005. Three-dimensional electromagnetic modelling and inversion from theory to application. Surveys in Geophysics, 26(6): 767-799. |
| [2] | Avdeev D B, Avdeeva A. 2009. 3D magnetotelluric inversion using a limited-memory quasi-Newton optimization. Geophysics, 74(3), F45-F57. |
| [3] | Börner R U. 2010. Numerical modelling in Geo-Electromagnetics: Advances and challenges. Surveys in Geophysics, 31(2): 225-245. |
| [4] | Cagniard L. 1953. Basic theory of the magnetotelluric method of geophysical prospecting. Geophysics, 18(3): 605-635. |
| [5] | Chen L S, Wang G E. 1990. The Magnetotellurics Method. Beijing: Geological Publishing House: 14-16. |
| [6] | Chen P, Hou Z Z, Fan G H. 1998. Three-dimensional topographic responses in MT using finite difference method. Acta Seismologica Sinica, 11(5): 631-635. |
| [7] | Dai Y H, Yuan Y. 1999. A nonlinear conjugate gradient method with a strong global convergence property. SIAM Journal on Optimization, 10(1): 177-182. |
| [8] | Haber E, Ascher U M, Oldenburg D W. 2004. Inversion of 3D electromagnetic data in frequency and time domain using an inexact all-at-once approach. Geophysics, 69(5): 1216-1228. |
| [9] | Han N, Nam M J, Kim H J, et al. 2008. Efficient three-dimensional inversion of magnetotelluric data using approximate sensitivities. Geophysical Journal International, 175(2): 477-485. |
| [10] | Hestenes M, Stiefel E. 1952. Methods of conjugate gradients for solving linear systems. Journal of Research of the National Bureau of Standards, 49(6): 409-436. |
| [11] | Hohmann G W. 1983. Three-dimensional EM modeling. Surveys in Geophysics, 6(1-2): 27-53. |
| [12] | Ledo J. 2005. 2D versus 3D magnetotelluric data interpretation. Surveys in Geophysics, 26(5): 511-543. |
| [13] | Lin C H, Tan H D, Tong T. 2008. Three-dimensional conjugate gradient inversion of magnetotelluric sounding data. Applied Geophysics, 5(4): 314-321. |
| [14] | Mackie R L, Madden T R, Wannamaker P E. 1993. Three-dimensional magnetotelluric modeling using difference Equations-Theory and comparisons to integral equation solutions. Geophysics, 58(2): 215-226. |
| [15] | Mackie R L, Rodi W, Watts D M. 2001. 3D magnetotelluric inversion for resource exploration. 2001 SEG Annual Meeting, 9-14 September, San Antonio, Texas. |
| [16] | Mackie R L, Smith J T, Madden T R. 1994. Three-dimensional electromagnetic modeling using finite difference equations: The magnetotelluric example. Radio Science, 29(4): 923-935. |
| [17] | Mitsuhata Y, Uchida T. 2004. 3D magnetotelluric modeling using the T-Ω finite-element method. Geophysics, 69(1): 108-119. |
| [18] | Nam M J, Kim H J, Song Y, et al. 2007. 3D magnetotelluric modelling including surface topography. Geophysical Prospecting, 55(2): 277-287. |
| [19] | Newman G, Alumbaugh D L. 2002. Threedimensional magnetotelluric inversion using non-linear conjugate gradients. Geophysical Journal International, 140(2): 410-424. |
| [20] | Newman G A, Alumbaugh D L. 1997. 3D electromagnetic modeling using staggered finite differences. Geoscience and Remote Sensing, 1997. IGARSS'97., 2: 930-932. |
| [21] | Polak E, Ribiere G. 1969. Note sur la convergence de méthodes de directions conjuguées. Revue Franaise d'informatique et de Recherche Operationnelle, 3(1): 35-43. |
| [22] | Press W H, Flannery B P, Teukolsky S A, et al. 1992. Secant Method, False Position Method, and Ridders' Method. In Numerical Recipes in FORTRAN: The Art of Scientific Computing. Cambridge, England: Cambridge University Press: 347-352. |
| [23] | Pridmore D F, Hohmann W H, Ward S H, et al. 1981. An investigation of finite-element modeling for electrical and electromagnetic data in three dimensions. Geophysics, 46(7): 1009-1024. |
| [24] | Ruan B Y, Wang Y X. 2005. A boundary element modeling method for the electromagnetic field by artificial source in frequency domain with 3-D topography. Chinese Journal of Geophysics, 48(5): 1197-1204. |
| [25] | Sasaki Y. 2001. Full 3-D inversion of electromagnetic data on PC. Journal of Applied Geophysics, 46(1): 45-54. |
| [26] | Siripunvaraporn W. 2011. Three-Dimensional magnetotelluric inversion: An introductory guide for developers and users. Surveys in Geophysics, 33(1): 5-27. |
| [27] | Siripunvaraporn W. 2005. Three-dimensional magnetotelluric inversion: data-space method. Physics of the Earth and Planetary Interiors, 150(1-3): 3-14. |
| [28] | Smith J T. 1996. Conservative modeling of 3-D electromagnetic fields, Part II: Biconjugate gradient solution and an accelerator. Geophysics, 61(5): 1319-1324. |
| [29] | Tan H D, Yu X F, Booker J, et al. 2003. Magnetotelluric three-dimensional modeling using the staggered-grid finite difference method. Chinese Journal of Geophysics, 46(3): 705-711. |
| [30] | Tikhonov A N. 1950. On determining electrical characteristics of the deep layers of the earth's crust. Doklady, 73(2): 295-297. |
| [31] | Ting S C, Hohmann G W. 1981. Integral equation modelling of three-dimensional response. Geophysics, 46(2): 182-197. |
| [32] | Wannamaker P E, Stodt J A, Rijo L. 1986. Two-dimensional topographic responses in magnetotellurics modeled using finite elements. Geophysics, 51(11): 2131-2144. |
| [33] | Wu X P, Xu G M. 2000. Study on 3-d resistivity inversion using conjugate gradient method. Chinese Journal of Geophysics, 43(3): 420-427. |
| [34] | Xu S Z, Ruan B Y, Zhou H, et al. 1997. Numerical modeling of 3-D terrain effect on MT field. Science in China Series D: Earth Sciences (in Chinese), 40(3): 269-275. |
| [35] | Ypma T J. 1995. Historical development of the Newton-Raphson method. SIAM Review, 37(4): 531-551. |
| [36] | 陈乐寿, 王光鄂. 1990. 大地电磁测深法. 北京: 地质出版社, 14-16. |
| [37] | 陈伯舫, 侯作中, 范国华. 1998. 三维大地电磁有限差分法的地形响应. 地震学报, 11(5): 631-635. |
| [38] | 林昌洪, 谭捍东, 佟拓. 2008. 大地电磁全信息资料三维共轭梯度反演研究. 应用地球物理, 5(4): 314-321. |
| [39] | 阮百尧, 王有学. 2005.三维地形频率域人工源电磁场的边界元模拟方法. 地球物理学报, 48(5): 1197-1204. |
| [40] | 谭捍东, 余钦范, Booker J等. 2003. 大地电磁法三维交错采样有限差分数值模拟. 地球物理学报, 46(3): 705-711. |
| [41] | 吴小平, 徐果明. 2000. 利用共轭梯度法的电阻率三维反演研究. 地球物理学报, 43(3): 420-427. |
| [42] | 徐世浙, 阮百尧, 周辉等. 1997. 大地电磁场三维地形影响的数值模拟. 中国科学(D辑):地球科学, 40(3): 269-275. |
 2014, Vol. 57
2014, Vol. 57

