2014, Vol. 57
数值求解波动方程是计算地球物理领域的重要研究内容，一种好的数值算法能够提供精确的正演波场、具有高的计算效率和小的计算机存储量需求，有助于我们更准确地认识地震传播规律和反演成像.20世纪以来，人们已发展了许多的正演数值模 拟方法.如有限差分法(Kelly et al., 1976; Dablain, 1986; 董良国等, 2000)，有限元法(Chen, 1984)，伪谱法(Komatitsch and Vilotte, 1998)等.但是，由于我们采用的是数值近似计算，所以当数值求解波动方程时会带来数值频散.所谓数值频散实际上是一种伪波动，不仅没有实际意义，而且还会影响到对真正波动现象的认识.所以，在数值计算中，我们应该消除这种非物理振荡的数值频散.本文就其中重要的数值计算方法：RKDG方法(Cockburn and Shu, 1989, 1998, 2001)、近似解析离散化方法(Yang et al, 2003, 2006)、Lax-Wendroff 修正方法(Dablain, 1986) 以及交错网格方法(Virieux, 1984, 1986; Moczo et al., 2000)的数值频散进行比较研究，以期发现这些方法的数值频散规律和它们的优缺点，以便为使用这些方法进行正、反演计算时提供参考，并为未来的数值方法发展提出新的建议.Lax-Wendroff 修正方法以及交错网格方法是比较流行的数值模拟方法，近似解析离散化方法是Yang等近年来提出的一种新的波场模拟方法，而间断有限元方法则是首先在计算流体力学领域发展起来的一种数值方法.在下面我们将针对这几种方法的优缺点作一简单回顾.
有限差分方法因其编程简易、同等网格点条件下存储量小、计算速度快等优点，在地球物理领域得 到广泛应用.传统的有限差分方法例如Lax-Wendroff correction方法(简称LWC方法)和交错网格方法是地球物理学中被广泛使用的数值方法.它们除了具有上述优点外，还易扩展到高阶精度，而且计算稳定性好.但是它们有严重的缺陷，即在粗网格情况下会产生假波，引起严重的数值频散(Fei and Larner, 1995; Zheng et al., 2006).
Yang等在2003年率先将一种近似解析离散化算子(Kondoh et al., 1994)引入到波动方程的数值求解中.该方法是基于截断的泰勒展式来构造空间局部插值函数，由相邻网格点之间的连接联系，通过该点与邻近点的位移及其梯度的线性组合来逼近该点的高阶空间偏导数.由于高阶偏导数的计算表达式中包含了位移及梯度信息，由此我们可以期望能够获得更为精确的波场模拟结果，因为：波场的重要信息主要包含于位移及其梯度中.而且，该方法由于仅使用该点及邻近点的位移和梯度信息，所以其离散算子具有高度局部化的性质，这有利于大规模并行计算和人为边界处理.基于这种思想已发展了一 系列方法，例如ONAD(Yang et al., 2006)，INADM (Yang et al., 2007)，WNADM(王磊等，2009), NSPRK(Ma et al., 2011; 马啸等, 2010)法等.本文将使用Yang等在2006年提出的ONAD方法与其他方法进行对比研究.事实上，Yang等在其文中已对这种方法的数值频散进行了分析，我们看到该方法确实有很好的压制数值频散的效果.
间断有限元方法最早是由Reed and Hill(1973) 在求解中子输运方程时提出，经过几十年的发展，已发展了多种多样的间断有限元方法(Cockburn and Shu, 1989, 1998, 2001; Arnold et al., 2002; Käser and Dumbser, 2006; Dumbser and Käser, 2006; Hesthaven and Warburton, 2008)，其中以Cockburn & Shu 提出的求解双曲守恒方程的龙格-库塔间断有限元方法(Runge-Kutta discontinuous Galerkin method，简称RKDG方法)尤其引人注目.RKDG是一种基于通量形式的间断有限元方法.它具有如下优点：易处理复杂边界和边值问题；可以很好地捕捉间断；易于提高精度(这从方法本身的构造可以看出)，即只要选取足够多的基函数即可实现提高精度；在RKDG方法中，由于单元基函数在单元交界处允许出现间断，于是我们实际上是在每一个单元上处理一个自由度很小的问题，这样避免了全局求解大规模线性方程组，而且由于只需要相邻单元的信息，这有利于并行算法的实现.在Hu等(1999)的工作中，已针对求解二维声波方程的基于迎风数值通量和中心数值通量的RKDG方法进行了半离散化的频散分析，但其分析并未包括时间离散所引起的数值频散.本文将基于另一种广泛被使用且编程简单，易于处理复杂通量的局部 Lax-Friedrichs数值通量(Cockburn and Shu, 1989, 1998, 2001)，对时间和空间全离散的RKDG方法进行数值频散分析且作比较研究.
考虑二维无源标量声波方程：
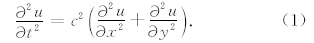
设求解区域为Ω，我们将区域Ω划分为不重叠 的子区域{Ωi}.间断有限元的试验函数空间是 Vh={v ∈ L1(Ω):v|Ωi ∈ Pk(Ωi)}，其中Pk(Ωi)表示区域Ωi上次数不超过k次的多项式.试验函数不必在整个区域上连续，可以在子区域{Ωi}之间有间断，这也是间断有限元与传统有限元最大的区别.本文中提到的RKDG方法均指不带限制器的RKDG方法.
引入两个变量p和q，p和q满足条件pt=ux，qt=uy，则方程(1)可以改写为：utt=c2(ptx+qty)=〖c2(px+qy)〗t，即ut=c2(px+qy).于是将方程(1)改写成如下形式：
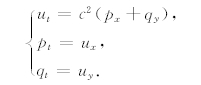
即
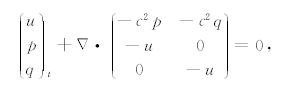
其中 Δ =(∂x,∂y).那么我们就将二维声波方程化成了适于用RKDG求解的双曲守恒形式：
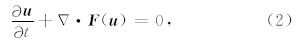
其中，
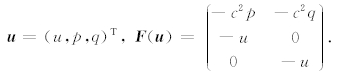
在(2)式两边同乘以试验函数v，并在Ωi上积分，利用格林公式，得到：
∂Ωi表示区域Ωi的边界， n 表示边界∂Ωi处的单位外法向量.由于 u 在∂Ωi处不一定是连续的，所以 (3)式中的 F ( u )· n 没有定义，因此需将通量 F ( u )· n 替换为数值通量：
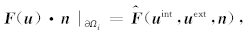其中 u int表示 u 在区域Ωi内部逼近∂Ωi处的值， u ext表示 u 在区域Ωi外部逼近∂Ωi处的值.这里采用一种 常用通量，即局部Lax-Friedrichs通量，其表达式为：
其中C∂Ωi取 ∂F/∂u( u int)· n 和 ∂F/∂u( u ext)· n 的绝对值最大的特征值.由于我们考虑的是线性问题，可像Hu(1999)的工作一样，不妨将通量 F ( u )写成 F ( u )=( A 1 u , A 2 u )的形式，其中
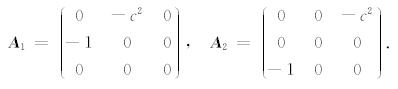
由此可将数值通量 F ( u int, u ext, n )写成下列形式：
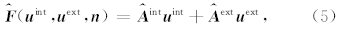
其中，
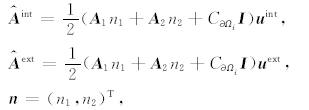
I 表示单位矩阵.将 u 与v限制在试验函数空间Vh，则可得到如下公式：
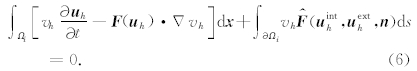
在下面，我们将区域划分为一致均匀的规则矩形Enm=[xn,xn+1]×[ym,ym+1](图1)，且令δx=xn+1－xn，δy=ym+1－ym.图1中L1、L2、L3及L4表示Enm的四条边界.令向量形式的 u h具有以下形式(Hu et al., 1999)：
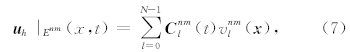
其中(7)式中的上标nm代表所属单元Enm，vnml( x )表示Enm内的基函数，在本文中采用Cockburn和Shu(1989, 1998, 2001)使用的有序完全(order complete)的基于一维Legendre多项式的基函数，N表示单元Enm内的基函数总的个数.当空间精度为2阶时，N的值是3，我们简称该方法为2阶RKDG方法；空间精度为3阶时，N的值是6，我们简称该方法为3阶RKDG方法. C nml(t)表示 u h在Enm内投影到基函数vnml( x )上的系数向量.
将(7)和(5)式代入(6)式中，可以得到如下方程：
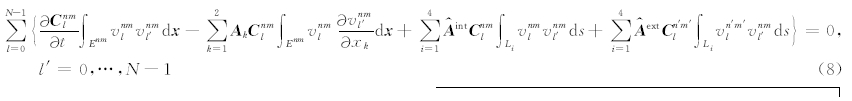
其中n′m′与Li相对应，n′对应L1、L2、L3及L4分别为n+1、n、n-1及n，m′对应L1、L2、L3及L4分别为m、m+1、m及m-1(图1).
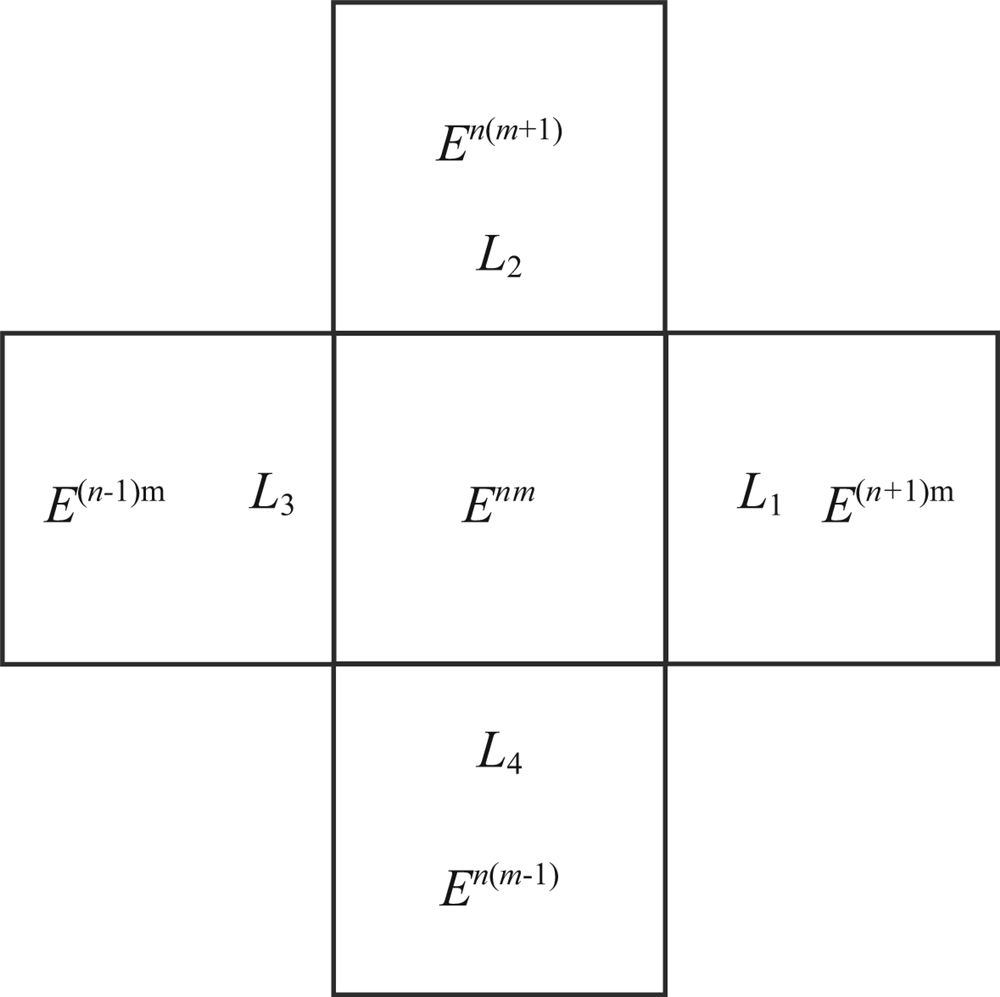 | 图1 单元Enm及其相邻单元，以及与相邻单元相交的边界示意图 Fig.1 Schematic diagram of finite element Enm, neighboring elements and boundaries |
令 C nm(t)=( C nm0(t), C nm1(t),…, C nmN－1(t))T，那么(8)式可以写成以下形式：
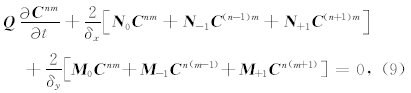
其中 Q 、 N 0以及 N -1等矩阵的表达式详见附录A.
为了应用求解常微分方程的基本思想和数值方法，我们将方程(9)写成一般的常微分方程形式： d u h/dt =L( u h).关于时间方向的离散我们采用3阶总变差不增的Runge-Kutta离散化方法(简称TVD-Runge-Kutta 时间离散方法)(Cockburn and Shu,1989,1998,2001)，其计算公式如下：
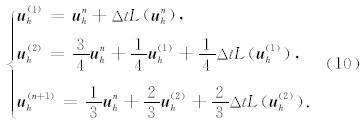
我们采用Von Neumann的分析方法进行数值频散分析.为此，假设一个平面波传播经过有限元区域，假定此区域是均匀、无界区域，方程右端无源项，另外，我们还假设有限元网格是周期矩形， 矩形的边平行于坐标轴，这些假设在有限元频散分析中是通常的假设(如：Hu et al., 1999; Cohen, 2002; Ainsworth et al., 2006; De Basabe and Sen, 2007; De Basabe et al., 2008).
将谐波解 C nm(t)= C (t)exp[i(kcosθnδx+ksinθmδy)] 代入(9)式，可以得到：
为了方便表述，将该式写为：
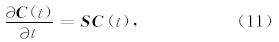
其中
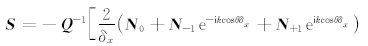
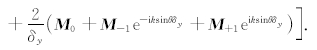
根据(11)式以及3阶TVD-Runge-Kutta时间离散格式，得到：
其中 I 是单位矩阵，(I +Δt S + 1/2 Δt2 S 2+ 1/6 Δt3 S 3 )是关于波传播入射角θ和波数k以及网格步长δx和δy有关的矩阵.
再令 C n= C 0e-iωnΔt，并将其代入(12)式，可得如下关系式：
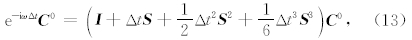
令Λ为矩阵(I +Δt S + 1/2 Δt2 S 2+ 1/6 Δt3 S 3 )的特征值，由(13)式可以推出e-iωΔt=Λ.其中ω=ωr+iωi，其实部ωr表示ω中与频散有关的量，虚部ωi表示ω中与耗散有关的量.由于在这里， 我们主要考查频散情况，所以想要获得ωr的表达式.令Λ=Λr+iΛi，其中Λr表示Λ的实部，Λi表示Λ的虚部，
则根 据e-iωΔt=Λ，可求得ωr的表达式ωrΔt=arctan(－ Λi/Λr). 若令δx=δy=h，则可以得到数值速度与真实速度 的比值为：R= ωrΔt/αkh ，其中α=c Δt/h 为库朗数.若定义采样率：Sp=h/λ，则有关系式：Sp= kh/2π .于是R= ωrΔt/α2πSp .根据|Λ|≤1可获得RKDG方法的稳定性条件，例如，空间精度为2阶的RKDG方法需满足c Δt/h ≤0.32，空间精度为3阶的RKDG方法需满足c Δt/h ≤0.16.可以看出，RKDG方法的稳定性条件限制比较严格.
在本节，我们将对比研究几种重要方法：2阶 RKDG方法、3阶RKDG方法、ONAD方法、4阶LWC 方法、8阶LWC方法以及4阶SG方法的数值频散，以期获得对这几种重要方法数值频散的规律性认识.为此，选取Courant数α=0.16，根据2节以及 附录A，B中给出的公式分别计算各种方法的数值频散 (R)随采样率Sp和波传播方向θ之间的变化规律.
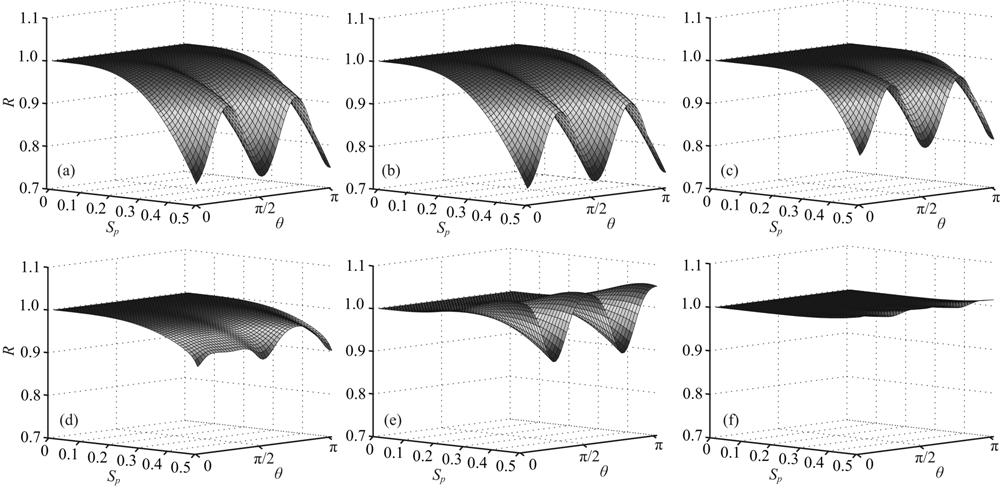 | 图2 几种不同方法的数值频散R随采样率Sp和波传播方向θ变化的比较 (a) 4阶SG方法；(b) 4阶LWC方法；(c) 8阶LWC方法；(d) ONAD方法；(e) 2阶RKDG方法；(f) 3阶RKDG方法. Fig.2 Comparison of numerical dispersion R changing with different propagation direction θ and different sampling rate Sp for different methods (a) Fourth-order SG method; (b) Fourth-order LWC method; (c) Eighth-order LWC method; (d) ONAD method; (e) Second-order RKDG method; (f) Third-order RKDG method. |
从图2可以看到，随着采样率Sp增大，R偏离1越大，即数值频散越严重.由于Sp=kh/2π，当震源确定后，波数k即给定，随着Sp增大(即h增大)，数值频散越严重.但是不同方法的数值频散是不一样的，从图2可以看出,3阶RKDG方法、2阶RKDG方法和ONAD方法的数值频散显著小于其他方法.例如，在库朗数α=0.16的条件下，3阶RKDG方法、2阶RKDG方法和ONAD方法的最大数值频散误差分别为：1.67%、9.73%、9.78%，而8阶LWC、4阶SG方法、4阶LWC方法的数值频散最大误差分别为18.70%、25.29%、26.38%.而在数值频散较小的前三种方法中，3阶RKDG方法的数值频散为最小.通过图2和图3还可以看出数值频散随传播角度的变化规律.图中除了ONAD方 法，其他方法的数值频散在[0°,90°]和[90°,180°]具有对称性.4阶SG、4阶LWC以及 8阶LWC方法的数值频散误差在传播方向θ=0°时最大，并随着θ的增大而减小，在θ=45°的时候取最小值.对于ONAD方法，数值频散在θ=0°的时候最大，但是最小值出现在θ≈135°，而对于3阶RKDG方法，从图3b可以看出，最小的数值频散误差是在45°的方向取得，但是最大的数值频散误差却不是在0°方向. 同时，还可以看出，在α=0.16的情况下，3阶RKDG 方法的数值速度大于真实波速c，而ONAD方法、8阶LWC、4阶SG方法以及4阶LWC方法的数值速度均大于c，但是2阶RKDG方法计算的数值速度随着传播角度θ的不同，有时小于真实速度，有时大于真实速度.
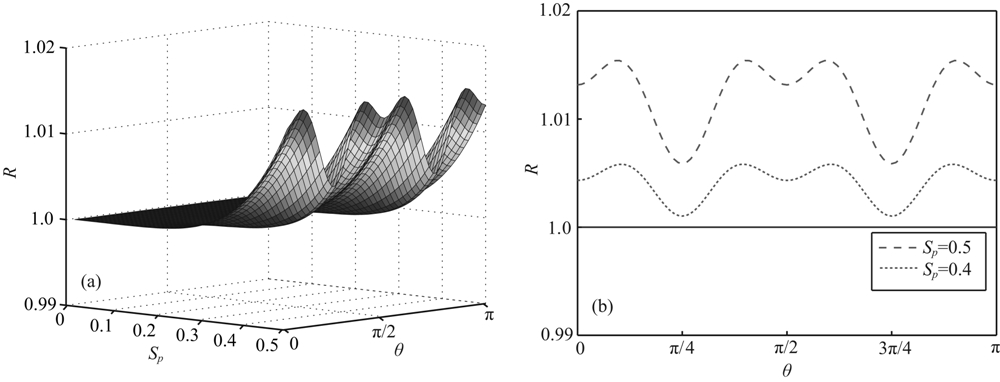 | 图3 (a)是3阶RKDG方法的数值频散R随采样率Sp和波传播方向θ变化的情况(此图对应图2f的放大图)， (b)是在给定采样率为0.5和0.4的情况下，3阶RKDG方法的数值频散R随波传播方向θ的变化 Fig.3 (a) Numerical dispersion R for different propagation directions (θ) and different sampling rates (Sp) for the third- order RKDG method, which is the clearer version of Fig.2f; (b)Numerical dispersion R for different propagation directions θ for the third-order RKDG method with sampling rate Sp=0.5 and Sp=0.4, respectively |
为了更全面地对比这几种数值方法的数值频散，我们将这几种方法在不同库朗数条件下的最大数值频散误差列于表1.从表1也可以得出和上述分析类似的结论.另一方面，从表1可看出，随着库朗数的增大，ONAD方法的数值频散误差有所减小，这有利于ONAD方法的进一步加速.换言之，如果取较大库朗数的话，可进一步加快ONAD方法的计算速度(因为从稳定性条件可知，可进一步选取更大的时间步长).
|
表1 不同库朗数条件下不同数值方法的最大数值频散误差(%) Table 1 Maximum numerical dispersive errors of different numerical methods for different Courant numbers (%) |
为进一步说明前述各种方法的优缺点，我们对均匀各向同性介质模型进行波场模拟并分析其效率.考虑到精度要求，将3阶RKDG方法、4阶LWC 方法、4阶SG方法、4阶ONAD方法以及8阶LWC 方法进行效率比较.为此，就RKDG方法来说，选取如下二维声波方程：
方程(14)中所选Ricker子波随时间变化的函数如下：
在我们的数值实验中选取频率f0=30 Hz.为了一致性，针对其他差分方法，选取声波方程的形式为：
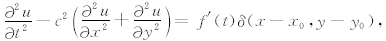
其中f′(t)是f(t)关于时间的导数.
在这个数值实验中，选取波速c=4 km/s，库朗数α=cΔt/Δx≈0.16，计算区域为0≤x,y≤12 km，震源位于区域中心，波传播时间为T=1.2 s.由于RKDG方法的稳定性条件限制非常严格，所以比较的时候对3阶RKDG方法，选取其最大库朗数0.16，而对于其他差分方法，均取库朗数为0.4进行比较.
 | 图4 粗网格(Δx=Δy=60 m)条件下T=1.2 s时刻的波场瞬时快照 (a)4阶SG方法；(b)4阶LWC方法；(c)8阶LWC方法；(d)ONAD方法；(e) 3阶RKDG方法. Fig.4 Snapshots of acoustic wave fields at time T=1.2 s on the coarse grid (Δx=Δy=60 m) Generated by the (a) fourth-order SG method, (b) fourth-order LWC method, (c) eighth-order LWC method, (d) ONAD method, and (e) third-order RKDG method. |
图4给出了粗网格(Δx=Δy=60 m)情况下不同数值方法所模拟的波场快照比较.从图4中可以看出，3阶RKDG方法(e)具有最小的数值频散.4阶SG方法(a)、4阶LWC方法(b)与8阶LWC方法(c)均具有严重的数值频散， ONAD方法(d)也有少量数值频散.显然3阶RKDG方法给出了最好的波场结果.
为了比较在消除数值频散情况下不同方法的计算效率和存储需求量，我们分别将4阶SG方法、4阶LWC方法、8阶LWC方法和4阶ONAD方法进行网格加密.图5给出了在消除可见数值频散条件下上述四种方法计算到T=1.2 s时刻的波场快照.比较图5与图4e，可以看到它们均无可见数值 频散.但是产生这些快照的CPU时间和存储量是 不一样的.表2给出了在Intel ○ R CorTM2 Quad CPU 2.66 GHz、 4 G内存的计算机环境下，得到这些图形所花费的计算时间和存储量.
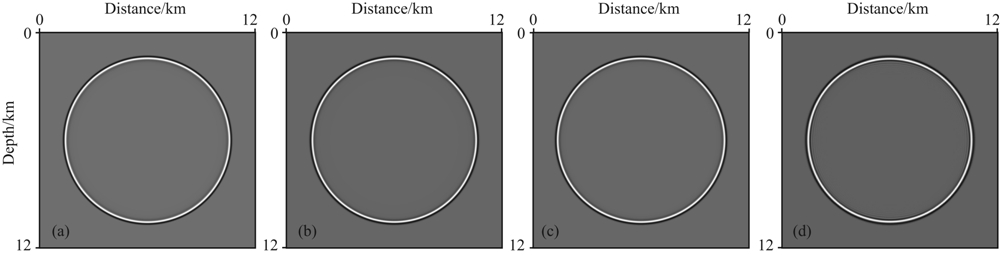 | 图5 无可见数值频散条件下T=1.2 s时刻的波场快照 (a)4阶SG方法(Δx=Δy=15 m)；(b)4阶LWC方法(Δx=Δy=15 m)； (c)8阶LWC方法(Δx=Δy=20 m)；(d)ONAD方法(Δx=Δy=40 m). Fig.5 Snapshots of acoustic wave fields at time T=1.2 s Generated by the (a) fourth-order SG method (Δx=Δy=15 m), (b) fourth-order LWC method (Δx=Δy=15 m), (c) eighth-order LWC method (Δx=Δy=20 m), and (d) ONAD method (Δx=Δy=40 m), respectively. |
从表2可以看出，在同样无可见频散的情况下，ONAD方法所用的计算时间是最短的，为58 s，而3阶RKDG方法所用的计算时间最长，大约是ONAD 方法的77倍.从存储量的角度分析，ONAD方法所用的存储量也最小，约为最大存储量(4阶SG方法与4阶LWC方法)的25%.另外，从表2的比较可得出，虽然3阶RKDG方法在粗网格下能很好地压制数值频散，但是其CPU计算时间非常大，所需存储量也较大，这不利于大尺度波场模拟、基于波动方程的地震偏移和波形反演成像.这说明，若是采用一致网格剖分计算区域，则DG方法的计算效率将很低.因此，为了提高DG方法的计算效率，应该发展多尺度、非一致网格的DG算法.例如，在地质结构复杂区或者速度变化较大的研究区，可采用细网格的DG方法，而在速度变化缓慢或者是均匀介质区 域，可以采用粗网格DG算法或其他数值频散低的差分方法(如：ONADM方法(Yang et al., 2006)).
|
|
表2 不同数值方法的计算CPU计时和存储量比较 Table 2 Comparison of CPU time and computer memory for different numerical methods |
为进一步说明我们对RKDG方法及前述各种方法在压制数值频散方面所得之结论，在本节选取两种不同的介质模型进行波场模拟.
在这个双层模型实验中，主要考查RKDG方法在间断处压制数值频散方面的效果.其中上、下层介质中的波速分别为2 km/s和5 km/s，下、上层速度之比为2.5，选取库朗数α=cΔt/Δx≈0.16，计算区域0≤x,y≤4 km，间断面位于z方向区域中心，接收器位于间断面上方0.2 km处，震源位于接收器上方0.2 km处，接收器与震源的x坐标均为x= 2 km，具体可见图6.震源函数与前面(15)式一致，其中f0=35 Hz.图7给出了在20 m×20 m正方形网格单元情况下采用3阶RKDG方法计算所得的波形记录和波场快照.从图7可以看出， 3阶RKDG方法给出了非常清晰的波场结果，在间断处几乎不会产生数值频散.
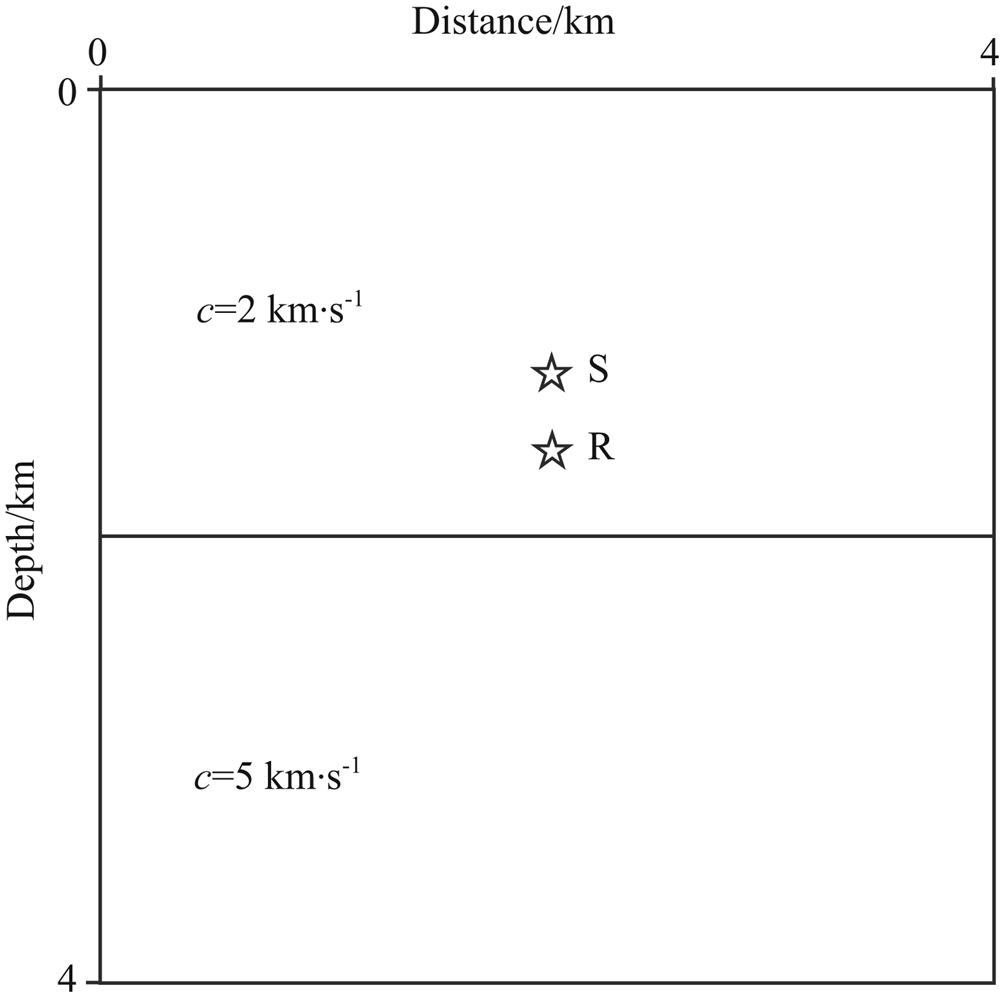 | 图6 双层介质模型，在深度z=2 km处有一强间断 震源S位于z=1.6 km处，接收点R位于z=1.8 km处. Fig.6 Two-layer medium model with a strong discontinuity at depth of z=2 km The explosive source denoted by S is located at z=1.6 km, while the receiver R is located at z=1.8 km. |
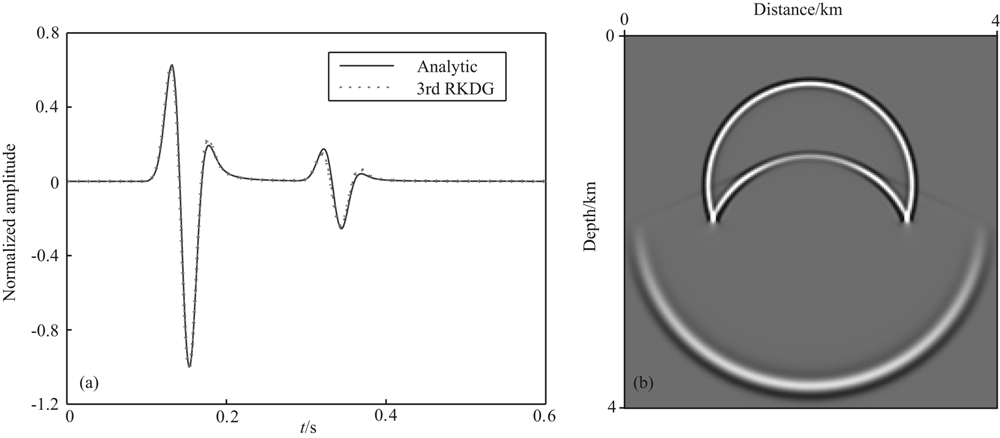 | 图7 对于双层介质模型，3阶RKDG方法在空间步长Δx=Δy=20 m，T=0.6 s 时刻的(a)波形记录(其中实线为解析解，虚线为数值解)和(b)波场快照 Fig.7 Waveforms (a) (where the solid line denotes the analytic solution and the dotted line denotes the numerical solution) and the snapshot of seismic wave fields (b) on the grid Δx=Δy=20 m, at time T=0.6 s, generated by the third-order RKDG method for the two-layer medium model |
在这个例子中，我们选取Marmousi速度模型 (Versteeg & Grau, 1991)以测试3阶RKDG方法在非均匀复杂介质情况下的计算效果.Marmousi模型有很强的非均匀性，其速度变化范围是1500~ 5500 m/s，如图8所示.实验中，选取网格单元为24 m×24 m 的正方形网格单元，网格数为384×122.频率为f0=25 Hz的点震源位于(4608 m，12 m)处，震源函数详见(15)式.模拟中取库朗数为α=cΔt/Δx≈0.16.图9给出了不同时刻的波场快照，并无可见的数值频散.这说明RKDG方法可以有效模拟复杂介质中的声波场.
 | 图8 Marmousi速度模型 Fig.8 Marmousi model |
 | 图9 对于Marmousi模型，利用3阶RKDG方法模拟声波所得到的不同时刻的波场快照 (a) T=0.6 s; (b) T=0.9 s; (c) T=1.2 s. Fig.9 Snapshots at different times generated by the third-order RKDG method for the Marmousi model |
本文从理论推导和数值计算，以及波场模拟的角度，深入细致地研究了Runge-Kutta间断有限元方法的数值频散，并与其他方法(如ONAD方法，高阶LWC方法和交错网格(SG)方法)进行了比较.结果表明：2阶和3阶RKDG方法、ONAD方法比其 他方法具有更强的压制数值频散的能力，考虑到精 度的要求，3阶RKDG方法和ONAD方法比2阶RKDG方法要好；如果从计算速度、压制频散能力和稳定性等综合角度考虑，ONAD方法是最好的一种方法，因为其计算速度和稳定性都比RKDG方法更快和更强；但如果从网格剖分的灵活性和压制数值频散的角度考虑，RKDG方法具有明显的优越性.然而由于RKDG方法的计算量和存储量均较其他方法大很多，因此，如何加快RKDG方法的计算速度、减小存储量需求，是间断有限元方法未来发展所面临的巨大挑战，若能解决这些问题，那么间断有限元方法将具有巨大应用前景.这就是说，为提高计算效率，对于复杂地质结构的波场模拟，应该发展多尺度、非一致网格的数值模拟方法，以克服一致网格DG方法计算量和存储需求量大的缺点.例如，可以将DG方法与ONADM方法相互交替使用，或对RKDG方法进行分区域使用粗网格和细网格相结合的算法，等等，这些都是我们今后提高DG方法计算和存储效率需要研究的问题.
我们给出(9)式中的矩阵具体的表达式(Hu, 1999).
假设在参考单元E=[－1,1]×[－1,1]上的基函数为{vl(x,y)|l=0,1,…,N－1}，(11)式中的矩阵表达式为：
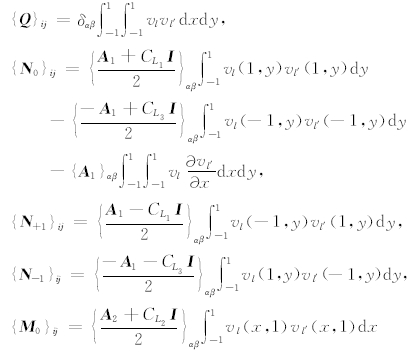
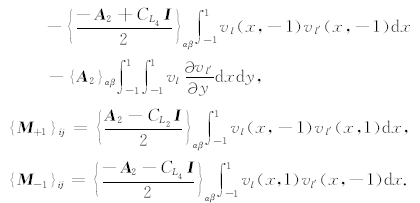
其中：
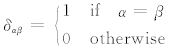
i=ml′+α, j=ml+β;α,β=0,1,…,m－1;l′,l=0,1,…,N－1. N为单元上基函数的个数，m为 u 中未知量的个数.
为求解声波方程， Yang等提出的优化近似解析离散化方法(ONAD)具有如下基本的时间推进计算公式：
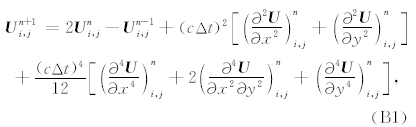
其中方程(B1)右端各高阶导数计算公式可由外推方法获得.
对于上述格式(B1)，我们应用Von Neumann的分析方法进行频散分析.ONAD的频散分析过程如下：
考虑(B1)式的简谐波解：
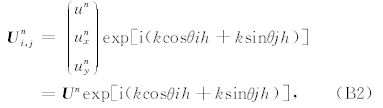
其中h为空间步长.将(B2)式代入(B1)式，可以得到： U n+1=2 U n－ U n－1+ HU n, (B3) H 是3×3矩阵，元素的具体表达式较复杂，这里仅给出(1,1)元素的表达式：
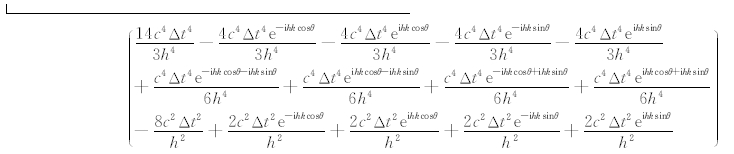再令 U n= U 0e－iωnΔt并代入(B3)式，可得
(e－iωΔt－2+eiωΔt) U 0= HU 0.
不妨设ΛH为矩阵 H 的特征值，由上述方程可得2(cosωΔt－1)=ΛH，即ωΔt=arcsin 1+ ΛH/2 .由此可以得到数值速度与真实速度的比值为： R= ωΔt/αkh .
高阶LWC方法(Dablain, 1986)已成为计算地球物理领域一种流行的差分方法.对于二维声波方程(1)，该方法的具体表达式为：
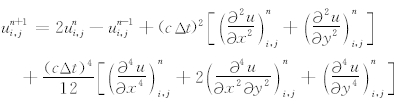
其中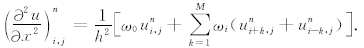
M=2,3,4分别表示精度为O(Δt4,Δx4),O(Δt4,Δx6),O(Δt4,Δx8)的格式.关于此格式的数 值频散分析， 可类似地应用前述分析方法，这里 给 出4阶LWC的数值频散的表达式(Yang et al., 2010)：
R= cnum/c = arccos(1+α2e1/6+α4e2/72)/2παSp ,
其中：
e1=－30+16d1－d2,
e2=152－125d1+20d2－d3+64f1,1－2f1,2, dn=cos(2πnSpcosθ)+cos(2πnSpsinθ),n=1,2,3 fm,n=cos(2πmSpcosθ)+cos(2πnSpsinθ),m=1,2.SG交错方法最初由Virieux(1984，1986)提出，最初针对速度应力方程，后来推广到位移应力方程.其中Moczo(2000)的文中给出了详细的格式说明与频散分析.我们将格式列出如下：
对于二维声波方程：∂2u/∂t2 =c2 (∂2u/∂x2 + ∂2u/∂y2) ，令τ= ∂u/∂x ，η=∂u/∂y .则4阶SG方法的格式为：
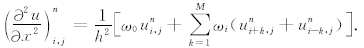其中u定义在整网格点(i,j)上，τ定义在整网格点(i+1/2,j)上，η定义在整网格点(i,j+1/2)上，a=－1/24，b=9/8.
关于格式(B4)的频散分析，不在这里详细推导了，具体过程可见Moczo等人的工作，这里仅给出频散结果表达式：
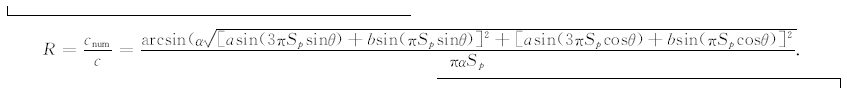
| [1] | Arnold D N, Brezzi F, Cockburn B, et al. 2002. Unified analysis of Discontinuous Galerkin Methods for elliptic problems. SIAM Journal on Numerical Analysis, 39(5): 1749-1779, doi: 10.1137/S0036142901384162. |
| [2] | Chen K H. 1984. Propagating numerical model of elastic wave in anisotropic in homogeneous media-finite element method. The 54th SEG Annual meeting Expanded Abstracts, 631-632. |
| [3] | Cohen G C. 2002. Higher-order Numerical Methods for Transient Wave Equations. Springer. |
| [4] | Cockburn B, Shu C W. 1989. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws II: General framework. Mathematics of Computation, 52(186): 411-435. |
| [5] | Cockburn B, Shu C W. 1998. The Runge-Kutta discontinuous Galerkin method for conservation laws V: Multidimensional systems. Journal of Computational Physics, 141(2): 199-224, doi: 10.1006/jcph.1998.5892. |
| [6] | Cockburn B, Shu C W. 2001. Runge-Kutta discontinuous Galerkin methods for Convection-Dominated problems. Journal of Scientific Computing, 16(3): 173-261, doi: 10.1023/ A:1012873910884. |
| [7] | Dablain M A. 1986. The application of high-order differencing to scalar wave equation. Geophysics, 51(1): 54-66, doi: 10.1190/1.1442040. |
| [8] | De Basabe J D, Sen M K. 2007. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations. Geophysics, 72(6): T81-T95, doi: 10.1190/1.2785046. |
| [9] | De Basabe J D, Sen M K, Wheeler M F. 2008. The interior penalty discontinuous Galerkin method for elastic wave propagation: Grid dispersion. Geophysical Journal International, 175(1): 83-93, doi: 10.1111/j.1365-246X.2008.03915.x. |
| [10] | Dong L G, Ma Z T, Cao J Z, et al. 2000. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese J. Geophys. (in Chinese), 43(3): 411-419. |
| [11] | Dumbser M, Käser M. 2006. An arbitrary high order discontinuous Galerkin method for elastic waves on unstructured meshes—II: The three-dimensional case. Geophysical Journal International, 167(1): 319-336, doi: 10.1111/j.1365-246X.2006.03120.x. |
| [12] | Fei T, Larner K. 1995. Elimination of numerical dispersion in finite difference modeling and migration by flux-corrected transport. Geophysics, 60: 1830-1842, doi: 10.1190/1.1443915. |
| [13] | Hesthaven J S, Warburton T. 2008. Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications. Springer. |
| [14] | Hu F Q, Hussaini M Y, Rasitarinera P. 1999. An analysis of the discontinuous Galerkin method for wave propagation problems. Journal of Computational Physics, 151(2): 921-946, doi: 10.1006/jcph.1999.6227. |
| [15] | Käser M, Dumbser M. 2006. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes—I: The two-dimensional isotropic case with external source terms. Geophysical Journal International, 166(2): 855-877, doi: 10.1111/j.1365-246X.2006.03051.x. |
| [16] | Kelly K R, Wave R W, Treitel S, et al. 1976. Synthetic seismograms: a finite-difference approach. Geophysics, 41(1): 2-27, doi: 10.1190/1.1440605. |
| [17] | Komatitsch D, Vilotte J P. 1998. The spectral element method: an efficient tool to simulate the seismic responses of 2D and 3D geological structures. Bulletin of the Seismological Society of America, 88(2): 368-392. |
| [18] | Kondoh Y, Hosaka Y, Ishii K. 1994. Kernel optimum nearly-analytical discretization algorithm applied to parabolic and hyperbolic equations. Computers & Mathematics with Applications, 27(3): 59-90, doi: 10.1016/0898-1221(94)90047-7. |
| [19] | Ma X, Yang D H, Liu F Q. 2011. A nearly analytic symplectically partitioned Runge-Kutta method for 2-D seismic wave equations. Geophysical Journal International, 187(1): 480-496, doi: 10.1111/j.1365-246X.2011.05158.x. |
| [20] | Ma X, Yang D H, Zhang J H. 2010. Symplectic partitioned Runge-Kutta method for solving the acoustic wave equation. Chinese J. Geophys. (in Chinese), 53(8): 1993-2003, doi: 10.3969/j.issn.0001-5733.2010.08.026. |
| [21] | Moczo P, Kristek J, Halada L. 2000. 3D 4th-order staggered-grid finite-difference schemes: stability and grid dispersion. Bulletin of the Seismological Society of America, 2000, 90(3): 587-603, doi: 10.1785/0119990119. |
| [22] | Reed W H, Hill T R. 1973. Triangular mesh methods for the neutron transport equation. Los Alamos Scientific Laboratory Report. LA-UR-73-479. |
| [23] | Versteeg R J, Grau G. 1991. The Marmousi Experience. Proc. EAGE Workshop on Practical Aspects of Seismic Data Inversion, Eur. Assoc. Explor. Geophysicists, Zeist. |
| [24] | Virieux J. 1984. SH-wave propagation in heterogeneous media: velocity-stress finite-difference method. Geophysics, 49(11): 1933-1957, doi: 10.1190/1.1441605. |
| [25] | Virieux J. 1986. P-SV wave propagation in heterogeneous media: velocity-stress finite-difference method. Geophysics, 51(4): 889-901, doi: 10.1190/1.1442147. |
| [26] | Wang L, Yang D H, Deng X Y. 2009. A WNAD method for seismic stress-field modeling in heterogeneous media. Chinese J. Geophys. (in Chinese), 52(6): 1526-1535, doi: 10.3969/j.issn.0001-5733.2009.06.014. |
| [27] | Yang D H, Peng J M, Lu M, et al. 2006. Optimal nearly-analytic discrete approximation to the scalar wave equation. Bulletin of the Seismological Society of America, 96(3): 1114-1130, doi: 10.1785/0120050080. |
| [28] | Yang D H, Song G J, Chen S, et al. 2007. An improved nearly analytical discrete method: an efficient tool to simulate the seismic response of 2-D porous structures. Journal of Geophysics and Engineering, 4(1): 40-52, doi: 10.1088/1742-2132/4/1/006. |
| [29] | Yang D H, Song G J, Hua B L, et al. 2010. Simulation of acoustic wavefields in heterogeneous media: A robust method for automatic suppression of numerical dispersion. Geophysics, 75(3): T99-T110, doi: 10.1190/1.3428483. |
| [30] | Yang D H, Teng J W, Zhang Z J, et al. 2003. A nearly-analytic discrete method for acoustic and elastic wave equations in anisotropic media. Bulletin of the Seismological Society of America, 93(2): 882-890, doi: 10.1785/0120020125. |
| [31] | Zheng H S, Zhang Z J, Liu E. 2006. Non-linear seismic wave propagation in anisotropic media using flux-corrected transport technique. Geophysical Journal International, 165(3): 943-956, doi: 10.1111/j.1365-246X.2006.02966.x. |
| [32] | 董良国, 马在田, 曹景忠等. 2000. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报, 43(3): 411-419. |
| [33] | 马啸, 杨顶辉, 张锦华. 2010. 求解声波方程的辛可分Runge-Kutta方法. 地球物理学报, 53(8): 1993-2003, 10.3969/j.issn.0001-5733.2010.08.026. |
| [34] | 王磊, 杨顶辉, 邓小英. 2009. 非均匀介质中地震波应力场的WNAD方法及其数值模拟. 地球物理学报, 52(6):1526-1535, doi: 10.3969/j.issn.0001-5733.2009.06.014. |