地球物理学报  2014, Vol. 57 Issue (2): 345-353   PDF    
引用本文
姚宜斌, 汤俊, 张良, 何畅勇, 张顺. 电离层三维层析成像的自适应联合迭代重构算法. 地球物理学报,2014,57(2): 345-353   
YAO Yi-Bin, TANG Jun, ZHANG Liang, HE Chang-Yong, ZHANG Shun. An adaptive simultaneous iteration reconstruction technique for three-dimensional ionospheric tomography. Chinese J. Geophys. (in Chinese),2014,57(2): 345-353
电离层三维层析成像的自适应联合迭代重构算法
姚宜斌1,2, 汤俊1, 张良1, 何畅勇1, 张顺1    
1. 武汉大学测绘学院, 武汉 430079;
2. 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉 430079
投稿时间:2013-10-17    最后修改时间: 2014-1-6 .
基金项目：国家自然科学基金面上项目（41174012，41274022）、国家高技术研究发展计划（863计划）项目（2013AA122502）和教育部新世纪优秀人才支持计划项目（NCET-12-0428）联合资助.
第一作者简介：姚宜斌，男，1976年生，教授，主要从事GNSS空间环境学及数据处理理论方法等研究.E-mail：ybyao@whu.edu.cn
摘要：在电离层层析成像过程中，联合迭代重构算法是一种常用的反演算法.然而，该算法迭代收敛较慢，反演结果精度不高.为此，本文发展了一种自适应的联合迭代重构算法，该算法利用上一轮的电离层电子密度反演结果，自适应地调整松弛因子和加权参数.通过模拟数据和实测数据对该算法的反演结果进行了验证，并将得到的反演结果与电离层测高仪数据进行了比较，结果表明，该算法能够有效地反演电离层电子密度，且反演结果精度优于常用的联合迭代重构算法.
关键词： 电离层层析成像     电子密度     总电子含量     联合迭代重构算法    
An adaptive simultaneous iteration reconstruction technique for three-dimensional ionospheric tomography
YAO Yi-Bin1,2, TANG Jun1, ZHANG Liang1, HE Chang-Yong1, ZHANG Shun1    
1. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
Abstract: The three-dimensional reconstruction of a tilt series for ionospheric tomography is commonly carried out using one of iterative algorithms such as the simultaneous iteration reconstruction technique (SIRT). This reconstruction algorithm cannot do the high computation efficiency and reconstruction accuracy is low. Here, we develop an adaptive simultaneous iteration reconstruction technique for ionospheric tomography, which is based on an adaptive adjustment method for the relaxation factor and weighted parameter by the reconstruction results of the previous iterative ionospheric electron density. Using a combination of simulation and real datasets for the experiment and comparing with ionosonde observations, it is shown that this new algorithm ASIRT has a better reconstruction quality than the SIRT. Moreover, it is able to accelerate the reconstruction speed.
Key words: Computerized ionospheric tomography     Ionospheric electron density     Total electron content     Simultaneous iteration reconstruction technique    

1 引言

电离层是日地空间环境的一个重要组成部分，与人类的高新技术和日常生活息息相关. 为了深入研究电离层电子密度时空分布的精细结构，Austen等(1986, 1988)首次提出了电离层层析 成像(Computerized Ionospheric Tomography, CIT) 技术的设想.随后，国际上利用该技术相继开展了许多实验和理论研究(Pryse, 2003; Raymund et al., 1990; Raymund， 1994; Rius et al., 1997; Spencer et al., 1998).顾及电离层层析成像过程中投影视角的有限性和测站布设的稀疏性，电离层层析成像中需要解决的核心问题是由于观测数据的缺失而引起的不适定问题，近年来，许多学者通过引入电离层电子密度的先验信息，来克服反演过程中的不适定性，由此出现了各种不同的反演算法(Arikan et al., 2007; Chartier et al., 2012; Hobiger et al., 2008; Lee and Kamalabadi, 2009; Li et al., 2012; Liu et al., 2010; Ma et al., 2005; Nesterov and Kunitsyn, 2011; Wen et al, 2007, 2008).其中， 联合迭代重构算法(Simultaneous Iteration Reconstruction Technique, SIRT)由于计算简便且易于实现，在电离层层析成像中得到广泛应用.Pryse 和Kersley (1992)最早将联合迭代重构算法应用于电离层层析成像；Hobiger等(2008)利用先验约束的联合迭代重构算法反演电离层电子密度，并与常用的联合迭代重构算法进行对比，发现其迭代收敛速度和反演结果精度均有所提高；Liu等(2010)针对边缘缺少约束的问题，提出了改进的先验约束联合迭代重构算法，并对其优越性进行了验证；Nesterov和 Kunitsyn (2011)提出了基于正则化的联合迭代重构算法，分别利用全球和区域的数据验证了该方法的有效性.这些算法都有效的反演了电离层电子密度，并能够反映电离层电子密度的时空特性变化规律，然而，由于在每轮迭代过程中，松弛因子和加权参数固定不变，从而使得电离层电子密度反演过程中迭代收敛较慢，反演结果精度不高.

针对上述问题，本文发展了一种自适应的联合 迭代算法(Adaptive Simultaneous Iteration Reconstruction Technique, ASIRT)，并通过模拟数据和实测数据实验来验证该方法的有效性和优越性.

2 电离层层析成像原理

电离层层析成像就是根据反演区域内的一系列卫星信号传播路径上的TEC信息来反演所选定区域内电离层电子密度的时空分布.如图1所示，在利用卫星信号观测进行的电离层层析成像过程中，所获得的电离层电子总含量(Total Electron Content, TEC)是电离层电子密度沿卫星至接收机射线路径上的积分(Liu, 2004; 邹玉华, 2003)，可表示为

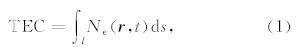
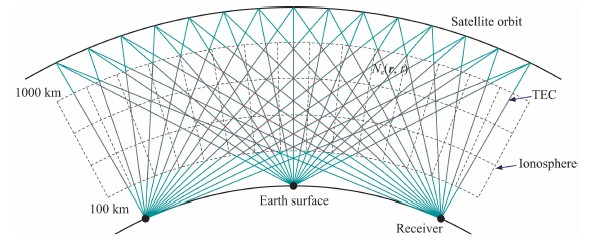图1 电离层层析几何分布示意图 Fig.1 Schematic diagram of the computation domain of IED tomography
式中，Ne为电离层电子密度，l为卫星信号传播路径，r为t时刻经度、纬度和高度所组成的位置向量.电离层电子密度与电离层TEC之间是非线性的.在实际反演过程中，为了反演方便，通常采用离散的反演方法将待反演的电离层空间离散化.对于离散化的像素基层析反演模型，选取像素指标函数bj作为基函数，如果射线穿过某像素，则bj为1，否则为0；并将电离层按经度、纬度以及高度方向上离散化为三维的格网，其公式表示为

式中，n为离散化的格网数(总的像素数)，xj(j=1,…,n)为模型参数(离散化后的电离层格网电子密度).那么对每条射线路径上的TEC测量值可以表示为

式中，m为电离层TEC观测值总数，aij为投影矩阵元素，即第i条射线在第j个格网内的截距.考虑到测量中观测噪声和离散误差的影响，且假定在一定时间段格网内电子密度是不变的，则每条射线传播路径上的电离层TEC测量数据可表示为

将(5)式用矩阵形式表示如下：

式中， y 为电离层TEC观测值组成的m维列向量， A 为投影矩阵(射线在对应像素内的截距构成的m个n维的行向量，由于可视卫星数有限，其通常是一个稀疏矩阵)， x 为未知参数组成的n维列向量， e 为观测噪声和离散误差组成的m维列向量.

3 自适应联合迭代重构算法
3.1 算法原理

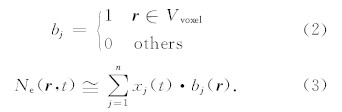
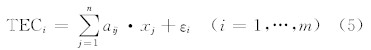
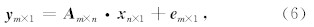
联合迭代重构算法是基于平方优化技术的一种并行迭代方法.每一次对所有观测路径上的电离层电子密度进行迭代，并根据每一次迭代的修正量再对电子密度分布做整体修正(Lytle, 1979).其迭代式表示如下：

式中，k为迭代次数，xjk为第k次迭代后第j个格网的电子密度值，yi为第i条射线的TEC观测值，

λk为迭代松弛因子.设加权参数W=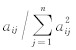，则式(7)可表示为

从式(8)中可以看出，加权参数只与投影矩阵 A 相关，而投影矩阵 A 本身又附加了很多的前提假设，如假定一定时间段内格网电子密度不变，由此，这一方法并不完全符合实际的电离层层析成像过程.因此，本文将自适应的思想引入联合迭代重构算法，即考虑将上一轮的迭代电子密度值引入到权值中，以便在某种程度上改正投影矩阵的不精确性.则改正后的加权参数为

将其代入方程式(7)中，即

将(10)式进一步写成矩阵的表示形式

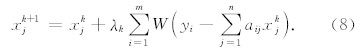
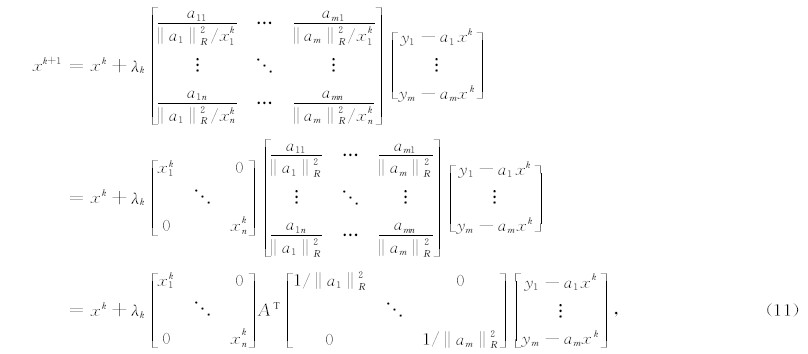
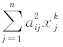式中，定义对角矩阵 R =diag(xjk)， M =diag(1/ ‖ ai ‖R 2)， 范数 ‖ a i ‖R2=〈 a i, Ra i〉=， a i为矩阵 A 的第i行，其中， x k=[xk1,xk2,…,xkn].则式(11)可表示为

式中， M 和 R 为对称正定矩阵.该算法中的松弛因子λk对于迭代过程中结果的精度及收敛速度有很 重要的影响.本文中松弛因子(Elfving et al., 2012) 的选择如下：

式中， r k= y － Ax k.

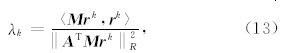
由此，本文在联合迭代重构算法的基础上，通过利用上一轮的电离层电子密度反演结果，自适应地调整松弛因子和加权参数，发展了一种新的自适应的联合迭代重构算法.

3.2 收敛性分析

考虑到如下线性方程的形式：

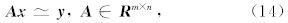
式中， A 具有非负性.以下推导过程中，向量都是列向量，ai为系数矩阵 A 的第i行的转置，内积的标准形式为〈 x , y 〉= x T y ，ρ(·)为谱半径(最大正特征值).对于每一个线性方程(14)，定义超平面Hi= { x ∈ R n|〈 a i, x 〉= y i } .

如果

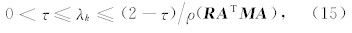
则迭代方程(12)收敛于解 x *(minx ‖ Ax － y ‖ M).其中，τ是一个任意小的固定常数.

由收敛条件可知： y = Ax *； 假定 r k= y - Ax k， 令 d k= M k r k， e k= x k－ x ?，则

根据(16)式可得

由式 r k= y - Ax k 和 e k= x k－ x ? 可得

因此，式(18)右边的最后一个被加项为

当 d ki≤0时，则由式 d k= M k r k可知

式中， M i为矩阵 M 的第i行.从(20)式可以看出，由于 M ki≥0， 则 r ki≤0.因此可 以得出〈 d k, r k〉≥0，当 d ki>0时，〈 d k, r k〉>0.

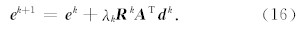
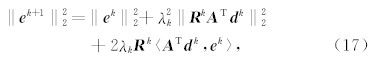
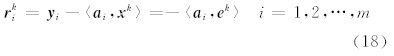
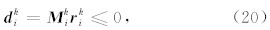
对于式(17)右边的第二个被加项，矩阵 M 可分 解为 M k= W T W ，利用如下不等式(Demmel, 1997)：

式中， Q 为任意对称正定矩阵.进一步可得

将式(19)和(22)代入式(17)，可得

式中，〈 d k, r k〉=〈 Wr k, Wr k〉≥0， 所以当且仅当0<τ≤λk≤(2－τ)/ρ( RA T MA )，可以得出 ‖ e k+1 ‖ 22≤ ‖ e k ‖ 22.因此对于序列 ‖ e k ‖ 2 k≥0是单调递减的，其是收敛的.

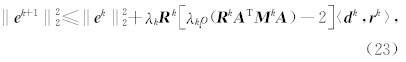
根据式(23)，得

由式(12)，式 r k= y － Ax k和 d k= M k r k以及式(23)，得

所以

由于λ2k R kρ( R k A T M k A )＞0，并根据式(26)，得

所以方程(12)是收敛的.

4 计算结果与分析
4.1 模拟数据实验

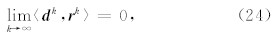
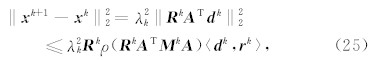
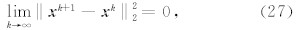
为验证算法ASIRT的可行性以及相对于SIRT的优越性，本文首先利用模拟的TEC数据来进行实验.利用模拟数据进行反演时，所选取的经度范围为0°—20°E，纬度范围为40°N—60°N，高度范围为100~1000 km，格网间隔在经度和纬度方向上为1°，在高度方向上为50 km.为了更加接近实际情况，测站数据和卫星数据均取真实值，选取欧洲地区的IGS跟踪站并计算卫星在反演时段内的坐标，获得相应反演时段内射线穿过格网内的截距，并构成观测方程(6)中的投影矩阵 A .利用IRI2007模型得到2012年4月8日UT10 ∶ 00时待反演区域内各网格中心点处的电离层电子密度 x <sub>IRI，并且将各条射线传播路径上的电离层TEC用 y simu表示.考虑到实际观测中观测误差和离散误差的存在，进行模拟时，加入一定量的随机误差 e ，即

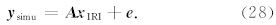
分别采用ASIRT和SIRT算法进行反演，并将反演的结果进行对比.图2给出了10°E子午面上电离层电子密度随纬度和高度的变化特性，其中图2a为IRI2007模型计算出的结果，图2b和图2c分别为ASIRT和SIRT算法迭代相同次数后的反演结果.从中可以看出， ASIRT算法反演的电离层电子密度分布整体上与IRI2007模型计算的电离层电子密度分布符合得较好，且优于SIRT算法，这说明利用ASIRT算法进行电离层电子密度反演是可行、有效的.

表1给出了两种算法在不同经度面上的反演结果误差统计，从中可以看出，在不同经度面上，利用ASIRT算法反演结果误差均小于SIRT算法.统计结果显示，利用ASIRT反演的重构区域内所有像素的电离层电子密度的平均绝对误差约为2.1×109el/m3，最大电离层电子密度误差的绝对值约为5.8×1010el/m3，SIRT反演的重构区域内所有像素的电离层电子密度的平均绝对误差约为5.0×109el/m3，最大电离层电子密度误差的绝对值约为9.8×1010el/m3， 且ASIRT算法经过9次迭代后收敛，SIRT算法经过16次迭代后收敛，这说明了本文算法在收敛速度和反演结果精度上均有提高，从而证实了该算法的优越性.

表1 不同经度面上两种算法误差统计分析表(单位: 1010el/m3) Table 1 Error analysis of IED reconstructed by two algorithms at different longitudes (unit:1010el/m3)

图2 10°E子午面上电离层电子密度剖面图
(a) IRI2007模型获取的；(b) ASIRT算法重构的；(c)SIRT算法重构的. Fig.2 IED profiles at 10°E by different algorithms
(a) IRI2007 model; (b) ASIRT algorithm; (c) SIRT algorithm.

为了进一步检验该算法，给出了高度面上的反 演结果.图3给出了两种算法在300 km高度面上电子密度分布及反演误差分布，图3b和3d分别为利用ASIRT算法反演的电子密度分布和误差分布，图3c和3e分别为利用SIRT算法反演的电子密度分布和误差分布.从中可以看出，相对于SIRT算法，ASIRT算法反演的结果总体来说更加接近于真值.表2给出了两种算法在不同高度面上的反演结果误 差统计，从中可以看出，在不同高度面上，利用ASIRT 算法反演结果误差均小于SIRT算法，这进一步说明了该ASIRT的优越性.

表2 不同高度面上两种算法误差统计分析表(单位: 1010el/m3) Table 2 Error analysis of IED reconstructed by the two algorithms at different heights (unit: 1010el/m3)

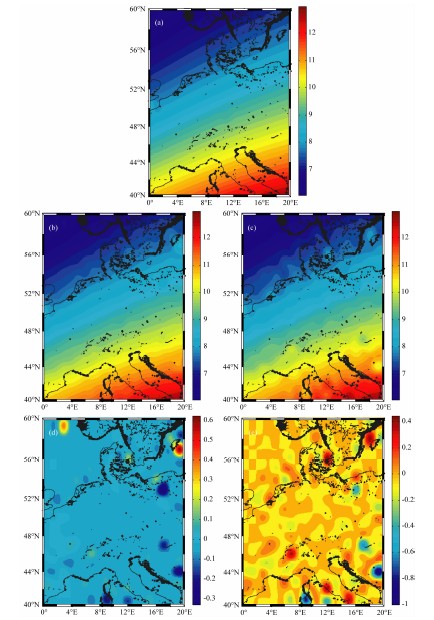图3 300 km高度面上电离层电子密度剖面图和误差图(单位：1011el/m3)
(a) IRI2007电离层模型给出的电子密度剖面图；(b)和(d)分别为ASIRT反演的电子密度剖面图和误差图；
(c)和(e)分别为SIRT反演的电子密度剖面图和误差图. Fig.3 The maps of IED profile and error at 300 km (unit: 1011el/m3)
(a) IED by IRI2007; (b) IED by ASIRT; (c) IED by SIRT; (d) Error of ASIRT; (e) Error of SIRT.
4.2 实测数据实验

利用实测数据对ASIRT算法进行了检验.重构时间为2012年4月8日，重构区域及格网划分与 上述模拟实验一致.本文采用的观测数据来自欧洲地区IGS观测网络，选取重构区域内的台站观测信息进行反演，并利用该区域内的一个垂直探测站PRUHONICE (50.00°N, 14.60°E)的观测数据进行独立检核.该电离层垂直站安装的是数字测高仪 DPS-4D，发射天线为两只交叉的双三角天线，高36 m； 接收天线场为四交叉天线循环；标准测定设置为每15分钟产生一幅0.05 MHz分辨率的电离层图.

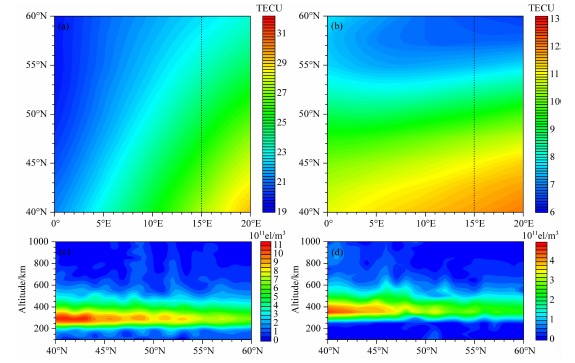图4 TEC分布及重构电离层电子密度分布
(a)和(c)是9 ∶ 00UT；(b)和(d)是23 ∶ 00UT.(a)和(b)为TEC图; (c)和(d)为15°E的垂直剖面图. Fig.4 Images of TEC distribution and reconstruction IED
(a) and (c) 9 ∶ 00UT; (b) and (d) 23 ∶ 00UT. (a) and (b) TEC; (c) and (d) Vertical cross-sections along 15°E.

如图4所示，(a)和(c)给出了UT9 ∶ 00时的分 布，(b)和(d)给出了UT23 ∶ 00时的分布，分别代表了白天和夜晚电离层电子密度的空间分布.(a)和(b)是实际空间的TEC分布，(c)和(d)是15°E的垂直剖面.从中可看出，利用ASIRT反演的电离层电子密度随着纬度的增大而逐渐降低，大体上与实际空间的TEC分布走向相符合，说明该算法是可行的.为了验证算法的可靠性，将反演结果与测高仪数据进行比较.图5展示了不同时刻的电离层测高仪 所得剖面与ASIRT和SIRT两种算法反演结果的比较， (a)和(b)分别为UT9 ∶ 00时和UT23 ∶ 00时的电子密度剖面的比较结果.从比较结果来看，ASIRT反演结果整体上与测高仪数据更为接近.说明ASIRT反演的精度确实优于SIRT.然而，在垂直方向上，这两种算法反演的结果与测高仪数据均存在一定差异，原因是观测信息不足导致垂直分辨率不高.

图6展示了一天12个反演时段内两种算法层析反演获得的F2层电子密度峰值(NmF2)和F2层 电子密度峰值高度(hmF2)与电离层测高仪站观测数据的比较结果.从中可以看出，两种算法反演获得的F2层电子密度峰值与测高仪观测结果总体上符合较好，但ASIRT算法总体上更接近于测高仪观 测结果.然而，F2层的峰值高度与测高仪存在一定 的差异.由于观测噪声、电离层空间离散误差以及测站几何结构限制等因素，使得反演结果的垂直分辨率较差.这说明在电离层层析成像过程中仅仅通过改进反演算法来改善电子密度空间结构(特别是垂直分辨率)是不够的，利用其他技术增加用于反演的观测信息是解决这一问题的最根本的手段.

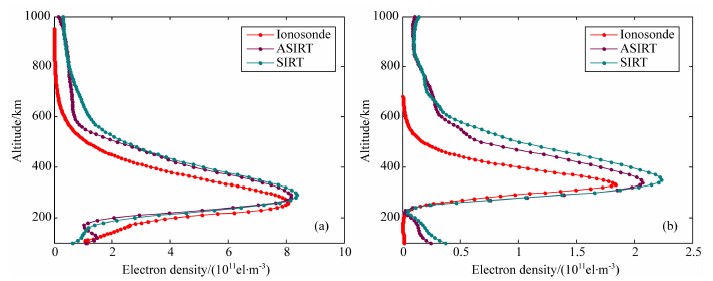图5 重构电离层电子密度剖面与电离层测高仪测量剖面的比较((a) UT9 ∶ 00; (b) UT23 ∶ 00) Fig.5 Comparison of estimated IED profiles by two algorithms and IED profiles measured by ionosonde ((a) UT9 ∶ 00; (b) UT23 ∶ 00)

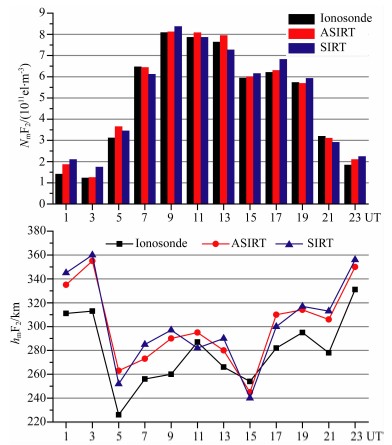图6 两种算法反演的F2层电子密度峰值以及峰值高度与测高仪结果的比较 Fig.6 Comparison of NmF2 and hmF2 values from CIT reconstruction by two algorithms and ionosonde data
5 结论

本文利用一种新的自适应的联合迭代重构算法研究了电离层层析成像的问题，实验结果表明，该算法在一定程度上能够改善常用的联合迭代重构算法的反演效果.相对于常用的联合迭代重构算法，新算法的收敛速度和反演精度均有所提高.尽管该算法改善了电离层层析成像的效果，但仍然不能很好地提高层析成像的垂直分辨率，解决这一问题，需要进一步增加观测信息.

参考文献
[1] Arikan O, Arikan F, Erol C B. 2007. Computerized ionospheric tomography with the IRI model. Adv. Space Res., 39(5): 859-866.
[2] Austen J R, Franke S J, Liu C H, et al. 1986. Application of computerized tomography techniques to ionospheric research. //Tauriainen A ed. Radio Beacon Contributions to the Study of Ionization and Dynamics of the Ionosphere and to Corrections to Geodesy and Technical Workshop. Oulu, Finland, Part 1, 25-35.
Austen J R, Franke S J, Liu C H. 1988. Ionospheric imaging using computerized tomography. Radio Sci., 23(3): 299-307.
[3] Chartier A T, Smith N D, Mitchell C N, et al. 2012. The use of ionosondes in GPS ionospheric tomography at low latitudes. J. Geophys. Res., 117: A10326, doi:10.1029/2012JA018054.
[4] Demmel J W. 1997. Applied numerical linear algebra. SIAM: Philadelphia, PA.
Elfving T, Hansen P, Relaxation T. 2012. Semiconvergence and relaxation parameters for projected SIRT algorithms. SIAM J. Sci. Comput., 34(4): A2000-A2017.
[5] Hobiger T, Kondo T, Koyama Y. 2008. Constrained simultaneous algebraic reconstruction technique (C-SART)—a new and simple algorithm applied to ionospheric tomography. Earth Planets Space, 60: 727-735.
Lee J K, Kamalabadi F. 2009. GPS-based radio tomography with edge-preserving regularization. IEEE Trans. Geosci. Remote Sens., 47(1): 312-324.
[6] Li H, Yuan Y, Li Z, et al. 2012. Ionospheric electron concentration imaging using combination of LEO satellite data with ground-based GPS observations over China. IEEE Trans. Geosci. Remote Sens., 50(5):1728-1735.
[7] Liu S, Wang J, Gao J. 2010. Inversion of ionospheric electron density based on a constrained simultaneous iteration reconstruction technique. IEEE Trans. Geosci. Remote Sens., 48(6): 2455-2459.
[8] Liu Z Z. 2004. Ionosphere tomographic modeling and applications using global positioning system (GPS) measurements [Ph. D. thesis]. Calgary: The University of Calgary.
Lytle R J. 1979. Computerized geophysical tomography. Proc. IEEE, 67(7): 1065-1073.
[9] Ma X F, Maruyama T, Ma G, et al. 2005. Three-dimensional ionospheric tomography using observation data of GPS ground receivers and ionosonde by neural network. J. Geophys. Res., 110: A05308, doi: 10.1029/2004JA010797.
[10] Nesterov I A, Kunitsyn V E. 2011. GNSS radio tomography of the ionosphere: The problem with essentially incomplete data. Adv. Space Res., 47(10): 1789-1803.
[11] Pryse S E, Kersley L. 1992. A preliminary experimental test of ionospheric tomography. J. Atmos. Terr. Phys., 54(7-8): 1007-1012.
[12] Pryse S E. 2003. Radio tomography: a new experimental technique. Surv. Geophys., 24(1): 1-38.
[13] Raymund T D, Austen J R, Franke S J, et al. 1990. Application of computerized tomography to the investigation of ionospheric structures. Radio Sci., 25(5): 771-789.
[14] Raymund T D. 1994. Ionospheric tomography algorithms. Int. J. Imag. Syst. Tech., 5(2): 75-85.
[15] Rius A, Ruffini G, Cucurull L. 1997. Improving the vertical resolution of ionospheric tomography with GPS occultations. Geophys. Res. Lett., 24(18): 2291-2294.
[16] Spencer P, Kersley L, Pryse S E. 1998. A new solution to the problem of ionospheric tomography using quadratic programing. Radio Sci., 33(3): 607-616.
[17] Wen D B, Yuan Y B, Ou J, et al. 2007. Three-dimensional ionospheric tomography by an improved algebraic reconstruction technique. GPS Solut., 11(4): 251-258.
[18] Wen D B, Yuan Y B, Ou J, et al. 2008. A hybrid reconstruction algorithm for 3-D ionospheric tomography. IEEE Trans. Geosci. Remote Sens., 46(6): 1733-1739.
[18] 邹玉华．2003．GPS地面台网和掩星观测结合的时变三维电离层层析［博士论文］．武汉：武汉大学