逆时偏移是一种基于全波方程的地震偏移方法,由于全波方程能够更加精确地描述地震波在地球介质中各个方向的传播,所以相比于Kirchhoff偏移、射线束偏移和单程波偏移等传统偏移技术,逆时偏移的成像精度大为提高. Whitmore(1983)首次提出逆时偏移方法,同年,Baysal等(1983)详细阐述了逆时偏移的概念和方法,利用伪谱法实现了逆时偏移,McMechan(1983)利用有限差分方法实现了逆时偏移.最初上述各方法用于叠后偏移.Chang和McMechan(1986,1987,1990,1994)先后采用有限差分方法实现了声波、弹性波的叠前逆时偏移;Wu等(1996)分析了高阶有限差分叠前逆时偏移的成像精度;Yoon等(2003)采用高阶有限差分方法和伪谱法实现了三维叠前逆时偏移;Xu等(2010)利用频率域外推方法实现了叠前逆时偏移;Duveneck和Bakker(2011)和Zhang等(2011)利用有限差分方法均实现了各向异性声波叠前逆时偏移.在国内,底青云和王妙月(1997)开展了弹性波有限元逆时偏移研究;杜启振和秦童(2009)、刘红伟等(2010)、严红勇和刘洋(2013)先后利用高阶有限差分方法实现了叠前逆时偏移;Liu等(2011)提出了利用多次波进行逆时偏移.另外,Chattopadhyay和McMeehan(2008)对几种成像条件进行了对比分析;Zhang和Sun(2009)提出了利用拉普拉斯算子滤波方法来压制低频噪声.
求解全波方程是逆时偏移的关键步骤之一,运用快速、高精度的数值算法是逆时偏移中一个非常重要的问题. 有限差分方法因其编程易实现、相同网格点数情况下存储量小、计算速度快、并行性高等优点,在地球物理学中得到广泛应用.但传统的差分格式会因为数值波速与真实波速的不同步,在粗网格情况下产生假波,引起严重的数值频散(Moczo et al., 2000). 为了消除数值频散,目前通常采用的方法有三种: 一是加细网格,二是构造高阶数值格式(Dablain,1986),三是对差分系数进行优化(Liu,2013; Zhang and Yao, 2013). 加细网格会增加计算量和存储量,这种做法不现实. 而高阶数值格式虽然具有高阶精度,但不一定具有低数值频散,且高精度导致长的差分算子,不利于边界处理和并行的实现. 对差分算子进行优化,能在一定程度上有效降低数值频散. 除了上述三种方法之外,Yang 等(2003)提出一种新的方法,将一种近似解析离散化算子(Kondoh et al., 1994)引入到地球物理领域. 该算子基于截断的泰勒展式以构造空间局部插值函数,并通过局部网格点之间的连接关系,用位移及梯度的线性组合来逼近空间高阶偏导数,包含了更多的波场信息,进而能有效压制数值频散. 在使用该离散算子的同时,结合不同的时间离散方法,可以得到具有低数值频散的数值格式,如NADM(Yang et al., 2003)、ONADM(Yang et al., 2006,2007a)、INADM(Yang et al., 2007b)、WNADM(王磊等,2009)等基于泰勒公式展开进行时间离散的数值方法,以及同时使用了三阶Runge-Kutta和算子级数方法的IRK-DSM方法(Yang et al., 2009),这些方法的共同特点是均具有良好的压制数值频散的能力,计算效率高.另一方面,波动方程可以表述为哈密尔顿系统的形式,且其时间上具有辛结构. 冯康和秦孟兆(2003)认为,对于哈密尔顿系统的离散格式应当采用保辛的数值格式. 保辛格式具有计算快速稳健、能长时间跟踪等优点(李一琼等,2011;Li et al., 2011,2012). 为了保证在求解哈密尔顿系统时离散方法的保辛性,马啸等(2010)基于声波方程的哈密尔顿表述,时间上采用二阶显式的辛可分Runge-Kutta III A-III B格式,空间上采用近似解析离散的方法,得到了一种时间精度为二阶、空间精度为四阶的新型辛格式(NSPRK).
本文的目的主要是基于四阶NSPRK数值格式的思想,发展新的具有六阶空间精度的格式,以提高现在NSPRK方法的精度,在此基础上进一步研究新格式稳定性条件和数值频散关系,并进行计算效率比较和波场模拟,然后和声波叠前逆时偏移理论相结合,给出基于六阶NSPRK方法的声波叠前逆时偏移方法,最后利用该方法对Sigsbee2B模型进行了偏移成像. 基本步骤是,在正演过程中采用六阶NSPRK方法,而边界处采用PML吸收边界条件(Komatitsch and Tromp, 2003),并利用归一化互相关成像条件进行成像,最后利用拉普拉斯算子滤波(Zhang and Sun, 2009),进而得到成像结果,同时和四阶NSPRK方法以及传统的有限差分方法如六阶差分方法、四阶Lax-Wendroff correction方法(简称LWC)(Dablain,1986)的偏移结果进行比较.数值结果表明,基于六阶NSPRK方法的声波叠前逆时偏移能得到更好的偏移结果,是一种优于四阶NSPRK方法、六阶传统差分方法、四阶LWC方法的叠前逆时偏移方法的新算法,尤其是在粗网格情况下具有更加明显的优越性. 2 正演算法 2.1 保辛格式
二维声波方程可写为:

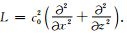 若令v=
若令v= ,则可将方程(1)写成如下线性可分的哈密尔顿系统:
,则可将方程(1)写成如下线性可分的哈密尔顿系统:
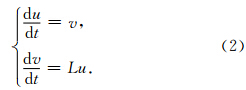
针对可分的哈密尔顿系统(2),时间上采用孙耿(1997)提出的二阶对称辛可分Runge-Kutta III A-III B格式,得到:

令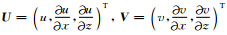 ,则方程(2)可变成:
,则方程(2)可变成:

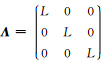 .针对哈密尔顿系统(4),采用近似解析离散化方法(Yang et al., 2003)离散方程(4)中的高阶空间偏导数,于是得到时间精度二阶、空间精度四阶的NSPRK(马啸等,2010)正演数值算法. 为了提高保辛算法的空间精度,我们利用四阶近似解析离散化算子的基本思想(Yang et al., 2003,2012),发展了具有六阶空间精度的计算公式,然后参照马啸等(2010)的做法,将时间保辛格式与六阶近似解析离散化算子相结合,于是得到时间精度二阶、空间精度六阶的NSPRK算法. 由于这种算法在时间上采用了辛格式,因此它在时间上具有保辛性,另一方面,由于在空间上采用六阶近似解析离散化方法,因此它具有低数值频散的特点. 在后面,我们将通过数值算例来说明这一点.
.针对哈密尔顿系统(4),采用近似解析离散化方法(Yang et al., 2003)离散方程(4)中的高阶空间偏导数,于是得到时间精度二阶、空间精度四阶的NSPRK(马啸等,2010)正演数值算法. 为了提高保辛算法的空间精度,我们利用四阶近似解析离散化算子的基本思想(Yang et al., 2003,2012),发展了具有六阶空间精度的计算公式,然后参照马啸等(2010)的做法,将时间保辛格式与六阶近似解析离散化算子相结合,于是得到时间精度二阶、空间精度六阶的NSPRK算法. 由于这种算法在时间上采用了辛格式,因此它在时间上具有保辛性,另一方面,由于在空间上采用六阶近似解析离散化方法,因此它具有低数值频散的特点. 在后面,我们将通过数值算例来说明这一点.
参照原四阶近似解析离散化算子(Yang et al., 2003,2012)的基本思想,本文详细推导了具有六阶精度的高阶空间偏导数计算公式,为了方便起见,以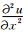 为例,新的六阶精度计算公式如下:
为例,新的六阶精度计算公式如下:
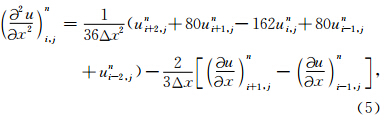
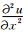 的四阶精度近似解析离散化方法(Yang et al., 2003)计算公式如下:
的四阶精度近似解析离散化方法(Yang et al., 2003)计算公式如下:

对于传统的有限差分方法,在离散高阶空间偏导数时,只利用函数值.
例如四阶LWC方法(Dablain,1986),首先通过泰勒展开和时空转换得到波动方程的差分格式如下:

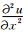 为例,其四阶精度的计算公式如下:
为例,其四阶精度的计算公式如下:
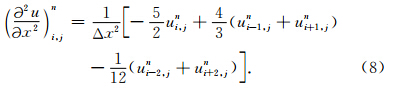
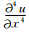 为例,计算公式如下:
为例,计算公式如下:
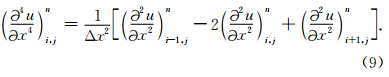

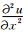 为例,其计算公式如下:
为例,其计算公式如下:
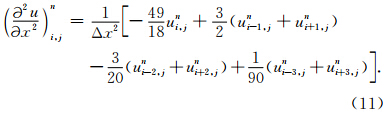
对于显式的差分方法,需要满足一定的稳定性条件. 仿照Yang等(2006)的稳定性分析方法,可得到本文六阶NSPRK方法在二维情况下满足的稳定性条件如下:
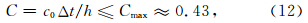
数值算法会带来数值波速和真实波速之间的差距,称之为数值频散. 数值频散的大小是衡量数值算法好坏的重要指标. 本节对我们发展的六阶NSPRK方法进行数值频散分析,并和原来的四阶NSPRK方法、四阶LWC方法、六阶CFD方法进行对比.
首先定义数值频散比率如下(Moczo et al., 2000):

 ,其中h和λgrid分别为网格步长和数值波长. 根据Nyquist-Shannon采样定理,Sp≤0.5才有意义(Dablain,1986). 经过简单推导,我们有
,其中h和λgrid分别为网格步长和数值波长. 根据Nyquist-Shannon采样定理,Sp≤0.5才有意义(Dablain,1986). 经过简单推导,我们有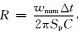 ,其中wnum为数值角频率,Δt为时间步长,C为库郎数,因此,只要推出wnumΔt的表达式,就可以得到数值频散关系. 对于本文发展的六阶NSPRK方法,其数值频散关系及推导过程详见附录B.
,其中wnum为数值角频率,Δt为时间步长,C为库郎数,因此,只要推出wnumΔt的表达式,就可以得到数值频散关系. 对于本文发展的六阶NSPRK方法,其数值频散关系及推导过程详见附录B. 图 1给出了库郎数C=0.3时,在不同方向的六阶NSPRK方法、四阶NSPRK方法、六阶CFD方法、四阶LWC方法所对应的数值频散关系. 由图 1可以看出,六阶NSPRK方法、四阶NSPRK方法、六阶CFD方法、四阶LWC方法的最大数值 频散误差分别为:1.61%、7.02%、18.19%、25.82%. 这表明,相比于传统的差分方法,六阶NSPRK方法和四阶NSPRK方法由于采用了近似解析离散化算子离散空间高阶偏导数,均能有效压制数值频散,特别地,在这四种方法中,六阶NSPRK方法的数值频散最小. 另一方面,由图 1可以看出,方向不同,四种方法的数值频散误差也不同,这种现象称为数值频散各向异性,其中六阶NSPRK方法的数值频散各向异性最小.
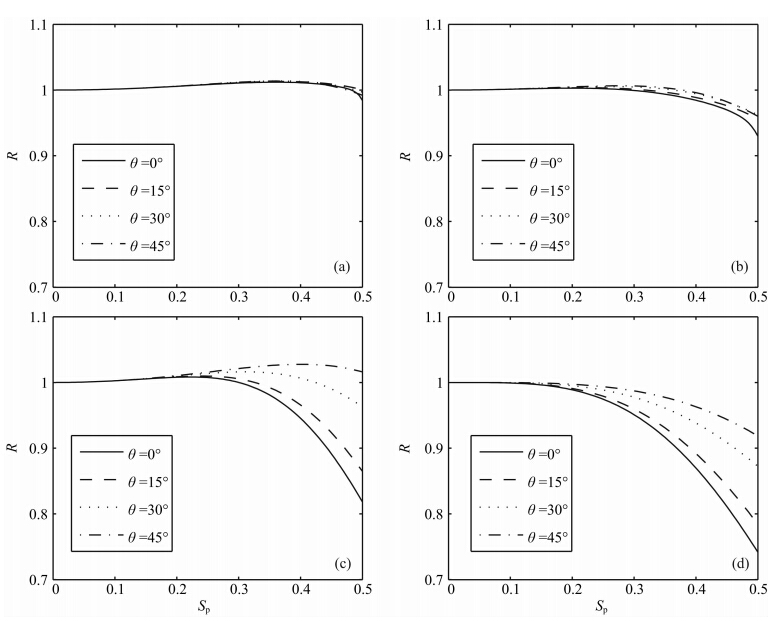 |
图 1 几种不同方法的数值频散比较 (a)六阶NSPRK方法;(b)四阶NSPRK方法;(c)六阶CFD方法;(d)四阶LWC方法. Fig. 1 Comparison of numerical dispersion for several methods (a)Sixth-order NSPRK method;(b)Fourth-order NSPRK method;(c)Sixth-order CFD method;(d)Fourth-order LWC method. |
下面研究我们发展的六阶NSPRK方法的计算效率. 为此,选取如下的波动方程:
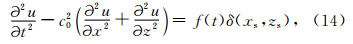
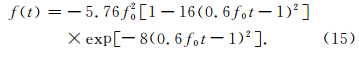
图 2给出了T=1.8 s时刻的波场快照,其中图 2a、图 2b、图 2c、图 2d分别由六阶NSPRK方法、四阶NSPRK方法、六阶CFD方法、四阶LWC方法这四种方法在粗网格(Δx=Δz=75 m)情况下计算所得. 对比这四个波场快照图,可以看出,在相同条件下,六阶CFD方法和四阶LWC方法有严重的数值频散,四阶NSPRK方法数值频散较弱,而六阶NSPRK方法没有可见的数值频散. 由此可见,相比于六阶CFD方法和四阶LWC方法这两种传统的差分方法,六阶NSPRK方法和四阶NSPRK方法能有效地压制数值频散,同时,六阶NSPRK方法比四阶NSPRK方法压制数值频散的能力更强.
 |
图 2 粗网格(Δx=Δz=75 m)情况下T=1.8 s时刻的波场快照 (a)六阶NSPRK方法;(b)四阶NSPRK方法;(c)六阶CFD方法;(d)四阶LWC方法. Fig. 2 Snapshots at time T=1.8 s on the coarse grid(Δx=Δz=75 m) (a)Sixth-order NSPRK method;(b)Fourth-order NSPRK method;(c)Sixth-order CFD method;(d)Fourth-order LWC method. |
对于四阶NSPRK方法、六阶CFD方法和四阶LWC方法,为了消除数值频散,需要加细网格. 当网格步长分别加细到Δx=Δz=50 m、Δx=Δz=25 m、Δx=Δz=18 m时,四阶NSPRK方法、六阶CFD方法和四阶LWC方法即可消除数值频散,得到清晰的波场快照(图 3a、图 3b和图 3c).比较图 2a和图 3a、图 3b、图 3c,它们都没有可见的数值频散,但是计算得到这些波场快照所需要的CPU时 间以及存储量是不一样的. 表 1给出了六阶NSPRK方法、 四阶NSPRK方法、六阶CFD方法和四阶LWC方法分别计算得到图 2a、图 3a、图 3b、图 3c所需要的计算时间和存储量. 由表 1知,在消除数值频散方面达到相同效果的情况下,六阶NSPRK方法需要的计算时间是7 s,而四阶NSPRK方法、六阶CFD方法、四阶LWC方法所需的计算时间分别为16 s、28 s、173 s,这表明,六阶NSPRK方法的计算速度大约分别是四阶NSPRK方法的2.3倍、六阶CFD方法的4.0倍、四阶LWC方法的24.7倍. 从存储量上看,六阶NSPRK方法需要241×241的12个存储数组,而四阶NSPRK方法、六阶CFD方法、四阶LWC方法分别需要361×361的12个、721×721的3个、1001×1001的3个存储数组. 这表明,六阶NSPRK方法所需要的存储量大约分别是四阶 NSPRK方法、六阶CFD方法、四阶LWC方法的 44.6%、44.7%、23.2%.因此,相比于四阶NSPRK方法、 六阶CFD方法和四阶LWC方法,六阶NSPRK方法是一种计算速度快、低存储、能有效压制数值频 散的保辛差分格式. 同时,六阶NSPRK方法和四阶NSPRK方法一样,与传统方法相比,可以提供除了位移之外更多的信息,包括位移的梯度场、粒子速度场、粒子速度的梯度场等信息.
| 表 1 几种不同方法的计算代价比较 Table 1 Comparison of computational costs for different methods |
 |
图 3 细网格情况下T=1.8 s时刻的波场快照 (a)四阶NSPRK方法(Δx=Δz=50 m);(b)六阶CFD方法(Δx=Δz=25 m);(c)四阶LWC方法(Δx=Δz=18 m). Fig. 3 Snapshots at time T=1.8 s on the fine grid (a)Fourth-order NSPRK method(Δx=Δz=50 m);(b)Sixth-order CFD method(Δx=Δz=25 m);(c)Fourth-order LWC method(Δx=Δz=18 m). |
为了进一步说明六阶NSPRK方法的计算效 果,本节选取了两个不同的模型,分别进行波场模拟. 2.6.1 双层介质模型
在本数值试验中,我们选取双层介质模型,其 上、下层介质的波速分别为4.0 km·s-1、6.0 km·s-1,选取计算区域0≤x≤12 km,0≤z≤12 km,速度的间断面位于竖直方向的中心,空间步长为Δx=Δz= 60 m,时间步长为Δt=3 ms,震源位于(6 km,5.1 km)处,震源是主频为f0=20 Hz的Ricker子波,震源随时间变化的函数如(15)式.
图 4给出了由四种方法计算得到的在T=1.0 s 时刻的波场快照图. 由图 4可以看出,六阶CFD方法和四阶LWC方法具有严重的数值频散,四阶NSPRK方法具有较弱的数值频散,而六阶NSPRK方法没有可见的数值频散. 这表明,六阶NSPRK方法在较粗的网格情况下,对于强间断层状介质中的波场模拟也十分有效.
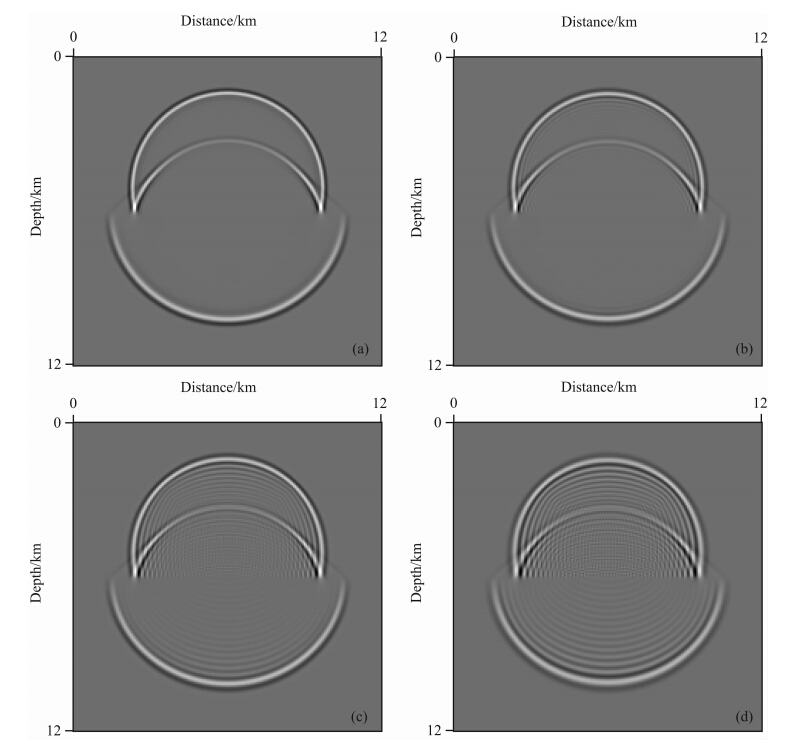 |
图 4 T=1.0 s时刻的波场快照 (a)六阶NSPRK方法;(b)四阶NSPRK方法;(c)六阶CFD方法;(d)四阶LWC方法. Fig. 4 Snapshots at time T=1.0 s (a)Sixth-order NSPRK method;(b)Fourth-order NSPRK method;(c)Sixth-order CFD method;(d)Fourth-order LWC method. |
在接下来的试验中,我们选取Sigsbee2B模型,来研究六阶NSPRK方法在非均匀复杂介质中的计 算效果.Sigsbee2B模型的速度结构如图 5所示,它具有很强的非均匀性.
 |
图 5 Sigsbee2B速度模型 Fig. 5 Velocity model of Sigsbee2B |
选取空间步长为Δx=Δz=75 ft,时间步长为Δt=2 ms,震源位于计算区域的(37500 ft,25 ft)处,震源是主频为f0=15 Hz的Ricker子波,震源随时间变化的函数如(15)式. 图 6给出由六阶NSPRK方法计算所得各个时刻的波场快照图. 由这些波场快照图可以看出,六阶NSPRK方法可以计算得到清晰的波场快照图,能有效模拟声波在复杂介质中传播. 图 7为由六阶NSPRK方法计算得到的0 s至9.6 s时刻的地表地震记录,其中图 7a 使用了PML(Perfectly Matched Layer,完全匹配层)吸收边界条件(Komatitsch and Tromp, 2003),图 7b使用了刚性边界条件. 对比图 7a和图 7b可以看出,六阶NSPRK方法能与PML吸收边界条件有效结合,吸收来自人为边界的反射波.
 |
图 6 由六阶NSPRK方法计算所得各个时刻的波场快照 (a)T=2.0 s;(b)T=3.0 s;(c)T=4.0 s;(d)T=5.0 s. Fig. 6 Snapshots generated by the sixth-order NSPRK method at different times |
 |
图 7 由六阶NSPRK方法计算所得的地表合成记录 (a)使用PML吸收边界条件;(b)使用刚性边界条件. Fig. 7 Synthetic seismograms on the surface generated by the sixth-order NSPRK method(a)PML absorbing boundary condition;(b)Stiff boundary condition. |
叠前逆时偏移实现的基本步骤为:首先,正演计算震源波场,计算时间从T0时刻开始到T时刻结束,各个时刻的震源波场记为s(t,x,z);然后反向逆时外推记录波场,计算时间从T时刻开始反推到T0时刻结束,各个时刻的记录波场记为r(t,x,z);最后,利用合适的成像条件以及震源波场 s(t,x,z)和记录波场r(t,x,z),计算得到偏移成像结果,偏移结果记为I(x,z).其中计算震源波场s(t,x,z)和记录波场r(t,x,z)的过程就是数值求解全波方程的过程,该过程利用本文发展的六阶NSPRK方法来计算.
叠前逆时偏移成像条件的选取和计算也是叠前逆时偏移中的核心问题之一,成像条件的好坏会直接影响最终成像结果的质量. 目前叠前逆时偏移中常用的成像条件主要有三种:激发时刻成像条件,互相关成像条件,振幅比成像条件. Chattopadhyay和McMeehan(2008)对几种成像条件进行了对比分 析,认为震源归一化互相关成像条件能够反映地下 界面的反射系数,提供较为准确的成像结果,因此,本文利用震源归一化互相关成像条件进行叠前逆时偏移成像,其表达式如下:
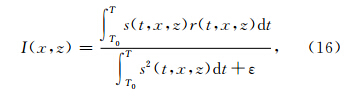
在叠前逆时偏移的过程中往往会产生低频噪声,这些噪声的产生是由潜水波、首波和绕射波等引起的,噪声的存在会影响到成像的结果,所以要得到最终清晰的成像结果,我们需要抑制噪声,对偏移产生的最初成像结果进行去噪处理. Zhang和Sun(2009)提出了利用拉普拉斯算子滤波方法来压制低频噪声,拉普拉斯算子滤波相当于对波场进行角度域衰减,该方法简单易操作被广泛使用. 本文利用拉普拉斯算子滤波方法对成像结果进行去噪处理. 4 声波叠前逆时偏移算例
我们选取被国际广为认可的Sigsbee2B模型进行偏移成像并进行对比研究. Sigsbee2B速度模型如图 5所示. 该模型的合成数据共496炮,其中每一炮最大的道集数为348,最小的道集数为65,而对Sigsbee2B模型进行偏移成像时,选取其中的248炮数据,同时选取两套网格,粗网格 情形下网格步长为Δx=Δz=75 ft,时间步长为Δt=2 ms,细网格情形下网格步长为Δx=Δz=37.5 ft,时间步长为Δt=1 ms. 震源选择主频为f0=15 Hz的Ricker子波,其随时间变化的函数如(15)式.
图 8给出了在粗网格(Δx=Δz=75 ft)情况下由六阶NSPRK方法、四阶NSPRK方法、六阶CFD方法和四阶LWC方法计算所得的逆时偏移结果.对比图 8,可以看到,在粗网格步长情况下,相比于四阶NSPRK方法、六阶CFD方法和四阶LWC方法,由六阶NSPRK方法进行逆时偏移得到的成像结果更清晰一些,尤其是在四个虚线框标示的区域,这四个小区域包含了盐下的小散射点以及盐丘底部的高速区域. 这是由于粗网格情况下,六阶CFD方法和四阶LWC方法计算波动方程时会有严重数值频散,四阶NSPRK方法具有较弱的数值频散,相比之下,六阶NSPRK方法能有效地压制数值频散. 图 9给出了在细网格(Δx=Δz=37.5 ft)情况下由六阶NSPRK方法、四阶NSPRK方法、六阶CFD方法和四阶LWC方法计算所得的逆时偏移结果.对比图 9,可以看到,在细网格步长情况下,由六阶NSPRK方法、四阶NSPRK方法、六阶CFD方法和四阶LWC方法进行逆时偏移得到的成像结果基本没有差别. 事实上,由六阶NSPRK方法在粗网格情况下的逆时偏移结果和另外三种方法在细网 格情况下的逆时偏移结果,也基本没有差别. 这 也表明,六阶NSPRK方法能有效压制数值频散,可以采用粗网格步长进行偏移成像,从而提高计算效率.
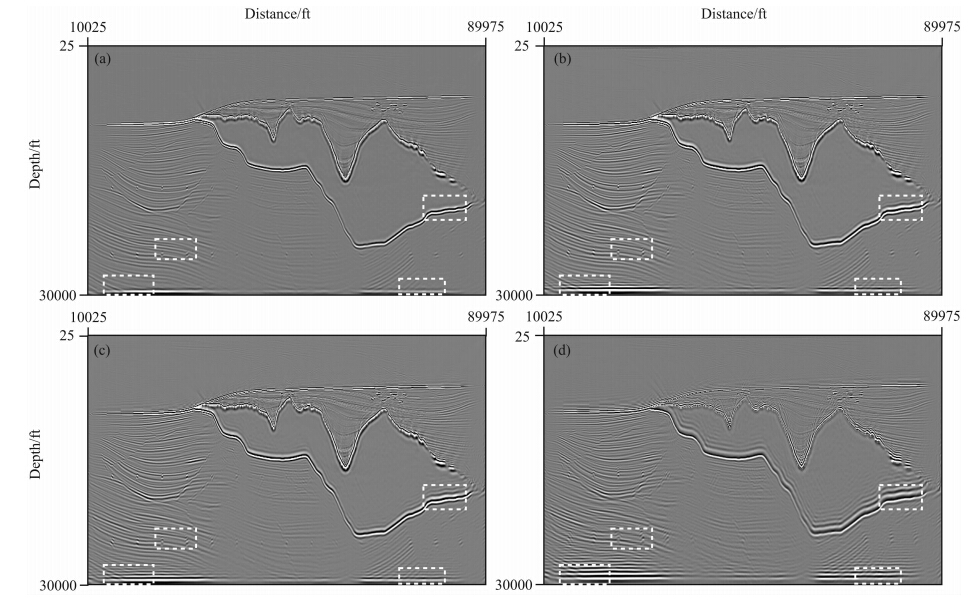 |
图 8 粗网格(Δx=Δz=75 ft)情况下的逆时偏移结果 (a)六阶NSPRK方法;(b)四阶NSPRK方法;(c)六阶CFD方法;(d)四阶LWC方法. Fig. 8 RTM results on the coarse grid(Δx=Δz=75 ft) (a)Sixth-order NSPRK method;(b)Fourth-order NSPRK method;(c)Sixth-order CFD method;(d)Fourth-order LWC method. |
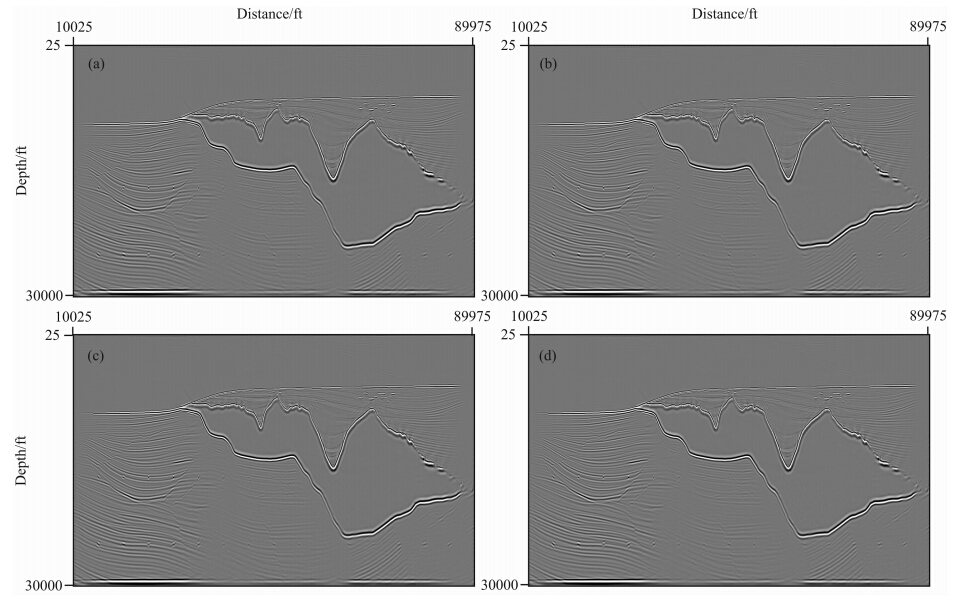 |
图 9 细网格(Δx=Δz=37.5 ft)情况下的逆时偏移结果 (a)六阶NSPRK方法;(b)四阶NSPRK方法;(c)六阶CFD方法;(d)四阶LWC方法. Fig. 9 RTM results on the fine grid(Δx=Δz=37.5 ft) (a)Sixth-order NSPRK method;(b)Fourth-order NSPRK method;(c)Sixth-order CFD method;(d)Fourth-order LWC method. |
本文详细推导了具有六阶精度的近似解析离散化方法,给出了高阶空间偏导数的计算公式,将原四阶NSPRK保辛算法的计算精度提高到了六阶,并对新的六阶NSPRK方法进行了稳定性和数值频散分析,以及计算效率比较和波场模拟,进一步将六阶NSPRK方法应用于RTM,得到一种时间上保辛、同时保持低数值频散的且可以应用大步长进行波场延拓的叠前逆时偏移方法. 数值结果表明,这种六阶NSPRK新方法与原四阶NSPRK方法、传统的六阶差分方法以及四阶LWC方法相比,可以有效压制数值频散,且具有计算速度快、低存储量等优 点. 对Sigsbee2B模型的偏移结果显示,六阶NSPRK 方法可以通过使用较大的空间步长和较大的时间步长来提高计算效率和节约存储量,有望在大尺度波场模拟和逆时偏移成像方面具有广泛应用. 附录A 六阶精度近似解析离散化算子推导
参照Yang 等(2003)的基本思想,首先利用截断的泰勒公式,有

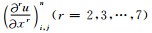 为未知数,求解式(A1)、式(A2)、式(A3)组成的线性方程组,即可得到x方向高阶空间偏导数的表达式,z方向高阶空间偏导数的表达式可类似得到. 由泰勒展式可以看出,得到的计算公式具有六阶精度. 为了方便起见,下面给出本文中所使用到的计算式:
为未知数,求解式(A1)、式(A2)、式(A3)组成的线性方程组,即可得到x方向高阶空间偏导数的表达式,z方向高阶空间偏导数的表达式可类似得到. 由泰勒展式可以看出,得到的计算公式具有六阶精度. 为了方便起见,下面给出本文中所使用到的计算式:
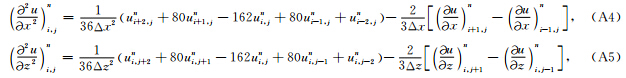

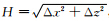 ,我们有关于方向偏导数的式子如下:
,我们有关于方向偏导数的式子如下:
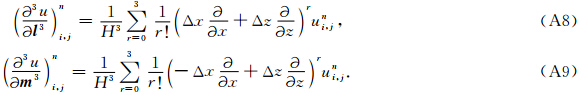
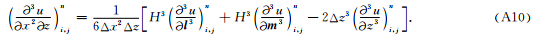

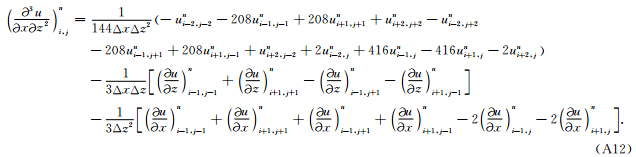
我们采用Von Neumann的分析方法进行稳定性及数值频散分析(Moczo et al., 2000; Yang et al., 2006). 将声波方程的谐波解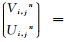
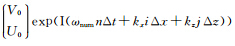 代入六阶保辛算法的格式中,即式(3)中,其中
代入六阶保辛算法的格式中,即式(3)中,其中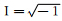 为虚数单位,则可以得到如下的迭代关系式:
为虚数单位,则可以得到如下的迭代关系式:
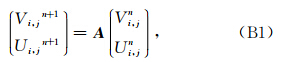
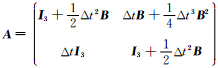 Ι3 为3×3的单位矩阵,B =(bij)3×3的元素如下:
Ι3 为3×3的单位矩阵,B =(bij)3×3的元素如下:
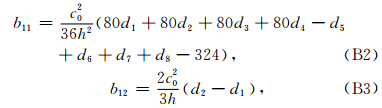
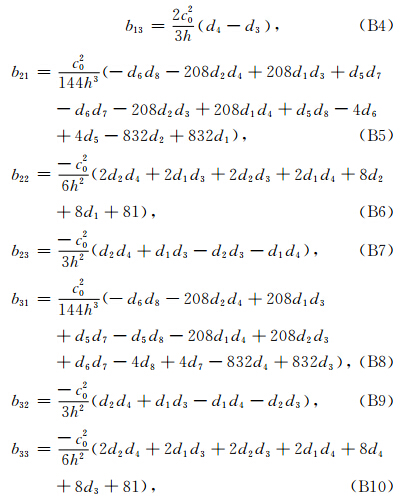
为了使得该算法稳定,需要满足ρ(A)≤1,从而可以得到库郎数满足的条件为C=c0Δt/h≤Cmax.同时,有
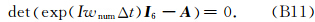
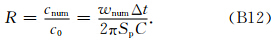
| [1] | Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration. Geophysics, 48(11): 1514-1524, doi: 10.1190/1.1441434. |
| [2] | Chang W F, McMechan G A. 1986. Reverse-time migration of offset vertical seismic profiling data using the excitation time imaging condition. Geophysics, 51(1): 67-84, doi: 10.1190/1.1442041. |
| [3] | Chang W F, McMechan G A. 1987. Elastic reverse-time migration. Geophysics, 52(10): 1365-1375, doi: 10.1190/1.1442249. |
| [4] | Chang W F, McMechan G A. 1990. 3D acoustic prestack reverse-time migration. Geophysical Prospecting, 38(7): 737-755, doi: 10.1111/j.1365-2478.1990.tb01872.x. |
| [5] | Chang W F, McMeehan G A. 1994. 3-D elastic prestack, reverse-time depth migration. Geophysics, 59(4): 597-609, doi: 10.1190/1.1443620. |
| [6] | Chattopadhyay S, McMeehan G A. 2008. Imaging conditions for prestack reverse-time migration. Geophysics, 73(3): S81-S89, doi: 10.1190/1.2903822. |
| [7] | Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66, doi: 10.1190/1.1442040. |
| [8] | Di Q Y, Wang M Y. 1997. The study of finite element reverse-time migration for elastic wave. Chinese J. Geophys. (in Chinese), 40(4): 570-579. |
| [9] | Du Q Z, Qin T. 2009. Multicomponent prestack reverse-time migration of elastic waves in transverse isotropic medium. Chinese J. Geophys. (in Chinese), 52(3): 801-807. |
| [10] | Duveneck E, Bakker P M. 2011. Stable P-wave modeling for reverse-time migration in tilted TI media. Geophysics, 76(2): S65-S75, doi: 10.1190/1.3533964. |
| [11] | Feng K, Qin M Z. 2003. Symplectic Geometric Algorithms for Hamiltonian Systems (in Chinese). Hangzhou: Zhejiang Science &Technology Press, 185-206, 271-278. |
| [12] | Komatitsch D, Tromp J. 2003. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation. Geophysical Journal International, 154(1): 146-153, doi: 10.1046/j. 1365-246X. 2003.01950.x. |
| [13] | Kondoh Y, Hosaka Y, Ishii K. 1994. Kernel optimum nearly-analytical discretization (KOND) algorithm applied to parabolic and hyperbolic equations. Computers & Mathematics with Applications, 27(3): 59-90, doi: 10.1016/0898-1221(94)90047-7. |
| [14] | Li X F, Li Y Q, Zhang M G, et al. 2011. Scalar seismic-wave equation modeling by a multisymplectic discrete singular convolution differentiator method. Bulletin of the Seismological Society of America, 101(4): 1710-1718, doi: 10.1785/0120100266. |
| [15] | Li X F, Wang W S, Lu M W, et al. 2012. Structure-preserving modelling of elastic waves: a symplectic discrete singular convolution differentiator method. Geophysical Journal International, 188(3): 1382-1392, doi: 10.1111/j.1365-246X.2011.05344.x. |
| [16] | Li Y Q, Li X F, Zhu T. 2011. The seismic scalar wave field modeling by symplectic scheme and singular kernel convolutional differentiator. Chinese J. Geophys. (in Chinese), 54(7): 1827-1834, doi: 10.3969/j.issn.0001-5733.2011.07.016. |
| [17] | Liu H W, Li B, Liu H, et al. 2010. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys. (in Chinese), 53(7): 1725-1733, doi: 10.3969/j.issn.0001-5733.2010.07.024. |
| [18] | Liu Y. 2013. Globally optimal finite-difference schemes based on least squares. Geophysics, 78(4): T113-T132, doi: 10.1190/GEO2012-0480.1. |
| [19] | Liu Y K, Chang X, Jin D G, et al. 2011. Reverse time migration of multiples for subsalt imaging. Geophysics, 76(5): WB209-WB216, doi: 10.1190/geo2010-0312.1. |
| [20] | Ma X, Yang D H, Zhang J H. 2010. Symplectic partitioned Runge-Kutta method for solving the acoustic wave equation. Chinese J. Geophys. (in Chinese), 53(8): 1993-2003, doi: 10.3969/j.issn.0001-5733.2010.08.026. |
| [21] | McMechan G A. 1983. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting, 31(3): 413-420, doi: 10.1111/j.1365-2478.1983.tb01060.x. |
| [22] | Moczo P, Kristek J, Halada L. 2000. 3D fourth-order staggered-grid finite-difference schemes: Stability and grid dispersion. Bulletin of the Seismological Society of America, 90(3): 587-603, doi: 10.1785/0119990119. |
| [23] | Sun G. 1997. A class of explicitly symplectic schemes for wave equations. Mathematica Numerica Sinica (in Chinese), (1): 1-10. |
| [24] | Wang L, Yang D H, Deng X Y. 2009. A WNAD method for seismic stress-field modeling in heterogeneous media. Chinese J. Geophys. (in Chinese), 52(6): 1126-1535, doi: 10.3969/j.issn.0001-5733.2009.06.014. |
| [25] | Whitmore N D. 1983. Iterative depth migration by backward time propagation. // The 53rd SEG Annual meeting Expanded Abstracts. SEG-1983-0382. Las Vegas, Nevada. |
| [26] | Wu W J, Lines L R, Lu H X. 1996. Analysis of higher-order, finite-difference schemes in 3-D reverse-time migration. Geophysics, 61(3): 845-856, doi: 10.1190/1.1444009. |
| [27] | Xu K, Zhou B, McMechan G A. 2010. Implementation of prestack reverse time migration using frequency-domain extrapolation. Geophysics, 75(2): S61-S72, doi: 10.1190/1.3339386. |
| [28] | Yan H Y, Liu Y. 2013. Acoustic prestack reverse time migration using the adaptive high-order finite-difference method in time-space domain. Chinese J. Geophys. (in Chinese), 56(3): 971-984, doi: 10.6038/cjg20130325. |
| [29] | Yang D H, Teng J W, Zhang Z J, et al. 2003. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media. Bulletin of the Seismological Society of America, 93(2): 882-890, doi: 10.1785/0120020125. |
| [30] | Yang D H, Peng J M, Lu M, et al. 2006. Optimal nearly analytic discrete approximation to the scalar wave equation. Bulletin of the Seismological Society of America, 96(3): 1114-1130, doi: 10.1785/0120050080. |
| [31] | Yang D H, Song G J, Lu M. 2007a. Optimally accurate nearly analytic discrete scheme for wave-field simulation in 3D anisotropic media. Bulletin of the Seismological Society of America, 97(5): 1557-1569, doi: 10.1785/0120060209. |
| [32] | Yang D H, Song G J, Chen S, et al. 2007b. An improved nearly analytical discrete method: an efficient tool to simulate the seismic response of 2-D porous structures. Journal of Geophysics and Engineering, 4(1): 40-52, doi: 10.1088/1742-2132/4/1/006. |
| [33] | Yang D H, Wang N, Chen S, et al. 2009. An explicit method based on the implicit Runge-Kutta algorithm for solving wave equations. Bulletin of the Seismological Society of America, 99(6): 3340-3354, doi: 10.1785/0120080346. |
| [34] | Yang D H, Tong P, Deng X Y. 2012. A central difference method with low numerical dispersion for solving the scalar wave equation.Geophysical Prospecting, 60(5): 885-905, doi: 10.1111/j.1365-2478.2011.01033.x. |
| [35] | Yoon K, Shin C, Suh S, et al. 2003. 3D reverse time migration using the acoustic wave equation: An experience with the SEG/EAGE data set. The Leading Edge, 22(1): 38-41, doi: 10.1190/1.1542754. |
| [36] | Zhang J H, Yao Z X. 2013. Optimized finite-difference operator for broadband seismic wave modeling. Geophysics, 78(1): A13-A18, doi: 10.1190/GEO2012-0277.1. |
| [37] | Zhang Y, Sun J. 2009. Practical issues in reverse time migration: true amplitude gathers, noise removal and harmonic source encoding. First Break, 26: 29-35. |
| [38] | Zhang Y, Zhang H Z, Zhang G Q. 2011. A stable TTI reverse time migration and its implementation. Geophysics, 76(3): WA3-WA11, doi: 10.1190/1.3533964. |
| [39] | 底青云, 王妙月. 1997. 弹性波有限元逆时偏移技术研究. 地球物理学报, 40(4): 570-579. |
| [40] | 杜启振, 秦童. 2009. 横向各向同性介质弹性波多分量叠前逆时偏移. 地球物理学报, 52(3): 801-807. |
| [41] | 冯 康, 秦孟兆. 2003. 哈密尔顿系统的辛几何算法. 杭州: 浙江科学技术出版社, 185-206, 271-278. |
| [42] | 李一琼, 李小凡, 朱童. 2011. 基于辛格式奇异核褶积微分算子的地震标量波场模拟. .地球物理学报, 54(7): 1827-1834, doi: 10.3969/j.issn.0001-5733.2011.07016. |
| [43] | 刘红伟, 李博, 刘洪等. 2010. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报, 53(7): 1725-1733, doi: 10.3969/j.issn.0001-5733.2010.07.024. |
| [44] | 马啸, 杨顶辉, 张锦华. 2010. 求解声波方程的辛可分Runge-Kutta方法. 地球物理学报, 53(8): 1993-2003, doi: 10.3969/j.issn.0001-5733.2010.08.026. |
| [45] | 孙耿. 1997. 波动方程的一类显式辛格式. 计算数学, (1): 1-10. |
| [46] | 王磊, 杨顶辉, 邓小英. 2009. 非均匀介质中地震波应力场的WNAD方法及其数值模拟. 地球物理学报, 52(6): 1126-1535, doi: 10.3969/j.issn.0001-5733.2009.06.014. |
| [47] | 严红勇, 刘洋. 2013. 基于时空域自适应高阶有限差分的声波叠前逆时偏移. 地球物理学报, 56(3): 971-984, doi: 10.6038/cjg20130325. |
 2014, Vol. 57
2014, Vol. 57


