地球物理学报  2014, Vol. 57 Issue (12): 4123-4131   PDF    
引用本文
李丽丽, 黄大年, 韩立国. 2014. 归一化总水平导数法在位场数据解释中的应用. 地球物理学报, 57(12): 4123-4131, doi: 10.6038/cjg20141223   
LI Li-Li, HUANG Da-Nian, HAN Li-Guo. 2014. Application of the normalized total horizontal derivative (NTHD) in the interpretation of potential field data. Chinese J. Geophys. (in Chinese), 57(12): 4123-4131, doi: 10.6038/cjg20141223   
归一化总水平导数法在位场数据解释中的应用
李丽丽, 黄大年, 韩立国    
吉林大学地球探测科学与技术学院, 长春 130061
投稿时间:2013-10-29    最后修改时间: 2014-10-11 .
基金项目：中国博士后科学基金项目(2014M551188)资助.
作者简介：李丽丽,女,1983年生,讲师,主要从事地球物理数据处理及解释方面的研究.E-mail:lilili@jlu.edu.cn
摘要：本文提出归一化总水平导数法,通过对总水平导数进行空间归一化计算实现了异常体水平位置和深度的估计,此外还推导出基于归一化总水平导数的欧拉反褶积法来估算地下地质体的空间位置,两种方法反演结果的相互验证可有效地提高反演结果的可信度.理论模型试验证明空间归一化总水平导数法和归一化总水平导数欧拉反褶积法均能有效地完成异常体的水平位置和深度的估计,所获得的位置参数与理论值相一致.在利用归一化总水平导数法进行磁异常解释时,对数据进行化磁极计算可得到更加准确的结果.将其应用于实际航磁数据的解释,获得了岩脉的大致分布特征.
关键词： 总水平导数     归一化     水平位置     深度    
Application of the normalized total horizontal derivative (NTHD) in the interpretation of potential field data
LI Li-Li, HUANG Da-Nian, HAN Li-Guo    
College of Geoexploration Science and Technology, Jilin University, Changchun 130061, China
Abstract: We propose the normalized total horizontal derivative method, which normalizes the total horizontal derivative to estimate the horizontal location and depth of the source. We also derive the Euler method based on the normalized total horizontal derivative to estimate the location of the source. The comparison of the inversion results computed by the two methods can increase the reliability of the inversion results. The theoretical tests show that the normalized total horizontal derivative method and Euler method based on normalized total horizontal derivative both can finish the computation of horizontal location and depth of the causative source effectively, and the obtained parameters are consistent with the theoretical values. In the interpretation of magnetic data, we reduce the data to the magnetic pole that can obtain more accurate results. We also apply the proposed methods to interpretation of real magnetic data and obtain the rough distribution of dykes.
Key words: Total horizontal derivative     Normalization     Horizontal location     Depth    
1 引言

边界识别是位场(重、磁)数据解释中的主要任务之一，依据边界识别结果能有效地识别出场源体 的水平位置(Miller and Singh，1994; Blakely，1995). 重磁异常水平导数的极值与垂直导数的零值对应地质体的边界(Verduzco et al.，2005; Cooper and Cowan，2006; 2008; Wang et al.，2009)，为此人们利用此特性构建边界识别滤波器来进行地质体边界的识别(Wijns et al.，2005; Ma，2013).总水平导数法是一种进行地质体边界识别的常用方法(Nabighian，1972; Roest et al.，1992; 马国庆等，2012)，其极大值点与地质体的边界相对应，但该方法并不能给出较深地质体的边界.Ma和Li(2012)提出正则化总水平导数法，其通过对局部水平导数进行正则化处理使浅部与深部地质体的边界同时显示出来，但该方法的输出结果依赖于窗口尺寸的大小.王万银等(2009)给出了总水平导数的空间变化特征，从结果中可知利用总水平导数所识别出的边界随着地质埋深的增加与理论边界的误差越大，且总水平导数法不能给出地质体的深度信息.

为了提供地质体的水平位置和深度信息，本文提出归一化总水平导数法，通过空间归一化总水平导数的极大值点可获得异常体的水平位置和深度，并推导出基于归一化总水平导数的欧拉反褶积法来估算出地下地质体的空间位置，两种方法计算结果的相互验证可有效地提高反演结果的准确性.通过理论模型试验和实际数据应用验证了归一化总水平导数法的应用效果.

2 归一化总水平导数法

总水平导数(Total Horizontal Derivative，THD)是进行地质体边界识别的常用方法，其表达式为：

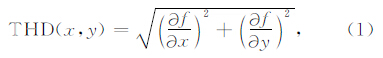
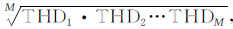其中，f为原始重力或磁异常.总水平导数仅能给出较浅地质体的边界，而对于较深地质体的边界分辨率较差，且总水平导数极值点所识别的边界与地质体埋深也存在关系，随着埋深的增加所识别边界与理论边界的误差也增大.归一化总梯度法在地质体中心点处取得最大值(肖鹏飞等，2006)，依据此理论提出空间归一化总水平导数法，可知归一化总水平导数到达场源体边界时表现为最大值，根据其最值点可判断异常体的水平位置和深度，且在异常体位置时埋深对总水平导数法所识别边界的影响可忽略不计，因此归一化总水平导数法所获得结果是最为准确的.本文采用几何平均对总水平导数进行空间归一化处理，空间归一化总水平导数(Normalized Total Horizontal Derivative，NTHD)的表达式为：

其中，GMT表示相应深度上总水平导数的几何平均，GMT= ，M为总测点数，THD(x，y，z)为深度z上的THD值.下延延拓结果的稳定是本文方法计算结果准确性的保障，为此本文采用Ma等(2013)提出的稳定迭代延拓方法来进行异常的延拓工作(计算过程见附录)，该方法是利用向上延拓和水平导数的组合来完成异常的向下延拓工作，可更加有效和准确地完成不同深度的延拓工作.

本文还推导出基于归一化总水平导数的欧拉反褶积法来估算地质体的空间位置.常规欧拉反褶积方程(Thompson，1982; Dewangan et al.，2007)的表达式为

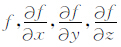其中，x，y，z为已知的观测点坐标；x0，y0，z0为待求的场源体中心坐标；分别为位场异常和其在x，y，z方向上的导数；B为未知背景场值；N为构造指数，不同地质构造对应特定的构造指数(Reid et al.，1990; Barbosa et al.，1999).表 1列出了不同地质构造所对应的构造指数.
表 1 不同类型地质体对应的构造指数 Table 1 Corresponding structural indexes of geological bodies of different types

在利用式(3)进行场源体位置计算时需要给定构造指数的大小，因此式(3)反演结果的准确度取决于给定的构造指数与实际构造指数的差距，但由于实际测量中区域构造指数是难以获取且不唯一的，为反演结果带来了很大的不确定性，将构造指数与位置参数一起作为未知数进行反演将是有效的解决手段(Fitzgerald et al.，2004; Salem and Ravat，2003).计算式(3)在x和y方向上的导数

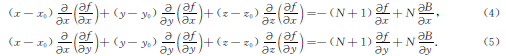
由于背景异常的变化较为平缓，因此其导数项较小可以忽略(Silva and Barbosa，2003).式(4)和(5)可改写为：

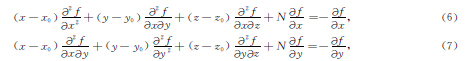
分别对(6)式和(7)式做如下的操作，，相加后得到：

计算归一化总水平导数在x，y和z方向的导数

将式(9)，(10)和(11)代入式(8)后，整理可得

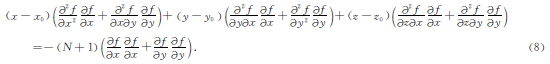
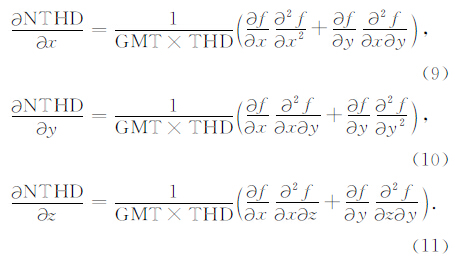
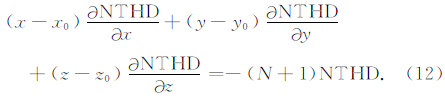
根据式(12)可以得到地质体的空间位置及其构造指数，该方法相对常规欧拉反褶积法具有不受构造指数选取误差的影响，且有效地综合了不同方向的水平导数，能获得更多的构造信息.对于式(12)反演得到的结果采用如下的筛选准则来获得更加准确的结果.

(1)计算点(xi，yi)与利用该点值求解得到的坐标x0，y0之间的距离小于窗口长度，因为当窗口在场源附近时解的准确性较高；

(2)利用一个较小窗口滤除一些孤立的解；

(3)滤除独立的求解结果后，针对已经集中的解进行筛选，当求解结果与集中解均值的距离大于窗口时该解无效；

(4)集中解的个数小于一定数量时直接滤除，因为当解的个数小于一定数量时不认为是有效异常.

经过上述的筛选后就已经获得比较准确的场源位置坐标x0，y0，z0.

3 理论模型试验

利用长方体产生的剖面重力异常来验证归一化总水平导数法的应用效果(图 1).图 1a为中心位置 分别为50 m和130 m，上、下顶埋深均为12 m和15 m，与围岩的密度差为1 g/cm3，宽度为10 m的两个板状体所产生的重力异常.

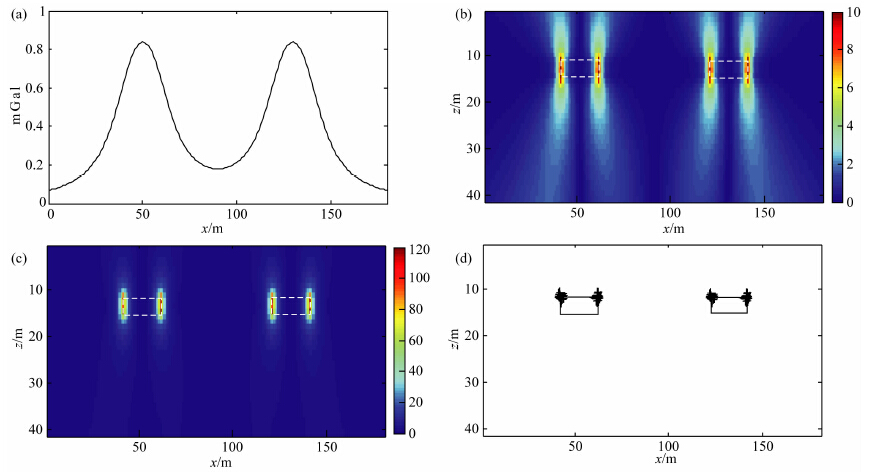图 1(a)长方体产生的重力异常；(b)算术平均归一化总水平导数；(c)基于几何平均的归一化总水平导数；(d)归一化总水平导数欧拉反褶积法反演结果Fig. 1 a)Synthetic gravity anomalies generated by a rectangular prism;(b)Normalized total horizontal derivative based on arithmetic mean;(c)Normalized total horizontal derivative based on geometric mean;(d)Inversion results computed by the Euler deconvolution of normalized total horizontal derivative

大多数归一化方法均采用算术平均作为归一化函数.图 1b为基于算术平均的归一化总水平导数结果，其中白框代表地质体的真实位置，可以看出其最大值对应的地质体的埋深为13.3 m，也能准确地标识出地质体的位置.采用公式(2)计算空间归一化总水平导数，其结果如图 1c所示.从计算结果中可以看出归一化总水平导数最大值的深度为13.4 m，与地质体的真实深度13.5 m之间误差很小，反演结果能准确地给出异常体的位置和深度信息，且得到的结果相对算术平均归一化总水平导数结果更加聚焦，发散程序较小.图 1d为利用归一化总水平导数欧拉反褶积法计算得到的结果，窗口大小为7.反演结果显示异常体的顶面深度为12.2 m，与异常体的真实空间位置相一致.通过该模型试验可知空间归一化总水平导数和归一化总水平导数欧拉反褶积法能准确地完成异常的反演工作.

实际数据中噪声是不可避免的干扰因素.图 2a为在图 1a所示异常中加入幅度为异常最大值5%噪声后异常，利用本文提出的归一化总水平导数法对图 2a所示异常进行解释(图 2).图 2b为基于算术平均的归一化总水平导数结果，可以看出最大值对应的地质体埋深为12.9 m，水平位置与地质体的真实位置相一致，能准确地完成异常的反演工作.图 2c为利用公式(2)计算得到的空间归一化总水平导数，根据其最大值判断出异常的埋深为13.1 m，水平位置与理论位置吻合较好，但由于受到噪声的影响，埋深与理论深度之间的误差加大.图 2d为归一化总水平导数欧拉反褶积法计算结果，窗口大小为7，反演得到的异常体的顶面深度11.6 m，反演得到的异常体的水平位置与真实位置吻合较好.总体来 讲，归一化总水平导数法具有一定的抗噪声干扰能力.

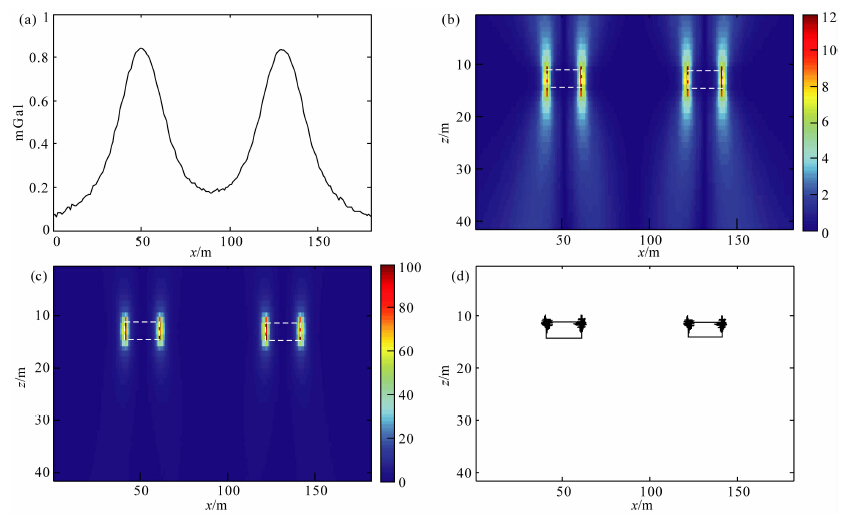图 2(a)含噪重力异常；(b)算术平均归一化总水平导数；(c)式(2)计算得到的空间归一化总水平导数；(d)归一化总水平导数欧拉反褶积法反演结果Fig. 2(a)Noise-bearing gravity anomalies;(b)Normalized total horizontal derivative based on arithmetic mean;(c)Spatially normalized total horizontal derivative computed by Eq.(2);(d)Inversion results computed by the Euler deconvolution of normalized total horizontal derivative

下面验证一下本文方法在二维情况下的应用效果.图 3a为埋深分别为11 m和13 m的正方体所产生的重力异常.图 3b为图 3a所示异常的总水平导数，从图中可以看出总水平导数能清晰地识别出较浅地质体的边界，而所得到的较深地质体的边界则比较模糊，且相对理论边界要大一些.图 3c为空间归一化总水平导数结果，通过空间归一化总水平导数空间不同位置的幅值特征可判断出地质体的埋深.为了更加清晰地显示出地质体的边界，图 3d给出了3、5、7、9、11、13 m深度上归一化总水平导数的极大值点的位置，通过该结果可以看出随着下延深度的增加归一化总水平导数所识别出的异常体的水平位置与真实边界更加接近，通过最大值的分布可判定出正方体的埋深分别为11 m和13 m.利用归一化总水平导数欧拉反褶积法估算异常体的位置参数，窗口大小为7×7.图 3e为利用该方法计算得到的异常体的位置分布，图 3f为该方法反演结果的三维显示，反演得到的异常体的平均深度分别为10.7 m和12.6 m，结果与理论埋深相一致.

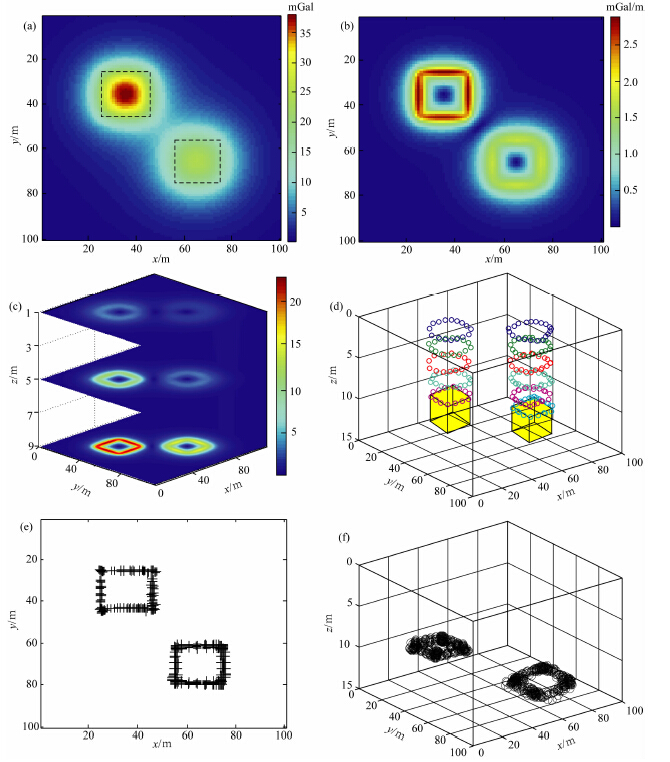图 3(a)原始重力异常；(b)图 3a所示异常的总水平导数；(c)空间归一化总水平导数；(d)空间归一化总水平导数不同深度极大值点的三维显示；(e)归一化总水平导数欧拉反褶积法得到的异常体的位置；(d)归一化总水平导数欧拉反褶积法反演结果的三维显示Fig. 3(a)Original gravity anomalies;(b)Total horizontal derivative of data in(a);(c)Spatially normalized total horizontal derivative;(d)3D view of the maximum values of spatially normalized total horizontal derivative at different depths;(e)Locations of sources computed by Euler deconvolution of normalized total horizontal derivative;(f)3D view of results computed by Euler deconvolution of normalized total horizontal derivative

为了验证方法的适用性，将其应用于磁异常的解释.图 4a为埋深分别为10 m和12 m板状体在磁化倾角为70°时产生的磁异常.图 4b为埋深分别为10 m和12 m板状体在垂直磁化时候产生的磁异常.图 4c为图 4a所示异常的空间归一化总水平导数，根据其最大值依旧能判断出地质体的埋深，但是由于倾斜磁化的影响所获得水平位置与真实水平位置存在一定的差距.图 4d为图 4a所示异常的空间 归一化总水平导数，标识出的异常体的水平位置与实际水平位置吻合较好.图 4e为图 4a所示异常归一化总水平导数欧拉反褶积法得到的结果，异常体的深度分别为8.2 m和10.1 m；图 4f为图 4b所示异常归一化总水平导数欧拉反褶积法得到的结果，异常体的平均深度为9.1 m和11.1 m.通过试验可知，由于倾斜磁化的干扰造成反演结果与理论结果之间的差距较大，因此为了获得更加准确的结果，在利用本文方法进行磁异常解释前需要对数据进行化磁极处理.此外还可以发现即使在垂直磁化条件下反演结果与理论值之间还是存在一定的差距，这是由于异常体距离较近，受邻近异常体干扰较大造成的.

图 4(a)磁倾角为70°时板状体产生的磁异常；(b)垂直磁化时板状体产生的磁异常；(c)图 4a所示数据的空间归一化总水平导数；(d)图 4b所示数据的空间归一化总水平导数；(e)图 4a所示数据的归一化总水平导数欧拉反褶积法反演结果；(d)图 4b所示数据的归一化总水平导数欧拉反褶积法反演结果Fig. 4(a)Synthetic magnetic anomalies of a prism with inclination of 70°;(b)Synthetic magnetic anomalies of a prism with inclination of 90°;(c)Spatially normalized total horizontal derivative of data in(a);(d)Spatially normalized total horizontal derivative of data in(b);(e)Inversion results of data in(a)computed by Euler deconvolution of normalized total horizontal derivative;(f)Inversion results of data in(b)computed by Euler deconvolution of normalized total horizontal derivative
4 实际数据应用

将归一化总水平导数方法用于实际磁测数据的解释，由于水平导数受磁化方向的干扰而使识别结果会出现较大误差(Ma，2013; 王万银，2010)，因 此在对其进行计算之前首先对磁异常进行磁极计算.

图 5a为朱日和地区化极后磁异常，测量点距为250 m.图 5b为空间归一化总水平导数结果.可以看出异常体的走势及异常体的大致埋深，深度在400～600 m之间，且根据不同深度极大值点的变化可判断出异常体的延深方向为东南.图 5c为归一化总水平导数欧拉反褶积计算结果，窗口大小为5×5.可以看出异常体的深度大多集中在400～600 m之间，与前一种方法得到的结果一致.图 5d为反演得到的异常体的构造指数，构造指数范围为0.42～1.71，其均值为1.12，地下地质体接近于脉状分布.由于异常体的不规则形与异常体之间的相互干扰造成构造指数并不是一个整数，很多作者也证明了这一点(Salem et al.，2008; Fedi et al.，2012).

图 5(a)朱日和地区化极后磁异常；(b)空间归一化总水平导数；(c)归一化总水平导数欧拉反褶积法得到的异常体的位置参数；(d)归一化总水平导数欧拉反褶积法得到的异常体的构造指数Fig. 5(a)Reduction to the north pole of magnetic anomalies in the Zhurihe area;(b)Spatially normalized total horizontal derivative of data in(a);(c)Locations of data in(a)computed by Euler deconvolution of normalized total horizontal derivative;(d)Structural index estimated by Euler deconvolution of normalized total horizontal derivative
5 结论

本文提出归一化总水平导数法，其通过两种方式来完成异常的解释工作，一提出空间归一化总水平导数，通过其最大值点可获得异常体的空间位置，二推导出基于归一化总水平导数的欧拉反褶积法来完成异常体位置参数的反演，且避免了构造指数选取误差为反演结果带来的不确定性.理论模型试验证明空间归一化总水平导数的最大值能准确地获得异常体的空间位置，基于归一化总水平导数的欧拉 反褶积法能同时完成场源体位置和构造指数的计算，与理论值之间的误差较小，且归一化总水平导数法具有一定的抗噪声能力.此外试验结果表明在利用归一化总水平导数法进行磁异常解释时，事先对磁异常进行化磁极处理可获得更加准确的结果.将本文方法应用于实际航磁数据的解释，获得了岩脉的大致延伸趋势及深度. 附录 位场数据向下延拓的稳定算法

Fedi和Florio采用泰勒展开式来完成数据的向下延拓，其表达式为：

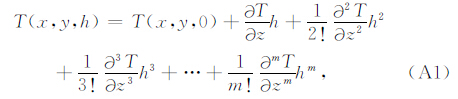
其中，T(x，y，h)是观测面h上的异常，h为延拓高度，T(x，y，0)是观测面上异常.该方法是通过垂直导数来进行向下延拓操作，但垂直导数的计算会明显增大噪声的干扰，且当点距较大时，垂直导数的计算是不稳定的.

向上延拓是一种稳定的运算，且受噪声干扰较小，因此本文提出利用向上延拓运算来完成异常的向下延拓.向上延拓运算的泰勒展开式可表示为：

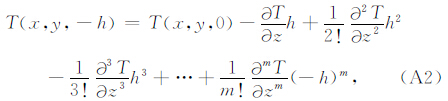
其中，T(x，y，－h)为观测面-h上的异常.三阶或更高阶垂直导数值较小，且计算结果稳定性差，因此设定展开式的项数为3，并将公式(A1)和(A2)相加后可得到：

由于垂直导数的计算会增大噪声的干扰，为此采用Laplace方程来计算异常的二阶垂直导数：

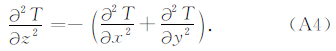
水平导数是空间域中进行，不会增大噪声的影响.因此利用公式(A3)进行异常的向下延拓工作只需要计算异常的水平导数和向上延拓结果，可有效地增强向下延拓的稳定性.但由于该方法所保留的泰勒展开式的项数较少，因此对于复杂异常所获得的结果精度较低.为了获得更加准确的结果，给出一种迭代的方法来计算向下延拓结果.

将公式(A3)计算得到的下界面异常T(x，y，h)向上延拓高度h得到异常T1(x，y，0)，理论上T(x，y，0)与T1(x，y，0)是相等的，但由于T(x，y，h)仅是一个近似值，因此两者之间会存在一定的差距，本文通过下面的迭代过程来消除这一差距.计算观测面上原始异常T(x，y，0)与T1(x，y，0)的差

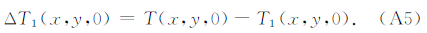
利用公式(A3)将ΔT1(x，y，0)向下延拓高度h，可以得到

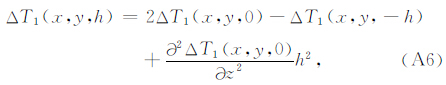
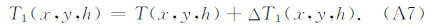
其中，ΔT1(x，y，h)为异常ΔT1(x，y，0)下延h后异常，ΔT1(x，y，－h)为异常ΔT1(x，y，0)上延h后异常.ΔT1(x，y，h)作下界面异常的一个修正量，则下界面异常可改写为

重复式(A5)—(A7)的计算过程，直至ΔTm(x，y，0)的均方差小于给定值，因此观测面h上的最终异常可写为：

参考文献
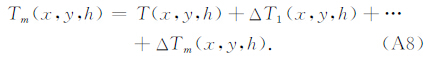
[1] Barbosa V C F, Silva J B C, Medeiros W E. 1999. Stability analysis and improvement of structural index estimation in Euler deconvolution. Geophysics, 64(1): 48-60.
[2] Blakely R J. 1995. Potential Theory in Gravity and Magnetic Applications. Cambridge: Cambridge University Press.
[3] Cooper G R J, Cowan D R. 2006. Enhancing potential field data using filters based on the local phase. Computers & Geosciences, 32(10): 1585-1591.
[4] Cooper G R J, Cowan D R. 2008. Edge enhancement of potential-field data using normalized statistics. Geophysics, 73(3): H1-H4.
[5] Dewangan P, Ramprasad T, Ramana M V, et al. 2007. Automatic interpretation of magnetic data using Euler Deconvolution with nonlinear background. Pure Appl. Geophys., 164(11): 2359-2372.
[6] Fedi M, Florio G, Cascone L. 2012. Multiscale analysis of potential fields by a ridge consistency criterion: the reconstruction of the Bishop basement. Geophys. J. Int., 188(1): 103-114.
[7] Fitzgerald D, Reid A, Mcinerney P. 2004. New discrimination techniques for Euler deconvolution. Computers & Geosciences, 30(5): 461-469.
[8] Ma G, Li L L. 2012. Edge detection in potential fields with the normalized total horizontal derivative. Computers & Geosciences, 41: 83-87.
[9] Ma G Q, Liu C, Huang D N, et al. 2013. A stable iterative downward continuation of potential field data. J. Appl. Geophys., 98: 205-211.
[10] Ma G Q. 2013. Edge detection of potential field data using improved local phase filter. Explor. Geophys., 44(1): 36-41.
[11] Ma G Q, Huang D N, Yu P, et al. 2012. Application of improved balancing filters to edge identification of potential field data. Chinese J. Geophys. (in Chinese), 55(12): 4288-4295.
[12] Miller H G, Singh V. 1994. Potential field tilt—A new concept for location of potential field sources. J. Appl. Geophys., 32(2-3): 213-217.
[13] Nabighian M N. 1972. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section: its properties and use for automated anomaly interpretation. Geophysics, 37(3): 507-517.
[14] Reid A B, Allsop J M, Granser H, et al. 1990. Magnetic interpretation in three dimensions using Euler deconvolution. Geophysics, 55(1): 80-91.
[15] Roest W R, Verhoef J, Pilkington M. 1992. Magnetic interpretation using the 3-D analytic signal. Geophysics, 57(1): 116-125.
[16] Salem A, Ravat D. 2003. A combined analytic signal and Euler method (AN-EUL) for automatic interpretation of magnetic data. Geophysics, 68(6): 1952-1961.
[17] Salem A, Williams S, Fairhead D, et al. 2008. Interpretation of magnetic data using tilt-angle derivatives. Geophysics, 73(1): L1-L10.
[18] Silva J B C, Barbosa V C F. 2003. 3D Euler deconvolution: Theoretical basis for automatically selecting good solutions. Geophysics, 68(6): 1962-1968.
[19] Thompson D T. 1982. EULDPH: A new technique for making computer-assisted depth estimates from magnetic data. Geophysics, 47(1): 31-37.
[20] Verduzco B, Fairhead J D, Green C M. 2004. New insights into magnetic derivatives for structural mapping. The Leading Edge, 23(2): 116-119.
[21] Wang W Y, Pan Y, Qiu Z Y. 2009. A new edge recognition technology based on the normalized vertical derivative of the total horizontal derivative for potential field data. Appl. Geophys., 6(3): 226-233.
[22] Wang W Y. 2010. Spatial variation law of the extreme value positions of total horizontal derivative for potential field data. Chinese J. Geophys. (in Chinese), 53(9): 2257-2270.
[23] Wijns C, Perez C, Kowalczyk P. 2005. Theta map: Edge detection in magnetic data. Geophysics, 70(4): L39-L43.
[24] Xiao P F, Li M, Xu S Z, et al. 2006. Stable solution of normalized total gravity gradient. Oil Geophysical Prospecting, 41(5): 596-598.
[25] 马国庆, 黄大年, 于平等. 2012. 改进的均衡滤波器在位场数据边界识别中的应用. 地球物理学报, 55(12): 4288-4295.
[26] 王万银. 2010. 位场总水平导数极值位置空间变化规律研究. 地球物理学报, 53(9): 2257-2270.
[27] 肖鹏飞, 李明, 徐世浙等. 2006. 重力归一化总梯度的稳定解法. 石油地球物理勘探, 41(5): 596-598.