地球物理学报  2014, Vol. 57 Issue (10): 3422-3430   PDF    
引用本文
李宏兵, 张佳佳. 2014. 多重孔岩石微分等效介质模型及其干燥情形下的解析近似式. 地球物理学报, 57(10): 3422-3430, doi: 10.6038/cjg20141028   
LI Hong-Bing, ZHANG Jia-Jia. 2014. A differential effective medium model of multiple-porosity rock and its analytical approximations for dry rock. Chinese J. Geophys. (in Chinese), 57(10): 3422-3430, doi: 10.6038/cjg20141028   
多重孔岩石微分等效介质模型及其干燥情形下的解析近似式
李宏兵1, 张佳佳2    
1. 中国石油勘探开发研究院, 北京 100083;
2. 中国石油大学(华东)地球科学与技术学院, 青岛 266580
投稿时间:2013-10-30    最后修改时间: 2014-8-22 .
基金项目：国家自然科学基金(41404088),国家油气重大专项(2011ZX05001)资助.
作者简介：李宏兵, 男, 1965年生, 博士, 教授级高级工程师.主要从事地震岩石物理及储层流体识别的方法研究及软件开发工作. E-mail:hbingli@petrochina.com.cn
摘要：经典的微分等效介质(DEM)理论可用于确定多孔介质的弹性性质,但由于缺乏多重孔DEM方程,其估计的多重孔岩石的等效弹性模量依赖于包裹体(即不同孔隙纵横比的孔或缝)的添加顺序.本文首先从Kuster-Toksöz理论出发建立了Zimmermann和Norris两种形式的多重孔DEM方程.Norris形式的多重孔DEM方程预测的等效弹性模量总是位于Hashin-Shtrikman上下限内,而Zimmermann形式的多重孔DEM方程有时会越界.然后,通过使用干燥岩石模量比的解析近似式,对两个相互耦合的Norris形式DEM方程进行解耦得到干燥多重孔岩石的体积和剪切模量解析式.用全DEM方程的数值解对解析近似式的有效性进行了测试,解析公式的计算结果在整个孔隙度分布区间与数值解吻合良好.对实验室测量数据在假设岩石含有双重孔隙的情形下用双重孔DEM解析公式对岩石的弹性模量进行了预测,结果表明,解析式准确地预测了弹性模量随孔隙度的变化.双重孔(即软、硬孔)DEM解析模型可用来反演各孔隙类型的孔隙体积比,它可以通过实验室测量与理论预测之间的平方误差最小反演得到.砂岩样品的反演结果揭示,软孔的孔隙体积百分比与粘土含量没有明显的相关性.
关键词： 微分等效介质理论     多重孔隙类型     弹性模量     干岩石     数学公式     砂岩    
A differential effective medium model of multiple-porosity rock and its analytical approximations for dry rock
LI Hong-Bing1, ZHANG Jia-Jia2    
1. Research Institute of Petroleum Exploration and Development, Beijing 100083, China;
2. School of Geosciences, China University of Petroleum, Qingdao 266580, China
Abstract: The classic differential effective medium (DEM) theory can be used to determine the elastic properties of the porous medium, but the final elastic properties of multiple-porosity rock depend on the added order of the different pore-type inclusions due to the lack of DEM equations for multiple-porosity rock. This paper first derives the differential equations of both Zimmermann's and Norris's versions for multiple-porosity rock from the Kuster-Toksöz theory. The elastic moduli predicted by the DEM equations of Norris's version never violate Hashin-Shtrikman bounds while those predicted by the DEM equations of Zimmermann's version violate bounds in some cases. Then, we derive analytical solutions of the bulk and shear moduli for dry rock from the differential equations of Norris's version by applying an analytical approximation for dry-rock modulus ratio, in order to decouple these equations. The validity of these analytical approximations is tested by integrating the full DEM equation numerically. The analytical formulae give good estimates of the numerical results over the whole porosity range. The analytical formulae have been used to predict the elastic moduli for the sandstone experimental data by assuming that the porous rock contains dual-porosity of both cracks and pores. The results show that they can accurately predict the variations of elastic moduli with porosity for dry sandstones. We also apply nonlinear global optimization algorithm to find the best estimate for the pore volume percentage of both cracks and pores by minimizing the error between theoretical predictions and experimental measurements based on the dual-porosity DEM analytical model. The inversions for the sandstone experimental data show that there is no direct correlation between the crack volume percentage and clay volume.
Key words: Differential effective medium theory     Multiple-porosity type     Elastic moduli     Dry rock     Mathematical formula     Sandstone    

1 引言

岩石的弹性性质显著依赖于孔隙系统的微观结构.绝大部分岩石通常发育两种乃至两种以上不同孔隙类型(孔隙、裂缝、洞等)的孔隙结构，复杂的孔隙系统使得岩石的速度与孔隙度之间的关系高度分散(Sayers，2008；Baechle et al., 2008)，因此，需要发展多重孔岩石物理模型来准确表征多孔岩石的弹性模量随孔隙度变化规律.

等效介质理论可用来研究多重孔岩石的弹性性质.常见的等效介质理论有Kuster-Toksöz理论和微分等效介质理论.Kuster和Toksöz(1974)基于波散射理论，考虑包裹体弹性性质、体积百分比和形状的影响，推导出多重孔岩石等效体积和剪切模量的显式表达式.但Kuster-Toksöz理论没有考虑孔隙间的相互作用，而且要求孔隙度与孔隙纵横比之比要远小于1.Kuster-Toksöz理论已被证明在某些情况下其估计的等效弹性模量与Hashin-Shtrikman上下限相冲突(Berryman，1980).微分等效介质(DEM)理论通过往固体矿物相中逐渐加入包裹体来模拟双相混合物，利用微分方程数值解研究干燥和饱和流体的多重孔岩石的等效弹性性质(Berryman，1980；Norris，1985；Zimmerman，1985；Berryman et al., 2002).与Kuster-Toksöz理论相比，DEM理论 从不越过Hashin-Shtrikman上下限(Berryman，1980； Berryman and Berge， 1996；Berryman et al., 2002).但是，由于关于体积和剪切模量的两个常微分方程是隐式的并且相互耦合，很难得到准确的便于分析的弹性模量解析公式.因此，体积和剪切模量的性质只能通过微分方程的数值解来模拟，而且，对于多孔介质来说，利用DEM所模拟的岩石等效弹性性质依赖于包裹体(即不同孔隙纵横比的孔或缝)的添加顺序(Norris，1985).

Xu和White(1995)在Kuster-Toksöz理论的基础上发展了一种针对泥质砂岩的双孔(软、硬孔)模型——Xu-White模型，两类孔隙的体积百分比分别由砂岩和粘土矿物的含量确定.但是该模型继承了Kuster-Toksöz存在问题，而且由于该模型采用了迭代算法，还存在计算效率的问题.Keys和Xu(2002)对Xu-White模型进行了改进，通过假设耦合方程中的干燥岩石的泊松比为常数的情形下得到干岩石骨架弹性模量，提高了运算效率.但是由他们给出的关系式推得的泊松比或模量比并不为常数.Xu和Payne(2009)把泥质砂岩的Xu-White模型推广到碳酸盐岩，得到Xu-Payne模型，但模型同样有Xu-White模型中存在的问题.

针对DEM理论缺乏解析式的问题，不少学者在这一方面做出了一些努力，取得一系列成果.Zimmerman(1991)从球孔的DEM方程得到干岩石骨架弹性模量的隐式解析式.Berryman等(2002)基于DEM理论得到干燥和完全饱和裂隙型岩石弹性 模量的近似解析式.Li和Zhang(2010，2012)为了解决体积和剪切模量方程组的耦合问题，借助于干燥岩石模量比的近似解析式，考虑三个特定孔隙形状：球孔、针形孔和币形缝，由微分方程推导出干燥岩石体积和剪切模量及弹性模量比的显式解析式.同样，Li和Zhang(2011)基于DEM理论还给出了椭球孔的干岩石 骨架模量的显式解析式.这些DEM解析模型目前是基于单重孔隙系统提出的，并已用于岩石的等效 孔隙纵横比反演及横波速度预测中(Li et al., 2013).

本文基于等效介质理论得到夹杂多重椭球孔的干燥岩石的体积和剪切模量的解析公式，利用它们来表征干燥多重孔岩石弹性模量随孔隙度的变化.首先，从Kuster-Toksöz理论的等效体积和剪切模量表达式出发，推导出Kuster-Toksöz理论的微分形式；然后，基于微分等效理论得到夹杂椭球形孔的干燥多重孔岩石的模量比公式，同时为了解决体积和剪切模量的两个常微分方程间的耦合问题，利用干燥多重孔岩石的模量比近似公式推导干燥多重孔岩石体积和剪切模量的解析式；接着，我们使用理论模型检查解析近似式的计算结果并与DEM微分方程的数值计算相比较，在所计算孔隙度的整个区间内讨论它们之间的一致性.最后，对实验室测量的干燥砂岩数据(Han et al., 1986)，利用解析近似式来预测多重孔岩石的弹性性质.

2 Kuster-Toksöz理论的微分形式及其数值解

Kuster和Toksöz(1974)用长波长一阶散射理论推导了含N种包裹体的岩石等效弹性模量的Kuster-Toksöz理论表达式K*KT和G*KT：

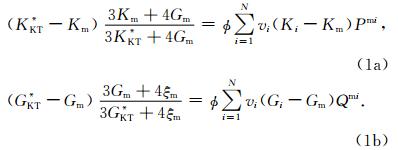
式中，Km和Gm分别是背景基质的体积和剪切模量，vi是第i种包裹体在孔隙度φ中所占的体积百分比(1≤i≤N)，Ki和Gi分别是第i种包裹体的体积和剪切模量，Pmi和Qmi是极化因子，描述了在背景介质m中加入包裹体i之后的效果，ξm= Gm(9Km+8Gm)/8(Km+2Gm)，上标*表示等效介质.

Kuster-Toksöz理论可以与微分等效介质理论结合在一起来估计多重孔岩石的弹性性质(Xu and White， 1995；Keys and Xu， 2002)，微分等效介质理论认为复合材料可通过在作为背景基质的复合材料中逐步加微小变化的包裹体来构造(Norris，1985；Mavko et al., 1998；Berryman et al., 2002).因此，当在孔隙度为y的复合材料中添加微量孔隙度dy时，此时式(1)中的Km和Gm分别相当于添加前的K*(y)和G*(y)，K*KT和G*KT分别相当于添加后的K*(y+dy)和G*(y+dy)，Pmi和Qmi变为P*i和Q*i，相当于添加前的等效介质中加入包裹体i之后的效果，因此式(1)重新写成

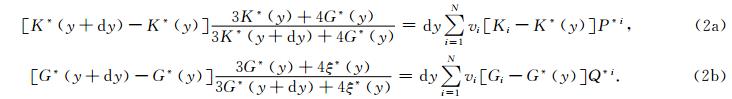
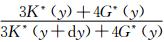由于dy<<1，因此式(2)中的≈1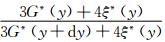，≈1. 令dK*(y)=K*(y+dy)－K*(y)，dG*(y)=G*(y+dy)－G*(y)，式(2)两边同时除以dy，则有

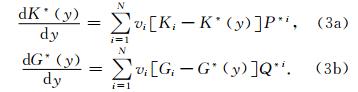
式(3)即为Kuster-Toksöz理论的微分形式.Zimmerman(1984)给出了包裹体为单一球孔的类似微分方程，该方程所蕴含的假设是当把新的孔隙加入到复合材料中时，它总是替代先前复合材料中的固体部分(Mavko et al., 1998)，式(3)目前常称之为Zimmermann形式的DEM方程.而Norris(1985)则认为新加入的孔隙既可能取代先前复合材料中的固体部分，也可能取代已存在于复合材料中的孔隙，它们的概率分别为1－y和y(Norris，1985；Mavko et al., 1998)，这样式(3)中的dy应为dy/(1－y)(Mavko et al., 1998)，因此式(3)变为

该式即为多重孔情形下Norris形式的微分等效介质模型，当N=1时，与经典的DEM表达式相同(Norris，1985；Mavko et al., 1998；Li and Zhang， 2010).这些方程通常从孔隙度y=0开始积分，并满足初始条件K*(0)=Km和G*(0)=Gm，然后继续从y=0至所需的最高值y=φ积分.

等效微分介质方程(4a)和(4b)一般是相互耦合的，因为这两个方程都取决于复合材料的体积和剪切模量.因此，很难通过对DEM方程积分得出复合材料体积和剪切模量的解析公式.

我们对微分方程(3)和(4)进行数值求解并对其结果进行比较.以石英作为主介质，其体积和剪切模量分别取为Km=44 GPa和Gm=37 GPa.岩石中含有三种不同形状的孔隙，其孔隙纵横比α分别为1.0，0.5和0.01，它们的孔隙体积百分比分别取为98.99%，1%和0.01%，以满足Kuster-Toksöz理论中假设的每种包裹体的孔隙度与孔隙纵横比要远小于1的要求(Kuster and Toksöz，1974).使用四阶龙格-库塔法来计算微分方程的数值解，数值积分中应用的步长取为Δy=0.01.考虑孔隙中充填了两种不同类型的材料，一种是固体，一种是干燥空腔，固体包裹体的弹性模量分别取为Ki=14 GPa和Gi=10 GPa，而干燥空腔的弹性模量则简单置为零.图 1是两种形式的DEM方程数值解结果对比，式(3)的数值解用粉红点显示，式(4)的数值解用蓝点显示，我们还给出了Kuster-Toksöz理论的估计结果，图中用黑点显示，同时还计算了Hashin-Shtrikman边界(Mavko et al., 1998)，图中用红线显示.图 1a，1b分别是含固体包裹体的岩石等效体积和剪切模量数值比较结果.图 1c，1d分别是含干燥空腔的岩石等效体积和剪切模量数值比较结果.可以看到，两种包裹体的Kuster-Toksöz理论计算结果与Hashin-Shtrikman上边界完全相同，式(3)的数值解在孔隙度较低时与Kuster-Toksöz理论相接近，而随着孔隙度的增大，式(3)的数值解则与Kuster-Toksöz理论相差越来越大，远超Hashin-Shtrikman上边界，而不具有物理意义.可见式(3)只适合于孔隙度很低时的多孔岩石弹性模量模拟.而式(4)的数值解始终位于Hashin-Shtrikman边界之间.由于式(3)在孔 隙度较大时其估计的等效弹性模量与Hashin-Shtrikman上下限相冲突，在下面的数值试验中，我们只使用式(4)来估计多重孔岩石的等效弹性模量.

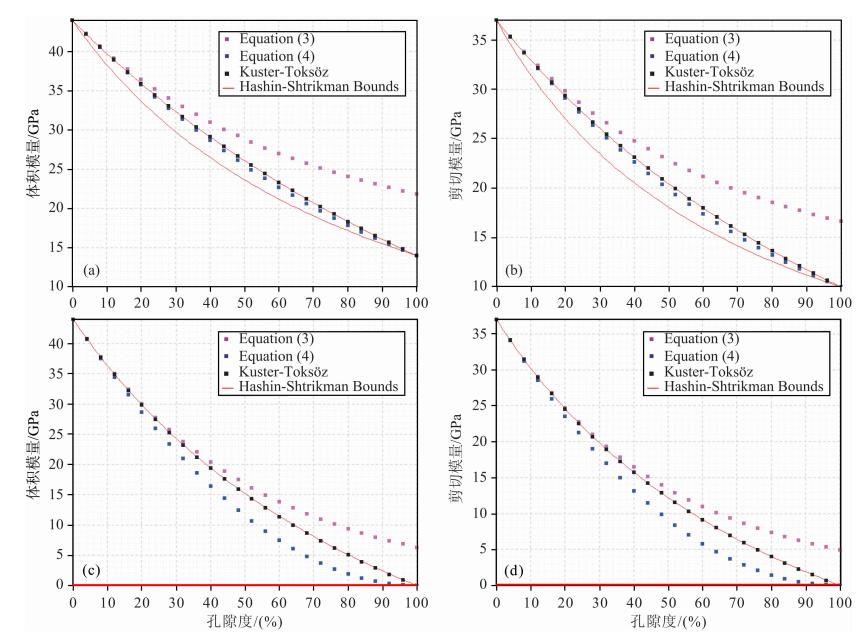图 1 多重孔岩石DEM方程数值解与Kuster-Toksöz理论结果对比
(a)含固体包裹体的岩石体积模量；(b)含固体包裹体的岩石剪切模量；(c)含干燥空腔的岩石体积模量；(d)含干燥空腔的岩石剪切模量. Fig. 1 Comparison of the numerical solutions of the DEM equations and Kuster-Toksöz estimates for porous rock
The bulk(a) and shear(b)moduli for solid inclusions. The bulk(c) and shear(d)moduli for dry-inclusions.
3 干燥多重孔岩石弹性模量DEM解析近似式

对于干燥岩石，每种包裹体的弹性模量Ki=0和Gi=0(1≤i≤N)，式(4)变成

和

同样，式(5a)和(5b)也是相互耦合的，因为这两个方 程也依赖于复合材料的体积和剪切模量(Berryman，1980； Li and Zhang， 2011).因此，同样很难对DEM方程积分得到干燥多重孔岩石体积和剪切模量的解析公式.采用Li和Zhang(2010，2011)类似的假设，即等效极化因子之差P*eff－Q*eff和等效模量比K*(y)/G*(y)之间存在一个几乎线性的关系，我们可以得到干燥多重孔岩石的模量比解析公式(公式推导见附录A)

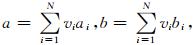式中，Kdry和Gdry分别为干燥多重孔岩石的体积模量和剪切模量，常数a和b分别为满足P*eff－Q*eff=a+bK*(y)/G*(y)的截距和梯度(Li and Zhang， 2010)，常数ai和bi分别为第i种孔隙(由于包裹体中没有流体，此时包裹体实为孔隙)的P*i－Q*i的截距和梯度，常数bi可以简单设置为极化因子之差P*i－Q*i的一阶导数在K*/G*=Km/Gm时所取的值，bi已知后常数ai就能够由公式P*i－Q*i=a+bK*(y)/G*(y)来计算得到(Li and Zhang， 2011，2012)，椭球包裹体的极化因子之差P*i－Q*i及其一阶导数见Li和Zhang(2011)论文的附录A.

为了解决体积模量和剪切模量微分方程间的耦合问题，把式(6)代入到式(5a)中，然后在积分区间[0，φ]对之进行积分，直接得到有关Kdry的解析式，接着用Kdry的解析式除以式(6)就得到相应的Gdry的解析式，因此有(公式推导见附录B)

式中

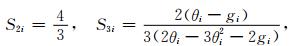
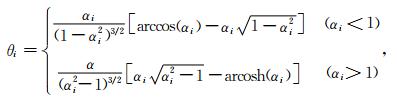
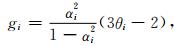，αi为第i种椭球孔的纵横比.

4 理论和实验室数据比较

式(7)—(8)可以用来研究孔隙岩石中含有两种或两种以上孔隙形状的干燥岩石等效弹性性质.目前大多数研究主要针对双重孔岩石(Xu and White， 1995)，为了方便对比，我们这里也只对干燥双重孔岩石体积和剪切模量的解析式作理论和实验室数据分析.

首先对微分方程的数值解与解析式的结果作比较.同样以石英作为主介质，其体积和剪切模量与图 1相同，分别取为Km=44 GPa和Gm=37 GPa.岩石中含有两种不同形状的孔隙，其孔隙纵横比α分别为0.15和0.005，分别代表孔和缝.为了表征不同孔缝发育程度对岩石弹性性质的影响，考虑了三种不同的孔缝体积百分比，分别为(90%，10%)、(50%，50%)和(10%，90%).同样使用四阶龙格-库塔法来计算微分方程(5)的数值解.图 2是解析和数值解的比较结果，图中，点代表数值结果，实线代表由式(7)—(8)计算的解析结果，式(7)—(8)中的常数b简单设置为极化因子之差的一阶导数在K*/G*=Km/Gm=1.1892时所取的值，b已知后常数a就可由公式P*i－Q*i=a+bK*(y)/G*(y)来计算(具体公式见附录A中).结果表明，无论是体积模量还是剪切模量，三种不同孔缝体积百分比情况下的解析解与数值解都充分吻合.随着裂缝体积百分比的增大，岩石的等效弹性模量总体呈下降趋势，裂缝体积百分比从10%增加到50%时弹性模量的下降速率比其从50%增加到90%时的速率要大很多.

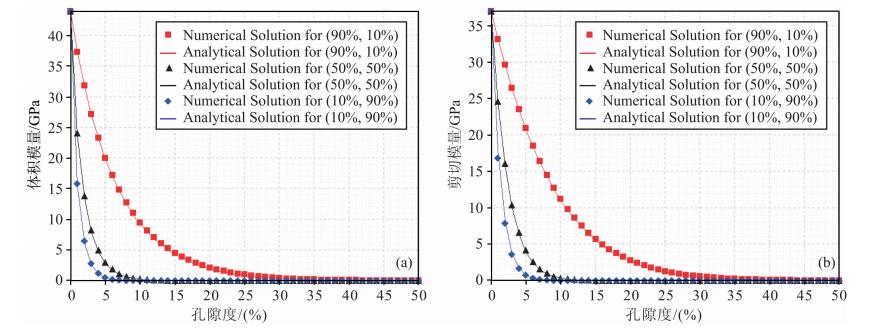图 2 干燥双重孔岩石不同孔隙体积比的(a)体积和(b)剪切模量数值解与解析式预测结果对比 Fig. 2 Comparison of the numerical and analytical solutions of dry-rock bulk(a) and shear(b)moduli for dual-porosity rock with different pore volume percentages

我们利用Han等(1986)测量的69个干燥砂岩 的岩石物理数据来分析解析式的预测效果.所测量的纵波和横波速度数据是在围压40 MPa下分别采用超声频率1 MHz和0.6 MHz完成的，砂岩样品的孔隙度分布范围为5％~30％，粘土含量分布范 围为0~50％.图 3a是69个干燥样品的纵波速度 与孔隙度之间的关系.测量结果表明，干燥碎屑岩的纵波速度随孔隙度增加而降低，随着粘土含量的增大而下降.用于分析的矿物弹性模量由Han提供，其中矿物石英的体积和剪切模量分别为40 GPa和43.7 GPa，粘土的体积和剪切模量分别为20.9 GPa和6.85 GPa.我们采用双重孔DEM解析模型来研究测量样品的弹性模量，硬、软孔的孔隙纵横比分别取为0.18和0.04.在运用式(7)和(8)预测弹性模量随孔隙度的变化时还需提供两种孔隙的体积百分比.图 3b显示了69个样品中10个纯砂岩样品的干燥岩石的体积模量在不同的孔隙体积百分比条件下随孔隙度的变化特征，从图中可以看到，当软孔的孔隙体积百分比Vcp=0时，只有两个点位于预测的曲线上，而有一个点(孔隙度等于6%)偏离Vcp=0的预测曲线最远.逐步增加软孔的体积百分比，直至Vcp=25%时，其模量预测曲线才与这个点接近吻合.这说明10个样品中只有2个样品不发育软孔，其他8个样品同时发育软硬孔，但各个样品的软硬孔发育程度不尽相同.我们使实验室测量的纵波模量与式(7)和(8)理论预测的模量之间的平方误差最小来估计每个砂岩样品的软孔体积百分比.图 3c显示了反演的软孔体积百分比与粘土含量之间的关系，总体看，岩石的孔隙度越大，其软孔体积百分比越小，但软孔体积百分比与粘土含量没有明显的正相关.根据式(7)和(8)和反演的软孔体积百分比可以正演得到干燥岩石样品的横波速度，图 3d是预测与测量的横波速度之间的对比，图中还显示了每个点在置信水平为95%的误差棒.可以看到，绝大多数样品的预测值与实测值吻合良好，这说明碎屑砂 岩的孔隙结构可以用双重孔DEM解析模型来表征.

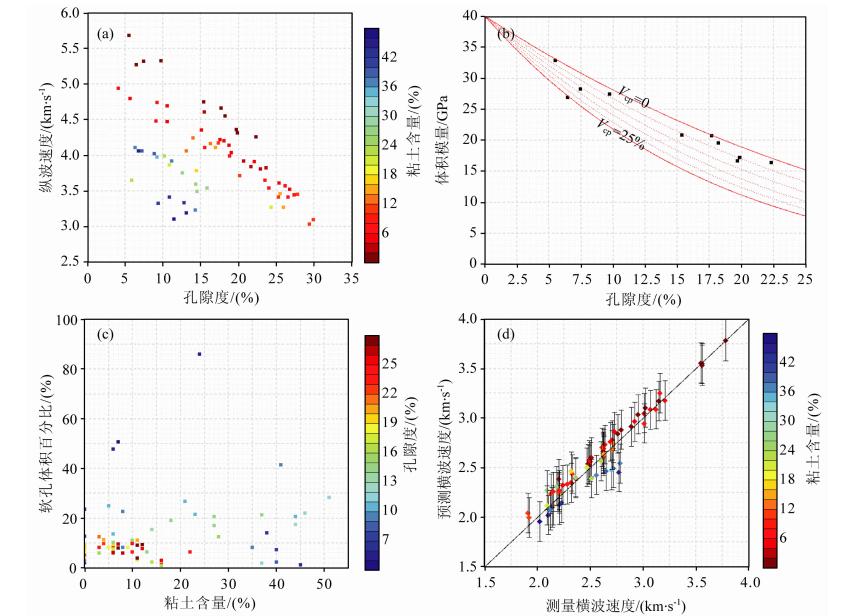图 3 实验室测量的干燥砂岩样品的速度与解析式预测结果对比
(a)纵波速度与孔隙度之间的关系；(b)纯净砂岩样品的体积模量与理论预测比较；(c)估计的软孔体积百分比 与粘土含量之间的关系；(d)实验室测量的横波速度与理论预测. Fig. 3 Result analysis of the experimental s and stone data measured by Han(1986) and theoretical estimations of the DEM analytical formulae for dual-porosity rock
(a)P wave versus porosity for experimental data;(b)Bulk modulus versus porosity for 10 samples of clean s and stone and the theoretical predictions;(c)The estimated compliant pore volume percentage versus clay volume;(d)Comparison of S wave between the experimental result and the theoretical calculation from the estimated pore volume percentage.
5 结论

借助于Kuster-Toksöz理论，本文建立了Zimmermann和Norris两种形式的多重孔岩石微分等效介质方程，并由Norris形式的微分方程推导出干燥多孔岩石体积和剪切模量的解析式.解析式是矿物颗粒的体积和剪切模量、孔隙度、孔隙体积百分比和孔隙几何形状的函数，孔隙几何形状由参数截距a和梯度b来表征，它可以根据每种孔隙的极化因子之差及其一阶导数在等效模量比等于矿物颗粒模量比取的值近似计算得到.

多重孔岩石微分等效介质模型避免了经典的DEM方程在用于研究多重孔岩石的弹性性质时其估计的等效弹性模量依赖于包裹体的添加顺序问题.当多重孔退化为单重孔时，多重孔岩石DEM方程即为经典的DEM方程.

数值试验结果表明，Norris形式的多重孔DEM方程估计的等效弹性模量始终位于Hashin-Shtrikman 上下限内，而Zimmermann形式的多重孔DEM方程在孔隙度较大时其估计的等效弹性模量与Hashin-Shtrikman上下限相冲突，因此后者只适合于孔隙度很低时的多重孔岩石弹性模量模拟.

理论模型和实验室数据试算表明：解析式的计算结果与全DEM方程的数值解吻合良好.多重孔DEM解析式可以准确地预测弹性模量随孔隙度的变化.双重孔(即软、硬孔)DEM解析模型可以用来反演各孔隙类型的孔隙体积比，它可以通过实验室测量与理论预测之间的平方误差最小反演得到.砂岩样品的反演结果揭示，软孔的孔隙体积百分比与粘土含量没有明显的正相关.

致谢 感谢匿名评阅人对本文提出的宝贵修改意见.

附录A 多重孔干燥岩石模量比的解析式推导

首先定义等效极化因子，它们是介质中包含的所有孔隙的极化因子的体积加权，即

和

于是式(5)变成

和

由此可见，式(A3)—(A4)与经典的单重孔DEM微分方程形式(Norris，1985；Mavko， et al.， 1998；Li and Zhang， 2010)完全一致，其解析近似式可用类似于Li和Zhang(2011，2012)的方法得到.

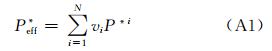
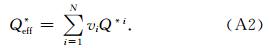
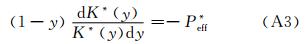
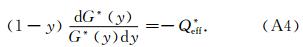
式(A3)减去式(A4)得到

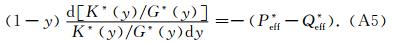
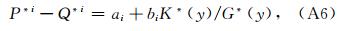
Li和Zhang(2010)假设干燥单重孔岩石的极化因子P*i和Q*i之差(P*i－Q*i)与干岩石模量比K*(y)/G*(y)之间存在近似线性关系，也就是说对于多重孔岩石中的第i个孔隙来说，有

式中ai和bi取决于孔隙形状，而且ai<0，bi≥0.这种假设对多重孔隙系统同样适用，因为

式中

将式(A7)代入到式(A5)中，可得到

式(A8)进一步分解成

在积分区间[0，φ]对式(A9)进行积分，并满足初始条件

得到

式中0≤φ<1.式(A11)进一步整理写成

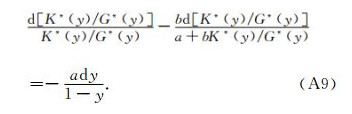
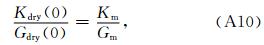
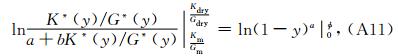
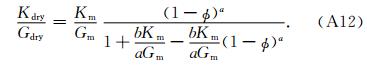
附录B 多重孔干燥岩石体积和剪切模量的解析式推导

根据Li和Zhang(2011)论文的附录A，干燥多重孔岩石中第i个椭球孔的极化因子为

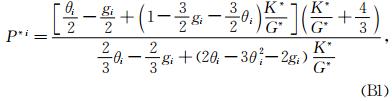
式中， αi为第i个椭球孔的孔隙纵横比.因此，极化因子P*i是等效模量比K*/G*和孔隙纵横比的函数.

由式(5a)和式(B1)，有

式(B2)右边进一步分解成

式中

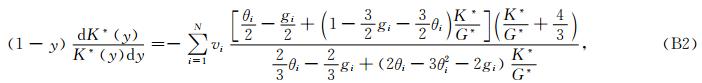
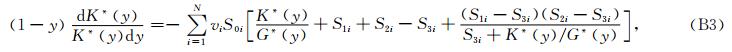
对式(B3)右边的最后一项在y=0附近作泰勒展开，则式(B3)可写为

对于干燥岩石，式(B8)中的K*(y)/G*(y)=Kdry(y)/Gdry(y).把式(6)代入到式(B8)，并对其在y=0到φ积分，由于0≤y≤φ和0≤φ≤1，忽略φ的平方以上项，得到

对式(B9)整理得到

式(B10)除以式(6)，得到

参考文献
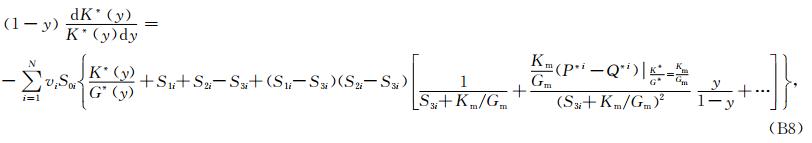
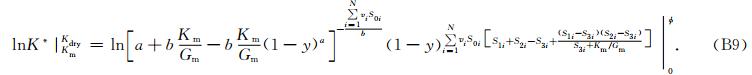
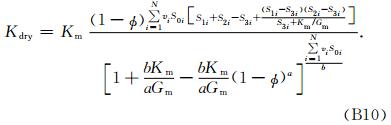
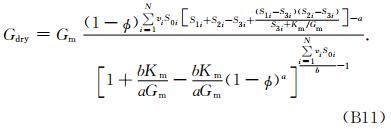
[1] Baechle G T, Colpaert A, Eberli G P, et al. 2008. Effects of microporosity on sonic velocity in carbonate rocks. The Leading Edge, 27(8): 1012-1018.
[2] Berryman J G. 1980. Long-wavelength propagation in composite elastic media II. Ellipsoidal inclusions. J. Acoust. Soc. Am., 68(6): 1820-1831.
[3] Berryman J G, Berge P A. 1996. Critique of two explicit schemes for estimating elastic properties of multiphase composites. Mech. Materials, 22(2): 149-164.
[4] Berryman J G, Pride S R, Wang H F. 2002. A differential scheme for elastic properties of rocks with dry or saturated cracks. Geophys. J. Int., 151(2): 597-611.
[5] Han D H, Nur A, Morgan D. 1986. Effects of porosity and Clay content on wave velocities in sandstones. Geophysics, 51(11): 2093-2107.
[6] Keys R G, Xu S Y. 2002. An approximation for the Xu-White velocity model. Geophysics, 67(5): 1406-1414.
[7] Kuster G T, Toksöz M N. 1974. Velocity and attenuation of seismic waves in two media, Part I. Theoretical considerations. Geophysics, 39(5): 587-606.
[8] Li H B, Zhang J J. 2010. Modulus ratio of dry rock based on differential effective-medium theory. Geophysics, 75(2): N43-N50.
[9] Li H B, Zhang J J. 2011. Elastic moduli of dry rocks containing spheroidal pores based on differential effective medium theory. J. Appl. Geophys., 75(4): 671-678.
[10] Li H B, Zhang J J. 2012. Analytical approximations of bulk and shear moduli for dry rock based on the differential effective medium theory. Geophys. Prospect., 60(2): 281-292.
[11] Li H B, Zhang J J, Yao F C. 2013. Inversion of effective pore aspect ratios for porous rocks and its applications. Chinese J. Geophys. (in Chinese), 56(2): 608-615.
[12] Mavko G, Mukerji T, Dvorkin J. 1998. The Rock Physics Handbook: Tools for Seismic Analysis in Porous Media. New York: Cambridge University Press.
[13] Norris A N. 1985. A differential scheme for the effective moduli of composites. Mech. Materials, 4(1): 1-16.
[14] Sayers C M. 2008. The elastic properties of carbonates. The Leading Edge, 27(8): 1020-1024.
[15] Xu S Y, Payne M A. 2009. Modeling elastic properties in carbonate rocks. The Leading Edge, 28(1): 66-74.
[16] Xu S Y, White R E. 1995. A new velocity model for clay-sand mixtures. Geophys. Prospect., 43(1): 91-118.
[17] Zimmerman R W. 1984. Elastic moduli of a solid with spherical pores: new self-consistent method. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 21(6): 339-343.
[18] Zimmerman R W. 1985. The effect of microcracks on the elastic moduli of brittle materials. J. Mater. Sci. Lett., 4(12): 1457-1460.
[19] Zimmerman R W. 1991. Elastic moduli of a solid containing spherical inclusions. Mech. Materials, 12(1): 17-24.
[20] 李宏兵, 张佳佳, 姚逢昌. 2013. 岩石的等效孔隙纵横比反演及其应用. 地球物理学报, 56(2): 608-615.