2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
电磁波信号穿过地球大气到达接收机的过程中,大气折射使信号的传播速度和方向同时发生变化,产生延迟效应.中性大气层分为对流层和平流层,对流层包括80%以上的大气质量和几乎全部的水汽,而气体和水汽的密度直接决定着信号延迟的程度,因此发生在中性大气层中的电磁波信号延迟被统称为对流层延迟.对流层延迟是无线电导航定 位的主要误差源之一,例如在GNSS(Global Navigation Satellite System)导航定位中,对流层延迟在天顶方向约为2 m,随着高度角的降低这一值将增大至20 m(Dodson et al.,1999).由于中性大气层不是色散介质,为了进行信号传播路径上的延迟改正,通常需要先借助对流层天顶延迟模型计算天顶方向的延迟量(Zenith Tropospheric Delay,ZTD),再将天顶延迟通过映射函数投影到斜方向.即使是在将对流层延迟作为待解参数进行数据处理的过程中,仍然需要模型确定的天顶延迟作为先验值.因此对流层天顶延迟的建模一直是一项非常重要的工作.
目前国际上常用的对流层天顶延迟模型有Hopfield、Saastamoinen、EGNOS、UNB系列等模 型.其中传统的Hopfield(Hopfield,1971)、Saastamoinen(Saastamoinen,1972)模型改正精度可达厘米或分米级,但该类模型需要已知目标位置实测的气象参数,当利用参考大气进行计算时,其精度显著下降,这在很大程度上限制了它们在实时动态定位导航中的应用.为了适应增强导航系统中的对流层延迟改正的需求,一系列不依赖实测气象参数的模型得到 了发展,如EGNOS(Dodson et al.,1999;Penna et al.,2001)、UNB系列模型(Collins and Langley 1996a,1996b; Le and ro et al.,2006,2008).这类模型将气象参数(压强、温度、水汽压、温度递减率、水汽递减率)沿纬度带网格化,每15°纬度提供一组年均值及振幅,用户利用自己的位置信息获得这些参数从而进一步计算天顶延迟,精度也可达厘米级.但该类模型空间分辨率低,提供的仅仅是一个全球平均的修正结果,而且模型中南北半球对称、低纬地区参数年际变化缺失等不合理设置导致这些模型在某些区域的误差较大.
对流层延迟的值与目标高程密切相关,对流层延迟改正不当引起的误差将会影响数据处理中所有待估参数的解算精度,特别是待定点垂直坐标分量的精度.近年来,直接模制天顶延迟时空变化特征的方法在一些对流层天顶延迟建模的研究中得到了应用,如Song等(2011)建立的SHAO-C模型、陈钦明等(2011a)建立的SHAO-G模型、Li等(2012)建立的IGGtrop模型以及姚宜斌等(2013)建立的GZTD模型等.这些模型采用二次多项式或指数函数表征天顶延迟随高程的变化,但我们通过研究发现,这两种方法均会引起模型随高程变化的系统误差,不适宜目标位置与模型中的参考位置高差过大时的对流层延迟改正.随着航空航天科技的发展,GNSS、VLBI等观测技术已经广泛应用于各类空间飞行器的导航和制导,飞行器动态导航定位的过程中需要在不同大气高度上对对流层延迟误差进行修正,飞行器位置变化随机性强、延迟修正计算实时性要求高,已有的对流层延迟模型难以满足该类应用需求.
本文利用ERA-Interim再分析气象资料计算获得全球1.5°×1.5°格网点上天顶延迟垂直剖面时间序列,对天顶延迟在全球范围内随高度变化的模制方法进行了详细的讨论,并以此为基础建立了新的对流层天顶延迟改正模型SHAO-H.精度检验表明,该模型适宜中性大气范围内任意高度的对流层天顶延迟计算,在全球范围内的精度优于UNB3m模型,用户可以根据目标三维位置直接确定对应的延迟改正,计算简便. 2 天顶延迟随高程变化最佳拟合形式的探讨
ERA-Interim是欧洲中尺度天气预报中心(European Centre for Medium-Range Weather Forecast,ECMWF)提供的最新的全球大气再分析产品,它重点改进了之前产品在水文循环、平流层环流质量以及再分析物理场时间一致性等方面遇到的问题(Dee et al.,2011).相较于之前的产品,该数据集具有更高的精度、更精细的空间分辨率以及更稳定的长期一致性.根据Chen等(2011b;2012)的研究结果,与实测的天顶延迟相比,采用ECMWF分层气象资料积分方法计算的天顶延迟的精度约为3 cm,可用于高精度天顶延迟建模的研究.本文采用的ERA-Interim分层格网资料平面分辨率为1.5°×1.5°,时间分辨率为6 h,每个格网点包括按等压层分布的37层数据,最高层高度约为50 km,几乎覆盖全部对流层以及平流层.ZTD根据成因进一步可分为天顶静力学延迟(Zenith Hydrostatic Delay,ZHD)和天顶非静力学延迟(Zenith Wet Delay,ZWD),由各层气象参数计算大气折射率,进而对折射率在各层高度上积分,最终可以获得ZTD、ZHD和ZWD在每个格网点上的垂直剖面.具体公式(Thayer,1974)概述如下:

SHAO模型(Song et al.,2011;陈钦明等,2011a)利用二次多项式模制10 km以下ZTD随高程的变化,其精度满足地面导航用户的需求.利用上述ZTD垂直剖面对10 km以下ZTD和高程的变化关系采用如式(7)所示的二次多项式进行拟合,其中Z表示剖面上各点位的积分ZTD,a0,a1和a2为拟合所得多项式系数.将由拟合系数计算得到的ZTD和原始积分ZTD进行比较,如图 1所示是以2005年四个季节中任选的一个时刻为例全球全部1.5°格网点上的残差分布情况.由图 1可知该拟合方法的残差呈现一定的系统性变化,其中最大值可达到5 cm.IGGtrop模型(Li et al.,2012)和GZTD模型(姚宜斌等,2013)采用指数关系模制ZTD在垂直方 向的变化.其中IGGtrop模型参数表为2.5°×2.5°×1 km 的三维结构,可以从一定程度上避免引起系统误差,但过多的参数个数给模型的使用带来了困难.GZTD模型在全球范围内使用一个统一的高程改正常数将平均海平面处的ZTD改正到目标高程位置.利用上述ZTD垂直剖面对ZTD和高度的变化关系采用如式(8)所示的指数函数进行拟合,参数意义同上,得到了如图 2所示四个季节任选的一个时刻全球1.5°格网点上拟合ZTD和原始积分ZTD的残差序列集合.由图 2可知,在较大高程范围内采用单一的指数高程改正数模制ZTD在垂直方向上的变化,仍然会引起最大约为5 cm的系统偏差.
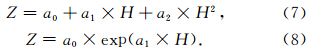
 | 图 1 全球1.5°格网点上二次多项式拟合ZTD随高程变化与原始积分ZTD的残差集合(10 km以下)Fig. 1 Residuals of fitting ZTD variation with height by quadratic polynomial,compared with integral ZTD at all 1.5° grid points(under 10 km) |
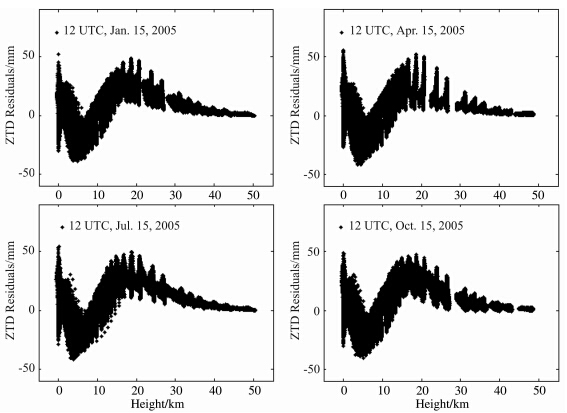 | 图 2 全球1.5°格网点上指数函数拟合ZTD随高程变化与原始积分ZTD的残差集合Fig. 2 Residuals of fitting ZTD variation with height by exponential function,compared with integral ZTD at all 1.5° grid points |
由以上分析可知,采用单一的函数模制ZTD在垂直方向上的变化往往存在一定的不足,因此我们考虑引入分段函数.ZTD由ZHD和ZWD两部分组成,如图 3—5显示了任取的一个时刻(2005年7月15日12 UTC)分布于不同纬度带的所有格网点上的ZHD、ZWD和ZTD的垂直剖面集合.由图可知,由于ZHD主要由干大气决定,而干大气的分布在全球范围内比较均匀,整体上ZHD随高程的增大平稳地减小,不同高程范围内减小的速率不同,不同地理位置的ZHD剖面没有明显的差别.对于由水汽引起的ZWD,不同地理位置的ZWD差异较大,且存在随纬度增大而减小的现象,总体上虽然ZWD仍然随着高程的增高而减小,但变化过程比较复杂.由于ZHD约占ZTD的90%以上,图 5显示的ZTD随高程变化的规律与ZHD相似.空气中的水汽变化随机性强,ZWD模型化的精度一直是制约ZTD模型精度的主要因素.通常对流层指从地面向高空延伸到对流层顶的大气,对流层集中了约75%的大气质量和几乎全部的水汽.对流层顶的高度随纬度和季节的变化而变化,在低纬地区平均约为17 km,极区平均约为8 km(盛裴轩等,2003;Seidel and R and el,2006).水汽在对流层内不同高度下降 速率不同,约有50%的水汽集中在地面附近1.5 km 以内,而5 km以上的水汽含量则不足10%(盛裴轩等,2003).根据大气中水汽的这一变化规律,我们将ERA-Interim资料涵盖的全部50 km大气以5 km和17 km为分段点分为三个高度区间,在三个区间内分别利用前文中的指数函数、二次多项式以及(9)式所示的三次多项式三种函数形式对每个格网点上ZHD和ZWD随高度的变化进行拟合,以评估得出每个区间内ZTD的最佳拟合函数形式.
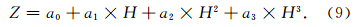
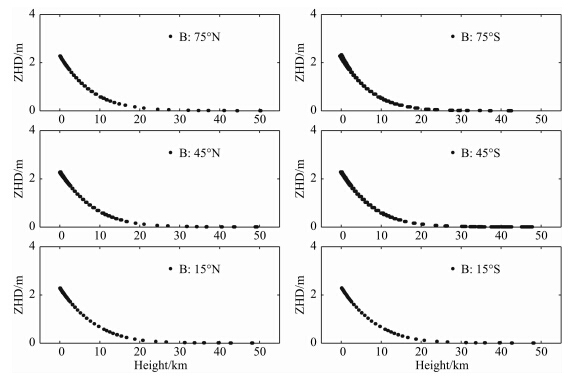 | 图 3 不同纬度带上的1.5°格网点的ZHD垂直剖面集合(2005-07-15 12 UTC)Fig. 3 ZHD vertical profiles at all 1.5° grid points in different latitude b and s(12 UTC,July 15,2005) |
 | 图 4 不同纬度带上的1.5°格网点的ZWD垂直剖面集合(2005-07-15 12 UTC)Fig. 4 ZWD vertical profiles at all 1.5° grid points in different latitude b and s(12 UTC,July 15,2005) |
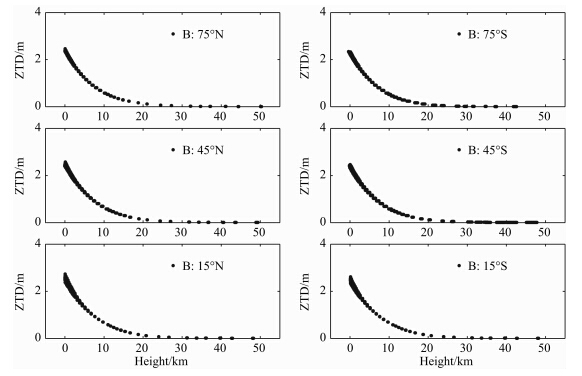 | 图 5 不同纬度带上的1.5°格网点的ZTD垂直剖面集合(2005-07-15 12 UTC)Fig. 5 ZTD vertical profiles at all 1.5°grid points in different latitude b and s(12 UTC,July 15,2005) |
采用上述策略对2005年和2006年不同时刻每个网格点处的ZHD和ZWD随高程的变化进行拟合试验,试验结果显示:对于ZHD,与其他两种拟合方法比较,在17 km以下使用两个三次多项式、在17 km以上使用指数函数拟合的残差最小且分布比较平稳,与积分ZHD相比,以上最佳分段函数形式在任意时刻任意位置拟合计算ZHD的偏差均不超过4 mm;对于ZWD,首先由于对流层顶以上水汽含量极其有限,我们定义17 km以上的ZWD值为0,其次在5~17 km范围内,指数函数与三次多项式的拟合精度相差不多而均好于二次多项式的拟合精度,与积分ZWD相比,以上最佳分段函数形式拟合计算的ZWD的偏差最大约为10 mm,较大的偏差多发生在靠近地面的区域.由于ZTD可以看作是ZHD和ZWD的线性叠加,根据以上分析,最终确立的ZTD随高程变化的模型形式如下:
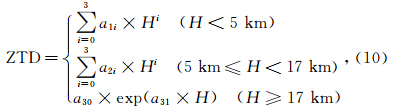
式中i表示多项式的次数,a为拟合函数系数.
如图 6显示了4个季节任选的一个时刻由(10)式所示的分段函数拟合ZTD与积分ZTD在全球全部1.5°格网点上的残差集合.由该图可知以上确定的分段函数可以较好地匹配任意区域内ZTD随高度的变化趋势,不同季节的拟合精度差异不大,拟合残差比较均匀地分布在0附近,但在地面附近的值偏大,最大值约为1 cm.
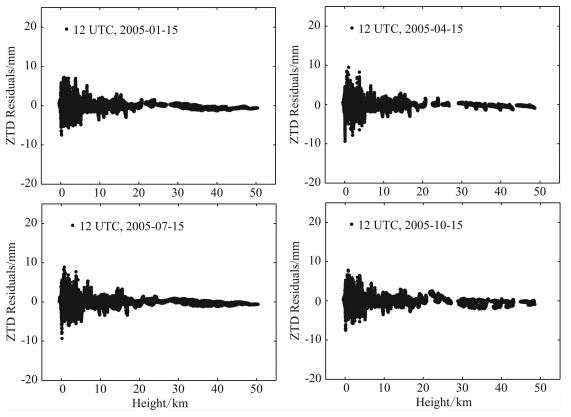 | 图 6 全球1.5°格网点上分段函数拟合ZTD随高程变化与原始积分ZTD的残差集合Fig. 6 Residuals of fitting ZTD variation with height by piecewise function,compared with integral ZTD at all 1.5°grid points |
根据第2节确定的ZTD随高程变化的函数表达式,适合任意高度用户使用的ZTD模型SHAO-H的基本形式确立如下:
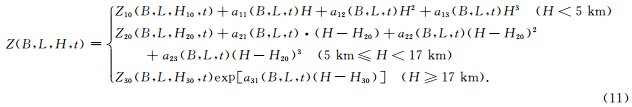
利用2005到2006年两年每个格网点的每个时刻上ERA-Interim分层气象资料计算的ZTD垂直剖面按(11)式进行拟合,生成(11)式中各参数的时间序列.(11)式中B表示纬度,L表示经度,H表示高程,Z表示由三维位置和时间决定的ZTD.SHAO-H模型将ZTD表示为高程的分段函数,在不同高程范围内均设置一个参考高度作为起算点,各层的起算高度分别为H10=0 km((11)式中省略未写明),H20=5 km,H30=17 km,则Z10、Z20以及Z30分别表示各层起算高度上的ZTD,不同脚标的参数a表示与ZTD随高程变化有关的改正系数.
根据姚等(2013)的分析,采用如(12)式所示的均值加周年和半周年周期函数的形式可对ZTD随时间的变化达到较好的拟合效果,IGGtrop(Li et al.,2012)和SHAO(Song et al.,2011;陈钦明等,2011a)模型中则利用了(13)式所示的均值加周年周期函数的形式对ZTD进行拟合.两式中mean表示年均值,amp表示周期函数振幅,d表示以年积日为单位的周期函数相位.分别采用(12)式和(13)式对前文得到的全球范围内1.5°格网点上的Z10、Z20和Z30时间序列进行拟合,年均值、振幅以及相位均由拟合具体获得,图 7—9显示了各参数由两种函数形式进行拟合与原始值统计的RMS的差异.由图可知,相比仅考虑周年变化,加入半周年周期变化的拟合方法会引起Z10拟合最大约为1.4 cm的精度提升,而两种拟合方法的差异对Z20拟合精度产生的影响在全球绝大部分地区在0.1 cm以内且最大不超过0.5 cm、对Z30拟合精度的影响在全球范围内不超过0.2 cm.由以上分析可知忽略Z20和Z30半周年变化对拟合精度的影响很小,考虑到模型参数的简化,采用(13)式所示的形式模拟Z20和Z30在时间域内的变化,对于Z10随时间的周期性变化则同时保留周年项和半周年项,模型形式如(12)式所示.

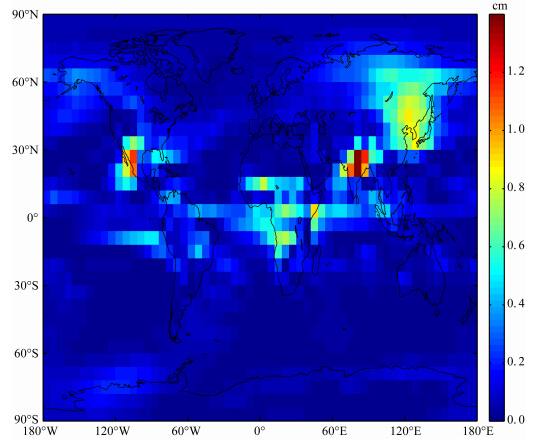 | 图 7 式(12)和式(13)两种函数形式拟合Z10的RMS的差异Fig. 7 Differences of RMS between the fittings of Z10 with equation(12) and equation(13) |
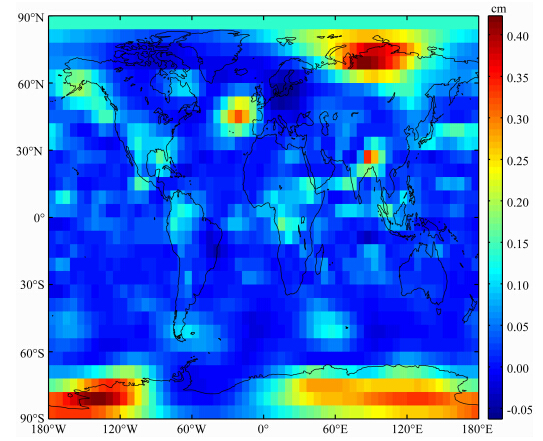 | 图 8 式(12)和式(13)两种函数形式拟合Z20的RMS的差异Fig. 8 Differences of RMS between the fittings of Z20 with equation(12) and equation(13) |
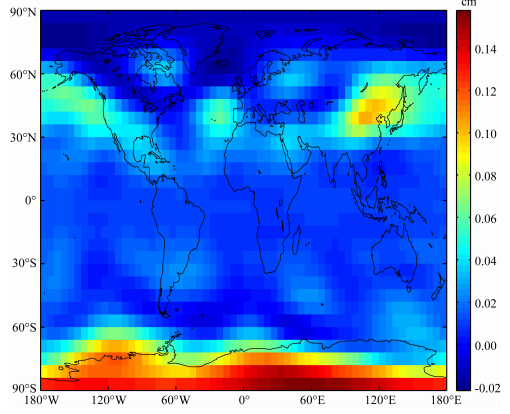 | 图 9 式(12)和式(13)两种函数形式拟合Z30的RMS的差异Fig. 9 Differences of RMS between the fittings of Z30 with equation(12) and equation(13) |
图 10显示了任选的一个格网点上SHAO-H模型中各ZTD高程改正参数的时间序列图,由图可知各参数均有明显的季节性变化,对各参数采用式(13)所示的函数形式进行时间域内的拟合,所得年均值和周年振幅在全球1.5°格网点上的均值如表 1所示.由该表可知,高阶项系数比低阶项系数的年均值和周年振幅均明显小得多,但考虑到高差过大时这些参数的变化引起的ZTD的变化也会达到数个厘米,SHAO-H模型中对a11、a12、a13、a21、a22和a23等参数随时间的变化均采用式(13)所示的函数形式 进行模型化.由于模型中最高层中的ZTD普遍较小,a31的季节性变化引起的最终ZTD的变化为极小值、可以忽略,模型中a31在每个网格点上仅取年均值.
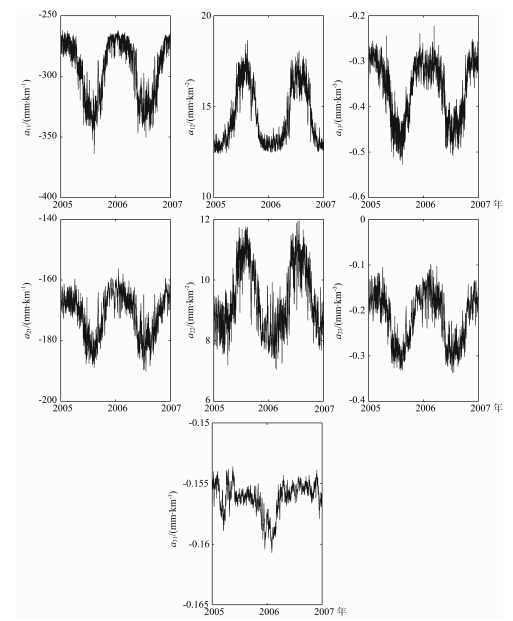 | 图 10 SHAO-H模型中高程改正参数时间序列图Fig. 10 Time series of the correction factors with respect to height in the SHAO-H model |
| | 表 1 SHAO-H模型中高程改正参数年均值和周年振幅的全球均值(单位:mm) Table 1 Global means of annual average and amplitude of the correction factors with respect to height in the SHAO-H model(unit: mm) |
以上分析确定的SHAO-H模型最终共包含30个模型参数,利用ERA-Interim2005、2006两年的分层气象资料在全球1.5°格网点上拟合各模型参数,每一个参数单独存储为一个文件,用户根据目标的三维坐标查找到离目标最近的格网点上的各模型系数进而可以计算所需任意时刻的ZTD.表 2以位于上海的IGS站SHAO为例,给出了SHAO-H模型中对应该站的格网点上各模型系数的具体数值.
| | 表 2 SHAO-H模型对应SHAO站位置的格网点的各模型系数 Table 2 Parameters in the SHAO-H model corresponding to the grid nearby SHAO |
利用ERA-Interim 2011年分层气象资料计算 的积分ZTD剖面对SHAO-H模型计算的不同高 度的ZTD的精度进行了分析,同时利用2011年117个IGS测站实测的ZTD序列对SHAO-H模型 计算地面测站ZTD的精度进行了评估,并与UNB3m 模型的精度进行了对比. 4.1 与积分ZTD垂直剖面的比较
利用SHAO-H模型计算了2011年全年水平分辨率为6°(纬向)×12°(经向)的格网点处不同等压层上的ZTD,时间分辨率为6 h,将其与对应时刻对应位置ERA-Interim分层气象资料积分方法计算的ZTD进行比较,统计了bias和RMS.表 3给出了部分等压层上所有网格点统计的两组ZTD序列的平均bias和RMS,表中第2列为各等压层在全部格网点上的平均高程.由表 3可知,不同高度上的平均bias绝大部分都在±1 mm以内,bias没有明确的随高度变化的规律,其最大值为1.3 mm发生在450 hPa等压层;平均RMS最大为39 mm,发生在最底层等压层,随着高度的上升RMS不断减小,到最高层等压层RMS减小至不足1 mm.
| | 表 3 与积分ZTD相比,SHAO-H模型ZTD在不同等压层的平均bias和RMS统计 Table 3 Statistics of mean bias and RMS of SHAO-H ZTD at different isobaric layers,compared with integral ZTD |
将以上全部三维格网点按照高程分为6个区间,统计SHAO-H模型ZTD和积分ZTD在每个高程区间内的纬度平均RMS和经度平均RMS如图 11所示.由该图可以看出:与积分ZTD相比,北半球SHAO-H模型计算的ZTD的RMS在2 km以上随着纬度的增大而增大、在2 km以下整体上随着纬度的增大而减小;南半球SHAO-H模型计算 的ZTD的RMS在2~15 km范围内的纬度54°存 在一个明显的波峰、在15 km以上整体随着纬度的 增大而增大、在2 km以下整体上随着纬度的增大而减小;SHAO-H模型计算的ZTD的RMS在5 km以上的范围内不存在明显的随经度的趋势性变化,但在5 km以下呈现锯齿状分布.由于大气中的水汽的来源是地球表面的蒸发,地面大气中的水汽含量随着纬度的增加而减少,海洋上空的水汽含量高于陆地上空的水汽含量(盛裴轩等,2003),分析认为SHAO-H模型的精度在近地面表现出的随纬 度和经度的趋势性变化主要与大气中的水汽含量 相关,水汽含量高的地区精度相对较差.高空中SHAO-H模型精度随纬度规律性变化的成因有待日后进一步研究.
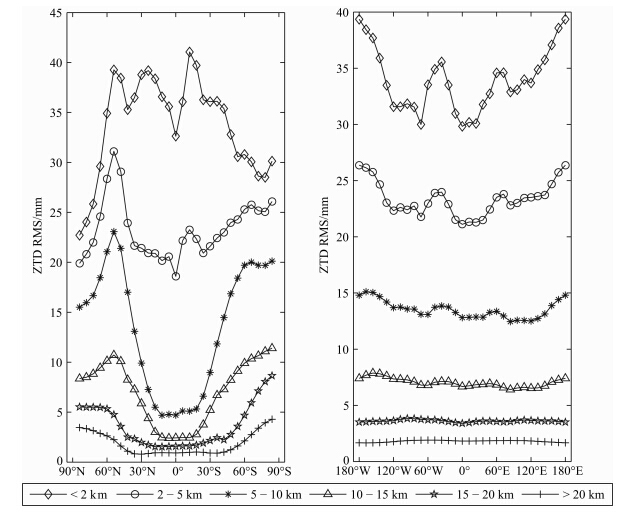 | 图 11 与积分ZTD相比,不同高程范围内SHAO-H模型ZTD纬度平均RMS和经度平均RMSFig. 11 Latitudinal mean RMS and longitudinal mean RMS of SHAO-H ZTD in different height range,compared with integral ZTD |
IGS(International GNSS Service)提供的ZTD是目前国际上公认的精度最高的实测ZTD,其典型误差在1.5~5 mm之间(Byun and Bar-Server,2009).UNB3m模型改进了估计ZWD的方式,是目前精度最高的UNB系列全球模型(Le and ro et al.,2006,2008).为了进一步验证SHAO-H模型的精度,本文收集了IGS提供的2011年均匀分布于全 球的117个测站时间分辨率为2 h的ZTD序列 作为评估基准,对SHAO-H模型和UNB3m模型的精度进行对比分析.IGS测站分布图如图 12所示.
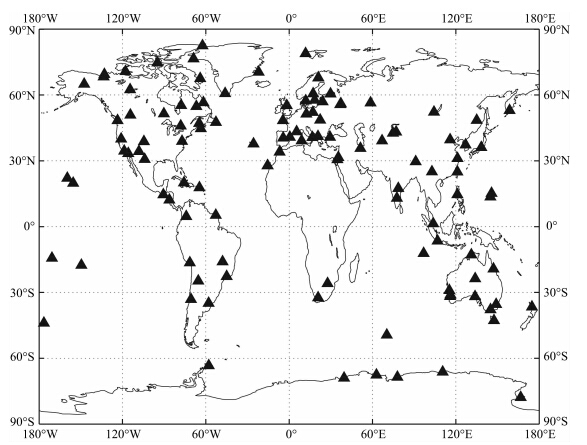 | 图 12 IGS测站分布图Fig. 12 The distribution of IGS stations |
统计结果显示117个测站上SHAO-H模型计 算的ZTD的平均bias为7.02 mm(最大值41.73 mm,最小值-19.72 mm),平均RMS为38.50 mm(最大 值66.57 mm,最小值19.65 mm),UNB3m模型计 算的ZTD的平均bias为14.67 mm(最大值93.31 mm,最小值-53.81 mm),平均RMS为51.95 mm(最大值 106.70 mm,最小值23.58 mm).图 13给出了两个模型全部测站bias和RMS的分布直方图,可以看出SHAO-H模型的bias和RMS分布的集中程度均高于UNB3m模型,表明SHAO-H模型在全球范围内具有良好的精度一致性.
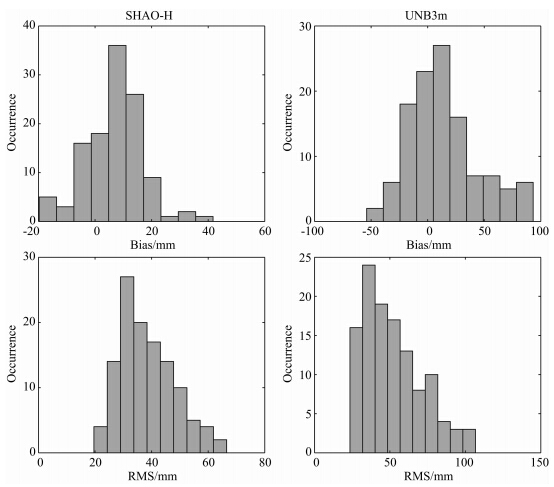 | 图 13 Bias和RMS分布直方图Fig. 13 Histograms of bias and RMS |
为了检验SHAO-H模型计算的ZTD在不同季节的精度特点,将在117个测站上按季节统计的bias和RMS列于表 4.由该表可以看出,除了北半 球的夏季和秋季的bias,南北半球不同季节UNB3m 模型的bias和RMS均大于对应的SHAO-H模型的bias和RMS;尽管不同季节的bias和RMS差异不是很大,但不管在南半球还是北半球,两个模型计算的ZTD在夏季精度最差,而冬季精度最高.分析认为造成这种现象的原因是由于夏季空气中水汽含量最高而冬季相反,而水汽是制约ZTD模型精度的重要因素.
| | 表 4 SHAO-H 模型和UNB3m 模型在不同季节的精度统计 Table 4 Seasonal accuracy statistics for both SHAO-H model and UNB3m model |
图 14显示了SHAO-H模型和UNB3m模型平均 bias和RMS随纬度、经度和高度的分布.由图 14可知:相比UNB3m模型,SHAO-H模型在南北半球的精度不存在明显差异,说明在ZTD模型中采用南北半球对称的假设具有不合理性,而SHAO-H采用全球分布的格网化参数有效避免了这一缺点;SHAO-H模型bias没有明显的随纬度、经度以及高度变化的规律,但RMS有随着纬度的增高而降低、随着高度的升高而减小的趋势,这与上述与积分ZTD比较时得出的结论一致;SHAO-H模型的RMS并未表现出与积分ZTD比较时呈现的随经度的变化趋势,分析认为造成这一差异的主要原因是因为IGS测站绝大部分位于陆地之上,受海洋上的水汽影响有限.
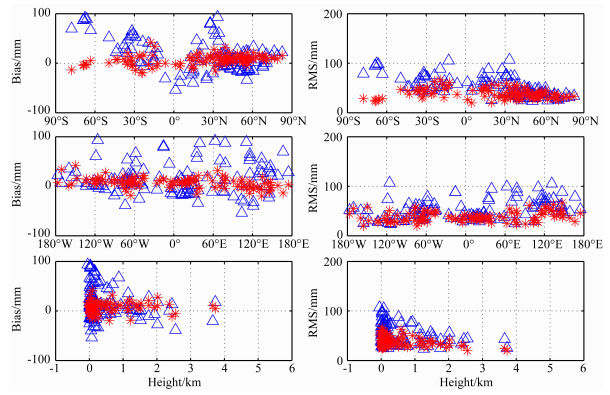 | 图 14 SHAO-H模型(红色*)和UNB3m模型(蓝色Δ)bias和RMS随纬度、经度和高度的分布Fig. 14 Bias and RMS with respect to latitude,longitude and altitude for both SHAO-H(red *) and UNB3m(blue Δ) |
表 5列出了SHAO-H模型和UNB3m模型计算中国境内6个IGS站ZTD的精度统计结果,由表 5可以发现,在中国区域内整体上SHAO-H模型的精度仍然优于UNB3m模型的精度,而且SHAO-H模型的RMS在中国境内也存在明显的随测站高度升高不断减小的特点,其在6个测站上的平均值为40.61 mm.
| | 表 5 SHAO-H模型和UNB3m模型在中国境内的精度统计 Table 5 Accuracy statistics for both SHAO-H model and UNB3m model over China |
本文以ERA-Interim再分析资料计算的ZTD、ZHD和ZWD垂直剖面为基础,详细地讨论了ZTD随高程变化的最佳拟合形式,建立了适宜任意高度ZTD改正的模型SHAO-H.SHAO-H模型以与高程相关的分段函数表达式为基础,利用30个全球1.5°分辨率的格网参数文件,直接模制ZTD时空变化的特征.分段函数根据空气中水汽在垂直方向的变化规律分别选定平均海平面、5 km和17 km作为三个起算高程,在17 km以下表示为两个三次多项式,在17 km以上表示为指数函数.通过与ERA-Interim再分析资料计算的积分ZTD垂直剖面以及IGS发布的实测ZTD序列比较,证明SHAO-H模型具有以下特点:
(1)较以往模型中二次函数、指数函数等单一函数拟合ZTD随高程变化的方法引起的最大约为6 cm的系统差,将ZTD随高程的变化表示为分段函数在50 km高程范围内残差较小、在不同的高程范围内精度一致性较高.最终确定的分段函数表达式拟合ZTD与积分ZTD的内符合残差随着高程升高不断减小,最大值约为1 cm.
(2)与全球870个格网点上2011一年的积分ZTD垂直剖面相比,SHAO-H模型计算的ZTD在不同等压层上的平均bias绝大部分均在±1 mm以内,平均RMS最大为39 mm,随着高度的上升平均RMS逐渐减小至不足1 mm.与IGS 2011年117个测站的实测ZTD相比,SHAO-H模型计算的ZTD的平均bias为7.02 mm,RMS为38.50 mm,较UNB3m模型计算的ZTD 的bias减小了52%、RMS减小了26%.在中国区域,SHAO-H模型的精度仍然优于UNB3m模型,6个测站统计的平均RMS为40.61 mm.
(3)SHAO-H模型计算的地面附近的ZTD的RMS有明显的随着纬度增高不断减小、夏季大于冬季等变化特点,此外其沿经向与积分ZTD统计的RMS也显示出与海陆分布有关的分布特点,分析认为SHAO-H模型在近地面的精度主要与空气中的水汽含量有关,水汽含量大的地区精度相对较差.
综上所述,SHAO-H模型能够有效反映ZTD在空间域和时间域内的变化特征,计算简便,可以满足不同高度的用户实时定位导航的需要.由于缺乏相应的实测数据,本文中模型与实测ZTD的精度验证仅局域于与地面实测值的比较,与不同高度的实测数据的验证比较有待于在以后的工作中进一步进行.
致谢 感谢欧洲中尺度天气预报中心、IGS数据中心以及iGMAS提供相关数据.| [1] | Byun S H, Bar-Server Y E. 2009. A new type of troposphere zenith path delay product of the international GNSS service. J. Geod., 83(3-4): 1-7. |
| [2] | Chen Q M, Song S L, Zhu W Y. 2011. Preliminary establishment of the global model(SHAO-G)for the zenith tropospheric delay. // China Satellite Navigation Conference (in Chinese). Shanghai. |
| [3] | Chen Q M, Song S L, Heise S, et al. 2011. Assessment of ZTD derived from ECMWF/NCEP data with GPS ZTD over China. GPS Solut, 15(4): 415-425. |
| [4] | Chen Q M, Song S L, Zhu W Y. 2012. An analysis of the accuracy of zenith tropospheric delay calculated from ECMWF/NCEP data over Asian area. Chinese J. Geophys., 55(5): 1541-1548. |
| [5] | Collins J P, Langley R B. 1996. Mitigating tropospheric propagation delay errors in precise airborne GPS navigation. // Proceedings of the IEEE Position, Location and Navigation Symposium. Atlanta, Georgia, USA: IEEE, 582-589. |
| [6] | Collins P, Langley R, LaMance J. 1996. Limiting factors in tropospheric propagation delay error modelling for GPS airborne navigation. // The Institute of Navigation 52nd Annual Meeting. Cambridge, Massachusetts, USA. |
| [7] | Dee D P, Uppala S M, Simmons A J, et al. 2011. The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Quart. J Roy. Meteor. Soc., 137(656): 553-597. |
| [8] | Dodson A H, Chen W, Baker H C, et al. 1999. Assessment of EGNOS tropospheric correction model. // Proceedings of the 12th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1999). Nashville, TN, 1401-1408. |
| [9] | Hopfield H S. 1971. Tropospheric effect on electromagnetically measured range: prediction from surface weather data. Radio Sci., 6(3): 357-367. |
| [10] | Leandro R, Santos M, Langley R B. 2006. UNB neutral atmosphere models: Development and performance. // ION NTM 2006. Monterey, California, USA, 564-573. |
| [11] | Leandro R F, Langley R B, Santos M C. 2008. UNB3m_pack: A neutral atmosphere delay package for radiometric space techniques. GPS Solut., 12(1): 65-70. |
| [12] | Li W, Yuan Y B, Ou J S, et al. 2012. A new global zenith tropospheric delay model IGGtrop for GNSS applications. Chin. Sci. Bull., 57(17): 2132-2139. |
| [13] | Penna N, Dodson A, Chen W. 2001. Assessment of EGNOS tropospheric correction model. J. Navig.J. Navig., 54(1): 37-55. |
| [14] | Saastamoinen J. 1972. Contributions to the theory of atmospheric refraction. Bull. Geo., 105(1): 279-298. |
| [15] | Seidel D J, Randel W J. 2006. Variability and trends in the global tropopause estimated from radiosonde data. J. Geophys. Res., 111: D21101. |
| [16] | Sheng P X, Mao J T, Li J G, et al. 2003. Atmospheric Physics (in Chinese). Beijing: Peking University Press |
| [17] | Song S L, Zhu W Y, Chen Q M, et al. 2011. Establishment of a new tropospheric delay correction model over China area. Sci. China Phys. Mech. Astron., 54(12): 2271-2283. |
| [18] | Thayer G D. 1974. An improved equation for the radio refractive index of air. Radio Sci., 9(10): 803-807. |
| [19] | Yao Y B, He C Y, Zhang B, et al. 2013. A new global zenith tropospheric delay model GZTD. Chinese J. Geophys. (in Chinese), 56(7): 2218-2227. |
| [20] | 陈钦明, 宋淑丽, 朱文耀. 2011. 全球对流层延迟改正模型(SHAO-G)的初步建立. ∥ 第二届中国卫星导航学术年会电子文集.上海. |
| [21] | 盛裴轩, 毛节泰, 李建国等. 2003. 大气物理学. 北京: 北京大学出版社. |
| [22] | 姚宜斌, 何畅勇, 张豹等. 2013. 一种新的全球对流层天顶延迟模型GZTD. 地球物理学报, 56(7): 2218-2227. |
 2014, Vol. 57
2014, Vol. 57

