2. 陕西延长石油集团有限责任公司研究院, 西安 710075
2. Research Institute, Shaanxi Yanchang Petroleum (Group) Co., LTD, Xi'an 710075, China
面波是陆上地震资料中一种主要的规则干扰波,沿着近地表传播,能量衰减缓慢,在风化地表出露区尤其发育.在单炮地震记录中面波波场一般呈扇形分布,具有能量强、频率低、视速度低等特点.地震记录中面波与反射波的同相轴互相交织干涉在一起,严重降低了地震资料的信噪比,影响地震资料处理质量.合理地压制面波干扰,有利于提高地震资料的信噪比,改善静校正、速度分析、偏移成像以及叠前属性分析等处理解释效果.
通常,通过野外地震数据采集阶段合理的检波器组合可以达到压制面波的目的[1].然而,这种检波器组合的方式只能部分地压制面波,还需要在数据处理阶段采用各种滤波方法来衰减面波干扰.目前大多数面波滤除方法利用面波与体波单一特征的不同,包括基于频率分布不同的带通滤波、高通滤波和多通道滤波等以及基于视速度特征差异的F-K滤波、沿时间-偏移距的加窗F-K滤波等[2-5].这些方法都存在自身的缺点,如带通滤波在去除面波时压制了体波的低频成分,而低频信息对于深层目标勘探和阻抗参数反演都非常重要;F-K滤波在遇到面波能量远强于体波时会造成有效信号严重的波形失真.为了克服这些缺点,许多滤波方法利用了面波或者体波的相干特性,如KL变换方法通过对单炮记录进行适当的处理来排齐体波或者面波分量,从而实现体波和面波的识别与分离[6-8].此外,Karsli等[9]根据面波的频散特性,构造线性或者非线性扫频信号来模拟面波干扰,利用Wiener-Levinson算法通过预测相减方法将面波干扰从原始地震道中去除,该方法可较好地保持有效波的波形特征和频谱结构.
由于地震信号是典型的非平稳信号,各种基于时频变换的信号分析方法被广泛用于地震资料的面波衰减.一维小波变换由于其多尺度特性[10-13]以及高维小波变换带来的方向分辨特性[14-18],被许多学者用于地震资料的面波衰减.Askari等[19]基于S变换的思想引入t-f-k变换和x-f-k变换,给出随时间位置或者偏移距改变的视速度滤波器,对于面波受到地表非均质体散射或者频散严重的地震记录,能够取得有效的滤波效果.另外,近些年发展起来的Ridgelet变换、Curvelet变换等也被成功地用于面波干扰的衰减[20-21],利用不同波场分量的频率、方向和空间位置差别实现有效波和面波的分离.
上述小波变换、Ridgelet变换与Curvelet变换等数学变换可以看作是采用不同的波形字典来表示信号,如果分析信号在某种波形字典中可由少数几个波形元素表示,即认为分析信号在这种波形字典中可得到稀疏表示.然而,考虑到实际地震数据非常复杂,仅仅选择单一的变换方法,很难对地震信号进行稀疏表示.如果把上述多种信号表示方法联合起来组成超完备冗余表示字典,就可能对复杂信号进行稀疏表示.由于超完备波形字典在捕捉地震波形特征方面具有独特的优势,结合信号的稀疏表示理论,能够取得更好的噪声衰减效果.Trad等[22-23]将单炮地震记录建模为具有线性同相轴的面波与具有双曲同相轴的反射波的线性叠加,提出将线性Radon变换和双曲Radon变换联合构成一种混合Radon变换,结合稀疏约束,对符合模型要求的地震记录取得完美的波场分离结果.Yarham等[24]利用Curvelet变换对地震波形结构优异的描述性能,结合两种波场分量的初始估计,在Curvelet域建立稀疏优化分离模型,利用分块坐标松弛算法(Block-Coordinate Relaxation,BCR)[25]得到更精确的波场分离结果.Wang等[26-27]根据面波与体波在一维平稳小波域的时间、尺度分布的差异性,以及单炮记录中相邻地震道中体波波形的相关性,初步探索了两种波场分量的自适应稀疏分解途径.
分析单炮地震记录中两种波场分量的波形结构特征,面波干扰在频域表现出低频和窄带特性,如果将小波变换作为面波信号的表示工具,其主要能量分布在小波变换域少数几个尺度中,这表明面波可在小波域中得到稀疏表示;此外,由于地层沉积过程的韵律特征,使得体波信号局部表现出具有一定相关度的波形结构,这样就非常适宜于利用局部离散余弦变换作为其稀疏表示字典[28].基于上述认识,本文基于用于复杂信号稀疏表示的形态成分分析(Morphological Component Analysis,MCA)理论[29],提出将一维平稳小波变换与局部离散余弦变换联合构成超完备波形字典,作为单道地震记录的稀疏表示字典;在两种变换组成的联合域内建立单炮记录中两种波场分量的稀疏分解模型,通过求解该稀疏优化问题得到最终的波场分离结果.
2 形态成分分析方法原理
近年来随着信号稀疏表示理论的发展[30-31],Starck等[29]提出基于形态成分分析的信号稀疏表示理论,将多种具有不同原子特征的波形字典联合起来构成超完备冗余字典,从而获得更加稀疏的信号表示方式和更加有效的特征识别能力.对于某种待分析信号s∈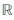
(1)针对第一种信号分量s1,存在超完备字典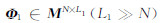
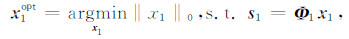
|
(1) |
式中,‖·‖0为l0范数,建立针对信号稀疏程度的一种度量.优化问题(1)本质上是通过对信号s1进行超完备变换,获得在字典Φ1中非常稀疏的表示系数x1.
(2)针对第二种信号分量s2,当采用超完备字典Φ1对其进行表示时,有

|
(2) |
得到的表示系数x12将是非常不稀疏的,即稀疏度量‖x12‖0非常大.这表明字典Φ1对于两种波形结构类型的信号分量在稀疏表示方面存在明显的区别.
(3)针对第二种信号分量s2,存在超完备字典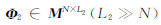
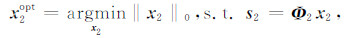
|
(3) |
同样地,要求字典Φ2对于第一种类型的信号分量的表示极其不稀疏.
这个三个假设条件说明形态成分分析理论假设对于线性组合信号中的每一种信号分量,都存在着对应的能够对其进行稀疏表示的超完备字典,并且认为该字典仅能稀疏表示该信号分量,对于其它类型的信号分量不能有效地表示(即非常不稀疏).因而,在形态成分分析方法中,两种超完备字典Φ1和Φ2的差异性以及它们对相应信号分量的分辨能力,直接影响对复杂信号的有效表示的能力.
根据上面的假设条件,对于任意由两种波形类型信号线性混合的信号s,可分别选取两种类型信号的最佳表示字典Φ1和Φ2,从而在由Φ1和Φ2联合构造的超完备字典中得到信号s的最稀疏表示形式,即需要求解如下问题:
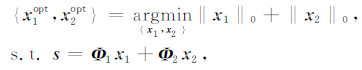
|
(4) |
式中,Φ1x1对应于s中的第一类信号分量s1,Φ2x2对应于中s的第二类信号分量s2.通过求解优化问题(4),不仅获得信号s的稀疏表示,同时也实现了两种类型信号分量的有效分离.
利用式(4)描述解决实际问题时,通常还存在着两方面的困难:首先这个问题是非凸的,从一个随机冗余字典中搜索信号的稀疏解是NP问题,其计算复杂度非常高;其次实际信号往往受到噪声干扰,并且表示字典与对应信号分量之间往往不能完全匹配,使得优化问题中的等式约束很难成立.因而,根据MP算法和BP算法[30-31]的思想,可对优化问题(4)中的约束条件进行适当松弛,使得问题变得可解,并且保证了稀疏解的稳定性:
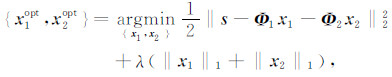
|
(5) |
式中,‖·‖1及‖·‖2分别表示l1范数和l2范数.式(5)表示一种典型的凸集优化问题,Elad等[32]将BCR算法进行推广,成功用于形态成分析问题的快速数值求解.由于BCR算法不作为本文的主要内容,此处不作详细讨论.
3 基于形态成分分析的面波噪声衰减方法 3.1 基于形态成分析的面波噪声分离模型假设单炮地震记录中的每道信号可看作体波和面波两种信号分量的线性叠加,那么单道地震记录s可表示为
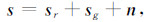
|
(6) |
式中,sr、sg和n分别表示体波信号分量、面波信号分量以及随机噪声向量.式(6)中引入加性的噪声分量n,有助于提高该信号模型的普适性,使其不仅适用于受噪声干扰的地震数据,也允许实际数据中包含适当的测量误差或者其它杂波干扰.针对面波干扰的衰减问题,仅需简单地假设噪声向量n服从零均值的高斯白噪分布.
式(6)表示在噪声干扰下的一种多源混合信号恢复重建和分离问题,这里的两种源信号分别指体波信号和面波信号.根据近年来信号处理领域发展的稀疏表示理论,如果信号在某种超完备的波形字典中能够获得稀疏表示,那么信号完全可以从噪声背景甚至不完整的采样中恢复.形态成分分析作为稀疏表示理论的发展,给出针对包含多源信号或者多种信号分量的复杂信号的稀疏表示和多源信号或者多种信号分量分离的实用方法.根据形态成分分析理论,如果可以分别获得体波和面波信号的稀疏表示字典Φr和Φg,并且Φr不能稀疏表示面波信号,Φg也不能稀疏表示体波信号,那么单道地震信号s可以在由Φr和Φg联合组成的超完备波形字典中得到稀疏表示,从而通过求解如下的最优化问题实现体波和面波两种信号分量的恢复和分离:
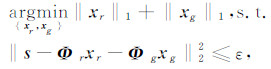
|
(7) |
式中,xr为体波sr在字典Φr中的表示向量,xg为面波sg在字典Φg中的表示向量;ε表示信号重建的误差门限,选择合理的误差门限参数,可使该优化问题在噪声干扰以及数据缺失的情况下仍然能够取得合理的稀疏解.
3.2 稀疏表示字典选择求解式(7)中的稀疏优化问题,还需要确定体波的稀疏表示字典Φr和面波的稀疏表示字典Φg.根据形态成分分析理论可知,两种波形字典不仅需要对相应信号成分获得足够稀疏的表示形式,而且它们的原子波形特征之间还需要体现出明显的差异性.近年来发展出许多信号表示方法[33],其中可用于一维信号的分析方法包括傅里叶变换、局部余弦变换、加窗傅里叶变换、Gabor变换以及小波变换等.分析单道地震记录中两种波场分量的波形特征,虽然两种地震波都是由相同的震源激发,但是面波沿着表层地层传播,通常表现出主频低、带宽窄和频散的波形特征;而体波波场可简单地看作,由传播到一定位置的震源子波与该处地层界面反射系数褶积形成,考虑到地层的沉积韵律特性,宽频带的体波信号往往局部地表现出明显的波动信号特征.因而,本文选择一维平稳小波变换作为面波信号的稀疏表示字典Φg,由于其时频局部化性质以及在低频段的良好频率分辨率,将非常有利于对面波信号的分析刻画;选择局部余弦变换作为体波信号的稀疏表示字典Φr,由于其基本原子为加窗调制的单频余弦波,相比小波变换更适合于描述具有波动信号特征的体波信号.
与正交小波变换相比,平稳小波变换更接近于连续小波变换,其不对平移参数离散化,具有平移不变特性,但是需要对尺度参数沿着二进制序列进行离散采样,降低了计算复杂度.当给定小波变换的尺度函数ф(t)和小波函数ψ(t),s(t)∈ L2(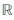

|
(8) |
式中,Wj表示第j级尺度的平稳小波变换分解系数.
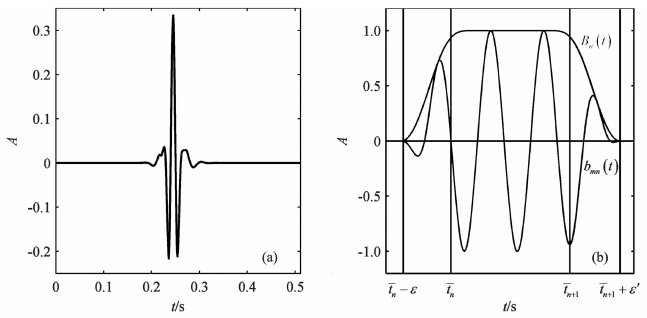
平稳小波变换将时域信号分解成一系列不同分辨率下的光滑分量和细节分量.与正交小波变换不同,平稳小波变换在每个分解尺度不对得到的分解系数进行下采样处理,这样每级分解得到的光滑分量系数和细节分量系数长度就与原始信号序列相同,并且每级的分解系数的分辨率随着分解级数的增加而降低,从而将时域信号分解成不同频带的分量.本文将一维平稳小波变换作为面波信号的稀疏表示字典,由于其冗余性以及多分辨率性质都有助于对面波波形特征的识别和稀疏表示.文中取具有4阶消失矩的Coiflet小波[34]作为平稳小波变换的基本小波函数,其时域波形如图 1a所示.Coiflet小波函数不仅具有近似对称的波形结构,还拥有近似线性的相位特性,有利于小波变换域处理操作的信号相位保真.
|
图 1 时域基函数对比 (a)第4尺度的Coiflet小波函数;(b)IV型局部余弦基函数. Fig. 1 Comparison of basis functions in time domain (a) Coiflet wavelet at scale 4;(b) Local Cosine IV basis. |
离散余弦变换是与傅里叶变换相关的一种实值变换,它对具有高度相关性的信号有非常好的能量聚集性.局部离散余弦变换作为离散余弦变换的一种局部化分析方式,不仅继承了离散余弦变换对相关信号的稀疏表示能力,而且能够有效地捕捉信号的局部结构特征.由于其双正交特性及对局部信号特征优异的描述能力,局部离散余弦变换已在地震数据压缩[35]、随机噪声压制[36]以及偏移成像[35, 37]等多方面得到应用.本文将局部离散余弦变换作为体波信号的稀疏表示字典,将非常有利于对具有局部相关特性的体波波形的描述和稀疏表示.
局部离散余弦变换常用的局部余弦基有Ⅰ型和Ⅳ两种,本文采用Ⅳ型余弦基.局部Ⅳ型余弦基函数的定义为[28]
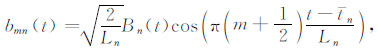
|
(9) |
式中,bmn(t)表示具有波数指标m和位置指标n的局部余弦基,如图 1b所示,tn为区间起始位置,tn+1为区间终止位置,Ln=tn+1-tn为区间长度,Bn(t)为定义在闭区间[tn-ε,tn+1+ε']的钟形窗光滑函数,且tn+ε≤tn+1 -ε',ε和ε'分别为区间左、右两侧的重叠半径.在实际计算中,局部离散余弦变换一般不直接通过离散信号与局部离散余弦基的内积求得,而是先对数据进行分段折叠预处理[28],然后利用具有快速算法的离散Ⅳ型余弦变换求得.对于离散信号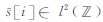
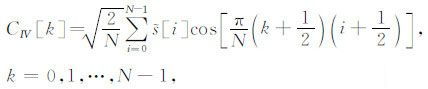
|
(10) |
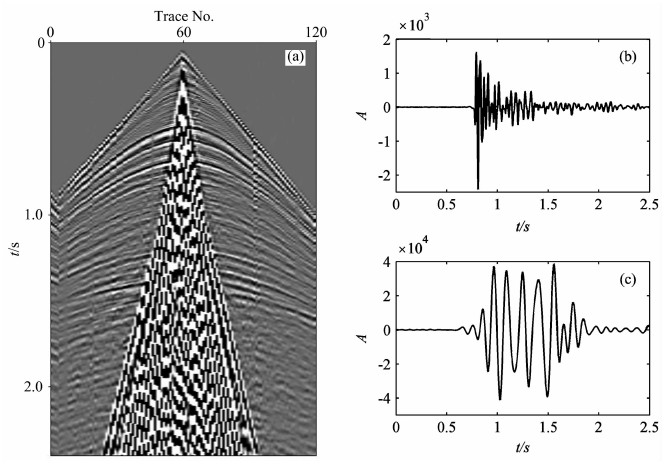
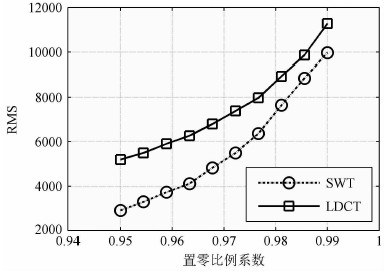
下面利用一个简单的试验来对比说明平稳小波变换和局部离散余弦变换分别对面波和体波信号的稀疏表示性能.试验中取某油田的实际单炮地震记录如图 2a所示,从其远偏移距中取出一道不受面波噪声干扰的信号作为试验体波信号,其波形如图 2b所示;从其近偏移距中取出一道体波能量完全被面波噪声干涉覆盖的信号,通过选取适当的参数进行低通滤波,将得到的滤波结果近似作为试验面波信号,其波形如图 2c所示.对两道试验信号分别进行平稳小波变换和局部离散余弦变换.针对每道试验信号,将两种变换的系数根据振幅进行排序,并按相同的比例系数将其中部分最小能量值的系数置为0,再分别通过两种变换的逆变换求出各自的重构信号,计算重构信号和原始信号之间的均方差(MSE),以此评价两种变换对体波和面波的稀疏表示性能.针对图 2b的试验体波信号,平稳小波变换和局部离散余弦变换的均方差值随置零比例系数的变化曲线如图 3所示.从图中可以看出,局部离散余弦变换的均方差更小,具有更好的能量压缩效果,也即与平稳小波变换相比,局部离散余弦变换能够用更少的系数表征体波信号,对体波信号有着更为优异的稀疏表示性能.类似地,针对图 2c的试验面波信号,从图 4中可以看出,与局部离散余弦变换相比,平稳小波变换能够用更少的系数表征面波信号,对面波信号具有更稀疏表示.两种波形字典对两种信号分量稀疏表示性能的差异性,使得形态成分析方法可用于解决单炮记录中体波和面波的分离问题.
|
图 2 实际单炮地震记录及两种试验信号 (a)实际炮集记录;(b)从远偏移距地震道获取的试验体波信号;(c)从近偏移距地震道获取的试验面波信号. Fig. 2 Real seismic record and two test signals (a) Real shot gather; (b) Test body-wave signal acquired from far offset traces; (c) Test ground-roll signal acquired from near offset traces. |

|
图 3 平稳小波变换与局部余弦变换用于体波表示的稀疏性对比 Fig. 3 Comparison of body-wave representation sparsity between the SWT and the LDCT |
|
图 4 平稳小波变换与局部余弦变换用于面波表示的稀疏性对比 Fig. 4 Comparison of ground-roll representation sparsity between the SWT and the LDCT |
在实际地震记录中,面波不仅呈现高振幅、低主频、低视速度以及同相轴近似线性的特征,而且具有频散特性.因此为了验证本文方法对面波干扰的衰减性能,在合成记录中,利用扫描信号来模拟面波干扰[9],公式为

|
(11) |
式中,g(t)为模拟的面波信号,A为信号振幅,T表示信号持续时间.函数F(t)为
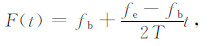
|
(12) |
式中,fb和fe分别表示单道模拟面波信号的起始频率和终止频率.
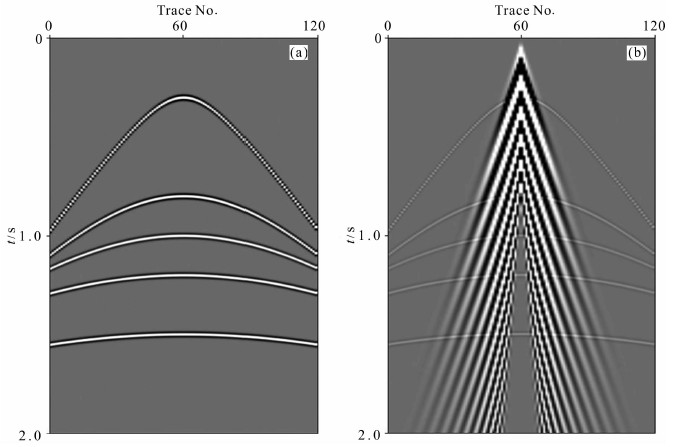
图 5a为包含5个反射同相轴的双边带合成炮集记录,其中Ricker子波的主频为35Hz,信号时间采样间隔为2ms,记录长度为2s,最大振幅为1.图 5b为加入频带范围为5~15Hz、最大振幅为6的扫频信号作为模拟面波噪声的含噪合成地震记录.从图中可以看出,由于模拟的面波频谱全部落在体波频带范围内,面波干扰在其影响区域扭曲和掩盖了体波信号,特别在近偏移距区域对体波信号的影响更为突出.应用本文提出的基于形态成分分析的面波干扰分离方法来处理该含噪炮集记录,得到体波信号如图 6a所示,分离的面波干扰如图 6b所示.将本文方法得到的体波信号与模拟体波对比可见,本文方法几乎衰减了全部的面波干扰且具有有很好的有效信号保真度.为了进一步说明本文方法的有效性,应用F-K滤波器和低截频为15Hz的高通滤波器来处理该含噪合成记录,得到的滤波结果分别如图 6c和e所示,滤除的面波噪声分别如图 6d和f所示.综合分析图 6a、c和e中三种方法的去噪结果可见,虽然F-K滤波方法和高通滤波方法都能够压制绝大部分的面波能量,但是这两种方法都造成有效信号波形失真,产生一些虚假的反射同相轴.为了更清楚地显示各种方法的优劣,我们选取含噪记录、原始记录以及三种方法处理结果的第45道数据与其振幅谱进行分析.图 7a、c、e、g和i分别为含噪合成记录、无噪的体波记录以及分别由本文方法、F-K滤波和高通滤波得到体波信号分量,它们对应的振幅谱分别如图 7b、d、f、h和j所示.通过对比发现,各种方法都能够衰减面波干扰.然而,相比高通滤波和本文方法,F-K滤波更容易导致强面波影响区域的有效信号产生波形畸变;相比F-K滤波和本文方法,高通滤波对有效信号的低频分量损失非常严重.综合整体剖面对比和单道信号的分析,本文方法不仅很好地保持了有效信号的波形结构,在时间剖面中取得良好的视觉效果,而且体波信号的频谱带宽也得到较好地保持,为后继地震资料的处理解释提供了有利的数据条件.
|
图 5 理论合成地震记录 (a)不含面波的合成地震记录;(b)包含面波干扰的合成地震记录. Fig. 5 Theoretically synthetic seismic records (a) Synthetic seismic data free ground-roll; (b) Synthetic seismic data containing ground-roll. |

|
图 6 合成地震记录面波衰减效果对比 (a)基于形态成分分析方法得到的体波;(b)基于形态成分分析方法得到的面波干扰;(c)F-K滤波方法得到的体波;(d)F-K滤波方法得到的面波干扰;(e)高通滤波方法得到的体波;(f)高通滤波方法得到的面波干扰. Fig. 6 Comparison of ground-roll attenuation results of synthetic shot gather (a) Body wave obtained by MCA method; (b) Ground-roll noise obtained by MCA method; (c) Body wave obtained by F-K filtering method; (d) Ground-roll noise obtained by F-K filtering mentod; (e) Body wave obtained by high pass filtering method; (f) Ground-roll noise obtained by high pass filtering method. |

|
图 7 合成地震记录单道信号分析 (a)图 5b中第45道信号;(b)图 5a中第45道信号;(c)图 6c中第45道信号;(d)图 6e中第45道信号;(e)图 6a中第45道信号;(f)图 7a的振幅谱;(g)图 7b的振幅谱;(h)图 7c的振幅谱;(i)图 7d的振幅谱;(j)图 7e的振幅谱. Fig. 7 Analysis of single seismic trace in synthetic shot gather (a) The 45th trace signal in Fig.5b; (b) The 45th trace signal in Fig.5a; (c) The 45th trace signal in Fig.6c; (d) The 45th trace signal in Fig.6e; (e) The 45th trace signal in Fig.6a; (f) Amplitude spectrum of (a); (g) Amplitude spectrum of (b); (h) Amplitude spectrum of (c); (i) Amplitude spectrum of (d); (j) Amplitude spectrum of (e). |
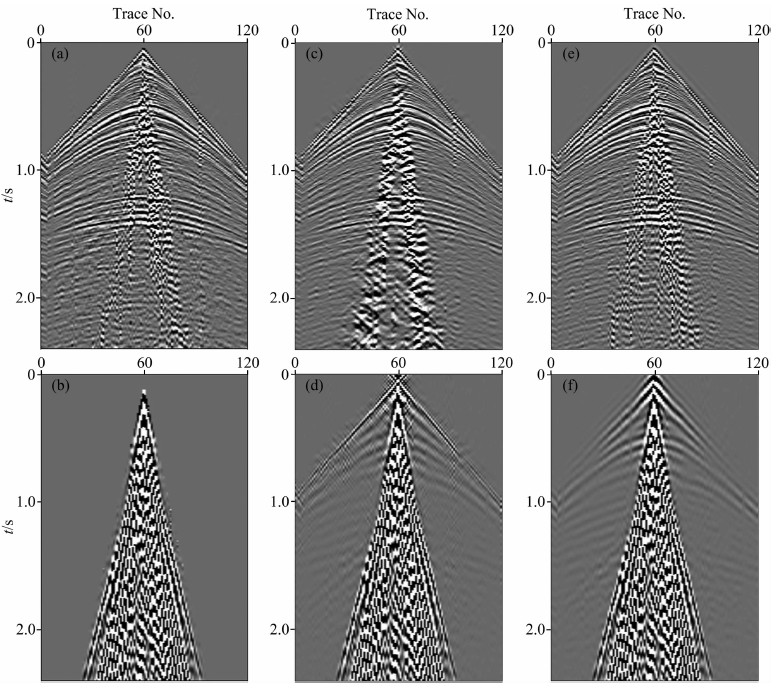
利用图 2中某油田的单炮记录来检验基于形态成分分析的面波分离方法处理实际地震资料的有效性.该单炮记录为120道双边接收,采样时间间隔为2ms,记录长度为2.5s.可以看出,该记录中面波干扰非常发育,在面波影响区域的有效波几乎完全被面波掩盖.另外,一方面由于空间采样密度不够,面波频谱存在严重的混叠现象;一方面由于面波的能量太强,记录的信号波形在一些地方存在削顶现象,这些都增加了处理难度.应用本文方法处理该单炮记录,得到体波信号和去除的面波干扰分别如图 8a和b所示.对比处理前后记录可见,面波干扰被完整地分离且未造成非面波影响区域内有效信号的损伤.为了检验本文方法的有效性,同样利用F-K滤波和高通滤波方法来处理该记录,得到的滤波结果分别如图 8c和e所示,滤除的面波干扰如图 8d和f所示.
|
图 8 实际地震记录面波衰减效果对比 (a)基于形态成分分析方法得到的体波;(b)基于形态成分分析方法得到的面波干扰;(c)F-K滤波方法得到的体波;(d)F-K滤波方法得到的面波干扰;(e)高通滤波方法得到的体波;(f)高通滤波方法得到的面波干扰. Fig. 8 Comparison of ground-roll attenuation results of real seismic record (a) Body wave obtained by MCA method; (b) Ground-roll noise obtained by MCA method; (c) Body wave obtained byF-K filtering method; (d) Ground-roll noise obtained byF-K filtering mentod; (e) Body wave obtained by high pass filtering method; (f) Ground-roll noise obtained by high pass filtering method. |
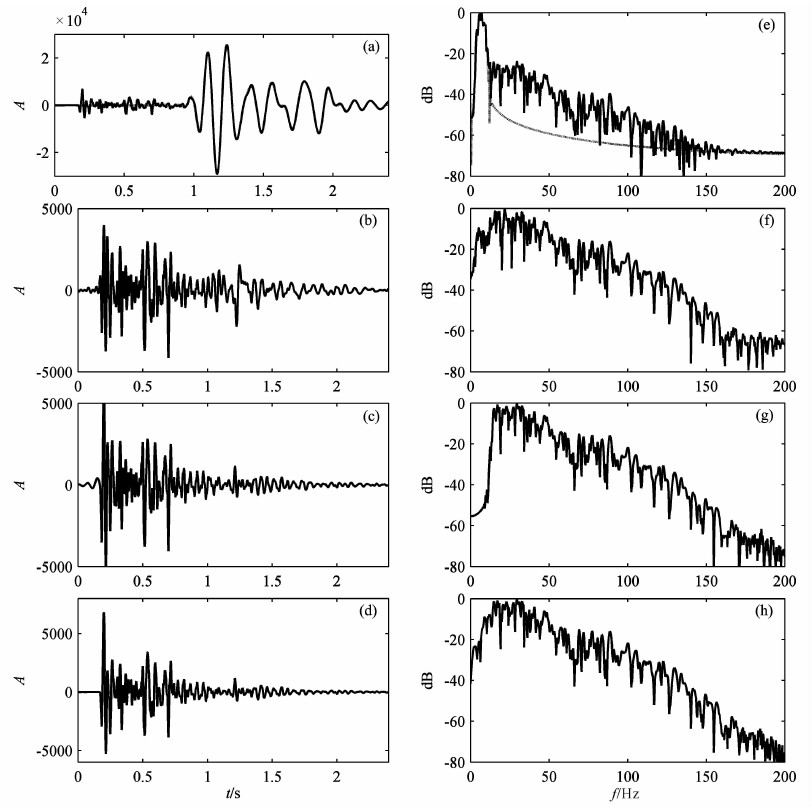
比较三种方法的处理结果可见,本文方法和高通滤波都衰减掉绝大部分的干扰噪声,而F-K滤波结果中仍有部分面波能量残留;对比三种方法得到的噪声剖面可见,F-K滤波和高通滤波都损伤了面波影响区域外的有效波,进而推测这两种滤波方法对面波区域的有效波也会造成严重损伤,而本文方法作为一种单道处理方法,几乎没有影响到面波干扰区域外的有效波,说明该方法能够较好地识别体波和面波信号,进而推测该方法对面波区域的体波信号也有较好的保真度.为了更清楚地比较这几种方法的优劣,选取原始记录、本文方法得到的面波噪声以及三种方法处理结果的第50道数据与其振幅谱进行比较.图 9a、b、c、和d分别为原始记录、F-K滤波、高通滤波和本文方法得到的有效信号,而本文方法得到的噪声分量以点划线的形式与原始记录重叠显示,它们对应的振幅谱分别如图 9e、f、g和h所示.可以看出,图 9b中F-K滤波对体波波形产生明显的变形失真,而图 9c中高通滤波在取得面波噪声衰减效果时也损伤了体波的低频分量,这从图 9g中其频谱结构分布得到证实.与两种常用的面波衰减方法相比,基于形态成分分析的面波衰减方法适用于强面波干扰噪声的处理,不仅分离了绝大部分面波干扰能量,而且能够很好地保持体波信号的波形特征与其低频分量.此外,本文方法作为一种单道处理方法,适用于横向非均匀采样炮集资料的处理,并且处理结果受频谱混叠现象的影响也较小.
|
图 9 实际地震记录单道信号分析 (a)图 2a中第50道信号与图 8b中第50道信号(点划线); (b)图 8c中第50道信号; (c)图 8e中第50道信号; (d)图 8a中第50道信号; (e)图 9a的振幅谱; (f)图 9b的振幅谱; (g)图 9c的振幅谱; (h)图 9d的振幅谱. Fig. 9 Analysis of single trace in real seismic record (a) The 50th trace signal in Fig.2a; (b) The 50th trace signal in Fig.8c; (c) The 50th trace signal in Fig.8e; (d) The 50th trace signal in Fig.8a; (e) Amplitude spectrum of (a); (f) Amplitude spectrum of (b); (g) Amplitude spectrum of (c); (h) Amplitude spectrum of (d). |
面波是陆上地震资料中一种主要的规则干扰波,如何合理地消除面波噪声始终是地震资料处理中的关键问题.本文基于形态成分分析的复杂信号稀疏表示理论,给出一种基于形态成分分析的炮集记录面波噪声衰减方法.根据单道地震记录中体波和面波信号波形结构特征的差异性,分别选择一维平稳小波变换和局部离散余弦变换作为体波和面波信号的稀疏表示字典,建立基于双波形字典的形态成分分析模型,通过求解该稀疏优化问题得到面波与体波两种波场分量的分离.通过理论合成模型和实际地震资料处理以及与两种传统处理方法对比,表明本文方法不仅能够衰减绝大部分面波干扰能量,并且可以很好地保持体波信号的波形特征与低频分量,为地震资料的后续处理和分析提供有利的数据基础.
| [1] | 何樵登. 地震波理论. 北京: 地质出版社, 1988 . He Q D. Theory of Seismic Wave (in Chinese). Beijing: Geological Publishing House, 1988 . |
| [2] | Embree P, Burg J P, Backus M M. Wide-band velocity filtering-the pie-slice process. Geophysics , 1963, 28(6): 948-974. DOI:10.1190/1.1439310 |
| [3] | Gelisli K, Karsli H. F-k filtering using the Hartley transform. Journal of Seismic Exploration , 1988, 7(2): 101-108. |
| [4] | Treitel S, Shanks J L, Frasier C W. Some aspects of fan filtering. Geophysics , 1967, 32(5): 789-800. DOI:10.1190/1.1439889 |
| [5] | 刘法启, 张关泉. 小波变换与F-K算法在滤波中的应用. 石油地球物理勘探 , 1996, 31(6): 782–791. Liu F Q, Zhang G Q. Application of wavelet transform and F-K algorithm in filtering. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 1996, 31(6): 782-791. |
| [6] | Liu X W. Ground roll supression using the Karhunen-Loeve transform. Geophysics , 1999, 64(2): 564-566. DOI:10.1190/1.1444562 |
| [7] | Montagne R, Vasconcelos G L. Optimized suppression of coherent noise from seismic data using the Karhunen-Loeve transform. Physical Review E , 2006, 74(1 Pt 2): 16213. |
| [8] | Porsani M J, Silva M G, Melo P E M, et al. SVD filtering applied to ground-roll attenuation. Journal of Geophysics and Engineering , 2010, 7(3): 284-289. DOI:10.1088/1742-2132/7/3/007 |
| [9] | Karsli H, Bayrak Y. Using the Wiener-Levinson algorithm to suppress ground-roll. Journal of Applied Geophysics , 2004, 55(3-4): 187-197. DOI:10.1016/j.jappgeo.2003.11.003 |
| [10] | 罗国安, 杜世通. 小波变换及信号重建在压制面波中的应用. 石油地球物理勘探 , 1996, 31(3): 337–349. Luo G A, Du S T. Application of wavelet transform and signal reconstruction in surface wave elimination. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 1996, 31(3): 337-349. |
| [11] | Deighan A J, Watts D R. Ground-roll suppression using the wavelet transform. Geophysics , 1997, 62(6): 1896-1903. DOI:10.1190/1.1444290 |
| [12] | 孙学文, 陈文超, 高静怀, 等. 小波域强面波衰减方法研究. 石油地球物理勘探 , 2008, 43(1): 22–28. Sun X W, Chen W C, Gao J H, et al. Study on attenuation of strong surface wave in wavelet domain. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 2008, 43(1): 22-28. |
| [13] | 陈文超, 高静怀, 包乾宗, 等. 基于连续小波变换的自适应面波压制方法. 地球物理学报 , 2009, 52(11): 2854–2861. Chen W C, Gao J H, Bao Q Z, et al. Adaptive attenuation of ground roll via continuous wavelet transform. Chinese Journal of Geophysics (in Chinese) (in Chinese) , 2009, 52(11): 2854-2861. |
| [14] | Nguyen M Q, Mars N J I. Filtering surface waves using 2D Discrete Wavelet Transform.//69th Annual International Meeting, SEG. Expanded Abstract, 1999: 1228-1231. |
| [15] | Abdul-Jauwad S H, Khène M F. Two-dimensional wavelet-based ground roll filtering.//70th Annual International Meeting, SEG. Expanded Abstract, 2000. |
| [16] | 刘财, 王典, 杨宝俊. 二维小波变换在地震勘探面波消除中的应用. 地球物理学进展 , 2003, 18(4): 711–714. Liu C, Wang D, Yang B J. Apply of 2-D wavelet transforms in surface wave eliminations of seismic exploration. Progress in Geophysics (in Chinese) (in Chinese) , 2003, 18(4): 711-714. |
| [17] | Zhang R F, Ulrych T J. Physical wavelet frame denoising. Geophysics , 2003, 68(1): 225-231. DOI:10.1190/1.1543209 |
| [18] | Zhang R F, Trad D, Ulrych T J. Hybrid, wavelet transform based, noise attenuation. Integrated Computer-Aided Engineering , 2005, 12(1): 91-98. |
| [19] | Askari R, Siahkoohi H R. Ground roll attenuation using the S and x-f-k transforms. Geophysical Prospecting , 2008, 56(1): 105-114. |
| [20] | 包乾宗, 高静怀, 陈文超. 面波压制的Ridgelet域方法. 地球物理学报 , 2007, 50(4): 1210–1215. Bao Q Z, Gao J H, Chen W C. Ridgelet domain method of ground-roll suppression. Chinese Journal of Geophysics (in Chinese) (in Chinese) , 2007, 50(4): 1210-1215. |
| [21] | Zheng J J, Yin X Y, Zhang G Z, et al. The surface wave suppression using the second generation curvelet transform. Applied Geophysics , 2010, 7(4): 325-335. DOI:10.1007/s11770-010-0257-x |
| [22] | Trad D, Sacchi M D, Ulrych T J. A hybrid linear-hyperbolic Radon transform. Journal of Seismic Exploration , 2001, 9(4): 303-318. |
| [23] | Trad D, Ulrych T J, Sacchi M. Latest views of the sparse radon transform. Geophysics , 2003, 68(1): 386-399. DOI:10.1190/1.1543224 |
| [24] | Yarham C, Boeniger U, Herrmann F J, et al. Curvelet-based ground roll removal.//76th Annual International Meeting, SEG. Expanded Abstract, 2006: 2777-2781. |
| [25] | Sardy S, Bruce A G, Tseng P. Block coordinate relaxation methods for nonparametric wavelet denoising.//Proceedings of the SPIE-The International Society for Optical Engineering, 1998: 75-86. |
| [26] | Wang W, Chen W C, Lei J L, et al. Ground-roll separation by sparsity and morphological diversity promotion.//80th Annual International Meeting, SEG. Expanded Abstract, 2010: 3705-3710. |
| [27] | Wang W, Gao J H, Chen W C, et al. Data adaptive ground-roll attenuation via sparsity promotion. Journal of Applied Geophysics , 2012, 83: 19-28. DOI:10.1016/j.jappgeo.2012.04.004 |
| [28] | Mallat S. A Wavelet Tour of Signal Processing. (3rd ed). Boston: Academic Press, 2009 . |
| [29] | Starck J L, Elad M, Donoho D L. Image decomposition via the combination of sparse representations and a variational approach. IEEE Transactions on Image Processing , 2005, 14(10): 1570-1582. DOI:10.1109/TIP.2005.852206 |
| [30] | Mallat S G, Zhang Z F. Matching Pursuits with Time-Frequency Dictionaries. IEEE Transactions on Signal Processing , 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [31] | Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit. Siam Journal on Scientific Computing , 1998, 20(1): 33-61. DOI:10.1137/S1064827596304010 |
| [32] | Elad M, Bruckstein A M. A generalized uncertainty principle and sparse representation in pairs of bases. IEEE Transactions on Information Theory , 2002, 48(9): 2558-2567. DOI:10.1109/TIT.2002.801410 |
| [33] | Rubinstein R, Bruckstein A M, Elad M. Dictionaries for sparse representation modeling. Proceedings of the IEEE , 2010, 98(6): 1045-1057. DOI:10.1109/JPROC.2010.2040551 |
| [34] | Daubechies I. Orthonormal bases of compactly supported wavelets Ⅱ: Variations on a theme. Siam Journal on Mathematical Analysis , 1993, 24(2): 499-519. DOI:10.1137/0524031 |
| [35] | Wang Y Z, Wu R S. Seismic data compression by an adaptive local cosine/sine transform and its effects on migration. Geophysical Prospecting , 2000, 48(6): 1009-1031. DOI:10.1046/j.1365-2478.2000.00224.x |
| [36] | 陆文凯. 基于离散余弦变换的地震随机噪声压制技术. 石油地球物理勘探 , 2011, 46(2): 202–206. Lu W K. Seismic random noise suppression based on the discrete cosine transform. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 2011, 46(2): 202-206. |
| [37] | Mao J A, Wu R S, Gao J H. Directional illumination analysis using the local exponential frame. Geophysics , 2010, 75(4): S163-S174. DOI:10.1190/1.3454361 |
 2013, Vol. 56
2013, Vol. 56


