2. 中国地质大学(北京)地球物理与信息技术学院, 北京 100083
2. School of Geophysics and Information Technology, China University of Geosciences, Beijing 100083, China
随着地球深部探测工作的大力开展和地球物理各种单方法正反演技术的日趋成熟,利用多种方法对同一地质体进行探测并做综合解释已经得到广泛应用[1-8].但由于受制于方法本身的单一性和局限性,利用单方法反演结果进行综合解释往往很难获得较为统一的地质-地球物理模型.为了突破这一限制,国内外学者对联合反演方法进行了深入研究[9-30].在大地电磁与地震走时资料的联合反演方面,研究主要集中在依靠先验资料所获得的参数换算关系来解决电阻率与速度模型的耦合问题[13-21].但事实证明,只有在一定地质条件下电阻率与速度之间才存在直接的函数关系,例如Meju和Gallardo就曾对英国Quorn地区某沉积地层进行了岩石物性标本的测定,发现电阻率的对数与速度的对数之间呈某种线性关系[24].不过这一参数耦合方法对先验物性关系的依赖性较大,具有不确定性,而且一旦这种关系得不到正确描述,联合反演结果会适得其反,因而其实用价值十分有限.
近年来,采用模型结构耦合的联合反演方法在国际上较为流行[25],比较有代表性的成果是由Gallardo和Meju提出的交叉梯度(cross-gradient)耦合方法[26].他们进行了大地电磁和折射地震二维联合反演算法的研究[27],通过在联合反演的目标函数中引入交叉梯度函数来约束不同参数.这种方法相比传统的直接关系的耦合更具普遍适用性,于是一些学者沿用这一耦合方法进行了各类地球物理数据联合反演的研究,也都取得了良好的效果[28-29].最近,已经有研究者分别采用直接关系耦合和交叉梯度耦合研究了大地电磁、重力与地震走时资料的三维联合反演的算法,提出了整个算法的架构,并对相容和不相容模型做了模型测试[30].相比国外,国内的已有成果更多地关注数据拟合,较少考虑不同物性参数间的耦合问题[23].
在研究地球深部壳幔构造方面,大地电磁法和天然地震方法一起被视为两大支柱方法.大地电磁提供的非常低的电阻率一般是地下连通的流体的反应,这通常与宽频地震所获得的低速体相对应,在综合解释中相互验证,互为补充.本文在大地电磁和地震走时资料的三维联合反演研究中首次引入交叉梯度,通过设计单棱柱体模型和双棱柱体模型对联合反演算法进行模型测试,探讨该联合反演方法的可行性和适用性.
2 大地电磁和地震走时资料的三维正反演方法 2.1 大地电磁三维正反演求解大地电磁正演问题所常用的数值模拟方法包括有限单元法、有限差分法、积分方程法和边界单元法,本文联合反演中大地电磁的正演采用三维交错采样有限差分算法[31].
大地电磁反演方法主要包括OCCAM反演,快速松弛反演(RRI),数据空间反演(Data Space)和共轭梯度反演法(CG)等.为了使OCCAM反演理论适用于大地电磁三维反演,Siripunvarapor等人在OCCAM法基础上进行了改进:通过一系列数学变换将M行M列的模型空间的叉积矩阵转化为N行N列的数据空间的叉积矩阵,演变成数据空间反演法.由于模型参数M比数据个数N大得多,反演中直接求取模型协方差矩阵Cm,因而大大减小了计算量并减低了计算机内存需求,是一种较为实用的大地电磁三维反演方法.考虑到上述优点,本文联合反演算法中的大地电磁模块采用数据空间反演.读者可参考Siripunvarapor等人的相关文献[32, 33]详细了解该反演方法,本文不做赘述.
2.2 地震走时资料三维正反演通过记录地表观测到的首波初至,获取从震源(人工震源和天然地震)到地震台站之间的走时,可以反演观测台站下方的速度结构.地震走时数据的正演问题通过求解程函方程来实现:
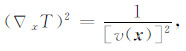
|
(1) |
式中,T为走时,x为某点的位置向量,v代表该点地震波速度,这一方程描述了不同时刻波前的几何形态的变化.
地震走时资料的正演算法主要包括三类:基于斯奈尔定律的两点射线追踪法(如打靶法和弯曲法),基于图论、费马原理、惠更斯原理的最短路径算法以及基于程函方程波前扩散类的有限差分数值求解算法(如快速行进法).本文采用快速行进三维有限差分算法(Fast Marching Method,简称为FMM)作为联合反演中地震模块的正演算法.这一算法由Sethian等人[34]首次提出,算法采用迎风差分格式,以窄带技术为波前扩展方式,通过窄带来近似代表波前,并用窄带的扩展推进来近似模拟波前的传播过程.此后,De Kool和Rawlinson[35]将该方法做了改进,能同时计算折射波和反射波的射线路径.
联合反演中地震走时资料的反演则采用子空间(Subspace)反演法[36-37].这一方法同时构建多个方向进行最小化迭代,扩展成在模型空间中的n维子空间.在每次迭代过程中,子空间反演的模型更新量可以写成n个M维基向量{aj}的加权和:
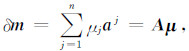
|
(2) |
式中,A=[aj]为M行n列的投影矩阵,加权系数为μj相应基向量aj的长度.
子空间反演的关键问题取决于基向量的构造,一般以最速下降向量作为构造基础.该方法的优势在于模型更新的计算量小,只需要求解n×n阶的线性方程.一般n取值较小,例如Rawlinson等[38]对澳大利亚Tasmania的地震走时反演所采用的子空间维数n小于20.
3 基于交叉梯度耦合的三维联合反演算法 3.1 交叉梯度函数对大地电磁和地震走时资料做联合反演首先要解决电阻率与速度之间的参数耦合问题.考虑到岩石物性关系耦合方法不适用于复杂地质条件,本文采用交叉梯度来对电阻率和速度进行耦合[25-27],其函数表达式可写成
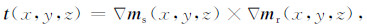
|
(3) |
式中,t代表交叉梯度,▽ms和▽mr分别代表地震波速度和电阻率的梯度.
交叉梯度函数表示为速度和电阻率两种模型单元参量的梯度的叉积,在联合反演中通过直接加入到目标函数来实现大地电磁电阻率模型和地震波速度模型的有效连接.交叉梯度具有以下主要性质:
(1)两种模型的梯度向同一方向变化或者其中一个模型的值为常数时,交叉梯度函数为零;
(2)模型参数改变的大小不影响交叉梯度函数值的大小;
(3)只有当两个模型参数朝不同方向变化时交叉梯度函数的值才不为零.这一耦合方法通过增强不同参数模型间结构的相似性,达到结构化的参数耦合的目的.
对于三维联合反演而言,交叉梯度为矢量,可以展开为沿x,y,z三个方向的分量:
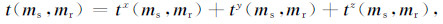
|
(4) |
其中,
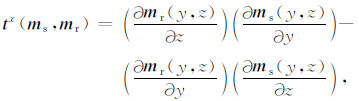
|
(5) |
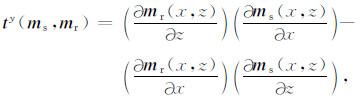
|
(6) |
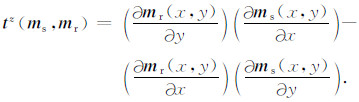
|
(7) |
对于各交叉梯度分量,分别采用差分算法进行二维空间的离散化,求取各个分量的长度,再对交叉梯度三维矢量作求模计算.
3.2 联合反演目标函数本文联合反演算法包括大地电磁和地震两大模块,其核心思想是:每次联合反演迭代过程中,电阻率模型的更新不仅考虑数据拟合和模型约束,而且还兼顾上次迭代更新的地震波速模型,通过计算它与电阻率模型的交叉梯度来连接两者,与此同时,迭代中地震波速模型的更新也兼顾上次迭代更新的电阻率模型.因此,联合反演算法所采用的目标函数包含以下两部分:

|
(8) |
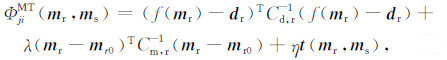
|
(9) |
式中,ms和mr分别为地震波速和电阻率模型向量;ms0和mr0分别为地震波速和电阻率先验模型向量;Cm为模型协方差矩阵,Cd为数据协方差矩阵,在(8)和(9)式中具有不同Cm和Cd;ds和dr分别为地震走时和大地电磁观测数据向量,g(·)和f(·)分别为地震和大地电磁的正演算子,α、β、λ和η为权重因子,本文选取的权重因子如下:α=0.1,β=1.0~3.0,λ=1.0,0.5(初始值为1.0,对数比率上的步长为0.5),η=1.0~3.0;t(·)为交叉梯度算子,其表达式见式(3).
由此可见,当未加入交叉梯度项时,大地电磁模块和地震模块之间没有数据关联,所获得的结果就是大地电磁或地震单独反演的结果.与单一反演不同,联合反演目标函数中都加入了交叉梯度函数,每迭代一次所修改生成的电阻率(或速度)模型参数都会传递给地震(或大地电磁)模块,通过计算交叉梯度来实现两者的耦合,增强两者的相似性,以达到联合反演的目的.
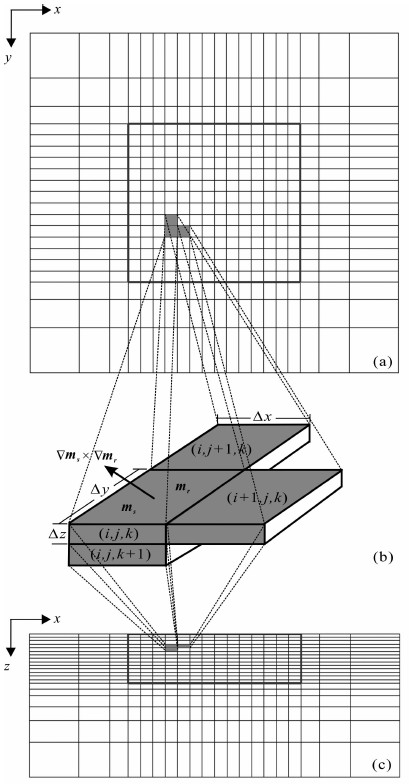
3.3 网格匹配方式为了获得稳定而且足够精确的正演解,不同方法对正演模拟的网格剖分有着不同要求.考虑大地电磁方法的分辨能力、场的衰减特点以及正演计算效率,大地电磁正演网格一般按照不等间隔剖分,且随深度的增加以及在研究区域的外围网格变得稀疏.地震走时反演的正演网格可采用等间隔剖分,也可采用不等间隔剖分.在联合反演中,为了对两种模型的物性参数进行耦合,需要计算电阻率和速度模型的交叉梯度值,但网格的差异势必给参数耦合带来困难.为解决这一问题,我们在大地电磁地下网格中定义一块公共反演网格(图 1),并采用如下网格匹配方法:
|
图 1 联合反演三维网格剖分示意图 (a)沿水平方向网格剖分;(b)三维有限差分网格单元;(c)沿垂直方向网格剖分,(a)、(c)图中粗线框内为大地电磁与地震走时反演的公共反演网格,该网格以等间隔剖分. Fig. 1 Diagram of 3-D grid for joint inversion (a) Horizontal mesh grid; (b) A 3-D element for forward difference calculation; (c) Vertical meshgrid, in the figure (a) and (c).Dlue bound represents common inversion grid of magnetotelluric grid and seismic grid, which is divided by equal interval. |
(1)公共网格为大地电磁和地震方法探测能力相当的范围,在此公共网格范围内地震反演网格和大地电磁网格一样,交叉梯度值也只在这一公共范围内计算,即电阻率和速度值只在这一公共范围内相互约束.
(2)对地震方法分别定义正演网格和反演网格,地震反演网格的范围可大于所定义的公共反演网格,但公共部分的网格和大地电磁是一样的;公共网格外为大地电磁的不等间隔剖分网格.
(3)本文的地震正演网格采用等间隔剖分方式,且正演网格要比反演网格精细,反演初始速度值和反演获得的新模型速度值通过插值在正演网格和反演网格之间传递.
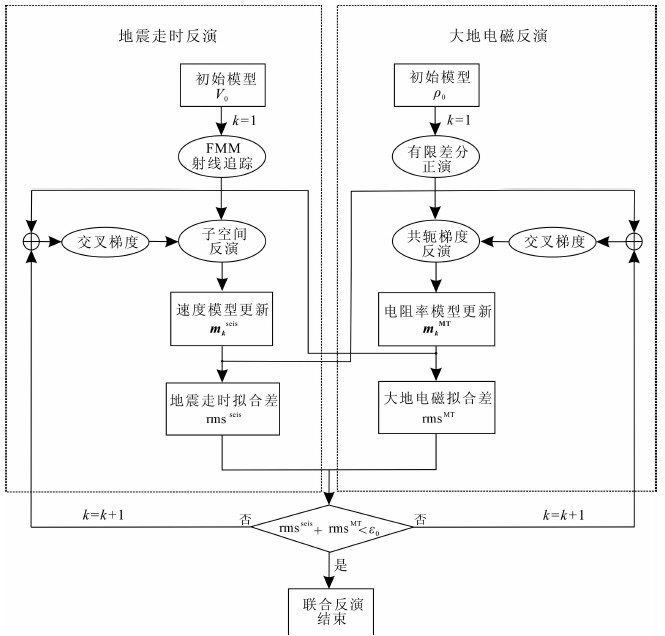
3.4 联合反演算法流程大地电磁与地震走时资料的三维联合反演的算法流程图如下(图 2).
|
图 2 联合反演流程示意图 Fig. 2 The flow chart of the joint inversion algorithm |
联合反演的算法框架可划分为两大模块:地震走时反演和大地电磁反演.两大程序模块之间不是彼此独立的,它们之间通过交叉梯度连接.对于地震走时反演模块,首先输入地震初始速度模型,对该模型进行FMM射线追踪,求取理论走时,并利用梯度类反演方法(本文采用子空间反演)计算速度模型的扰动量,获得新速度模型.再对新速度模型做正演以计算地震数据的拟合差(rmsseis).另一方面,大地电磁的反演与地震反演同时进行,在模型迭代环节中与速度模型交替更新;模型更新后以交叉梯度来耦合电阻率模型和速度模型.大地电磁的正演采用三维交错采样有限差分算法,反演采用三维MT梯度类反演法(如数据空间反演法).当每次电阻率模型和速度模型都更新完成后,比较地震拟合差与大地电磁拟合差(rmsMT)之和与期望值(ε0)的大小,如果rmsseis+rmsMT≥ε0,那么继续迭代,直至第k次迭代的联合反演满足rmsseis+rmsMT<ε0为止.
另需强调的是,为了使地震速度模型参数与大地电磁的反演模型参数相匹配,在反演计算中(包括交叉梯度计算)需对电阻率取对数,当下次迭代进行大地电磁的正演计算时再将对数电阻率转换回来.另外,该算法结构与传统的顺序反演类的联合反演算法有显著不同.后者首先对某一方法(如地震)进行单独反演,生成新速度模型,然后通过岩石物性关系将它转化为另一方法的模型参数(如电阻率),使其作为该方法反演的初始模型进行反演,生成的模型作为联合反演模型.
4 算例分析基于以上理论和算法,在Linux操作系统下采用Fortran语言并结合Shell脚本成功开发了三维联合反演程序.为了检验算法的有效性和正确性,同时对比联合反演结果与单方法反演的差别,本文进行了理论模型合成数据的反演研究,分别设计了单棱柱体模型和双棱柱体模型,下面依次作分析讨论.
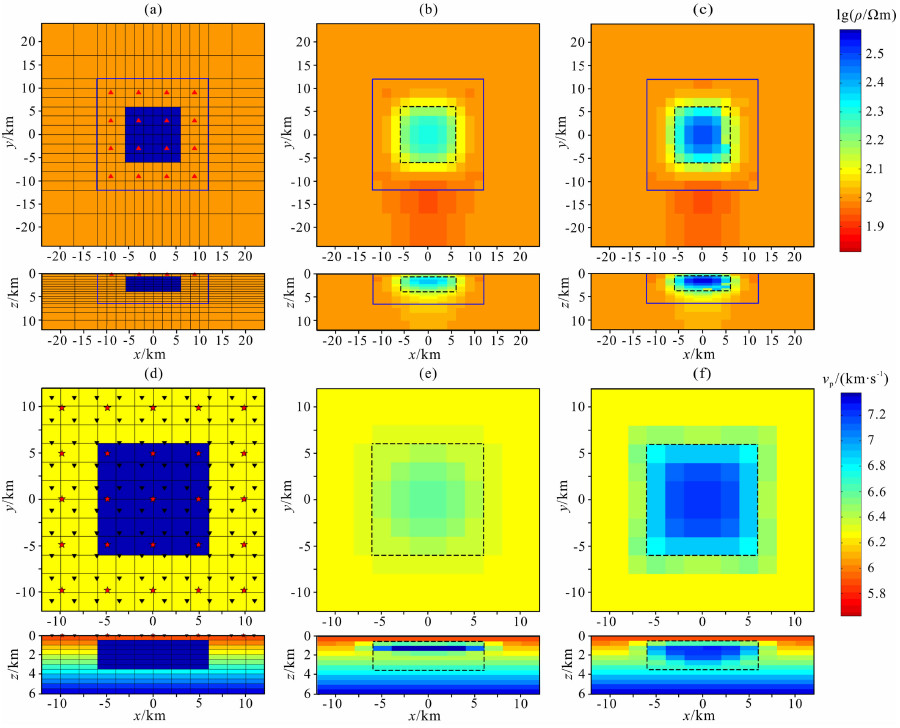
4.1 单棱柱体模型电阻率为1000 Ωm,P波速度大小为7.4 km/s,大小为12 km×12 km×3 km的单棱柱体顶面埋深为500 m,埋藏于电阻率为100 Ωm的地下均匀半空间,围岩的速度为递增的一维模型,第一层速度大小为5.87 km/s,每层递增0.13 km/s,直到第12层为7.33 km/s.P波速度模型的地下三维网格剖分为12×12×12,x,y方向分别以单元网格2 km进行等间隔剖分,z方向以每个网格0.5 km进行等间隔剖分.电阻率模型的网格剖分在速度模型网格的基础上向外进行了延展,延展网格以不等间隔剖分:沿x,y方向的延展网格间距在两侧均依次为5 km和7 km,沿z方向的延展网格间距向下依次为0.8、1、1.5和2 km,总体网格剖分为16×16×16.如图 3a、d所示,地面设计了16个大地电磁测点(红色三角),25个震源(红色五角星)和100个地震观测台站(黑色倒三角).
|
图 3 单棱柱体模型联合反演与单一反演结果对比图 (a)电阻率理论模型;(b)大地电磁单一反演结果;(c)联合反演电阻率模型;(d)P波速度理论模型;(e)地震走时资料单一反演结果;(f)联合反演P波速度模型.各子图中上图为沿z方向俯视2 km切片图,下图为沿x方向y=0 km位置剖面图,图中黑色虚线所示为棱柱体边界范围,(a)、(b)、(c)中蓝色实线为P波速度模型的网格边界. Fig. 3 The comparison of joint inversion and separate inversion by a single-prism model (a) Theoretical resistivity model; (b) Separate MT inversion results; (c) Resistivity model from joint inversion; (d) Theoretical P-wave velocity model; (e) Separate seismic inversion results; (f) P-wave velocity model from joint inversion, in each figure, the one above shows the horizontal slices at 2 km depth and the one below shows the vertical slices at y=0 km along the x axis, the black dashed lines show the prism margins and the blue solid lines show seismic grid margins in the figure (a)、(b) and (c). |
大地电磁采用全部波阻抗张量元素,正演采用0.01、0.1、1、10 Hz和100 Hz五个频率计算出合成数据;利用地震FMM三维正演程序计算走时,再分别加入1%的高斯随机误差作为观测数据.对模型的合成数据分别进行了单独反演和联合反演,初始模型采用电阻率为100 Ωm的均匀半空间和P波速度递增的一维模型(与棱柱体围岩结构相同,前文已做描述).图 3b和e为单棱柱体模型的单独反演结果图.
结果显示:电阻率的反演结果对单棱柱体的空间形态有较好的恢复,但对棱柱体真实电阻率(1000 Ωm)却反演得不够好,围岩电阻率出现一定范围的假异常;P波速度的反演结果只对单棱柱体浅部有较好恢复,对棱柱体真实波速(7.4 km/s)也恢复得不好.相比单独反演,图 3c和f的联合反演结果对单棱柱体的空间形态有更好的恢复,棱柱体的反演电阻率更接近于真实电阻率;联合反演不仅对单棱柱体浅部速度结构有较好恢复,而且单棱柱体深部的速度特征也得到了一定程度的恢复.
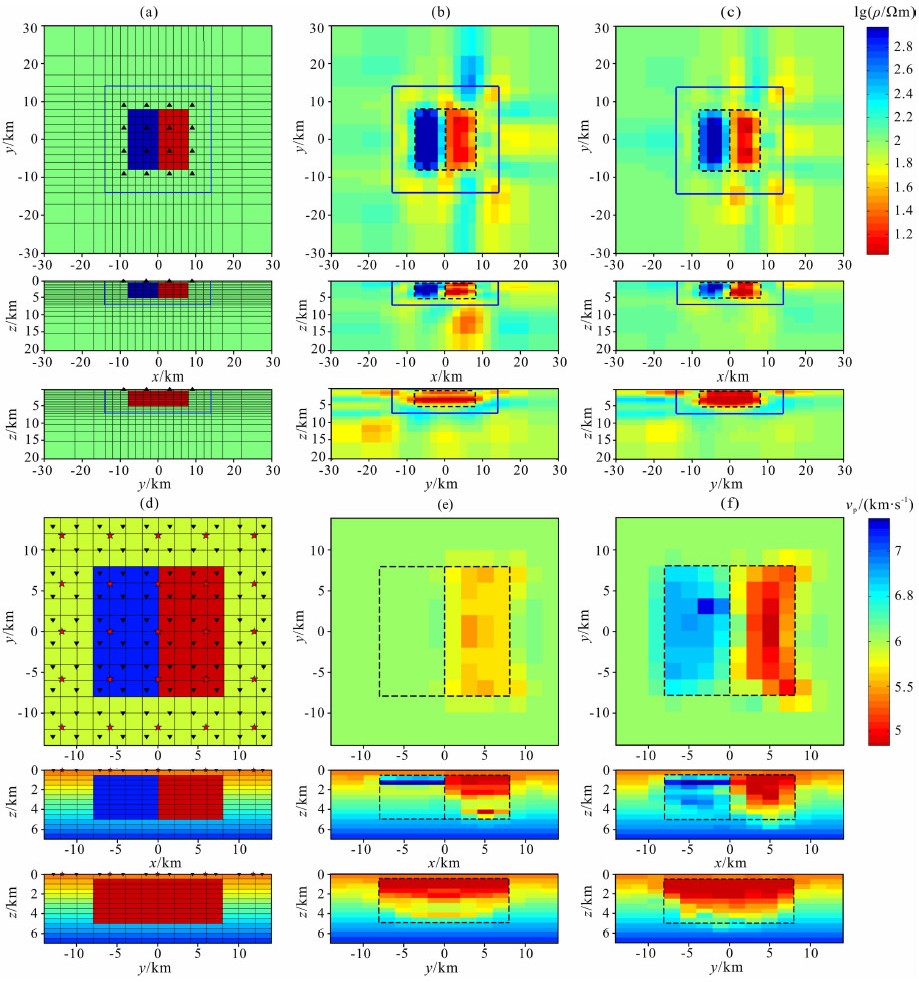
4.2 双棱柱体模型首先设计了一个含高阻高速和低阻低速异常体的双棱柱体模型:左侧为高阻高速棱柱体(电阻率为1000 Ωm,P波速度大小为7.2 km/s),右侧为低阻低速棱柱体(电阻率为10 Ωm,P波速度大小为4.8 km/s),大小均为16 km×8 km×4.5 km,顶面埋深500 m.双棱柱体埋藏于电阻率为100 Ωm的地下均匀半空间,围岩为速度递增的一维模型,第一层速度大小为5.36 km/s,每层递增速度为0.14 km/s,直到第14层为7.14 km/s.P波速度模型的地下三维网格剖分为14×14×14,x,y方向分别以单元网格2 km进行等间隔剖分,z方向以每个网格0.5 km进行等间隔剖分.电阻率模型的网格向外进行了延展,延展网格以不等间隔剖分:沿x,y方向的延展网格间距在两侧均依次为3 km、5 km和7 km,沿z方向的延展网格间距向下依次为0.8、1、1.5、2、3 km和5 km,总体网格剖分为20×20×20.如图 4a和d所示,地面设计了16个大地电磁测点(黑色三角),25个震源(红色五角星)和100个地震观测台站(黑色倒三角).
|
图 4 高阻高速-低阻低速双棱柱体模型联合反演与单一反演结果对比图 (a)电阻率理论模型;(b)大地电磁单一反演结果;(c)联合反演电阻率模型;(d)P波速度理论模型;(e)地震走时资料单一反演结果;(f)联合反演P波速度模型.各子图中由上至下依次为沿z方向俯视3 km切片图,沿x方向y=0 km位置剖面图和沿y方向x=2 km位置剖面图,黑色虚线所示为棱柱体边界范围,(a)、(b)、(c)中蓝色实线为P波速度模型的网格边界. Fig. 4 The comparison of joint inversion and separate inversion by a resistive-high velocity and conductive-low velocity double-prism model (a) Theoretical resistivity model; (b) Separate MT inversion results; (c) Resistivity model from joint inversion; (d) Theoretical P-wave velocity model; (e) Separate seismic inversion results; (f) P-wave velocity model from joint inversion, each figure from the top down shows the horizontal slices at 3 km depth, the vertical slices at y=0 km along the x axis and the vertical slices at x=2 km along the y axis, the black dashed lines show the prism margins and the blue solid lines show seismic grid margins in figure (a)、(b) and (c). |
大地电磁正演采用0.01、0.1、1、10 Hz和100 Hz五个频率计算出全部阻抗张量的合成数据,利用地震FMM三维正演程序计算走时,分别加入1%的高斯随机误差作为观测数据.对模型的合成数据分别进行了单独反演和联合反演,图 4b和e所示的单独反演结果显示:电阻率的反演结果对双棱柱体的空间形态有较好恢复,但围岩电阻率出现一定范围的假异常,特别是在右侧低阻棱柱体深部出现明显的假低阻异常区,该假异常应是由于三维网格剖分比较稀疏所致(剖分过密会大大增加内存需求和计算量);P波速度的反演结果则只对浅部有较好恢复,而且左侧高速棱柱体明显不如右侧低速棱柱体恢复得好.联合反演在同等网格剖分条件下进行.相比单独反演,图 4c和f的联合反演结果对异常体的空间形态和位置都恢复更好,特别是对速度模型异常体的深部特征有更好恢复,而且部分消除了电阻率模型中双棱柱体围岩的假异常,使反演结果得到明显改善.
为了讨论交叉梯度与岩石物性关系耦合方法的区别,考虑异常体的电阻率和速度不是同向变化的情形(高阻低速或低阻高速),本文进一步设计了含高阻高速与低阻高速的双棱柱体模型:由两个相隔8 km的高速的(P波速度大小为7.2 km/s)单棱柱体组成,左侧为高阻棱柱体(电阻率为1000 Ωm),右侧为低阻棱柱体(电阻率为10 Ωm),大小均为12 km×6 km×3 km,顶面埋深500 m.围岩为速度递增的一维模型,第一层速度大小为5.96 km/s,每层递增速度为0.04 km/s,直到第16层为6.54 km/s.网格剖分方式、设计的震源和测点位置如图 5(a)和(d).
|
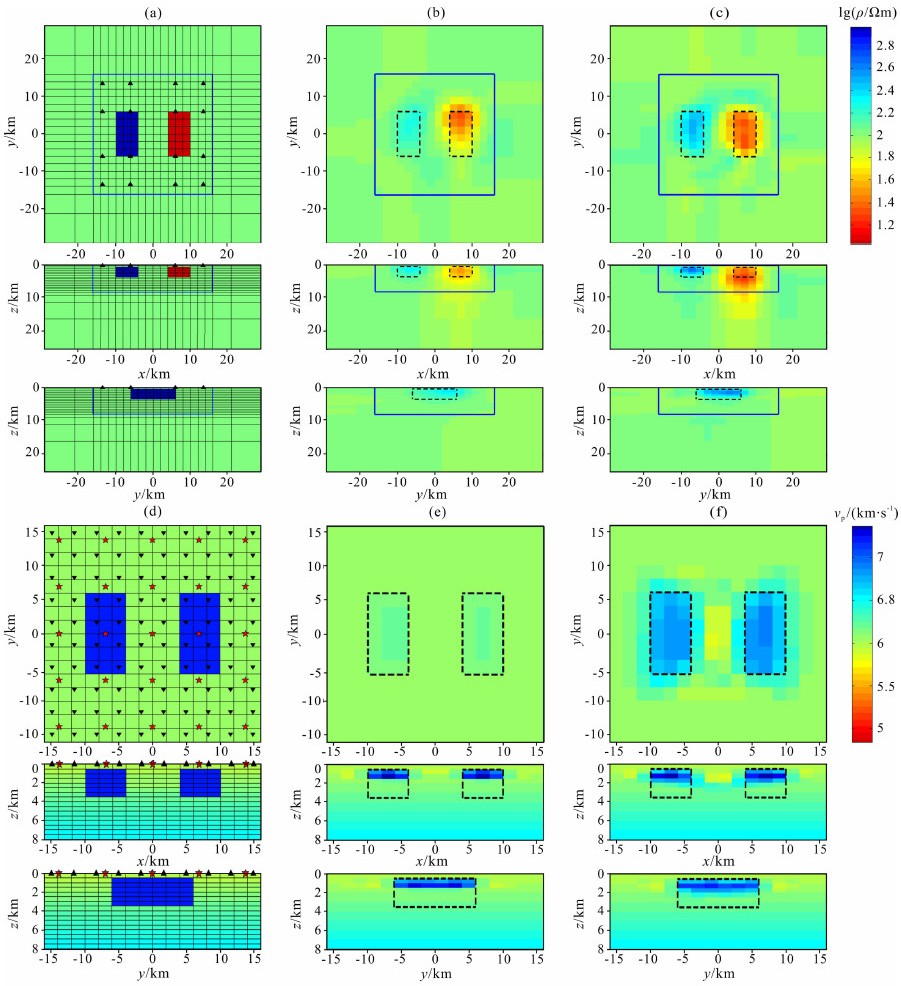
图 5 高阻高速-低阻高速双棱柱体模型联合反演与单一反演结果对比图 (a)电阻率理论模型;(b)大地电磁单一反演结果;(c)联合反演电阻率模型;(d)P波速度理论模型;(e)地震走时资料单一反演结果;(f)联合反演P波速度模型.各子图中由上至下依次为沿z方向俯视2 km切片图,沿x方向y=0 km位置剖面图,沿y方向x=-6 km位置剖面图,黑色虚线所示为棱柱体边界范围,(a)、(b)、(c)中蓝色实线为P波速度模型的网格边界. Fig. 5 The comparison of joint inversion and separate inversion by a resistive-high velocity and conductive-low velocity double-prism model (a) Theoretical resistivity model; (b) Separate MT inversion results; (c) Resistivity model from joint inversion; (d) Theoretical P-wave velocity model; (e) Separate seismic inversion results; (f) P-wave velocity model from joint inversion, each figure from the top down shows the horizontal slices at 2 km depth, the vertical slices at y=0 km along the x axis, the vertical slices at x=-6 km along the y axis, the black dashed lines show the prism margins and the blue solid lines show seismic grid margins in the figure (a)、(b) and (c). |
同样以电阻率为100 Ωm的均匀半空间和P波速度递增的一维模型作为初始模型,对模型的合成数据分别进行了单独反演和联合反演.大地电磁的单独反演使异常体得到一定恢复,但左侧高阻体的反演值普遍不足200 Ωm,与真实电阻率(1000 Ωm)有一定差距;对右侧低阻体的反演虽然更接近真实电阻率(10 Ωm),但与真实空间位置出现一定偏离.地震波速的反演结果同样只对浅部(1.5 km以上)有较好恢复,深度2 km切片已显示所恢复得到的P波速度值普遍不到6.5 km/s,而高速异常体的真实P波速度则为7.2 km/s,说明对于这一模型地震走时的单独反演很难恢复深度在1.5 km以下的高速异常体.而图 5c和f所示的联合反演结果不仅使左侧高阻体和右侧低阻体的反演值都更加接近于真实电阻率,而且对右侧低阻体的空间形态和位置也有更好的恢复.深度2 km切片显示所恢复得到的P波速度值可达到7 km/s,很接近真实速度值;而且深度在1.5 km至2.5 km间的高速异常体得到了一定程度的恢复.
通过对比双棱柱体模型合成数据反演算例,我们认为对于电阻率和速度不是同向变化的异常体,通过联合反演依然可以同时改善大地电磁和地震走时的单独反演结果,这也进一步说明了交叉梯度耦合的特点和优势:并不依赖于不同物性间的特定关系,而是依靠地下结构的相似性进行反演,因而具有更普遍的适用性.
5 结论联合反演能够克服单一方法的局限性,减小地球物理反演的多解性,是今后地球物理反演发展的方向.基于大地电磁数据空间三维反演和地震走时资料的子空间三维反演方法,本文实现了在交叉梯度耦合下的三维联合反演算法.设计了单棱柱体模型和双棱柱体模型对联合反演程序进行了理论模型测试.通过对比合成数据的联合反演和单一反演结果,分析表明:
(1)无论是单棱柱体模型还是双棱柱体模型,大地电磁联合反演结果比单独反演对异常体的空间形态都有更好的恢复,其中单棱柱体模型反演的异常体电阻率更接近于真实电阻率,双棱柱体模型的联合反演消除了围岩的部分假异常.
(2)速度模型的单一反演很难恢复深部的高速异常体,而联合反演不仅对异常体浅部速度结构有更好恢复,而且使异常体深部的速度特征也能得到一定程度的恢复.
(3)高阻高速-低阻高速的双棱柱体组合模型的合成数据反演算例表明:联合反演能同时改善电阻率和速度反向变化异常体的单独反演结果,进一步说明叉梯度耦合并不依赖于不同物性间的特定关系,而是依靠地下结构的相似性,因而具有更普遍的适用性.
致谢研究过程中得到了德国学者Dr.Moorkamp的帮助和有益的建议,两位匿名评审专家为本文修改提出了细致而宝贵的意见,在此一并表示感谢.
| [1] | Aric K, Adam A, Smythe D K. Combined seismic and magnetotelluric imaging of upper crystalline crust in the Southern Bohemian Massif. First Break , 1997, 15(8): 265-271. DOI:10.1046/j.1365-2397.1997.00670.x |
| [2] | Favetto A, Pomposiello C, Booker J, et al. Magnetotelluric inversion constrained by seismic data in the Tucumán Basin (Andean Foothills, 27°S, NW Argentina). J. Geophys. Res. , 2007, 112(B9): B09104. |
| [3] | Muñoz, Bauer K, Moeck I, et al. Exploring the Groβ Schönebeck (Germany) geothermal site using a statistical joint interpretation of magnetotelluric and seismic tomography models. Geothermics , 2010, 39(1): 35-45. DOI:10.1016/j.geothermics.2009.12.004 |
| [4] | 高德章, 赵金海, 薄玉玲, 等. 东海重磁地震综合探测剖面研究. 地球物理学报 , 2004, 47(5): 853–861. Gao D Z, Zhao J H, Bo Y L, et al. A profile study of gravitative-magnetic and seismic comprehensive survey in the East China Sea. Chinese J. Geophys. (in Chinese) , 2004, 47(5): 853-861. |
| [5] | 胡平, 刘保金, 白立新, 等. 奥林匹克公园地区隐伏断裂综合探测. 地球物理学报 , 2010, 53(6): 1486–1494. Hu P, Liu B J, Bai L X, et al. Synthetic exploration of the buried faults in Olympic park area. Chinese J. Geophys. (in Chinese) , 2010, 53(6): 1486-1494. |
| [6] | 李德春, 杨书江, 胡祖志, 等. 三维重磁电震资料的联合解释--以库车大北地区山前砾石层为例. 石油地球物理勘探 , 2012, 47(2): 353–359. Li D C, Yang S J, Hu Z Z, et al. Integrated interpretation of 3D gravity, magnetic, electromagnetic and seismic data: a case study of conglomerate mass investigation in piedmont area of Kuche Depression. Oil Geophysical Prospecting (in Chinese) , 2012, 47(2): 353-359. |
| [7] | 姜枚, 谭捍东, 钱辉, 等. 金川铜镍矿床的地球物理深部结构与成因模式. 矿床地质 , 2012, 31(2): 207–215. Jiang M, Tan H D, Qian H, et al. Geophysical deep structure and genetic model of Jinchuan copper-nickel deposit. Mineral Deposits (in Chinese) , 2012, 31(2): 207-215. |
| [8] | 姜枚, 彭淼, 王有学, 等. 喜马拉雅东构造结岩石圈板片深俯冲的地球物理证据. 岩石学报 , 2012, 28(6): 1755–1764. Jiang M, Peng M, Wang Y X, et al. Geophysical evidence for deep subduction of Indian lithospheric plate beneath Eastern Himalayan Syntaxis. Acta Petrologica Sinica (in Chinese) , 2012, 28(6): 1755-1764. |
| [9] | Moorkamp M, Jones A G, Eaton D W. Joint inversion of teleseismic receiver functions and magnetotelluric data using a genetic algorithm: Are seismic velocities and electrical conductivities compatible?. Geophys. Res. Lett. , 2007, 34(16): L16311. |
| [10] | Moorkamp M, Jones A G, Fishwick S. Joint inversion of receiver functions, surface wave dispersion, and magnetotelluric data. J. Geophys. Res. , 2010, 115(B4): B04318. |
| [11] | Roux E, Moorkamp M, Jones A G, et al. Joint inversion of long-period magnetotelluric data and surface-wave dispersion curves for anisotropic structure: Application to data from Central Germany. Geophys. Res. Lett. , 2011, 38(5): L05304. |
| [12] | 彭淼, 谭捍东, 姜枚, 等. 利用接收函数和大地电磁数据联合反演南迦巴瓦构造结中部地区壳幔结构. 地球物理学报 , 2012, 55(7): 2281–2291. Peng M, Tan H D, Jiang M, et al. Joint inversion of receiver functions and magnetotelluric data: Application to crustal and mantle structure beneath central Namche Barwa, eastern Himalayan syntaxis. Chinese J. Geophys. (in Chinese) , 2012, 55(7): 2281-2291. |
| [13] | Kozlovskaya E, Hjelt S E. Modeling of elastic and electrical properties of solid-liquid rock system with fractal microstructure. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy , 2000, 25(2): 195-200. DOI:10.1016/S1464-1895(00)00031-4 |
| [14] | Heincke B, Jegen M, Hobbs R. Joint inversion of MT, gravity and seismic data applied to sub-basalt imaging.//SEG Technical Program Expanded Abstracts, 2006, 25(1): 784-789. |
| [15] | Colombo D, Stefano M D. Geophysical modeling via simultaneous joint inversion of seismic, gravity, and electromagnetic data: application to prestack depth imaging. The Leading Edge , 2007, 26(3): 326-331. DOI:10.1190/1.2715057 |
| [16] | Vermeesch P M, Morgan J V, Christeson G L, et al. Three-dimensional joint inversion of traveltime and gravity data across the Chicxulub impact crater. J. Geophys. Res. , 2009, 114(6): B02105. |
| [17] | 杨辉, 王家林, 吴健生, 等. 大地电磁与地震资料仿真退火约束联合反演. 地球物理学报 , 2002, 45(5): 723–734. Yang H, Wang J L, Wu J S, et al. Constrained joint inversion of magnetotelluric and seismic data using simulated annealing algorithm. Chinese J. Geophys. (in Chinese) , 2002, 45(5): 723-734. DOI:10.1002/cjg2.v45.5 |
| [18] | 于鹏, 戴明刚, 王家林, 等. 电阻率和速度随机分布的MT与地震联合反演. 地球物理学报 , 2009, 52(4): 1089–1097. Yu P, Dai M G, Wang J L, et al. Joint inversion of magnetotelluric and seismic data based on random resistivity and velocity distributions. Chinese J. Geophys. (in Chinese) , 2009, 52(4): 1089-1097. |
| [19] | 陈高, 于鹏, 陈晓, 等. 改进的大地电磁与地震资料联合反演方法在黔中隆起区的适用性研究. 石油物探 , 2010, 49(2): 158–163, 197. Chen G, Yu P, Chen X, et al. Adaptability research on improved joint inversion method of magnetotelluric and seismic data in middle Guizhou Uplift. Geophys. Pros. for Petroleum. (in Chinese) , 2010, 49(2): 158-163, 197. |
| [20] | 陈晓, 于鹏, 张罗磊, 等. 地震与大地电磁测深数据的自适应正则化同步联合反演. 地球物理学报 , 2011, 54(10): 2673–2681. Chen X, Yu P, Zhang L L, et al. Adaptive regularized synchronous joint inversion of MT and seismic data. Chinese J. Geophys. (in Chinese) , 2011, 54(10): 2673-2681. |
| [21] | 陈华根, 李嘉虓, 吴健生, 等. MT-重力模拟退火联合反演研究. 地球物理学报 , 2012, 55(2): 663–670. Chen H G, Li J X, Wu J S, et al. Study on simulated-annealing MT-gravity joint inversion. Chinese J. Geophys. (in Chinese) , 2012, 55(2): 663-670. |
| [22] | 何委徽, 王家林, 于鹏. 地球物理联合反演研究的现状与趋势分析. 地球物理学进展 , 2009, 24(2): 530–540. He W H, Wang J L, Yu P. Overview of the status and prospect of geophysical joint inversion. Progress in Geophysics. (in Chinese) , 2009, 24(2): 530-540. |
| [23] | 刘彦, 吕庆田, 孟贵祥, 等. 大地电磁与地震联合反演研究现状与展望. 地球物理学进展 , 2012, 27(6): 2444–2451. Liu Y, Lu Q T, Meng G X, et al. Joint electromagnetic and seismic inversion survey: status and prospect. Progress in Geophysics (in Chinese) , 2012, 27(6): 2444-2451. |
| [24] | Meju M A, Gallardo L A, Mohamed A K. Evidence for correlation of electrical resistivity and seismic velocity in heterogeneous near-surface materials. Geophys. Res. Lett. , 2003, 30(7): 1373-1376. |
| [25] | Haber E, Oldenburg D. Joint inversion: a structural approach. Inverse Problems , 1997, 13(1): 63-77. DOI:10.1088/0266-5611/13/1/006 |
| [26] | Gallardo L A, Meju M A. Characterization of heterogeneous near-surface materials by joint 2D inversion of DC resistivity and seismic data. Geophys. Res. Lett. , 2003, 30(13): 1658. |
| [27] | Gallardo L A, Meju M A. Joint two-dimensional cross-gradient imaging of magnetotelluric and seismic traveltime data for structural and lithological classification. Geophys. J. Int. , 2007, 169(3): 1261-1272. DOI:10.1111/gji.2007.169.issue-3 |
| [28] | Linde N, Binley A, Tryggvason A, et al. Improved hydrogeophysical characterization using joint inversion of cross-hole electrical resistance and ground-penetrating radar traveltime data. Water Resources Research , 2006, 42(12): W04410. |
| [29] | Hu W Y, Abubakar A, Habasshy T M. Joint electromagnetic and seismic inversion using structural constraints. Geophysics , 2009, 74(6): R99-R109. DOI:10.1190/1.3246586 |
| [30] | Moorkamp M, Heincke B, Jegen M, et al. A framework for 3-D joint inversion of MT, gravity and seismic refraction data. Geophys. J. Int. , 2011, 184(1): 477-493. DOI:10.1111/gji.2010.184.issue-1 |
| [31] | 谭捍东, 余钦范, BookerJ, 等. 大地电磁法三维交错采样有限差分数值模拟. 地球物理学报 , 2003, 46(5): 705–711. Tan H D, Yu Q F, Booker J, et al. Magnetotelluric three-dimensional modeling using the staggered-grid finite difference method. Chinese J. Geophys. (in Chinese) , 2003, 46(5): 705-711. |
| [32] | Siripunvaraporn W, Egbert G. An efficient data-subspace inversion method for 2-D magnetotelluric data. Geophysics , 2000, 65(3): 791-803. DOI:10.1190/1.1444778 |
| [33] | Siripunvaraporn W, Egbert G, Lenbury Y, et al. Three-dimensional magnetotelluric inversion: data-space method. Phys. Earth Planet. Interiors , 2005, 150(1-3): 3-14. DOI:10.1016/j.pepi.2004.08.023 |
| [34] | Sethian J A, Popovici A M. 3-D traveltime computation using the fast marching method. Geophysics , 1999, 64(2): 516-523. DOI:10.1190/1.1444558 |
| [35] | De Kool M, Rawlinson N, Sambridge M. A practical grid-based method for tracking multiple refraction and reflection phases in three-dimensional heterogeneous media. Geophys. J. Int. , 2006, 167(1): 253-270. DOI:10.1111/gji.2006.167.issue-1 |
| [36] | Kennett B L N, Sambridge M S, Williamson P R. Subspace methods for large inverse problems with multiple parameter classes. Geophys. J. Int. , 1988, 94(2): 237-247. DOI:10.1111/j.1365-246X.1988.tb05898.x |
| [37] | Sambridge M S. Non-linear arrival time inversion: constraining velocity anomalies by seeking smooth models in 3-D. Geophys. J. Int. , 1990, 102(3): 653-677. DOI:10.1111/gji.1990.102.issue-3 |
| [38] | Rawlinson N, Reading A M, Kennett B L N. Lithospheric structure of Tasmania from a novel form of teleseismic tomography. J. Geophys. Res. , 2006, 111(B2): B02301. |
 2013, Vol. 56
2013, Vol. 56

