2. 宁夏大学数学计算机学院, 银川 750021
2. School of Mathematics and Computer Science, Ningxia University, Yinchuan 750021, China
地震波数值模拟是研究地震波在复杂介质中传播规律的有效手段, 常用的地震波数值模拟方法有:几何射线法[1-2]、积分方程法[3-4]和地震波方程数值解法[5-9].几何射线法又简称射线法或射线追踪法, 是以弹性动力学方程的渐进解为基础, 主要考虑地震波的高频渐进解.积分方程法是将散射体内的波场表示成第一类或第二类方程的未知函数, 积分方程的数值求解用数值积分得到.地震波方程的数值解法能够得到完整的波场信息, 且对复杂介质有着广泛的适应性和有效性.常用的地震波动方程数值解法有:有限差分法, 傅里叶伪谱法, 有限元法, 谱元法, 有限体积法等.这些方法都有各自的优点和不足, Carcione[10]、Yang [11]对这些方法做了回顾和讨论.
传统的有限差分法基于Taylor展开原理具有较高的计算效率[12], 但算子无法覆盖高波数域, 对地震波高频部分模拟并不理想[13-14].基于快速Fourier变换的伪谱法虽能对波数有效覆盖, 但伪谱法缺乏因果律, 有悖于微分局部性的特点[15], 且计算效率较低.鉴于此, Mora[16]和Holberg [17]在伪谱法基础上设计了隐式褶积微分算子, 算子兼顾了有限差分和伪谱法的特点.随后, Zhou等[18]发展了显式褶积算子, 对算子进行加窗改造, 并运用至声波方程数值模拟中, 发现有限长度的算子精度能达到谱精度.张中杰等[19]将Shannon核褶积微分算子运用至地震波数值模拟中, 加窗后的算子对声波和弹性波场模拟得到了较好的效果; 戴志阳等[20]给出了功率窗和哈密窗下的算子系数; 龙桂华等[21]提出最优窗系数的思想, 将算子作用后的位移函数变换至波数域, 此时的波数应与理论波数最为接近, 依此可以计算不同窗半径和不同波数上限的最优系数, 但由于追求高波数的逼近使得低波数误差较为明显.
与Shannon离散奇异核褶积微分算子(SCD)相比, 广义Shannon离散奇异核褶积微分算子(GCD)通过增加Gauss包络线, 使得算子随长度衰减更快, 这意味着GCD更有利于体现微分的局部性, 使得我们可以进一步缩短算子长度以加大空间步长, 提高计算效率的同时保证较高的计算精度. Wei[22]首先讨论了GCD与SCD之间的联系, 通过大量的数值实验证实了GCD在求解偏微分方程时的高精度特点, Qian[23]推导了GCD的截断误差, 验证了GCD高精度高稳健的特点.
本文首次利用GCD逼近地震波方程空间微分, 并运用导数逼近的思想提出了一种优化GCD算子的方法, 使得有限长度的GCD获得较高的精度.然后将波动方程变换至Hamilton体系, 引入了Lie算子[24-25], 将指数算子运用BCH公式[24-26]展开, 基于最小误差原理构造得到了优化的二级二阶辛格式, 即每一步广义动量和广义坐标只需计算两次, 相比于三级三阶辛格式, 计算效率明显提升.对于辛系数中含有一个自由度的辛差分格式而言, Ruth[27]、Iwatsu[28]、李一琼等[29-30]将一个辛系数或两个辛系数的组合指定为特点的数值, 未从优化角度确定辛差分系数, 汪文帅等[31]虽提出了一种基于相位误差最下原理选取辛系数的优化方法, 但此方法只对简单振动方程有效, 并不具普遍意义, 而本文截断误差最小原理优化辛差分系数是一种适普方法.将优化的辛格式与GCD算子结合得到了优化保结构的OSGCD算子, 通过与几类其它辛格式作比较如辛PRK Lobatto ⅢA-ⅢB格式[32-35], Iwatsu三级三阶辛格式[28-30, 36], 本文的最优二级二阶辛格式的精度要高于常见的二阶格式, 而与Iwatsu的三阶辛格式精度相当, 但是计算效率比三阶格式大幅提升.说明该方法更适合于大尺度长时程地震波模拟.
2 OSGCD方法构造 2.1 保结构时间离散格式各向同性弹性介质中地震波传播的波动特征可以由运动方程完全描述.若不计体力, 三维齐次弹性波运动方程可以表示如下:
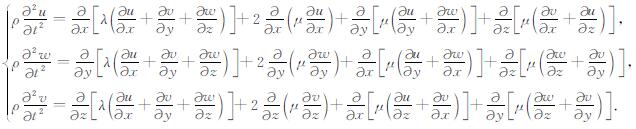
|
(1) |
其中, (u, w, v)为位移的三分量, u, w为水平方向位移, v为垂直方向位移, ρ为介质密度, λ, μ为拉梅常数.若只考虑弹性波情形, 则二维情况下方程(1)可变为:
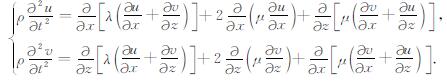
|
(2) |
(2)式中的两等式可以写成如下统一形式:
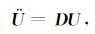
|
(3) |
其中, 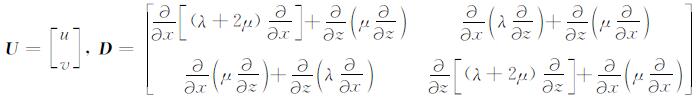
引入广义动量p=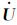

|
(4) |
其中, J为2n维反对称矩阵, J-1为矩阵J的逆矩阵, In为n阶单位矩阵, H为Hamilton函数, 可以表示如下:
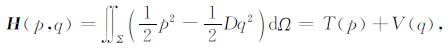
|
(5) |
其中, T(p), V(q)分别为Hamilton体系广义动能和广义势能. H描述了系统的整体能量, 若H与时间无关, 则系统能量守恒.在辛变换下Hamilton方程的正则形式(4)式不变[37], Hamilton动力学的基本定理是:对于任意的Hamilton体系必定依赖于H以及初始时刻和t时刻辛变换族GHt使得:

|
(6) |
其中, Z(0)为初始相, Z(t)为t时刻的相.由0时刻至t时刻的演进过程中辛变换保证了辛结构不变, 即微分二形式守恒.由(5)知波动方程为一可分的Hamilton系统, 对于可分的Hamilton系统可以构造任意阶精度的显式辛格式[38].为了方便构造辛格式, 分别以A和B约定T(p)和V(q)的Lie算子[24, 25]为:

|
(7) |
其中, {}为泊松括号.三阶或高阶辛格式虽有较高的精度, 但高精度的获取往往以牺牲计算效率为代价, 为了适应高效地震波模拟的需要, 本文由Lie算子设计了二级二阶辛格式表示为
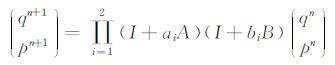
|
(8) |
其中, a1, a2, b1, b2为待定辛差分系数.
(8)式辛格式四个系数需满足三个等式, 故方程组有一个自由度, 反复使用指数算子展开的BCH公式[24-26]基于截断误差最小原理可以得到优化的二级二阶辛格式: a1=1-



传统的基于泰勒展开的有限差分算子在进行地震波模拟时具有较高的计算效率, 但有限差分短算子在粗网格的情况下精度较低, 数值频散明显[39-40].如何保证有限差分计算效率的同时提高计算精度是本文研究的重点.本文引进广义离散Shannon奇异核褶积微分算子(GCD)计算空间微分.
广义Shannon奇异函数定义如下[22]:

|
(9) |
其中, Δ为空间网格间距, r为任意常数.若Δ →0时δΔ为Delta函数的一个很好近似, 广义Shannon插值基函数的离散形式为
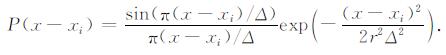
|
(10) |
根据广义函数理论, 对于任意函数序列{u(xi)}, 其空间任意阶微分可由其离散序列近似表示如下:
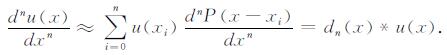
|
(11) |
波动方程的数值求解涉及空间的一阶导数、二阶导数、混合导数, 混合导数由两个方向的一阶导数实现.对(10)式求一阶导数可以得到一阶微分算子为

|
(12) |
在空间均匀采样情况下(x=mΔ), 一阶算子退化为如下简洁的形式:

|
(13) |
同理均匀空间采样的二阶微分算子为

|
(14) |
(13)、(14)式算子为全局长算子, 需要用到空间所有节点值, 实际计算中为了提高计算效率, 需要对算子截断, 使长算子变为短算子.如对算子强行截断, 势必引起Gibbs现象, 为了消除这种现象, 需要采用使算子主瓣能量集中旁瓣波动较小的窗函数截断, 本文采用Hanning窗函数[41], 其具体形式如下:

|
(15) |
其中, W为算子半径.
加窗后的一阶、二阶微分算子可以表示如下:

|
(16) |
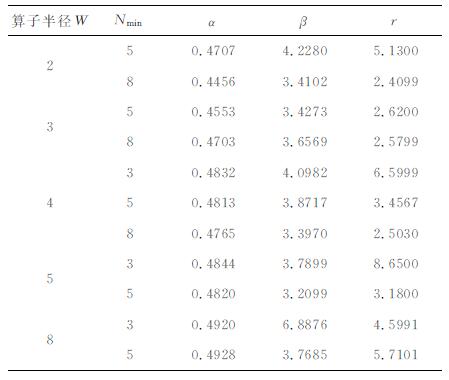
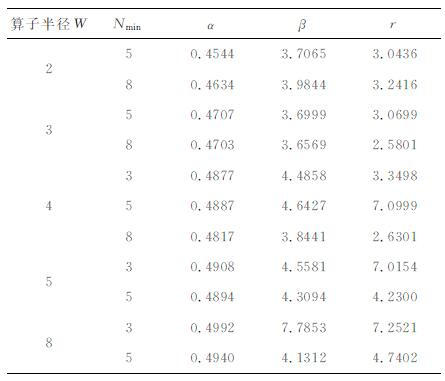
可以看出, 一阶微分算子为反对称算子, 二阶算子为对称算子, 为了使群速度误差尽量最小, 差分算子应满足能量守恒定律, 一阶算子自然满足, 二阶算子需修正中心点值为其它对称值和的负数[20].算子中有三个系数α, β, r需要确定.合理的选择系数使得求导精度尽量最高, 基于导数逼近原理可以得到稳定的优化系数, 表 1, 表 2给出了优化结果, 具体推导见附录B.从表 1和表 2可以看出, 优化系数由算子半径和最短波长内采样点数决定.根据实际情况灵活选择优化系数以获得更好效果, 实际地震波模拟时最短波长内采样点数大于5, 所以选择Nmin=5的最优算子系数就已经足够.若一味求最高波数范围内的精度, 选择采样下限较小的优化系数, 虽能在高波数获得较高精度, 但这必然以牺牲低波数范围内精度为代价.本文数值算例中考虑计算效率和精度均选择W=4, Nmin=5对应的系数.
|
|
表 1 一阶最优褶积微分算子窗函数系数 Table 1 Optimal coefficients of window function for first order GCD |
|
|
表 2 二阶最优褶积微分算子窗函数系数 Table 2 Optimal coefficients of window function for second order GCD |
利用f(x)的一阶导数分析GCD的精度, f′(x)做Fourier变换得到ikxF(kx), F(kx)为Fourier变换的像函数, 空间导数的Fourier变换可以看成是f(x)线性滤波的结果, 滤波响应为ikx.空间离散点f(xi)用GCD估计空间导数的滤波响应为

|
(17) |
其中, Cn(W)为GCD算子系数, G=Δ/λ为一个波长内的采样点数的倒数.
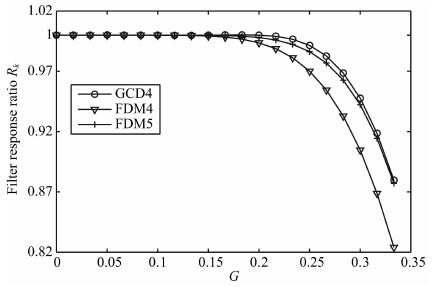
算子滤波响应比为Rk=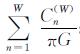
|
图 1 GCD和FDM算子滤波响应对比 Fig. 1 Comparison of filter response ratio of GCD and FDM operators |
OSGCD进行地震波模拟时, 计算时间步长和空间网格间距应满足一定的关系计算过程才稳定, 否则计算结果会产生无物理意义的按指数增长的数值结果[32], 参照文献[30]的分析方法, 将稳定条件设定为如下形式:

|
(18) |
其中, Δt为时间步长, a和C为待定常数.
附录C给出二维情形下(18)式中a和C的推导过程, 结果为a=0. 6986, C=0. 8138.
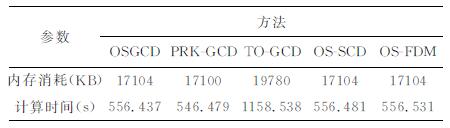
3 数值实验 3.1 半无限均匀模型为了检验方法的有效性及精度, 将本文提出OSGCD分别与以下几类方法进行比较: (1) 辛PRK Lobatto Ⅲ A-ⅢB格式[32-35]与GCD结合(PRK-GCD); (2) Iwatsu三级三阶辛格式[15, 28-30, 36]与GCD结合(TO-GCD); (3) 二级二阶最优辛格式与SCD[15, 28-29, 41]结合(OS-SCD); (4) 二级二阶最优辛格式与有限差分[42]结合(OS-FDM).选择半无限空间模型, 模型大小为2000 m×2000 m, 纵波速度2000 m/s, 横波速度1250m/s, 介质密度2400kg/m3, 震源位于(1000m, 1000m)处, 接收点位于(1200m, 1200m)处.震源为集中力源, 由主频为30 Hz的Ricker子波激发产生, 时间步长为0. 5 ms, 空间网格间距为5m.模拟均在主频为3.0 G Hz的Intel (R) Core (TM) i5-2320 CPU、内存为16GB的计算机上进行.模拟结果如图 3、图 4、表 3所示.

|
图 2 弹性波传播二维半无限空间模型 Fig. 2 2-D half infinite space for elastic wave propagation |
|
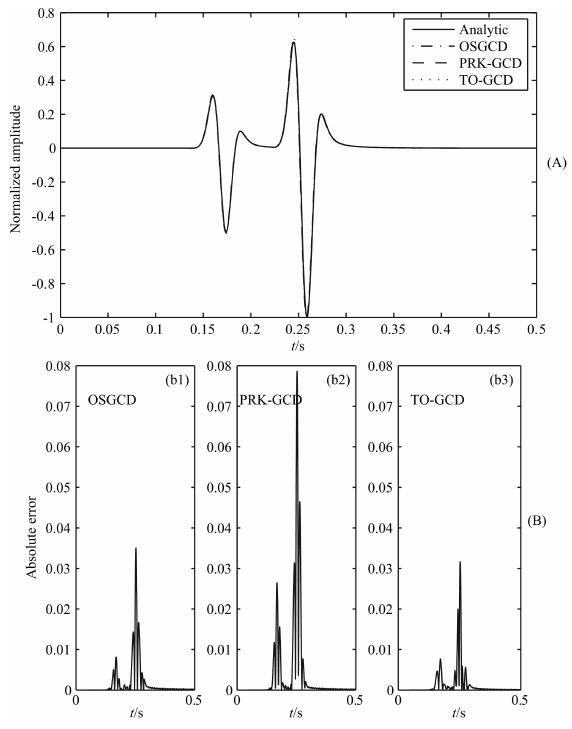
图 3 三种辛格式模拟结果波形对比(A)及三种辛格式模拟结果绝对误差对比(B) Fig. 3 (A) Comparison of waveforms generated by OSGCD, PRK-GCD and TO-GCD and (B) Comparison of absolute error generated by three different time discretization methods |
|
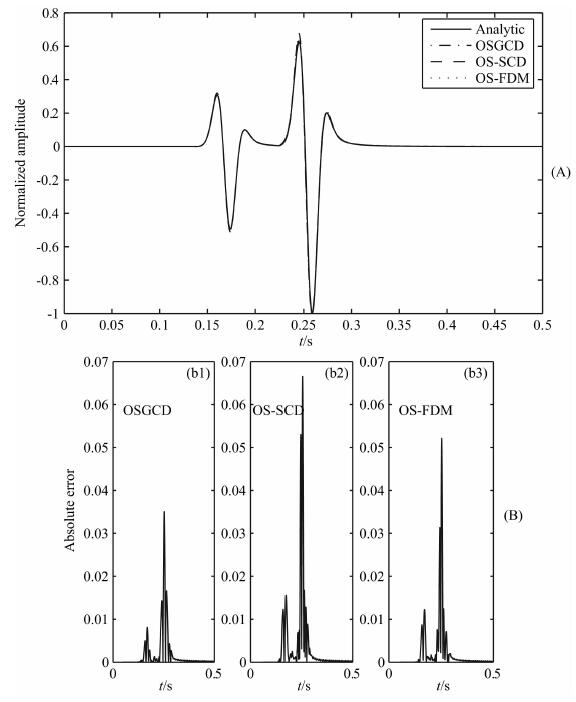
图 4 三种空间微分格式模拟结果波形对比(A)及三种空间微分格式模拟结果绝对误差对比(B) Fig. 4 (A) Comparison of waveforms generated by OSGCD, OS-SCD and OS-FDM; (B) Comparison of absolute error generated by three different spatial derivative methods |
|
|
表 3 五种算法计算效率对比 Table 3 Comparison of computational efficiency of five methods |
由图 3a可以看出三种辛格式与GCD结合能对地震波有效模拟, 计算的地震波到时与波形都能与解析解很好的逼近; 图 3b显示TO-GCD高阶辛格式误差最小, OSGCD误差其次, 而PRK-GCD误差最大, 但由表4可知TO-GCD内存要求明显增加, 而计算时间几乎为OSGCD和PRK-GCD的两倍, 而OSGCD与PRK-GCD计算效率基本相同; 由图 4a可知三种空间微分格式亦能得到有效结果, 但图 4b显示GCD计算精度明显优于SCD和FDM, 而三种空间微分格式内存和时间消耗几乎一致.从上述对比中, 我们发现在相同的计算时间和内存消耗下OGSCD可获得更高的精度.
3.2 长时程模拟为了检验OSGCD长时间地震波模拟能力, 与常用的Runge-Kutta有限差分法(RK-FDM)对比.模型为6000m×6000 m的均匀介质模型, 纵波速度为3000m/s, 横波速度为2000m/s, 介质密度2000kg/m3.震源为剪切力源, 位于模型中心, 选取主频为20 Hz的Ricker子波, 空间网格间距为10m, 时间步长为1ms.模型周围为刚性界面.模拟结果如图 5所示.
对比图 5(a, b)可知, 在短时间内, 两种方法对地震波模拟结果几乎无明显差别; 随着时间增加, RK-FDM (图 5c)数值频散和误差累积明显超过OSGCD (图 5d), 在快照中表现为RK-FDM等时面(图 5c)较为模糊, 而OSGCD等时面(图 5d)较为清晰, 说明OSGCD较常规方法更具有长时间地震波模拟的优势.

|
图 5 RK-FDM (a, c)和OSGCD (b, d)得到的1.5 s和25 s时的波场快照 Fig. 5 Snapshots of wavefield generated by RK-FDM (a, c) and OSGCD (b, d); (a, b) timestep=1500; (c, d) timestep=25000. |
为了验证OSGCD在处理非均匀介质中地震波模拟的有效性, 选择Marmousi模型对OGSCD进行检验.模型网格点数为384×122, 模型中存在若干个起伏弯曲速度强烈间断面, 模型纵波速度结构如图 5所示, 纵波速度变化范围为1500~5500m/s, 横波速度可用公式VS=VP/ 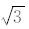

|
图 6 Marmousi速度模型示意图 Fig. 6 Marmousi velocity model |
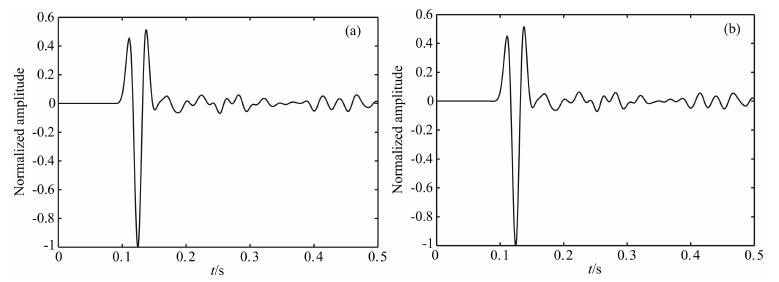
对比图 7(a, b)、图 8(a, b)可知, OSGCD和PSM无论快照和地震记录都一致, 由于介质的非均匀性, 在速度突变的地方产生了强烈的绕射和散射, 主要表现在主要震相过后的区域尾震荡明显.模拟结果表明OSGCD处理非均匀介质的能力与PSM一致.

|
图 7 OSGCD (a)和PSM (b)模拟Marmousi模型0.25 s时的波场快照 Fig. 7 Snapshots of wave field at 0.25 s in Marmousi model (a) is generated by PSM; (b) is generated by OSGCD. |
|
图 8 OSGCD (a)和PSM (b)模拟Marmousi接收点处地震记录 Fig. 8 Seismograms in Marmousi model (a) isgenerated by PSM; (b) is generated by OSGCD |
将波动方程变换至Hamilton体系, 基于最小误差原理构造了一种新的二级二阶辛格式, 用广义褶积微分算子逼近空间微分算子, 运用导数逼近原理提出了一种优化微分算子系数的方法.空间域优化的离散褶积微分算子与新推导的时间域二级二阶辛离散格式相结合, 得到了一种适用于地震波高效高精度模拟的保结构算法(OSGCD), 并给出了OSGCD稳定性条件.在数值算例中OSGCD与多种常见方法对比, 证实了OSGCD在精度和计算效率上都具有明显优势, 在长时程地震波模拟中, OSGCD能有效地压制数值频散和误差累积, 在非均匀介质中地震波模拟时, OSGCD表现出较好的稳定性并得到了可靠的结果. OSGCD为高效高精度地震波模拟与成像提供了一种新的、有效的选择.
附录A约定互易子[45][A, B]=AB-BA且[A, B, A]=[A, [B, A]], 则:

|
(A1) |
运用Baker-Campell-Hausdroff (BCH)公式, (A1)展成幂级数形式:
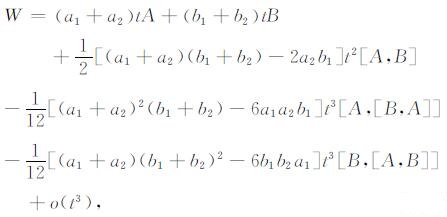
|
(A2) |
a1, a2, b1, b2须满足:

|
(A3) |
其中, Minimum表示η1, η2平方和最小
由(A3)可知:

|
考虑如下形式的简谐平面波
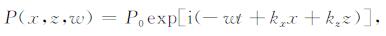
|
(B1) |
其中, kx=ksinθ, kz=kcosθ, k=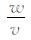
GCD作用(B1)后的导数为

|
(B2) |
其中, G=kΔ/2π=Δ/λ为一个波场内采样点数的倒数.
(B2)为非线性最优化问题可以用最速下降法构造如下迭代[46]:
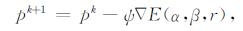
|
(B3) |
其中, 
假设OSGCD稳定性条件服从如下形式[35]:
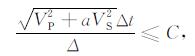
|
(C1) |
其中, Δ=Δx=Δz, a, C为待定常数.
广义坐标与广义动量某时刻的误差向量为

|
(C2) |
其中, E=exp[i (kxx+kzz)].
误差增长格式可以写成如下形式:
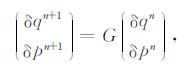
|
(C3) |
其中,
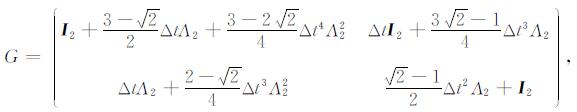
|
I2为二阶单位矩阵, Λ2=(aij)2×2, a11=VP2kx2+VS2kz2, a12=(VP2-VS2)kxkz, a21=a12, a22=VS2kx2+VP2kz2, kx=ksinθ, kz=kcosθ, k=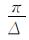
令r=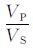

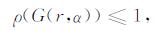
|
(C4) |
用数值方法求解(C4), r从1增加至4, 步长为0. 01, 计算对应的最大α, 用非线性拟合求(C1)中的待定常数a和C.最后求得a=0.6986, C=0.8138.
| [1] | 陈景波, 秦孟兆. 辛几何算法在射线追踪中的应用. 数值计算与计算机应用 , 2000, 21(4): 254–265. Chen J B, Qin M Z. Ray tracing by symplectic algorithm. Journal of Numerical Methods and Computer Applications (in Chinese) , 2000, 21(4): 254-265. |
| [2] | Červeny V. Seismic Ray Theory. Cambridge: Cambridge University Press, 2001 . |
| [3] | Pao Y H, Varatharajulu V. Huygen's principle, radiation conditions, and integral formulas for the scattering of elastic wave. J. Acoust. Soc. Am. , 1976, 59(6): 1361-1371. DOI:10.1121/1.381022 |
| [4] | Ursin B. Review of elastic and electromagnetic wave propagation in horizontally layered media. Geophysics , 1983, 44(8): 1063-1081. |
| [5] | 牟永光, 裴正林. 三维复杂介质地震数值模拟. 北京: 石油工业出版社, 2005 . Mou Y G, Pei Z L. Seismic Numerical Modeling for 3-D Complex Media (in Chinese). Beijing: Petroleum Industry Press, 2005 . |
| [6] | 董良国, 马在田, 曹景忠. 一阶弹性波方程交错网格高阶差分解法稳定性研究. 地球物理学报 , 2000, 43(6): 856–864. Dong L G, Ma Z T, Cao J Z. A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation. Chinese J. Geophys. (in Chinese) , 2000, 43(6): 856-864. |
| [7] | 张美根, 王妙月, 李小凡, 等. 各向异性弹性波场的有限元数值模拟. 地球物理学进展 , 2002, 17(3): 384–389. Zhang M G, Wang M Y, Li X F, et al. Finite element forward modeling of anisotropic elastic waves. Progress in Geophysics (in Chinese) , 2002, 17(3): 384-389. |
| [8] | Gazdag J. Modeling of the acoustic wave equation with transform methods. Geophysics , 1981, 46(6): 854-859. DOI:10.1190/1.1441223 |
| [9] | Komatitsch D. Spectral and spectral-element methods for the 2D and 3D elastodynamics equations in heterogeneous media. Paris, France: Institut de Physique du Globe, 1997. |
| [10] | Carcione J M, Herman G C, ten Kroode A P E. Seismic modeling. Geophysics , 2002, 67(4): 1304-1325. DOI:10.1190/1.1500393 |
| [11] | Yang D H, Song G J, Lu M. Optimally accurate nearly analytic discrete scheme for wave-field simulation in 3D anisotropic media. Bull. Seism. Soc. Am. , 2007, 97(5): 1557-1569. DOI:10.1785/0120060209 |
| [12] | Bayliss A, Jordan K E, Lemesurier B J, et al. A fourth-order accurate finite-difference scheme for the computation of elastic wave. Bull. Seism. Soc. Am. , 1986, 76(4): 1115-1132. |
| [13] | Fornberg B. The Pseudospectral method: Comparisons with finite differences for the elastic wave equation. Geophysics , 1987, 52(4): 483-501. DOI:10.1190/1.1442319 |
| [14] | Fornberg B. The Pseudospectral method: Accurate representation of interfaces in elastic wave calculations. Geophysics , 1988, 53(5): 625-637. DOI:10.1190/1.1442497 |
| [15] | Li X F, Wang W S, Lu M W, et al. Structure-preserving modelling of elastic waves: a symplectic discrete singular convolution differentiator method. Geophys. J. Int. , 2012, 188(3): 1382-1392. DOI:10.1111/gji.2012.188.issue-3 |
| [16] | Mora P. Elastic Finite Differences with Convolutional Operators. California: Stanford Exploration Project Report, 1986: 277-290. |
| [17] | Holberg O. Computational aspects of the choice of operator and sampling interval for numerical differentiation in large-scale simulation of wave phenomena. Geophysical Prospecting , 1987, 35(6): 629-655. DOI:10.1111/gpr.1987.35.issue-6 |
| [18] | Zhou B, Greenhalgh S. Seismic scalar wave equation modeling by a convolutional differentiator. Bull. Seism. Soc. Amer. , 1992, 82(1): 289-303. |
| [19] | 张中杰, 滕吉文, 杨顶辉. 声波与弹性波场数值模拟中的褶积微分算子法. 地震学报 , 1996, 18(1): 63–69. Zhang Z J, Teng J W, Yang D H. The convolutional differentiator method for numerical modeling of acoustic and elastic wave-field. Acta Seismologica Sinica (in Chinese) , 1996, 18(1): 63-69. |
| [20] | 戴志阳, 孙建国, 查显杰. 地震波场模拟中的褶积微分算子法. 吉林大学学报(地球科学版) , 2005, 35(4): 520–524. Dai Z Y, Sun J G, Zha X J. Seismic wave field modeling with convolutional differentiator algorithm. Journal of Jilin University (Earth Science Edition) (in Chinese) , 2005, 35(4): 520-524. |
| [21] | 龙桂华, 赵宇波, 赵家福. 地震波数值模拟中的最优Shannon奇异核褶积微分算子. 地震学报 , 2011, 33(5): 650–662. Long G H, Zhao Y B, Zhao J F. Optimal Shannon singular kernel convolutional differentiator in seismic wave modeling. Acta Seismologica Sinica (in Chinese) , 2011, 33(5): 650-662. |
| [22] | Wei G W. Quasi wavelets and quasi interpolating wavelets. Chemical Physics Letters , 1998, 296(3-4): 215-220. DOI:10.1016/S0009-2614(98)01061-6 |
| [23] | Qian L W. On the regularized Whittaker-kotel' nikov-Shannon sampling formula. American Mathematical Society , 2002, 131(4): 1169-1176. |
| [24] | Li R, Wu X. Two new Fourth-order Three-stage symplectic integrators. Chin. Phys. Lett. , 2011, 28(7): 070201. DOI:10.1088/0256-307X/28/7/070201 |
| [25] | Li R, Wu X. Application of the fourth-order three-stage symplectic integrators in chaos determination. Eur. Phys. J. Plus , 2011, 126(8): 73-80. DOI:10.1140/epjp/i2011-11073-1 |
| [26] | Casas F, Murua A. An efficient algorithm for computing the Baker-Campbell-Hausdorff series and some of its applications. Technical report, Universitat Jaume I, 2008. |
| [27] | Ruth R D. A canonical integration technique. IEEE Transactions on Nuclear Science , 1983, 30(4): 2669-2671. DOI:10.1109/TNS.1983.4332919 |
| [28] | Iwatsu R. Two new solutions to the third-order symplectic integration method. Physics Letter A , 2009, 373(34): 3056-3060. DOI:10.1016/j.physleta.2009.06.048 |
| [29] | 李一琼, 李小凡, 朱童. 基于辛格式奇异核褶积微分算子的地震标量波场模拟. 地球物理学报 , 2011, 54(7): 1827–1834. Li Y Q, Li X F, Zhu T. The seismic scalar wave field modeling by symplectic scheme and singular kernel convolutional differentiator. Chinese J. Geophys. (in Chinese) , 2011, 54(7): 1827-1834. |
| [30] | 李一琼, 李小凡, 张美根. 基于辛格式离散奇异褶积微分算子的弹性波场模拟. 地球物理学报 , 2012, 55(5): 1725–1731. Li Y Q, Li X F, Zhang M G. The elastic wave fields modeling by symplectic discrete singular convolution differentiator method. Chinese J. Geophys. (in Chinese) , 2012, 55(5): 1725-1731. |
| [31] | 汪文帅, 李小凡. 一种新的三阶非力梯度辛积分算法. 武汉大学学报(理学版) , 2012, 58(3): 221–228. Wang W S, Li X F. A new solution to the third-order non-gradient symplectic integration algorithm. J. Wuhan Univ. (Nat. Sci. Ed.) (in Chinese) , 2012, 58(3): 221-228. |
| [32] | 罗明秋, 刘洪, 李幼铭. 地震波传播的哈密顿表述及辛几何算法. 地球物理学报 , 2001, 44(1): 120–128. Luo M Q, Liu H, Li Y M. Hamiltonian description and symplectic method of seismic wave propagation. Chinese J. Geophys. (in Chinese) , 2001, 44(1): 120-128. |
| [33] | 孙耿. 波动方程的一类显式辛格式. 计算数学 , 1997(1): 1–10. Sun G. A class of explicitly symplectic schemes for wave equations. Mathematica Numerica Sinica (in Chinese) , 1997(1): 1-10. |
| [34] | 马啸, 杨顶辉, 张锦华. 求解声波方程的辛可分Runge-Kutta方法. 地球物理学报 , 2010, 53(8): 1993–2003. Ma X, Yang D H, Zhang J H. Symplectic partitioned Runge-Kutta method for solving the acoustic wave equation. Chinese J. Geophys. (in Chinese) , 2010, 53(8): 1993-2003. |
| [35] | Ma X, Yang D H, Liu F Q. A nearly analytic symplectically partitioned Runge-Kutta method for 2-D seismic wave equations. Geophys. J. Int. , 2011, 187(1): 480-496. DOI:10.1111/gji.2011.187.issue-1 |
| [36] | Li X F, Li Y Q, Zhang M G, et al. Scalar seismic-wave equation modeling by a multisymplectic discrete singular convolution differentiator method. Bull. Seism. Soc. Am. , 2011, 101(4): 1710-1718. DOI:10.1785/0120100266 |
| [37] | 冯康, 秦孟兆. 哈密尔顿系统的辛几何算法. 杭州: 浙江科学技术出版社, 2003 . Feng K, Qin M Z. Symplectic Geometric Algorithm for Hamiltonian Systems (in Chinese). Hangzhou: Zhejiang Science & Technology Press, 2003 . |
| [38] | Suzuki M. General theory of higher-order decomposition of exponential operators and symplectic integrators. Phys. Lett. A , 1992, 165(5-6): 387-395. DOI:10.1016/0375-9601(92)90335-J |
| [39] | Dablain M A. The application of high-order differencing to the scalar wave equation. Geophysics , 1986, 51(1): 54-56. DOI:10.1190/1.1442040 |
| [40] | Fei T, Larner K. Elimination of numerical dispersion in finite-difference modeling and migration by flux-corrected transport. Geophysics , 1995, 60(6): 1380-1842. |
| [41] | 龙桂华, 李小凡, 张美根. 基于Shannon奇异核理论的褶积微分算子在地震波场模拟中的应用. 地球物理学报 , 2009, 52(4): 1014–1024. Long G H, Li X F, Zhang M G. The application of convolutional differentiator in seismic modeling based on Shannon singular kernel theory. Chinese J. Geophys. (in Chinese) , 2009, 52(4): 1014-1024. |
| [42] | Smith G D. Numerical Solution of Partial Differential Equations: Finite Difference Methods. Oxford: Glarendon Press, 1978 . |
| [43] | 李信富, 李小凡. 地震波传播的褶积微分算子法数值模拟. 地球科学-中国地质大学学报 , 2008, 33(6): 861–866. Li X F, Li X F. Numerical simulation of seismic wave propagation using convolutional differentiator. Earth Science-Journal of China University of Geosciences (in Chinese) , 2008, 33(6): 861-866. DOI:10.3799/dqkx.2008.103 |
| [44] | Berenger J. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. , 1994, 114(2): 185-220. DOI:10.1006/jcph.1994.1159 |
| [45] | Xu J, Wu X. Several fourth-order force gradient symplectic algorithms. Research in Astronomy and Astrophysics , 2010, 10(2): 173-188. DOI:10.1088/1674-4527/10/2/009 |
| [46] | Jo C H, Shin C, Suh J H. An optimal 9-point, finite-difference, frequency-space, 2-D Scalar wave extrapolator. Geophysics , 1996, 61(2): 529-537. DOI:10.1190/1.1443979 |
 2013, Vol. 56
2013, Vol. 56