地球物理学报  2013, Vol. 56 Issue (7): 2447-2451   PDF    
引用本文
刘璐, 刘洪, 张衡 等. 基于修正拟牛顿公式的全波形反演. 地球物理学报, 2013, 56(7): 2447-2451, doi: 10.6038/cjg20130730.  
Liu L, Liu H, Zhang H, et al. Full waveform inversion based on modified quasi-Newton equation. Chinese J. Geophys. (in Chinese), 2013, 56(7): 2447-2451, doi: 10.6038/cjg20130730.  
基于修正拟牛顿公式的全波形反演
刘璐1,2 , 刘洪1 , 张衡1,2 , 崔永福3 , 李飞3 , 段文胜3 , 彭更新3     
1. 中国科学院地质与地球物理研究所中国科学院油气资源研究重点实验室, 北京 100029;
2. 中国科学院大学, 北京 100049;
3. 中国石油塔里木油田分公司勘探开发研究院, 新疆 库尔勒 841000
收稿日期 2012-04-06, 2012-06-28 收修定稿
基金项目: 国家自然科学基金重点项目(40830424);国家油气重大专项(2011ZX05008-006-50)和国家863主题项目(2012AA061202)联合资助
作者简介: 刘璐, 男, 1988年生, 中国科学院地质与地球物理研究所在读博士研究生, 主要从事地震波成像和反演方法的研究. E-mail:liulu@mail.iggcas.ac.cn
通讯作者: 刘洪, 男, 1959年生, 研究员, 主要从事油储地球物理研究.E-mail:liuhong@mail.iggcas.ac.cn
摘要: 波形反演是一种利用全波场信息, 通过最小化预测波场和实际波场的残差来揭示地下岩性和构造信息的方法.本文首先简述了常规拟牛顿算法的原理, 之后利用一种新的拟牛顿公式对Davidon-Fletcher-Powell (DFP)和Broyden-Fletcher-Goldfarb-Shanno (BFGS)算法进行了修正, 改进后的BFGS算法在近似Hessian矩阵逆矩阵时, 不仅考虑了梯度和模型信息, 还加入了目标函数本身的信息, 而且对于每次迭代, 基本没有增加计算量.数值试验表明, 相对常规拟牛顿方法, 修正BFGS算法在保证反演精度的同时, 明显提高了反演效率.
关键词: 修正BFGS算法      波形反演      Hessian矩阵      拟牛顿法     
Full waveform inversion based on modified quasi-Newton equation
LIU Lu1,2, LIU Hong1, ZHANG Heng1,2, CUI Yong-Fu3, LI Fei3, DUAN Wen-Sheng3, PENG Geng-Xin3     
1. Key Laboratory of Petroleum Resources Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Research Institute of Exploration and Development, Tarim Oilfiled Company, PetroChina, Korla, Xinjiang 841000, China
Abstract: Waveform inversion is a kind of method to reveal the underground structure and lithology information through minimizing the residual error between predicted wavefield and true seismic record using full-wavefield information. In this paper, we briefly state the principle of conventional Quasi-Newton algorithm, and then exploit a new modified Quasi-Newton equation to modify the conventional Davidon-Fletcher-Powell (DFP) and Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm. Different from past Quasi-Newton methods, this modified BFGS algorithm considers gradient value, model information and objective function value together to approximate the inverse matrix of Hessian matrix; moreover it almost does not increase the calculation amount for each iteration. Finally, numerical experiment shows that compared with conventional Quasi-Newton method, modified BFGS algorithm can not only preserve the inversion accuracy, but significantly improve calculation efficiency..
Key words: Modified BFGS algorithm      Waveform inversion      Hessian matrix      Quasi-Newton method     
1 引言

全波形反演综合利用了地震记录中振幅、走时和相位等信息, 通过拟合实际波场和预测波场来定量提取地下介质的弹性参数, 进而为深部大尺度构造演化分析[1-2], 为勘探地震成像及速度建模等方面提供可靠依据.相对时间域反演, 频率域反演采用一部分频率参与反演就可以得到可靠的结果[3], 而且低频到高频的反演策略可以更好地解决全频段反演遇到的局部极小值问题[4].

20世纪80年代, Tarantola等人通过梯度寻优来更新模型参数, 在时间域实现了波形反演, 并将目标函数对参数偏导数的求取转换成残差反传波场和入射波场的互相关运算[5-6], 从而避开了直接计算Jacobi矩阵, 减小了计算量.基于该思想, Pratt等率先利用五点差分格式实现了频率域全波形反演[7].由于该方法运算量和内存占用量都很大, 而且应用到实际数据尚有一段距离, 所以起初全波形反演并没有得到足够的重视; 近几年, 人们不断从计算机硬件, 反演算法和地震野外采集等多方面解决这些问题[8-9].反演算法方面, 一阶近似的梯度法往往不能满足收敛要求, 于是Pratt等将高斯牛顿法和全牛顿法应用到了频率域波形反演中[10]; 但牛顿法中Hessian矩阵逆矩阵的求取极耗费机时, 而且可能非正定, 而拟牛顿法采用近似矩阵Hk来对其进行逼近, 避开了Hessian矩阵逆矩阵的直接求取, 是一种行之有效的方法; 其中, 有限存储的BFGS算法(L-BFGS)不需要直接存储矩阵Hk, 仅存储近m次迭代(m取值为3~6)的梯度信息和模型信息就可以估计出Hk[11], 节省了内存开销; Brossier等人将L-BFGS算法应用到全波形反演中, 较高效地求解了大规模无约束的优化问题[12].同时, Ma等人也对反演算法做了深入研究, 他们利用投影的Hessian矩阵, 修改了BFGS算法, 减少了计算耗时和内存占用量[13], 还将影像引导插值技术应用到全波形反演中, 通过减少模型参数个数加速了收敛速度[14].但是, 常规拟牛顿法在近似Hessian逆矩阵时, 仅仅是考虑了梯度和模型信息, 却忽视了目标函数本身的数值信息.基于此, Zhang等人推导了新的拟牛顿条件, 在近似矩阵Hk的构造上同时利用了目标函数梯度和其本身的信息, 进而得出了修正的BFGS公式[15-16].

本文将Zhang的修正拟牛顿条件引入到全波形反演中, 并对常规DFP算法和BFGS算法进行了修正, 进而给出了修正算法的反演流程图; 修正的公式相对常规拟牛顿算法, 在每次迭代过程中基本没有增加计算量; 之后, 我们以BFGS算法为例进行了对比验证, 通过与常规BFGS算法在反演效果和收敛性上的对比, 证明修正BFGS算法由于综合考虑了梯度信息、模型差值信息和目标函数信息, 可以更好地逼近Hessian矩阵的逆矩阵, 从而在保证精度的前提下, 加快收敛, 减少反演耗时.

2 常规拟牛顿算法

全波形反演通常被表示为一个非线性目标函数的优化问题.目标函数的选取有多种, 包括残差波场的L2范数, L1范数, Huber范数和混合范数[17]等, 其中L2范数可以表示为

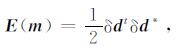
(1)

(2)

其中, m表示模型参数向量, δd是预测波场u和实际波场d的差值, 角标t和*分别代表转置和共轭.在Born近似条件下, 更新的模型参数可以表示为初始模型m0加上模型扰动量Δm, 即m=m0 +Δm, 反演的目的就是利用目标函数梯度信息和其他信息来求取模型参数的扰动量Δm.而拟牛顿法用不包含二阶导数的矩阵来近似牛顿法中的Hessian矩阵的逆矩阵Hk, 在反演方法中占有重要地位.

DFP和BFGS算法是Broyden族成员中最常用的两种, 两者都是基于同一个拟牛顿条件,

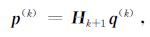
(3)

其中,

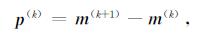
(4)

(5)

进一步可得到DFP和BFGS的迭代公式分别为

(6)

(7)

3 修正拟牛顿算法的推导

如(3)-(7)式所示, 常规拟牛顿法的一个弊端是, 仅利用梯度和模型信息来构造Hk, 没有充分利用目标函数的信息[16]; 对此, Zhang等人进行了算法修正[15].首先将目标函数(1)式在mk+1处进行三阶Taylor展开, 并令m=mk, 则有

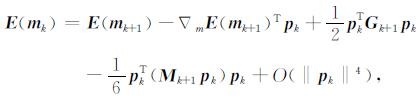
(8)

其中,

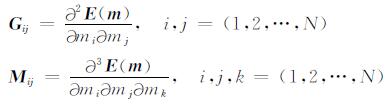
对(8)式两边对模型参数求导, 同时左乘pkT,

(9)

由(8)式和(9)式消去Mk+1, 并省去无穷小项, 可得

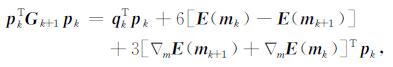
(10)

进而, 令校正矩阵Bk来代替Hessian矩阵Gk, 则有

(11)

进一步, 我们可以得到,

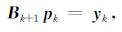
(12)

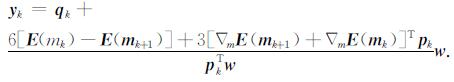
(13)

式(12)和(13)即为修正后的新拟牛顿公式, w的取值满足pkTw≠0, 本文取w=pk, 可以看出, 修正后的拟牛顿公式在近似Hessian矩阵Hk时, 同时利用了梯度信息, 模型信息和目标函数自身信息.另外, 在运算量方面, 相对常规的拟牛顿条件, 修正后的公式(12)和(13)只是增加了简单的向量乘加运算, 基本没有增加额外计算量.基于式(12)和(13), 常规的DFP和BFGS算法可修改为

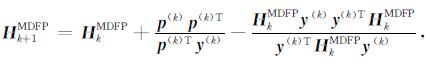
(14)

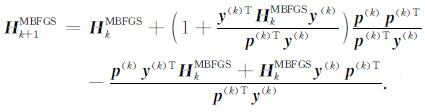
(15)

波形反演中, 通过引入虚震源可以避免Jacobi矩阵的直接求取[10], 目标函数(1)的梯度可以表示为

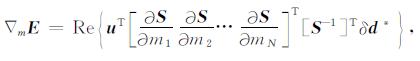
(16)

其中, S是与当前迭代频率和速度场相对应的系数矩阵, u是当前速度模型的预测波场.当模型垂向和纵向网格间距一样时, 系数矩阵S是对称矩阵, 此时上式就可以看作是入射波长与残差反传波场的互相关, 进而结合(14)和(15)式, 可得与修正拟牛顿法相应的模型更新扰动量为

(17)

其中, ωd是加权系数; Hk是不同拟牛顿法求得的近似矩阵; α为迭代步长, 本文通过抛物线拟合来求取之[18].相应的算法流程图见图 1.

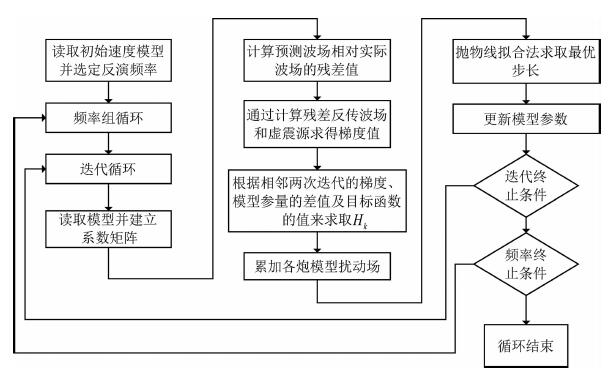
图 1 基于修正拟牛顿公式的FWI流程图 Fig. 1 Flow chart of FWI based on modified Quasi-Newton equation
4 方法对比

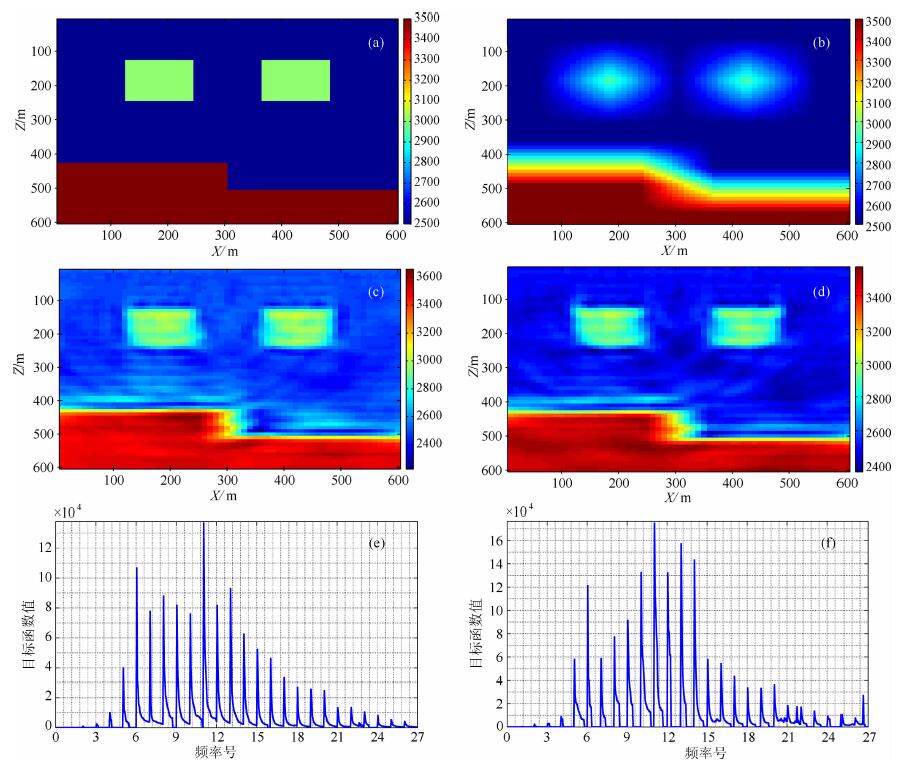
下面以BFGS算法为例, 来对比用新拟牛顿公式(12)修正后的BFGS算法和常规BFGS算法的收敛性和反演效果.我们建立如图 2a所示的速度模型, 网格大小为60×60, 纵横网格间距均为10m, 共30炮, 炮点位于z=40 m的界面上, 检波器布设在地表, 每炮60道, 震源主频选取为22 Hz, 频率域正演采用完全匹配层(PML)边界条件, 反演频率以1. 5Hz为步长从1 Hz选取到40 Hz, 共27个反演频率, 每个频率最大的迭代次数为20次.迭代终止条件取

图 2 BFGS和修正BFGS算法收敛性和反演效果对比 (a) 模型真实模型; (b) 反演初始模型; (c) BFGS得到的反演结果; (d) 修正BFGS得到的反演结果; (e) BFGS的反演收敛曲线; (f) 修正BFGS反演收敛曲线. Fig. 2 Comparison between BFGS and modified BFGS algorithm on convergence and inverse result (a) True model; (b) Initial model; (c) Inverse result by BFGS algorithm; (d) Inverse result by modified BFGS algorithm; (e) Convergence curve of BFGS; (f) Convergence curve of modified BFGS.

(18)

图 2b是用12×12的网格光滑之后的初始速度模型.基于以上参数, 分别于PC机上进行BFGS算法和修正BFGS算法的频率域波形反演. 图 2c和d分别是BFGS和修正BFGS的反演结果; 图 2e和f分别是BFGS和修正BFGS反演收敛曲线, 横轴代表参与反演的27个频率, 每个频率号对应着迭代循环中每次迭代对应的目标函数值.当一个频率内迭代终止时, 图中即将目标函数充零来表示迭代结束. 表 1是两种算法的耗时和迭代次数对比.

表 1 BFGS和修正BFGS算法耗时对比 Table 1 Comparison between BFGS and modified BFGS on consuming time

从图 2e、2f可以看出, BFGS算法进行反演时, 多数反演频率内的迭代次数都要达到最大迭代次数(20次), 而修正BFGS算法则多数频率不需要20次迭代就已经满足迭代终止条件; 进而结合表 1, 可以得出, 相对BFGS算法, 修正后的BFGS具有更快的收敛速度和更少的耗时, 而且两者每次迭代的耗时基本一样, 这是由于修正的算法综合利用了梯度, 模型和目标函数等多种信息来近似Hessian矩阵的逆矩阵, 并且相对常规算法只是增加了向量乘加运算, 所以可以在保证每次迭代耗时的前提下, 加快收敛.另外对比图 2c和d可以看出, 修正后的BFGS算法可以用较少的收敛次数和较少的耗时来获得与BFGS基本一样的反演结果.

5 结论

通过将一种新的拟牛顿条件应用到频率域全波形反演中, 基于此条件修改了常规的DFP和BFGS算法, 修改后的算法在近似Hessian矩阵逆矩阵Hk的时候综合利用了梯度信息, 模型差值信息和目标函数信息, 可以更好的地对Hk进行近似, 而且每次迭代几乎没有增加运算量.数值实验结果表明, 修正的BFGS算法在保证反演精度的同时明显地加快了收敛速度, 并减少了反演运算时间.

参考文献
[1] Bleibinhaus F, Hole J A, Ryberg T, et al. Structure of the California Coast Ranges and San Andreas Fault at SAFOD from seismic waveform inversion and reflection imaging. Journal of Geophysical Research , 2007, 112: B06315. DOI:10.1029/2006JB004611
[2] Operto S, Virieux J, Dessa J X, et al. Crustal seismic imaging from multifold ocean bottom seismometer data by frequency domain full waveform tomography: Application to the eastern Nankai trough. Journal of Geophysical Research , 2006, 111: B09306. DOI:10.1029/2005JB003835
[3] Sirgue L, Pratt R G. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies. Geophysics , 2004, 69(1): 231-248. DOI:10.1190/1.1649391
[4] 李国平, 姚逢昌, 石玉梅, 等. 频率域叠前波动方程反演及其应用. 石油地球物理勘探 , 2011, 46(3): 411–416. Li G P, Yao F C, Shi Y M, et al. Pre-stack wave equation inversion and its application in frequency domain. Oil Geophysical Prospecting (in Chinese) , 2011, 46(3): 411-416.
[5] Tarantola A. Inversion of seismic reflection data in the acoustic approximation. Geophysics , 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754
[6] Tarantola A. Inverse Problem Theory and Methods for Model Parameter Estimation. Society for Industrial and Applied Mathematics, 2005.
[7] Pratt R G, Worthington M H. Inverse theory applied to multi-source cross-hole tomography. Part1: Acoustic wave-equation method. Geophysical Prospecting , 1990, 38(3): 287-310. DOI:10.1111/gpr.1990.38.issue-3
[8] 刘璐, 刘洪, 刘红伟. 优化15点频率-空间域有限差分正演模拟. 地球物理学报 , 2013, 56(2): 644–652. Liu L, Liu H, Liu H W. Optimal 15-point finite difference forward modeling in frequency-space domain. Chinese J. Geophys (in Chinese) , 2013, 56(2): 644-652.
[9] Jo C H, Shin C, Suh J H. An optimal 9-point, finite-difference, frequency-space, 2-D scalar wave extrapolator. Geophysics , 1996, 61(2): 529-537. DOI:10.1190/1.1443979
[10] Pratt R G, Shin C, Hicks G J. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion. Geophys. J. Int. , 1998, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x
[11] Virieus J, Operto S. An overview of full-waveform inversion in exploration geophysics. Geophysics , 2009, 74(6): WCC1. DOI:10.1190/1.3238367
[12] Brossier R, Operto S, Virieus J. Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion. Geophysics , 2009, 74(6): WCC105. DOI:10.1190/1.3215771
[13] Ma Y, Hale D. A projected Hessian matrix for full waveform inversion. 81st Annual International Meeting. SEG, Expanded Abstracts 30, 2011, 2401-2405.
[14] Ma Y, Hale D. Full waveform inversion with image-guided gradient. 80th Annual International Meeting, SEG, Expanded Abstracts 29, 2010, 1003-1007.
[15] Zhang J Z, Deng N Y, Chen L H. New quasi-Newton equation and related methods for unconstrained optimization. Journal of Optimization theory and applications , 1999, 102(1): 147-167. DOI:10.1023/A:1021898630001
[16] Zhang J Z, Xu C X. Properties and numerical performance of quasi-Newton methods with modified quasi-Newton equations. Journal of Computational and Applied Mathematics , 2001, 137(2): 269-278. DOI:10.1016/S0377-0427(00)00713-5
[17] 卞爱飞, 於文辉, 周华伟. 频率域全波形反演方法研究进展. 地球物理学进展 , 2010, 25(3): 982–993. Bian A F, Yu W H, Zhou H W. Progress in the frequency-domain full waveform inversion method. Progress in Geophysics (in Chinese) , 2010, 25(3): 982-993.
[18] Vigh D, Starr W E, Kapoor J. Developing earth models with full waveform inversion. The Leading Edge , 2009, 28(4): 432-435. DOI:10.1190/1.3112760