2. 武汉大学测绘学院, 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
GPS坐标时间序列呈现显著的非线性变化(尤其是垂直方向的季节性变化),通常认为地球物理效应及与GPS技术相关的系统误差是造成测站非线性变化的主要因素.从产生形变的本质入手,定量分析不同因素造成的测站位移对时间序列的贡献是GPS技术应用领域的发展新方向[1-2],有助于研究造成测站非线性运动的物理机制,进而改正各种误差模型.其结果不但可以获得测站准确的位置和速度,为合理解释板块构造运动,建立和维持动态地球参考框架提供基础数据,而且还能更好地研究冰后回弹及海平面变化,反演冰雪质量变迁等地球动力学过程,具有重要的理论意义及应用价值[3-4].
国内外学者针对地表质量负载造成的位移进行了广泛的研究,取得了丰富的成果,证实了大气压负载、非潮汐海洋负载及水文负载与GPS测站垂直位移的强相关性[5-11].然而,已有研究仅给出了不同地表质量负载引起的测站垂向位移与GPS垂直位移及其周年振幅之间的关系,并未涉及负载改正对测站坐标各分量时间序列噪声特性的影响,同时考虑到地球物理效应的地域性特征,深入研究不同地表质量负载对中国区域IGS基准站各分量坐标时间序列的贡献很有必要.
除地表质量负载造成的位移外,GPS数据处理模型及策略的不完善同样可能导致测站产生虚假的非线性位移,包括电离层延迟高阶项、大气潮汐、海洋潮汐、对流层延迟处理方式等其它原因[12-22].目前,国际上关于基准站虚假非线性变化的成因尚处于起步阶段.就中国区域IGS基准站而言,国内尚无此方面的研究.
本文的主要目的在于分析中国区域IGS基准站非线性变化的成因,建立地表质量负载与ITRF2005框架下中国区域11个IGS基准站各分量坐标时间序列噪声特性、周年及半周年振幅之间的定量关系.在此基础上深入分析造成基准站非线性变化的其他可能因素,重点探讨周日(S1)、半周日(S2)大气潮汐对基准站非线性运动的贡献.
2 数据本文采用独立地球物理模型计算不同地表质量负载造成的测站位移,利用此结果对ITRF2005框架下中国区域11个IGS基准站1995-2010年的位置时间序列1)进行修正,时间序列最短跨越年限5.1a,最长15.2a,平均9.9a.计算大气压负载所需的全球地表气压由美国国家环境预测中心(National Centers for Environmental Prediction,即NCEP)再分析数据提供2),时间分辨率为6 h,空间分辨率为2.5°×2.5°;非潮汐海洋负载使用美国国家海洋合作计划(National Oceanographic Partnership Program,即NOPP)制定的海洋环流及气候估值(Estimating the Circulation & Climate of the Ocean,即ECCO)模型提供的全球海底压力格网数据计算3),时间分辨率为12 h,空间分辨率为1°× (0.3~1.0°).水文负载考虑积雪深度和土壤湿度引起的地表储水量变化,同样由NCEP再分析数据提供4),空间分辨率为1.875°×1.875°.
2) http://www.esrl.noaa.gov/psd/data/gidded/data.ncep.reanalysis.surface.html
3) http://ecco.jpl.nasa.gov/thredds/las/kf080/catalog.html
4) http://www.esrl.noaa.gov/psd/data/gidded/data.ncep. reanalysis.surfaceflux. html
3 数据分析 3.1 数据处理策略采用QOCA软件5)计算不同地表质量负载,包括非潮汐大气压负载,海洋负载,积雪深度及土壤湿度负载造成的测站位移,根据此结果对选取的ITRF2005框架下中国区域11个IGS基准站的坐标时间序列进行修正.为了分析地表质量负载对测站位置时间序列特征的影响,利用CATS软件[23]估计白噪声+闪烁噪声(White Noise+Flicker Noise,即WN+FN),闪烁噪声+可变白噪声(Variable White Noise+Flicker Noise,即FN+VWN),白噪声+随机漫步噪声(Random Walk Noise+ White Noise,即RWN+WN),白噪声+随机漫步噪声+闪烁噪声(Random Walk Noise+Flicker Noise+ White Noise,即RWN+FN+WN),非整数谱指数幂律噪声+白噪声(Power Law Noise+ White Noise,即PLN+WN),带通+幂律+白噪声(Band Pass+Power Law Noise+ White Noise,即BP+ PL+WN),以及一阶高斯马尔科夫+随机漫步噪声+白噪声(First Order Gauss-Markov+ Random Walk Noise+White Noise,即FOGM+RWN+WN)七种噪声模型下修正前后基准站位置时间序列的线性趋势,周年及半周年振幅.时间序列最优噪声模型的确定采用Langbein提出的保守估计准则[24-25].
5) http://gipsy.jpl.nasa.gov/qoca
3.2 地表质量负载造成的测站位移就季节性尺度来说,地表质量负载引起的测站位移是GPS位置时间序列的主要特征[5].为了分离地球物理效应的影响,通常采用Farrell格林函数与独立地表质量负载数据的卷积计算不同质量负载引起的测站位移,然后从GPS时间序列里扣除这部分影响[26-27].
3.2.1 CM、CE、CF、CN定义地球参考框架的原点通常定义为三种中心:包括大气和海洋在内的整个地球质量中心(Center of Mass,CM),不包括地表质量负载的固体地球中心(Center of Solid Earth,CE),以及固体地球外表面的形状中心(Center of Figure,CF).理想情况下,如果跟踪站无限密集,均匀分布全球,那么CF表现为理论定义的CF,但是如果用于定义参考框架的网络核心站较为稀疏,不能实现全球均匀分布,则CF表现为框架网中心(Center of Network,CN),此时CF与CN之间的季节振幅差异将达到亚毫米或者更大.空间大地测量领域通常选用CM框架,因为卫星动力学仅对CM敏感;CE框架主要用于理论地球物理(例如负载勒夫数)研究,CF框架则通常应用于与地面测量相关的学科领域[10, 28-29].
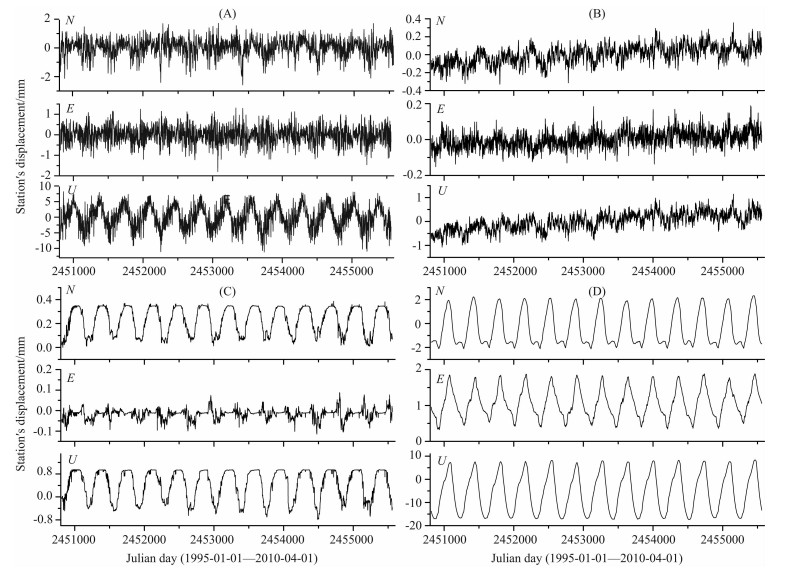
3.2.2 地表质量负载造成的测站位移计算采用QOCA软件根据Farrell格林函数计算了1995年1月1日-2010年4月1日期间大气压负载、非潮汐海洋负载、积雪深度及土壤湿度负载对中国区域11个IGS基准站的日位移影响.图 1表示四种质量负载造成的URUM站N、E、U分量的日位移.Farrell格林函数是基于质量负载勒夫数理论在CE (Center of Solid Earth)框架下创建的,因此该方法计算得到的测站位移同样属于CE框架.
|
图 1 不同质量负载造成的URUM站N、E、U分量位移 (A)大气压负载;(B)非潮汐海洋负载;(C)积雪深度负载;(D)土壤湿度负载. Fig. 1 Daily displacement of URUM in N(top)、E (middle)、U (bottom) directions resulted from different surface mass loadings (A) Atmospheric loading; (B) Non-tidal ocean loading; (C) Snow depth loading; (D) Soil moisture loading. |
从图 1可以看到,不同地表质量负载对测站的影响均表现为U分量最大,N、E分量影响较小,与已有研究成果一致[10-11, 30].部分质量负载对测站的影响与其地理环境密切相关,例如土壤湿度对URUM站U分量的位移影响为-20~10 mm,对L hAS站U分量的位移影响却为-10~0 mm.同一测站对不同质量负载的敏感度也不同,例如大气压负载造成的URUM站E分量位移变化为-2~2 mm,非潮汐海洋负载和积雪深度负载的影响为-0.2~0.2 mm,土壤湿度负载却为0~2 mm.
就选取的11个IGS基准站而言,土壤湿度负载造成的测站位移最大,E、N、U分量分别小于2 mm、5、10 mm;大气压负载对测站位移的影响次之,与测站地理位置无密切联系,N、E分量变化约为-2~2 mm,U分量最大达到10 mm;非潮汐海洋负载造成的位移较小,E、N、U分量分别小于0.5、1、2 mm;积雪负载对测站位移影响最小,且随纬度降低而减小,E、N、U分量分别小于0.2、0.5、1 mm.不同地表质量负载造成的测站位移呈现不同的周期特性.例如,非潮汐海洋负载造成的测站N、E、U分量位移呈现显著的线性趋势,积雪深度及土壤湿度负载则更多表现为不规则谐波变化.
3.2.3 地表质量负载对GPS坐标时间序列的修正Tregoning等[12]研究发现,在观测值层面施加非潮汐大气压负载(这里称大气压负载)改正与采用地球物理模型获得的负载日平均值直接对坐标时间序列进行改正相比并无优越性.后者更易于实现,且能避免对多年数据进行重新处理的巨大工作量,因此本文选择采用地球物理模型对GPS坐标时间序列进行大气负载改正.考虑到地表质量负载的相似性,对非潮汐海洋负载、积雪深度及土壤湿度负载也做同样的处理.
ITRF2005的原点定义为相对于SLR时间序列平均值确定的CM的平移量及平移速率为零[31],其实现的本质在长时间尺度上(20年或更久)表现为CM,短时间尺度或季节性尺度上表现为CF[28-29, 32],因此ITRF2005框架下的中国区域IGS基准站的坐标时间序列属于CF框架.采用QOCA软件计算得到的地表质量负载引起的测站位移属于CE框架.严格来说,根据地球物理模型计算得到的位移需减去CF原点在CE框架下的坐标才能得到CF框架下的测站位移与GPS解直接对比.CE框架与CF框架之间的差异约等于观测到的地心运动的2%[28],也就是说,如果观测到的季节性地心运动振幅为4 mm,则CE、CF框架之间的季节性振幅差异仅为约0.08 mm,因此实际应用中可以忽略CE和CF的差异,将CE框架下得到的地表质量负载引起的测站位移直接从CF框架下的GPS位置时间序列中扣除.
根据3.2.2节的计算结果对中国区域11个IGS基准站N、E、U分量的位移进行地表质量负载改正,并对改正后的坐标时间序列采用CATS软件进行分析即可得到适合于扣除地表质量负载影响后的中国区域IGS基准站分量最优噪声模型、线性速度及季节性振幅.
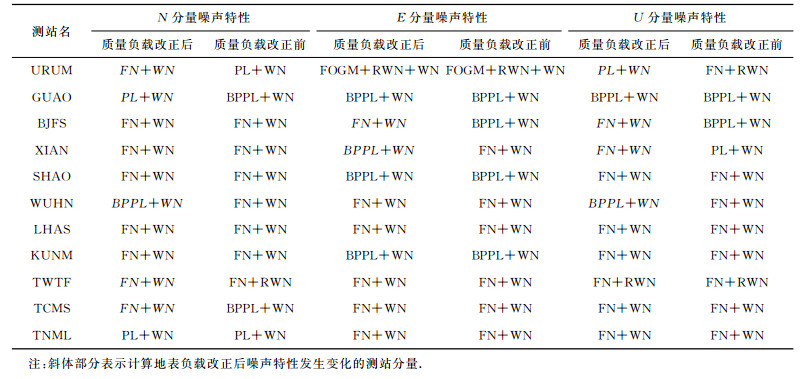
4 地表质量负载对基准站非线性运动的贡献 4.1 地表质量负载对测站噪声特性的影响理想情况下,GPS测站位置时间序列的噪声特性应表现为纯白噪声,然而实际情况下并非如此.未进行地表负载改正前,全球GPS坐标时间序列表现为有色噪声特征[33].通常认为地球物理效应及与GPS技术相关的系统误差是产生有色噪声的潜在来源.为了分析计算的四种地表质量负载对中国区域IGS基准站噪声特性的影响,表 1给出了负载改正前后11个基准站N、E、U分量的噪声特性.
|
|
表 1 地表质量负载改正前后各测站分量的噪声特性 Table 1 Noise characteristics of station components before and after surface mass loading correction |
表 1数据表明,去除计算的四种地表质量负载影响后,33%的测站分量噪声特性发生了变化(主要表现为N、U分量的变化).噪声类型的变化无显著规律,FN+WN模型比例增大,其余噪声模型比例减小.从噪声分析结果我们还可以看到,经地表质量负载改正后,各测站分量的BP (这里指的是周期为0.5~1.5年的谐波)及RWN噪声振幅普遍发生变化,由此认为本文计算的四种地表质量负载会造成除周年、半周年以外的谐波运动.
4.2 地表质量负载对测站周年、半周年振幅的影响为了研究计算的四种地表质量负载与中国区域IGS基准站周期振幅之间的关系,我们分别估计了不同噪声模型下考虑、未考虑质量负载影响的测站周年、半周年振幅,最优噪声模型下的结果如表 2所示.
|
|
表 2 计算地表质量负载改正前后测站分量的周年、半周年振幅 Table 2 Annual and semi-annual amplitude of station components before and after surface mass loading correction |
负载改正前后各测站分量的周年振幅变化值随纬度分布如图 2所示.从图 2及表 1可以看出,不论计算质量负载改正与否,各测站运动均存在显著的周年振幅.未考虑负载影响时,U分量最大,约为3~10 mm,E分量次之,约为1~5 mm,N分量最小,约为1~2 mm,与文献[34]结果一致.计算负载改正后,U分量周年振幅仍然最大,约为1~10 mm,N、E分量较小,约为1~5 mm,其中N分量周年振幅略大于E分量.所有测站N分量周年振幅全部变大,变化约为0~2.8 mm,E分量变化较为平缓集中,约为-0.6~0.7 mm,U分量除2测站分别增大4 mm、2 mm外,其余全部减小(80%),约为0.2~6.3 mm,且变化较为剧烈.

|
图 2 地表质量负载改正造成的各测站分量周年振幅变化随纬度分布图 Fig. 2 Annual amplitude change of station components varying with latitude caused by surface mass loading |
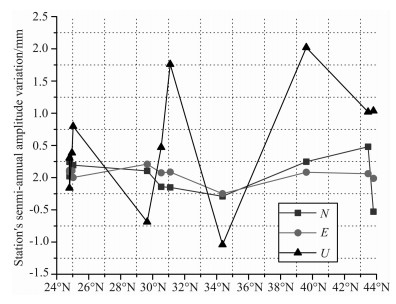
负载改正前后各测站分量的半周年振幅变化值随纬度分布如图 3所示.从图 3及表 2可以看出,各测站半周年振幅明显小于周年振幅.计算负载改正前,测站U分量半周年振幅较大,约为0.4~2.1 mm,E分量次之,约为0.4~1.6 mm,N分量最小,约为0.1~1.2 mm.负载改正后,U分量半周年振幅约为1~3 mm,E分量约为0.4~1.7 mm,N分量约为0.1~1 mm.U分量变化最大,约为-1~2 mm,N分量次之,约为-0.5~0.5 mm,E分量最小,约为-0.2~0.2mm.
|
图 3 地表质量负载改正造成的各测站半周年振幅变化随纬度分布图 Fig. 3 Semi-annual amplitude change of station components varying with latitude caused by surface mass loading |
由此可以得出结论,计算的四种地表质量负载确实会造成中国区域IGS基准站的周年、半周年运动,其影响因站而异,与测站周围地理环境相关,引起的周年运动较半周年运动幅度大,但是并不能完全减小GPS位置时间序列的周年、半周年振幅,尤其是半周年振幅.经质量负载改正后,73%的测站分量半周年振幅增大(某些测站U分量的增大量达1~2 mm),52%的测站分量周年振幅增大(包括所有测站N分量),不过仅U分量而言,80%测站分量的周年振幅显著减小.也就是说,就中国区域IGS基准站而言,包括大气压负载、非潮汐海洋负荷、积雪深度和土壤湿度负载在内的四种地表质量负载对测站位置时间序列的贡献较少,主要表现为测站U分量的周年运动,但是并不能很好地解释测站的半周年运动以及水平方向的周年运动,相反会增大测站N分量的周年运动.
5 造成中国区域IGS基准站非线性变化的其它因素从4.2节的分析结果我们可以看到,大气压负载、非潮汐海洋负载及包括积雪深度及土壤湿度在内的水文负载仅能解释中国区域IGS基准站的小部分季节性变化,本节从GPS数据处理策略及地球物理模型的可靠性两个方面讨论可能导致基准站非线性变化的其他因素.
5.1 与GPS相关的可能因素近年来,GPS数据处理模型及策略取得了显著的进步.许多研究成果表明数据处理策略的不完善及未模型化的GPS系统误差可能导致虚假周期性信号的产生.较最新的策略相比,本文选取的ITRF2005框架下的中国区域IGS基准站坐标时间序列的生成采用的数据处理策略存在许多不足,其中可能导致虚假周期性信号的因素主要包括:
5.1.1 S1-S2大气潮汐大气的昼夜加热使得地表气压呈现周日(S1)、半周日(S2)及更高谐波频率的振荡.这种“大气潮汐”会造成地球表面的周期性运动[35],其造成的地表垂直形变的振幅与海洋潮汐负载中某些潮汐分量的影响量级相同.目前SOPAC提供的IGS基准站坐标时间序列包括S1-S2大气潮汐造成的周期性位移.我们采用GGFC提供的S1-S2大气潮汐负载服务[36]计算了CF框架下S1-S2大气潮造成的中国区域11个IGS基准站的平均周年振幅,结果如表 3所示.
|
|
表 3 S1-S2大气潮造成的中国区域IGS基准站平均周年振幅 Table 3 S1-S2 atmospheric tides induced average annual amplitude of IGS stations inside China |
从表 3可以看出,S1-S2大气潮汐造成的中国区域IGS基准站平均周年运动不可忽视.S1-S2对U分量的影响最大,且随纬度升高而减小,北部地区的影响较小,周年振幅约为0.5~0.8 mm,可以解释SOPAC坐标时间序列垂向约6%~10%的周年变化;中部、南部区域的平均振幅超过1 mm,可以解释基准站垂向约19%~95%的周年变化.S1-S2大气潮造成的水平方向的平均周年振幅约为垂向的1/10~1/5,对基准站N分量的周年振幅贡献较E分量大,分别能够解释SOPAC坐标时间序列水平方向约6%~67%及3%~37%的周年变化.
由此得出结论,S1-S2大气潮汐是造成SOPAC提供的中国区域IGS基准站坐标时间序列周年变化的潜在影响源,对于中国中部、南部地区基准站周期运动的影响尤其不可忽视.考虑到其量级与部分海洋潮汐分量的影响相同,IERS协议2010建议测站运动模型必须考虑S1-S2负载的影响[37].在观测值水平对GPS观测数据施加S1-S2大气潮改正有望显著减小中国区域(尤其是中、南部地区) IGS基准站的周年振幅.
5.1.2 其它因素除S1-S2大气潮汐外,SOPAC采取的数据处理策略未计算高阶电离层延迟的影响及未模型化周期性海洋潮汐造成的测站位移,对流层延迟建模采用标准气象数据及Niell经验投影函数.已有研究表明,忽略高阶电离层延迟会造成南北方向GPS坐标时间序列虚假的半周年、周年变化信号[11, 13-15].未模型化的周期性(周期为一天甚至更小)地表位移会扩散为长周期谐波信号进入GPS高程时间序列[16-18].不适当的先验对流层延迟及投影函数同样会导致太阳周年及半周年虚假周期信号的产生[12, 19-22].忽略这些因素造成的地表位移改正都可能使得中国区域IGS基准站产生周年、半周年运动.从理论上来说,采用IERS协议2010推荐的最新模型及策略对GPS数据从观测值水平重新处理可能大幅度减少SOPAC坐标时间序列包括的周年、半周年及其他频率谐波的振幅.我们针对现有数据处理模型及策略不完善导致的虚假非线性位移对全球IGS基准站坐标时间序列的影响展开了细致深入的分析,研究结果表明,实施未模型化的高阶电离层延迟及周期性海洋潮汐改正能显著减小中纬测站的垂直周年、半周年及南北方向的半周年运动[38].
5.2 与地球物理模型相关的可能因素 5.2.1 温度变化造成的热效应闫昊明等[39]研究了温度变化造成的热膨胀效应对中国区域GPS台站垂直位移的影响,认为其产生的测站位移对GPS观测结果总体属于正反馈,最大周年振幅达2.8 mm (BJFS),特别是对于水泥墩较高的基准站(例如BJFS、URUM),一定要考虑温度变化引起的测站垂直位移.此结果为我们提供了研究中国区域IGS基准站周期性特征的新线索.由于闫昊明等采用NCEP/NCAR全球格网化地表空气温度数据(空间分辨率为2.5°×2.5°)计算温度对基准站的位移影响,并未考虑地形影响,其空间分辨率是否足以满足高精度大地测量的需求尚须大量数据加以验证.van Dam等[40]研究表明,采用经地形改正的高分辨率地表气压数据代替原始的NCEP数据计算大气压负载造成的测站位移可以显著降低复杂地形及较低空间分辨率导致的气压数据偏差影响.与此类似,采用经地形改正的高分辨率地表空气温度数据同样能够进一步精化热膨胀效应造成的更为准确的测站位移.
另外,Prawirodirdjo等[41]通过研究发现南加州GPS连续监测站水平方向坐标时间序列的大部分周年振幅可以通过大气温度变化造成的弹性地壳的热弹性应变解释.关于此作用机制对于中国及全球IGS基准站位移的影响目前尚无文献涉及.
5.2.2 QOCA用于GPS坐标时间序列修正的局限性本文地表质量负载造成的测站位移时间序列采用QOCA计算,得到的结果属于CE框架.由于CE与CF的细微差别,我们将CE框架下的负载位移时间序列直接从CF框架下的坐标时间序列中扣除.关于不同地表质量负载造成的CE及CF框架下的测站位移的差异及其对GPS坐标时间序列的影响,目前全球地球物理流体中心(Global Geophysical Fluids Center,GGFC)所属的负载特殊管理局(Special Bureau on Loading,SBL)为用户提供CM、CF、及CE框架下大气压负载、非潮汐海洋负载及水文负载造成的地表位移6),为开展上述研究提供了方便快捷的途径,我们已将其列入下一步的研究计划.
6) http://geophy.uni.lu/ggfc-about/products.html
除CE、CF框架之间的差异外,根据不同地球物理数据源计算得到的地表质量负载位移各不相同,QOCA用于计算负载影响的地球物理数据源的精度是否足以满足高精度大地测量的需求有待进一步验证.GGFC所属的SBL提供了丰富的近实时全球地表负载数据,其精度显著优于已有文献,使得采取统一的数据和方法分析处理各项地球物理负载对测站位移的影响成为可能.我们分别采用QOCA、GGFC及自主开发的最优模型数据(Optimum Model Data,OMD)对全球IGS基准站坐标时间序列进行修正[42].研究结果表明,QOCA仅对格陵兰地区测站具有满意的修正效果,GGFC具有足够的精度应用于除格陵兰地区以外的全球GPS坐标时间序列修正,考虑地形影响的OMD能显著提高亚洲地区GPS坐标时间序列的修正效果.因此,采用的地球物理模型误差在中国区域带来的噪声影响不可忽略,利用GGFC或者OMD结果对中国区域基准站坐标时间序列进行修正有望显著提高其改正效果,降低由于地球物理模型误差带来的噪声影响[38].
6 结论本文计算了包括大气压负载、非潮汐海洋负载、土壤湿度和积雪深度负载在内的四种地表质量负载造成的测站位移,分析并确定了其对中国区域IGS基准站坐标时间序列非线性变化的贡献,在此基础上探讨了可能造成基准站非线性变化的其它因素,重点研究了周日、半周日大气潮汐造成的基准站周年运动特征,得出了以下结论:
(1) 地表质量负载会造成测站的噪声特性变化,占分量总数的33%,主要表现在N、U分量,E分量受到的影响较小.噪声类型的变化与测站所处地理环境相关.就中国区域IGS基准站而言,除周年、半周年运动外,计算的四种地表质量负载对测站位置时间序列的影响还可能表现为BP及RWN特征.考虑到质量负载模型的准确性和选取测站数目的局限性,关于其确定影响还需要做进一步系统的研究.
(2) 计算地表质量负载改正仅能减小中国区域大部分IGS基准站的U分量周年振幅,并不能很好地解释测站的半周年运动以及水平方向的周年运动.负载改正后70%测站分量半周年振幅增大,52%的测站分量周年振幅增大(包括所有测站的N分量).
(3) S1-S2大气潮汐会造成中国区域IGS基准站的周年运动,其影响随着纬度升高而降低.中部、南部地区的垂向S1-S2周年振幅超过1 mm,能够解释SOPAC提供的坐标时间序列包括的19%~95%的垂直周年运动.水平方向S1-S2平均周年振幅约为垂向影响的1/10~1/5,能够解释SOPAC坐标时间序列约3%~67%的周年变化.在观测值层面对GPS数据实施S1-S2大气潮改正有望显著减小中国区域IGS基准站的周年振幅(尤其是中、南部区域测站的垂向周期运动).
(4) 给出了可能造成中国区域IGS基准站非线性变化的其它潜在来源,包括与GPS相关的技术性误差,如高阶电离层延迟、未模型化周期性海洋潮汐负载的影响、对流层延迟模型的选择,以及与地球物理模型相关的因素,如温度变化造成的热膨胀效应及热弹性应变作用,明确了解释中国区域IGS基准站非线性变化的下一步研究目标.
致谢感谢SOPAC提供的IGS基准站坐标时间序列,感谢S.D.P.Williams博士提供的CATS软件及在本文确定IGS基准站分量最优噪声模型过程中给予的建议和帮助,感谢董大南博士提供的QOCA软件,感谢Tonie van Dam博士提供的S1-S2大气潮汐负载计算服务.计算大气压、土壤湿度和积雪深度负载改正采用的全球地表气压及地表储水量变化数据由美国国家环境预测中心NCEP提供,计算非潮汐海洋负载采用的全球海底压力格网数据由美国国家海洋合作计划NOPP提供.
| [1] | 田云锋, 沈正康. GPS坐标时间序列中非构造噪声的剔除方法研究进展. 地震学报 , 2009, 31(1): 68–81. Tian Y F, Shen Z K. Progress on reduction of non-tectonic noise in GPS position time series. Acta Seismologica Sinica (in Chinese) , 2009, 31(1): 68-81. |
| [2] | 姜卫平, 李昭, 刘万科, 等. 顾及非线性变化的地球参考框架建立与维持的思考. 武汉大学学报(信息科学版) , 2010, 35(6): 665–669. Jiang W P, Li Z, Liu W K, et al. Some thoughts on establishment and maintenance of terrestrial reference frame considering non-linear variation. Geomatics and Information Science of Wuhan University (in Chinese) , 2010, 35(6): 665-669. |
| [3] | 陈俊勇. 大地坐标框架理论和实践的进展. 大地测量与地球动力学 , 2007, 27(1): 1–6. Chen J Y. Progress in theory and practice for geodetic reference coordinate frame. Journal of Geodesy and Geodynamics (in Chinese) , 2007, 27(1): 1-6. |
| [4] | Altamimi Z, Boucher C, Willis P. Terrestrial reference frame requirements within GGOS perspective. Journal of Geodynamics , 2005, 40(4-5): 363-374. DOI:10.1016/j.jog.2005.06.002 |
| [5] | van Dam T M, Blewitt G, Heflin M B. Atmospheric pressure loading effects on global positioning system coordinate determinations. Journal of Geophysical Research , 1994, 99(B12): 23939-23950. DOI:10.1029/94JB02122 |
| [6] | van Dam T M, Wahr J, Chao Y, et al. Predictions of crustal deformation and of geoid and sea-level variability caused by oceanic and atmospheric loading. Geophysical Journal International , 1997, 129(3): 507-517. DOI:10.1111/gji.1997.129.issue-3 |
| [7] | Zerbini S, Matonti F, Raicich F, et al. Observing and assessing nontidal ocean loading using ocean, continuous GPS and gravity data in the Adriatic area. Geophysical Research Letters , 2004, 31(23): L23609. DOI:10.1029/2004GL021185 |
| [8] | van Dam T, Wahr J, Milly P C D, et al. Crustal displacements due to continental water loading. Geophysical Research Letters , 2001, 28(4): 651-654. DOI:10.1029/2000GL012120 |
| [9] | Dong D, Fang P, Bock Y, et al. Anatomy of apparent seasonal variations from GPS-derived site position time series. Journal of Geophysical Research , 2002, 107(B4): ETG9-1-ETG9-16. DOI:10.1029/2001JB000573 |
| [10] | 王敏, 沈正康, 董大南. 非构造形变对GPS连续站位置时间序列的影响和修正. 地球物理学报 , 2005, 48(5): 1045–1052. Wang M, Shen Z K, Dong D N. Effects of non-tectonic crustal deformation on continuous GPS position time series and correction to them. Chinese J. Geophys (in Chinese) , 2005, 48(5): 1045-1052. |
| [11] | 袁林果, 丁晓利, 陈武, 等. 香港GPS基准站坐标序列特征分析. 地球物理学报 , 2008, 51(5): 1372–1384. Yuan L G, Ding X L, Chen W, et al. Characteristics of daily position time series from the Hong Kong GPS fiducial network. Chinese J. Geophys (in Chinese) , 2008, 51(5): 1372-1384. |
| [12] | Tregoning P, Watson C. Atmospheric effects and spurious signals in GPS analyses. J. Geophys. Res. , 2009, 114(B9): B09403. DOI:10.1029/2009JB006344 |
| [13] | Kedar S, Hajj G A, Wilson B D, et al. The effect of the second order GPS ionospheric correction on receiver positions. Geophys. Res. Lett. , 2003, 30(16): 1829. DOI:10.1029/2003GL017639 |
| [14] | Petrie E J, King M A, Moore P, et al. Higher-order ionospheric effects on the GPS reference frame and velocities. J. Geophys. Res. , 2010, 115(B3): B03417. DOI:10.1029/2009JB006677 |
| [15] | Chen W, Gao S, Hu C W, et al. Effects of ionospheric disturbances on GPS observation in low latitude area. GPS Solutions , 2008, 12(1): 33-41. DOI:10.1007/s10291-007-0062-z |
| [16] | Penna N T, Stewart M P. Aliased tidal signatures in continuous GPS height time series. Res. Lett. , 2003, 30(23): 2184. DOI:10.1029/2003GL018828 |
| [17] | Penna N T, King M A, Stewart M P. GPS height time series: Short-period origins of spurious long-period signals. J. Geophys. Res. , 2006, 112(B2): B02402. DOI:10.1029/2005JB004047 |
| [18] | Stewart M P, Penna N T, Lichti D D. Investigating the propagation mechanism of unmodelled systematic errors on coordinate time series estimated using least squares. J. Geod. , 2005, 79(8): 479-489. DOI:10.1007/s00190-005-0478-6 |
| [19] | Tregoning P, Herring T A. Impact of a priori zenith hydrostatic delay errors on GPS estimates of station heights and zenith total delays. Geophys. Res. Lett. , 2006, 33(23): L23303. DOI:10.1029/2006GL027706 |
| [20] | Kouba J. Testing of Global Pressure/Temperature (GPT) model and global mapping function (GMF) in GPS analyses. J. Geod. , 2009, 83(3-4): 199-208. DOI:10.1007/s00190-008-0229-6 |
| [21] | Steigenberger P, Rothacher M, Dietrich R, et al. Reprocessing of a global GPS network. J. Geophys. Res. , 2006, 111(B5): B05402. DOI:10.1029/2005JB003747 |
| [22] | Steigenberger P, Boehm J, Tesmer V. Comparison of GMF/GPT with VMF1/ECMWF and implications for atmospheric loading. J. Geod. , 2009, 83(10): 943-951. DOI:10.1007/s00190-009-0311-8 |
| [23] | Williams S D P. CATS: GPS coordinate time series analysis software. GPS Solution , 2008, 12(2): 147-153. DOI:10.1007/s10291-007-0086-4 |
| [24] | Langbein J. Noise in GPS displacement measurements from Southern California and Southern Nevada. Journal of Geophysical Research , 2008, 113(B5): B05405. DOI:10.1029/2007JB005247 |
| [25] | Langbein J. Noise in two-color electronic distance meter measurements revisited. Journal of Geophysical Research , 2004, 109(B4): B04406. DOI:10.1029/2003JB002819 |
| [26] | Farrell W E. Deformation of the Earth by Surface Loads. Reviews of Geophysics , 1972, 10(3): 761-797. DOI:10.1029/RG010i003p00761 |
| [27] | Tregoning P, van Dam T. Effects of atmospheric pressure loading and seven-parameter transformations on estimates of geocenter motion and station heights from space geodetic observations. Journal of Geophysical Research , 2005, 110(B3): B03408. DOI:10.1029/2004JB003334 |
| [28] | Dong D, Dickey J O, Chao Y, et al. Geocenter variations caused by atmosphere, ocean and surface ground water. Geophysical Research Letters , 1997, 24(15): 1867-1870. DOI:10.1029/97GL01849 |
| [29] | Dong D, Yunck T, Heflin M. Origin of the International Terrestrial Reference Frame. Journal of Geophysical Research , 2003, 108(B4): B42200. DOI:10.1029/2002JB002035 |
| [30] | 朱文耀, 符养, 李彦. GPS高程导出的全球高程振荡运动及季节变化. 中国科学(D辑) , 2003, 46(8): 765–778. Zhu W Y, Fu Y, Li Y. Global elevation vibration and seasonal changes derived by the analysis of GPS height. Science in China: Series D (in Chinese) , 2003, 46(8): 765-778. DOI:10.1007/BF02879521 |
| [31] | Altamimi Z, Collilieux X, Legrand J, et al. ITRF2005: A new release of the International Terrestrial Reference Frame based on time series of station positions and Earth Orientation Parameters. Journal of Geophysical Research , 2007, 112(B9): B09401. DOI:10.1029/2007JB004949 |
| [32] | Blewitt G. Self-consistency in reference frames, geocenter definition, and surface loading of the solid Earth. Journal of Geophysical Research , 2003, 108(B2): B22103. DOI:10.1029/2002JB002082 |
| [33] | Williams S D P, Bock Y, Fang P, et al. Error Analysis of Continuous GPS position time series. Journal of Geophysical Research , 2004, 109(B3): B03412. DOI:10.1029/2003JB002741 |
| [34] | Meisel B, Angermann D, Krugel M. Influence of time variable effects in station positions on the terrestrial reference frame. Geodetic Reference Frames , 2009, 134: 89-93. DOI:10.1007/978-3-642-00860-3_14 |
| [35] | Petrov L, Boy J P. Study of the atmospheric pressure loading signal in very long baseline interferometry observations. J. Geophys. Res. , 2004, 109(B3): B03405. DOI:10.1029/2003JB002500 |
| [36] | van Dam T, Ray R. S1 and S2 Atmospheric Tide Loading Effects for Geodetic Applications. Updated October 2010, Data set/Moddel accessed YYYY-MM-DD at http://geophy.uni.lu/ggfc-atmosphere/tide-loading-calculator.html. |
| [37] | Petit G, Luzum B. IERS Conventions 2010, IERS Technical Note 36, 2010, http://tai.bipm.org/iers/conv2010/. |
| [38] | 李昭. GPS坐标时间序列的非线性变化研究.武汉:武汉大学, 2012. Li Z. Research on the non-linear variation of GPS coordinate time series. Wuhan: Wuhan University (in Chinese), 2012. |
| [39] | 闫昊明, 陈武, 朱耀仲, 等. 温度变化对我国GPS台站垂直位移的影响. 地球物理学报 , 2010, 53(4): 825–832. Yan H M, Chen W, Zhu Y Z, et al. Thermal effects on vertical displacement of GPS stations in China. Chinese J. Geophys (in Chinese) , 2010, 53(4): 825-832. DOI:10.3969/j.issn.0001-5733.2010.04.007 |
| [40] | van Dam T, Altamimi Z, Collilieux X, et al. Topographically induced height errors in predicted atmospheric loading effects. J. Geophys. Res. , 2010, 115: B07415. DOI:10.1029/2009JB006810 |
| [41] | Prawirodirdjo L, Ben Zion Y, Bock Y. Observation and modeling of thermoelastic strain in Southern California Integrated GPS Network daily position time series. J. Geophys. Res. , 2006, 111: B02408. DOI:10.1029/2005JB003716 |
| [42] | Jiang W P, Li Z, van Dam T, et al. Comparative analysis of different environmental loading methods and their impacts on the GPS height time series. Journal of Geodesy , 2013. DOI:10.1007/s00190-013-0642-3 |
 2013, Vol. 56
2013, Vol. 56