2. 中石化胜利石油管理局地球物理勘探开发公司, 山东 东营 257086;
3. 中国石油勘探开发研究院 中东研究所, 北京 100083;
4. 青海油田公司勘探开发研究院地球物理研究中心, 甘肃 敦煌 736202
2. Geophysical Exploration and Development Company, SINOPEC Shengli Oil Field, Dongying 257086, China;
3. Department of Middle East, Research Institute of Petroleum Exploration and Development, Beijing 100083, China;
4. Geophysics Research Center, Exploration and Development Research Institute, Qinghai Oil field, Dunhuang 736202, China
从叠前AVO三参数反演中可以提取出纵波速度、横波速度和密度, 其中密度项具有描述储层流体饱和度的信息[1].出于计算成本经济和计算过程简易等方面考虑, 常规的AVO三参数反演通常是利用Zoeppritz方程的近似公式(Aki-Richards近似和Fatti近似等)来建立AVO正演模拟的过程, 然而在P波入射角过临界角以及纵向上弹性参数变化剧烈的情况下, 近似公式精度有限, 因此限制了常规AVO三参数反演的应用范围.针对这个问题, 可以使用精确的Zoeppritz方程来改善反演的精度.由于Zoeppritz方程和弹性参数之间是复杂的非线性关系, 通常使用非线性反演或者广义线性反演作为反演的优化算法, 非线性反演由于其计算量巨大并未得到推广; 广义线性反演通过利用泰勒一阶展开式将反射振幅用线性关系式近似表达, 在给定初始模型的条件下, 经过几次迭代, 在理论上可以达到很高的精度.Larsen曾在1999年提出将广义线性反演应用到PP波和PS波数据的联合反演上[2]; 李录明[3]成功将广义线性反演应用到多波叠前AVA参数反演, 该反演可以同时获得三参数以及各向异性参数.然而广义线性反演的核心部分——Jacobian矩阵通常由于矩阵条件数过大, 造成反演算法的不稳定, 因此需要在反演目标函数中加入合适的正则化项来提高反演的稳定性.
基于统计理论的贝叶斯反演, 通过引入模型参数的先验信息结合噪声的似然函数生成模型参数的后验概率分布, 将求取反演目标函数的极小值问题转化为求取模型参数后验概率分布最大化问题.将加入模型参数的先验信息作为反演的约束条件, 可以有效的降低反演的不适定性, 根据不同情况, 模型参数的先验信息可以服从不同的统计分布:该方法假设三参数自然对数服从三变量高斯分布[4]; Karimi和Omre[5]在此方法基础上提出三参数自然对数服从三变量斜歪高斯分布, Buland和Omre[4]将贝叶斯反演应用到AVO三参数同步反演中, 进一步提高了反演的精度; Downton[6]针对二项和三项AVO波形反演, 提出采用三种不同的长尾巴分布来描述三参数反射系数, 相对高斯分布, 长尾巴分布可以产生稀疏脉冲反演的效果, 提高了反演的分辨率.Alemie和Sacchi[7]提出三参数反射系数服从三变量柯西分布, 通过引入相关矩阵来消除三参数反射系数之间的统计相关性, 进一步降低了反演的不适定性.
本文在Alemie等[7]工作的基础上, 基于广义线性反演的思想利用精确的Zoeppritz方程构建AVO正演模拟的过程, 并结合贝叶斯理论通过引入模型参数的先验分布来构建反演的约束项, 其中假设模型参数的先验信息服从三变量柯西分布, 通过该约束项可以有效降低由于Jacobian矩阵条件数过大而引起的反演不适定问题, 相对基于近似公式的AVO三参数反演可以进一步提高反演的精度.
2 AVO正演过程为了避免Zoeppritz方程的近似公式带来的计算误差, 选用精确的Zoeppritz方程构建AVO正演过程, 其表达式如下:
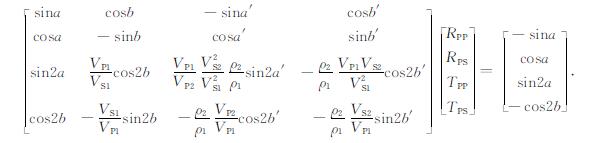
|
(1) |
可以看出RPP是关于VP1, VP2, VS1, VS2, ρ1, ρ2这个6个弹性参数的函数, 未知数较多.因此对(1)式的系数矩阵进行修改, 将其表达成关于P波速度反射系数RVP, S波速度反射系数RVS, 密度反射系数Rd和上层介质的纵横波速度比γ的函数:
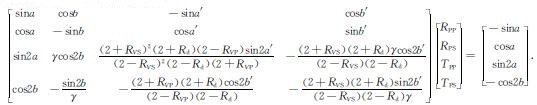
|
(2) |
其中,
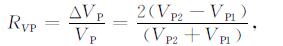
|
(3a) |
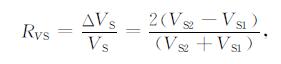
|
(3b) |
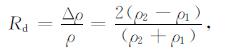
|
(3c) |
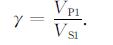
|
(3d) |
由于γ相当于背景纵横波速度比, 作为反演的已知项, 因此RPP是三参数反射系数RVP, RVS和Rd的非线性函数, 令三参数反射系数作为反演的模型参数.基于广义线性反演的基本思想, 通过将RPP用泰勒一阶展开式展开后, 用线性关系近似表达非线性关系可以将问题简单化:
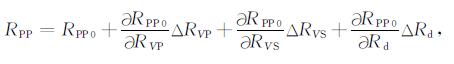
|
(4) |
式中RPP为实际观测的P波反射系数, RPP0为由初始模型参数RVP0, RVS0和Rd0计算的P波反射系数,
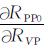
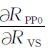
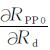
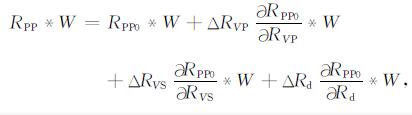
|
(5) |
于是:
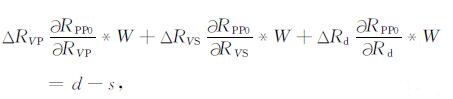
|
(6) |
其中, d=RPP*W表示实际观测的地震数据, s=RPP0*W, 其中*代表褶积运算, ΔRVP, ΔRVS, ΔRd分别是模型参数RVP, RVS, Rd的更新量.为了求解出模型参数的更新量, 至少需要联立N(N≥3)个方程(每个角度对应一个方程)形成线性方程组:
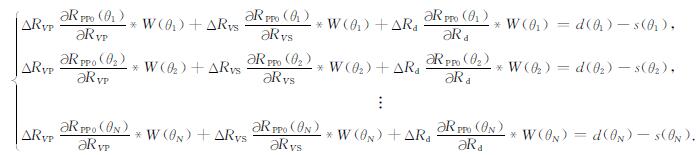
|
(7) |
将方程组(7)扩展到包含K个时间采样点的矩阵表达式:
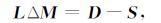
|
(8) |
式中, L表示由一阶偏导数和角度子波组成的NK ×3K维矩阵, ΔM表示3K×1维的模型参数的更新量矩阵, D和S分别代表NK×1维的实际观测的地震数据向量和NK×1维的由初始模型计算的合成地震数据向量.
通过(8)式可以直接得到ΔM, 但是ΔM的先验分布是未知的, 如果用ΔM作为反演参数, 无法构建反演的约束项.而M的先验分布是已知的, 因此用M作为反演参数.通过在(8)式的等号两边同时加上LM0, 使反演参数由ΔM转化为M:
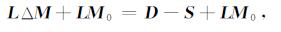
|
(9) |
即:
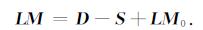
|
(10) |
为简化起见, 令H=D-S+LM0, 则:
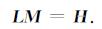
|
(11) |
通过对(11)式求解便可以直接得到M, 其中L, M和H的具体表达式参见附录B.但是由于(11)式的系数矩阵的条件数过大, 直接对(11)式进行求解将导致反演结果的不稳定, 因此需要引入反演正则化项来降低反演问题的不适定性, 反演的正则化项是通过利用贝叶斯理论引入三参数反射系数的先验分布构建的, 本文假设三参数反射系数的先验分布服从三变量柯西分布.
3 反演问题的不确定性和非唯一性分析Macdonald[8]和Russell[9]曾指出在开展广义线性反演之前, 应该对所选的模型参数和目标函数之间的不确定性以及目标函数的单极值性进行分析, 以确保目标函数的非线性关系能够成功地线性展开.
针对利用(2)式建立的广义线性反演问题, 通过分析不同角度范围下的反演不确定性, 来确定该广义线性反演对入射角度的限定.分析方法是采用的Macdonald和Russell提出的残差函数分布图(RFM)[8-9], 如果RFM中等值线围绕给定模型参数值呈椭圆分布, 则说明该反演问题的不确定性较低, 适合于广义线性反演; 如果RFM中的等值线呈现带状分布, 则该反演问题的不确定性较大, 不适合用广义线性反演方法进行反演[8].RFM的计算公式如下:
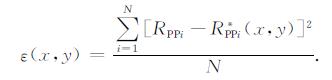
|
(12) |
式中, RPPi代表在给定的模型参数下, 第i个角度对应的P波反射系数; R PPi*(x, y)代表任意改变模型参数中的两个参数, 重新计算得到第i个角度对应的P波反射系数.给定的模型参数如表 1所示, 固定其中的一个参数, 不断变化剩下两个参数(变化范围都在-0.3~0.7之间), 利用(2)式和(3)式分别计算了入射角范围为1~10°, 1~20°, 1~30°和1~40°这四种情况下的RFM.
|
|
表 1 模型参数 Table 1 The model parameters |
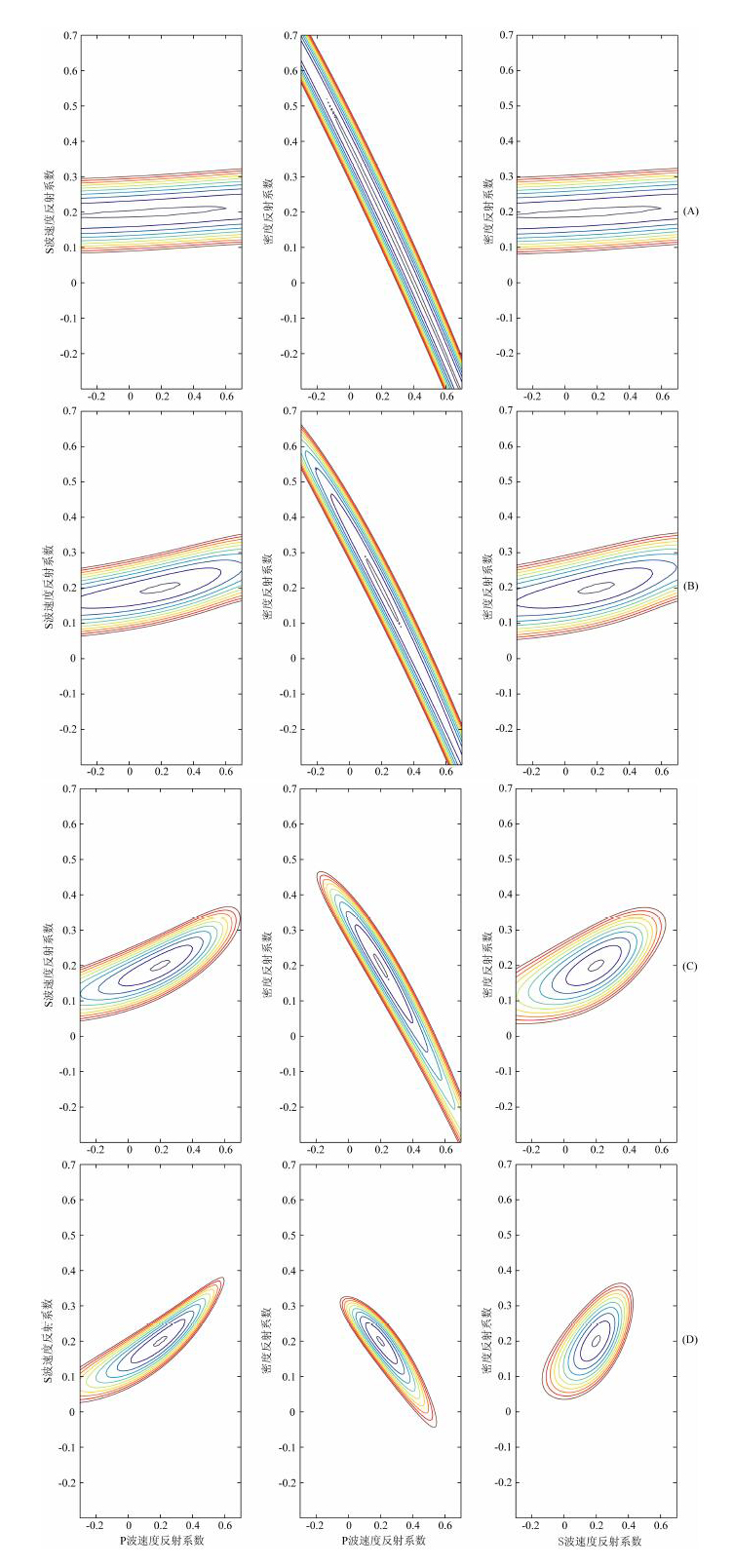
从图 1A可以看出在入射角范围为1~10°的情况下, 全部的RFM图中的等值线呈现带状分布.随着入射角范围的增大, RFM中的等值线逐渐呈现椭圆分布, 并且椭圆的范围逐渐缩小.因此随着入射角范围的不断增大, 反演问题的不确定性逐渐降低.如果仅使用小角度的叠前数据进行反演, 将无法得到可靠的反演结果.中角度和大角度的叠前数据在反演中起到了降低反演不确定性的作用, 对反演的准确度提供了可靠的保证.
|
图 1 不同入射角的残差函数分布图 (A)入射角度1~10°; (B)入射角度1~20°; (C)入射角度1~30°; (D)入射角度1~40°. Fig. 1 (A) The RFMs with respective to the incidence angle from 1 to 10°; (B) The RFMs with respective to the incidence angle from 1 to 20°; (C) The RFMs with respective to theincidence angle from 1 to 30°; (D) The RFMs with respective to the incidence angle from 1 to 40°. |
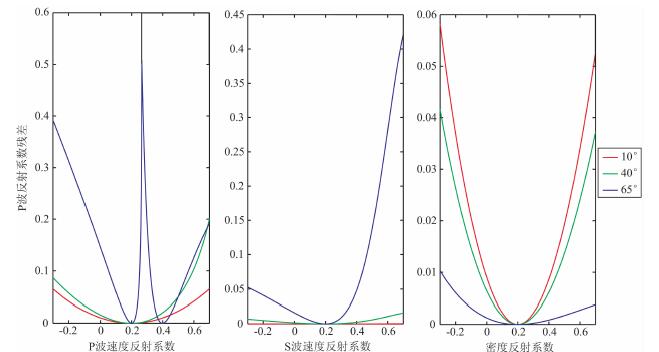
广义线性反演如同所有基于模型反演的方法一样, 对初始模型的准确度都有所依赖.如果目标函数是关于模型参数的单极值函数, 那么该反演方法对初始模型的依赖程度较低; 如果目标函数是关于模型参数的多极值函数, 那么对初始模型的依赖程度较高, 需要慎重的选择初始模型, 防止在反演迭代过程中落入目标函数的极小值, 造成错误的反演结果.针对表 1给定的模型参数, 图 2给出了不同入射角度下目标函数(这里指P波反射系数残差)随各模型参数的变化关系.其中红线、绿线和蓝线代表入射角为10°、40°和65°情况下对应的函数关系.从图 2可以看出, 在入射角为10°和40°的情况下, 目标函数是关于模型参数的单极值函数, 但是在超大入射角65°的情况下, 目标函数与P波速度反射系数之间的非线性关系增强, 由单极值函数变为双极值函数.模型参数的真实值在RVP=0.2;如果不适当的选取初始模型, 可能会得到错误的反演结果RVP=0.4.因此在利用超大入射角的叠前数据进行反演时, 需要建立准确的P波速度初始模型, 以确保反演的准确度和精度.
|
图 2 不同角度下目标函数随模型参数变化关系 Fig. 2 The objective function versus the changing of model parameters at the different incidence angle |
在叠前道集中存在微弱噪声时, 噪声n可用下式表达:
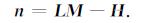
|
(13) |
假设噪声n服从均值为0, 协方差矩阵为Cn的多变量高斯分布:
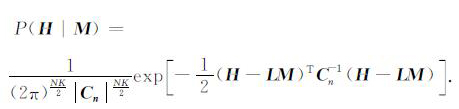
|
(14) |
假设噪声n是均匀分布的, 则Cn=σn2I, 其中σn表示噪声的均方差, I表示NK×NK维的单位矩阵.
5 模型参数的先验分布贝叶斯反演通过引入模型参数的先验分布来构建反演的正则化项, 从而可以提高反演的适定性.模型参数的先验分布可以假定为不同的统计分布(高斯分布, 柯西分布, Huber分布等)进而可以获得不同的反演结果.常用的模型参数的先验分布可以分为两大类: (1)单随机变量统计分布; (2)多随机变量统计分布.
其中单随机变量分布方式见表 2.
|
|
表 2 单随机变量统计分布 Table 2 The univariate distributions |
多随机变量分布方式见表 3.
|
|
表 3 多随机变量统计分布 Table 3 The multivariate distributions |
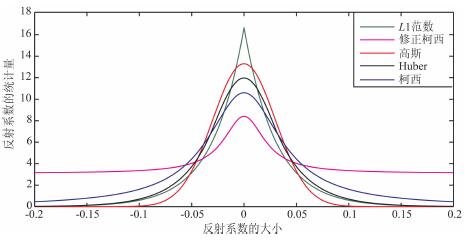
表 1中的四种单变量统计分布均属长尾巴分布, 从图 3中可以看出这4种单变量分布相比高斯分布将会有更大的概率落入反演参数的较大值, 其中修正柯西分布表现最为明显.它们作为反射参数的先验约束项可以产生非一致性加权系数, 相对较大的反演参数将会产生较小的加权系数, 而较小的反演参数将会产生较大的加权系数, 加权系数越大, 反演结果也越平滑, 因此非一致性加权系数可以突出较大的反演参数, 平滑较小的反演参数, 从而产生稀疏脉冲反演的效果.
|
图 3 几种常见的模型参数的统计分布 Fig. 3 The common distribution for describing the model parameters |
然而单随机变量统计分布可以作为反演参数的先验约束项的假设前提是:同一时间采样点, 三参数之间是统计独立不相关的.然而大量的研究表明, 在有地质背景的情况下, 三参数之间是存在一定的统计相关性的, Castagna等[10]研究了P波和S波速度之间存在线性关系, 例如, Castagna等[10, 13]研究了P波和S波速度之间存在线性关系, Gardner等[11, 13]发现了P波速度和密度之间关系, Potter等[12-13]讨论了S波速度和密度之间关系.Downton等[6]提出通过对三参数反射系数的协方差矩阵进行特征值分解, 进而达到对三参数反射系数进行去相关, 从而使其符合同一时间采样点三参数之间是统计独立不相关这一假设.
多随机变量统计分布包括多变量高斯分布和三变量柯西分布, 多变量高斯分布通过引入三参数反射系数的协方差矩阵, 表征了三参数之间的统计相关性, 使得这种统计分布更加符合有地质背景的情况, 但是高斯分布只能产生一致性加权系数, 对各个反射系数产生相等的加权系数, 这样无法突出较大的反射系数, 不会产生稀疏脉冲反演的效果[14].
三变量柯西分布作为学生t分布的一种特殊情况, 其数学表达式如下:
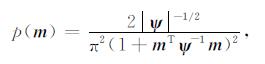
|
(15) |
其中, m=[RVP RVS Rd]T, 表示每一个时间采样点处的三参数反射系数.通过相关矩阵ψ, 引入了三参数反射系数之间的相关性, 在有地质背景的情况下, 这种统计分布更适合描述三参数反射系数的联合概率密度分布.同时作为长尾巴分布的一种, 会产生非一致性加权系数, 可以有效突出强反射边界, 形成稀疏脉冲反演的效果, 因此用三变量柯西分布作为AVO反演的先验分布要优于以上几种先验分布.考虑K个时间采样点, 模型参数的先验联合分布概率密度函数为
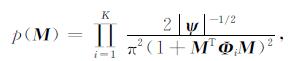
|
(16) |
式中, Φi=DiTψ-1Di, 其中Di为3K×3K矩阵, 其表达式如下:
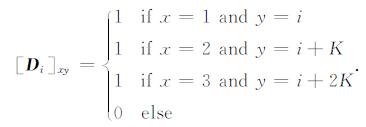
|
(17) |
根据贝叶斯理论, 模型参数的后验概率密度函数为[15]
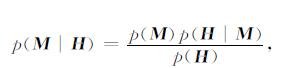
|
(18) |
由于p(H)为一常数, 不决定模型参数后验概率密度函数的形状, 因此:
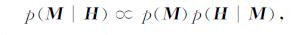
|
(19) |
结合公式(14)和公式(16):
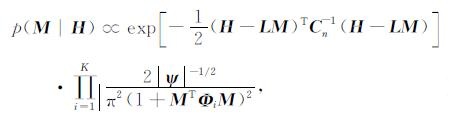
|
(20) |
对公式(20)两边取自然对数并乘以-1, 将求取p(M|H)的极大值转化为求取反演目标函数极小值, 反演目标函数为
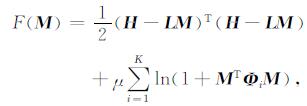
|
(21) |
其中, μ=2σn2, 式右边的第一项表示地震数据拟合差的L2模, 主要控制反演精度, 右边第二项表示反演参数的先验分布约束项, 主要控制反演的稀疏性.当μ越大, 反演结果的稀疏性越高, 反之, 反演的结果将出现明显的带限特征[16].
为了求取目标函数的极小值, 令F(M)对M的一阶偏导数为0:
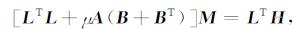
|
(22) |
其中,
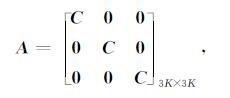
|
(23) |
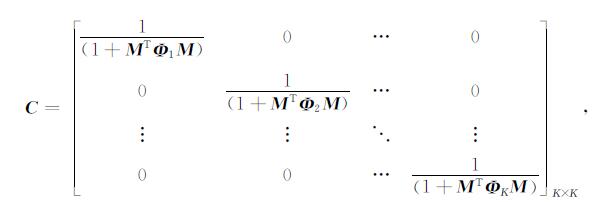
|
(24) |

|
(25) |
(25)式中为维的单位矩阵.三参数反射系数的相关矩阵可以通过EM算法求取[7].由于矩阵A中包含模型参数M, 因此不能直接求取, 采取迭代重加权最小二乘算法(IRLS)[17], 在每次迭代过程中利用共轭梯度法求取方程组(22)的解[7], 一般经过5次迭代便可以完成收敛, 最后对得到的三参数反射系数进行道积分和低频补偿便可以获得绝对的VP, VS和ρ.
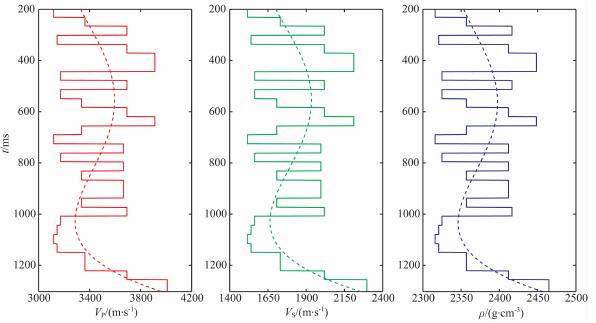
7 模型试算为了检验该反演算法的优越性以及抗噪性, 针对图 4给出的一套模型参数进行反演算法试算:
|
图 4 弹性参数 Fig. 4 The Elastic parameters |
对图 4中的弹性参数利用精确的Zeoppritz方程分别计算出不同时间采样点, 不同角度处(10°, 20°, 30°, 40°和50°)的反射系数, 并和30 Hz的雷克子波褶积后得到合成的角道集(图 5).为了检验该算法的抗噪性, 在合成道集上加入了随机噪声, 信噪比为3.
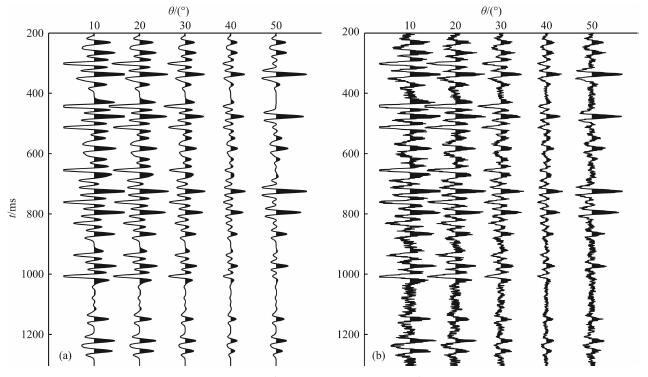
|
图 5 合成角道集(a)及含噪声合成角道集(b) Fig. 5 The synthetic angle gather (a) and The synthetic angle gather with the random noise (b) |
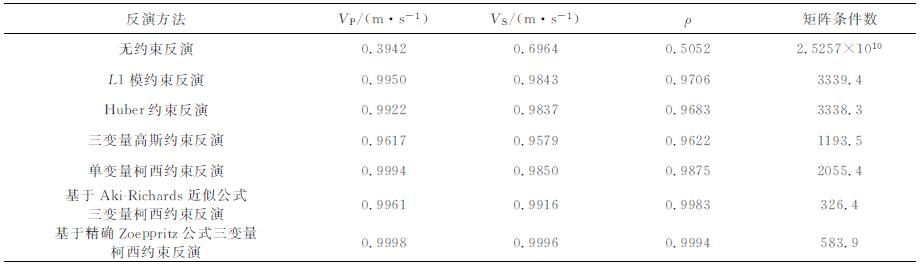
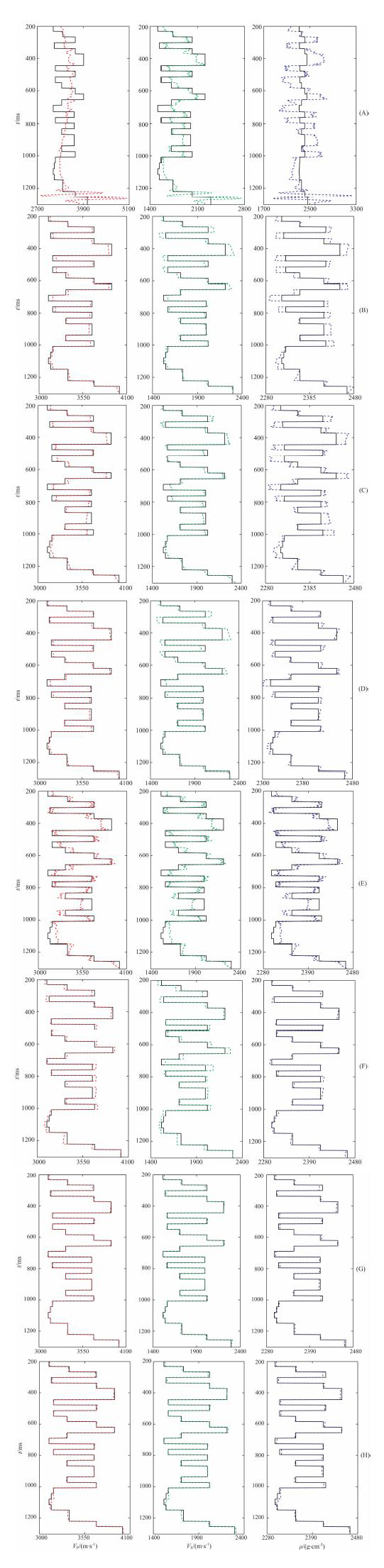
针对无噪声的合成角道集分别进行了如下7种反演:基于精确Zoeppritz方程的无约束反演、L1模分布先验约束的反演、Huber分布先验约束的反演、单变量柯西分布先验约束的反演、多变量高斯分布先验约束的反演和三变量柯西分布先验约束的反演以及基于Aki-Richards近似公式的三变量柯西约束的反演.其反演结果分别如图 6(a-f)所示.初始模型参数是通过对实际的模型参数进行4阶多项式拟合得到的, 如图 4中虚线.单变量分布先验约束反演的迭代次数为10次, 三变量分布先验约束反演的迭代次数为5次.其中三变量柯西约束的相关矩阵是通过初始模型参数利用EM算法构建的.
|
图 6 (A)无约束反演结果; (B)L1模分布约束反演结果; (C) Huber分布约束反演结果; (D)单变量柯西约束反演结果; (E)多变量高斯约束反演结果; (F)基于Aki-Richards近似三变量柯西约束反演结果; (G)基于Zoeppritz方程三变量柯西约束反演结果; (H)基于Zoeppritz方程三变量柯西约束含噪声反演结果 Fig. 6 (A) The inversion result with no constraint; (B) The inversion result with the constraintof L1 norm distribution; (C) The inversion result with the constraint of Huber distribution; (D) The inversion result with the constraint of Univarite Cauchy distribution; (E) The inversion result with the constraint of multivariate Guass distribution; (F) The inversion resul with the constraint of trivariate Cauchy distribution based on Aki-Richardsa pproximation; (G) The inversion result with the constraint of trivariate Cauchy distribution based on Zoeppritz equation; (H) The inversion result from the synthetic data with random noise. |
图 6中彩线代表反演结果, 黑线代表真实的弹性参数, 从图 6A可以看出在无任何先验约束的情况下, 反演是异常不稳定的, 这主要是由Jacobian矩阵的条件数过大引起的; 图 6(B-D)分别给出了几种单变量分布先验约束的反演结果, 即L1模分布、Huber分布和单变量柯西分布.由于加入了模型参数的先验分布作为反演的约束项, 提高了反演的稳定性, 对比无约束的反演结果可以看出反演的准确度得到了较大的提高, 但是单变量分布忽略了三参数反射系数之间的统计互相关性, 这种互相关会在一定程度引起三参数反演的不稳定性和病态性, 从而造成了横波和密度的反演不准确; 利用多变量高斯分布作为先验约束虽然可以有效消去三参数反射系数之间的统计相关性, 但是高斯分布并不能产生稀疏脉冲反演的效果, 其反演的分辨率有所下降, 从图 6E中可以看出在弹性参数分界面处的反演结果有类似于"吉布斯现象"的抖动, 这是由于反演过程中无法将子波进行有效压缩, 由子波旁瓣造成的假象; 利用三变量柯西分布作为先验约束可以有效降低由于三参数反射系数之间的统计相关造成的反演不稳定性, 同时作为长尾巴分布可以产生稀疏脉冲反演的效果, 其反演的稳定性和分辨率都得到了有效提高; 由于试算的角道集模型中最大的入射角度为50°, 而Aki-Richards近似公式在大入射角情况下精度有限, 因此在对大入射角的叠前数据进行反演时会引入误差, 对比图 6F和图 6G可以看出, 通过引入精确Zoeppritz方程构建反演目标函数后, 精度进一步提高.表 4给出了这几种反演结果和实际弹性参数之间相关系数和矩阵条件数.
|
|
表 4 不同反演结果和真实值的相关系数以及系数矩阵条件数 Table 4 The conditional number of the coefficient matrixes and the coefficient of correlation between the inversion results and the true value |
从表 4的统计结果可以看出, 基于精确Zoeppritz方程三变量柯西约束的反演结果最为精确, 三参数反演结果与真实值的相关系数都达到了0.99以上, 其次是基于Aki-Richards近似公式三变量柯西约束反演的反演结果.
反演目标函数系数矩阵的矩阵条件数是衡量反演稳定性的一个重要指标, 矩阵条件数越大, 反演相对越不稳定.在无任何约束项时, 反演的系数矩阵, 也就是Jacobian矩阵的条件数是异常大, 达到了1010数量级.通过引入先验分布约束项作为反演目标函数的正则化项, 系数矩阵的条件数降低很多, 使得反演变得稳定, 而利用三变量柯西分布作为约束时, 不管是利用Aki-Richards近似公式还是利用精确Zoeppritz方程构建的系数矩阵的矩阵条件数都在103数量级以下, 较低的矩阵条件数确保了反演的稳定性.
为了检验该反演算法的抗噪性, 对信噪比为3的含噪声的合成角道集进行了基于精确Zoeppritz方程三变量柯西约束的贝叶斯反演.从图 6H的带噪声反演结果可以看出, 随机噪声对强反射系数影响较小, 但是弱反射系数会淹没在随机噪声中, 造成对弱反射系数的影响较大, 注意图 6H中1000ms到1200ms区域, 该处的模型参数纵向变化缓慢, 对应弱反射系数, 由于随机噪声的影响, 该处的反演结果不准确.但是强反射系数区域的反演结果还是较为精确的.总体上, 可以看出该反演算法的抗噪性还是较高的.
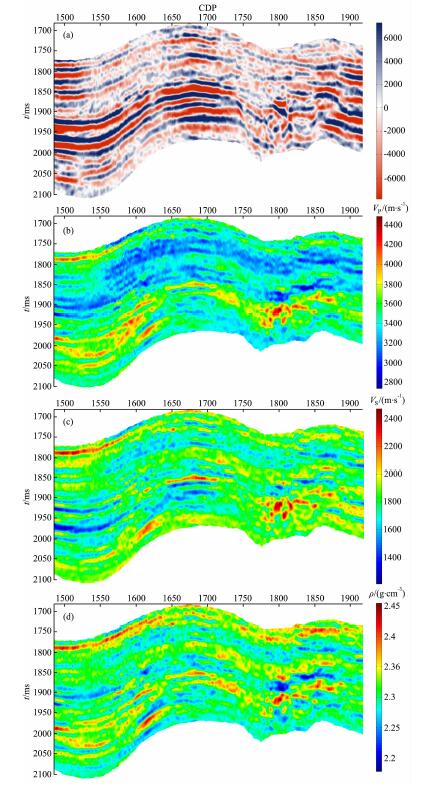
8 实际资料实际资料取自某工区, 该工区构造继承性发育, 为多套盐岩交错相变.图 7给出了实际资料的叠加剖面, 实际资料的处理经过了地表一致性振幅校正、地表一致性反褶积、去除多次波、动校正、球面扩散补偿、吸收衰减补偿以及叠前时间偏移等环节.
|
图 7 (a)实际资料叠加剖面; (b) P波速度反演剖面; (c) S波速度反演剖面; (d)密度反演剖面 Fig. 7 (a) The stack section of the real data; (b) The inverted P-wave velocity section; (c) The inverted S-wave velocity section; (d) The inverted density section |
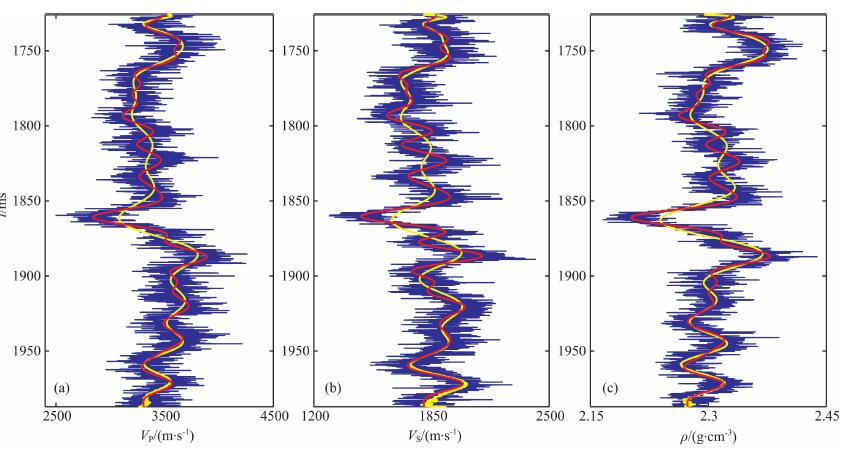
为了研究该反演算法在实际资料的应用效果, 井A并没有参与到反演当中, 起到用于验证反演结果的作用.该井位于第1840CDP处, 为了更好地对比井曲线和反演结果, 图 8分别给出了实际的井曲线(蓝色), 地震资料的反演结果(红色)以及井曲线低通滤波后的结果(黄色).从图 8可以看出反演结果和实际井曲线变化趋势一致, 并且与井曲线低通滤波后的结果也较吻合.该井1850~1860 ms处对应气层, 储层含气后相应的P波速度值较低, 但是单一从P波速度变化并不能确定到底是由于受到含气的影响还是由于受到岩性变化的影响, 通过结合密度的反演剖面, 发现该处的密度值较低, 较好的表征了储层含气后的特征.因此通过联立多种弹性参数进行解释, 可以有效降低储层预测和流体识别中的多解性.
|
图 8 实际的井曲线(蓝色)、井曲线低通滤波结果(黄色)和井旁道反演结果(红色)对比图 Fig. 8 The compare among the true value of well A (blue), the low-passed filter result of the true value (yellow) and the inverted result from seismic data (red) |
(1)本文基于广义线性反演的思想, 利用精确的Zoeppritz方程代替其近似公式构建AVO正演模拟的过程, 可以有效避免由于引入近似公式而带来的反演误差, 特别是在大角度入射的情况下.
(2)通过结合贝叶斯理论, 引入模型参数的先验分布作为反演的约束项, 可以有效降低由于Jacobian矩阵条件数过大而引起的反演不适定性.本文假设三参数反射系数服从三变量柯西分布, 三变量柯西分布作为长尾巴分布的一种, 可以形成稀疏脉冲反演的效果, 同时该分布引入了相关矩阵, 消除了三参数之间的统计相关, 可以降低由统计相关带来的反演不适定性, 提高了反演的稳定性和准确度.
(3)通过模型中7种反演算法试算的对比, 可以看出基于精确Zoeppritz方程三变量柯西约束的反演算法, 相比基于近似公式的反演算法在对大角度地震数据进行反演时, 精度有了进一步提高, 而相对单变量分布约束的反演算法, 由于相关矩阵的引入, 稳定性得到了提高, 较大幅度地改善了横波速度和密度的反演结果的精度; 相对于多变量高斯分布约束, 可以有效压缩地震子波, 产生稀疏脉冲反演的效果, 提高了三参数的纵向分辨率.在对实际资料进行处理时, 反演结果和井曲线的吻合度较高.
(4)该反演方法属于基于模型类的反演, 对初始模型的精度有所依赖.特别是在利用超大入射角的叠前地震数据进行反演时, 对初始模型的依赖程度增强, 需要建立准确的P波速度初始模型, 才能获得可靠的反演结果, 这是该反演方法的不足之处.
附录A 反射系数对模型参数的一阶偏导数原Zoeppritz方程如下所示:
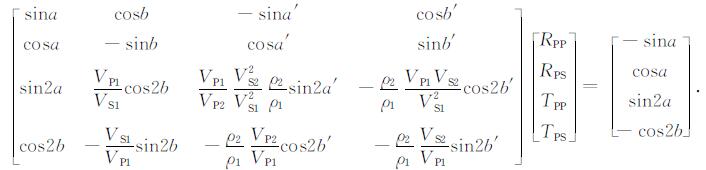
|
(A1) |
将(A1)式改写成关于三参数反射系数的表达式如下:
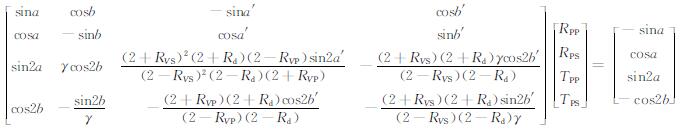
|
(A2) |
为了方便起见, 令(A2)式的系数矩阵为Z, 反射系数和透射系数项为R, 右边常数项为C, 则:
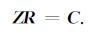
|
(A3) |
分别对(A3)两边对RVP, RVS和Rd求导[18]
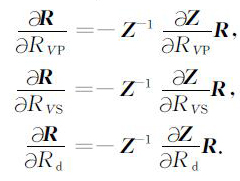
|
(A4) |
通过求取(A4)式的方程组便可以得到P波反射系数对三参数反射系数的一阶偏导数.
其中,
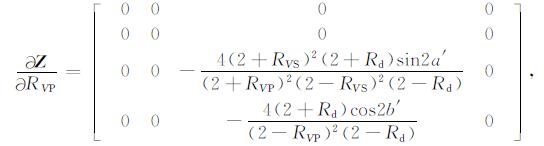
|
(A5) |
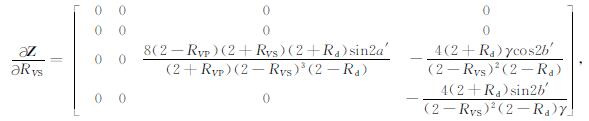
|
(A6) |
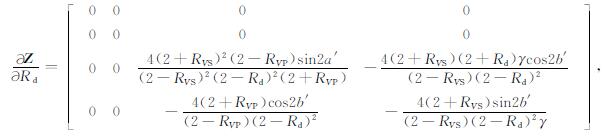
|
(A7) |
基于精确Zoeppritz方程建立的AVO正演模拟矩阵表达式如下:
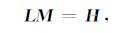
|
(B1) |
其中, H=D-S+LM0. D表示叠前地震数据, 为KN×1维矩阵:
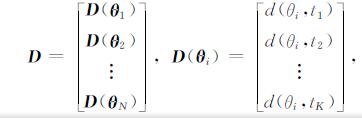
|
(B2) |
D(θi)表示角道集中入射角为θi地震数据向量, 由K个时间采样点的地震数据组成.
S表示由初始模型参数计算得到的合成地震数据, 为KN×1维矩阵:
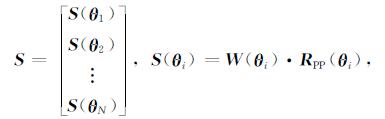
|
(B3) |
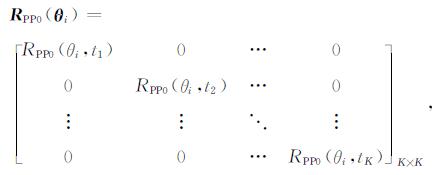
|
(B4) |
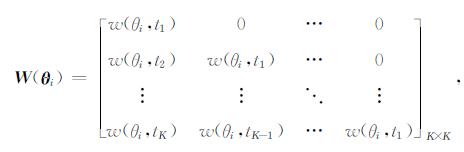
|
(B5) |
其中W(θi)表示入射角为θi的角度子波褶积矩阵, RPP0(θi, tj)表示利用给定的初始模型参数, 由Zoeppritz方程计算得到的入射角为θi、时间采样点为tj处的反射系数.
L表示由反射系数对模型参数的偏导数矩阵和子波矩阵组成的KN×3K维矩阵:
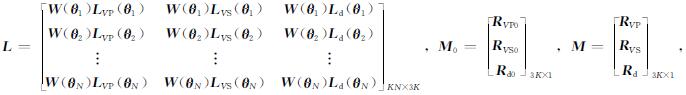
|
(B6) |
M0表示初始模型参数矩阵, 以RVP0为例:
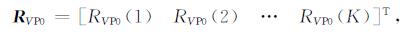
|
(B7) |
M表示模型参数矩阵, 以RVP为例:
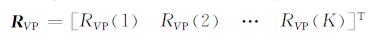
|
(B8) |
LVP(θi), LVS(θi)和Ld(θi)分别表示RPP0(θi)对RVP, RVS和Rd一阶偏导数组成的对角阵, 以LVP(θi)为例:

|
(B9) |
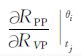
| [1] | 陈建江. AVO三参数反演方法研究[学位论文].东营:中国石油大学(华东), 地质资源与地质工程系, 2007. Chen J J. Study of three-term AVO inversion method[Doctor's thesis]. Dongying: Geological Resources and Geological Engineering, China University of Petroleum (East China) (in Chinese), 2007. http://cdmd.cnki.com.cn/Article/CDMD-10425-2007226441.htm |
| [2] | Larsen J A. AVO Inversion by simultaneous P-P and P-S inversion. Calgary: University of Calgary Department of Geology and Geophysics, 1999 . |
| [3] | 李录明, 罗省贤, 王明春, 等. 各向异性介质三维纵横波联合叠前反演方法及应用. 石油地球物理勘探 , 2010, 45(1): 60–65. Li L M, Luo X X, Wang M C, et al. 3D PP-PS joint inversion method and application inanisotropic medium. OGP (in Chinese) , 2010, 45(1): 60-65. |
| [4] | Buland A, Omre H. Bayesian linearized AVO inversion. Geophysics , 2003, 68(1): 185-198. DOI:10.1190/1.1543206 |
| [5] | Omid Karimi, Henning Omre. Bayesian closed-skew Gaussian inversion of seismic AVO data for elastic material properties. Geophysics , 2010, 75(1): 1-11. |
| [6] | Downton J E. Seismic Parameter Estimation from AVO inversion[Doctor's thesis]. Calgary: University of Calgary, 2005. http://adsabs.harvard.edu/abs/2005PhDT........87D |
| [7] | Alemie W, Mauricio D.Sacchi. High-resolution three-term AVO inversion by means of a Trivariate Cauchy probability distribution. Geophysics , 2011, 76: 43-55. |
| [8] | Macdonald C, Davis P M, Jackson D D. Inversion of reflection traveltimes and amplitudes. Geophysics , 1987, 52: 606-617. DOI:10.1190/1.1442330 |
| [9] | Russell B H. Introduction to seismic inversion methods. SEG Continuing Education Course Note Series, 1988, Vol. 2, Soc. Expl. Geophys. http://library.seg.org/doi/abs/10.1190/1.9781560802303.ch4 |
| [10] | Castagna J P, Batzle M L, Eastwood R L. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks. Geophysics , 1985, 50(4): 571-581. DOI:10.1190/1.1441933 |
| [11] | Gardner G H F, Gardner L W, Gregory A R. Formation velocity and density: The diagnostic basics for stratigraphic traps. Geophysics , 1974, 39(6): 770-780. DOI:10.1190/1.1440465 |
| [12] | Potter C C, Dey A K, Stewart R R. Density prediction using P-and S-wave sonic velocity. CREWES Research Report (University of Calgary) , 1998, 10: 1-10. |
| [13] | 张世鑫, 印兴耀, 张繁昌. 基于三变量柯西分布先验约束的叠前三参数反演方法. 石油地球物理勘探 , 2011, 46(5): 737–747. Zhang S X, Yin X Y, Zhang F C. Prestack three term inversion method based on Trivariate Cauchy distribution prior constraint. Oil Geophysical Prospecting (in Chinese) , 2011, 46(5): 737-747. |
| [14] | 杨培杰, 印兴耀. 非线性二次规划贝叶斯叠前反演. 地球物理学报 , 2008, 51(6): 1876–1882. Yang P J, Yin X Y. Non-linear quadratic programming Bayesian prestack inversion. Chinese J. Geophys. (in Chinese) , 2008, 51(6): 1876-1882. |
| [15] | Tor Erik Rabben. Non-linear Bayesian joint inversion of seismic reflection coefficients. Geophys.J.Int , 2008, 173: 265-280. DOI:10.1111/gji.2008.173.issue-1 |
| [16] | Tor Erik Rabben. Non-linear least-squares inversion with data-driven Bayesian regularization. Geophys.J.Int , 2000, 142: 43-72. |
| [17] | Mauricio D.Sacchi. Reweighting strategies in seismic deconvolution. Geophys.J.Int , 1997, 129: 651-656. DOI:10.1111/gji.1997.129.issue-3 |
| [18] | 张丰麒.纵波、转换波匹配与联合反演方法研究[硕士论文].青岛:中国石油大学(华东), 地球探测与信息技术系, 2011. Zhang F Q. Methodology of PS-to-PP time mapping and simultaneous inversion using P-P and P-S wave seismic data[Master's thesis]. Qingdao: Earth exploration and Information Technology, China University of Petroleum (East China), 2011. http://www.oalib.com/references/18987473 |
 2013, Vol. 56
2013, Vol. 56