2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
多波多分量地震勘探技术是具有极大的科学价值和发展前途的勘探地震学前缘学科之一.它在提高地震资料的分辨率,提高成像精度,精细预测岩性,研究地下介质方位各向异性等方面有着常规纵波勘探无法比拟的优势[1].多波多分量地震勘探技术将应用于所有的陆地或是海底地震勘探[2].
随着多波多分量地震勘探技术的发展,多波多分量地震资料处理技术也得到了快速发展.基于波场分离的多波多分量处理技术便是其中很重要的一类处理方法.这类方法以标量波场理论为基础,首先将多波多分量地震数据分解为纵波数据和转换横波数据,然后对这两种数据分别进行处理[3].因此,纵、横波的分离是多波多分量地震资料处理中很重要的一步.
纵、横波的分离方法有许多种,例如:偏振滤波法[4-5],Radon变换法[6],波动方程法[7]等.本文依据Helmholtz分解理论分离纵、横波利用的是这两种波场偏振特性的差异,属于偏振滤波法.
由Helmholtz分解理论可知,一个矢量场可以被分解成一个无旋的标量场和一个无散的矢量场.而在各向同性介质中,纵波是无旋场,横波是无散场,因此根据Helmholtz分解理论,对地震波场分别求取散度和旋度,可以提取出纯纵波和纯横波[8].但是在各向异性介质中,纵波的偏振方向并不完全平行于波的传播方向,横波的偏振方向也不完全垂直于波的传播方向.因此对于各向异性介质中的波场,直接求散度和旋度无法得到纯的纵、横波.为了在各向异性介质中也能够分离出纵、横波,Dellinger和Etgen[9]以Helmholtz分解理论为基础,在频率-波数域求解Christoffel方程,得到纵、横波质点的振动方向,继而得到所谓的波型分离算子(类似于散度和旋度算子),然后再反变换回时间-空间域,从而实现了二维VTI介质中的纵、横波分离.Dellinger[10]又将此方法推广到三维各向异性介质中.但是此分离算子对于均匀介质效果很好,而对于非均匀介质,其适用性不佳.
Yan和Sava[11-12]在Dellinger理论的基础上,利用Christoffel方程在每个网格节点上计算分离算子,从而将其适用性从均匀VTI介质推广到非均匀的TTI介质和VTI介质中.Zhang和McMechan[13]对比研究了前几种方法,提出了适用性更广的波场分离方法.该方法以Helmholtz分解理论和Christoffel方程为基础,推导出可以直接获得纵、横波各分量的公式.其物理意义明确,而且可以很好的适用于3D各向异性介质中.Yan和Sava[14]针对该方法计算成本高、效率低的问题,提出了更为高效的计算方法.郭鹏等[15]也研究了非均匀VTI介质中的纵、横波分离.
上述的纵、横波的分离方法,只适用于正演模拟.对于给定的地震记录,尧德中等[16]从Helmholtz分解理论出发,在频率-波数域对VSP地震记录求取散度和旋度,从而解决了地震记录中有一个方向上的偏导数无法求取的问题.然后再反变回时间-空间域,得到纯的纵、横波地震记录.但是该方法要求各地层的纵、横波速度为已知.Sun[17]将Helmholtz分解理论与波场延拓相结合,先将地面地震记录在均匀空间中延拓到某一位置,然后利用求散度和旋度的方法得到纯的纵、横波,最后再将分离后的波场分别逆向延拓回地面,从而实现地面地震记录的纵、横波的分离.Sun等[18]将此方法应用到3D介质中.但是此方法对波场进行了散度和旋度的运算,使分离后的波场产生了相移,并且使得纵、横波的振幅比也发生了改变.因此需要对产生的相移进行校正[19],并恢复真实的纵、横波振幅比[20].
本文依据Helmholtz分解理论,在频率-波数域求解散度和旋度来进行纵、横波分离.针对地表速度不准确造成纵、横波分离不彻底的问题,提出了准确估算地表速度值的方法.针对进行散度和旋度运算后,纵、横波的相位和振幅比会发生改变的问题,提出了相应的相位校正以及纵、横波振幅比校正的方法.
2 利用散度和旋度进行纵横波分离的原理尧德中等[16]指出在频率-波数域进行散度和旋度运算可以解决地震记录中某个方向的偏导数无法求取的问题.
根据Helmholtz分解理论,位移场U可表示为一个标量势的梯度与一个矢量势的散度之和[8].用公式表示为
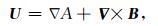
|
(1) |
其中,A表示标量拉梅势,B表示矢量拉梅势,ΔA和
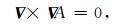
|
(2) |
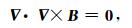
|
(3) |
根据(2)、(3)两式对(1)式两边分别求旋度和散度,可得:
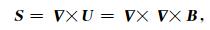
|
(4) |
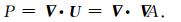
|
(5) |
由于S只包含了横波分量,P只包含了纵波分量,因此可以用S和P来分别表示横波波场和纵波波场.
在二维情况下,令U=[u,w],其中u表示位移场的水平分量,w表示位移场的垂直分量.将(4)、(5)两式展开,可得(二维情况下S是一标量):
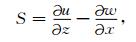
|
(6) |
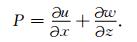
|
(7) |
在时间-空间域中,地面地震记录z方向的偏导数是无法求得的.将(6),(7)两式变换到频率-波数域求解[16, 21],有:
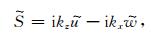
|
(8) |
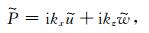
|
(9) |
其中,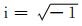

|
(10) |
由于在地面接收到的是上行波,所以(10)式取负号.对于(8)式,v取纵波波速,对于(9)式,v取横波波速[16].求得
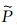
图 1为合成的地面地震记录.模型为一均匀介质,速度是vp=3000m/s,vs=1700m/s,所用震源为集中力震源,置于模型中心.

|
图 1 合成地震记录 (a)水平分量; (b)垂直分量. Fig. 1 Synthetic seismic data (a) horizontal component (b) vetical component |
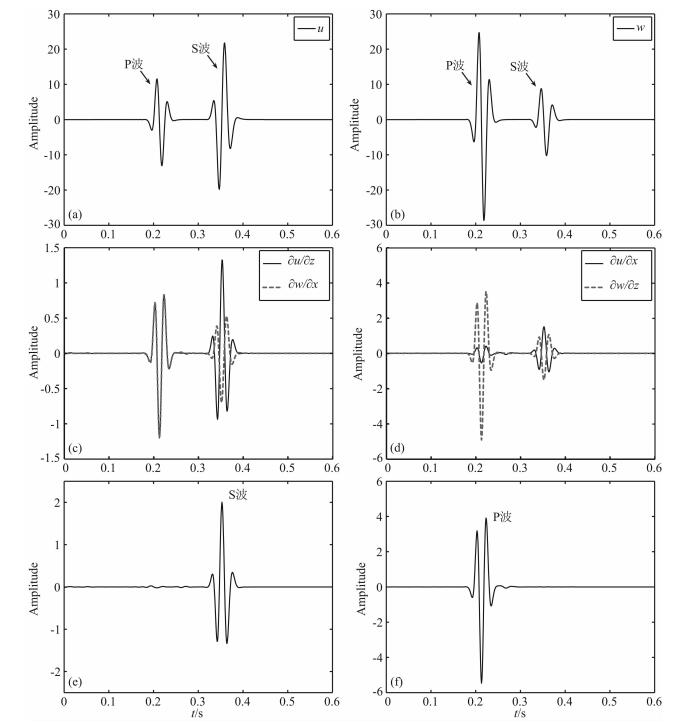
从图 1中抽取一道地震数据显示在图 2中,图 2a是水平分量(用u表示),图 2b是垂直分量(用w表示).图 2c中的实线是u对z的偏导数,虚线是w对x的偏导数;图 2e是图 2c中两条线相减的结果.从图 2c和图 2e中可以看出,(6)式中之所以能将纵波成分消除掉,是因为u/z和w/x中的纵波成分相等,横波成分不相等,两者相减便可将纵波成分消除,只保留横波成分.图 2d中的实线是u对x的偏导数,虚线是w对z的偏导数;图 2f是图 2d中两条线相加的结果.从图 2d和图 2f中可以看出,(7)式中之所以能将横波成分消除,是因为u/x和w/z中的横波成分振幅大小相等,相位相差π,而纵波成分振幅不等,相位相差很小,两者相加便可将横波成分消除,只保留纵波成分.
|
图 2 图 1中的一道地震数据 (a)水平分量u; (b)垂直分量w; (c)∂u/∂z和∂w/∂x的波形图; (d)∂u/∂x和∂w/∂z的波形图; (e)分离出的横波; (f)分离出的纵波. Fig. 2 A trace data of Fig. 1 (a) Horizontal component u; (b) Vetical component w; (c) Waveform of ∂u/∂z and ∂w/∂x; (d) Waveform of ∂u/∂x and ∂w/∂z; (e) The separated P-waves; (f) The separated S-waves. |
在上述计算过程中,给出的速度为真实速度.如果给出的速度不准确,结果如何?我们知道,(8)式和(9)式中的kx是与速度无关的,由(10)式可知,kz与速度有关.也就是说,速度影响的只是u和w对z的偏导数(u/z和w/z).
图 3a为纵波速度分别为2500、3000、3500m/s时,u/z的波形图.从图中可以看出速度对u/z的振幅影响很明显,而且速度越快振幅越小,速度越慢振幅越大.速度对相位也有影响,但是影响比较小,在图中很难看出.这表明,如果速度给的不准确,u/z-w/x是不能够将纵波成分消除掉的,如图 3c所示,纵波有残留.图 3b为横波速度分别为1200、1700、2200m/s时,w/z的波形图.从图中可以看出速度对w/z的影响与对u/z的影响一样有着相同的规律.在速度不准确的情况下,u/x+w/z也无法将横波成分消除掉,如图 3d所示,横波有残留.从上面分析可以知,只有在速度准确的情况下,纵横波才能分离开.因此,需要估算地表的纵、横波速度.

|
图 3 (a)纵波速度取不同值时, u/z的波形图; (b)横波速度取不同值时, w/z的波形图; (c)纵波速度为3500m/s时, 分离出的横波; (d)横波速度为1200m/s时, 分离出的纵波 Fig. 3 (a) Waveforms of u/z on different P velocities; (b) Waveforms of w/z on different S velocities; (c) The separated S-waves using P velocity 3500m/s; (d) The separated P-waves using S velocity 1200 m/s |
令uP(ω)和wP(ω)分别表示单频ω上,平面纵波的水平分量和垂直分量,则(x,z)处的uP(ω)和wP(ω)可表示为[20]
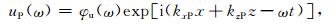
|
(11) |
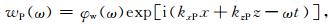
|
(12) |
其中,φu(ω)和φw(ω)分别表示单频ω上,纵波水平分量以及垂直分量的振幅;kxP和kzP分别为水平方向和垂直方向上的波数.
令UP和WP分别为平面纵波的水平分量和垂直分量
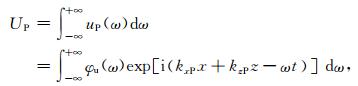
|
(13) |
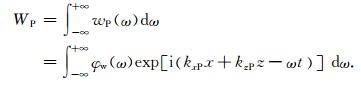
|
(14) |
UP和WP分别对z和x求偏导数得:
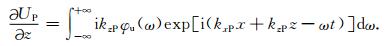
|
(15) |
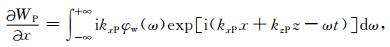
|
(16) |
通过前面的分析可知,若要消除掉纵波,(15)、(16)两式应相等,于是有:
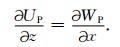
|
(17) |
当所给速度不准确时,令所求波数为k zP*,则

|
(18) |
由(15)-(18)式可得
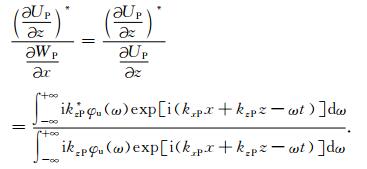
|
(19) |
由(10)式可得

|
(20) |
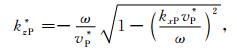
|
(21) |
其中,vP为真实的纵波速度,v
P*为不准确的纵波速度.根号下的数值为非负值,所以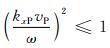
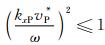
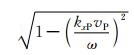
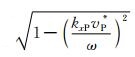
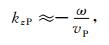
|
(22) |
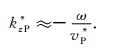
|
(23) |
将(22)、(23)两式代入(19)式得
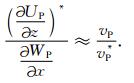
|
(24) |
结合第二节的分析,同理可得:
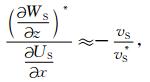
|
(25) |
其中US和WS为平面横波的水平分量和垂直分量,vS为真实的横波速度,v S*为不准确的横波速度.
由(24)、(25)式可知,(UP/z)*和WP/x的振幅比近似等于真实纵波速度与所给纵波速度之比.(WS/z)*和US/x的振幅比近似等于真实横波速度与所给横波速度之比的负数.因此利用(24)、(25)式,可以估算出地表的真实速度值.但这两个式子是一个粗略的近似,可利用多次迭代提高速度估算的精度.具体的做法是(以估算纵波速度为例):
(1) 预先给定一个速度值v P1*;
(2) 计算出(UP/z)*和WP/x,求得两者振幅之比;
(3) 判断振幅比是否满足要求(接近于1),若满足,停止计算,若不满足由(24)式,计算出v P2*,重复步骤2;
同理,可估算出地表的横波速度值.
在实际计算时,我们选取一个子波长度的时间窗口,该窗口内的纵波子波或横波子波与其它子波有很小的干涉.在该窗口内计算(UP/z)*和WP/x最大振幅之比或(WS/z)*和Us/x最大振幅之比.
例如,对于上述地震地面记录,给定初始的纵波速度值为3500m/s,经两次迭代后,求得(UP/z)*和WP/x最大振幅之比为0.9628,利用(24)式求得纵波速度为3012.7m/s.再以此速度计算(WP/z)*和WP/x最大振幅之比为0.9956,已经非常接近于1,此时估算的纵波速度为2999.4m/s,与真实速度只差0.6m/s.同样,当给定初始的横波速度值为2200m/s时,经过两次迭代,求得(WS/z)*和US/ x最大振幅之比-0.9955,估算的横波速度为1701.1m/s,与真实速度相差1.1m/s.图 4(a,b)分别为纵、横波的初始速度为3500m/s以及1200m/s时分离的横波和纵波,可以看到图 3c中残留的纵波以及图 3d中残留的横波已经消除掉.
|
图 4 (a)初始纵波速度为3500m/s时分离出的横波; (b)初始横波速度为2200m/s时分离出的纵波; (c)初始纵波速度为8000m/s时分离出的横波; (d)初始横波速度为6700m/s时分离出的纵波; (e)初始纵波速度为20m/s时分离出的横波; (f)初始横波速度为10m/s时分离出的纵波. Fig. 4 (a) The separated S-waves using initial P velocity 3500 m/s; (b) The separated P-waves using initial S velocity 2200 m/s; (c) The separated S-waves using initial P velocity 8000 m/s; (d) The separated P-waves using initial S velocity 6700 m/s; (e) The separated S-waves using initial P velocity 20 m/s; (f) The separated P-waves using initial S velocity 10 m/s. |
本文也验证了所给速度与真实速度相差非常大的情况.如当纵波初始速度给出8000m/s,经过5次迭代,估算出的纵波速度为3021.7m/s;横波初始速度给出6700m/s时,经过4次迭代,估算出的横波为1704.6m/s.分离的纵、横波如图 4(c,d)所示.又如,当纵波初始速度为20m/s时,经过5次迭代,估算出的纵波速度为3022m/s;横波初始速度为10m/s时,经过4次迭代,估算出的横波速度为1704.6m/s.分离的纵、横波如图 4(e,f)所示.从图 4(c-f)可以看出在所给出的纵、横波速度与真实速度相差很大的情况下,也能够很好地分离纵、横波.
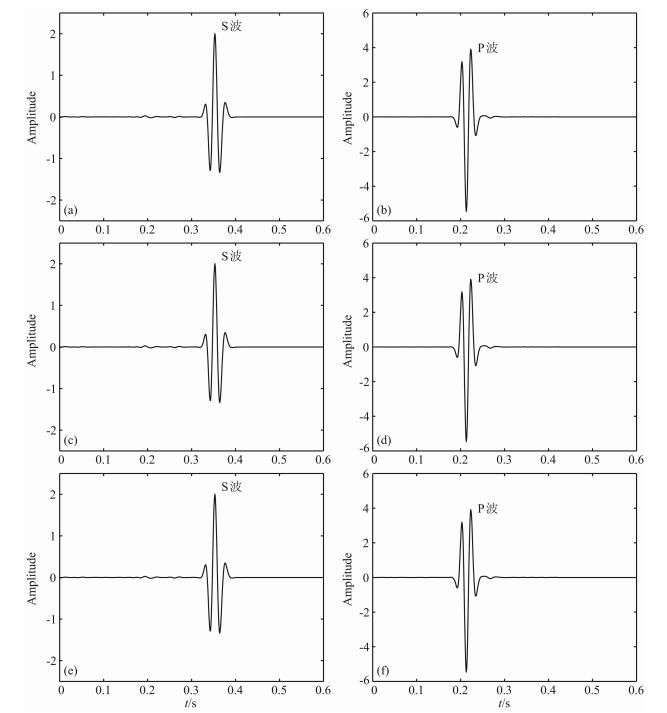
4 相位和纵横波振幅比的校正 4.1 相位的校正Sun等[19]指出在对波场进行散度和旋度计算后,纵、横波的相位将产生π/2的移动.从(8)式和(9)式可以看出,对波场求取散度和旋度后,等式的右边被乘上了一个i因子(i=exp(iπ/2)),从而使分离后的P波和S波产生了π/2的相移.由于Sun是在空间域求取的散度和旋度,因此无法直接在计算的过程中对相位进行校正,需要在求取散度和旋度之后,将分离的纵、横波分别通过对时间t做Hilbert变换[22]来进行校正.而本文是在频率波数域求取的散度和旋度,因此可以在计算过程中将(8)式和(9)式两边同乘以-i(-i=exp(-iπ/2)),直接将产生的π/2的相移校正回去,即:

|
(26) |
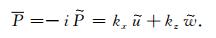
|
(27) |
S和P是相位校正后的波场.在实际计算时,用(26)式和(27)式代替(8)式和(9)式来计算.
4.2 纵、横波振幅比的校正
Sun等[20]指出在对波场进行散度和旋度计算后,使得纵、横波的振幅比产生了vP/vS的变化,需要在分离后的横波波场乘以vS/vP,从而将纵、横波振幅比校正到真实的纵、横波振幅比上.而对于本文来说,由于在计算(8)式时,为了保证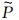

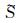
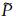
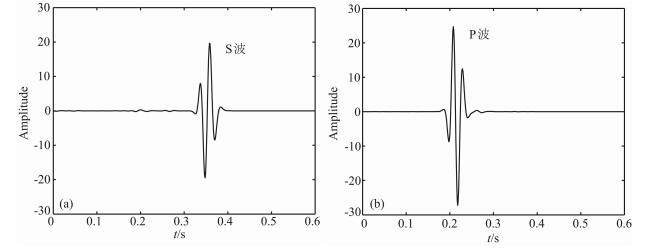
图 5是做了相位与纵横、波振幅比校正的纵、横波波场图.在成图时将分离后的纵、横波振幅进行了规格化[20].通过图 5a与图 2a中的横波(横波能量主要集中在水平分量上),图 5b与图 2b中的纵波(纵波能量主要集中在垂直分量上)对比可以看到相位和振幅比得到了恢复.
|
图 5 对分离后的纵、横波进行相位、纵横波振幅比校正以及规格化 (a)横波; (b)纵波 Fig. 5 The separated S-and P-waves after correcting phase, balanceing amplitude and normalizating (a) S-waves; (b) P-waves |
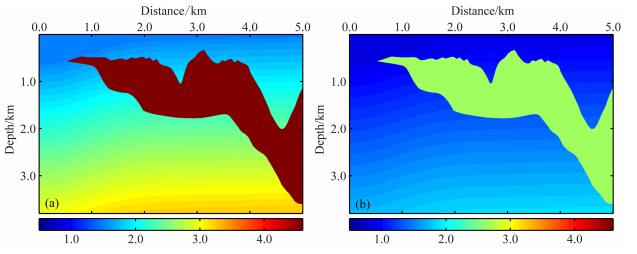
图 6为Sigsbee盐丘模型.模型表层的纵波速度为1517m/s,横波速度为876m/s.正演模拟时,震源放在地下50m,采用爆炸震源,检波器置于地表,中间放炮,两边接收,模型四周使用了混合吸收边界[23].
|
图 6 Sigsbee盐丘模型 (a)纵波速度, 从1517~4564m/s; (b)横波速度, 876~2635m/s Fig. 6 The sigsbee salt model (a) The P-wave velocity ranging from 1517 to 4564 m/s; (b) The S-wave velocity ranging from 876 to 2635 m/s. |
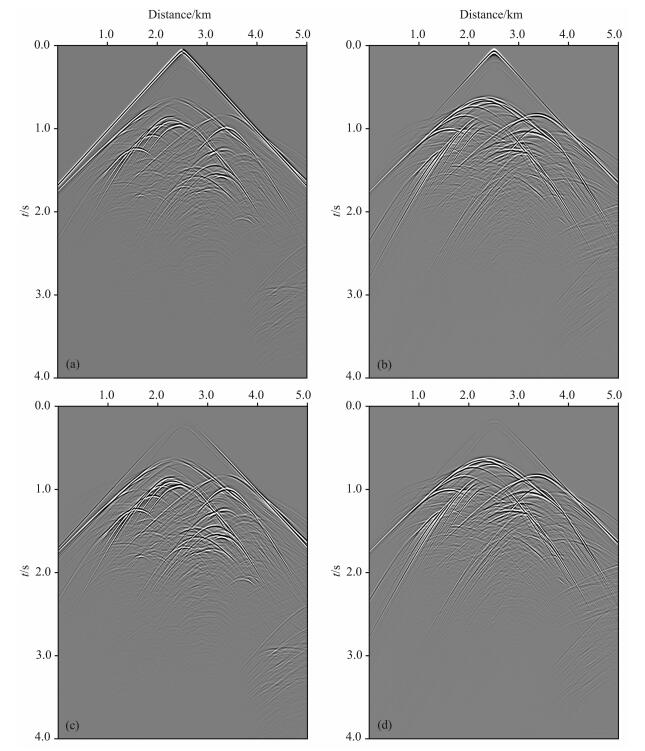
图 7是利用图 6所示模型正演出的地面地震记录.从图中可以看出记录中波场的主要能量是来自盐丘表面的反射,浅部地层的反射能量很微弱.波场很复杂,纵、横波混叠在一起,尤其是在1.5s以后,几乎无法将两者区分出来.
|
图 7 (a)模拟地震记录的水平分量; (b)模拟地震记录的垂直分量; (c)切除直达波后模拟地震记录的水平分量; (d)切除直达波后模拟地震记录的垂直分量. Fig. 7 (a) Horizontal component of synthetic seismogram; (b) Vetical component of synthetic seismogram; (c) Horizontal component of synthetic seismogram after removing direct arrival; (d) Vertical component of synthetic seismogram after removing direct arrival. |
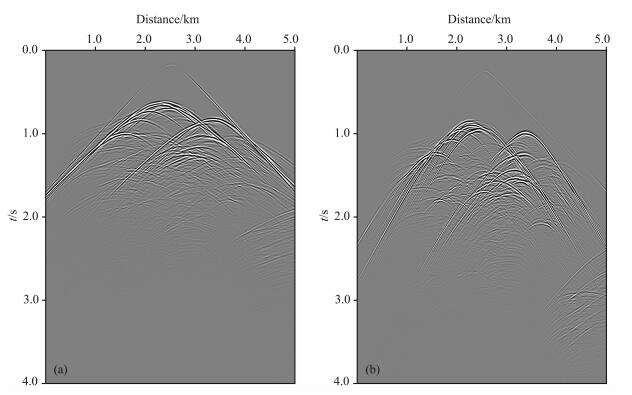
在进行纵、横波分离时,假定地表速度未知,给出的初始纵波速度为3000m/s,初始横波速度为1800m/s.利用上述估算速度值的方法,分别经过10次和9次迭代,估算出的地表纵波速度为1517m/s,横波速度为877m/s,与表层的纵、横波速度非常接近.图 8(a,b)为最终分离的纵波和横波,在频率波数域计算散度和旋度时,使用的是(26)式和(27)式,并进行了纵、横波振幅比的校正,以及规格化[19].从图 8中可以看出,原本混叠在一起无法区分的纵、横波得到了很好的分离.
|
图 8 分离出的纵波和横波 (a)分离出的纵波; (b)分离出的横波. Fig. 8 The separated P-and S-wavefield (a) The separated P-waves; (b) The separated S-waves |
本文依据Helmholtz分解定理,利用对地面地震记录求散度和旋度的方法,分离出了纵、横波.分析了地表纵、横波的速度在波场分离中的重要性,针对速度值不准确会使纵、横波分离不彻底的问题,提出了估算地表速度值的方法.利用此方法,可以在地表速度值未知时,将其估算出来.虽然(24)式和(25)式只是近似式,但通过盐丘模型验证可以看出,经过几次迭代后依然可以比较准确地估算出地表速度值,并且利用估算出的速度值很好地分离出了纵、横波,说明了本文方法的有效性.估算速度值时,子波的选取很关键,选取比较纯净的纵波子波或横波子波,估算的速度值才能更加接近真实值.根据本文波场分离的方法提出了相应的相位校正以及纵、横波振幅比校正的公式.在实际计算时,直接利用(26)和(27)两式进行计算,不需要再额外进行相位校正,节省了计算成本.本文只对位移形式表示的波场进行了分离,对于速度形式表示的波场,本文的方法依然是适用的.
附录A这部分证明主要参考了文献[20].与其不同的是,在对波场求取完散度和旋度后,文献[20]中的纵、横波振幅比变为cvP/vS,而本文中变为cvS/vP.主要原因是,本文需要人为选取波数,而文献[20]则不需要.
令UP和US分别表示在坐标(x,z)处的纵波和横波的位移矢量,则有
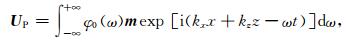
|
(A1) |
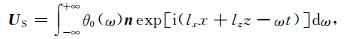
|
(A2) |
其中,φ0(ω)和θ0(ω)分别是频率为ω时纵波和横波的振幅;m和n是单位矢量,分别平行于纵波和横波的偏振方向;kx,kz分别为纵波x方向和z方向上的波数;lx,lz分别为横波x方向和z方向上的波数.
令φ0(ω)和θ0(ω)满足如下关系式:
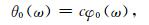
|
(A3) |
c是常量
弹性波波场U可以表示为纵波波场和横波场的线性叠加:
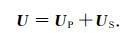
|
(A4) |
(1)利用散度求取纵波时,由于
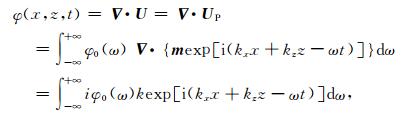
|
(A5) |
其中,k=(k x2+k z2)1/2=ω/α,α是波速.
在求散度时,尧德中[16]指出为保证得到纯纵波,求取波数kz时,α应该取横波速度,因此k=ω/vS,则
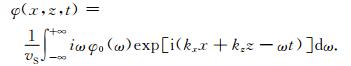
|
(A6) |
(2)利用旋度来求取横波时,由于 ×UP=0,则
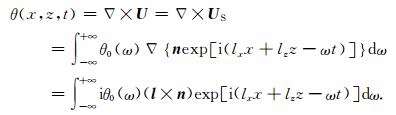
|
(A7) |
其中l=(lx,lz).
令p为单位向量,方向平行于l×n的方向,则
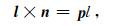
|
(A8) |
其中l=(l x2+l z2)1/2=ω/β,β是波速.
同样,在求旋度时,为保证得到纯横波,求取波数lz时,β应该取纵波速度,因此l=ω/vP,则
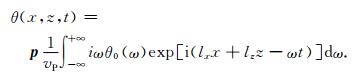
|
(A9) |
将式(A3)代入(A9)式,可得
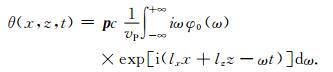
|
(A10) |
对比(A6)式和(A10)式可以看出,经过了散度和旋度运算后,横波与纵波的振幅比由c变成了cvS/vP.
| [1] | 赵邦六. 多分量地震勘探在岩性气藏勘探开发中的应用. 石油勘探与开发 , 2008, 35(4): 397–423. Zhao B L. Application of multi-component seismic exploration in the exploration and production of lithologic gas reservoirs. Petroleum Exploration and Development (in Chinese) , 2008, 35(4): 397-423. DOI:10.1016/S1876-3804(08)60088-9 |
| [2] | Davis T L. Multicomponent seismology: The next wave. Geophysics , 2001, 66(1): 49. DOI:10.1190/1.1444920 |
| [3] | 孙歧峰, 杜启振. 多分量地震数据处理技术研究现状. 石油勘探与开发 , 2011, 38(1): 67–72. Sun Q F, Du Q Z. A review of the multi-component seismic data processing. Petroleum Exploration and Development (in Chinese) , 2011, 38(1): 67-72. |
| [4] | 胡天跃, 张广娟, 赵伟, 等. 多分量地震波波场分解研究. 地球物理学报 , 2004, 47(3): 504–508. Hu T Y, Zhang G J, Zhao W, et al. Decomposition of multicomponent seismic wavefileds. Chinese J. Geophys. (in Chinese) , 2004, 47(3): 504-508. |
| [5] | 李英康, 崔作舟. 分离纵波和横波的偏振旋转法. 地球物理学报 , 1994, 37(Supp. 1): 372–382. Li Y K, Cui Z Z. P and S-waves separated by polarization revolving method. Acta Geophysica Sinica (Chinese J. Geophys.) (in Chinese) , 1994, 37(Supp. 1): 372-382. |
| [6] | 冯晅, 张先武, 刘财, 等. 带有多道相关的抛物线Radon变换法分离P-P、P-SV波. 地球物理学报 , 2011, 54(2): 304–309. Feng X, Zhang X W, Liu C, et al. Separating P-P and P-SV wave by parabolic Radon transform with multiple coherence. Chinese J. Geophys. (in Chinese) , 2011, 54(2): 304-309. |
| [7] | Devaney A J, Oristagliot M L. A plane-wave decomposition for elastic wave fields applied to the separation of P-waves and S-waves in vector seismic data. Geophysics , 1986, 51(2): 419-423. DOI:10.1190/1.1442102 |
| [8] | Aki K, Richards P G. Quantitative Seismology. (2nd ed). California: University Science Books, 2002 . |
| [9] | Dellinger J, Etgen J. Wave-field separation in two-dimensional anisotropic media. Geophysics , 1990, 55(7): 914-919. DOI:10.1190/1.1442906 |
| [10] | Dellinger J. Anisotropic Seismic Wave Propagation. California: Stanford University , 1991: 65-69. |
| [11] | Yan J, Sava P. 3D elastic wave mode separation for TTI media. 79th Annual International Meeting, SEG, Expanded Abstracts , 2009: 4294-4298. |
| [12] | Yan J, Sava P. Elastic wave-mode separation for VTI media. Geophysics , 2009, 74(5): WB19-WB32. DOI:10.1190/1.3184014 |
| [13] | Zhang Q S, McMechan G A. 2D and 3D elastic wavefield vector decomposition in the wavenumber domain for VTI media. Geophysics , 2002, 75(3): D13-D26. |
| [14] | Yan J, Sava P. Improving the efficiency of elastic wave-mode separation for heterogeneous tilted transverse isotropic media. Geophysics , 2011, 76(4): T65-T78. DOI:10.1190/1.3581360 |
| [15] | 郭鹏, 何兵寿, 张一凡. VTI介质中的波场分离. 工程地球物理学报 , 2011, 8(3): 261–268. Guo P, He B S, Zhang Y F. Wave-field Separation in VTI Media. Chinese Journal of Engineering Geophysics (in Chinese) , 2011, 8(3): 261-268. |
| [16] | 尧德中, 周熙襄, 钟本善. VSP记录的纵、横波分离方法与应用. 石油地球物理勘探 , 1993, 28(5): 623–628. Yao D Z, Zhou X X, Zhong B S. Method for separating out P-wave or S-wave in VSP data, and its application. OGP (in Chinese) , 1993, 28(5): 623-628. |
| [17] | Sun R. Separating P-and S-waves in a prestack 2-dimensional elastic seismogram. 61th Ann. Mtg., Eur. Assn. Geosci. Eng., Extended Abstracts, 1999: 6-23. |
| [18] | Sun R, McMechan G A, Hsiao H H, et al. Separating P-and S-waves in prestack 3D elastic seismograms using divergence and curl. Geophysics , 2004, 69(1): 286-297. DOI:10.1190/1.1649396 |
| [19] | Sun R, Chow J D, Chen K J. Phase correction in separating P-and S-waves in elastic data. Geophysics , 2001, 66(5): 1515-1518. DOI:10.1190/1.1487097 |
| [20] | Sun R, McMechan G A, Chuang H H. Amplitude balancing in separating P-and S-waves in 2D and 3D elastic seismic data. Geophysics , 2011, 76(3): S103-S113. DOI:10.1190/1.3555529 |
| [21] | 尧德中. 单程弹性波逆时偏移和相移偏移方法. 石油地球物理勘探 , 1994, 29(4): 449–455, 461. Yao D Z. Reverse-time and phase-shift migrations of single-way elastic waves. OGP (in Chinese) , 1994, 29(4): 449-455, 461. |
| [22] | Claerbout J F. Fundamentals of Geophysical Data Processing: With Applications to Petroleum Prospecting. California: Blackwell Scientific Publications , 1985: 20-24. |
| [23] | Liu Y, Sen M K. A hybrid absorbing boundary condition for elastic wave modeling with staggered-grid finite difference. 80th SEG meeting, Denver, Colorado, USA, Expanded Abstracts , 2010: 2945-2949. |
 2013, Vol. 56
2013, Vol. 56


