2. 中国科学院大学地球科学学院, 北京 100049
2. College of Earth Science, University of Chinese Academy of Sciences, Beijing 100049, China
反演静态高阶引力场和对大洋环流进行研究是GOCE(Gravityfieldandsteady-stateOceanCirculation Explorer)卫星计划的最主要两个目的[1].针对前者,国外如:Rummel,Visser,Klees,Pail,Ditmar,Baur等学者进行了大量研究和模拟计算[2-7],国内如:罗志才、于锦海等学者对相应算法进行了讨论[8-11].这些研究为利用GOCE实际数据反解高精度引力场模型作了很好铺垫.不仅如此,目前欧空局已经发布三组利用GOCE数据计算的引力场模型[12],这些模型高精度地给出了重力场的中高阶位系数,可为海洋学研究提供高精度的大地水准面数据.本文研究的目的即是利用GOCE卫星提供的引力场模型,并结合卫星测高提供的海面高数据(CNES-CLS2010 MSS),对稳态海面地形及大洋环流进行研究.
利用GOCE卫星数据研究大洋环流是当前该领域的研究热点之一.LeGrand等[13-14]评估了GOCE对未来大洋环流研究的作用,特别是重点研究了对北大西洋区域的影响;利用气候反演模型讨论了GOCE数据对极地环流、巴西暖流等研究的作用;Schroter等[15]结合容量和热流讨论了GOCE可能的影响;Vossepoel等[16]指出GOCE卫星将提高小尺度空间稳态海面地形的精度;Bingham等[17]利用GOCE数据,给出了北大西洋稳态地转流的初步估计,指出仅仅用两个月的GOCE数据,其MDT的计算精度已经好于采用GRACE(GravityRecovery andClimateExperiment)八年观测数据的计算精度;Haines等[18]从空间分辨率、时间分辨率、误差协方差等角度讨论了利用GOCE大地水准面产品需要注意的问题;Janjic等[19]结合GRACE和GOCE重力场模型及卫星测高数据研究了大洋环流;Knudsen等[20]利用GOCE卫星提供的初步重力场模型详细讨论了其在稳态海面地形及大洋环流中的应用.在国内也有许多学者利用卫星重力模型研究了海洋学的相关问题,例如:张子占等[21-22]先后讨论了GRACE卫星资料确定的稳态海面地形及其谱特征,并讨论了小波滤波方法在探测表层地转流中的应用,指出小波滤波比高斯滤波更能保留海面地形的局部特征;王正涛等[23]在反解了GRACE卫星重力场模型WHU-GM-05的基础上联合卫星测高数据计算了稳态海面地形.但目前国内所进行的类似工作仍停留在GRACE的基础上,而对于GOCE数据及模型的应用还很缺乏.这可能是由于数据滞后等原因产生的.总体来看,国际上利用GOCE初步的重力场模型并结合具体的区域进行实算,已经得出了许多结论.然而其存在的问题是GOCE数据的使用仍远远不够,以上文献最多仅利用了GOCE提供的前两个月数据.
而到目前为止,GOCE已经可以提供2009年11月1日到2011年6月1日之间的数据,主要缺失2010年7月5日到2010年10月15日时间段.数据量较之前已大大改观,含有的相关信息值得进一步挖掘,本文研究的目的也在于此.
2 计算方法稳态海面地形的基本计算公式如下[24]:
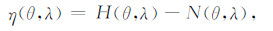
|
(1) |
其中(θ,λ)为计算点的余纬、经度,η为稳态海面地形,H为平均海面高,N为大地水准面高.在具体计算中,H、N所含的频谱成分有差别,原因为H来源于卫星测高,理论上按球谐展开,可展至无限阶次;但N由重力场模型计算得到(本文中重力场模型由GOCE提供),而重力场模型的阶次是有限的,如GOCE数据只能提供到约250阶次的重力场模型.因此二者对应的空间分辨率不一致.针对此问题,一般有两种解决方案[18].
第一是对H在球域内作球谐展开,让其展至与N同阶次,然后为了进一步削弱高频误差的影响,可利用高斯滤波器等对二者在频域内进行同样的滤波.但需要注意的是,一般H在陆地上没有值,此时需用大地水准面数据来代替.
第二是计算各点处N的值,然后与该点H的值作差,最后利用高斯滤波器等在空间进行平滑滤波.
本质上讲,这二种算法是等价的.本文主要采用第二种算法.需要注意的是,H和N所采用的参考椭球和潮汐系统必须一致.根据文献[24],参考椭球和潮汐系统不同所引起的差异最高可达30cm,而稳态海面地形的量级一般在1m以内,因此这种差异不可忽略.
在计算得到了η之后,可采用(2)式来计算海表处洋流的速度[17, 20, 24]:

|
(2) |
其中us、vs分别为洋流速度的北向、东向分量;f为科氏系数,值为2Ωcosθ,Ω为地球自转速度;g为该点的重力;re为该点到地心的距离.
3 采用的数据资料本文中的海面高数据采用由法国空间中心(CNES)利用16年卫星测高数据计算得到的CNES-CLS2010MSS,所涉及的测高卫星包括:T/P、T/PTDM、ERS2ERM、ENVISAT、Jason-1、GFO、ERS-1.数据以经纬度都为2′的格网给出,采用TOPEX参考椭球和平均潮汐系统.
关于从GOCE观测数据来解算引力场模型存在多种方法[2-12, 25-26],但欧空局主要推荐了三组引力场模型[12],即:分别使用直接法、时域法、空域法解算的引力场模型,后文中分别用DIR、TIM、SPA来表示.到目前为止,欧空局利用不同时段的数据及不同的方法,发布了三组引力场模型.其时段大致为:2009年11月1日到2010年1月11日,2009年11月1日到2010年7月5日,2009年11月1日到2011年4月30日,目前共有8个模型,仅缺第三时段的空域法解.依据时段的不同,本文将其模型分别命名为:DIR1、DIR2、DIR3、TIM1、TIM2、TIM3、SPA1、SPA2.考虑到第一组解仅采用了两个月数据,且已有文献主要采用该组解进行讨论[17, 20],因此本文的讨论主要利用DIR2、DIR3、TIM2、TIM3、SPA2来进行.为了对比,本文还选用了由德国地学中心(GFZ)和法国空间大地测量研究小组(GRGS)利用4.5年的GRACE数据联合研制的静态引力场模型EIGEN-GRGS_ RL02_MEAN-FIELD,模型最大阶数为160.
4 结果与讨论 4.1 海面地形本节利用上述数据,根据第2节所述原理对海面地形进行计算,计算工具采用欧空局提供的GOCE USER Toolbox(GUT)软件[24].在具体计算中,利用GOCE引力场模型时,高斯平滑的半径取为80km,GRACE取为125km.结果如图 1所示.
|
图 1 不同模型计算所得MDT(单位:m) Fig. 1 MDT calculated with different models (units:m) |
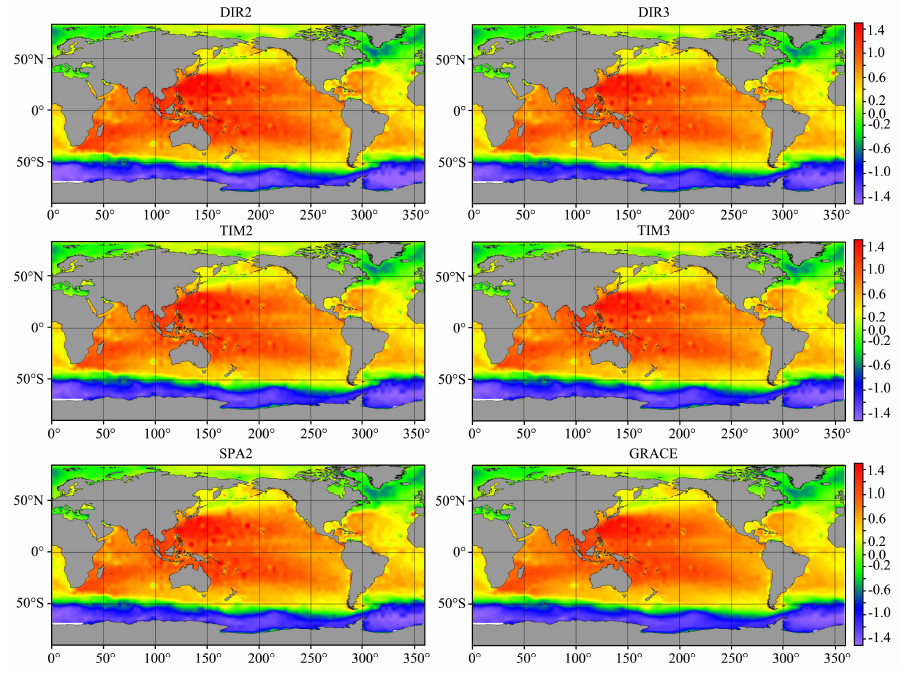
易见,由各模型得到的MDT差异不大,均能反映其大致的轮廓,这主要是由于稳态海面地形的主量由低阶控制[21],而低阶的相对精度往往都很高,因此彼此之间很难有较大差异.由于GOCE卫星的贡献主要在中高阶,为了评估不同GOCE引力场模型之间的差异,现分别给出第二时段直接法、空域法与时域法的对比;也计算了第二、三时段直接法、时域法所得模型的对比,结果如图 2、图 3所示.
|
图 2 第二时段直接法、空域法与时域法模型的对比(单位:m) Fig. 2 Comparisons between DIR2, SPA2 and TIM2 (units:m) |

|
图 3 第二、三时段直接法、时域法各自模型的对比(单位:m) Fig. 3 Comparisons between DIR3 and DIR2, TIM3 and TIM2 (units:m) |
从图 2、图 3易知不同方法所得模型在MDT计算中产生的差异并不大,大部分区域的差异均在2cm以内.需要说明的是,两极比较大,可达10cm,这主要是因为GOCE卫星由于受轨道倾角所限,观测无法覆盖两极地区.在反解模型时,需要添加相应的约束信息,因此两极的差异主要来自约束信息的不同,而并非来自GOCE数据.具体来看,第二组GOCE模型中,直接法与时域法的差大约在-2~2cm之间,空域法也如此,但在更多局部空域法差异稍大,可达±4cm左右,这说明与时域法的差异,空域法比直接法更大;不同时段的对比中,差也基本维持在-2~2cm之间.由于采用的是同样的测高数据,因此这种差异主要反映的是大地水准面的差异,这从侧面反映了GOCE所得解具有较好的稳定性,基本维持在厘米量级内.由于时域法所得模型没有采用先验模型,且考虑到第三组解采用数据时段较长,更能体现GOCE数据的特性,因此在此后对洋流的讨论中,主要采用TIM3模型来进行讨论.
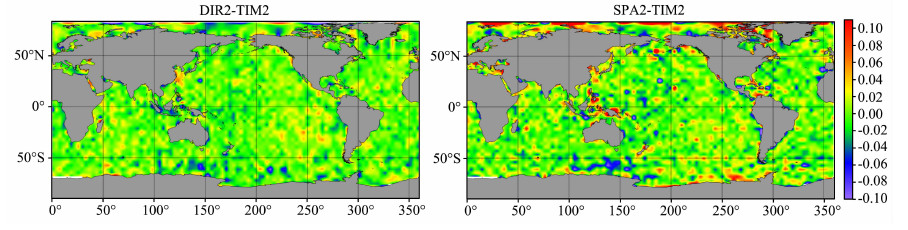
4.2 洋流计算稳态海面地形的主要作用之一是对洋流进行讨论.本节根据公式(2)并在4.1节所得MDT的基础上对洋流进行讨论.图 4给出了分别由GOCE引力位模型TIM3及GRACE引力位模型所得到的全球地转流速度图.
|
图 4 由TIM3及GRACE模型解算的地转流速度图(单位:m/s) Fig. 4 Geostrophic current velocity calculated with TIM3 and GRACE gravity field model (units:m/s) |
需要说明,赤道附近由于f趋近于0,公式(2)存在奇异性等问题[22],GUT无法计算.为了不影响格网平滑的精度,现将赤道附近南北纬3°之间的区域,值取为零.总体来看,两图基本一致,均能反映全球洋流的主要特征,例如:黑潮、墨西哥湾流、阿古拉斯海流等均清晰可见;全球的速度基本位于40cm/ s以内,且大部分区域小于10cm/s,局部区域(如洋流附近)稍大,这些特征与文献[20]的结论一致.这表明结合卫星重力和卫星测高数据能很好地反映洋流的相关特征.另一方面,两图也有差别:
①从各个洋流,如:黑潮、墨西哥湾流、阿古拉斯海流、巴西洋流、南极洲环流等均可发现GOCE所得结果条纹更细更清晰.如位于60°N,314°E的拉布拉多洋流,GRACE所得结果极为模糊,因为该洋流近岸分支宽度仅约100km,GRACE空间分辨率显然不够;
②赤道附近差异显著,一是因为GOCE的空间分辨率更高,展现了更多的高频信号;二是因为GOCE模型的阶数更高,公式(2)由奇异因子产生的累积误差更大;
③在许多区域,GOCE计算结果局部量值比GRACE所得结果稍大,特别是靠近陆地的边界流,如北半球的黑潮和墨西哥湾流等.
为了对比,现从图 4取出离我国较近的黑潮区域(20°N-60°N,120°E-170°W)进行分析,其地转流速度如图 5所示.
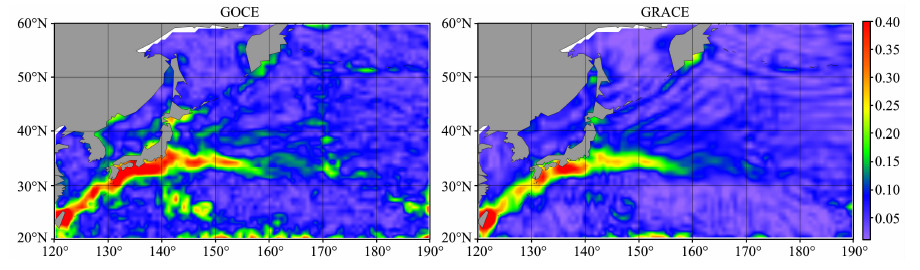
|
图 5 GOCE模型和GRACE模型在黑潮流域解算的地转流速度图(单位:m/s) Fig. 5 Geostrophic current velocity of Kuroshio calculated with GOCE and GRACE gravity field models (units:m/s) |
从该图可知,GOCE和GRACE均可展现黑潮的基本特征,即大致从中国台湾东北部沿着东北方向流向日本,然后大约在35°N,140°E朝东流去,且流速逐渐变弱.整个流域,大约在34°N,135°E的日本南部海域流速达到最大.然而两图差异也较明显:
①GRACE比GOCE更加平滑,GOCE能显示更多的局部特征;
②在中国台湾北端和日本九州之间的区域,GOCE所得洋流速度约35 cm/s左右,这和Knudsen[20]所给值基本一致(37cm/s),而GRACE引力场模型的计算值仅约27cm/s,由此可见,利用GOCE重力场模型解出的洋流速度较GRACE的结果精度更高;
③在东京以东的海域GRACE所得解也明显偏小.
不难发现,墨西哥湾流也有类似差别.而黑潮和墨西哥湾流均从赤道向北极流去,同属于边界流,受地球自转和大陆边界的共同影响,具有速度快、水流窄的特点,该特点的存在对稳态海面地形的空间分辨率提出了更高的要求.因此上述各种差异的根本原因是GOCE提高了大地水准面的空间分辨率,可达80km,而GRACE仅达到125km.
5 结论本文利用最新的GOCE引力场模型,对稳态海面地形及洋流速度进行了计算和讨论.从已有结果来看,GOCE所得不同解具有很好的一致性,差异在厘米量级内,均可用于洋流的解算;与GRACE的对比中,不难发现GOCE已经表现了一定的优越性,根本原因是GRACE模型的空间分辨率不够.同时值得一提的是,GRACE引力场模型是集4.5年数据所得,而GOCE模型最多仅利用了不到1.5年的数据.随着GOCE数据的进一步积累和模型精度的进一步提升,GOCE数据将在海洋学研究中逐步发挥更重要的作用.
致谢感谢欧空局(ESA)提供GOCE数据及GOCE USER Toolbox软件!也感谢两位匿名审稿专家的宝贵意见!
| [1] | Balmino G, Rummel R, Visser P, et al. Gravity Field and Steady-State Ocean Circulation Mission. The Four Candidate Earth Explorer Core Missions, ESA Publications Division, 1999. |
| [2] | Rummel R, Gelderen M V, Koop R, et al. Spherical Harmonic Analysis of Satellite Gradiometry. Netherlands: Delft: Nederlandse Commissie Voor Geodesie, 1993 . |
| [3] | Visser P. Gravity field determination with GOCE and GRACE. Adv. Space Res. , 1999, 23(4): 771-776. DOI:10.1016/S0273-1177(99)00154-4 |
| [4] | Klees R, Koop R, Visser P, et al. Efficient gravity field recovery from GOCE gravity gradient observations. Journal of Geodesy , 2000, 74(7-8): 561-571. DOI:10.1007/s001900000118 |
| [5] | Pail R, Plank G. Assessment of three numerical solution strategies for gravity field recovery from GOCE satellite gravity gradiometry implemented on a parallel platform. Journal of Geodesy , 2002, 76(8): 462-474. DOI:10.1007/s00190-002-0277-2 |
| [6] | Ditmar P, Klees R, Kostenko F. Fast and accurate computation of spherical harmonic coefficients from satellite gravity gradiometry data. Journal of Geodesy , 2003, 76(11/12): 690-705. DOI:10.1007/s00190-002-0298-x |
| [7] | Baur O, Sneeuw N, Grafarend E W. Efficient GOCE satellite gravity field recovery based on least-squares using QR decomposition. Journal of Geodesy , 2008, 82(4/5): 207-221. DOI:10.1007/s00190-007-0178-5 |
| [8] | 罗志才.利用卫星重力梯度数据确定地球重力场的理论和方法[博士论文].武汉:武汉测绘科技大学, 1996. Luo Z C. The theory and methodology for determining the Earth's gravity field using satellite gravity gradiometry data [Ph. D. thesis](in Chinese). Wuhan: Wuhan Technical University of Surveying and Mapping, 1996. |
| [9] | 于锦海, 赵东明. 引力梯度不变量与相关边界条件. 中国科学D辑:地球科学 , 2010, 53(5): 781–790. Yu J H, Zhao D M. The gravitational gradient tensor's invariants and the related boundary conditions. Sci. China Ser. D-Earth Sci. (in Chinese) , 2010, 53(5): 781-790. DOI:10.1007/s11430-010-0014-2 |
| [10] | 徐新禹.卫星重力梯度及卫星跟踪卫星数据确定地球重力场的研究[博士论文].武汉:武汉大学, 2008. Xu X Y. Study of determing the Earth's gravity field from satellite gravity gradient and satellite-to-satellite tracking data [Ph. D. thesis](in Chinese). Wuhan: Wuhan University, 2008. |
| [11] | 钟波.基于GOCE卫星重力测量技术确定地球重力场的研究[博士论文].武汉:武汉大学, 2010. Zhong B. Study on the determination of the Earth's gravity field from satellite gravimetry mission GOCE [Ph. D. thesis](in Chinese). Wuhan: Wuhan University, 2010. |
| [12] | Pail R, Bruinsma S, Migliaccio F, et al. First GOCE gravity field models derived by three different approaches. Journal of Geodesy , 2011, 85(11): 819-843. DOI:10.1007/s00190-011-0467-x |
| [13] | LeGrand P, Minster J F. Impact of the GOCE gravity mission on ocean circulation estimates. Geophysical Research Letters , 1999, 26(13): 1881-1884. DOI:10.1029/1999GL900440 |
| [14] | LeGrand P. Impact of the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE) mission on ocean circulation estimates 1.Volume fluxes in a climatological inverse model of the Atlantic. Journal of Geophysical Research-Oceans , 2001, 106(C9): 19597-19610. DOI:10.1029/2000JC000556 |
| [15] | Schroter J, Losch M, Sloyan B. Impact of the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE) mission on ocean circulation estimates 2.Volume and heat fluxes across hydrographic sections of unequally spaced stations. Journal of Geophysical Research-Oceans , 2002, 107(C2): 4-1. |
| [16] | Vossepoel F C. Uncertainties in the mean ocean dynamic topography before the launch of the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE). Journal of Geophysical Research-Oceans , 2007, 112(C5). DOI:10.1029/2006JC003891 |
| [17] | Bingham R J, Knudsen P, Pail P. An initial estimate of the North Atlantic steady-state geostrophic circulation from GOCE. Geophysical Research Letters , 2011, 38(1). DOI:10.1029/2010GL045633 |
| [18] | Haines K, Johannessen J A, Knudsen P, et al. An ocean modelling and assimilation guide to using GOCE geoid products. Ocean Science , 2011, 7(1): 151-164. DOI:10.5194/os-7-151-2011 |
| [19] | Janjić T, Schroter J, Savcenko R, et al. Impact of combining GRACE and GOCE gravity data on ocean circulation estimates. Ocean Science Discussions , 2011, 8(3): 1535-1573. DOI:10.5194/osd-8-1535-2011 |
| [20] | Knudsen P, Bingham R, Andersen O, et al. A global mean dynamic topography and ocean circulation estimation using a preliminary GOCE gravity model. Journal of Geodesy , 2011, 85(11): 861-879. DOI:10.1007/s00190-011-0485-8 |
| [21] | 张子占, 陆洋. GRACE卫星资料确定的稳态海面地形及其谱特征. 中国科学D辑:地球科学 , 2007, 37(6): 753–760. Zhang Z Z, Lu Y. Spectral analysis of quasi-stationary sea surface topography from GRACE mission. Sci. China Ser. D-Earth Sci. (in Chinese) , 2007, 37(6): 753-760. |
| [22] | 张子占, 陆洋, 许厚泽. 利用卫星测量技术和小波滤波方法探测表层地转流. 中国科学D辑:地球科学 , 2007, 37(6): 753–760. Zhang Z Z, Lu Y, Xu H Z. Detection of surface geostrophic current with technique of satellite measurement and method of wavelet filtering. Sci. China Ser. D-Earth Sci. (in Chinese) , 2007, 37(6): 753-760. |
| [23] | 王正涛, 党亚民, 姜卫平, 等. 联合卫星重力和卫星测高数据确定稳态海洋动力地形. 测绘科学 , 2006, 31(6): 40–42. Wang Z T, Dang Y M, Jiang W P, et al. Combining altimeter and gravity satellite to compute quasi-stable dynamic ocean topography. Science of Surveying and Mapping (in Chinese) , 2006, 31(6): 40-42. |
| [24] | Rio M H. GUT Tutorial Version 6.2, ESA, 2011. |
| [25] | 于锦海, 万晓云. 引力梯度归算的模拟计算. 地球物理学报 , 2011, 54(5): 1182–1186. Yu J H, Wan X Y. Reduction for gradiometry and corresponding imitation. Chinese J. Geophys. (in Chinese) , 2011, 54(5): 1182-1186. |
| [26] | 万晓云, 于锦海, 曾艳艳. GOCE引力梯度的频谱分析及滤波. 地球物理学报 , 2012, 55(9): 2909–2916. Wan X Y, Yu J H, Zeng Y Y. Frequency analysis and filtering processing of gravity gradients data from GOCE. Chinese J. Geophys. (in Chinese) , 2012, 55(9): 2909-2916. DOI:10.6038/j.issn.0001-5733.2012.09.010 |
 2013, Vol. 56
2013, Vol. 56

