重力数据反演是根据地面或空中观测数据求取地球内部物质分布或者异常源形态结构的方法.随着密度差解释模型的发展,可从重力数据中提取的有效信息量显著增加,因此重力数据反演成为定量解释中必不可少的重要环节.重力场只在地球表面是已知数据,在地面以下有多种等效的密度分布可产生与地面观测数据相同的已知场.所以如果想通过反演从地球物理数据求得太多信息,它的解就是不适定的,这是由基于位场的任何地球物理反演方法固有的不稳定性和不唯一性造成的.
引入异常源的先验信息是将不适定问题转换为适定问题的有效途径.在反问题中有两类不同的反演方法.第一类是当我们有足够的关于异常源形状、走向分布、密度差随深度的变换规律或者密度差确切值等先验信息时,可利用这些先验信息作为相对或者绝对约束反演重力数据[1-8].第二类是如果我们的先验信息不足,在最小化信息的情况下反演异常源的地下信息成为前人研究的重要分支.比如将先验信息以一个或者多个近似权函数的形式加入到算法中,通过最小化由模型目标函数和拟合数据误差构成的全体目标函数的方式获得反演结果,结合磁法数据反演并用相似的深度加权函数约束密度随深度变化的程序来处理近地面的质量集中[9-10];也可以在考虑核函数内部固有约束和外加约束前提下,通过随机子域方法在信息最小化条件下尽可能的减少计算所需存储空间,获得良好的反演结果[11-12];或者通过计算位场数据与地下各点在测区的位场数据的归一化之间的相关性,显示地下物性分布特点[13-14];再者基于非线性共轭梯度算法理论提出加权重力梯度反演方法,约束密度上下限的强制转换函数的引入,对于获得有物理和地球物理意义的解起到重要作用[15].
重力数据三维反演的病态性主要表现是其敏感矩阵的不稳定性,观测数据中的微小误差可使反演结果严重偏离真解,Tikhonov指出可在反演过程加入正则参数,对初始的反演方程进行微调,从而达到稳定反演解的目的[16-18],因此,Tikhonov正则化方法在改变位场反问题的病态性方面效果显著.本文在密度差解释模型基础上继续进行最小化先验信息情况下的三维加权反演的研究.Tikhonov正则化方法的正则参数选择和使用在解决非自共轭情况下不适定问题解的同时,也给近似解引进了新的误差[16-19].Hamarik等提出的Extrapolation Tikhonov正则化方法作为一个提高近似方法精度的工具是将不同的正则参数值对应的不同近似解通过线性结合的方式获得最终的近似解,因正则参数的使用使得解在误差扩大方面受到限制[20-21].本文第一部分研究用Extrapolation Tikhonov正则化方法解决反演中解的不唯一性和不稳定性问题,详细分析和讨论了如何利用三种后验的Extrapolation Tikhonov正则化参数的选择规则综合选择适合的正则参数以提高反演结果的精度.第二部分在反演过程中用改进后的深度加权函数作用于核函数以有效的抵消随深度增加核函数迅速衰减对反演结果产生的负面影响,模型试验表明,改进后的深度加权函数与原方法相比,改善了异常体底部密度分布存在的发散问题,对于埋深较深的异常体密度分布特征具有很好的反演效果.本文的第三部分引用上下限约束,用强制转换函数将平滑约束引进到反演中,将超出物理意义和地球物理意义范围的反演参数限制在解释者可接受的范围内,从而有效的限制了反演结果中物性分布的数值范围.
2 基于Extrapolation Tikhonov正则化方法的重力反演理论 2.1 重力数据三维反演理论本文将包含异常源的地下区域离散为多行列的并列单元立方体构成的网格状区域,每个具有特定尺寸的立方体单元网格被视为一个密度单元.这些密度单元是重力数据三维反演在右手坐标系中的待估计参数.设地下任一立方体单元网格中心坐标为(x′,y′,z′),x轴和y轴为水平面内方向相互垂直的两个坐标轴,z轴垂直与水平面指向地下.在观测点r=(x,y,z)处,单个立方体网格单元产生的万有引力积分形式[22]为

|
(1) |
式中γ是牛顿万有引力常量,ρ(r′)是异常体中r′=(x′,y′,z′)处的单元网格立方体的密度差分布,g(r)是测点距离异常源为r的万有引力.无限小体积dV′=dx′dy′dz′的万有引力垂直分量即重力异常用gz(r)表示,(1)式变成
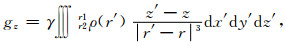
|
(2) |
(2)式的积分形式可以表示为如下的离散形式:
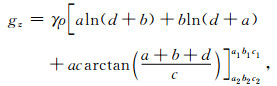
|
(3) |
式中d=|r′-r|是观测点到离散网格单元的距离,且a=x′-x,b=y′-y,c=z′-z.
重力异常可视为离散网格单元密度值ρ与常量核函数A的乘积,因此,(3)式的紧致形式为
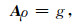
|
(4) |
其中A∈RM×N是核函数矩阵,ρ∈RN是地下物性分布向量,g∈RM是地面观测重力异常.M和N分别代表测量区域的观测异常数据数量和测量区域的网格单元数量.
2.2 基于Extrapolation Tikhonov正则化方法的物性反演公式(4)中核函数A中有一定数量的含有不同阶次的无限接近零的奇异值,因此核函数矩阵A的逆不存在.为了解决这个问题,前人曾使用过拟广义逆[23]、神经网络[24]等多种优化方法.本文利用基于原正则化近似方法的Extrapolation Tikhonov正则化方法反演重力数据[20-21].在正则化方法中假设含有噪声的重力数据gδ可代替精确重力数据g,且该噪声数据满足误差标准‖gδ-g‖≤δ,其中δ为解释人员设置的拟合误差标准,那么反演密度的近似值ρ在非自共轭的情况下可用Tikhonov正则化方法ρα(αI+A*A)-1=A*gδ求得,其中正则化参数α>0,I是与A*A维数相同的单位矩阵.为了减少因正则化参数的加入而扩展的反演误差,Hamarik等提出用拉格朗日插值方法将用不同的正则化参数获得的正则近似解经线性结合获得想要的近似解,即Extrapolation Tikhonov正则化方法.
我们设ραi,i=1,2,…,n是根据不同的正则化参数αi-1=αi/q(q>1)计算获得的密度正则近似解,其中q是用来产生一系列正则化参数的比例常数,其值的大小决定了产生的正则化参数序列收敛的快慢;与上述各参数相应的计算密度差的Extrapolation Tikhonov正则化公式ρn,α可表示为:
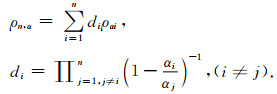
|
(5) |
基于Extrapolation Tikhonov正则化方法的重力三维反演,参数αi和n的选择直接影响着病态线性反演结果的好坏,也直接关系到近似解与精确解之间的近似程度.一般情况下我们先确定αi和n中的一个,另外一个成为要求的正则化参数.本文中先确定一组α1,α2,…,αN,N为已知的常数,然后根据拟合误差水平确定α,进一步确定参数n(1≤n≤N).本文选取离散原则、单调误差原则和平衡原则(见附录A)来确定参数序列中满足先验误差水平的正则化参数α和n,并分析由上述选择方法获得的参数值计算的Tikhonov正则近似解及拟合误差,同时计算相应的Extrapolation Tikhonov正则近似解及拟合误差,经数值分析证明后者在相同的拟合误差水平下能够获得更为精确的反演结果.若设定相同的误差标准,新方法与原方法相比,根据所使用的数值模型不同,拟合精度可提高1到5个数量级不等.
在Extrapolation Tikhonov正则参数计算中,本文设αn=0.95,αi-1=αi/q(q>1),n=500,q分别取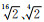
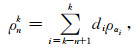
|
(6) |
(6)式中di同(5)式,此处的n值为外推总项数,经数值试算表明n可取2~10的任意常数,k=1,2,…,n,此处的k值为附录A中的n值,确定方法详见附录A.
2.3 改进的深度加权函数在重力数据三维反演中,核函数随深度增加而自然衰减的特点使反演获得的密度分布具有明显的趋肤效应,这种情况下获得的密度分布与真实异常源的密度分布相背.为了抵消这种衰减,前人讨论了多种适用于重磁数据反演的深度加权方法[9-10, 15].在重力数据反演及重力梯度反演中,这些方法分别用深度加权函数直接作用于核函数或者通过再加权抵消核函数随深度自然衰减,消除其近地表权重过大而使反演密度分布不符合真实异常源的情况.本文使用的加权函数由Commer提出的深度加权函数发展而来,Commer的深度加权函数适用于重力梯度三维反演,其表达式为[15]

|
(7) |
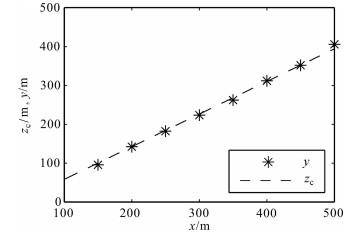
式中θ=0.001(由Commer给出)或者其它很小的值,它的大小直接决定近地表顶层压制作用的大小,其值越小压制作用越大,反演结果越集中,反之亦然.d=Lz,即离散区域垂直深度值,若模型顶部和底部深度已知,在Commer的函数中zc=(z1+z2)/2是一个设定的常数,其中z1和z2是异常源顶部和底部埋深值.为了获得适合重力数据三维反演的深度加权函数,我们做了大量的实验来研究(7)式中各参数与ρ之间的关系.通过单个立方体模型的实验我们获得一系列关于zc与异常体平均深度的数值关系,见图 1.图 1中x是模型的平均深度值,y是zc随x变化能获得好的反演结果时的值.由图 1可见,这两个参数之间存在着如下线性关系,因此,适应于重力数据三维反演的深度加权函数可表示为如下形式:
|
图 1 参数zc与平均深度之间的线性关系图 Fig. 1 The linear relation ship between zc and mean depth |

|
(8) |
式中α的范围是0.8~0.9,β的范围是24~26.上述数据是根据大量模型试验反演拟合初始模型在获得好的效果时所得,若核函数为A,深度加权函数按照设定的尺寸网格化参数获得离散值,再作用于核函数并参与反演过程即可.当应用于实测重力数据时,根据已知地质或者地球物理信息给出异常体的中心埋深,先将数据做位场分离,然后用上述方法反演局部重力异常场数据,即可获得异常体形态和分布特征等信息.
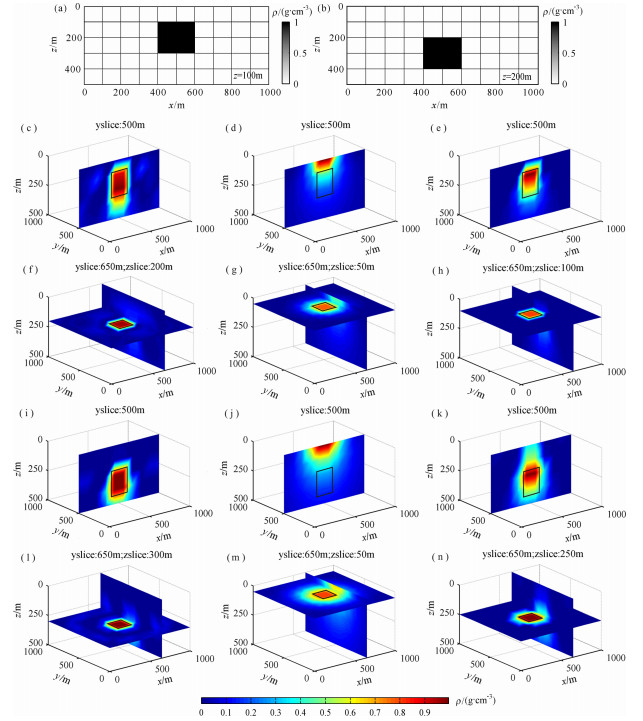
本文理论模型纵向切面图如图 2a和2b所示,立方体尺寸为200m×200m×200m,x和y坐标范围分别是:(400,600)和(400,600),测区范围是1000m×1000m.异常体的密度值为1g/cm3,背景场密度值为0g/cm3.图中黑色代表异常体模型纵切面分布特征.图 2c-2n是图 2a和2b在不同深度加权作用下的反演结果切面图,图中黑色线框代表异常体实际所在位置.由图 2可见,对于埋深不同的异常体,在改进后的深度加权函数作用下,反演结果的横向和纵向分辨率都比较理想(见图 2(c,f,i,l)),与之相比如果不做深度加权处理,反演密度分布都集中在地表面附近,其纵向分辨率非常差(见图 2(d,g,j,m)),趋肤效应十分严重,当Commer的深度加权函数应用到反演中时(见图 2(e,h,k,n)),对于埋深较浅的异常体,反演结果的横向分辨率较好,异常体顶部位置的确定较为准确,异常体底部密度分布形态失真,对于埋深较深的异常体,其反演结果明显高于实际异常体所在位置,反演结果发散较严重.
|
图 2 不同深度的单个立方体模型在不同的深度加权作用下的反演结果切面图 (a)顶部埋深100m的立方体模型;(b)顶部埋深200m的立方体模型.(c-n)中黑色边界范围代表正演模型所在位置.(c-e)是图(a)分别在本文改进的深度加权、未加权及Commer的深度加权作用下获得的反演结果纵切面图;图(f-h)是(a)在上述深度加权顺序作用下获得的反演结果横切面图;图(i-k)是(b)在上述深度加权顺序作用下获得的反演结果纵切面图;图(l-n)是(b)在上述深度加权顺序作用下获得的反演结果横切面图. Fig. 2 The inversion density distribution on different depth weighting slices of the single cube model at different depths (a) Single model with the upper depth 100m. (b) Single model with the upper depth 200m. The black boundariesin (c)-(n) represent the location of the forward model. (c)-(e) are the inversion solutions displayed in vertical slices corresponding to (a) and worked by the improved depth weighting function in this paper, unweighting and Commer′s depth weighting function, respectively. (f)-(h) are the inversion solutions displayed in horizontal slices corresponding to (a); (i)-(k) are the inversion solutions displayed in vertical slices corresponding to (b). (l)-(n) are the inversion solutions displayed in horizontal slices corresponding to (b). |
地球物理反问题解的不唯一和不稳定性导致反演过程中不符合实际的模型计算的响应与观测数据的拟合差与观测数据和由真正的模型计算的响应的拟合差相一致.因此约束的使用对于减少解的奇异性起到至关重要的作用,我们可使用通过不同方式得到的先验信息约束反演结果.在重力数据反演中,早期通过固定上下限的方法将密度值限制在一定的区域内,后来发展了强制密度差为正的方法约束反演结果,本文使用的上下限约束是较小程度的限制解的约束方法之一.反演结果中不具有物理意义的负的或者不真实的过高密度值可以通过上下限约束函数转换到合理的值域中.Kim等通过对数约束实现了将电导率值限制在合理的值域范围内[25].那么如果我们获得了关于密度范围的信息,在反演中可用上下边界约束处理反演结果,处理后极少数不具有物理意义的结果再用强制为正的方法加以约束.Cardarelli等将对数转换方法成功地应用于电阻率层析成像中[26].除了对数转换,Commer等引进了反双曲正切转换将电导率参数限制在一个转换空间的无界区域[27].这说明这种转换函数在限制电导率可能发生的无界反演的结构边界方面很有意义.本文中我们使用的上下限约束函数[27]表示为:
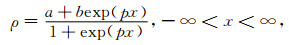
|
(9) |
式中a和b分别为强制边界约束的上下限,通过公式(9)可将反演密度中不具有地球物理意义的密度值限制在由先验信息确定的有意义的密度分布范围内.函数中参数p控制着转换区域中x=0处的值的转换结果,此时方程变为ρ=(a+b)/2.如图 3a所示,不同的p值,对边界约束的结果是有差异的,其值越大,则由x向ρ转换的函数越陡峭,也就是说在x=0附近很快达到ρ的上下限;反之,转换函数的曲线则较缓,在x=0周围更大的数值区域内才可达到ρ的上下限.参数p值相同的情况下,虽然不同的上下限对应的转换空间的值不同,转换函数的陡峭程度也不同,如图 3b所示,但是能在相同的x的值域内达到ρ的上下限,本文中p值取-1.2~1.4之间可使反演结果较合理的转换到符合地球物理意义的数值范围内.在处理实测数据时,将反演结果视为(9)式中的x,通过该式实现反演数据的上下限约束.

|
图 3 上下限约束函数中参数变化对转换空间值的影响 (a)不同的p值的数据转换特征;(b)同p值时不同上下限的数据转换特征. Fig. 3 Influence of the change of the parameter on the transform space in the upperand lower function (a) The characteristic of transform values with different p. (b) The characteristic of transform values of different upper and lower functions with the same p. |
下面使用与前期作者(李耀国,姚长利等)相似的岩脉组合模型验证基于Extrapolation Tikhonov正则化方法的重力数据3D反演方法的有效性[10-11].本文测区为一1000m×1000m的正方形区域,由10×10个数据点构成,点线距均为100m.网格化地下由10×10×5个网格单元构成,每个单元的尺寸为100m×100m×100m.
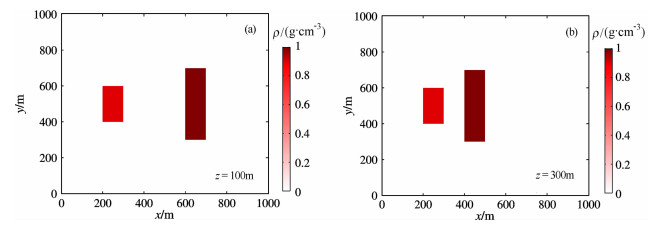
地下正演模型如图 4及图 5所示,模型由两个高密度体构成,左侧为一直立棱柱体,两个角点的坐标分别为(200,400,100)和(300,600,300),密度差为0.9g/cm3;右侧为倾角是45°倾斜岩脉,上顶埋深为100m,底部埋深为400m,上顶两对角角点坐标为(600,300)和(700,700),底部两对角角点坐标为(320,300)和(420,700),密度差为1g/cm3.图 4a所示为y=500m处的垂直切面,上面对应的是由该切面处模型体产生的剖面重力异常曲线,异常值单位为mGal;图 4b所示为由上述组合模型产生的原始异常等值线图.图中最大值与图 4a中剖面曲线的最大值一致.组合模型在z=100m及z=300m处的横截面示意图如图 5a和5b所示.

|
图 4 组合模型纵向剖面形态和异常曲线以及异常等值线平面图 Fig. 4 The morphology of vertical profile, the anomaly curve and the contours |
|
图 5 组合模型不同横截面示意图 (a)z=100m;(b)z=300m. Fig. 5 Synthetic model at different depths (a) z=100m; (b)z=300m. |
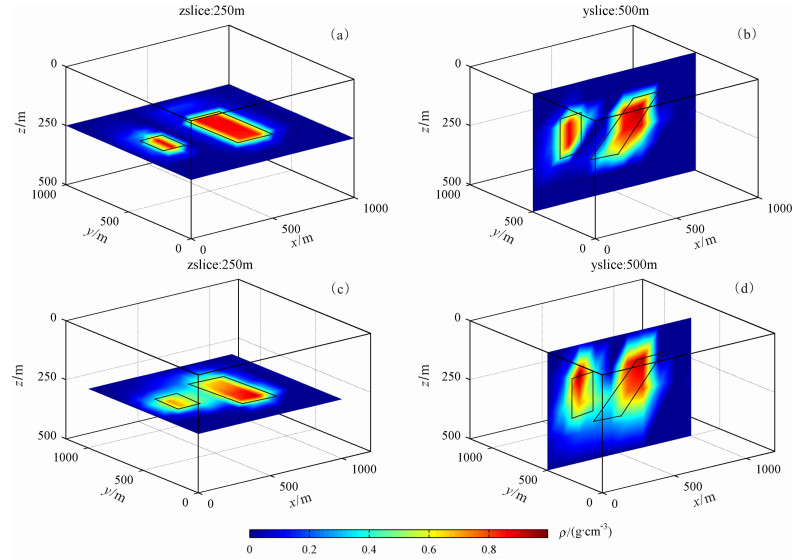
反演时,在模型原始异常中加入3%的高斯噪声,反演的密度分布在不同切面处的分布特点如图 6所示,图 6(a,b)是基于Extrapolation Tikhonov正则化方法反演的密度分布图,图 6(c,d)是基于Tikhonov正则化方法反演的密度分布图,黑色框所圈定的范围是正演组合模型体所在位置及分布范围,图 6(b,d)为y=500m处的切面图,由图中结果可看出,利用本文的正则化方法反演的异常位置及分布区域与模型中异常源的分布特征基本相符,图 6b较图 6d能够更加准确的给出正演模型体的位置,图 6d的反演结果显示,埋深较深的反演密度更发散.图 6(a,c)为z=250m处的切面图,两图都可较准确的给出模型体所在位置,但是图 6c两个相邻的模型体边界划分较图 6a更模糊,因此其反演效果较本文中的方法差.图 6所示的反演结果表明,与原正则化方法相比,新方法能将异常体在不同切面处的密度分布准确的呈现,与图 4及图 5所示的模型异常源的位置,倾向及区域范围吻合较好,两种方法的反演结果比模型体略分散一点,新旧正则化方法反演的密度的最大值分别较模型密度大0.06g/cm3和0.052g/cm3.反演时在不同的误差水平下由原正则化方法及Extrapolation Tikhonov正则化方法计算出的拟合误差如表 1所示,由此可见Extrapolation Tikhonov正则化方法在与原方法耗时几乎相同的情况下,显著减小反演密度分布计算的预测数据与观测数据之间的拟合误差,计算中n取5,q取2,迭代次数最小为12次,最大为27次.
|
图 6 反演密度在不同切面处的数值分布 (a)-(b)是基于Extrapolation正则化方法的反演切面图;(c)-(d)是基于Tikhonov正则化方法的反演切面图. Fig. 6 The recovered density distribution at different slices (a)-(b) the slice of the inversion results based on the Extrapolation regularization method; (c)-(d) the slice of the inversion results based on the Tikhonov regularization method. |
|
|
表 1 Tikhonov正则化方法与Extrapolation Tikhonov正则化方法在不同误差下的拟合误差 Table 1 The calculated errors with different error levels given by Tikhonov Regularization method and Extrapolation Tikhonov Regularization method |
(1) 将基于拉格朗日插值方法的Extrapolation Tikhonov正则化方法应用于重力数据的三维反演,深入讨论三种选择两个正则化参数的原则,详细计算分析数值.依据这些数值分析结果再结合三种参数选择方法,确定最终反演所需的正则化参数.该方法的引入很大程度上减小了因正则化参数的引入而在反演结果中介入的新的误差,进一步提高了反演拟合误差的精度.
(2) 改进后的深度加权函数更适宜重力数据的三维反演.在详细分析函数中各参数对趋肤效应的作用后,给出了参数合理的取值范围.该函数对消除核函数随深度增加快速衰减的自然属性起到有效的控制作用,进一步增强了对近地表的物性分布过度集中的压制效果,与未加权的反演方法及前人的反演方法相比,在反演异常体底部密度分布方面具有更大的优势.
(3) 本文引进了上下限约束函数,深入讨论了函数中参数选择与设定的量化细节,对反演具有重要意义,且该函数将不具有地球物理意义的反演结果转化到合理而有地球物理意义的数据范围内,给进一步的解释工作带来方便.
(4) 通过多组模型反演计算及结果比对,证明基于Extrapolation Tikhonov正则化方法的反演方法较基于原Tikhonov正则化方法的反演方法能够更准确的反演出异常体所在位置及密度分布特征,在计算时间几乎不变的情况下,减小了观测数据与预测数据的拟合误差.
附录A Extrapolation Tikhonov正则化参数的选择方法附录详细论述Extrapolation Tikhonov正则化方法三个参数选择原则,以用于选择适当的正则化参数[20-21].
1 分别使用三个原则选择正则化参数αD、αME以及αL和nD、nME以及nI的方法 1.1 基于离散原则的参数选择方法解释人员给定误差标准δ后,在αi序列中第一个满足Aραi-g<δ的αD即为所选第一个参数值,该参数所对应的k=iD为第二个参数值nD.
1.2 基于单调误差原则的参数选择方法αi序列中第一个满足下式的αME即为所求第一个参数值:
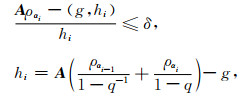
|
当αME确定后,再进一步确定k值.设ρn,α=A*wi,i=1,2,…,是Aρ=g的近似解序列.iME是第一个使(A1)式成立的序列号:
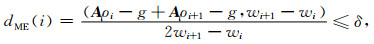
|
(A1) |
若(A1)式成立,则有ρi-ρ≤ρi-1-ρ,i=2,…,iME,因此,在用单调误差选择第一个参数后,满足(A1)式的k=iME为Extrapolation Tikhonov正则近似解ρnME的第二个参数值nME.
1.3 基于平衡原则的参数选择方法
αi序列中使得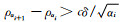
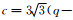
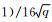
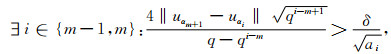
|
(A2) |
Extrapolation Tikhonov正则近似解在满足上述参数选择原则的基础上还要满足不等式(A3).设rn=Aρn,α-fδ,C为大于1的常数.函数dD(n)=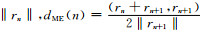
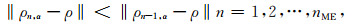
|
(A3) |
并且衰减无限序列α1,α2,…,满足下列条件:
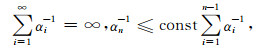
|
(A4) |
则项数n∈{nD,nME}能保证使‖ρn,α-ρ‖趋近于0,即如果(A3)式成立,我们认为ρn,α比ρn-1,α更精确,此时的解为所求近似解,n取nD和nME中较大的值作为第二个参数值,用同样的方法可从已选择出的n值及nI中确定最后的参数值.
| [1] | Blakely R J. Potential Theory in Gravity and Magnetic Applications. Cambridge:Cambridge University Press, 1995. http://journals.cambridge.org/action/displayAbstract?aid=4387744 |
| [2] | Last B J, Kubik K. Compact gravity inversion. Geophysics , 1983, 48(6): 713-721. DOI:10.1190/1.1441501 |
| [3] | Guillen A, Menichetti V. Gravity and magnetic inversion with minimization of a specific functional. Geophysics , 1984, 49(8): 1354-1360. DOI:10.1190/1.1441761 |
| [4] | Barbosa V C F, Silva J B C. Generalized compact gravity inversion. Geophysics , 1994, 59(1): 57-68. DOI:10.1190/1.1443534 |
| [5] | Medeiros W E, Silva J B C. Geophysical inversion using approximate equality constraints. Geophysics , 1996, 61(6): 1678-1688. DOI:10.1190/1.1444086 |
| [6] | 陈石, 王谦身, 卢红艳, 等. 三维重力反演新方法--调和密度成像理论与模型测试. 地球物理学进展 , 2010, 25(6): 1917–1925. Chen S, Wang Q S, Lu H Y, et al. A new method of gravity inversion-theory and model test of harmonic density imaging. Progress in Geophysics (in Chinese) , 2010, 25(6): 1917-1925. |
| [7] | 柯小平, 王勇, 许厚泽, 等. 青藏高原地壳三维密度结构的重力反演. 地球物理学进展 , 2009, 24(2): 448–455. Ke S P, Wang Y, Xu H Z, et al. The three-dimensional crustal density structure of the Tibetan plateau from gravity inversion. Progress in Geophysics (in Chinese) , 2009, 24(2): 448-455. |
| [8] | 柯小平, 王勇, 许厚泽. 基于变密度模型的位场界面反演. 地球物理学进展 , 2006, 21(3): 825–829. Ke S P, Wang Y, Xu H Z. Interface depths inversion of potential field data with variable density model. Progress in Geophysics (in Chinese) , 2006, 21(3): 825-829. |
| [9] | Li Y G, Oldenburg D W. 3-D inversion of magnetic data. Geophysics , 1996, 61(2): 394-408. DOI:10.1190/1.1443968 |
| [10] | Li Y G, Oldenburg D W. 3-D inversion of gravity data. Geophysics , 1998, 63(1): 109-119. DOI:10.1190/1.1444302 |
| [11] | 姚长利, 郑元满, 张聿文. 重磁异常三维物性反演随机子域法方法技术. 地球物理学报 , 2007, 50(5): 1576–1583. Yao C L, Zheng Y M, Zhang Y W. 3D gravity and magnetic inversion for physical properties using stochastic subspaces. Chinese J. Geophys. (in Chinese) , 2007, 50(5): 1576-1583. |
| [12] | 姚长利, 郝天珧, 管志宁, 等. 重磁遗传算法三维反演中高速计算及有效存储方法技术. 地球物理学报 , 2003, 46(2): 252–258. Yao C L, Hao T Y, Guan Z N, et al. High-speed computation and efficient storage in 3-D gravity and magnetic inversion based on genetic algorithms. Chinese J. Geophys. (in Chinese) , 2003, 46(2): 252-258. |
| [13] | 郭良辉, 孟小红, 石磊, 等. 重力和重力梯度数据三维相关成像. 地球物理学报 , 2009, 52(4): 1092–1106. Guo L H, Meng X H, Shi L, et al. 3-D correlation imaging for gravity and gravity gradiometry data. Chinese J. Geophys. (in Chinese) , 2009, 52(4): 1092-1106. |
| [14] | 孟小红, 刘国峰, 陈召曦, 等. 基于剩余异常相关成像的重磁物性反演方法. 地球物理学报 , 2012, 55(1): 304–309. Meng X H, Liu G F, Chen Z X, et al. 3-D gravity and magnetic inversion for physical properties based on residual anomaly correlation. Chinese J. Geophys. (in Chinese) , 2012, 55(1): 304-309. |
| [15] | Commer M. Three-dimensional gravity modelling and focusing inversion using rectangular meshes. Geophysical Prospecting , 2011, 59(5): 966-979. |
| [16] | Tikhonov A N, Arsenin V Y. Solution of Ill-Posed Problems. New York:V. H. Winston & Sons, 1977. |
| [17] | Tikhonov A N. Regularization of Ill-Posed Problems. Doklady Akad. Nauk, SSSR , 1963, 153: 49-52. |
| [18] | Zhdanov M S. Geophysical Inverse Theory and Regularization Problems. New York:Elsevier Science, 2002. |
| [19] | Lawson C J, Hanson R J. Solving Least Squares Problems. Englewood Cliffs:Prentice-Hall Inc, 1974. |
| [20] | Hämarik U, Palm R, Raus T. Extrapolation of Tikhonov and Lavrentiev regularization methods. Journal of Physics:Conference Series , 2008, 135(1): 1-8. |
| [21] | Hämarik U, Palm R, Raus T. Use of extrapolation in regularization methods. Journal of Inverse and Ill-Posed Problems , 2007, 15(3): 277-294. DOI:10.1515/jiip.2007.015 |
| [22] | Zhdanov M S. Integral Transforms in Geophysics. New York:Springer Verlag, 1988. |
| [23] | 刘天佑, 管志宁. 对二维磁异常利用广义逆矩阵的选择法. 地球物理学报 , 1986, 29(4): 390–398. Liu T Z, Guan Z N. Selective method of generalized inverse matrix for the interpretation of two-dimensional magnetic anomalies. Chinese J. Geophys. (in Chinese) , 1986, 29(4): 390-398. |
| [24] | 管志宁, 侯俊胜, 黄临平, 等. 重磁异常反演的拟BP神经网络方法及其应用. 地球物理学报 , 1998, 41(2): 242–251. Guan Z N, Hou J S, Huang L P, et al. Inversion of gravity and magnetic anomalies using pseduo-BP neural network method and its application. Chinese J. Geophys. (in Chinese) , 1998, 41(2): 242-251. |
| [25] | Kim H J, Song Y, Lee K H. Inequality constraint in least-squared inversion of geophysical data. Earth Planets Space , 1999, 51: 255-259. DOI:10.1186/BF03352229 |
| [26] | Cardarelli E, Fischanger F. 2D data modelling by electrical resistivity tomography for complex subsurface geology. Geophysical Prospecting , 2006, 54(2): 121-133. DOI:10.1111/gpr.2006.54.issue-2 |
| [27] | Commer M, Newman G A. New advances in three-dimensional controlled-source electromagnetic inversion. Geophysical Journal International , 2008, 172(2): 513-535. DOI:10.1111/gji.2008.172.issue-2 |
 2013, Vol. 56
2013, Vol. 56


