随着地震勘探对保幅成像及叠前反演的关注, 地震波入射角已成为地震偏移和照明分析所利用的重要信息.只有准确获得入射地震波与界面法线的夹角, 才能利用Zoeppritz方程进行泊松比等叠前反演处理, 获得储层的岩石物理参数[1]; 在观测系统设计中, 只有在目的层获得均匀、宽广的入射角覆盖, 才能实现观测系统设计的目标[2-3].实际上, 偏移距只是反映入射角的一个间接指标; 因此近年来, 生成角道集的偏移[4-5]以及基于角道集的速度拾取[6]、叠前反演[7]已成为叠前偏移研究的重要方向.
理论上, 地震波入射角作为射线追踪算法的副产品, 可在射线追踪的过程中得到, 射线理论也表明地震波走时的梯度反映了地震波入射角度[8].但在实际地震资料处理中, 并不能直接应用这类方法求得地震波入射角度.一个重要的原因是地震偏移总是使用一个近似的速度模型, 这个模型仅在较地震波主频更低的尺度上近似实际的速度模型.就地震波走时而言, 速度模型的不同近似(平滑)产生的走时误差几乎可以忽略; 由于入射角对应走时的空间导数, 速度模型的不同近似(平滑)却明显改变了地震波入射角, 这使得复杂构造情况下难以准确确定入射角度.出现这一问题的原因是由于射线理论对应着高频解, 而高频解的波前面入射角对速度变化就是很敏感, 因此不能简单地用高频解的入射角替代实际频带地震波的入射角.为此, 必须发展与实际地震资料频带相匹配的地震波入射角计算方法.
本文计算地震波入射角方法主要服务于叠前偏移与照明分析.一个重要的应用是波动方程偏移中合成角道集进而为岩性反演提供高质量的道集数据.为与波动偏移方法相匹配, 本文发展了基于单程波的入射角计算方法.由于单程波算子可考虑地震波的频带, 其传播特性对偏移速度模型不是很敏感, 因此可避免射线理论产生的诸多问题.应用单程波算子计算入射角的关键是其计算效率, 这是该方法能否在实际地震成像中得到应用的关键.为此本文发展了基于单程波算子(地震波主频)简谐波场的入射角计算方法.该方法通过利用空间导数与波数的对应关系, 由单频震源的脉冲响应求得全场的地震波入射角度; 其所需计算量与叠前偏移的全频带波场延拓相比, 几乎可以忽略.
本文方法使用与偏移计算完全相同的偏移速度模型和单程波算子, 因此得到的角度更真实地反映了震源波前面或反射波波前面的入射角度.该方法可灵活应用于二维和三维问题, 能一次求得整个成像空间内震源波场的入射角度.对存在多次到达的复杂介质情况, 本文得到的角度对应于主能量波场.由于本文方法在计算入射角度时考虑了地震波的幅值, 它得到的角度能更好地与实际波前面相对应(可有效剔除“阴影区”).
本文的组织如下:首先给出了基于单程波计算地震波入射角的理论基础, 然后给出了实际应用的计算流程, 最后给出了二维和三维算例, 并与理论值进行了对比, 数值算例证明了本文方法的稳定性、精度和效率.
2 基于单程波算子的入射角计算理论单程波算子是通过对标准的声波方程进行分解而得到的[9], 一般情况人们总是沿垂直方向分解单程波算子.单程波算子可正确模拟复杂介质中地震波的单向传播(存在大角度限制), 与标准的声波(双程波)方程相比, 单程波算子沿其分解方向不发生地震波反射.由于这一特征, 单程波算子所得到的简谐波场就对应着地震波传播波场中的波前面.而双程波方程存在的反射导致波场变的更复杂.地震波场的波数是与波前面的法线方向相联系的, 而波场的空间导数又与波数存在着对应关系, 因此, 我们可利用求取空间导数前后简谐波场的变化, 简单求得全场的地震波入射角方向.
由单程波方程可知, 下行的频率域波场P+(x, y, z; ω)满足
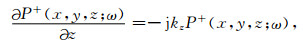
|
(1) |
其中j是单位虚数, kz是垂直波数, ω是角频率, x和y是水平位置坐标, z是深度坐标, 由频散关系得
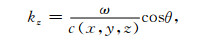
|
(2) |
式中c(x, y, z)是空间各位置处的介质波速, 角度θ即是空间位置(x, y, z)处波前面法线与深度轴z的夹角.将(2)式代入(1)式并做离散的时域傅氏反变换, 且令时间t=0, 可得
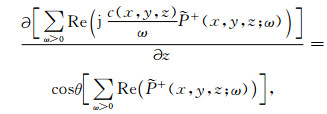
|
(3) |
式中符号Re代表求复波场值的实部.若令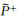
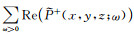
脉冲响应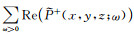
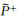

|
(4) |
式(4)中的分母将存在多个零点, 这些零点处将不能得到正确的入射波角度; 既然在一个波长范围内入射波的角度不会有显著变化, 可用波前面的波峰和波谷处的入射波角度插值得到邻近位置的入射波角度.我们设计了如下平滑算法, 实现这一思想.首先计算
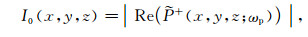
|
(5) |

|
(6) |
用四阶差分算法计算(4)式中的一阶导数, 令计算脉冲响应的深度方向的空间采样为Δz, 可得
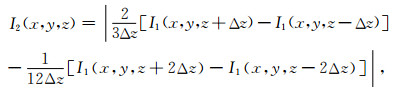
|
(7) |
式(5)和(7)中采用绝对值, 是因为对下行波而言cosθ总是正.由(4)式可知, I2(x, y, z)应该小于I0(x, y, z).但当偏移噪音较强时(即在入射波较弱的阴影区), 有时并不满足这一条件; 这表明该处不存在准确的入射波, 因此不能得到正确的入射角度.在计算中, 若I2(x, y, z)> 1.05I0(x, y, z), 可令I2(x, y, z)=0, 这样避免了阴影区角度计算的困难.
式(4)中采用地震波主频并不是必需的.理论上, 在地震波频带内的任意频率都可以用来计算式(4)中的角度; 采用的频率越高, 所需的计算量就越大.采用主频只是为使计算得到的角度精度与实际偏移结果更匹配.
为避免式(4)中除法计算的不稳定, 我们发展了高精度的稳定的相除算法, 这一算法的核心是利用级数展开近似式:
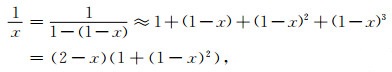
|
(8) |
当x趋于零, 式(8)仍可得到稳定的结果, 而当0.6 < x≤1.2时, 式(8)的近似有很好的精度.利用式(8), 我们发展了稳定的相除算法, 即
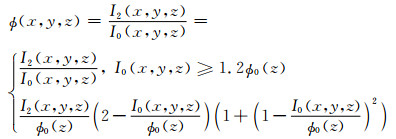
|
(9) |
式中I0(x, y, z)≥0.0, ϕ0(z)是I0(x, y, z)在深度z上的平均值.该式既保证了稳定性, 又可以得到光滑的相除结果.
对(9)式的结果, 先做沿深度方向的中值滤波, 然后进行空间三维平滑, 即可由波峰和波谷处的入射波角度插值得到邻近位置的入射角度; 为避免(7)式差分计算产生的误差, 将对每一深度上平滑处理后的ϕ(x, y, z)进行归一化处理, 保证垂直入射的存在.这样就可通过单个频率的简谐波场的深度延拓, 求得炮点出射波对地下各点的入射角度
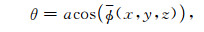
|
(10) |
式中ϕ(x, y, z)由ϕ(x, y, z)进行归一化处理得到, (x, y, z)即是地下各点的空间坐标.
3 基于单程波方法的入射角计算流程从2节基于单程波算子的入射角计算理论可看出, 该方法可使用任意的深度延拓方法, 这也使得本节将要讨论的入射角度方法流程可以借鉴使用业已发展成熟的任意一类单程波算子.但是, 不同的深度延拓方法所能够模拟的地震波的最大传播角度是不同的, 因此使用该方法计算出来的入射角度的有效角度范围也是不同的.这样就可以针对不同的精度和效率要求, 选择合适的深度延拓方法以达到足够的精度和较高的计算效率.由于本文计算地震波入射角度的方法是服务于地震偏移及照明分析等地震勘探方法, 有限的角度范围并不影响本文方法的实际应用(对波动方程偏移方法都不能正确处理的高角度波场, 获得准确的入射角度也是没有意义的).
本文采用了最优分裂步法进行波场延拓[10-12], 既保证了较高的计算效率, 还具有很高的计算精度.
由于在计算角度的过程中需要准确的波场信息, 尤其是本文方法仅利用了单频(通常是主频)的波场延拓信息, 因而在波场延拓过程中避免空间假频的产生至关重要, 否则会对最终的结果产生很大影响.通常, 深度方向的空间采样Δz应满足:Δz≤0.5cπ/ω, 即1/4波长, 否则将出现空间假频; 水平方向的空间采样Δx应满足:Δx≤cπ/ω, 即1/2波长.需指出的是, Δx≤cπ/ω或Δx=cπ/(ωsinθmax)仅能保证在深度延拓过程中避免假频.其中c为速度, ω为圆频率, θmax为最大成像角度.
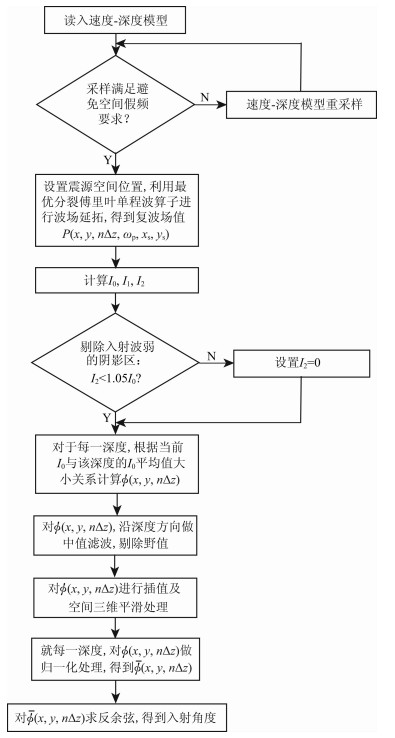
令震源的主频是ωp, 震源的空间位置为(xs, ys, 0), 介质的速度为c(x, y, z); 利用波动方程偏移的单程波算法, 对空间脉冲δ(x-xs, y-ys, ωp)进行深度延拓, 沿用图 1所示的基于单程波深度延拓的入射角计算流程图, 即可得到震源波场在各地下成像点的入射角度信息.
|
图 1 基于单程波深度延拓的入射角计算流程图 Fig. 1 Flow chart of angle field estimation based on the one-way wave equation wavefield extrapolation |
从图 1所示的流程图来看, 本文方法流程的计算量主要源于波场延拓及后期信号处理.由于仅利用了单一频率的波场延拓结果, 因而所建议的震源波场入射角计算方法具有较高的计算效率, 而这也是该方法能够工业应用的一个关键问题.
本文方法得到的是波场的入射角, 并不是角道集中使用的反射张角; 为获得反射张角, 或是同时利用震源波场的和反射波场的入射角进行点积计算, 或是利用震源波场的入射角与界面法线进行点积计算.实际应用中获得反射波场的入射角需要远大于本文方法的计算成本(不能应用单频波场、需逐炮估计), 且由于噪音干扰精度也不理想; 因此建议使用后一种方法.就匹配逆时偏移的双程波估计角度方法而言, 还需要进一步区分上下行波和克服上下行波的互相干扰.
4 数值算例 4.1 二维模型数值算例为验证本文提出的基于单程波深度延拓的入射角计算方法及流程, 首先将其应用于均匀速度模型(对此模型可容易得到入射角的理论值), 将其计算结果与理论角度值进行对比分析.其次, 给出一个速度扰动情况下入射角计算的实例, 以验证这一计算方法的稳定性.最后应用Marmousi模型考察该方法对复杂横向速度变化情况的适应能力.
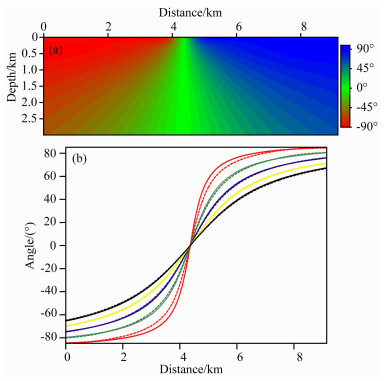
均匀模型 我们设计了一个横向9km, 纵向3km的均匀速度模型, 速度为3000 m/s, 炮点位于模型中心位置.该模型纵横向比达到1:3, 角度范围广, 不同深度角度变化明显, 能够很好地验证该入射角计算算法.在图 2a中给出了本文方法流程求得的入射角度.整体上看, 角度分布均匀平滑, 没有突变点, 符合常规认识.
|
图 2 均匀模型入射角度分布及其与理论值对比分析 (a)均匀模型入射角度图;(b)图(a)中不同深度横向位置角度与理论值对比,图中实线为理论值,虚线为本文方法计算值. Fig. 2 Comparisons of theoretical and estimated angles on 2D homogeneous model (a) Angle field of a 2D homogeneous model; (b) Comparisons of theoretical (illustrated by the solid line) and estimated (illustrated by the dashed line) angles at different depth. |
我们自深度400m开始, 每间隔400m取一个深度, 共取5个深度, 最深至2000m进行对比分析.分别在这5个深度层取每个横向位置的角度值, 与该位置的理论值进行对比, 总体结果显示在图 2b中.图中实线表示理论值, 虚线表示计算值, 红绿蓝黄黑五种颜色代表了不同的深度, 分别为:400 m, 800m, 1200m, 1600 m, 2000 m.从图中可以看出, 除最浅的第一层以外, 理论值和计算值都吻合较好, 误差小于1°.就浅层计算角度不准确而言, 一方面源于基于单程波波场延拓算法在延拓的初始深度即浅层精度较低, 且本算例中单程波波场延拓的算子设计最大角度为60°; 另一方面, 通常在实际应用中即使是人们所关心的浅层也要大于这一深度.因此可以认为本文建议的方法流程在均匀速度模型中得到的入射角度计算结果在应用层面上与理论角度值相比具有较高的符合度.
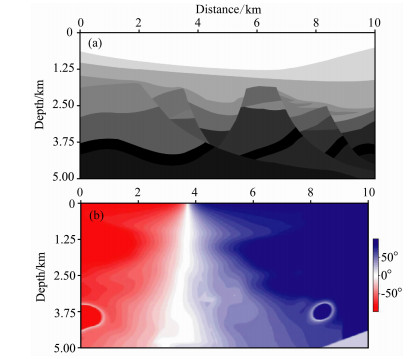
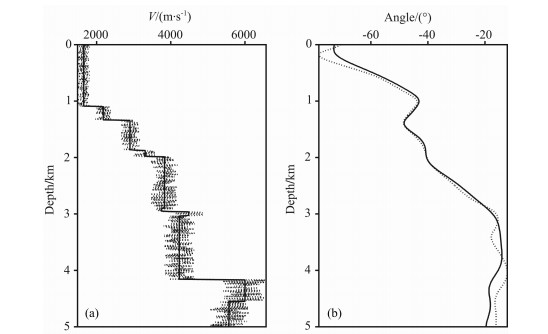
海上复杂地质模型 为考察本文计算方法流程在复杂构造模型且存在速度扰动情况下的稳定性, 设计如下算例.速度模型如图 3a所示, 其取值范围为1500~6000m/s.将炮点置于0.38km处, 运用本文方法流程得到的入射角示于图 3b.可以看出, 本文算法流程在此复杂构造模型中仍可得到较合理的入射角计算结果.至于入射角分布图左下角及右下角存在的角度异常区域, 在实际应用中因偏移孔径或者采集孔径的关系通常是不在有效范围之内的.基于图 3a所示的速度模型, 将其按照如下公式加入速度扰动:vel(x, z)=vel0(x, z)×[1+(rand(x, z)-0.5)×η].式中vel0(x, z)为原始速度, rand(x, z)为取值介于0与1间的随机函数, η为一调节系数, 本例中取值0.2, vel(x, z)为加入扰动后的速度模型.图 4a与图 4b分别给出了0.5km处加入速度扰动前后速度模型曲线与入射角计算结果曲线比较.比较图 4a与图 4b可见, 加入扰动后的速度模型若运用射线法计算入射角存在较大困难, 而运用本文方法流程仍能得到较稳定合理的入射角计算结果.
|
图 3 海上复杂地质模型(a)及其入射角计算结果分布(b) Fig. 3 (a) A fairly complicated model and (b) the estimated angle field with one-way wave equation based scheme |
|
图 4 本文计算入射角方法流程稳定性测试 (a)加入速度扰动前后的速度曲线对比,图中实线和虚线分别对应加入速度扰动前后的速度;(b)加入速度扰动前后本文方法计算的入射角度对比,图中实线和虚线分别对应加入速度扰动前后的入射角度. Fig. 4 Stability test of the proposed one-way wave equation based angle field estimation scheme (a) Comparison of velocity values without (illustrated by the solid line) andwith (illustrated by the dashed line) randomvelocity perturbation; (b) Comparison of estimated angles without (illustrated by the solid line) and with (illustrated by the dashed line) random velocity perturbation. |
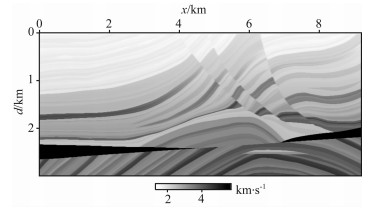
Marmousi模型 为进一步验证本文方法流程对复杂横向速度变化的适应能力, 将其应用于SEG Marmousi模型, 该模型存在断层、背斜、尖灭等复杂构造, 同时具有较强的横向变速.图 5显示了其速度模型.应用该方法计算炮点位于不同横向位置时模型的入射角分布, 为更好地分析角度的合理性, 选择较有代表性的位置将角度的等值线和速度模型叠合起来示于图 6.
|
图 5 Marmousi速度模型 Fig. 5 Marmousi velocity model |
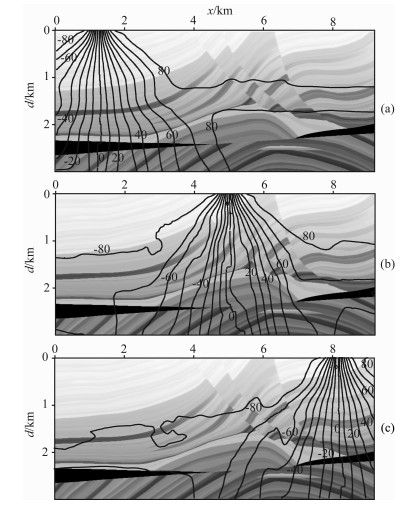
考察图 6可见, 对于CDP100和CDP650, 这两个位置具有一定的相似性, 炮点置于该位置时其下地层速度横向变化不大, 主要成层分布, 因此所对应的入射角度分布较均匀, 横向渐变, 纵向上存在因速度变化引起的角度变大或变小, 符合Snell定律; 入射角的等值线基本上垂直贯穿了各层, 符合费马原理.炮点置于CDP400这一位置时, 因其下介质速度横向变化大, 且有断层的切割以及背斜和两侧高速体的影响, 使得它们所对应的入射角度变得复杂, 零角度位置随之发生偏移, 不再位于炮点下方, 而是随速度变化而发生相应的变化.对比分析认为, 在较强的横向速度变化情况下, 本文方法计算的角度仍有较高的合理性.
|
图 6 震源位于不同位置时入射角等值线和速度模型 叠合图: (a) CDPl00,(b) CDP400,(c) CDP650 Fig. 6 The incident angle contour line underlying velocity model with the source at different position i. e. CDP100 (a), CDP400 (b) and CDP 650(c), respectively |
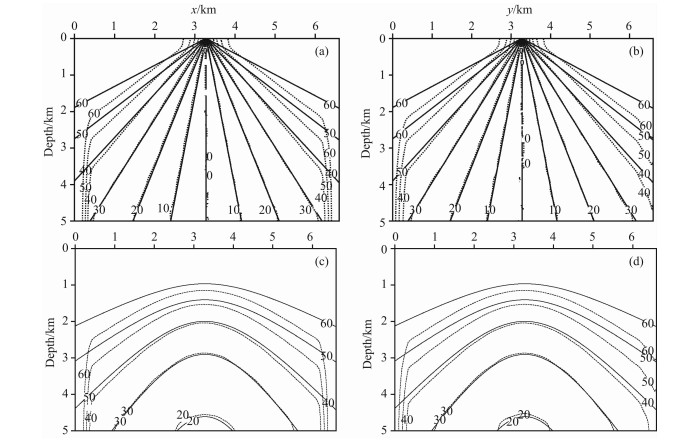
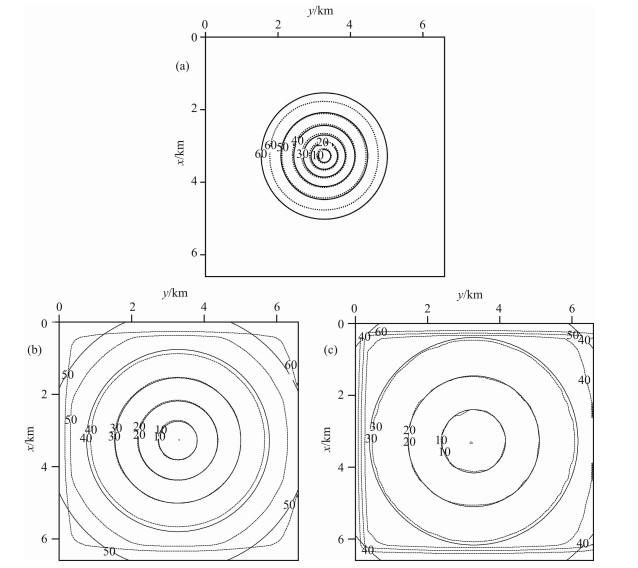
本节进一步应用三维均匀速度模型将本文计算方法及流程的计算结果与理论角度值进行对比分析.这一三维模型在inline方向和crossline方向上均为6600m, 纵向上5000m, 炮点置于水平面的中心点.为对比分析得到的入射角度及等值线计算结果, 选择inline及crossline方向的典型切片示于图 7, 图 8则展示了深度分别为1km, 3km, 5km的水平切片.
|
图 7 不同位置纵切面的理论值与计算值等值线对比分析:图中实线为理论值,虚线为本文方法计算值 Fig. 7 Comparisons of theoretical (illustrated by the solid line) and estimated (illustrated by the dashed line) angle field sections at (a) offset 0 mat inline direction, (b) offset 0 mat crossline direction, (c) offset 1680m at inline direction and (d) offset 1680m at crossline direction, respectively (a) Offset 0m inline; (b) Offset 0m crossline; (c) Offset 1680m inline; (d) Offset 1680m crossline. |
|
图 8 不同深度水平切片上理论角度与计算角度的等值线对比分析 图中实线为理论值,虚线为本文方法计算值. Fig. 8 Comparisons between the contour lines at different depth slices of theoretical (illustrated by the solid line) and estimated (illustrated by the dashed line) angles (a) Slice at the depth of 1 km; (b) Slice at the depth of 3 km; (c) Slice at the depth of 5 km. |
从图 7中可以看到, 在inline和crossline方向上距离炮点越近, 角度的准确度越高; 随着距离的增大, 计算角度误差有所增大.但从整体上来讲, 在45°左右仍均有很高的精度.在图 8所显示的水平切片对比中, 可以看到, 即使到了最深部, 其有效的角度范围内计算角度都吻合得很好.需要指出的是, 各图中边界处等值线急剧下降, 计算角度不准, 这是由于波场传播过程中为避免人工反射, 对边界波场值进行了衰减, 因此相应的角度计算也不准, 但实际应用中衰减区的计算结果是不采用的, 因而, 这一现象并不影响其应用.综合上面的对比分析, 可以认为在3D情况下, 本文方法仍是准确的.
5 结论本文给出了利用叠前偏移的单程波算子计算地震波入射角的方法.该方法能基于(近似的)偏移速度模型, 得到匹配震源频带的地震波入射角, 这规避了射线理论方法对精确速度模型的依赖, 也避免“焦散”等现象导致的难以应用射线理论求得波场入射角度.该方法可一次性求得整个成像区域的地震波入射角度, 可灵活应用于二维和三维问题.它使用与偏移计算完全相同的偏移速度模型和单程波算子, 因此得到的角度能更真实地反映震源波前面或反射波波前面的入射角度, 从而可更好地服务于叠前偏移合成角道集和角度域照明分析(可以此为基础得到反射张角).对单程波算法难以描述的传播特征(如大角度、回转波等), 本文方法也不能得到正确的地震波入射角度; 由于本文方法是服务于波动方程深度偏移, 这些限制并不影响方法的实际应用.
文中给出了该方法的实际应用流程和二维及三维计算实例, 数值算例表明, 本文方法既有很好的计算精度, 又有很好的稳定性, 其计算量与偏移计算相比几乎可以忽略.
| [1] | Wapenaar K, Goudswaard J, van Wijngaarden A J. Multi-angle, multi-scale inversion of migrated seismic data. The Leading Edge , 1999, 18(8): 928-932. DOI:10.1190/1.1438409 |
| [2] | Berkhout A J, Ongkeihong L, Volker A W F, et al. Comprehensive assessment of seismic acquisition geometries by focal beams-Part 1:Theoretical considerations. Geophysics , 2001, 66(3): 911-917. DOI:10.1190/1.1444981 |
| [3] | 张辉, 王成祥, 张剑锋. 基于单程波方程的角度域照明分析. 地球物理学报 , 2009, 52(6): 1606–1614. Zhang H, Wang C X, Zhang J F. One-way wave equation based illumination analysis in angle domain. Chinese J. Geophys. (in Chinese) , 2009, 52(6): 1606-1614. |
| [4] | de Bruin C G M, Wapenaar C P A, Berkhout A J. Angle-dependent reflectivity by means of prestack migration. Geophysics , 1990, 55(9): 1223-1234. DOI:10.1190/1.1442938 |
| [5] | Zhang Y, Xu S, Bleistein N, et al. True-amplitude, angle-domain, common-image gathers from one-way wave-equation migrations. Geophysics , 2007, 72(1): S49-S58. DOI:10.1190/1.2399371 |
| [6] | Biondi B, Symes W W. Angle-domain common-image gathers for migration velocity analysis by wavefield-continuation imaging. Geophysics , 2004, 69(5): 1283-1298. DOI:10.1190/1.1801945 |
| [7] | Kuhl H, Sacchi M D. Least-squares wave-equation migration for AVP/AVA inversion. Geophysics , 2003, 68(1): 262-273. DOI:10.1190/1.1543212 |
| [8] | Červeny V. Seismic Ray Theory. Cambridge: Cambridge University Press, 2001 . |
| [9] | Claerbout J F. Toward a unified theory of reflector mapping. Geophysics , 1971, 36(3): 467-481. DOI:10.1190/1.1440185 |
| [10] | Liu L N, Zhang J F. 3D wavefield extrapolation with optimum split-step Fourier method. Geophysics , 2006, 71(3): T95-T108. DOI:10.1190/1.2197493 |
| [11] | Zhang J F, Liu L N. Optimum split-step Fourier 3D depth migration:Developments and practical aspects. Geophysics , 2007, 72(3): S167-S175. DOI:10.1190/1.2715658 |
| [12] | 张剑锋, 卢宝坤, 刘礼农. 波动方程深度偏移的频率相关变步长延拓方法. 地球物理学报 , 2008, 51(1): 222–228. Zhang J F, Lu B K, Liu L N. Frequency-dependent varying-step depth extrapolation scheme for wave equation based migration. Chinese J. Geophys. (in Chinese) , 2008, 51(1): 222-228. |
 2013, Vol. 56
2013, Vol. 56

