2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
频率域正演是波形反演的基础,在波场模拟中占有重要地位,它具有适合多炮并行运算,无时间频散,频带选取灵活[1],及易于实现黏弹性介质波场模拟[2]等优点.相比而言,时间域正演精度高,但是由于其时间递推的思想,当时间采样点较多时,会产生误差累积,而频率域正演是对空间域所有网格整体计算波场,误差会分配到各个网格点上[3],并且不同频率的系数矩阵相对独立,特别适合并行加速[4].另一方面,频率域正演的效率在很大程度上取决于系数矩阵LU分解的快慢,而LU分解的效率则由矩阵的带宽决定,所以以较小的带宽来获取更高的精度才能同时保证频率域正演的精度和效率.
频率域正演模拟最初由Lysmer等(1972)提出[5];进而Marfurt(1984)指出频域-空间域正演不存在稳定性问题,而且适合大量炮点的同时模拟[6];基于该思想,Pratt(1990)率先将频率域正演引入到波形反演中,并对声波方程提出了5点差分格式[7],但是数值频散严重,每个波长需要13个网格才能使相速度误差低于1%;同时,Luo(1990)又提出了省时交错网格方法[8],这种方法后来被证实与Pratt的方法是一致的[9],而且,这种5点差分格式需要比时间域正演更多的网格点,才可以得到与其相近的精度[10],所以最初频率域正演由于数值频散和巨大的计算量等问题并没有得到广泛应用;为了压制频散,Jo等(1996)对声波方程提出了优化9点差分格式,频散曲线得到较大的改进,以相速度误差1%为准,每个波长只需要4个网格点来表示[10];之后,基于Jo的工作,Shin(1998)将坐标系进行三次旋转,利用0°,26.6°,45°和63.4°四个方向的差分项,得出了25点差分格式[11],每个波长只需要2.5个网格点来表示,但是系数矩阵的带宽却增加了一倍,明显地影响了LU分解的效率;Hustedt(2004)详细分析了频率域正演的多种差分格式,并基于Luo的省时交错网格方法和Jo的优化9点差分格式,提出了混合网格下的变密度优化9点差分算子[9, 12],而且指出在单频波场的求解中,LU分解约占用88%的机时[9];Min(2000)利用25点加权平均算子,对弹性波进行了频率空间域正演[13];吴国忱等(2007)将该方法进一步推广到了TTI介质中[14].
本文以用较小的系数矩阵带宽来获得较高正演精度为目标,首先根据加权平均算子和平均加速度项,构建了12个参数约束的15点差分格式,然后由Gauss-Newton法优化各项系数,再结合PML边界条件[9, 15],最终得到了优化15点频率域有限差分格式.在带宽上,此差分格式对应的系数矩阵将尽可能多的次对角线限定在了主对角线两侧,相对9点差分格式只增加了2条带,保证了机时;在压制频散方面,利用本文提出的方法,每个波长只需要2.97个网格就可以使相速度误差限制在1%以内,相对优化9点差分格式改善了正演精度;此外,正演过程中,系数矩阵是一个大型稀疏矩阵,本文采用压缩存储方式,极大地缩小了计算过程中系数矩阵的内存占用量.最后,我们利用模型数据,在耗用机时和精度方面与优化25点[11]和9点差分格式[10]进行对比,说明本文的15点优化差分格式,可以在不明显增加计算量的前提下,较好地压制频散.
2 优化15点差分格式的构造我们从频率-空间域的声波方程出发:
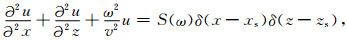
|
(1) |
其中,u(x,z,ω)是频域波场值,ω是角频率,v(x,z)是传播速度,S(ω)是频域震源项,xs,zs是震源点坐标.优化15点差分格式的构造主要包括三个方面:加权平均算子、平均加速度项和优化系数.此差分格式所需要的网格点如图 1所示,从后文可以看出,用这样网格构建的差分格式对矩阵带宽增加很小.相应的空间差分算子表示为:
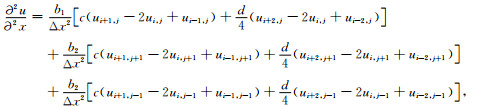
|
(2) |
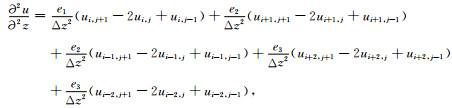
|
(3) |
式中,Δx,Δz分别是原坐标系中的网格间隔.这种多方向的数值差分形式被证实关于传播角度有相对较小的数值各向异性[10].
将加速度项
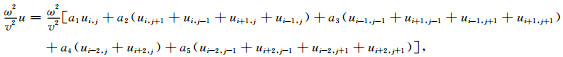
|
(4) |
将(2)-(4)式代入(1)式可得:

|
(5) |
将平面波u(x,z,ω)=u0e-i(kxx+kzz)代入(5)式,并令
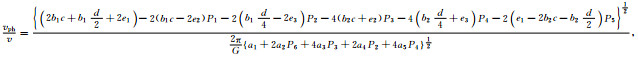
|
(6) |
其中,

|
(7) |

|
图 1 15点有限差分格式的数值网格点 Fig. 1 15-point finite difference computational grid |
由于差分格式的不对称性,系数优化时,角度θ取0~
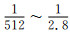


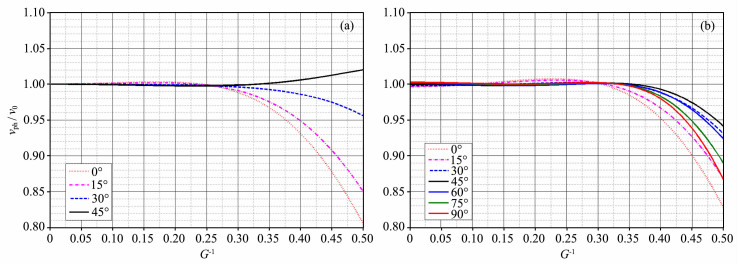
|
图 2 两种差分格式的频散曲线 (a)9点差分格式;(b)15点差分格式. Fig. 2 Dispersion curve of the two difference schemes (a) 9-point difference scheme; (b) 15-point difference scheme. |
下面我们对比本文方法和优化9点差分格式的带宽,以8×8的网格为例,来显示两种差分格式对应的系数矩阵形状,如图 3所示.9点差分格式非零元素的带宽是2nx+3,上带宽和下带宽均为nx+2;而15点差分格式非零元素的带宽是2nx+5,上带宽和下带宽为nx+3;可以看出,本文的差分格式将尽可能多的次对角线限定在了主对角线两侧,相对9点差分格式只增加了2个带宽,并且较大地提高了正演精度.

|
图 3 9点(a)和15点(b)优化差分格式系数矩阵结构图 Fig. 3 The structure of the impedance matrix of optimal 9-point (a) & 15-point (b) difference scheme |
另一方面,正演中系数矩阵是一个大型稀疏矩阵,本方法最多有15×(nx×nz)个元素是非零的;若直接对矩阵进行存储,需要8×(nx×nz)2个字节,现代计算机无法满足.本文通过记录系数矩阵中的非零值及对角线结构,来实现对系数矩阵的压缩存储,只需要8×15×(nx×nz)个字节.
3 PML边界条件的加载边界条件对边界反射的压制直接影响了正演质量.本文采取最佳匹配层(PML)吸收边界条件,它最初是由Berenger在电磁学中提出[16],其主要思想是在研究区域四周加上由幂函数或余弦函数组成的PML吸收层,使边界上传入吸收层的波随传播距离呈指数衰减,其衰减效果好,对于压制边界反射比旁轴近似的吸收边界条件要优越很多.我们从加入PML衰减项的波动方程出发:
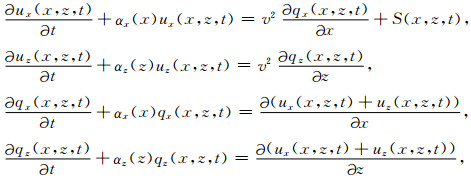
|
(8) |
式中,ux和uz代表不同方向的位移函数,qx和qz代表质点速度,αx和αz是衰减系数,在PML区域内部,衰减系数通常表示为:
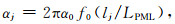
|
(9) |
式中,f0是震源子波主频,α0是一常数,经验取值为1.79,LPML是PML边界的厚度.进而将(8)式转换到频率域,并令ξx(x)=1+iαx(x)/ω,ξz(z)=1+iαz(z)/ω,则有:
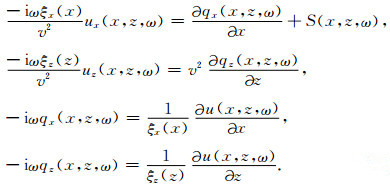
|
(10) |
设不加PML边界条件的空间变量为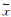


|
(11) |
对比(10)式和(11)式可得,引入匹配层后的空间偏微分算子

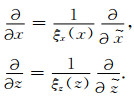
|
(12) |
结合(5)式,最终得出PML边界条件下的15点优化差分格式:

|
(13) |
其中:

|
(14) |
为了测试15点优化差分格式的精度与效率,我们采用单层介质模型来做试验.模型网格大小100×100,空间采样间隔均为5m,时间采样间隔为1ms,记录时间为1s,震源子波峰值频率为22Hz,第一层纵波速度为1000m/s,第二层纵波速度为2000m/s,PML边界厚度为50个网格点,如图 4a所示,震源位置在(250m,20m),检波器置于z=20m的界面上,对此模型分别进行9点差分格式和本文方法的正演模拟,并分别对正演中LU分解部分的耗时进行记录.

|
图 4 单层模型正演记录 (a)速度模型;(b)30Hz稳态波场;(c)9点差分格式求出的时间域波场;(d)本文方法求出的时间域波场. Fig. 4 Forward modeling result of single layer model (a) Velocity model; (b) 30 Hz monochromatic wavefield; (c) Time-domain wavefield acquired by 9-point difference scheme; (d) Time-domain wavefield acquired by our method presented here |
图 4b显示的是本文方法在30Hz的单频波场,图中可以看到入射波,透射波和反射波,入射波和反射波的相互干涉造成了反射界面附近波场的扰动;之后我们将波场转换到时间域,由于反傅氏变换的周期性影响,时间域剖面产生折叠效应(wraparound),本文采取Mallick的引入复频率的方法来消除[17],频率的虚部构造为imag(ω)=ln(50)/Δω.图 4c和图 4d是以相同振幅比例(perc=95)显示的两种差分格式得到的时间域正演结果.从图 4c和图 4d所标示的区域可以看出,9点差分格式的正演结果频散现象明显,而在图 4d相应的区域,频散却被较好地压制;所以,相对9点差分格式,优化15点差分格式波场特征保持良好,频散现象消除明显.
本模型共计算501个频率域波场,Jo的9点差分格式LU分解耗时817.226s,为了对比,我们首先测试了Shin的25点差分格式[11]的LU分解时间,其系数矩阵非零元素的带宽是9点差分格式的两倍,为4nx+5,相应的LU分解耗时为3455.098s,约为9点差分格式的4.23倍;可见,系数矩阵带宽的增加对LU分解耗时影响十分明显.而本文方法系数矩阵LU分解总耗时则为1107.901s;可以看出,本文的方法综合了高阶方法的精度和9点差分格式的效率,在不明显增加计算量的前提下,较好地压制了频散,提高了正演质量.
此外,由于15点差分格式构造上的不对称性,可能会在复杂介质情况下出现数值各向异性,下面我们构造一个复杂模型来进行测试.速度模型为200×200的网格,如图 5a所示,第一层界面是一个连续弯曲界面,第二层界面是一个锯齿状界面,三层介质纵波速度依次为:2200m·s-1,2500m·s-1,3000m·s-1,第一层介质内嵌一个高速异常体,纵波速度为2800m·s-1,模型横向变速明显;网格间距均为5m,时间采样间隔为1ms,采样时间为1s,震源峰值频率为25Hz,位置为(15m,15m),检波器置于z=15m的界面上.采用PML边界条件,分别对该模型进行时间域有限差分正演和频率域9点及15点差分格式正演,结果如图 5b-5f所示.图 5c和图 5d分别是利用本文方法和时间域正演方法得到410ms时刻的波场快照;图 5e是利用复频率得到的地表记录;图 5f是以PML为边界条件的常规时间域方法得到的地表记录.

|
图 5 复杂模型正演记录 (a)速度模型;(b)30Hz稳态波场;(c)(d)本文方法和时间域正演方法得到的410ms时刻的波场快照;(e)(f)15点差分格式和时间域方法求得的地震记录. Fig. 5 Forward modeling result of complex model (a) Velocity model; (b) 30 Hz monochromatic wavefield; (c) (d) The snapshot at 410 ms acquired by 15-point difference scheme and time-domain method; (e) (f) Seismic record acquired by 15-point difference scheme and time-domain finite difference method. |
对比图 5c和图 5d,图 5e和图 5f可以看出,在横向变速剧烈的情况下,15点差分格式和时间域有限差分方法正演结果同相轴位置和波至时间有很好的一致性,频散压制良好,前者存在一些背景噪声,这是频率域方法误差均匀分配的特性造成的.
5 结论本文综合利用加权平均算子、平均加速度项和优化系数三项技术,提出了一种新的频率空间域优化15点差分格式,该差分格式综合了高阶正演方法的精度和低阶方法的效率,它将系数矩阵的次对角线尽可能多地限定在主对角线两侧,保证了正演的计算效率.利用本文提出的差分方法,每个波长只需要用2.97个网格表示就可以限制相速度误差在1%以内;并且通过与其它频率域正演方法对比,说明该方法可以在不明显增加计算量的前提下,更好地压制频散,从而保证了后续成像及波形反演工作的精度.
同时,本文采用完全匹配边界条件,很好地衰减了边界反射;而且,可通过引入复频率压制频域波场转换到时间域产生的折叠效应.
附录A 频散曲线优化文中建立起来的频散关系式(6)是一个与传播角度、波长内网格点数以及各项系数有关的函数.我们的目标是最优化各项系数使式(6)与1最优逼近.
首先根据频散曲线,建立起目标函数,如式(A1)所示,
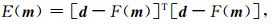
|
(A1) |
其中,F(m)即为式(6)所得到的频散关系,它是一个与传播角度θ、最短波长内网格点数G以及各项系数有关的函数.可以看出,目标函数是关于θ和G的一个积分式;角度θ取0~π/2,间隔0.001,1/G的范围取1/512~1/2.8,间隔为0.001.我们采用Gauss-Newton法来优化该问题.给定一个初始值m0,并将F(m)在m0处进行多元函数一阶泰勒展开.矩阵形式如(A2)所示:
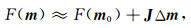
|
(A2) |
其中,J是F(m)的一阶偏导数,可表示为:Ji=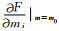

|
(A3) |
由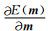

|
(a4) |
一次迭代后的新参数表示为:m=m0+Δm,反复迭代直到满足精度要求为止.
按照上述思路,我们给定初始值为:b1=1.3,b2=0.2,e1=0.6,e2=0.03,e3=0.07,c=0.4,d=0.0005,a1=0.5,a2=0.06,a3=0.02,a4=0.001,a5=-0.01.
利用上述反演原理得到的优化参数为:b1=1.4019,b2=0.1990,e1=0.6147,e2=0.0473,e3=0.0070,c=0.4062,d=0.0007,a1=0.4766,a2=0.0500,a3=0.0168,a4=0.0010,a5=-0.0042.
| [1] | 任浩然, 王华忠, 龚婷. 标量地震波频率-空间域有限差分法数值模拟. 石油物探 , 2009, 48(1): 20–26. Ren H R, Wang H Z, Gong T. Seismic modeling of scalar seismic wave propagation with finite-difference scheme in frequency-space domain. Geophysical Prospecting for Petroleum (in Chinese) , 2009, 48(1): 20-26. |
| [2] | Pratt R G. Frequency-domain elastic wave modeling by finite differences:A tool for crosshole seismic imaging. Geophysics , 1990, 55(6): 626-632. |
| [3] | 殷文, 印兴耀, 吴国忱, 等. 高精度频率域弹性波方程有限差分方法及波场模拟. 地球物理学报 , 2006, 49(2): 561–568. Yin W, Yin X Y, Wu G C, et al. The method of finite difference of high precision elastic wave equations in the frequency domain and wave-field simulation. Chinese J. Geophys. (in Chinese) , 2006, 49(2): 561-568. |
| [4] | Operto S, Virieux J, Sourbier F. Documentation of FWT2D program:Frequency-domain full-waveform modeling/inversion of wide-aperture seismic data for imaging 2D acoustic media, 2007.http://seiscope.oca.eu/spip.php?article13. http://www.oalib.com/references/19002452 |
| [5] | Lysmer J, Drake L. A finite element method for seismology.//Bolt B A ed. Methods in Computational Physics Ⅱ. Seismology:Surface Waves and Earth Oscillations. New York:Academic Press , 1972, 11: 181-216. |
| [6] | Marfurt K J. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics , 1984, 49(5): 533-549. DOI:10.1190/1.1441689 |
| [7] | Pratt R G, Worthington M H. Inverse theory applied to multi-source cross-hole tomography. Part 1:Acoustic wave-equation method. Geophysical Prospecting , 1990, 38(3): 287-310. |
| [8] | Luo Y, Schuster G. Parsimonious staggered grid finite-differencing of the wave equation. Geophys. Res. Lett. , 1990, 17(2): 155-158. DOI:10.1029/GL017i002p00155 |
| [9] | Hustedt B, Operto S, Virieus J. Mixed-grid and staggered-grid finite-difference methods for frequency-domain acoustic wave modelling. Geophys. J. Int. , 2004, 157(3): 1269-1296. DOI:10.1111/gji.2004.157.issue-3 |
| [10] | Jo C, Shin C, Suh J H. An optimal 9-point, frequency-space, 2-D scalar wave extrapolator. Geophysics , 1996, 61(2): 529-537. DOI:10.1190/1.1443979 |
| [11] | Shin C, Sohn H. A frequency-space 2-D scalar wave extrapolator using extended 25-point finite-difference operator. Geophysics , 1998, 63(1): 289-296. DOI:10.1190/1.1444323 |
| [12] | 卞爱飞, 於文辉, 周华伟. 频率域全波形反演方法研究进展. 地球物理学进展 , 2010, 25(3): 982–993. Bian A F, Yu W H, Zhou H W. Progress in the frequency-domain full waveform inversion method. Progress in Geophysics (in Chinese) , 2010, 25(3): 982-993. |
| [13] | Min D J, Shin C, Kwon B D, et al. Improved frequency-domain elastic wave modeling using weighted-averaging difference operators. Geophysics , 2000, 65(3): 884-895. DOI:10.1190/1.1444785 |
| [14] | 吴国忱, 罗明彩, 梁楷. TTI介质弹性波频率-空间域有限差分数值模拟. 吉林大学学报(地球科学版) , 2007, 37(5): 1023–1033. Wu G C, Luo M C, Liang K. Frequency-space domain finite difference numerical simulation of elastic wave in TTI media. Journal of Jilin University (Earth Science Edition) (in Chinese) , 2007, 37(5): 1023-1033. |
| [15] | Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics , 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [16] | Mallick S, Frazer L N. Practical aspects of reflectivity modeling. Geophysics , 1987, 52(10): 1355-1364. DOI:10.1190/1.1442248 |
| [17] | Pratt R G, Shin C, Hicks G J. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion. Geophys. J. Int. , 1998, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x |
 2013, Vol. 56
2013, Vol. 56


