2. 有色金属成矿预测教育部重点实验室, 长沙 410083;
3. 有色资源与地质灾害探查湖南省重点实验室, 长沙 410083
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education, Changsha 410083, China;
3. Non-ferrous Resources and Geologic Disasters Prospecting Emphases Laboratory of Hunan, Changsha 410083, China
基于波动方程的探地雷达(Ground Penetrating Radar, GPR)数值模拟一直是计算地球物理学的研究热点.时域有限差分法(Finite difference time domain method, FDTD)和有限单元法(Finite Element Method, FEM)是目前最常用的两类模拟算法. FDTD以算法简单、灵活、程序易实现, 而被广泛地采用, 如:刘四新[1]、冯德山[2]等基于K S Yee网格的FDTD进行了GPR二、三维正演, 但是该算法对于物性参数分布复杂或几何特征不规则的模型适应性差. FEM具有很好的适应复杂模型的特点, 如:底青云、王妙月[3-4]用Galerkin有限元法实现了复杂形体的雷达模型的正演及偏移; 但是FEM存在特殊的单元剖分要求、网格剖分(前处理)及人为造成场函数不连续(后处理)等缺陷[5].本文将计算力学、计算电磁学领域广泛应用的无单元Galerkin法(Element-Free Galerkin Method, EFGM)引入到GPR正演模拟中, 该算法只需节点无需单元, 摆脱了单元的束缚, 它将计算场域离散成若干个点, 采用滑动最小二乘法(Moving Least Squares, MLS)来拟合场函数, 其形函数及导数具有很好的连续性, 所得到的解也是高次连续的, 大大简化了前、后处理工作, 具有计算精度高、自适应能力强、灵活度大的特点[6].
EFGM是由Belytschko[7]及其同事于1994年在扩散元法基础上, 改进"近似导数确定、强加边界条件及数值积分处理"等一系列问题基础上提出来的. Cingoski等(1998)[8]首次将EFGM应用于电磁场计算领域中, 成功解决电压互感器中的二维静电场问题; Viana等(1999)[9]、Herault等(1999)[10]对EFGM边界条件和介质交界面条件问题进行了初步研究; 刘素贞等(1999)[11]应用EFGM计算平行板电容器的电场、长直接地金属槽电场和载流导线的磁场; Cingoski等(2000)[12]尝试将EFGM和FEM结合, 分析电磁场问题; Ho等(2001)[13]总结了EFGM计算电磁学中取得的初步研究成果; Brighenti(2005)[14]将EFGM应用于求解三维断裂力学中的问题中.近年来, 国内外对于EFGM的研究热度持续升温:杨庆新等(2008)[15]出版了《工程电磁场无单元法》专著, 为无单元方法引入电磁场的计算做出了贡献; Zhang等(2008)[16]应用改进的EFGM算法进行了二维工程裂纹问题分析; Khosravifard等(2010)[17]提出了一种新的无网格积分算法, 提高了EFGM算法计算速度和精度; Peng(2011)[18]应用复杂的可变EFGM进行了二维弹塑性问题的模拟, 对比常规EFGM具有更高的精度.在地球物理领域EFGM的应用相对滞后, 文献较少, 仅有贾晓峰[19]利用EFM进行了地震波模拟研究; 王月英[20]探讨了EFM应用于地震波正演模拟中的各种影响因素.而以滑动最小二乘法为基础的EFGM在地球物理电磁领域的研究, 还未见报道.本文利用EFGM对GPR模型进行了正演, 并将该正演结果与有限元的正演结果进行了对比, 结果表明EFGM算法的正确性及有效性, 它为GPR正演模拟提供了一种新的算法.
2 雷达波波动方程Maxwell方程组描述了电磁场的运动学和动力学规律, 由电磁波理论, 雷达波在媒质中的传播规律也应服从Maxwell方程组[21]:
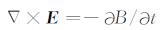
|
(1a) |

|
(1b) |
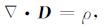
|
(1c) |

|
(1d) |
其中E为电场强度(V/m), H为磁场强度(A/m), B为磁感应强度(T), D为电位移(C/m2), J为电流密度(A/m2), ρ为电荷密度(C/m3).
本构方程:
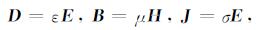
|
(2) |
式中ε为介电常数(F/m), μ为磁导率(H/m), σ为电导率(S/m).
把方程式(2)代入方程式(1a), 并求旋度, 得
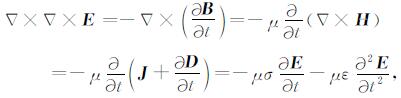
|
(3) |

|
(4) |
由于ε, μ, σ为坐标的函数, 它们的时间导数可以忽略, 把电场E代入(4)式中取代A, 则(4)式中第二项为零.
整理得
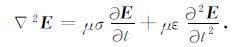
|
(5) |
假设雷达波激励源如电场源SE或磁场源SH, 代入到(5)式中, 有
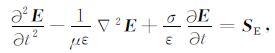
|
(6) |
同理对(1b)式两边求旋度, 可得
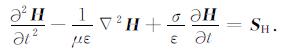
|
(7) |
(6)、(7)两式表明, 磁场H和电场E及其分量满足相同的微分方程.
3 EFGM理论基础--滑动最小二乘法拟合场函数EFGM算法的基础--滑动最小二乘法是由P. Lancaster[22]提出的, 其基本思想是将计算场域离散成若干个节点, 由滑动最小二乘法来拟合场函数, 这样构造的场函数光滑性好且高次导数连续.
如图 1所示, 用n个节点(实心点)离散二维地电模型.假设场函数为u(x), 对于二维空间, x=(x, y)T为场节点, 给定u(x)在n个节点上的值为
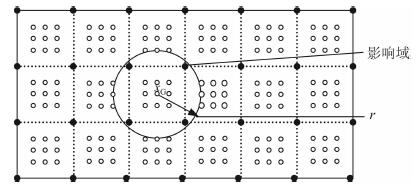
|
图 1 无单元法背景网格节点离散示意图 Fig. 1 Sketch showing discretization of background mesh nodes of the EFGM |
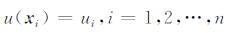
|
(8) |
其向量的形式为

|
(9) |
根据滑动最小二乘法的原理, 由这n个节点上的场值可确定一个近似场函数uh(x),
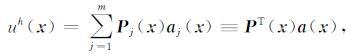
|
(10) |
其中PT (x)为m维基函数矢量; a(x)为m维系数矢量.对于二维情况, PT(x)可如下选取:
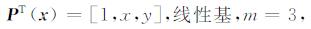
|
(11) |
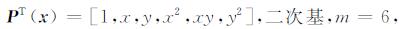
|
(12) |
式(11)和(12)分别称为线性基函数和二次基函数, m是基函数的项数, 本文采用线性基函数.通常情况下, 基函数是已知的, 需要确定的是系数矢量a(x), 与传统的最小二乘法不同, 系数向量a(x)不是常数, 而是空间场节点x(x, y)的函数, 因此被称为滑动最小二乘法.
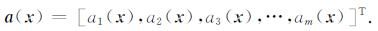
|
(13) |
为确定a(x), 在局部范围内构造带权重的加权离散L2范数得
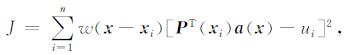
|
(14) |
式(14)中, n为权函数w(x-xi)非零域内的节点个数, 在点x周围一个有限的邻域内, 权函数w(x-xi) > 0;在这个邻域之外的权函数定义为0, 该邻域叫做点x的影响域[23], w(x-xi)的大小随着邻域点xi远离中心点x而逐渐减小.如图 1所示在二维情形下它为圆形, 其半径r被称为点xG的影响半径.以J取极小值求出参变量a(x)的支配方程为

|
(15) |
对式(15)展开, 将得到如下的线性关系:
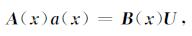
|
(16) |
式(16)中
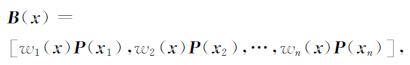
|
(18) |
其中A的具体形式为:

|
B的具体形式为
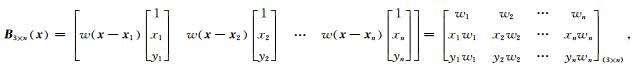
|
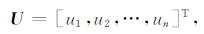
|
(19) |
由式(16)可导出
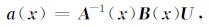
|
(20) |
将式(20)代入式(14)中得
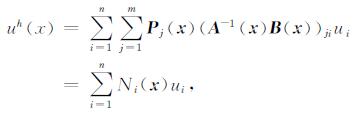
|
(21) |
Ni(x)为节点i的形函数, 它是坐标的函数.
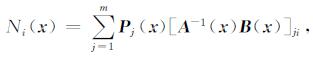
|
(22) |
式(22)可简写为
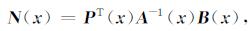
|
(23) |
节点i形函数Ni(x)关于k方向的空间导数为
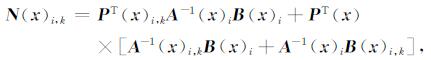
|
(24) |
其中
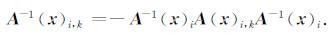
|
(25) |
式(24)和(25)中, k=x, y.从式(21)可以看出, 滑动最小二乘法拟合场函数并不满足插值条件uh(xi)≠ ui.而且MLS形函数的值可正可负, 形函数的分量具有与权函数相似的性质, 即远离x的那些节点所代表的分量具有较小的绝对值并趋近于零.而靠近x点的那些节点所代表的分量具有较大的绝对值, 形函数的这一性质决定了式(22)所表示的内插方法的一种权重分配.故权函数对MLS近似的性能将起着极其重要的作用.一般所选择的w(x-xi)均须具备如下性质[24]:
a.在支持域中的w(x-xi) > 0;
b.在支持域外的w(x-xi)=0;
c. w(x-xi)从计算点x开始单调递减;
d. w(x-xi)应足够光滑, 尤其是在边界上.
条件d将确保支持域移动时, 相应节点的进、出是光滑而平顺的, 故可保证MLS形函数在整个问题域上的相容性.权函数的选择具有一定的随意性, 只要能满足条件a, b, c, d即可.实际应用中常常选择指数函数和样条函数, 本文中采用如下指数权函数:
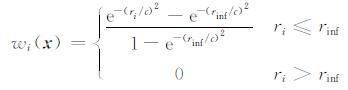
|
(26) |
式(26)中, rinf决定影响域的大小, 在二维情况下, 影响半径ri是点x与点xi之间的距离, c是一个控制相对权重的常数.
4 无单元法求解GPR方程边界条件处理 4.1 强加边界条件的处理由于EFGM不满足插值条件uh(xi)≠ui, 也就是说, 节点参数ui并不是节点的函数值uh(xi).这一特性使得强加边界条件的处理变得比较复杂, 一般使用拉格朗日乘子法[25]、与有限元耦合的方法[26]和罚因子法[27-28]等特殊方法来处理.本文采用罚因子法处理强加边界条件, 在GPR正演模拟中, 强加边界条件主要是激励源的加载, 罚因子的基本原理是引进罚泛函因子, 使得基本边界条件在物理上等效于边界被施加了一个力而产生一个位移.利用罚因子法处理方法, 式(6)可写为
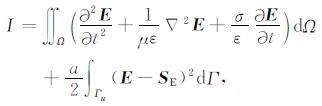
|
(27) |
其中a是罚因子.从式(27)可以看到, 罚因子本质上是一种力的刚度.把近似解函数式(21)代入式(23), 可得
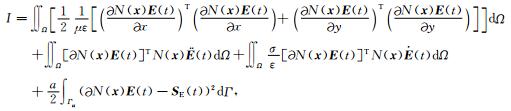
|
(28) |
将式(28)中第4项边界积分项的平方展开, 并将ET(t)提到积分号前面得
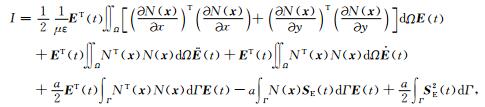
|
(29) |
再对式(29)求ET(t)的偏导数得

|
(30) |
根据变分原理, 求解波动方程(6)等效于求解泛函(30)的变分问题.令∂I/∂ET(t)=0, 并整理可得
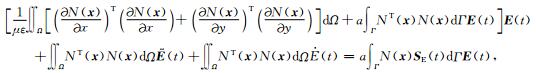
|
(31) |
式(31)可简化为以下方程:
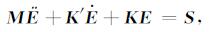
|
(32) |
式(32)中, S为等效的电场源向量. Ë为电场对时间的二次导数项, Ė为电场对时间的一次导数项. M为质量矩阵, K′为阻尼矩阵, K为刚度矩阵, 其中:
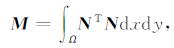
|
(33) |

|
(34) |
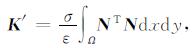
|
(35) |
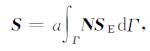
|
(36) |
其中Ω和Γ分别为所讨论雷达波场的区域及其边界.以上各矩阵的求解都需要计算高斯数值积分.标准的高斯数值积分公式如下[29]:
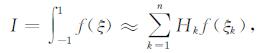
|
(37) |
式中, ξk为高斯积分点; Hk为高斯点相应的加权系数. 表 1给出对应于不同积分点的ξk, Hk的数值.
|
|
表 1 高斯积分点ξk与相应的加权系数Hk Table 1 Gauss integration points ξk and the corresponding weighting factor Hk |
一维及二维的高斯积分分别采用线段区间、矩形作为积分子域.一维高斯积分公式为:
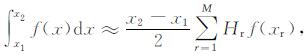
|
(38) |
二维高斯积分公式为:
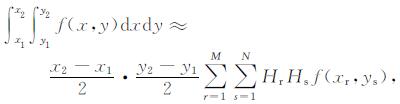
|
(39) |
式中, M, N分别为x, y方向高斯积分的阶数; Hr, Hs分别为x, y方向高斯点的积分权.
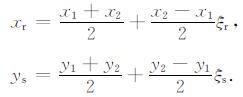
|
(40) |
目前应用于电磁场正演模拟的吸收边界条件研究主要集中于FDTD相关算法, 如辐射边界条件[30]、基于单行波方程的吸收边界条件[31]、超吸收边界条件[32]、完全匹配层(PML)[33-34]吸收边界条件等, 这些对人工截断边界反射波的处理都取得了一定的效果.而基于EFG算法的GPR正演尚无文献可查, 故本文借鉴地震波FEM及EFG正演中的透射边界条件实现GPR波在模型边界处的衰减, 则透射边界条件公式为[35]:

|
(41) |
式中L为微分算子.则在整个计算区域中有
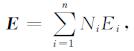
|
(42) |
这里的Ei为第i个节点的电场值.残余量R为:

|
(43) |
利用Galerkin余量法, 二维方程可写为:
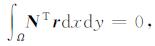
|
(44) |
其中Ω为计算区域的面积, r是残余量R的向量表示, 由式(43)代入式(44)得到.由于内边界的积分相互抵消, 所以只需求解区域外边界积分.在均匀各向同性介质中, 根据Claerbout推导的旁轴近似, 其下行波方程为:

|
(45) |
左行波方程为:
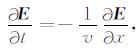
|
(46) |
右行波方程为:
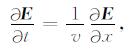
|
(47) |
由法向导数的定义知:
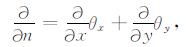
|
(48) |
其中θx和θy为边界外法线的方向余弦.将式(41), (42), (43)代入式(44)中, 并利用高斯定理可得:

|
(49) |
式(49)中Γl、Γr、Γd分别表示左、右及底边界, 上边界为自由边界条件.再将式(45), (46), (47)给出的边界条件代入到式(49), 可以得到:

|
(50) |
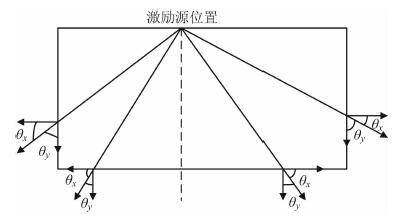
其中Ė为电场对时间的一阶导数, v为电磁波在媒质中的传播速度; 如图 2所示, Ni, Nj为左边界上的节点形函数; Ng, Nh为底边界上的节点形函数; Nk, Nm为右边界上的节点形函数.在加载透射边界条件时, 计算式(50)时, 还需求解外法线的方向余弦, 其求解示意图如图 3所示. θx为GPR发射天线激励源和边界线x方向的夹角, θy为y方向夹角,

|
图 2 边界上的节点 Fig. 2 Nodes on the boundary |
|
图 3 外法线的方向余弦角示意图 Fig. 3 Sketch map of direction Cosine angle of external normal |
其余弦值nx和ny均为正值.故边界的吸收阻尼矩阵F为:

|
(51) |
将边界阻尼加入到GPR的EFGM方程中去, 得到如下式子:
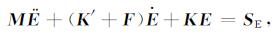
|
(52) |
这样, 就得到了加入透射吸收边界条件的EFGM雷达波波动方程式(52).
5 GPR波动方程的求解本文采用的EFGM为无网格法的一种, 它需要图 1所示的背景网格进行数值积分.应用中心差分法解方程式(52), 首先对初始条件离散化得到E(0)=E0, Ė(0)=Ė0, 把时间域[0, T]分为几个相等步长Δt=T/n, 则时刻t的微分方程记为:
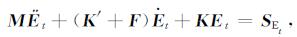
|
(53) |
用差商代替微分:
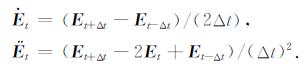
|
(54) |
中心差分法是一种条件稳定性的计算方法, 当时间步长Δt取的过大时, 计算结果就会出现数值色散, 为此本文采用Δt≤(ΔXmin/Vmax), 时间步长Δt与最小背景网格边长ΔXmin成正比, 与最大媒质速度Vmax成反比.差分网格空间步长满足稳定性条件Δx < (λmin/10), 其中λmin为最小波长长度, Δx为背景网格的最小尺寸.将式(58)代入到式(57)中得到
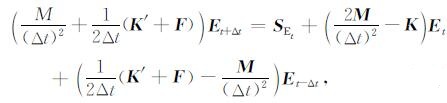
|
(55) |
此式即为GPR的EFGM正演递推公式.由于零时刻的E0、Ė0和Ë0及-Δt时刻的E-Δt、Ė-Δt和Ë-Δt均为0, 所以根据(55)式可计算出Δt时刻的EΔt, 然后依次递推可得到所有时刻的E值.令
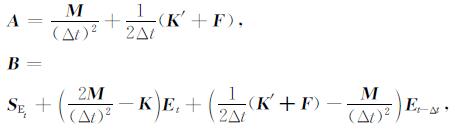
|
则式(55)可简化为Ax=B形式的线性方程组.由于系数矩阵A往往是大型的病态稀疏矩阵, 其条件数很大, 如果采取对其直接求逆, 计算量巨大, 为了提高计算效率, 采取集中质量和集中阻尼矩阵的方法来处理M, K′矩阵, 即将每一行(或列)的元素都加到对角线元素上去.采用集中质量矩阵和集中阻尼矩阵使得方程组的求解无需对矩阵求逆, 提高了计算效率.
6 数值算例 6.1 模型一图 4为三圆雷达模型示意图, 模型为3. 0 m× 2. 0m的矩形区域, 区域的背景介质为素填土, 其相对介电常数ε1为10. 0, 电导率σ1为0. 001S/m.在素填土中存在3个圆状异常体.它们的圆心位置如图 4所示, 半径为0. 1 m, 左边圆状异常体为混凝土, 其介电常数为6. 0, 电导率为0. 0005S/m, 中间为圆形金属体, 右边为圆形空洞.应用EFGM对该模型进行了正演模拟, 模拟时全域节点取101×51, 高斯积分阶次为4×4. GPR波脉冲激励源为调幅脉冲激励源, 其子波形式为f(t)=t2e-αtsinω0t, 其中ω0为发射天线中心频率, 电磁脉冲的衰减速度取决于系数α, 此处取α=0. 93ω0, 其中心频率为100 MHz.模拟时采用剖面法测量方式, 时间步长为0.1 ns, 时窗长度为50 ns.
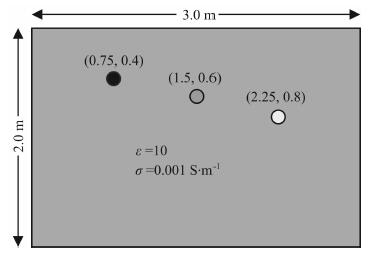
|
图 4 三圆模型示意图 Fig. 4 Sketch of the three-circle model |
图 5、图 6分别为相同节点条件下应用EFGM及基于矩形剖分、线性插值的FEM对模型一正演所得的GPR剖面.图中可见: 3个圆状异常体所在位置出现了双曲线绕射波, 只是双曲线弧形两翼的宽度比圆的直径大得多, 但双曲线的弧顶却准确对应3个圆状异常体的顶点; 对比图 5、图 6可知, 由于EFGM采用滑动最小二乘法拟合电磁场函数, 解具有导数高次连续的优点, 相比线性插值的FEM法, 它能更好地拟合随时间非线性变化雷达波场函数, 故图 5中产生的双曲线波形较图 6更光滑, 能量更强, 精度更高, 但需要更长的计算机时.

|
图 5 模型一的EFGM雷达波正演剖面图 Fig. 5 EFGM simulation profile of model 1 |
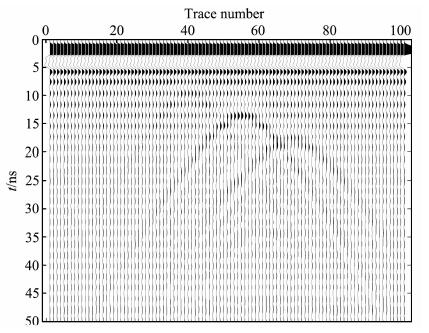
|
图 6 模型一的线性插值FEM雷达波剖面图 Fig. 6 Linear interpolation FEM simulation profile of model 1 |
图 7为EFGM模拟雷达波传播6. 0ns、8. 0ns、10. 0ns、15. 0ns、20. 0ns、30. 0ns时的波场快照图; 图 7中x、y轴分别对应图 4中的剖面长度与深度, 单位为m; z方向对应雷达波电场幅值, 单位为V/m, 该波场快照组图是取源点位于(x=1. 5 m, y=0m)的位置开始传播并取值的. 图 7a雷达波以球面波方式向地下传播(二维情况下为圆), 波前传播所到达的位置清楚可见; 图 7b可见雷达波到达了中间圆形金属处, 并产生了较强的波反射, 反射波以原一次波前相反的方向向地面传播; 图 7c中雷达一次波场继续向下传播, 而中间圆形金属产生的二次反射波向地面传播, 圆弧不断变大; 图 7d-7f中可见, 雷达波的一次波前继续向下传播, 传播的过程中, 遇到了左边混凝土圆形及右边的圆形空洞, 产生了圆弧形二次反射波及绕射波; 从图 7e中看出, 该异常体产生反射波前能量较一次波前能量明显要弱得多; 再分析图 7f, 由于模拟区域中异常体较多, 一次波前、反射波、绕射波、多次波混叠在一起, 导致后期雷达波场快照图中波场细节相对复杂, 难以区分.通过分析这些雷达剖面图及其不同时刻波场快照, 能更全面准确地推断模型特征, 深刻认识雷达波的传播规律, 指导GPR资料解释.
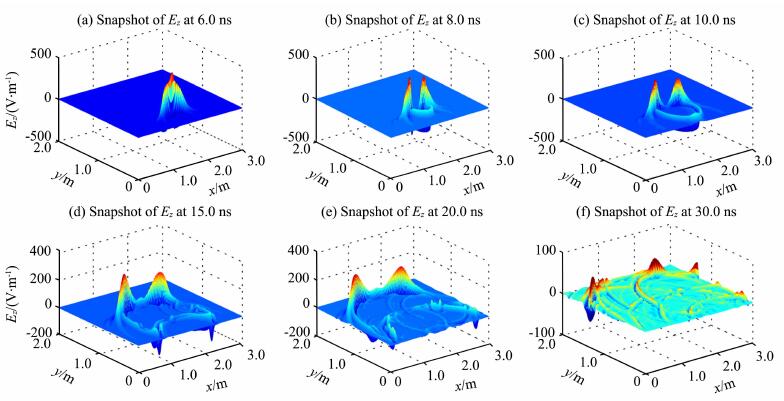
|
图 7 模型一的GPR不同时刻波场快照图 Fig. 7 Snapshots of GPR wave field on model 1 at difference times |
图 8为V字形模型示意图, 模型为一个10 m×5 m的矩形区域, 分为上下两层介质, 中间为一不平的"V"字形界面, "V"字形大约处在下层的中间位置, 宽度为3 m, 深度为1.5 m, 上层介质的相对介电常数ε1为5. 0, 电导率σ1为0.001S/m, 下层左侧位于2 m深的位置, 下层右侧位于1 m深的位置, 相对介电常数设置为30, 电导率设置为0.02 S/m.应用EFGM算法对该模型进行了正演模拟, 模拟时取全域节点为101×51, 高斯积分阶次为4×4. GPR波脉冲激励源的中心频率为100 MHz, 时间步长为0. 1 ns, 时窗长度为100 ns, 其它参数设置如模型一.
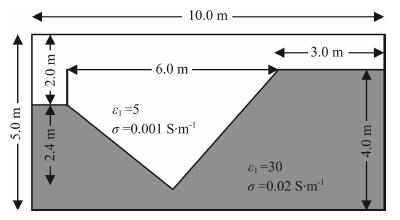
|
图 8 V字形模型示意图 Fig. 8 Sketch of V-shaped model |
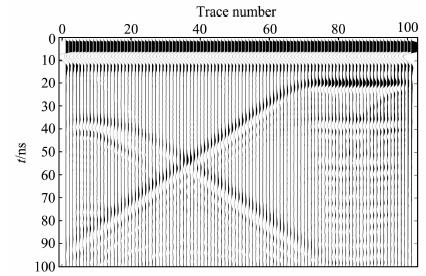
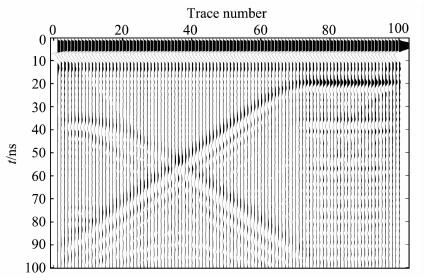
图 9、图 10分别为相同节点条件下, 应用EFGM及FEM对模型二正演所得的GPR剖面图.图中可见:分别在左、右两侧的35 ns、20 ns附近有一条能量较强的反射界面, 通过计算可以得出它与图 8模型中的上、下两层分界面位置相吻合; 而模型图中的"V"字形, 在正演剖面中"V"两条边的倾角变平缓且延长了, 两条边交叉的"V"顶点向上偏移了, 导致"V"字形凹陷变浅了, 模型图中的"V"字形在正演剖面图中变成了"×"字形.显然两图的结果存在较好的一致性, 这也说明了正演惟一性定理的正确性.进一步对比图 9、10可知: 图 9中反映"V"字形界面的两条反射波能量更强、界面更清晰、具有更好的连续性, 而图 10中V字形的下角点处产生的回转绕射波、反射界面下产生的类似"多次反射波"明显要较图 9中强.究其原因, 由于EFGM算法采用的高斯积分、影响区内有效节点搜索的特殊计算方式, 在同等背景网格条件下, 对数值频散压制得更好、精度更高所致.由此可见, 无单元法对于"V"字形模形态拟合更好, 模拟所得的正演剖面具有更高的分辨率、更利于指导雷达剖面的数据解译.
|
图 9 模型二的EFGM雷达波正演剖面图 Fig. 9 EFGM simulation profile of model 2 |
|
图 10 模型二的线性插值FEM雷达波剖面图 Fig. 10 FEM simulation profile of model 2 |
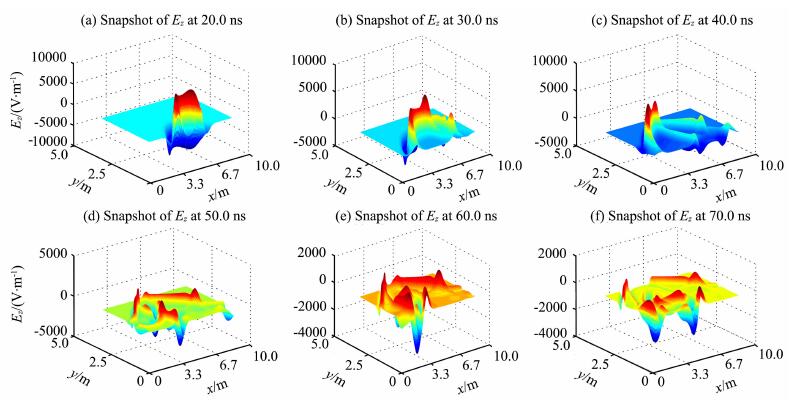
图 11为EFGM模拟雷达波传播20. 0ns、30. 0ns、40. 0ns、50. 0ns、60. 0ns、70. 0ns时的波场快照图; 图 11a-11b中清楚可见, 雷达波以球面波方式向地下传播, 波前传播所到达的位置清楚可见; 图 11c中可见, 由于模拟区域"V"字形异常体的存在, 导致波前传至异常体时改变了波前的形状, 雷达波前传播时先到达"V"字形凹陷的右边斜面再到达左边斜面, 右边斜面产生了反射波, 该波与原来的雷达波传播方向相反, 40ns时该反射波到达了"V"字形凹陷中间位置; 再分析图 11d-11f, "V"字形凹陷的顶点会产生回转波、"V"字形其它两个顶点会产生绕射波, 两个反射界面会产生反射波, 这些反射波、绕射波、多次波混叠在一起, 导致后期雷达波场快照图中波场细节相对复杂, 难以区分.通过分析这些雷达剖面图及其不同时刻波场快照, 能更全面准确地推断模型特征, 深刻认识雷达波的传播规律, 指导GPR资料解释.
|
图 11 模型二的GPR不同时刻波场快照图 Fig. 11 Snapshots of GPR wave field on model 2 at difference times |
(1) 采用EFGM计算所得的雷达剖面与采用FEM的计算结果非常一致, 在相同的节点条件下, EFGM所用的CPU时间比FEM长, 主要是由于高斯数值积分的影响区内有效节点的搜索及高斯积分计算时间过长.但EFGM毋需采用复杂的剖分网格, 仅需在求解域内合理配置一系列离散节点即可计算的优点得到了体现.
(2) 应用EFGM对典型的GPR模型进行了正演计算, 并把该模拟结果与有限单元模拟结果进行了对比, 对比结果表明了EFGM用于雷达波模拟的正确性、有效性, 说明了无单元法有望成为GPR高精度模拟的又一有效算法, 可成为常规FDTD、FEM算法的一个很好补充.
| [1] | 刘四新, 曾昭发. 频散介质中地质雷达波传播的数值模拟. 地球物理学报 , 2007, 50(1): 320–326. Liu S X, Zeng Z F. Numerical simulation for Ground Penetrating Radar wave propagation in the dispersive medium. Chinese J. Geophys. (in Chinese) , 2007, 50(1): 320-326. |
| [2] | 冯德山, 陈承申, 戴前伟. 基于UPML边界条件的交替方向隐式有限差分法GPR全波场数值模拟. 地球物理学报 , 2010, 53(10): 2484–2496. Feng D S, Chen C S, Dai Q W. GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD. Chinese J. Geophys. (in Chinese) , 2010, 53(10): 2484-2496. |
| [3] | Di Q Y, Wang M Y. Migration of ground-penetrating radar data with a finite-element method that considers attenuation and dispersion. Geophysics , 2003, 69(2): 472-477. |
| [4] | 底青云, 王妙月. 雷达波有限元仿真模拟. 地球物理学报 , 1999, 42(6): 818–825. Di Q Y, Wang M Y. 2D Finite element modeling for radar wave. Chinese J. Geophys. (in Chinese) , 1999, 42(6): 818-825. |
| [5] | Zhang Z, Zhao P, Liew K M. Improved element-free Galerkin method for two-dimensional potential problems. Engineering Analysis with Boundary Elements , 2009, 33(4): 547-554. DOI:10.1016/j.enganabound.2008.08.004 |
| [6] | Li X L. Meshless analysis of two-dimensional Stokes flows with the Galerkin boundary node method. Engineering Analysis with Boundary Elements , 2010, 34(1): 79-91. DOI:10.1016/j.enganabound.2009.05.009 |
| [7] | Belytschko T, Lu Y Y, Gu L. Element-free Galerkin methods. Int. J. Num. Methods Eng. , 1994, 37(2): 229-256. DOI:10.1002/(ISSN)1097-0207 |
| [8] | Cingoski V, Miyamoto N, Yamashitaet H. Element-free Galerkin method for electromagnetic field computations. IEEE Trans. Magnetics , 1998, 34(5): 3236-3239. DOI:10.1109/20.717759 |
| [9] | Viana S A, Mesquita R C. Moving least square reproducing kernel method for electromagnetic field computation. IEEE Trans. Magnetics , 1999, 35(3): 1372-1375. DOI:10.1109/20.767218 |
| [10] | Herault C, Marechal Y. Boundary and interface conditions meshless methods. IEEE Trans. Magnetics , 1999, 35(3): 1450-1453. DOI:10.1109/20.767239 |
| [11] | 刘素贞, 杨庆新. 二维电场的无单元数值解法. 河北工业大学学报 , 1999, 28(2): 10–15. Liu S Z, Yang Q X. Element-free method applied to 2D electrical field numerical calculation. Journal of Hebei University of Technology (in Chinese) , 1999, 28(2): 10-15. |
| [12] | Cingoski V, Miyamoto N, Yamashita. Hybrid element-free Galerkin-finite element method for electromagnetic field computations. IEEE Trans. Magnetics , 2000, 36(4): 1543-1547. DOI:10.1109/20.877733 |
| [13] | Ho S L, Yang S, Machado J M, et al. Application of a meshless method in electromagnetics. IEEE Trans. Magnetics , 2001, 37(5): 3198-3202. DOI:10.1109/20.952576 |
| [14] | Brighenti B. Application of the element-free Galerkin meshless method to 3-D fracture mechanics problems. Engineering Fracture Mechanics , 2005, 72(18): 2808-2820. DOI:10.1016/j.engfracmech.2005.06.002 |
| [15] | 杨庆新, 刘素贞, 陈海燕, 等. 工程电磁场无单元法. 北京: 科学出版社, 2008 . Yang Q X, Liu S Z, Chen H Y, et al. Meshless Method and Its Applications to Engineering Electromagnetic Field (in Chinese). (in Chinese) Beijing: Science Press, 2008 . |
| [16] | Zhang Z, Liew K M, Cheng Y M, et al. Analyzing 2D fracture problems with the improved element-free Galerkin method. Engineering Analysis with Boundary Elements , 2008, 32(3): 241-250. DOI:10.1016/j.enganabound.2007.08.012 |
| [17] | Khosravifard A, Hematiyan M R. A new method for meshless integration in 2D and 3D Galerkin meshfree methods. Engineering Analysis with Boundary Elements , 2010, 34(1): 30-40. DOI:10.1016/j.enganabound.2009.07.008 |
| [18] | Peng M J, Li D M, Cheng Y M. The complex variable element-free Galerkin (CVEFG) method for elasto-plasticity problems. Engineering Structures , 2011, 33(1): 127-135. DOI:10.1016/j.engstruct.2010.09.025 |
| [19] | 贾晓峰, 胡天跃, 王润秋. 无单元法用于地震波波动方程模拟与成像. 地球物理学进展 , 2006, 21(1): 11–17. Jia X F, Hu T Y, Wang R Q. Wave equation modeling and imaging by using element-free method. Progress in Geophysics (in Chinese) , 2006, 21(1): 11-17. |
| [20] | 王月英. 地震波正演模拟中无单元Galerkin法初探. 地球物理学进展 , 2007, 22(5): 1539–1544. Wang Y Y. Study of element-free Galerkin method in the seismic forward modeling. Progress in Geophysics (in Chinese) , 2007, 22(5): 1539-1544. |
| [21] | 曾昭发, 刘四新, 冯晅, 等. 探地雷达原理与应用. 北京: 电子工业出版社, 2010 . Zeng Z F, Liu S X, Feng X, et al. Ground Penetrating Radar Theory and Applications (in Chinese). (in Chinese) Beijing: Publishing House of Electronics Industry, 2010 . |
| [22] | Lancaster P, Salkauskas K. Surfaces generated by moving least squares methods. Math. Comput. , 1981, 37(155): 141-158. DOI:10.1090/S0025-5718-1981-0616367-1 |
| [23] | Liu G R. Mesh Free Methods:Moving Beyond the Finite Element Method. London: CRC Press, 2003 . |
| [24] | Liu G R, Gu Y T. An Introduction to Meshfree Methods and Their Programming. New York: Spring, 2005 . |
| [25] | 茅昕光, 林鹤云. 电磁场数值分析的无单元Galerkin方法. 东南大学学报(自然科学版) , 2003, 33(1): 30–33. Mao X G, Lin H Y. Element free Galerkin method for numerical analysis of electromagnetic fields. Journal of Southeast University (Natural Science Edition) (in Chinese) , 2003, 33(1): 30-33. |
| [26] | 刘天祥, 刘更, 徐华. 二维无网格伽辽金-有限元耦合方法的研究. 机械强度 , 2002, 24(4): 602–607. Liu T X, Liu G, Xu H. Studies on two dimensional element-free Galerkin-finite element coupling method. Journal of Mechanical Strength (in Chinese) , 2002, 24(4): 602-607. |
| [27] | 沈振中, 陈小虎, 孙粤琳. 用罚函数无单元法分析有自由面的稳定渗流场. 西安石油大学学报(自然科学版) , 2007, 22(2): 92–96. Shen Z Z, Chen X H, Sun Y L. Analysis of the steady seepage field with free surface using element-free Galerkin method. Journal of Xi'an Shiyou University (Natural Science Edition) (in Chinese) , 2007, 22(2): 92-96. |
| [28] | Gavete L, Benito J J, Falcón S, et al. Penalty functions in constrained variational principles for element free Galerkin method. European Journal of Mechanics-A/Solids , 2000, 19(4): 699-720. DOI:10.1016/S0997-7538(00)00168-6 |
| [29] | 刘素贞, 杨庆新, 陈海燕, 等. 无单元法在电磁场数值计算中的应用研究. 电工技术学报 , 2001, 16(2): 30–33. Liu S Z, Yang Q X, Chen H Y, et al. The element-free method for electromagnetic calculation. Transactions of China Electrotechnical Society (in Chinese) , 2001, 16(2): 30-33. |
| [30] | Bayliss A, Turkel E. Boundary conditions for the Helmholtz equation in duct-like geometries. International Association for Mathematics & Computers in Simulation , 1983: 455-458. |
| [31] | Engquist B, Majda A. Absorbing boundary conditions for numerical simulation of waves. Proceedings of the National Academy of Sciences of the United States of America , 1977, 74(5): 1765-1766. DOI:10.1073/pnas.74.5.1765 |
| [32] | Mei K K, Fang J Y. Superabsorption-A method to improve absorbing boundary conditions. IEEE Transactions on Antennas and Propagation , 1992, 40(9): 1001-1010. DOI:10.1109/8.166524 |
| [33] | Gedney S D, Liu G, Roden J A, et al. Perfectly matched layer media with CFS for an unconditionally stable ADI-FDTD method. IEEE Transactions on Antennas and Propagation , 2001, 49(11): 1554-1559. DOI:10.1109/8.964091 |
| [34] | Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics , 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [35] | 薛东川, 王尚旭, 焦淑静. 起伏地表复杂介质波动方程有限元数值模拟方法. 地球物理学进展 , 2007, 22(2): 522–529. Xue D C, Wang S X, Jiao S J. Wave equation finite-element modeling including rugged topography and complicated medium. Progress in Geophysics (in Chinese) , 2007, 22(2): 522-529. |
 2013, Vol. 56
2013, Vol. 56

