2. 中国科学院大学,北京100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
近年来随钻测井的服务产值在整个测井行业中的比重越来越大[1].随钻声波测井作为随钻测井的关键技术之一,也受到了越来越多的关注与研究.随钻声波测井仪器中钻铤的存在使得相对成熟的电缆测井的理论与技术不能直接用于随钻测井.早期的电缆测井偶极子声波测井技术被直接移植到随钻测井上,商业运用后却没能得到正确的测量结果,正是由于忽略了随钻测井的特殊井孔环境所致[2].所以针对随钻环境下的声波测井理论模型,进行必要的理论模拟及实验研究就显得尤为迫切和重要.近年来,国内外很多学者已经对随钻声波测井进行了很多理论与实验研究[2-8].
实际声波测井勘探中,地层介质往往不是各向同性的,而是具有不同程度的各向异性.横向各向同性(transversely isotropic,简记为TI)介质是测井中最普遍的各向异性模型,因为绝大多数沉积岩层都具有这种各向异性,而且在波长较长的情况下,对于油气藏具有重要意义的周期薄互层结构和裂隙定向分布的介质也可以等效为TI介质[9].通常情况下钻井方向与地面垂直,所以TI介质的对称轴和井轴平行的模型目前是最受关注的,而且这种情况可以严格求解.在电缆声波测井中关于TI地层的理论研究已经相对完善[10-14],但在随钻声波测井中关于TI地层的理论研究却很少[15-17].
随钻声波测井中各模式波的特征由于钻铤的存在而与在电缆测井中有显著的不同.电缆测井中TI地层各模式波的传播理论还能否应用于随钻测井,随钻测井测量地层各向异性是否可行,有待我们进一步验证.本文针对随钻声波测井时TI地层对称轴与井轴平行的模型,推导了井孔声场方程,计算各模式波的频散与激发强度特征,并与电缆测井中的相应特征进行比较;同时还计算了各模式波对TI地层弹性常数的灵敏度,并与电缆测井的结果进行比较,以充分验证随钻声波测井测量地层各向异性的可行性.实际测井中人们较多的用到了最低阶的模式波,所以本文重点分析各种声源条件下最低阶模式波的特征.
2 原理及方法 2.1 模型及参数图 1是随钻声波测井物理模型的剖面图,模型包括无限大地层、钻铤和泥浆等部分.本文中钻铤为各向同性介质,相关参数见表 1;地层为横向各向同性介质,相关参数见表 2.

|
图 1 随钻声波测井物理模型 Fig. 1 The plane of acoustic LWD model |
|
|
表 1 流体和钻铤的参数 Table 1 Parameters of the collar and the fluid |
|
|
表 2 横向各向同性地层的参数 Table 2 Parameters of the TI formations |
随钻声波测井时,声源放在钻铤外壁,所以钻铤内腔的流体声场是无源的且在r=0有限,因此钻铤内腔流体的位移uri及声压pfi为[3]

|
(1) |
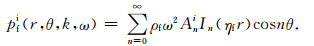
|
(2) |
钻铤与地层间的环形流体空间的声场既有入射场又有反射场,其位移uro及声压pfo为:
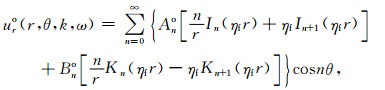
|
(3) |
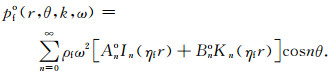
|
(4) |
In和Kn分别是n阶第一、第二类变形Bessel函数;ρf是流体密度,vf是流体声速,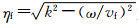
以上表达式中上n=0代表单极子,n=1代表偶极子,n=2代表四极子;上角标i和o分别代表钻铤内、外流体相对应的物理量,下角标f代表流体.
2.3 钻铤中的多极声场各向同性介质中势函数多极声场解可设为[6]:
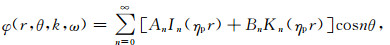
|
(5) |
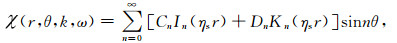
|
(6) |

|
(7) |
其中φ、χ和Γ分别对应P波SH波和SV波,ηp=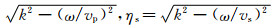
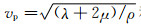
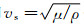
柱坐标系下位移分量与势函数的关系式为:
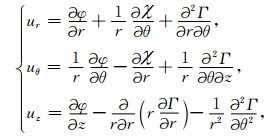
|
(8) |
应力应变关系为:

|
(9) |
kp2为纵波波数.
2.4 横向各向同性介质中的多极声场横向各向同性介质中P波和SV波耦合,SH波是独立的,而且由于地层无限大,则声场只有入射场而无反射场[3],其势函数的多极声场解设为[12]:
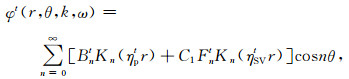
|
(10) |
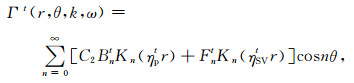
|
(11) |

|
(12) |
其中

|
以上两个系数中C1代表横向振动与纵波的耦合程度,C2代表纵向振动与横波的耦合程度.
P-SV波的径向波数为:
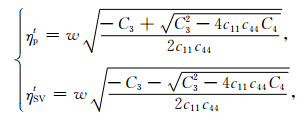
|
其中
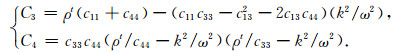
|
SH波的径向虚波数为:
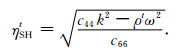
|
以上各式中c11,c33,c13,c44和c66是TI介质的5个独立弹性常数[15].以上各表达式中的上角标t代表地层,以示与钻铤各物理量的区别.
横向各向同性介质中位移分量与势函数的关系式与式(8)相同,而应力应变关系如下式所示:
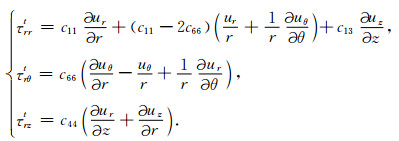
|
(13) |
上述模型的三个边界,即钻铤内流体与钻铤内壁边界处,钻铤外壁与钻铤外流体边界处,钻铤外流体与地层边界处,a,b和c分别代表钻铤内半径,钻铤外半径和井孔半径.在这些固-液边界处根据法向位移和应力的连续性可得所有边界条件如下:
在钻铤和钻铤内流体边界处(r=c)
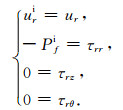
|
(14) |
在钻铤和钻铤外流体边界处(r=b)
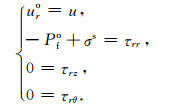
|
(15) |
在钻铤外流体和地层边界处(r=a)

|
(16) |
利用这12个边界条件可以将以上势函数假设解中的待定系数解出来.将边界条件写成矩阵形式为:
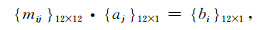
|
(17) |
其中,

|
σns是场源辐射贡献项,具体表达式为[3]
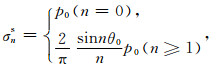
|
(18) |
{mij}12×12矩阵各元素的详细形式见附录.
2.6 模式波的频散、激发强度及灵敏度随钻声波测井中,发射器和接收器均置于钻铤外壁,那么井内(钻铤与地层之间流体环之间)声场由井内流体位移势表示为
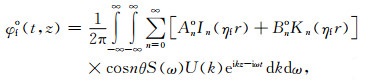
|
(19) |
若将上式改写为下式:

|
(20) |
Rn(ω,k)=Nn(ω,k)/Dn(ω,k)称为随钻测井本征响应函数,此函数中的极点对应着导波,这些极点可由下式求出,即
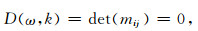
|
(21) |
此式即为频散方程.令c11=c33,c44=c66,c13=c11-2c66,C1=C2=0,则横向各向同性介质退化为各向同性介质.
对于给定的极点km,可作一阶极点处理,在频率域内对应导波的激发强度e(ω,k)可由其相应的留数给出
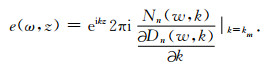
|
(22) |
导波的传播特征受模型中所有参数的影响,但影响程度不同.随钻声波测井模型中由于钻铤的存在使得问题比较复杂,三种介质的参数对模式波的传播都有影响,鉴于本文重点分析与地层密切相关的最低阶模式波,所以主要研究TI地层中各弹性常数对模式波的影响.这些常数对模式波的影响程度由灵敏度分析给出.
灵敏度计算公式由以下表达式[6]给出:

|
(23) |
即导波对某参数p的灵敏度实际上就是归一化后的波的相速度对该参数的偏微分.
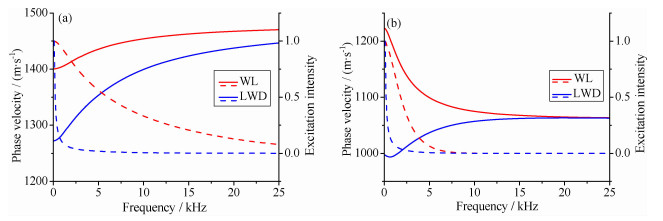
3 结果及分析 3.1 单极子模式波分析图 2给出了快速和慢速TI地层随钻单极子源条件下斯通利(stoneley)波的相速度频散和激发强度特征,并与电缆测井中的结果进行对比.其中实线为频散曲线,虚线为激发强度曲线,对比电缆测井时地层各参数与上文给出的保持一致(各弹性常数、密度、井孔半径都相同),只是不考虑钻铤,下文中偶极子和四极子模式波也是如此.由于随钻测井和电缆测井声源加载方式的不同,激发强度曲线暂时采取自归一化的方式.由图 2a可以得知快速TI地层的斯通利波(随钻测井中的斯通利波在本文中特指钻铤和地层间流体环内的斯通利波)在随钻测井和电缆测井中的相速度都低于流体速度,但随钻测井中的斯通利波频散性比电缆测井中严重,而且相速度都低于电缆测井时,这是因为由于钻铤的缘故,井孔有效半径减小,类似于前人关于测井仪器的加入对模式波的影响[18-19];虽然ST波的激发强度在随钻测井和电缆测井中的趋势一样,但在随钻测井时低频(小于2.5kHz)与高频(大于2.5kHz)时激发强度相差很大.由图 2b可以看出,慢速TI地层随钻斯通利波相较于电缆测井呈现正频散特征;激发强度特征与快速地层时类似.需要指出的是无论是快速地层还是慢速地层,随钻斯通利波的零频极限速度规律与电缆测井中不同,需要加入钻铤的影响.
|
图 2 单极子斯通利波相速度频散与激发强度 (a)快速TI地层;(b)慢速TI地层.WL为电缆测井,LWD为随钻测井. Fig. 2 Phase-velocity dispersion curves and excitation intensity curves of ST waves (a) Fast TI formation; (b) Slow TI formation. |
在传统的电缆测井中,可以通过ST波反演地层的各向异性参数[6],因为低频时的斯通利波主要产生径向位移,从而使井周变形,而井周变形由水平向剪切模量控制,对应于TI介质弹性常数中的c66.鉴于ST波只在低频时携带地层水平向横波信息的特性,本文的ST波灵敏度曲线着重给出频率小于10kHz时的数据.图 3是斯通利波对TI地层五个弹性常数的灵敏度曲线.随钻测井时,无论快、慢速TI地层,在低频时(快速地层小于6.5kHz,慢速地层小于2.5kHz),斯通利波对c66最为敏感,即斯通利波可以用来确定地层的横波各向异性.更为重要的是,相较于电缆测井,随钻斯通利波对c66的灵敏度无论在快速地层和慢速地层都有很大提高,这说明随钻ST波相较于电缆ST波更容易反演地层水平向横波速度.

|
图 3 斯通利波对TI地层弹性常数的灵敏度 (a)电缆测井快速TI地层;(b)电缆测井慢速TI地层;(c)随钻测井快速TI地层;(d)随钻测井慢速TI地层. Fig. 3 Sensitivity curves of ST waves (a) Fast TI formation of WL; (b) Slow TI formation of WL; (c) Fast TI formation of LWD; (d) Slow TI formation of LWD. |
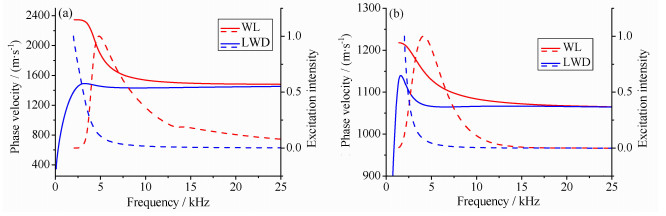
图 4给出了快速和慢速TI地层随钻偶极子源条件下弯曲波的相速度频散和激发强度特征,并与电缆测井中的结果进行对比.由图 4可以看出,由于钻铤的存在,TI地层的随钻弯曲波(这里仅指最低阶,下同)并无电缆测井中的截止频率,而且全频段速度在快速TI地层时低于流体速度,在慢速TI地层时低于地层垂直向横波速度;低频(小于3kHz)时与钻铤置于无限大流体中时的钻铤弯曲波特征类似,即由于地层与钻铤的耦合,随钻弯曲波在低频时不携带地层横波信息,所以无法直接利用随钻弯曲波(最低阶)直接获得地层横波信息.当然,在快速TI地层中,可以利用高阶弯曲波的低频段获得地层横波速度[3].随钻弯曲波的激发强度特征也与电缆测井中的不同,而是类似随钻ST波的特征,在频率低时强度更大.
|
图 4 偶极子弯曲波相速度频散和激发强度 (a)快速TI地层;(b)慢速TI地层. Fig. 4 Phase-velocity dispersion curves and excitation intensity curves of flexural waves (a) Fast TI formation; (b) Slow TI formation. |
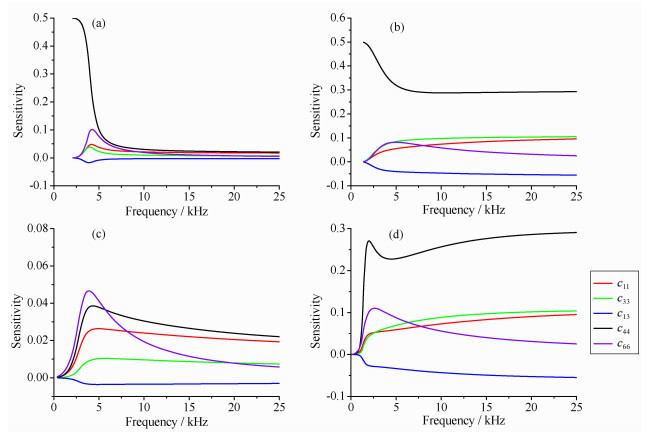
图 5是弯曲波对TI地层五个弹性常数的灵敏度曲线.由图 5c可知快速TI地层时最低阶弯曲波基本不携带地层信息,无法据其提取获得地层横波速度,这与快速各向同性地层的研究结果一致[3];而图 5d显示慢速TI地层中,当频率大于2.5kHz时,随钻弯曲波对表征地层垂直向横波信息的c44的灵敏度非常高,鉴于此点我们将深入研究慢速TI地层随钻弯曲波与地层垂直向横波速度的关系.
|
图 5 弯曲波对TI地层弹性常数的灵敏度 (a)电缆测井快速TI地层;(b)电缆测井慢速TI地层;(c)随钻测井快速TI地层;(d)随钻测井慢速TI地层. Fig. 5 Sensitivity curves of flexural waves (a) Fast TI formation of WL; (b) Slow TI formation of WL; (c) Fast TI formation of LWD; (d) Slow TI formation of LWD |
对表 2中的慢速地层参数,等间隔且只改变地层垂直向横波速度(VSV)分别计算随钻弯曲波的频散曲线,得到如图 6a的结果.由图可以看出在高频段(频率大于5kHz)时弯曲波频散效应很小,且随着VSV的改变,弯曲波的速度近似等间隔变化,这说明随钻偶极弯曲波在高频段主要受地层VSV的影响,且二者间的关系呈近似线性相关.进一步的研究发现其它五个弹性常数对随钻弯曲波的高频处的相速度影响较小,这与图 5d的灵敏度分析结果一致,鉴于篇幅原因同时考虑到论文的主题,这里不再一一给出具体的计算结果.

|
图 6 慢速地层中弯曲波相速度与地层垂直向横波速度的关系 Fig. 6 Relations between the phase-velocities of flexural waves and the velocities of vertically propagating shear wave in slow TI formation |
为了进一步考察弯曲波速度与地层VSV的关系,选取文献[6, 9-10]以及[20-23]中的慢速TI地层的参数,计算频率6kHz时各地层VSV对应的弯曲波相速度,得到图 6b中的星形数据点.用最简单的线性关系去拟合这些数据点,得到图 6b中的实线,发现这种线性拟合和实际数据之间的最大相对偏差只有5.04%,即地层VSV和随钻弯曲波相速度近似线性相关.通过此近似关系,可以根据随钻偶极弯曲波速度来估测出地层垂直向横波速度,即可以将随钻偶极声波测井测得的软地层弯曲波速度值“代入”图 6b所示的线性关系中,从而估测出地层真实垂直向横波速度.
3.3 四极子模式波分析图 7给出了快速和慢速TI地层随钻四极子源激发的螺旋波的相速度频散和激发强度特征,并与电缆测井中的结果进行对比.由图 6可知,无论是快、慢速TI地层,无论是电缆测井还是随钻测井,螺旋波都有一个低频截止频率,而且螺旋波在截止频率处相速度趋近于地层垂直向横波速度,但是随钻螺旋波的截止频率要低于电缆测井(快速TI地层中相差1.5kHz,慢速TI地层中相差0.8kHz),这使得螺旋波的艾里相在随钻测井中相较于在电缆测井中向低频移动,其激发强度峰值对应的频率也相应向低频移动.

|
图 7 四极子螺旋波相速度频散和激发强度 (a)快速TI地层;(b)慢速TI地层. Fig. 7 Phase-velocity dispersion curves and excitation intensity curves of screw waves (a) Fast TI formation; (b) Slow TI formation |
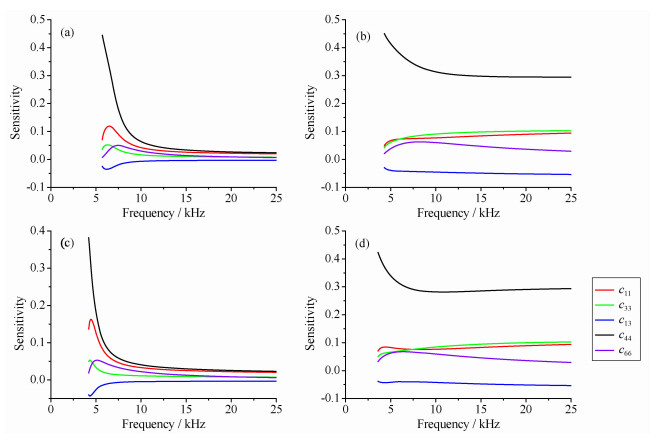
图 8是螺旋波对TI地层五个弹性常数的灵敏度曲线.不仅四极子螺旋波在电缆测井和随钻测井中的频散和激发强度特征相似,而且其灵敏度曲线特征也一样.由图 7a和7c可以看出快速TI地层中,无论是电缆测井还是随钻测井,螺旋波在低频(电缆测井低于7.5kHz,随钻测井低于5kHZ)时对c44最为敏感;由图 7b和7d可知,在慢速TI地层中,电缆测井和随钻测井在全频段都只对c44最为敏感.
|
图 8 螺旋波对TI地层弹性常数的灵敏度 (a)电缆测井快速TI地层;(b)电缆测井慢速TI地层;(c)随钻测井快速TI地层;(d)随钻测井慢速TI地层. Fig. 8 Sensitivity curves of screw waves (a) Fast TI formation of WL; (b) Slow TI formation of WL; (c) Fast TI formation of LWD; (d) Slow TI formation of LWD. |
四极子螺旋波在低频时携带地层垂直向横波速度信息,而且可以避开钻铤波的干扰[2],使得四极子声波技术成为随钻测井中获取地层横波信息的较好选择.
4 结论本文通过模式分析的方法,计算了TI地层对称轴与井轴平行时随钻声波测井模型中单极子、偶极子和四极子最低阶模式波的频散和激发强度曲线以及灵敏度曲线,并与电缆测井中的情况进行了详细对比分析.从这些分析中得到以下认识和结论:
(1)随钻ST波在低频时携带地层水平向横波信息,而且与电缆测井相比,随钻ST波在快速和慢速地层中对c66的灵敏度均有大幅提高,使随钻ST波更适合用于反演地层弹性常数c66;
(2)与电缆测井不同,慢速TI地层中随钻偶极子弯曲波(最低阶)无截止频率,不能在低频时得到准确的地层横波信息,但可以根据本文中近似线性关系间接估测出地层垂直向横波速度,从而反演慢速TI地层弹性常数c44;快速TI地层中最低阶随钻弯曲波无此特征.
(3)随钻四极子螺旋波的频散、激发强度和灵敏度特征与电缆测井中的类似,只是其截止频率相较于电缆螺旋波向低频移动;无论是快速TI地层还是慢速TI地层,在随钻螺旋波截止频率附近都可以获得地层垂直向横波速度,从而反演地层弹性常数c44.
附录 mij矩阵元素mij矩阵元素如下(所有未列出的矩阵元素都为0):
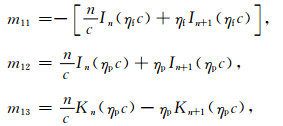
|
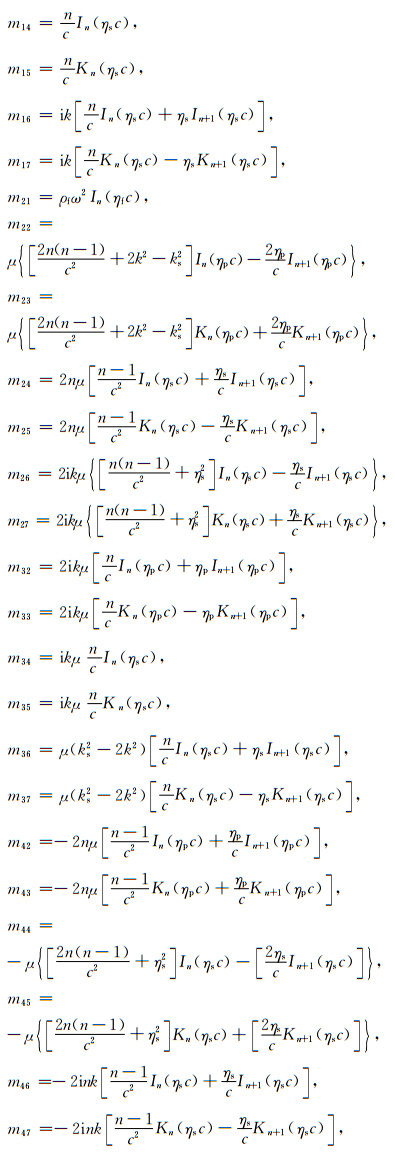
|

|
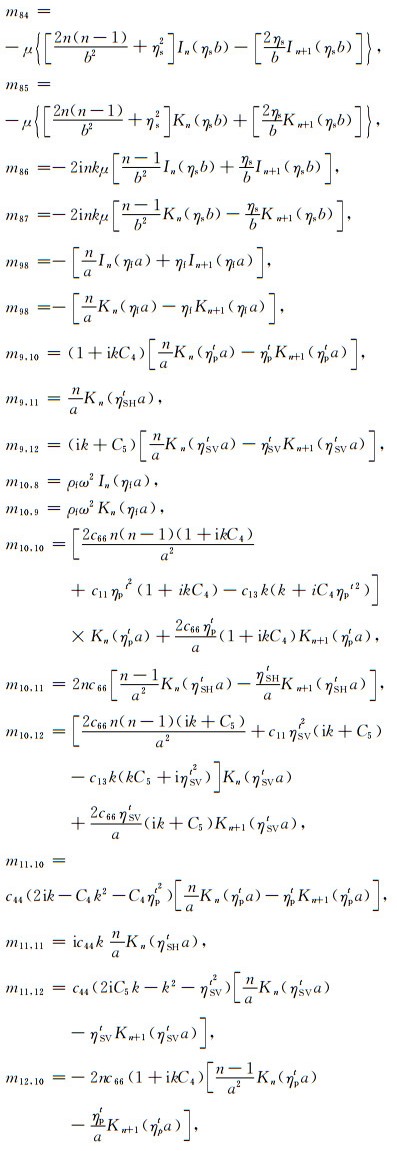
|
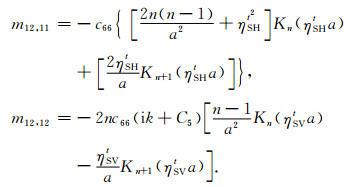
|
| [1] | 时鹏程. 随钻测井技术在我国石油勘探开发中的应用. 测井技术 , 2002, 26(6): 441–445. Shi P C. M/LWD technology plays an important role in China oilfield development. WLT (in Chinese) , 2002, 26(6): 441-445. |
| [2] | Tang X M, Dubinsky V, Wang T, et al. Shear-velocity measurement in the logging while drilling environment: modeling and field evaluations. SPWLA 43rd Annual Logging Symposium, Oiso, Japan, 2002, 6: 2-5, paper RR. |
| [3] | 崔志文.多孔介质声学模型与多极源声电效应测井和多极随钻声测井的理论与数值研究[博士论文].长春:吉林大学, 2004. Cui Z W. Theoretical and numerical study of modified Biot's models, acoustoelectric well logging and acoustic logging while drilling excited by multipole acoustic sources [Ph. D. thesis] (in Chinese). Changchun: Jilin University, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10183-2004100268.htm |
| [4] | 王华, 陶果, 王兵, 等. 多极子随钻声波测井波场模拟与采集模式分析. 地球物理报 , 2009, 52(9): 2402–2409. Wang H, Tao G, Wang B, et al. Wave field simulation and data acquisition scheme analysis for LWD acoustic tool. Chinese J. Geophys. (in Chinese) , 2009, 52(9): 2402-2409. |
| [5] | Sinha B K, Şimşek E, Asvadurov S. Influence of a pipe tool on borehole modes. Geophysics , 2009, 74(3): E111-E123. DOI:10.1190/1.3085644 |
| [6] | Tang X M, Cheng C H A. Quantitative Borehole Acoustic Methods. San Diego: Elsevier Science Publishing Co. Inc., 2004 : 39 -42. |
| [7] | Wang H, Tao G. Wave field simulation and data acquisition scheme analysis for LWD acoustic tools in very slow formations. Geophysics , 2011, 76(3): 59-68. DOI:10.1190/1.3552929 |
| [8] | Zhu Z Y, Toksoz M N, Rao R, et al. Experimental studies of monopole, dipole, and quadrupole acoustic logging while drilling (LWD) with scaled borehole models. Geophysics , 2008, 73(4): E133-E143. DOI:10.1190/1.2919827 |
| [9] | Thomsen L. Weak elastic anisotropy. Geophysics , 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [10] | White J E, Tongtaow C. Cylindrical waves in transversely isotropic media. J. Acoust. Soc. Am. , 1981, 70(4): 1147-1155. DOI:10.1121/1.386946 |
| [11] | Zhang B X, Dong H F, Wang K X. Multipole sources in a fluid-filled borehole surrounded by a transversely isotropic elastic solid. J. Acoust. Soc. Am. , 1994, 96(4): 2546-2555. DOI:10.1121/1.411383 |
| [12] | He X, Hu H S. Borehole flexural modes in transversely isotropic formations: low-frequency asymptotic velocity. Geophysics , 2009, 74(4): E149-E158. DOI:10.1190/1.3141442 |
| [13] | 陈雪莲, 王瑞甲. 横向各向同性弹性地层井孔中模式波的探测深度. 吉林大学学报 , 2008, 38(3): 502–507. Chen X L, Wang R J. Investigating depth of mode waves in the borehole surrounded by transversely isotropic elastic formation. Journal of Jilin University (in Chinese) , 2008, 38(3): 502-507. |
| [14] | Schmitt D P. Acoustic multipole logging in transversely isotropic porous formations. J. Acoust. Soc. Am. , 1989, 86(6): 2394-2421. |
| [15] | Wang T, Tang X M. LWD quadrupole shear measurement in anisotropic formations. 73rd Ann. Internat. Mtg., Soc. Explor. Geophys., Expanded Abstracts. |
| [16] | 王瑞甲, 乔文孝, 鞠晓东. 利用随钻正交偶极子声波测井评价地层各向异性的数值研究. 地球物理学报 , 2012, 55(11): 3870–3882. Wang R J, Qiao W X, Ju X D. Numerical study of formation anisotropy evaluation using cross dipole acoustic LWD. Chinese J. Geophys. (in Chinese) , 2012, 55(11): 3870-3882. |
| [17] | Briggs V A. A comparison of logging while drilling (LWD) and wireline acoustic measurements [Ph. D. thesis]. Cambridge: Massachusetts Institute of Technology, 2006. |
| [18] | Cheng C H, Toksöz M N. Elastic wave propagation in a fluid-filled borehole and synthetic acoustic logs. Geophysics , 1981, 46(7): 1042-1053. DOI:10.1190/1.1441242 |
| [19] | Sinha B K, Şimşek E, Liu Q H. Elastic-wave propagation in deviated wells in anisotropic formations. Geophysics , 2006, 71(6): D191-D192. DOI:10.1190/1.2358402 |
| [20] | Wang Z J. Seismic anisotropy in sedimentary rocks, Part 2: Laboratory data. Geophysics , 2002, 67(5): 1423-1440. DOI:10.1190/1.1512743 |
| [21] | Sinha B K, Andrew N N, Chang B K. Borehole flexural modes in anisotropic formations. Geophysics , 1994, 59(7): 1037-1052. DOI:10.1190/1.1443660 |
| [22] | Lev V, Liu X Z. Velocity anisotropy in shales: A petrophysical study. Geophysics , 1997, 62(2): 521-532. DOI:10.1190/1.1444162 |
| [23] | Urosević M, Juhlin C. Seismic anisotropy in the upper 500 m of the Southern Sydney Basin. Geophysics , 1999, 64(6): 1901-1911. DOI:10.1190/1.1444696 |
 2013, Vol. 56
2013, Vol. 56




