2. 中南大学数学与统计学院, 长沙 410083;
3. 复旦大学数学科学学院, 上海 200433
2. School of Mathematics and Statistics, Central South University, Changsha 410083, China;
3. School of Mathematical Sciences, Fudan University, Shanghai 200433, China
油气勘探难度的增大以及精确测井的发展要求,对测井技术不断提出新的要求,传统的双侧向或双感应测井仅能提供两种探测深度的电阻率信息,且易受相对井斜、薄层等因素的影响,难以满足精细油气勘探的新需求.
1998年,斯伦贝谢(Schlumberger)公司推出高分辨率阵列侧向测井仪器(High-Resolution Lateral Array tool,HRLA)[1],该电极系能同时提供6条不同探测深度的测井响应曲线,具有纵向分辨率高、径向探测信息丰富等优点,为精确反演地层参数提供了丰富的信息.快速、高精度的正演计算是最终反演的基础,因此研究快速正演响应计算方法进而分析测井响应曲线特性与地层参数之间的变化规律非常有必要.
数值模拟仍是电法测井研究、仪器研制及应用的重要手段.对轴对称非均匀分层介质模型,电位为径向和纵向坐标的函数.当径向方向上存在井眼、侵入带等边界,纵向方向上存在围岩等水平边界时,无法得到其解析解[2-3].迄今为止,解决这类测井响应计算的常用方法主要包括有限元法(FEM)[4-14]、有限差分法(FDM)[15-21]和数值模式匹配法(NNM)[22-32].其中,有限元法和数值模式匹配法在电测井数值模拟领域的研究和应用最为成熟.1980年,我国数学家李大潜的《有限元素法在电法测井中的应用》,是国内最早的有限元法在电法中应用的专著.之后,张庚骥[2]等人进行了更加具体和深入的工作,将FEM法推向实用.文献[6]提出一种电导率连续变化地层的普通电阻率测井二维有限单元数值模拟方法,并采用异常电位法提高电源点附近的精度;文献[7]将FEM应用于双频复电阻率双侧向测井的数值模拟,讨论了复电阻率测井的空间探测特性与频率响应特性;朱军[8]等利用FEM对高分辨率双侧向测井响应进行了数值模拟分析;刘振华[9]、仵杰[10]等人对阵列侧向测井的FEM正演及其特性进行了一定的研究;邓少贵[11-14]用FEM计算了各向异性倾斜地层双侧向测井、水平井双侧向测井以及裂缝性储层裂缝的阵列侧向测井响应.NNM法是地球物理电磁场计算中一种半数值、半解析的高效算法,最初用于分析二维非均匀介质中的电磁散射,后经W.C.Chew和聂在平等人的完善,成功应用于感应测井和电磁波测井响应的数值分析中[22].1994年,聂在平[23-24]等利用NNM法和“δ环电极”激励的位场格林函数研究了轴对称条件下非均匀介质的双侧向测井响应特性;之后,张庚骥等[25-26]利用NNM法研究了轴对称条件下纵向成层、径向不均匀地层模型中交流电测井和普通电阻率测井的数值模拟;袁宁等[27] (1998)成功将NNM推广到自然电位测井的数值模拟中;谭茂金等[28](2007)采用三维NNM法研究了非轴对称条件下普通电阻率测井响应;顿月芹等[29-31]基于点源模拟柱状电极,提出阵列侧向测井的NNM快速计算方案;最近,汪宏年等[32-33]应用NNM建立了水平层状非均质横向同性地层以及层状各向异性倾斜地层中多分量感应测井响应的快速算法.
电法测井正演计算本身为无界区域问题,为方便数值模拟必须将其计算区域有界化,故须在截断边界上施加人工边界条件.目前,电法测井中普遍使用的截断边界条件为设定其上的电势或者电流为零,即电位函数满足简单的第一类或第二类齐次边界条件.此处理方式实现比较简单,但边界近似精度不高.为满足实际应用的精度要求,必须将其计算区域取得足够大(径向至少数百米).而测井仪电极尺寸相对比较小(半径仅几厘米),因此过大的计算区域必然需要耗费大量的内存和计算时间,给快速正演带来很大的困难.为解决此问题,本文借鉴点源直流电法正演中截断边界条件的处理办法,推导了柱状电极情形下的阵列侧向测井正演中截断边界上的Robin边界条件,进而建立阵列侧向测井的偏微分方程数学模型,然后给出测井响应的有限元快速计算方案.定量地分析了地层厚度、井径、侵入带等因素对阵列侧向测井响应的影响,为测井作业人员和测井解释人员提供参考和指导.
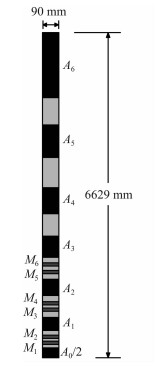
2 阵列侧向测井原理及其边值问题 2.1 阵列侧向测井工作原理高分辨率阵列侧向测井仪器采用多个聚焦线圈系组合,由1个主电极A0、6对屏蔽电极Ai,A′i(1≤i≤6)和6对监督电极Mi,M′i(1≤i≤6)组成,电极排列关于主电极对称,图 1为阵列侧向测井仪器上半部分示意图,共13个电极.
|
图 1 阵列侧向测井仪器 Fig. 1 Lateral array tool |
每次测量时,主电极A0发射单位电流,监督电极Mi,M′i(1≤i≤6)不发射电流.只有A0发射单位电流,其它屏蔽电极为回路电极时构成最浅探测深度的响应RLA0;当A0向两侧每次增加一对屏蔽电极为发射电流电极时,可依次得到5种不同探测深度的测井响应RLA1,RLA2,RLA3,RLA4和RLA5.具体工作原理如下:
(1)最浅探测RLA0
电流从主电极A0流出,返回至屏蔽电极A1(A′1)-A6(A′6).为唯一确定屏蔽电极上的返回电流值,必须附加等电位条件:
(2)浅探测RLA1
主电流电极为A0,屏蔽电流电极为A1(A′1),电流回路电极为A2(A′2)-A6(A′6).A0和A1(A′1)分别供同相位电流,测井时使M1(M′1)、M2(M′2)电压相等(M1,M′1,M2,M′2相当于取样电极功能),主电流I0在屏蔽电流I1屏蔽下,以垂直井壁方向进入地层.电流返回等电位屏蔽电极A2(A′2)-A6(A′6),由于距离A0很近,I0进入地层后不远即散开,探测深度浅.
(3)中浅探测RLA2
主电流由A0流出,屏流由A1(A′1),A2(A′2)流出,调整屏流大小使得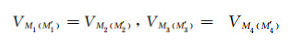
(4)中探测RLA3
A0供主电流,由A1(A′1),A2(A′2),A3(A′3)供屏流,并使得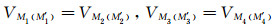
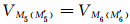
(5)中深探测RLA4
A0供主电流,由Ai(A′i)(1≤i≤4)供屏流,使得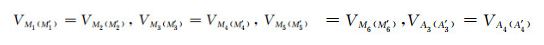
(6)深探测RLA5
A0供主电流,由Ai(A′i)(1≤i≤5)供屏流,电流全部返回至A6(A′6)电极.工作时使得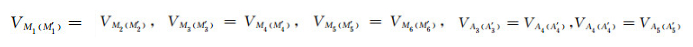
地层介质通常具有旋转对称性,阵列侧向测井仪器也具有轴对称,对称轴通过电极中心线;且有时介质和电极系还具有对z=0平面的反射对称性.以对称轴为z轴,电极中心为坐标原点,建立如图 2所示柱坐标系.对包含井眼、侵入带、围岩和原始地层的轴对称模型,在柱坐标系(r,z)中,电位函数u(r,z)满足如下偏微分方程边值问题[4, 18-19]:

|
图 2 轴对称地层模型示意图 Ωm,Ωx0,Ωt,Ωs分别为井眼、侵入带、原始地层和围岩;rh,ri分别为井眼半径和侵入带半径,H为原始地层厚度;z∞,r∞为适当大的有界化常数. Fig. 2 Schematic diagram of axisymmetric formation |
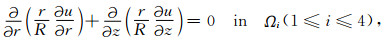
|
(1) |
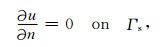
|
(2) |
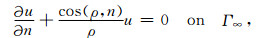
|
(3) |
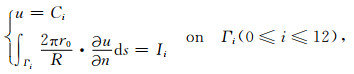
|
(4) |
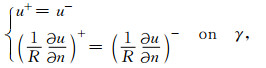
|
(5) |
其中,绝缘边界Γs包括对称轴r=0、对称面z=0以及电极系表面上的绝缘环;Γ∞表示无穷远边界(包括径向外边界r=r∞和水平外边界z=z∞);Γi表示第i个电极表面,Ci为待定常数,Ii为第i个电极发射的电流(计算区域内仅包含半个主电极,故I1为主电极A0发射电流的一半);γ为不同地层的交界面,“+”和“-”分别表示函数在交界面两侧的取值,n为边界外法线,ρ为边界点到发射电流电极中心的距离,r0为电极系半径.边界条件(2)表示绝缘边界及对称边界上电流为零;截断边界条件(3)为Robin边界条件,具体推导详见附录;等值面边界条件(4)表示第i个电极为等势体[34],且发射电流为Ii;条件(5)表示不同地层交界面上电位及电流均连续.Γ0表示主电极A0表面,Γi,Γ6+i(1≤i≤6)分别对应屏蔽电极Ai与监督电极Mi的表面,故Ii=0(7≤i≤12).电阻率R为分块常数,即
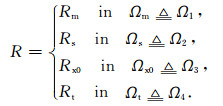
|
(6) |
由阵列侧向测井工作原理可知,每种测深都有多个电极发射电流.因此边界条件(3)中ρ边界点到发射电流电极中心的距离,指代不明.但是,真正进行有限元计算时,并非直接求解边值问题(1)-(5)(事实上也无法直接求解,因为事先并不知道各个屏蔽电极上的电流发射值),而是利用线性叠加原理,将原问题的解表示成若干个基本解的线性组合(组合系数即未知的电流发射值,可通过各种测深下的电位相等、总发射电流为零等条件确定),而每个基本解有且仅有一个电极发射单位电流,此时ρ的定义就有意义,详见2.3节边值问题的简化.
已有电法测井数学模型在无穷远截断边界上给定第一类齐次边界条件
为了得到各种测深情形下屏蔽电极上的电流发射值,记uj(0≤j≤6)分别为电极Aj发射单位电流,其它电极均不发射电流时,边值问题(1)-(5)的解.记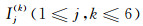

|
(7) |
其中,Ij(k)为待定电流值,要求满足如前所述各次测量屏蔽电极和监督电极上电位相等及返回电极上电位相等的条件.
考虑最浅测深RLA0,主电极发射单位电流,返回等电位电极A3,A4,A5,A6,且保持M3与M4等电位,M5与M6等电位.由此可得Ij(1)满足的6元线性方程组

|
(8) |
解此方程组即可得屏蔽电极上的发射电流值Ij(1)(1≤j≤6).方程组中第一个方程中0.5表示半空间对称情形下,只含有半个发射单位电流的主电极.
类似地,对第k次测量,利用其满足的平衡条件可得到关于Ij(k)(2≤k≤6)满足的6元线性方程组,解方程组即可得第k次测量时屏蔽电极上的电流发射值.
采用此种叠加原理的处理方法,不仅避开了事先屏蔽电极上电流不确定的困难,同时对6次不同的测量,只须计算一次电流发射情况相对比较简单的基本解uj(j=0,1,…,6),大大简化了计算.并且,基本解满足的边值问题,由于只有一个电极发射电流非零,其Robin边界条件(3)的推导更加简单,且ρ的意义更加明确.
3 阵列侧向测井有限元正演 3.1 变分原理构造下列泛函:
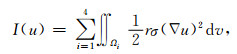
|
(9) |
其中电导率σ=1/R.由奥-高公式知其变分为
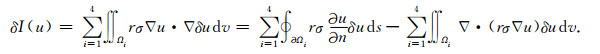
|
(10) |
根据方程(1)知(10)式右端第二项面积分为零.由边界条件(2)、(3)及(5),有

|
(11) |
由边界条件(4)知Γi上u为常数,δu亦为常数,故

|
(12) |
因此,
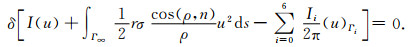
|
(13) |
即边值问题(1)-(5)与下列变分问题等价:
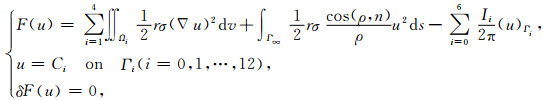
|
(14) |
其中,第i个电极上的电位Ci为常数.实际上在计算基本解uj(0≤j≤6)时,仅屏蔽电极Aj发射单位电流,故
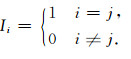
|
(15) |
此时,相应的变分问题简化为
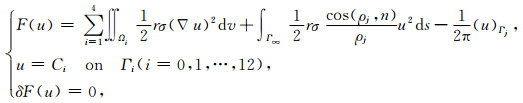
|
(16) |
其中,ρj为无穷远边界上的点到屏蔽电极Aj中心(0,zj)的距离,即
(1)单元分析
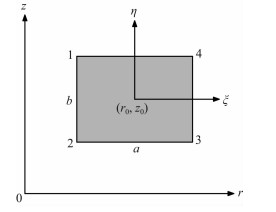
将区域Ω剖分成矩形单元,在单元e内进行双线性插值.单元节点编号及子单元、母单元的坐标系如图 3所示.其中(r0,z0)为子单元的中心坐标,a,b为子单元的两个边长.r,z为子单元所用坐标系,ξ,η为母单元所用坐标系,二者有如下对应关系:
|
图 3 单元编号 Fig. 3 Element numbering |

|
(17) |
单元e中函数u的双线性插值函数为
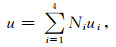
|
(18) |
其中ui为单元四个节点的待定u值,形函数
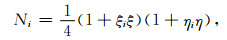
|
(19) |
ξi,ηi为点i(i=1,…,4)的坐标.
将(16)式中的积分,分解成各单元e上的积分.首先考虑面积分,

|
(20) |
其中Ue=(u1,u2,u3,u4)T为单元e的u值列向量,K1e=(kij)4×4为4阶对称矩阵,
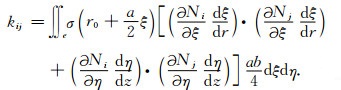
|
(21) |
若单元内电导率σ为常数σe,则将(17)、(19)两式代入(21)式可得具体计算公式如下:
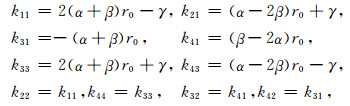
|
(22) |
其中,
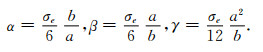
|
(23) |
考虑(16)式中的线积分.若单元e的边界34落在右边界r=r∞上,则线积分为
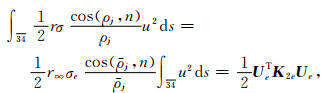
|
(24) |
其中
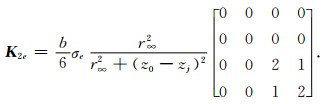
|
(25) |
若单元e的边界14落在上边界z=z∞上,则线积分为
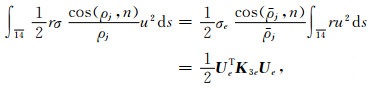
|
(26) |
其中
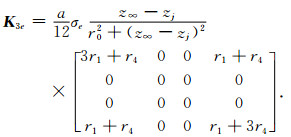
|
(27) |
下面考虑(16)式中的第三项,可将其写成
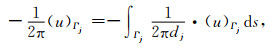
|
(28) |
式中dj为屏蔽电极Aj的长度.只有当单元e的边12落在Γj(1≤j≤m)上时,相应的积分(28)才出现,则线积分
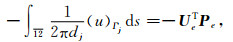
|
(29) |
其中单元荷载向量
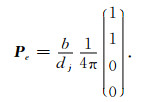
|
(30) |
(2)总刚合成
设区域Ω剖分为n个节点,将K1e,K2e和K3e相加可得4阶单元刚度矩阵Ke,并扩展成n阶方阵,然后叠加得
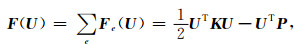
|
(31) |
其中,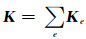
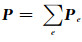
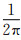
令式(31)变分为零,得到线性方程组
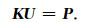
|
(32) |
(3)边界条件处理
外边界条件(2)、(3)和内部界面边界条件(5)均为自然边界条件,可自动得到满足,故只须处理等值面边界条件(4).
对等值面边界条件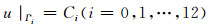
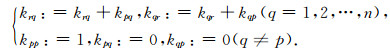
|
(33) |
最后,将右端向量P的第p个分量加到第r个分量,再令第p个分量为零,即
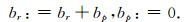
|
(34) |
经过等值面边界条件处理后,得到新的线性方程组
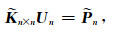
|
(35) |
其中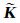

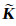
通常,式(35)中的系数矩阵是具有高度稀疏性的大型病态对称正定矩阵.若采用一维变带宽存贮方式,其中仍包含大量零元素,既浪费了内存也影响了求解速度.若对其直接采用共轭梯度法求解,则收敛速度非常慢,甚至根本不收敛.针对这两个关键问题,本文采用基于地址矩阵的稀疏矩阵压缩存贮模式[35-36],并利用预条件共轭梯度法求解大型线性方程组,起到了降低内存占用量和提高计算速度的作用.
4.1 基于地址矩阵的压缩存贮模式总体刚度矩阵K是具有高度稀疏性的对称正定矩阵,故对其可采取压缩存储,即只记录和存贮矩阵非零元素节省内存.基于地址矩阵的压缩存贮方式采用两个矩阵,一个整型矩阵G记录非零元素的地址,另一个实型矩阵M记录相应非零元素的数值.例如,n阶方阵A,若它每行最多有m个非零元素,则采用n×m阶矩阵G记非零元素的地址,用n×m阶矩阵M记非零元素的数值.则计算矩阵向量乘法Ax的第i个分量简化为计算m个乘法
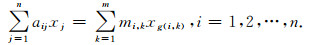
|
(36) |
基于地址矩阵压缩存贮模式,压缩效率高;地址矩阵物理意义非常明确,便于迭代法解方程组时调用,同时零元不参与运算,提高了计算效率.
4.2 预条件共轭梯度法考虑求解线性方程组
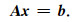
|
(37) |
假设有非奇异矩阵L,使得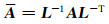
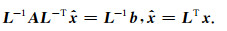
|
(38) |
此时,M=LLT为预条件子,当A条件数较小,且M矩阵便于求逆时即可达到加速收敛的目的.对同解线性方程组(38)利用共轭梯度法求解,即可得到预条件共轭梯度法(PCG).
算法:
(1)初始化: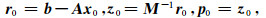
(2)对j=0,1,2,…计算
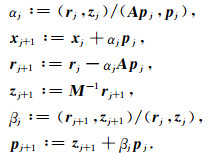
|
PCG算法收敛速度的快慢与预条件子M的选取密切相关.在上述PCG算法中,方程zj+1:=M-1rj+1的计算比较关键,本文选取最简单的预条件子,即取A矩阵的对角元素组成的对角阵为M矩阵,称为Jacobi预条件子.与其它预条件子相比,具有如下优点:① M中对角元素可直接从压缩刚度矩阵中索引,不必另行定义数组存贮,节省内存占有量;②由于M为对角矩阵,方程zj+1:=M-1rj+1无须利用Gauss消去法求解,省去了其它预条件法所必须的顺代和回代过程,大大简化了预条件子M的求逆运算.
对于阵列侧向测井响应数值模拟问题,由于各子区域电导率差异较大(往往跨几个数量级),且有限元网格剖分的严重非均匀性,导致有限元方程(35)中的刚度矩阵对角元素差异比较大,病态程度非常严重.若直接采用共轭梯度法(CG)、超松弛迭代法(SOR)等方法求解,收敛速度非常缓慢;而采用Jacobi预条件子的PCG算法,相比CG法加速十分明显,这点可从第5节数值例子得到验证.
常用的另外两种预条件方法:对称超松弛共轭梯度(SSORCG)法[37]和不完全Cholesky共轭梯度(ICCG)法[38-39].从迭代次数考虑,Jacobi预条件子的效果最差,其主要作用是提高迭代过程的稳定性;从内存需求考虑,雅可比共轭梯度(JCG)和SSORCG无需额外内存开销,而ICCG法需单独存贮预条件子;从预条件子的实现角度来说,Jacobi预条件法最为简洁,SSORCG次之,主要难度在于松弛因子ω的选取,ICCG方法最为繁琐.对于求解高分辨率阵列侧向测井响应,Jacobi预条件法已具有比较理想的加速效果,因此,本文仍采用Jacobi预条件技术.
5 数值模拟结果采用擅长数值计算的Fortran语言编制了阵列侧向测井有限元正演程序.本文的数值测试平台为CPUi57602.8 G,RAM 2 G;测试系统为Intel (R) FortranCompiler11.0,Window XP.
5.1 正演程序验证为了验证正演程序的正确性,构造如下典型地层模型:井径rh=0.1016m,侵入带半径ri=0.4016m;井眼泥浆电阻率Rm=1 Ωm,围岩电阻率Rs=10Ωm,侵入带电阻率Rx0=50Ωm,原始地层电阻率Rt=500Ωm;储层厚度H=2m.计算区域为矩形域[0,r∞]× [0,z∞]除去电极系所占区域[0,0.045]×[0,6.629],采用如下网格剖分方法:1)原点附近r,z方向均采用比较密的均匀剖分(根据电极系尺寸作适当调整);2)远离坐标原点采取对数均匀剖分.这种剖分方式既能保证电极系附近的计算精度,又能有效地节省计算时间和内存,提高正演的计算速度.
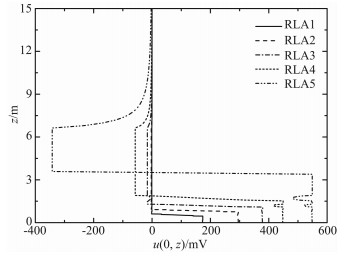
取有界化常数r∞=z∞=40m,JCG迭代残差控制精度10-8,对138×178的非均匀矩形网格,单元数为24564,节点数为24881,正演程序计算一次共耗时3.56s.5次测量得到的测量仪器上的电位值有限元计算结果如图 4所示,相应的屏蔽电极上的发射电流值与油田实际数据非常吻合,平均相对误差控制在2.39%以内,验证了本文方法及正演程序的正确性.
|
图 4 电极系表面上的电位值 Fig. 4 The electric potential on the surface of electrodes |
为比较无穷远边界条件对计算结果的影响,忽略电极大小,考虑位于原点的主电极发射单位电流,分别对具有解析解的纵向阶跃介质、径向阶跃介质地层模型进行了模拟与分析.
(1)两层径向阶跃介质地层模型(忽略围岩、侵入带影响)
模型参数:井径rh=0.1016m,泥浆电阻率Rm=0.1Ωm,原始地层电阻率Rt=10Ωm,此时利用分离变量法可求得井轴上的电位[2]:
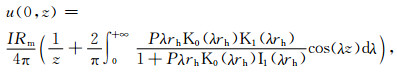
|
(39) |
其中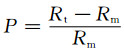
(2)两层纵向阶跃介质地层模型(忽略井眼、侵入带影响)
模型参数:原始地层厚度H=1m,围岩电阻率Rs=20Ωm,原始地层电阻率Rt=1Ωm,此时由分离变量法可求得井轴上电位[2]:
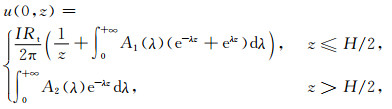
|
(40) |
其中,系数

|
(41) |
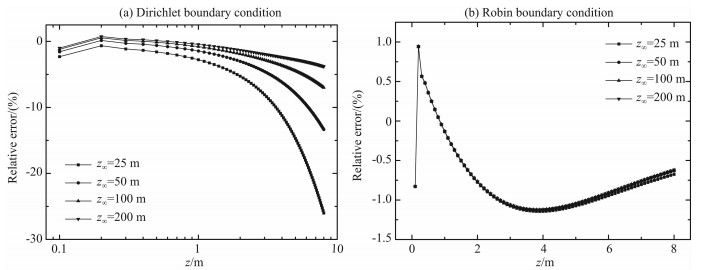
针对两个阶跃介质模型,建立4个有限元模型,模型的外边界到原点距离依次增大一倍,分别取为25m,50m,100 m,200 m.为了便于比较,网格剖分依次取为250×250,500×500,1000× 1000,2000×2000均匀剖分,此时相同区域的网格剖分完全相同.这样,仅仅是无穷远边界的选取以及边界条件的选择影响计算结果.图 5、图 6分别给出径向分层、纵向分层介质模型在两种边界条件(Dirichlet、Robin)下的井轴上的电位相对误差图.
|
图 5 径向分层介质两种边界条件下井轴上电位相对误差图 Fig. 5 Relative errors of potential on the well-axis for radially layered medium with two kinds of boundary conditions |
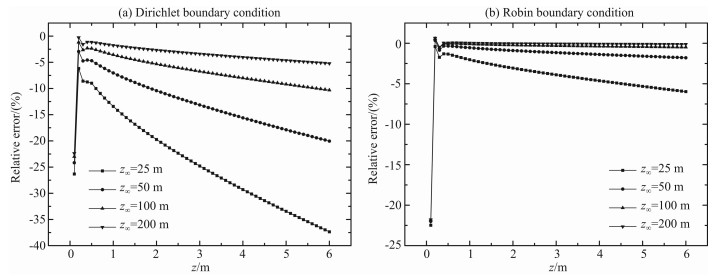
|
图 6 纵向分层介质两种边界条件下井轴上电位相对误差图 Fig. 6 Relative errors of potential on the well-axis for vertically layered medium with two kinds of boundary conditions |
从图 5a可以看出,由于点电源奇性的影响,最接近电源的第一个网格点的相对误差比较大,约为-2%,随着边界距离的增大基本保持不变;而远离原点的相对误差随着边界距离的增大逐渐减小.当边界距离由25m增大到200 m时,相对误差的最大值(z=8 m)由26%逐渐降为4%.并且发现,相对误差的最大值并非出现在点电源附近网格点,而出现在无穷远边界处,且当z>2 m时,相对误差随着到点电源距离的增大而迅速增大.这说明有限元解的误差主要是由于无穷远边界条件的误差引起的.
而Robin边界条件(3)是相对比较精确的.从图 5b可以看出,边界距离从25 m增大到200 m时,其计算结果的相对误差基本保持不变,也就是说无穷远边界距离的选择对有限元解误差的影响不大.此时,相对误差的最大值出现在具有奇性的原点附近,约为1%;远离电源点,随着到电源点的距离增大相对误差迅速减小,到z=8 m时相对误差仅为-0.6%.通过对比发现,Robin边界条件下r∞=25 m时的最大相对误差约为-1%,也比Dirichlet边界条件下r∞=200 m时的最大相对误差-4%小得多.
对纵向分层介质地层模型,从图 6可以看出,亦得到与径向分层介质地层模型时类似的结论.因此,采用Robin边界条件,可以把无穷远边界放得很近(如25m,甚至更小),从而大大缩小模型的计算区域,节省计算机内存和计算时间,提高正演计算速度,为进一步快速反演的研究奠定基础.
5.3 PCG收敛性分析为了验证本文采用预条件共轭梯度法的计算效率,分别用超松弛迭代法(SOR)、CG和PCG三种不同的迭代算法求解阵列侧向测井离散得到的有限元方程.
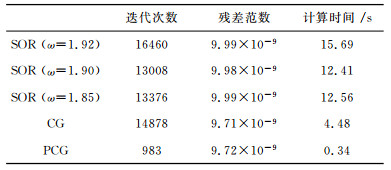
以计算基本解u0为例,三种方法(SOR,CG,PCG)均取相同的误差容限10-8,求解有限元方程的计算时间和迭代次数详见表 1.从表中可看出,不论从迭代次数还是计算时间来考虑,PCG算法较其它两种算法均具有绝对优势.基于Jacobi预条件的PCG算法耗时仅0.34s,不到CG计算时间的1/13,较SOR法加速36.5倍.值得指出的是,虽然总的迭代次数SOR (ω=1.9)法比CG法略少,但其计算时间却将近CG法的3倍,这是因为CG和PCG算法中单次迭代的时间要比SOR法少得多.由此可见,Jacobi预条件虽然十分简单,但对阵列侧向测井(尤其各个子区域电导率差异较大时)模拟时求解离散得到的有限元方程却非常有效,较直接CG法求解加速十几倍.
|
|
表 1 SOR、CG和PCG计算时间及其迭代次数 Table 1 Computing time and iterations of SOR,CG and PCG |
图 7给出了SOR、CG和PCG三种方法的收敛速度.从图中可看出:共轭梯度法收敛非常缓慢,迭代了1000次残差基本保持不变,尽管最终能收敛到问题的精确解,但在整个迭代过程中误差震荡得比较厉害;SOR法刚开始收敛速度比较快,但之后收敛趋于平缓,残差基本保持不变.而PCG法收敛速度非常快,且迭代过程中残差几乎严格单调下降趋于零,能迅速收敛到原问题的准确解.

|
图 7 SOR、CG和PCG收敛曲线 Fig. 7 The convergence curves of SOR, CG and PCG |
阵列侧向测井仪器不可避免地受到井眼的影响,下面仅对存在井眼的无限厚地层,研究泥浆电阻率Rm和井眼半径rh对测井响应的影响.
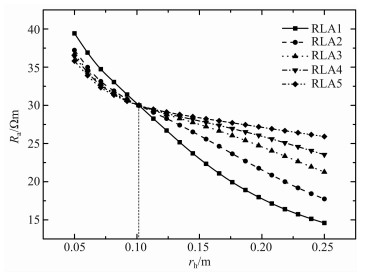
图 8为无侵入无限厚地层视电阻率随井眼半径变化的关系曲线,其地层模型为:Rm=30 Ωm,Rt=1Ωm.从图中可看出,阵列侧向测井曲线RLA1-RLA5受井径影响的程度依次减小,其中RLA1受井径影响最大,这与5条测井曲线的探测深度有关.并且,当井眼半径大于0.15m时,探测深度最浅的RLA0所测的视电阻率基本上不受井眼半径变化的影响.
|
图 8 井眼半径影响曲线 Fig. 8 The effect of the radius of the well |
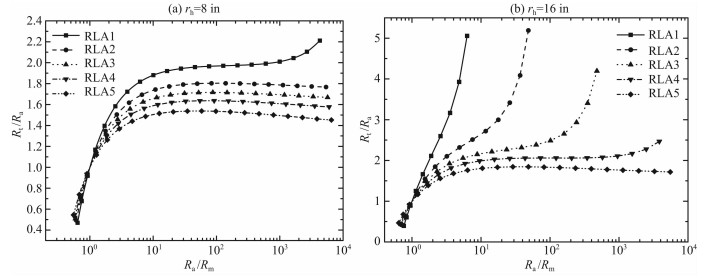
图 9a、9b分别给出8in和16in井眼无侵入无限厚地层阵列侧向测井计算结果.从图 9a可知,浅测深RLA1受井眼电阻率影响最大,而探测深度较深的RLA2-RLA5受井眼的影响相对较小.从图 9b可看出,测井曲线RLA1-RLA5受泥浆电阻率的影响依次减小;且随着井眼尺寸的增加,浅探测深度的仪器响应受井眼的影响较8in井径的情形明显加剧.
|
图 9 井眼泥浆电阻率影响曲线 Fig. 9 The effect of the resistivity of mud |
阵列侧向测井仪器的径向响应与泥浆滤液的侵入深度密切相关.为了研究仪器侵入响应,取无限厚地层,讨论存在井眼、侵入带和原始地层的情形.
图 10给出8in井眼在不同侵入半径ri下的阵列侧向测井响应.低侵模型地层参数:Rm=1Ωm,Rx0=10Ωm,Rt=100Ωm;高侵模型地层参数:Rm=1Ωm,Rx0=100Ωm,Rt=10Ωm.从图 10可看出,当侵入深度较小时,视电阻率接近地层真实电阻率;随着侵入深度的增加,仪器响应受侵入带的影响,逐渐偏离地层电阻率.并且,仪器径向探测深度越浅,受侵入的影响越严重,对地层真电阻率的偏离越大.与文献[9]得到的分析结果比较吻合.

|
图 10 测井响应随侵入半径变化曲线 Fig. 10 The curve of logging responses vs. the radius of invasion |
纵向分辨率是电阻率测井仪器的重要指标之一.为了研究层厚对测井响应的影响,考虑8in井眼的无侵模型,地层参数为Rt=50 Ωm,Rs=3Ωm,Rm=0.1Ωm.
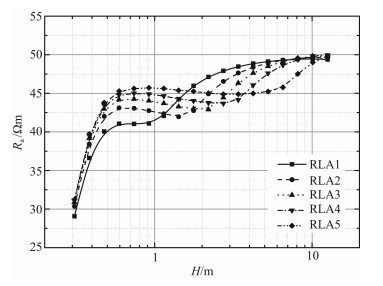
图 11给出了阵列侧向测井的计算结果,从图中可看出,层厚越大,仪器响应受围岩低阻的影响就越小.对于1m以上的目的层,仪器响应受围岩的影响比较小,最小视电阻率也超过42Ωm;当层厚达到10 m时,5条视电阻率测井曲线RLA1-RLA5几乎都能给出地层真电阻率50Ωm.并且,对于厚度仅为0.5m的高阻层,5条测井曲线仍有一定程度的分离,这说明阵列侧向测井仪具有较好的薄层分辨能力.
|
图 11 测井响应随地层厚度变化曲线 Fig. 11 The curve of logging responses vs. formation thickness |
本文推导了高分辨率阵列侧向测井问题中截断边界上的Robin边界条件,建立其具有等值面边界条件的椭圆边值问题数学模型,利用线性叠加原理、预条件、稀疏矩阵压缩存贮等技术,给出了轴对称地层中阵列侧向测井的快速有限元计算方案,并定量分析了地层厚度、井径、侵入带等因素对阵列侧向测井响应的影响.具体结论如下:
(1)对阵列侧向测井问题,Robin边界条件相对于传统的Dirichlet条件更加精确,可在保持精度的前提下大大减小问题的计算区域,节省计算机内存和正演时间.
(2)线性叠加原理,不仅能避开阵列侧向测井事先屏蔽电极上电流不确定的困难,且能大大简化原问题的计算.
(3) Jacobi预条件子不占用内存空间、实现非常简单,且对阵列侧向测井正演问题,能达到比较理想的加速效果.
(4)高分辨率阵列侧向测井具有纵向分辨率高、径向探测信息丰富等优点,可为同时反演侵入深度、侵入带电阻率和原始地层电阻率提供丰富的信息.
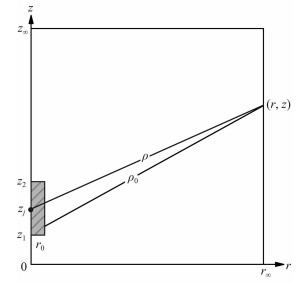
附录 轴对称均匀地层中柱状电极电场精确解及Robin边界条件考虑附图 1所示的轴对称均匀地层,发射电流的第j个电极位置为[z1,z2],半径为r0.
|
图 附图 1 均匀地层示意图 Fig. 附图 1 Schematic diagram of homogeneous formation |
利用微元分析法,柱状电极上取面积元素为
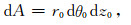
|
(A1) |
其上的电流微元

|
(A2) |
故产生的电场
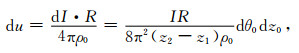
|
(A3) |
其中ρ0为点(r,θ,z)到点(r0,θ0,z0)的距离,即

|
(A4) |
因此,均匀地层柱状电极电场为:
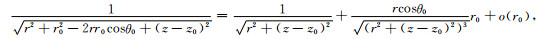
|
(A5) |
其中,常数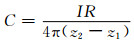
由于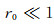
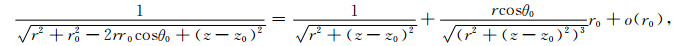
|
取一阶近似得
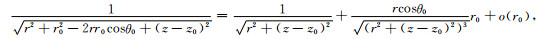
|
(A6) |
利用中点积分公式
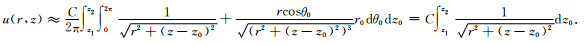
|
(A7) |
可得
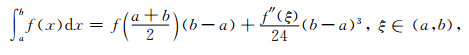
|
(A8) |
其中,zj为电极中心的z坐标.进一步考虑到电极尺寸相对其到区域边界的距离比较小,即

|
(A9) |
因此,

|
(A10) |
其中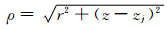

|
(A11) |
整理即得边界条件(3).
致谢作者衷心感谢两位匿名审稿专家提出的宝贵修改意见,特别感谢复旦大学“电法测井的数学建模及数值模拟”课题组李大潜院士和蔡志杰教授的有益指导
| [1] | Chen Y H, Chew W C, Zhang H J. A novel array laterolog method. The Log Analyst , 1998, 39(5): 23-30. |
| [2] | 张庚骥. 电法测井. 北京: 石油工业出版社, 1984 . Zhang G J. Electrical Well Logging (in Chinese). Beijing: Petroleum Industry Press, 1984 . |
| [3] | 张建华, 刘振华, 仵杰. 电法测井原理与应用. 西安: 西北大学出版社, 2002 . Zhang J H, Liu Z H, Wu J. Theory and Application of Electrical Well Logging (in Chinese). Xi'an: Northwest University Press, 2002 . |
| [4] | 李大潜, 郑宋穆, 谭永基, 等. 有限元素在电法测井中的应用. 北京: 石油工业出版社, 1980 . Li D Q, Zheng S M, Tan Y J, et al. Application of Finite Element Method in Electric Well Logging (in Chinese). Beijing: Petroleum Industry Press, 1980 . |
| [5] | 徐世浙. 地球物理中的有限单元法. 北京: 科学出版社, 1994 . Xu S Z. The Finite Element Method in Geophysics (in Chinese). Beijing: Science Press, 1994 . |
| [6] | 欧东新, 阮百尧, 王家林. 电导率线性变化测井二维有限单元法数值模拟. 同济大学学报(自然科学版) , 2005, 33(5): 692–695. Ou D X, Ruan B Y, Wang J L. 2-dimension finite element method to simulate logging when conductivity is piecewise linear variable. Journal of Tongji University (Natural Science) (in Chinese) , 2005, 33(5): 692-695. |
| [7] | 肖占山, 徐世浙, 罗延钟, 等. 复电阻率测井的数值模拟研究. 石油地球物理勘探 , 2007, 42(3): 343–347. Xiao Z S, Xu S Z, Luo Y Z, et al. Study on numeric simulation of complex resistivity logging. Oil Geophysical Prospecting (in Chinese) , 2007, 42(3): 343-347. |
| [8] | 朱军, 冯琳伟. 高分辨率双侧向测井响应数值模拟分析. 石油地球物理勘探 , 2007, 42(4): 457–462. Zhu J, Feng L W. Analysis on numeric simulation of high-resolution dual laterolog (DLL) response. Oil Geophysical Prospecting (in Chinese) , 2007, 42(4): 457-462. |
| [9] | 刘振华, 胡启. 阵列侧向测井响应的计算及其特征. 西安石油学院学报 , 2002, 17(1): 53–57. Liu Z H, Hu Q. Calculation and characteristics of array laterlog responses. Journal of Xi'an Petroleum Institute (in Chinese) , 2002, 17(1): 53-57. |
| [10] | 仵杰, 谢尉尉, 解茜草, 等. 阵列侧向测井仪器的正演响应分析. 西安石油大学学报(自然科学版) , 2008, 23(1): 73–76. Wu J, Xie W W, Xie X C, et al. Forward response analysis of array lateral logging tool. Journal of Xi'an Shiyou University (Natural Science Edition) (in Chinese) , 2008, 23(1): 73-76. |
| [11] | 范宜仁, 蒋建亮, 邓少贵, 等. 高分辨率阵列侧向测井响应数值模拟. 测井技术 , 2009, 33(4): 333–336. Fan Y R, Jiang J L, Deng S G, et al. Numerical simulation of high resolution array lateral logging responses. Well Logging Technology (in Chinese) , 2009, 33(4): 333-336. |
| [12] | 邓少贵, 仝兆岐, 范宜仁. 各向异性倾斜地层双侧向测井响应数值模拟. 石油学报 , 2006, 27(3): 61–64. Deng S G, Tong Z Q, Fan Y R. Numerical simulation of dual laterolog response in tilted anisotropic formation. Acta Petrolei Sinica (in Chinese) , 2006, 27(3): 61-64. |
| [13] | 邓少贵, 李竹强, 李智强. 水平井双侧向测井响应及层厚/围岩影响快速校正. 石油勘探与开发 , 2009, 36(6): 725–729. Deng S G, Li Z Q, Li Z Q. Response of dual laterolog and fast correction for layer thickness and shoulder bed in horizontal wells. Petroleum Exploration and Development (in Chinese) , 2009, 36(6): 725-729. DOI:10.1016/S1876-3804(10)60005-5 |
| [14] | 邓少贵, 李智强. 裂缝性储层裂缝的阵列侧向测井响应数值模拟. 地球科学-中国地质大学学报 , 2009, 34(5): 841–847. Deng S G, Li Z Q. Simulation of array laterolog response of fracture in fractured reservoir. Earth Science-Journal of China University of Geosciences (in Chinese) , 2009, 34(5): 841-847. DOI:10.3799/dqkx.2009.095 |
| [15] | 汪功礼, 张庚骥, 崔锋修, 等. 三维感应测井响应计算的交错网格有限差分法. 地球物理学报 , 2003, 46(4): 561–567. Wang G L, Zhang G J, Cui F X, et al. Application of staggered grid finite difference method to the computation of 3D induction logging response. Chinese J. Geophys. (in Chinese) , 2003, 46(4): 561-567. |
| [16] | 沈金松. 用有限差分法计算各向异性介质中多分量感应测井的响应. 地球物理学进展 , 2004, 19(1): 101–107. Shen J S. Modeling of the multi-component induction log in anisotropic medium by using finite difference method. Progress in Geophysics (in Chinese) , 2004, 19(1): 101-107. |
| [17] | 刘四新. 二维圆柱坐标下FDTD法对多频电磁波测井的数值模拟. 吉林大学学报(地球科学版) , 2004, 32(2): 283–286. Liu S X. Multi-frequency electromagnetic well logging simulation by 2-D cylindrical FDTD. Journal of Jilin University (Earth Science Edition) (in Chinese) , 2004, 32(2): 283-286. |
| [18] | Pan K J, Tan Y J, Hu H L. Mathematical model and numerical method for spontaneous potential log in heterogeneous formations. Applied Mathematics and Mechanics , 2009, 30(2): 209-219. DOI:10.1007/s10483-009-0208-z |
| [19] | 潘克家, 谭永基. 复杂地层中自然电位测井的高效数值模拟. 石油地球物理勘探 , 2009, 44(3): 371–376. Pan K J, Tan Y J. High-efficient numeric simulation of spontaneous potential log in complex beds. Oil Geophysical Prospecting (in Chinese) , 2009, 44(3): 371-376. |
| [20] | 杨守文, 汪宏年, 陈桂波, 等. 倾斜各向异性地层中多分量电磁波测井响应三维时域有限差分(FDTD)算法. 地球物理学报 , 2009, 52(3): 833–841. Yang S W, Wang H N, Chen G B, et al. The 3-D finite difference time domain (FDTD) algorithm of response of multi-component electromagnetic well logging tool in a deviated and layered anisotropic formation. Chinese J. Geophys. (in Chinese) , 2009, 52(3): 833-841. |
| [21] | 邓少贵, 李智强, 范宜仁, 等. 斜井泥浆侵入仿真及其阵列侧向测井响应数值模拟. 地球物理学报 , 2010, 53(4): 994–1000. Deng S G, Li Z Q, Fan Y R, et al. Numerical simulation of mud invasion and its array laterolog response in deviated wells. Chinese J. Geophys. (in Chinese) , 2010, 53(4): 994-1000. |
| [22] | Chew W C, Nie Z P, Liu Q H, et al. An efficient solution for the response of electrical well logging tools in a complex environment. IEEE Transactions on Geoscience and Remote Sensing , 1991, 29(2): 308-313. DOI:10.1109/36.73673 |
| [23] | 聂在平, 陈思渊. 复杂介质环境中双侧向测井响应的高效数值分析. 电子学报 , 1994, 22(6): 30–38. Nie Z P, Chen S Y. The numerical analysis for the response of dual lateral logging tool in a complex environment. Acta Electronica Sinica (in Chinese) , 1994, 22(6): 30-38. |
| [24] | 聂在平, 陈思渊, 曾昭光, 等. 二维完全非均匀介质中位场格林函数的数值解. 地球物理学报 , 1994, 37(5): 688–697. Nie Z P, Chen S Y, Zeng Z G, et al. The numerical solution of Green's function for potential in two dimension inhomogeneous media. Acta Geophysica Sinica (Chinese J. Geophys.) (in Chinese) , 1994, 37(5): 688-697. |
| [25] | 张庚骥, 汪涵明, 汪功礼. 成层介质中交流电测井响应. 地球物理学报 , 1995, 38(6): 840–849. Zhang G J, Wang H M, Wang G L. Logging response in stratified media. Chinese J. Geophys. (in Chinese) , 1995, 38(6): 840-849. |
| [26] | 张庚骥, 汪涵明. 普通电阻率测井的数值模式匹配解法. 石油大学学报(自然科学版) , 1996, 20(2): 23–29. Zhang G J, Wang H M. Solution of the normal resistivity logging with the numerical mode-matching method. Journal of the University of Petroleum, China (Edition of Natural Sciences) (in Chinese) , 1996, 20(2): 23-29. |
| [27] | 袁宁, 聂在平, 聂小春. 自然电位测井响应的高效数值模拟. 地球物理学报 , 1998, 41(S1): 429–436. Yuan N, Nie Z P, Nie X C. Numerical analysis of SP log response in complex heterogeneous media. Acta Geophysica Sinica (Chinese J. Geophys.) (in Chinese) , 1998, 41(S1): 429-436. |
| [28] | 谭茂金, 张庚骥, 运华云, 等. 非轴对称条件下用三维模式匹配法计算电阻率测井响应. 地球物理学报 , 2007, 50(3): 939–945. Tan M J, Zhang G J, Yun H Y, et al. 3-D numerical mode-matching (NMM) method for resistivity logging responses in nonsymmetric conditions. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 939-945. |
| [29] | 顿月芹, 唐章宏, 冯琳伟, 等. 侧向测井响应计算中模拟柱状电极的快速处理方法. 测井技术 , 2008, 32(4): 310–313. Dun Y Q, Tang Z H, Feng L W, et al. A fast method for simulating cylindrical electrodes in lateral log response calculation. Well Logging Technology (in Chinese) , 2008, 32(4): 310-313. |
| [30] | 顿月芹, 闵越, 袁建生. 阵列侧向测井正演响应的特性分析. 山东大学学报(工学版) , 2010, 40(1): 121–125. Dun Y Q, Min Y, Yuan J S. Characteristic analysis of the forward response of array lateral logging. Journal of Shandong University (Engineering Science) (in Chinese) , 2010, 40(1): 121-125. |
| [31] | Dun Y Q, Tang Z H, Zhang F, et al. Fast calculation and characteristic analysis of array lateral-logging responses. International Journal of Applied Electromagnetics and Mechanics , 2010, 33(1-2): 145-151. |
| [32] | 汪宏年, 陶宏根, 姚敬金, 等. 用模式匹配算法研究层状各向异性倾斜. 地球物理学报 , 2008, 51(5): 1591–1599. Wang H N, Tao H G, Yao J J, et al. Study on the response of a multicomponent induction logging tool in deviated and layered anisotropic formations by using numerical mode matching method. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1591-1599. |
| [33] | 汪宏年, 胡平, 陶宏根, 等. 水平层状非均质横向同性地层中阵列多分量感应测井响应的快速计算. 地球物理学报 , 2012, 55(2): 717–726. Wang H N, Hu P, Tao H G, et al. Fast algorithm of responses of array multicomponent induction logging tool in horizontally stratified inhomogeneous TI media. Chinese J. Geophys. (in Chinese) , 2012, 55(2): 717-726. |
| [34] | 李大潜, 郑宋穆, 谭永基, 等. 自共轭椭圆型方程具等值面边界条件的边值问题(I). 复旦学报(自然科学版) , 1976(1): 61–71. Li D Q, Zheng S M, Tan Y J, et al. Boundary value problems with equivalued surface boundary condition for self-adjoint elliptic equation (I). Journal of Fudan University (Natural Science) (in Chinese) , 1976(1): 61-71. |
| [35] | 潘克家, 汤井田, 胡宏伶, 等. 直流电阻率法2.5维正演的外推瀑布式多重网格法. 地球物理学报 , 2012, 55(8): 2769–2778. Pan K J, Tang J T, Hu H L, et al. Extrapolation cascadic multigrid method for 2.5D direct current resistivity modeling. Chinese J. Geophys. (in Chinese) , 2012, 55(8): 2769-2778. |
| [36] | 潘克家, 胡宏伶, 陈传淼, 等. 外推瀑布式多网格法的OpenMP并行化. 计算数学 , 2012, 34(4): 425–436. Pan K J, Hu H L, Chen C M, et al. Parallelization of extrapolation cascadic multigrid method using OpenMP. Mathematica Numerica Sinica (in Chinese) , 2012, 34(4): 425-436. |
| [37] | 吴小平, 汪彤彤. 利用共轭梯度算法的电阻率三维有限元正演. 地球物理学报 , 2003, 46(3): 428–432. Wu X P, Wang T T. A 3-D finite-element resistivity forward modeling using conjugate gradient algorithm. Chinese J. Geophys. (in Chinese) , 2003, 46(3): 428-432. |
| [38] | Wu X P, Xiao Y F, Qi C, et al. Computations of secondary potential for 3D DC resistivity modelling using an incomplete Choleski conjugate-gradient method. Geophys. Prospect. , 2003, 51(6): 567-577. DOI:10.1046/j.1365-2478.2003.00392.x |
| [39] | 吴小平, 徐果明, 李时灿. 利用不完全Cholesky共轭梯度法求解点源三维地电场. 地球物理学报 , 1998, 41(6): 848–855. Wu X P, Xu G M, Li S C. The calculation of three-dimensional geoelectric field of point source by incomplete Cholesky conjugate gradient method. Acta Geophysica Sinica (Chinese J. Geophys.) (in Chinese) , 1998, 41(6): 848-855. |
 2013, Vol. 56
2013, Vol. 56