地球物理学报  2013, Vol. 56 Issue (12): 4206-4214   PDF    
引用本文
段鹏飞, 程玖兵, 陈爱萍 等. TI介质局部角度域高斯束叠前深度偏移成像. 地球物理学报, 2013, 56(12): 4206-4214, doi: 10.6038/cjg20131223.  
Duan P F, Cheng J B, Chen A P, et al. Local angle-domain Gaussian beam prestack depth migration in a TI medium. Chinese J. Geophys. (in Chinese), 2013, 56(12): 4206-4214, doi: 10.6038/cjg20131223.  
TI介质局部角度域高斯束叠前深度偏移成像
段鹏飞1,2 , 程玖兵1 , 陈爱萍2 , 何光明2     
1. 同济大学海洋与地球科学学院, 上海 200092;
2. 中国石油川庆钻探工程有限公司地球物理勘探公司, 成都 610213
收稿日期 2012-09-20, 2013-10-30 收修定稿
基金项目: 国家自然科学基金（41074083）资助
作者简介: 段鹏飞, 男, 1987年生, 硕士, 主要从事各向异性介质地震波传播与成像方法研究.E-mail:duanpengfei7@gmail.com
通讯作者: 程玖兵, 副教授, 研究方向为地震各向异性、偏移速度模型构建、储层地震成像与描述方法.E-mail:cjb1206@tongji.edu.cn
摘要: 各向异性射线理论基础上的局部角度域叠前深度偏移方法能够为深度域构造成像与基于角道集的层析反演提供有力支撑，但是对于复杂地质构造而言，高斯度叠前深度偏移在不失高效、灵活等特点的情况下，具有明显的精度优势.为此，本文研究局部角度域理论框架下的高斯束叠前深度偏移方法.为提高算法效率与实用性，文中讨论了一种从经典弹性参数表征的各向异性介质运动学和动力学射线方程演变而来的由相速度表征的简便形式，并提出了一种比较经济的各向异性高斯束近似合成方案.结合地震波局部角度域成像原理，讨论一种适合高斯束偏移的角度参数计算方法.国际上通用的理论模型合成数据试验表明：相比局部角度域Kirchhoff叠前深度偏移成像方法，本文方法具有更高的成像精度与抗噪能力，既适用于复杂构造成像，也可为TI介质深度域偏移速度分析与模型建立提供高效的偏移引擎.
关键词: 横向各向同性      运动学射线追踪      动力学射线追踪      高斯束      局部角度域      叠前深度偏移     
Local angle-domain Gaussian beam prestack depth migration in a TI medium
DUAN Peng-Fei1,2, CHENG Jiu-Bing1, CHEN Ai-Ping2, HE Guang-Ming2     
1. School of Ocean and Earth Science, Tongji University, Shanghai 200092, China;
2. CNPC CDEC Sichuan Geophysical Company, Chengdu 610213, China
Abstract: Angle-domain prestack depth migration based on anisotropic ray theory can provide strong support to the structural imaging in the depth domain and angle-gather-based seismic tomography. The Gaussian beam prestack depth migration has shown its great advantages in accuracy of complex structural imaging, computational efficiency and flexibility. In this paper, we focus on implementing Gaussian beam perstack depth migration in the framework of local angle domain imaging. In order to improve the efficiency and practicability of proposed algorithm, we discuss a kind of phase velocity based kinematic and dynamic ray tracing systems, which is evolved from the classic ray tracing equation of anisotropic media. And we propose a more economical program for constructing anisotropic Gaussian beams. Combined with the principle of seismic local angle domain imaging, we discuss an angle parameter calculation method which is suitable for Gaussian beam migration. Numerical tests on the standard theoretical anisotropic models show that compared with local angle domain Kirchhoff migration, our approach has a higher imaging precision and better anti-noise ability. It also can be used as an imaging tool for complex geological structures and efficient migration engine for anisotropic migration velocity analysis and model construction..
Key words: Transversely isotropic      Kinematic ray tracing      Dynamic ray tracing      Gaussian beam      Local angle domain      Prestack depth migration     
1 引言

随着地震勘探目标越来越复杂、越来越精细, 长偏移距、宽方位三维地震资料采集得越来越多, 对改善复杂地质体成像、压制三维噪声、提高非构造型油气藏的勘探成功率起到了重要推动作用.随着地震观测的排列变长, 方位角分布变宽, 速度各向异性对地震波传播、成像与反演的影响变得越来越不可忽视.这就要求地震偏移成像与速度模型建立方法要根据实际观测系统的特点, 合理考虑速度各向异性.对于构造成像问题而言, 人们主要关注沉积地层最普遍的一种等效各向异性模型, 即横向各向同性(TI)介质, 包括具有垂直对称轴的VTI介质和具有倾斜对称轴的TTI介质.

叠前深度偏移是强横向非均匀介质复杂构造成像与速度模型建立依赖的关键技术.高斯束叠前深度偏移作为Kirchhoff偏移方法的一种有效改进, 它既克服了Kirchhoff偏移所固有的缺陷和不足(如不能有效应对多波至、焦散等复杂波现象), 又保留了其高效、灵活的优点以及对陡倾构造成像的能力; 其成像精度接近波动方程偏移, 但计算效率远远高于波动方程偏移.高斯束方法最早由Cerveny [1]引入地球物理领域, 并应用于地震波场模拟中.随后Hill提出高斯束叠后偏移[2], 并于2001年将其拓展到适用于共偏移距、共方位角道集的叠前偏移[3]. Nowack等[4]和Gray [5]分别针对Hill方法对观测系统适应性不足的问题, 提出了适用于共炮道集的叠前偏移方法.Gray [6]基于Bleistein提出的广义真振幅共炮道集偏移理论, 将高斯束偏移同真振幅单程波方程偏移相结合, 提出了基于炮道集的真振幅高斯束偏移.并且认为高斯束叠前深度偏移输出角度域共成像点道集存在一些优势[7].李振春等[8]提出了一种高斯束偏移角道集的提取方法(利用走时慢度), 岳玉波等[9]讨论了复杂地表情况下保幅高斯束叠前深度偏移方法.Alkhalifah[10]和Zhu等[11]分别讨论了各向异性介质中的高斯束叠后和叠前偏移方法.Zhu等[12-13]将各向异性介质射线追踪领域的工作使得高斯束叠前深度偏移可以很容易的拓展到一般TI介质及弱正交各向异性介质中.

在强横向非均匀介质中, 传统的偏移距域和炮域共成像点道集都可能都存在明显的相干性噪声.影响偏移速度分析和AVO分析[14-15].于是, 角度域成像方法引起了人们的关注, 并视其为解决上述问题的有效途径[15-16].本文是对段鹏飞等[17]所研究的各向异性射线理论基础上的局部角度域叠前深度偏移方法的继承和发展.根据强横向非均匀各向异性介质地震波成像与偏移速度模型建立的需要, 着重研究TI介质局部角度域高斯束叠前深度偏移成像方法.首先介绍各向异性介质射线追踪基础上的高斯束计算方法, 然后讨论局部角度域叠前深度偏移成像算法的实现过程, 最后借助国际上通用的理论模型检验算法的可靠性.

2 各向异性介质射线追踪基础上的高斯束计算 2.1 基于相速度表征的运动学与动力学射线方程

文献[17]详细介绍了从经典各向异性介质射线方程演变而来的由相速度表征的运动学射线方程的推导过程, 为此本文直接给出其表达式, 并以此为基础介绍相速度表征的各向异性动力学射线方程.

根据Zhu等[11-13]的工作, 各向异性介质中的相速度表征的运动学方程为

(1a)

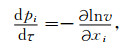
(1b)

其中v=v(xi, ni)为相速度, VGi为群速度VG在空间坐标xi方向上的分量, ni为单位慢度矢量.

在各向异性介质中, 群速度可以表达为, 为了方便动力学射线追踪的推导, 可将运动学射线追踪方程改写为

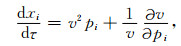
(2a)

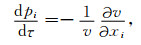
(2b)

设相速度法相矢量为n=-(cosφsinθ, sinφsinθ, cosθ), 其中, θ和φ分别为相角及其方位角.于是可将(2a)式偏微分项改为如下形式:

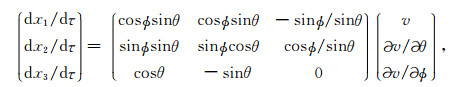
(3)

上式即为三维任意各向异性介质中, 由相速度计算群速度的显式的表达式.方程组(2)对射线参数求偏导可以得到笛卡尔坐标系中6个偏微分方程组成的由相速度表征的动力学射线追踪方程组:

(4)

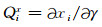
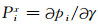
其中, , γ表示射线坐标系(γ1, γ1, τ)中γ1或γ2方向.系数为

(5)

2.2 基于波前正交坐标系的动力学射线方程

对于高斯射线束的计算, 人们通常用以射线为中心的局部坐标来描述动力学射线方程.这种局部坐标可使得方程组(4)式由6个一阶偏微分方程减少到4个.为此, 前人[1]讨论了两种局部坐标系:射线中心坐标系和波前正交坐标系.各向异性介质中, 射线中心坐标系不再是一个正交坐标系, 因此, 相比各向同性情况(射线中心坐标系为正交坐标系), 将动力学射线方程从笛卡尔坐标系转换到射线中心坐标系变得更加复杂.而各向异性介质中, 波前正交坐标系仍然是一个正交坐标系.本文仅讨论波前正交坐标系下的动力学射线追踪方程.

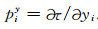
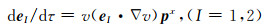
用y=(y1, y2, y3)表示波前正交坐标系, 该坐标系对应的慢度矢量可表示为.如图 1所示, 波前正交坐标系的一组基向量为(e1, e2, e3), 其中e3=n与波前垂直.单位向量e1和e2与波前相切, 并且满足:

(6)

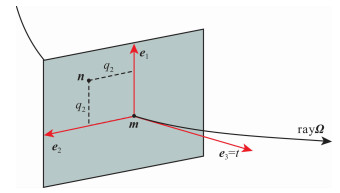
图 1 波前正交坐标系示意图 Fig. 1 Wavefront orthogonal coordinate

应用由上述基向量为元素所组成的转换矩阵可将方程组(4)由笛卡尔坐标系转化到波前正交坐标系, 最终得到由4个一阶偏微分方程组成的方程组:

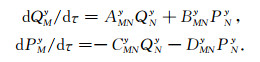
(7)

其中的系数满足:

(8)

其中VMy和VNy分别代表群速度在波前正交坐标系中沿y1和y2方向上的分量.与各向同性介质中运动学及动力学射线追踪方程相似, 射线方程组(1)和(7)右侧不再是复杂的弹性参数表达形式, 而是由相速度及群速度表达的形式.由于群速度可通过相速度计算得出, 因此它们就组成了相速度表示、适应一般各向异性介质的运动学及动力学射线方程组.

2.3 动力学射线方程近似与高斯束计算简化

观察方程组(7)不难发现, 其系数的表达式依然很复杂, 由多个相速度的一阶及二阶偏导数组成.这些偏导数在计算过程中, 不仅编程复杂, 而且计算成本很高.特别是当考虑TTI等更复杂各向异性介质时, 对称轴角度参数也是空间坐标的函数, 相速度关于空间坐标的偏导数变得更加复杂.为此, 本文引入一些近似来提高计算效率, 基本思路就是射线路径计算(运动学射线追踪部分)时考虑各向异性, 且不做其他近似, 但在高斯束合成(动力学射线追踪部分)时, 借用各向同性介质算法, 只不过其传播方向要考虑各向异性影响.由于地震波在各向异性介质中传播时相速度与群速度的传播方向不一致, 在合成高斯束时需要沿着相速度矢量的方向计算该高斯束上的振幅及走时.这样, 方程组(7)的系数可简化成:

(9)

3 高斯束局部角度域成像原理 3.1 共炮域高斯束叠前深度偏移

三维声学介质中, 地下一点x处的标量地震波场U(x, xs, ω)可用第二类Rayleigh积分表示:

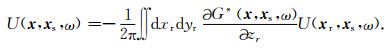
(10)

其中, xs=(xs, ys)为震源; xr=(xr, yr)代表检波点.另外, 检波点xr到成像点x处的格林函数G(x, xr, ω)可以通过高斯波束UGB(x, xs, p, ω)的积分叠加表示:

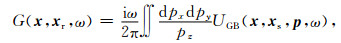
(11)

因为高斯波束UGB(x, xs, p, ω)在起始点处为局部平面波.Hill[2-3]利用这个特点将地表记录波场分解为同高斯波束初始方向相匹配的局部平面波分量, 然后将局部平面波通过相对应的由波束中心出射的高斯波束延拓至地下进行成像.但是, 高斯束波前仅在初始点为绝对的平面波, 远离初始点的波前曲率不再为零, 此时利用线性倾斜叠加合成的平面波同匹配的高斯束在远离波束中心的位置存在走时和振幅的误差.为此Hill[2-3]提出了加高斯窗局部倾斜叠加, 利用高斯函数沿两侧衰减的性质可减少上述误差, 其表达式为

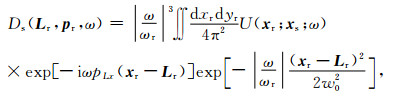
(12)

其中, Ds(Lr, pr, ω)为合成的局部平面波分量; Lr=(LxLy, 0)为高斯束中心位置坐标; ωr为参考频率; xr为高斯窗内检波点的位置; w0为高斯束的初始宽度; pr为波束中心初始慢度; U(xr; xs; ω)为高斯窗内的记录波场.

叠前高斯束偏移既适用于共偏移距域数据[2], 也适用于共炮域数据[4-5].相对于共偏移距的叠前高斯束偏移, 共炮域的高斯束偏移在处理陆地采集观测系统和地势落差大的资料时在灵活性方面具有优势.根据Nowack等[4]和Gray [5]的思路, 单炮记录在地下x点处的成像可表示为

(13)

其中, Is(x)为单炮记录在成像点x处的成像结果.系数C是一个与高斯束中心间隔及高斯束初始宽度有关的常数.将震源格林函数G(x, xs, ω)与束中心位置Lr有效范围内的检波点格林函数G(x, xr, ω)通过高斯束的积分叠加表示, 则上式可改写为

(14)

单个炮点成像结果Is(x)是式(14)所有束中心位置Lr计算结果的叠加, 最终成像结果为所有单炮偏移的叠加.叠前偏移中采用的其他公式(如束中心间隔和初始宽度)与Hill[2-3]给出的公式相似, 此处不再赘述.

3.2 高斯束局部角度参数计算

叠前偏移可视为从不同入射方向来的“源”波与不同方向出射的“接收”波在成像点的耦合(聚焦成像).在高频渐近意义下, 成像点处入射和散射波前面分别具有各自的格林函数属性, 如走时、几何扩散因子、走时梯度或慢度矢量等.如图 2所示, 三维情况下, 可用两类、四个角度参数共同定义地下成像点处局部传播方向.第一类是描述入射与散射(反射)方向特征的两个角度, 即入射角γ (散射张角θ的一半)和散射方位角(局部入射与散射慢度ps、pr所在平面的方位角)φ.AVA、AVAZ分析/反演就是考察和利用振幅随这两个角度的变化.第二类是描述局部照明方向的两个角度, 即照明矢量(入射与散射慢度矢量之和pm)的倾角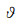与方位角φ.这4个角度参数可在射线理论框架下通过走时的空间梯度计算得到[18], 也可在波动理论框架下借助于波场局部方向分解隐式地获得[19].

图 2 成像点处地震波局部角度特征示意图 Fig. 2 Local angle characteristics of aselected ray pair at a subsurface image point

根据矢量运算法则, 前文所述4个局部角度参数分别满足[18]:

(15a)

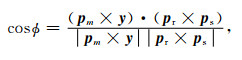
(15b)

(15c)

(15d)

式中pmz为照明矢量的垂向分量.x、y与z分别代表沿坐标轴的单位矢量, 其中y指向正北方向并作为定义方位角的参考方向.可见, 角度域成像的关键是计算得到成像点处入射与散射慢度矢量, 便可根据上述方程求取4个局部角度参数.运动学射线追踪过程中, 如果成像点落在追踪到的射线上时, 那么可以直接得到该点的慢度矢量.如果成像点落在射线附近, 则可通过以下步骤计算得到.

在三维波前正交坐标系中(如图 1), n点处高斯束的实值走时满足如下公式:

(16)

其中, T(m)为源点到中心射线Ω上参考点m的实值走时, qT=(qI, qJ)为描述波前正交坐标系中n点位置的二维矢量.M(m)为走时的二阶偏导数, 三维介质中为2×2矩阵; 二维介质中为一个标量.假设, 那么方程(16)及其空间偏导数为

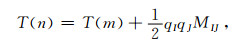
(17)

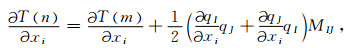
(18)

于是得到n点的射线慢度矢量为

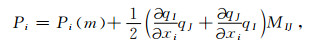
(19)

最终可以求得高斯束上n点的单位矢量:

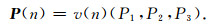
(20)

一旦获得入射与反射慢度矢量, 便可通过公式(15)求得成像点处的4个局部角度参数.

常规的成像结果相当于不同传播方向波场成像值的某种平均, 而局部角度域成像就是要在叠前偏移过程中保留这些像的局部方向信息.按上述理论得到的局部角度域共成像点道集是七维数据体, 其计算、存储与读写对目前的计算机仍是一项挑战.为了降低计算成本, 可输出入射角度(x, y, z, φ, γ)域或者照明角度(x, y, z, φ, )域的共成像点道集.前者适用于偏移速度分析、成像振幅随入射角或方位角变化(AVA/AVAZ)分析; 后者可用于提取地层走向与倾角属性, 也可用于绕射波的分离与成像等.当然, 也可以产生常规叠前深度偏移输出的成像叠加数据体与炮检距域共成像点道集.在具体实现时, 我们逐炮进行局部角度域高斯束偏移.

4 数值算例 4.1 SEG/HESSVTI模型

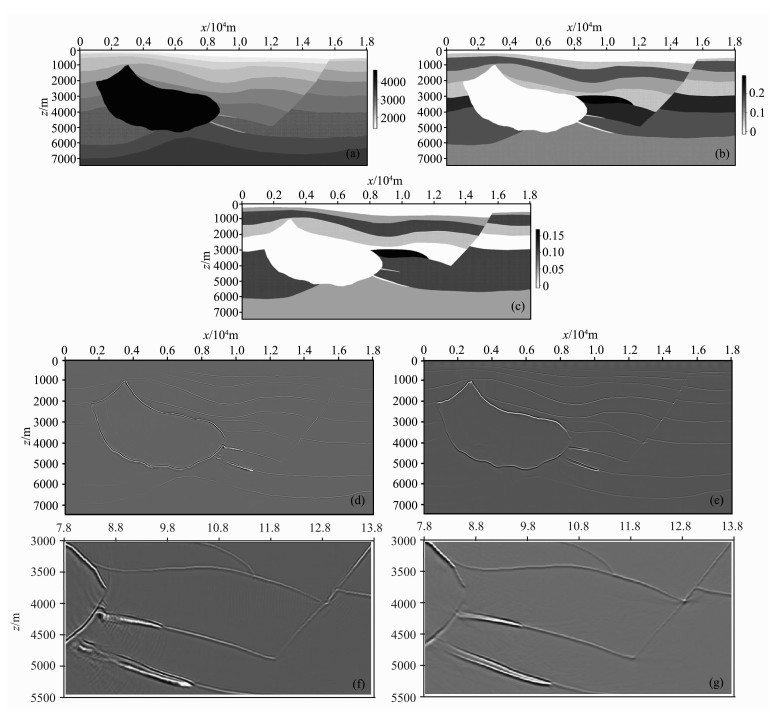
为了验证局部角度域高斯束叠前深度偏移在VTI介质中的应用, 本文对SEG/HESS理论模型合成数据进行了偏移试算.并将该算法偏移结果与局部角度域Kirchhoff叠前深度偏移结果进行对比[17].图 3(a、b、c)展示了SEG/HESS二维VTI模型垂直qP波速度、Thomsen参数ε和δ.模型左边有一个被各向异性岩层包围的盐丘, 右侧为一个断层面, 盐丘两侧与断层较为陡峭.图 3(d、e)分别展示了VTI介质局部角度域Kirchhoff叠前深度偏移结果[17]与VTI介质局部角度域高斯束叠前深度偏移结果.而图 3(f、g)分别展示了图 3(d、e)对应的该模型复杂构造区域放大显示的结果.可见, 虽然两种方法对盐丘边缘与断层都得到了很好的聚焦成像.但是在复杂的地质构造区域, 高斯束叠前深度偏移可以提供一个更加精细、准确的成像结果.不仅如此, 从成像剖面看, 高斯束偏移结果的信噪比明显优于Kirchhoff偏移结果.图 4(a、b)分别展示了Kirchhoff叠前深度偏移与高斯束叠前深度偏移对该模型偏移后的平均入射角域共成像点道集, 其中入射角范围为0°~60°.与Kirchhoff叠前深度偏移生成的角道集(图 4a)相比, 高斯束叠前深度偏移生成的角度域共成像点道集能量更聚焦, 信噪比也相对较好.图 4c展示了高斯束叠前深度偏移生成的照明倾角域共成像点道集.可见, 偏移后的反射波为似双曲线形状, 其中能量最强的顶点所对应的照明倾角与反射界面的倾角一致, 而偏移后的绕射波则具有明显不同的形态.

图 3 SEG/HESSVTI模型数值算例 (a) vp0模型; (b)ε模型; (c)δ模型; (d)各向异性Kirchhoff偏移结果; (e)各向异性高斯束偏移结果; (f)各向异性Kirchhoff偏移局部结果; (g)各向异性高斯束偏移局部结果. Fig. 3 Numerical example on SEG/HESS VTI model (a) vp0 model; (b)ε model; (c)δ model; (d) Anisotropic Kirchhoff migration; (e) Anisotropic Gaussian beam migration; (f) Anisotropic Kirchhoff migration; (g) Anisotropic Gaussian beam migration.
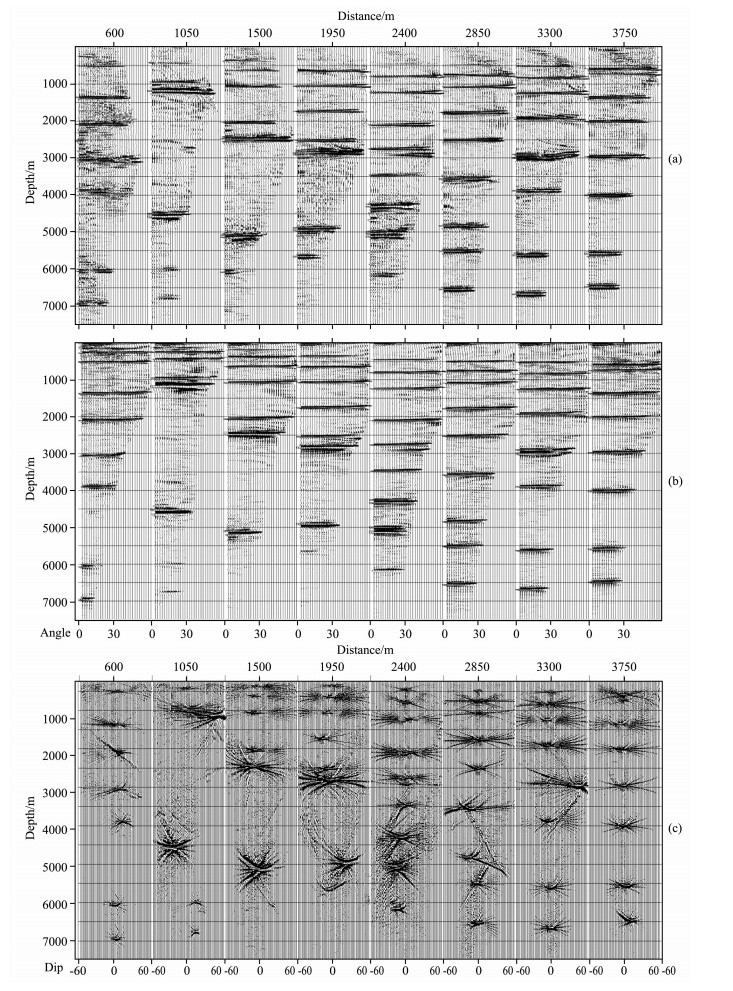
图 4 共成像点道集 (a) Kirchhoff平均入射角度域共成像点道集; (b)高斯束平均入射角度域共成像点道集; (c)高斯束照明倾角域共成像点道集. Fig. 4 Common image gathers (a) Kirchhoff average incident-angle domain CIGs; (b) Gaussian beam average incident-angle domain CIGs; (c) Gaussian beam illumination-dip domain CIGs.
4.2 TTI逆冲模型

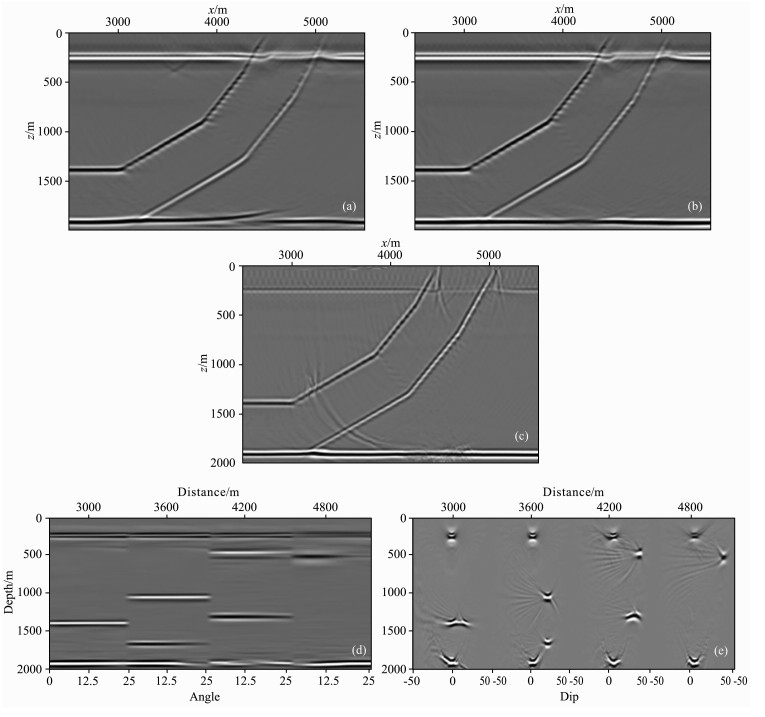
下面以国际上通用的逆冲模型为例来测试TTI介质局部角度域高斯束叠前深度偏移成像算法.其vp0、ε、δ、ν模型分别如图 5(a-d)所示.该模型数据正演模拟时底部放有一水平反射界面用于测试上覆各向异性介质对该界面反射地震波传播与成像的影响.首先对合成数据进行VTI介质高斯束叠前深度偏移(图 6a), 由于忽略对称轴倾角给走时计算带来明显误差, 进而导致该反射界面未能准确成像.图 6b显示了TTI介质高斯束叠前深度偏移结果, 此时底部的水平界面得到了正确成像, 相比TTI介质Kirchhoff叠前深度偏移结果(图 6c), 高斯束方法偏移结果更加的干净、精确.其成像剖面信噪比明显优于TTI介质Kirchhoff叠前深度偏移结果.图 6d为TTI介质局部角度域高斯束叠前深度偏移成像获得的平均入射角域共成像点道集.由于合成数据偏移距范围较小, 考虑的入射角范围为0°到25°.图 6e展示了TTI介质局部角度域高斯束叠前深度偏移成像获得的照明倾角域共成像点道集.

图 5 逆冲模型数 (a)vp0模型; (b)ε模型; (c)δ模型; (d)ν模型. Fig. 5 Overthrust model (a)vp0 model; (b)ε model; (c)δ model; (d)ν model.
图 6 逆冲模型偏移结果 (a)高斯束VTI偏移结果; (b)高斯束TTI偏移结果; (c) KirchhoffTTI偏移结果; (d)平均入射角域共成像点道集; (e)照明倾角域共成像点道集. Fig. 6 TTI data migration results (a) VTI migration; (b) TTI migration; (c) Kirchhoff TTI migration; (d) Average incident-angle CIGs; (e) Illumination-dip domain CIGs.
5 结论

本文基于简便、高效的各向异性运动学及动力学射线追踪, 实现了TI介质局部角度域高斯束叠前深度偏移成像方法.在各向异性介质射线追踪理论框架下, 提出了一种相对经济的动力学射线追踪近似方案.结合地震波局部角度域成像原理, 给出了一种适合高斯束计算的角度参数计算方法.文中VTI与TTI模型数值试验表明, 该高斯束局部角度域叠前深度偏移成像算法明显比Kirchhoff偏移方法精确, 能够给各向异性介质复杂构造成像与偏移速度分析提供强有力的支撑.局部角度域成像方法的优点还在于用到了成像孔径内所有波场数据而不是某些按地面炮检距与方位角分选的数据子集, 成像振幅更合理地反映了目的层“原位”的随入射角及其方位变化的带限反射系数信息.为后续的偏移速度分析、AVA分析等提供更加可靠的数据.下一步拟进一步将该算法推广到三维, 并使其适应更复杂的各向异性(如正交各向异性)介质.

致谢

感谢SEG提供文中使用的理论模型数据.

参考文献
[1] Cerveny V. Seismic Ray Theory. Cambridge: Cambridge University Press, 2001 .
[2] Hill N R. Gaussian beam migration. Geophysics , 1990, 55(11): 1416-1428. DOI:10.1190/1.1442788
[3] Hill N R. Prestack Gaussian-beam depth migration. Geophysics , 2001, 66(4): 1240-125. DOI:10.1190/1.1487071
[4] Nowack R, Sen M K, Stoffa P L, et al. Gaussian beam migration for sparse common-shot and common-receiver data. 73th Annual International Meeting, SEG, Expanded Abstracts, 2003: 1114.
[5] Gray S H. Gaussian beam migration of common-shot records. Geophysics , 2005, 70(4): S71-S77. DOI:10.1190/1.1988186
[6] Gray S H, Bleistein N. True-amplitude Gaussian-beam migration. Geophysics , 2009, 74(2): S11-S23. DOI:10.1190/1.3052116
[7] Gray S H. Angle gathers for Gaussian beam depth migration EAGE 69th Conference & Exhibition-London, UK, 11-14 June 2007.
[8] 李振春, 岳玉波, 郭朝斌, 等. 高斯波束共角度保幅深度偏移. 石油地球物理勘探 , 2010, 45(3): 360–365. Li Z C, Yue Y B, Guo C B, et al. Gaussian beam common angle preserved-amplitude migration. Oil Geophysical Prospecting (in Chinese) , 2010, 45(3): 360-365.
[9] 岳玉波, 李振春, 钱忠平, 等. 复杂地表条件下保幅高斯束偏移. 地球物理学报 , 2012, 55(4): 1376–1383. Yue Y B, Li Z C, Qian Z P, et al. Amplitude-preserved Gaussian beam migration under complex topographic conditions. Chinese J. Geophys. (in Chinese) , 2012, 55(4): 1376-1383.
[10] Alkhalifah T. Gaussian beam depth migration for anisotropic media. Geophysics , 1995, 60(5): 1474-1484. DOI:10.1190/1.1443881
[11] Zhu T F, Gray S H, Wang D L. Prestack Gaussian-beam depth migration in anisotropic media. Geophysics , 2007, 72(3): S133-S13. DOI:10.1190/1.2711423
[12] Zhu T F, Gray S H, Wang D L, et al. Kinematic and dynamic ray tracing in anisotropic media: Theory and application. 75th Annual International Meeting, SEG, Expanded Abstracts, 2005: 96-99.
[13] Zhu T F. Dynamic raytracing in inhomogeneous anisotropic media. GeoCanada , 2010.
[14] Nolan C, Symes W. Imaging in complex velocities with general acquisition geometry. The Rice Inversion Project (TRIP), Technical Report , 1996.
[15] ten Kroode A P E, Smit D J, Verdel A R. Linearized inverse scattering in the presence of caustic. SPIE-The International Society for Optical Engineering Expanded Abstracts , 1994: 28-42.
[16] de Hoop M V, Bleistein N. Generalized radon transform inversions for reflectivity in anisotropic elastic media. Inverse Problems , 1997, 13(3): 669-690. DOI:10.1088/0266-5611/13/3/009
[17] 段鹏飞, 程玖兵, 陈三平, 等. TI介质局部角度域射线追踪与叠前深度偏移成像. 地球物理学报 , 2013, 56(1): 269–279. Duan P F, Cheng J B, Chen S P, et al. Local angle-domain ray tracing and prestack depth migration in TI medium. Chinese J. Geophys. (in Chinese) , 2013, 56(1): 269-279.
[18] Cheng J B, Wang T F, Wang C L, et al. Azimuth-preserved local angle-domain prestack time migration in isotropic, vertical transversely isotropic and azimuthally anisotropic media. Geophysics , 2012, 77(2): S51-S64. DOI:10.1190/geo2011-0295.1
[19] Biondi B. Angle-domain common-image gathers from anisotropic migration. Geophysics , 2007, 72(2): 581-591.