2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Science, Beijing 100049, China
地震波正演模拟技术一直是地震学研究的热点, 无论是中小尺度的地震波逆时偏移[1-2]、全波形反演[3-4], 还是区域性地震动研究[5-6]以及全球地震波模拟[7-9]和地球介质非均匀性反演等方面, 正演模拟都起着关键作用.经过几十年的发展, 地震波模拟方法已逐渐完善, 总体而言, 这些方法可以分为三大类, 即射线法、积分方程法以及波动方程直接解法, Carcione等[10]和Yang等[11]对这些方法做了详细的回顾与讨论.本文主要讨论声波方程的直接解法.
无论是经典的有限差分法[12-14], 还是伪谱法[15-16]、有限元法[4, 6]、谱元法[17-18]等众多方法, 在时间离散上常常使用二阶中心差分或Newmark格式, 虽然计算效率较高, 但低阶的时间近似与高阶的空间离散格式往往不匹配, 以致影响了地震波模拟的精度.针对时间精度较低等问题, Dablain[19]将Lax等[20]提出的Lax-Wendroff方法运用至地震波模拟之中, 其思想是运用高次空间微分修正时间精度.为了计算方便, 一般得到时间四阶精度.但是直接运用有限长度的网格点波场值修正时间高次项, 精度往往不够, 针对此问题, Tong等[21]利用Yang等[22]发展的NearlyAnaylticDiscreteMethod (NAD)近似空间高阶微分, 得到了时间四阶、空间八阶的两步Stereo-Modeling Method (STEM)地震波模拟方法, 两步STEM法在实际地震波模拟中精度的提高、数值频散压制和数值方向各向异性控制等方面均明显优于Lax-Wendroff方法.
Chen在研究Lax-wendroff方法之后发现该方法在实际运用中误差增长较快[23], 针对此缺点, Chen将高阶的辛Runge-Kutta-Nyström (RKN)与辛Partitioned-Runge-Kutta (PRK)格式运用至声波模拟之中[24-25], 因辛格式严格保持Hamiltion系统微分二形式不变的特性[26], 有效地解决了地震波长时间计算中的误差累积等问题.Li等[27-28]在时间离散上采用三级三阶的辛PRK格式、空间离散上采用褶积微分算子法, 形成了一套较为高效的地震波模拟方法, 这些格式都是显式辛格式.与显式辛格式不同的隐式辛格式, 其优点为无条件稳定性, Luo等[29-30]主要讨论了二阶隐式辛格式, 但隐式辛格式涉及到微分算子的求逆运算, 直接LU分解消耗大量的时间, 谱因式分解虽计算速度快, 但面临着精度损失、边界处误差过大等弊端, 改进的混合算法虽然精度和计算效率上有所提高, 但仍无法满足高精度与高效率地震波模拟的要求.Ma等[31]在分析总结前人工作基础上, 提出在时间离散上采用二阶的辛PRK格式[32]、空间离散上采用NAD算子, 得到了一种高效、高精度的地震波模拟方法.
本文将伪谱法离散后的半离散声波方程变换至Hamilton系统, 在分析不同时间积分格式面临的诸多问题之后, 提出在时间离散上使用二级的辛RKN格式, 以保证较高的计算效率, 运用根数理论得到辛条件方程组.针对两个自由度的方程组, 为了实际模拟需要, 从精度、频散、稳定性三方面优化系数, 最后得到了三组优化系数, 理论上分析了新得到的优化格式在求解声波方程时的优良特性.在实际运用之中, 可以根据不同的实际需要选择不同的格式以得到更好的模拟结果.
2 辛RKN格式 2.1 声波方程的伪谱法离散在地震波模拟与成像中有限差分算子得到了广泛的应用[19], 但有限长度的有限差分算子精度较低、数值频散明显[11].伪谱法在精度和数值频散压制方面明显优于有限差分法[33], 随着计算机硬件的发展, 伪谱法有望运用至三维高精度地震波模拟与成像之中[16].
考虑如下形式的地震声波方程:
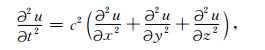
|
(1) |
其中, u(x, y, z, t)为声波波场值, c(x, y, z)为声速.在空间上采用均匀网格对(1)式离散, 即uijk≈ u(iΔx, jΔy, kΔz), i=1, 2, …, Ni, j=1, 2, …, Nj, k=1, 2, …, Nk, Δx, Δy, Δz为空间网格间距.若采用伪谱法计算(1)式中的空间微分, 得到的半离散方程如下:
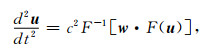
|
(2) |
其中, u为离散后的波场向量, F, F-1分别表示Fourier正变换和逆变换, 

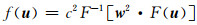
对于(2)式可以采用多种时间离散格式, 如三阶的Runge-Kutta方法(RK)[34]、Newmark格式[5, 7, 8]、二阶辛PRK格式[31-32]、三阶辛PRK格式[23, 27-28, 34]、四阶的辛RKN格式[24-26]以及最近Yang等发展的显式化后的RK格式与Adams格式[35-36].这些方法中二阶的辛PRK格式效率最高, 每一个时间步只需两次正反Fourier变换, 高阶格式虽然有较高的精度, 但每个时间步计算量过大以致严重影响计算效率.在大尺度以及全球尺度地震波模拟时, 由于空间微分计算量过大, 每个时间步无法承受过多中间步, 所以本文使用二阶辛RKN格式对(2)式进行离散.
引入变元
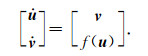
|
(3) |
考虑(3)式为Hamilton系统情形, 即(3)式可表示为如下形式:

|
(4) |
其中H(u, v)为一标量函数, 由(3)、(4)式知H满足如下等式:
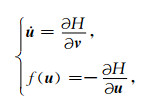
|
(5) |
因此H满足: 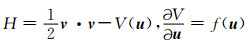

|
(6) |
其中, h为时间步长, ci, aij, bj, bj为辛系数.可以证明, 如果(6)式是显式辛的, (6)式应满足如下方程[26, 37]:
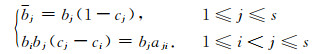
|
(7) |
在地震波模拟时, 希望格式(6)的计算效率与二阶的PRK格式相近[31-32], 当s=2时即满足高效地震波模拟的要求.在精度上希望格式(6)精度尽可能提高, 对于非约化的辛RKN格式[26, 37](即格式中无冗余级, bj≠0), 满足(7)式的格式(6)是p阶的, 可以用图形表示微分关系的根数理论[37-38], 即任何s-树sτ, 都有一个有根的s-树ρsτ由sτ的一胖节点提升得到, ρsτ的权与密度满足如下等式:

|
(8) |
其中φ为ρsτ的权, γ为ρsτ的密度.如果二级的辛RKN格式是三阶的, 有4个非多余有根s-树需满足(8)式, 将辛条件(7)带入(8)式化简得到如下等式:
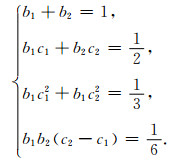
|
(9) |
求解(9)式发现, 方程无实数解, 即二级的辛RKN格式无法使精度达到三阶, 我们可以根据截断误差最小原理得到精度接近三阶的误差最小辛RKN格式, 即(9)式中的前两式满足的同时, 构造目标函数, 使目标函数尽量最小,
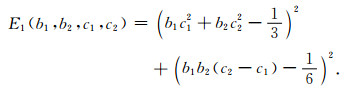
|
(10) |
运用非线性优化方法, 可以得到如下一种误差最小辛RKN格式(记为M1):

|
(11) |
运用二级辛RKN格式进行地震波模拟时, 时间步长与空间步长应满足一定的比例关系, 否则计算失稳以至无法进行.为了使分析过程中量纲一致, 引入变量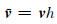

|
(12) |
由(6)式得到的时间演进方程为
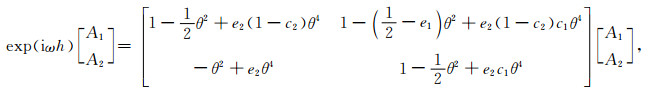
|
(13) |
其中, θ=ckh, e1=b1c12 + b1c22, e2=b1b2(c2 -c1).由(13)式知时间演进方程的特征值为

|
(14) |
其中
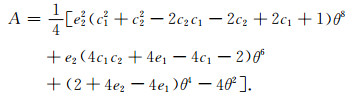
|
为了保证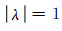

|
(15) |
选择不同的c1, c2, 满足(9)、(15)式的同时力图使θ取到最大值.最后得到的一种强稳定的辛RKN格式(记为M2):
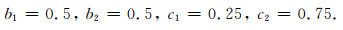
|
(16) |
由于用时间和空间的离散点值近似替代时间空间连续变化的函数, 必然导致真实信号中的部分信号无法拾取而导致数值频散.本文用伪谱法计算空间微分, 在Nyquist波数范围内伪谱法对波数完全覆盖, 用格式(6)进行地震波模拟时, 数值频散将主要来源于时间离散.由(13)、(14)式可知, (13)式左端的exp (iωh)应与λ相等, 由此可以得到相速度

|
(17) |
其中, θ又可以表示为θ=rkΔ, 库朗数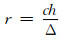
选择适当的库朗数(如r=1), 当kΔ由0变化至π, 选择不同的系数使得相速度与真实速度最接近, 为此构造如下目标函数:
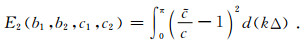
|
(18) |
用非线性最优化方法得到一种最小频散辛RKN格式(记为M3),
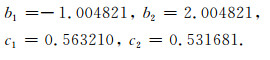
|
(19) |
第2节从精度、稳定性和数值频散优化三方面得到了3种辛RKN格式, 本节就这三方面与常见格式对比, 以凸显本文格式的特性.对比选用的格式包括:二阶辛PRK格式[31-32](记为M4)、二阶优化PRK格式[39](记为M5)和三级三阶PRK格式[27-28](记为M6).
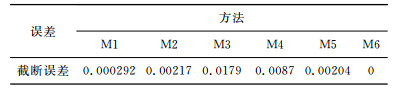
3.1 精度分析将(10)式中的E1视为截断误差, 对比M1-M6 6种格式的E1.对比结果如表 1所示.就精度而言, 三阶格式M6精度最高; M1精度其次, 其精度逼近三阶格式M6;M2与M5精度接近, M3和M4精度最差.
|
|
表 1 6种辛格式截断误差对比 Table 1 Error truncation of six symplectic schemes |
按照2.4节分析方法, 可以得到M1-M6的稳定性条件.表 2给出了6种格式从一维到三维的稳定性极限(即库朗数r所取的极大值).从表 2可以看出, 理论上M3稳定性最好.在常见格式中三阶格式M6稳定性最好, 二阶的M4格式稳定性最差, 优化的二阶格式M5介于两者之间, 整体而言常见格式稳定性要逊色于本文3种格式.
|
|
表 2 6种格式一维到三维稳定性比较 Table 2 Stability limits of sixsymplectic schemes for 1D, 2D, and 3D scalar wave simulations |
按照2.3节的分析方法, 可以得到M1-M6的频散关系, 图 1(a、b)为r=0.5和r=0.8时6种格式1D情形下的频散曲线.由图 1a可知, r取较小值时M6频散最小, M3频散其次, M4与M5频散较大; 在图 1b中当r=0.8时M4与M5已经失稳, 故未在图中显示, 当kΔx取较小值时, M6频散最小, 但kΔx取较大值时, M6频散将超过M3.由图对比可知, M3频散一直维持在较低范围.当r=0.8时, 按照Basabe和Sen[40]频散限定标准, 即频散小于0.01, 1D情况下, M3一个波长的最小采样点数为2.38;同理2D情形下, M3一个波场内的最小采样点数为3.36.

|
图 1 6种格式r=0.5和r=0.8时的频散关系对比 Fig. 1 Comparison of numerical dispersion of six symplectic schemes when r=0.5 (a) and r=0.8 (b) |
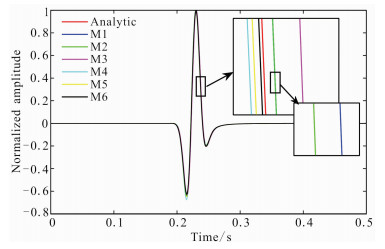
为了测试这组辛RKN格式对声波的模拟精度, 设计了2D均匀介质模型, 模型大小为2550 m× 2550 m, 震源位于模型中心, 接收点在震源左侧400 m处.震源由主频为30 Hz的Ricker子波激发, 空间网格间隔为10 m, 时间步长为1 ms.声波波速为3000 m/s.定义接收点的总体误差
|
图 2 6种格式计算得到的声波波形与解析解对比 Fig. 2 Comparison of waveforms generated by six sympletic methods and analytic solution |
|
|
表 3 6种辛格式计算效率和总体误差对比 Table 3 Computational efficiency and total error comparison of six symplectic methods |
由图 2可知, 6种方法模拟结果与解析解高度一致, M1、M2和M6与解析解最靠近, M3、M4和M5偏离解析解较远, 由于压制高波数处的数值频散, M3对低波数模拟的精度影响较大, 表现在图 2中为相位较为超前.由表 3可以看出, M6误差最小, M1与M2误差其次, 其中M1与M2精度足够接近; M3-M5误差较大; 就计算效率而言M6的计算时间为M1-M5的1.5倍, 在计算效率相同的情况下, M1、M2比M4、M5有较大的精度提升.
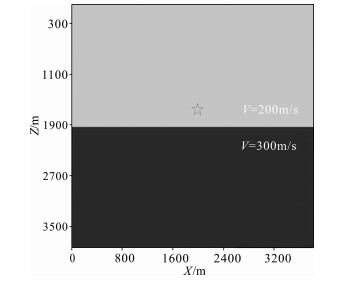
4.2 分层介质模型为了检验本文方法的数值频散压制能力, 设计如图 3的分层介质模型, 模型大小为3825 m×3825 m, 分界面位于1920 m深度处, 上层介质的波速为2000 m/s, 下层介质波速为3000 m/s, 震源位于(1920 m, -1710 m)处, 由主频为60 Hz的Ricker子波激发产生, 时间间隔为1 ms, 空间间隔为15 m.模拟结果如图 4所示.
|
图 3 分层均匀介质模型以及模型参数 Fig. 3 Two layer homogeneous media and model parameters |
|
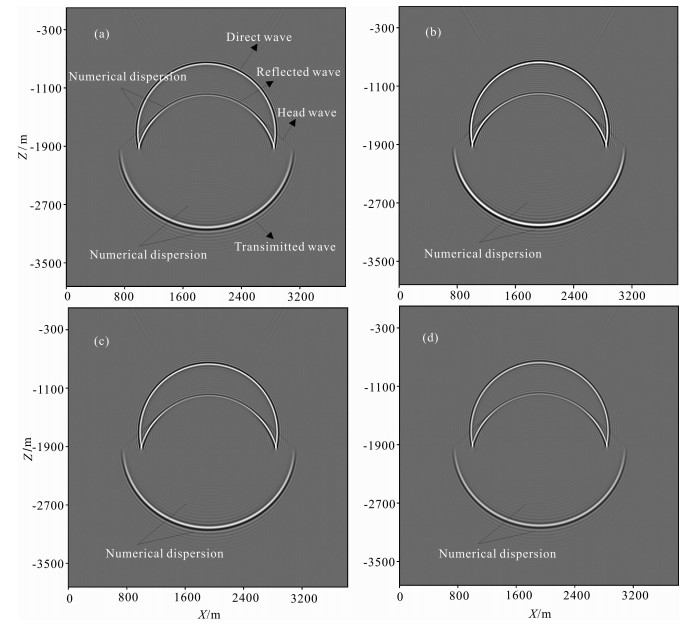
图 4 4种方法模拟分层声波介质中地震波传播0.5 s时的波场快照 (a-c) M4-M6方法; (d) M3方法. Fig. 4 The snapshots of scalar wave propagation in two layered medium at time t=0.5 s |
图 4(a-d)分别为M4-M6和M3四种方法计算得到的0.5 s时刻的波场快照.从图 4a可以看到除了直达波、反射波、透射波以及首波外, 还在直达波波前、透射波波前附近出现了强烈的数值频散, 图 4b在透射波波前也出现了强烈的数值频散; 图 4(c, d)中只在透射波前出现了轻微的频散, M3和M6计算结果较为一致.M3-M5计算效率基本相同, M6计算耗时为M3-M5的1.5倍, 在高频地震波模拟时使用M3, 在保证计算效率的同时, 能较好地压制数值频散.
4.3 非均匀介质模型---SEG/EAGE盐丘模型为了测试本文方法在非均匀介质中波场计算的有效性和稳定性, 选择SEG/EAGE模型做测试, 模型速度结构如图 5所示.模型中波速变化范围为1524~4480 m/s, 除了若干个起伏分层界面外, 还存在盐丘高阻体, 使得介质横向速度变化极为强烈.选择震源位于模型中心, 其为主频是40 Hz的Ricker子波, 空间网格间距为20 m, 时间间隔为1 ms时M2、M5和M6三种方法的模拟结果如图 6所示, 时间间隔为2 ms时的模拟结果如图 7所示.

|
图 5 SEG/EAGE盐丘模型 Fig. 5 The velocity profile of SEG/EAGE salt model |
|
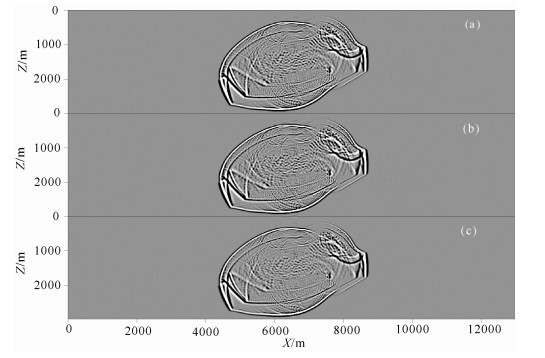
图 6 三种方法模拟得到的非均匀介质中0.5 s时的波场快照 (a) M2;(b) M5;(c) M6, 时间间隔为1 ms. Fig. 6 The snapshots of wavefields in heterogeneous media when t=0.5 s (a-c) are calculated by M2, M5, and M6, respectively. Time interval is 1 ms. |
|
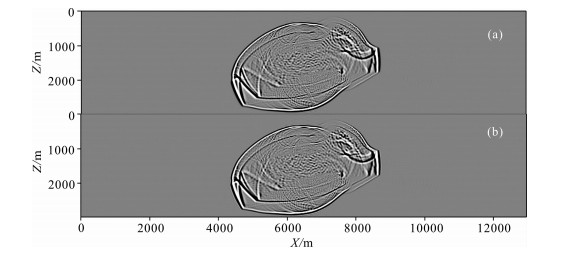
图 7 两种方法模拟得到的非均匀介质中0.5 s时的波场快照 (a) M2;(b) M6, 时间间隔为2 ms. Fig. 7 The snapshots of wavefields in heterogeneous media when t=0.5 s (a-b) are calculated by M2, and M6, respectively. Time interval is 2 ms. |
当时间间隔为1 ms时, M2、M5和M6可以得到几乎相同的波场快照, 从图 6中可以看到, 由于介质的非均匀性, 在速度突变的界面上产生了强烈的反射和多次反射, 以及在速度突变的角点处产生了明显的绕射和散射, 三种方法均是稳定的, 并得到了可靠的结果.当时间间隔增加一倍, 即为2 ms时, M5已经失稳, 而M2和M6依然稳定, 从图 7中可以看到两种方法得到的快照和图 6中的快照无论是整体还是细节上都极其一致, 说明本文M2使用大时间步长的模拟结果依然是可靠的.
5 讨论本文对地震声波方程空间上使用伪谱法离散, 时间离散上选用高效的二阶辛RKN格式, 通过以误差最小、稳定域最大和频散最小为依据构造了三种辛RKN格式.在理论分析中, 和常见格式对比, 理论上论证了本文方法在精度、稳定性和数值频散等方面的优势; 在数值实验中, 通过与解析解、分层介质和非均匀介质中不同方法波场模拟结果对比, 数值结果进一步佐证了本文方法在保证计算效率的同时, 在精度提高、稳定域增加和数值频散压制等方面均具有明显改进.可以根据不同实际需要选择不同方法, 如在高精度地震波模拟时选择M1, 在高频地震波模拟时选择M3, 在强烈非均匀介质中地震波模拟时选择M2.本文方法为高效地震波模拟、成像提供了一种可靠的选择.
| [1] | Whitmore N D. Iterative depth migration by backward time propagation. 53rd Annual International meeting, SEG, Expanded Abstracts, 1983: 827-830. |
| [2] | 刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报 , 2010, 53(7): 1725–1733. Liu H W, Li B, Liu H, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys. (in Chinese) , 2010, 53(7): 1725-1733. |
| [3] | Song Z M, Williamson P R, Pratt R G. Frequency-domain acoustic-wave modelling and inversion of cross-hole data, Part Ⅱ: Inversion method, synthetic experiments and real-data results. Geophysics , 1995, 60(3): 796-809. DOI:10.1190/1.1443818 |
| [4] | 张美根, 王妙月, 李小凡, 等. 时间域全波场各向异性弹性参数反演. 地球物理学报 , 2004, 46(1): 94–100. Zhang M G, Wang M Y, Li X F, et al. Full wavefield inversion of anisotropic elastic parameters in the time domain. Chinese J. Geophys. (in Chinese) , 2004, 46(1): 94-100. |
| [5] | Komatitsch D, Liu Q, Tromp J. Simulations of ground motion in the Los Angeles basin based upon the spectral-element method. Bull. Seismol. Am. Soc. , 2004, 94(1): 187-206. DOI:10.1785/0120030077 |
| [6] | 张怀, 周元泽, 吴忠良, 等. 福州盆地强地面运动特征的有限元数值模拟. 地球物理学报 , 2009, 52(5): 1270–1279. Zhang H, Zhou Y Z, Wu Z L, et al. Finite element analysis of seismic wave propagation characteristics in Fuzhou basin. Chinese J. Geophys. (in Chinese) , 2009, 52(5): 1270-1279. |
| [7] | Komatitsch D, Tromp J. Spectral-element simulations of global seismic wave propagation-I. Validation. Geophys. J. Int. , 2002, 149(2): 390-412. DOI:10.1046/j.1365-246X.2002.01653.x |
| [8] | Komatitsch D, Tromp J. Spectral-element simulations of global seismic wave propagation-Ⅱ. Three-dimensional models, oceans, rotation and self-gravitation. Geophys. J. Int. , 2002, 150(1): 303-318. DOI:10.1046/j.1365-246X.2002.01716.x |
| [9] | Yan Z Z, Zhang H, Yang C C, et al. Spectral element analysis on the characteristics of seismic wave propagation triggered by Wenchuan Ms8.0 earthquake. Science in China Series D: Earth Sciences , 2009, 52(6): 764-773. DOI:10.1007/s11430-009-0078-z |
| [10] | Carcione J M, Herman G C, ten Kroode A P E. Seismic modeling. Geophysics , 2002, 76(4): 1304-1325. |
| [11] | Yang D H, Tong P, Deng X Y. A central difference method with low numerical dispersion for solving the scalar wave equation. Geophysical Prospecting , 2012, 60(5): 885-905. DOI:10.1111/gpr.2012.60.issue-5 |
| [12] | Virieux J. SH-wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics , 1984, 49(11): 1933-1942. DOI:10.1190/1.1441605 |
| [13] | Virieux J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics , 1986, 51(4): 889-901. DOI:10.1190/1.1442147 |
| [14] | Yang D H, Liu E, Zhang Z J, et al. Finite-difference modelling in two-dimensional anisotropic media using a flux-corrected transport technique. Geophys. J. Int. , 2002, 148(2): 320-328. |
| [15] | Kolsoff D D, Baysal E. Forward modeling by a Fourier method. Geophysics , 47(10): 1402-1412. |
| [16] | 龙桂华, 李小凡, 江东辉. 基于交错网格Fourier伪谱微分矩阵算子的地震波场模拟GPU加速方案. 地球物理学报 , 2010, 53(12): 2964–2971. Long G H, Li X F, Jiang D H. Accelerating seismic modeling with staggered-grid Fourier Pseudo-spectral differentiation matrix operator method on graphics processing unit. Chinese J. Geophys. (in Chinese) , 2010, 53(12): 2964-2971. |
| [17] | Komatitsch D, Barnes C, Tromp J. Wave propagation near a fluid-solid interface: A spectral-element approach. Geophysics , 2000, 65(2): 623-631. DOI:10.1190/1.1444758 |
| [18] | Komatitsch D, Barnes C, Tromp J. Simulation of anisotropic wave propagation based upon a spectral element method. Geophysics , 2000, 65(4): 1251-1260. DOI:10.1190/1.1444816 |
| [19] | Dablain M A. The application of high-order differencing to the scalar wave equation. Geophysics , 1986, 51(1): 54-66. DOI:10.1190/1.1442040 |
| [20] | Lax P D, Wendroff B. Difference schemes for hyperbolic equations with high order of accuracy. Communications on Pure and Applied Mathematics , 1964, 17(3): 381-398. DOI:10.1002/(ISSN)1097-0312 |
| [21] | Tong P, Yang D H, Wang M X. A high-order stereo-modeling method for solving wave equations. Bull. Seism. Am. Soc. , 2013, 103(2A): 811-833. DOI:10.1785/0120120144 |
| [22] | Yang D H, Teng J W, Zhang J F, et al. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media. Bull. Seismol. Soc. Am. , 2003, 93(2): 882-890. DOI:10.1785/0120020125 |
| [23] | Chen J B. High-order time discretizations in seismic modeling. Geophysics , 2007, 72(5): 115-122. DOI:10.1190/1.2750424 |
| [24] | Chen J B. Modeling the scalar wave equation with Nyström methods. Geophysics , 2006, 71(5): 151-158. |
| [25] | Chen J B. Lax-Wendroff and Nyström methods for seismic modelling. Geophysical Prospecting , 2009, 57(6): 931-941. DOI:10.1111/gpr.2009.57.issue-6 |
| [26] | Okunbor D, Skeel R D. Explicit canonical methods for Hamiltonian systems. Math. Comp. , 1992, 59(200): 439-455. DOI:10.1090/S0025-5718-1992-1136225-3 |
| [27] | Li X F, Li Y Q, Zhang M G, et al. Scalar seismic-wave equation modeling by a multisymplectic discrete singular convolution differentiator method. Bull. Seismol. Am. Soc. , 2011, 101(4): 1710-1718. DOI:10.1785/0120100266 |
| [28] | Li X F, Wang W S, Lu M W, et al. Structure-preserving modelling of elastic waves: a symplectic discrete singular convolution differentiator method. Geophys. J. Int. , 188(3): 1382-1392. |
| [29] | Luo M Q, Liu H, Li Y M. LU decomposition with spectral factorization in seismic imaging. Chinese J. Geophys. , 2003, 46(3): 602-612. DOI:10.1002/cjg2.v46.3 |
| [30] | Luo M Q, Zhu G T, Liu H, et al. A hybrid matrix inversion method for 3-D implicit prestack depth migration. Chinese J. Geophys. , 2003, 46(5): 978-987. DOI:10.1002/cjg2.v46.5 |
| [31] | Ma X, Yang D H, Liu F Q. A nearly analytic symplectically partitioned Runge-Kutta method for 2-D seismic wave equations. Geophys. J. Int. , 2011, 187(1): 480-496. DOI:10.1111/gji.2011.187.issue-1 |
| [32] | 孙耿. 波动方程的一类显式辛格式. 计算数学 , 1997(1): 1–10. Sun G. A class of explicitly symplectic schemes for wave equations. Comput. Math. (in Chinese) , 1997(1): 1-10. |
| [33] | Fornberg B. High-order finite differences and the pseudospectral method on staggered grids. SIAM J. Numer. Anal. , 1990, 27(4): 904-918. DOI:10.1137/0727052 |
| [34] | 汪文帅, 李小凡, 鲁明文, 等. 基于多辛结构谱元法的保结构地震波场模拟. 地球物理学报 , 2012, 55(10): 3427–3439. Wang W S, Li X F, Lu M W, et al. Structure-preserving modeling for seismic wavefields based upon a multisymplectic spectral element method. Chinese J. Geophys. (in Chinese) , 2012, 55(10): 3427-3439. |
| [35] | Yang D H, Wang N, Chen S, et al. An explicit method based on the implicit Runge-Kutta algorithm for solving wave equations. Bull. Seismol. Soc. Am. , 2009, 99(6): 3340-3354. DOI:10.1785/0120080346 |
| [36] | Yang D H, Wang Lei, Deng X Y. An explicit split-step algorithm of the implicit Adams method for solving 2-D acoustic and elastic wave equations. Geophys. J. Int. , 2010, 180(1): 291-310. DOI:10.1111/gji.2010.180.issue-1 |
| [37] | 冯康, 秦孟兆. 哈密尔顿系统的辛几何算法. 杭州: 浙江科学出版社, 2003 . Feng K, Qin M Z. Symplectic Geometric Algorithms for Hamiltionian Systems (in Chinese). Hangzhou: Zhejiang Science & Technology Press, 2003 . |
| [38] | Hairer E. Geometric Numerical Intergration I (2nd ed). Berlin and New York: Springer-Verlag, . |
| [39] | MaLachlan R I, Atela P. The accuracy of symplectic integrators. Nonlinearity , 1992, 5(2): 541-562. DOI:10.1088/0951-7715/5/2/011 |
| [40] | Basabe J D D, Sen K M. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations. Geophysics , 2007, 72(6): T81-T95. DOI:10.1190/1.2785046 |
 2013, Vol. 56
2013, Vol. 56