2. 中国地质大学(北京)地球物理与信息技术学院, 北京 100083;
3. 国家地质实验测试中心, 北京 100037
2. School of Geophysics and Information Technology, China University of Geosciences, Beijing 100083, China;
3. National Research Center for Geoanalysis, Chinese Academy of Geological Sciences, Beijing 100037, China
在三维(3-D)地质环境中采集的大地电磁场(MT)数据, 一般情况下解释为二维(2-D)结果的近似值.在某些情况下, 可以谨慎且细心地用2-D模型和反演来实现3-D地质解释[1].但是, 在大多数情况下, 这种解释方法行不通, 尤其是在地质环境比较复杂的地区, 这就需要高效的3-D反演方法.而在3-D大地电磁数据解释中存在一个重要的问题, 即缺乏高效的3-D反演计算方法[2].
3-D MT反演问题的难点主要有两个, 一是由于观测数据远远少于网格节点产生的超欠定病态矩阵; 二是由超大节点数量造成的超大计算量.可以通过带约束的正则化方法解决或改善病态问题, 而大尺度的问题仍然存在, 为了精确反映3-D地下电性结构, 需要利用有限的测量数据估计大量的模型参数, 因此需要一种在保证计算精度的条件下, 能够实现快速计算的方法.Smith & Booker提出了快速松弛方法来解决3-D MT数据的成像问题[3], 该方法使用前一次迭代计算的场值代替场的水平导数, 将3-D问题简化为1-D问题, 提高了计算效率.但是, 这种简化忽略了灵敏度矩阵计算过程中的横向效应, 在电阻率重构中可能会产生假异常.
Mackie & Madden的共轭梯度反演方法[4]使用有限差分法作为正演方法, 能够高效地模拟MT场分量以及由复杂的3-D地质环境产生的敏感度和梯度变化, 是包含处理3-D灵敏度横向效应的可行方法, 很大程度上减小了数据的不适定性, 由于该方法有数据和变量存储上的优势以及相对简单的迭代过程, 能够解决大规模计算的问题.
Newman & Alumbaugh使用非线性优化方法解决3-D MT反演问题[2].在每次迭代中, 每个频率仅需6次拟正演就能得到模型修改量, 即2次响应计算和4次修改量计算, 将并行方法应用于反演计算中, 减少了计算时间.但是该方法的预处理部分较为复杂, 并且采用网格分区域并行计算可能会破坏模型的边界条件.
本文用预处理非线性共轭梯度方法构建3-D MT反演问题, 在Smith提出的交错网格有限差分方法[5-6]、Newman & Alumbaugh提出的3-D目标函数和梯度计算方法[2]和Rodi & Mackie提出的预处理方法[7]基础上, 结合前人的工作成果, 改进了2-D NLCG反演中的预处理方法, 用一个与当前迭代模型电阻率有关的参数代替Hessian矩阵的计算, 避免了每个频点中4次正演计算, 在保证计算精度的情况下, 最终实现每次迭代每个频点仅需6次正演计算, 即1次响应计算和5次模型修改量计算.此外, 使用OPENMP并行方法建立了反演算法的并行结构, 采用分频点并行计算, 提高了效率.通过正演模拟数据和实测数据测试了反演方法的正确性和预处理方法的高效性.
2 大地电磁场交错网格有限差分正演实现精确的大地电磁场的三维正演模拟, 必需满足计算资源的要求和场值分布的守恒定律以及适用性等诸多条件.早期的研究工作多集中在积分方程法上, 目前研究和使用最多的是交错网格有限差分法.
在对Randy Mackie和Smith等人的工作进行深入分析的基础上, 本文对交错网格有限差分法进行了系统的研究, 实现了以求解电场分布为基础的大地电磁三维数值模拟算法.
设随时间变化的谐波函数为eiωt, 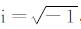
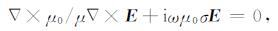
|
(1) |
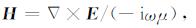
|
(2) |
其中, H为磁场, σ为电导率, μ为磁导率, μ0为真空磁导率.
在笛卡尔坐标系下沿x、y、z三个坐标轴将地下空间划分成Nx、Ny、Nz个小的长方体网格单元, 间距为Δx(i)(i=1, 2, …, Nx)、Δy(j)(j=1, 2, …, Ny)、Δz(k)(k=1, 2, …, Nz), i, j, k为节点位置参数.
图 1所示的是编号为(i, j, k)的长方体网格单元, 其长度、宽度和高度分别为Δx(i)、Δy(j)、Δz(k), 电阻率为ρ(i, j, k).其中电场取在各网格单元边缘的中点, 磁场取在各网格单元表面的中心.
节点(xi-1/2, yj, zk)在x方向上交错网格差分的近似表达式为:
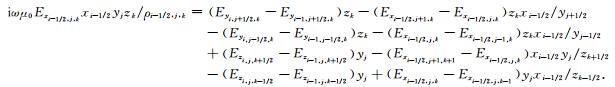
|
(3) |
通过方程(3)及其在y、z方向上的扩展可以得到所有网格节点Ex、Ey、Ez的表达式.此外, 在数值解中使用静态散度和Smith (1996)提出的大幅度减少计算时间的方法[6], 校正低频阻抗响应.
3 大地电磁场三维反演 3.1 正则化反演的目标函数最小二乘法的计算目标是使实测数据和正演数据之间的差值达到最小, 由于只有数据约束, 没有物理条件约束, 经常会得到违反物理现实情况的模型.考虑到这个问题, 将Tikhonov提出的正则化方法引入反演过程中, 排除不符合物理实际的模型[8].正则化方法附加一个约束条件到模型中, 重建包括平滑分项的电阻率模型.将地下半空间分成M个单元并给每个单元网格指定电阻率值, 假设地下磁导率为真空磁导率且保持不变.用m表示模型电阻率的有序矩阵元素.结合数据误差和平滑模型约束, 目标函数表示为[2]:
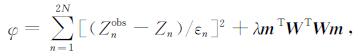
|
(4) |
其中Znobs和Zn表示观测阻抗数据和正演阻抗数据, ε为数据误差, W为正则化矩阵, 第1~N个数据为阻抗各分量的实部, 第(N+1)~2N个数据为阻抗各分量的虚部, 阻抗表达式如下:
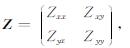
|
(5) |
综合使用阻抗各分量的数据及其误差, 能够充分权衡地下电性结构产生的综合电磁响应, 并且能够降低噪声对目标函数的影响.正则化矩阵W为控制模型平滑度的参数, 由近似拉普拉斯算子的有限差分多项式组成, 正则化因子λ用于控制平滑度的量级, 以保证数据拟合差与模型改变量保持在同一量级或者近似量级.因此在选取正则化因子时需要非常谨慎, 参数过大会产生超平滑模型, 但是通常不能拟合数据; 参数过小能很好地拟合数据, 但是最终的模型会很粗糙, 并且可能违反物理实际.当反演问题中使用线性查找方法时, λ不必再受约束, 变为在查找过程中可以改变的参数[9].但在本文算法的线性查找方法中λ保持不变, 因此通常选用几个λ值分别做反演, 挑选模型偏差与拟合差较为接近的结果或者拟合差在可接受范围内的反演模型作为计算结果.
小尺度反演问题中, 可以使用列举法确定搜索方向和尺度, 使方程(4)达到全局最小.而在大尺度反演问题中, 计算量很大, 无法使用列举法, 只能假设目标函数的导数为零(Δφ=0), 采用一种有效的计算方法寻找全局最小值, 才能得到合理的反演模型, 而且只能通过迭代方式求出Δφ=0的解, 因此, 我们采用非线性共轭梯度法解决大尺度反演问题[2].
3.2 非线性共轭梯度法非线性共轭梯度法的迭代速度较快, 收敛速度较最速下降法好, 属于计算效率较高的方法, 最早由Fletcher和Reeves (1964)在非线性规划[10]的基础上提出, 后来经Polyak和Ribiere (1969)改进[11]. Rodi和Mackie成功地将其应用于二维大地电磁反演[7], Newman和Alumbaugh将其应用于三维大地电磁反演[2].
目标函数的梯度表示为

|
(6) |
其中, φd为数据偏差函数, φm为模型光滑度函数, 令[2]:

|
(7) |
则有[2]:
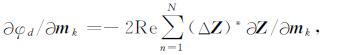
|
(8) |
非线性共轭梯度的模型由单减或沿搜索方向的线性查找确定[7]:
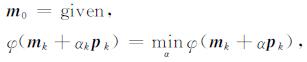
|
(9) |
搜索方向表示为[7]:
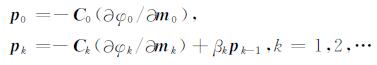
|
(10) |
引用Polak-Ribiere方法[11]:
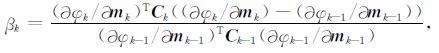
|
(11) |
pk为查找方向, -Ck(∂φk/∂mk)是另一个最速下降方向, 最小化φ在mk上的方向导数.
通过线性查找得到模型改变量[7]:
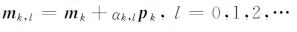
|
(12) |
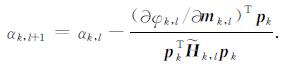
|
(13) |
通过迭代求解, 最终得到最佳拟合模型.
由式(13)可见, α的每一次计算都用到Hessian矩阵, 但是Hessian矩阵计算量十分巨大, 为了避免大量计算, 提高计算效率, 需要使用预处理方法代替它的计算.
3.3 预处理方法在本文的NLCG算法中使用了预处理矩阵C.对C的选取主要考虑两个方面:使用预处理矩阵的计算量大小以及使梯度向量成为有效的搜索方向的能力.
算法中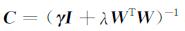

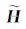
尽管本文的非线性共轭梯度方法在每一次迭代中已经减少了4次正演计算, 并且新的预处理因子和预处理过程计算量很小, 但是三维正演的计算效率仍是缩短消耗时间的瓶颈.阻抗、搜索步长和搜索方向三个参数需要进行(拟)正演计算, 而就目前的正演模拟现状而言, 三维交错有限差分方法是相对高效的方法之一, 但其串行计算速度受频点和网格节点数量限制.因此, 任何减少正演模拟运行时间的方法都将对减少反演时间产生相应的效果[2].此外, 模型网格数量可能达到百万量级, 而进行正演模拟时, 系数矩阵便是一个元素数量为万亿量级的矩阵, 这对内存的消耗十分巨大.
为了解决这些问题, 我们首先对所有稀疏矩阵进行一维定位存储, 减少内存消耗, 并且改进了算法, 使之适用于并行计算.该算法会根据计算机线程数量自动分配每个线程的工作量, 将各频点数据分配给不同的线程, 进行并行运算, 显著减少了计算时间, 但对计算机内存有了更高要求.
交错网格有限差分正演模拟方法在计算系数矩阵和场值时需要所有网格节点参数参与计算, 因此, 如果将模型分散为小块体分布于各计算线程, 会破坏正演模拟的边界条件, 从而影响计算精度.但是不同频点的数据在反演计算过程中彼此毫不相关, 将各频点数据分散于不同线程进行并行运算不会影响计算精度.
本文使用OPENMP并行计算开发平台, 根据计算机线程数量将各频点数据分配给不同的线程, 这样虽然使内存损耗接变为串行计算的线程数量倍, 但是计算效率也同时提高到线程数量倍.此外, 由于本文的并行反演方法是高效低损耗的方法, 对内存和CPU的要求较低, 因此并行程序能够适用于目前主流的PC上, 基本上不受硬件条件制约, 能够在多种操作系统上推广使用.
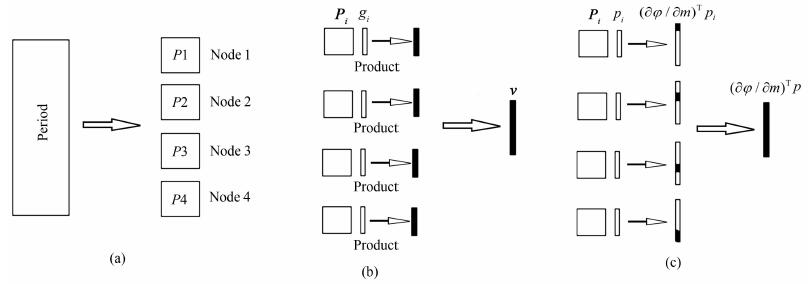
算法中的并行计算部分主要是通过类似正演模拟的计算, 求解不同频点对应的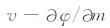
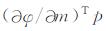
|
图 2 分布式存储和计算示意图.(a)分布式存储; (b)各线程v计算(P是与频点相关的正演系数矩阵, g是电磁场插值的线性组合系数, g的说明详见文献[3]); (c)各线程(∂φ/∂m)Tp计算 Fig. 2 Distributed storage and compute. (a) Distributed storage; (b) Compute v in every core (P is the frequency coefficient matrix of forward modeling, g is the linear combination coefficients of the electromagnetic field interpolation, g can be searched in Ref.[3]); (c) Compute (∂φ/∂m)Tp in every core |
在并行计算过程中, 加速比和效率是评价并行算法和程序的重要指标.其中加速比是单个线程上运行时间和n个线程上运行时间的比; 效率定义为加速比和计算线程个数之比.计算时由于将各参数定义n份, 分别传送给n个线程, 因此数据通信时间t与串行计算相同.并行效率e的估算方程为
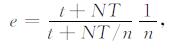
|
(14) |
其中N为频点总数, T为单个频点计算时间, 
(14)式表明, 计算时间随着线程数量的增加而减小(当线程数量小于频点数量时).
4 算例 4.1 合成数据反演算例该算例通过理论模型数据验证了反演算法的正确性, 并且对比了不同数量的CPU线程参与反演的计算效率.
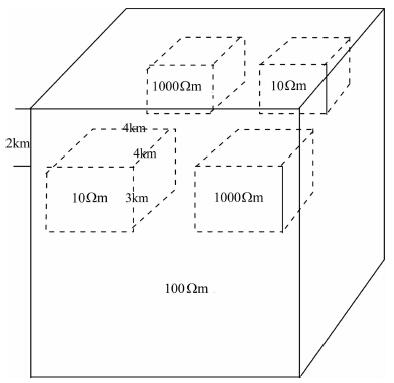
4.1.1 模型设计模型中设计4个异常体, 100 Ωm的半空间背景中包含2个低阻异常体和2个高阻异常体, 异常体电阻率分别为10 Ωm和1000 Ωm, 异常体顶深2 km、长4 km、宽4 km、厚3 km、间距2 km, 如图 3所示.
|
图 3 理论模型示意图 Fig. 3 Synthetic mode |
数据频率范围0.01~100s, 共8个频点, 初始数据频率范围0.01~100s, 共8个频点, 初始模型网格数为30×30×38(含8个空气层网格), 横向长度100 km, 纵向深度100 km, 初始电阻率为100 Ωm, 64个测点位于网格中心, 测点数据误差限为10%, 添加噪声为响应数据的1%, 正则化因子为0.01, 反演目标拟合差为1, 最大迭代次数为100, 反演结果如图 4所示.
|
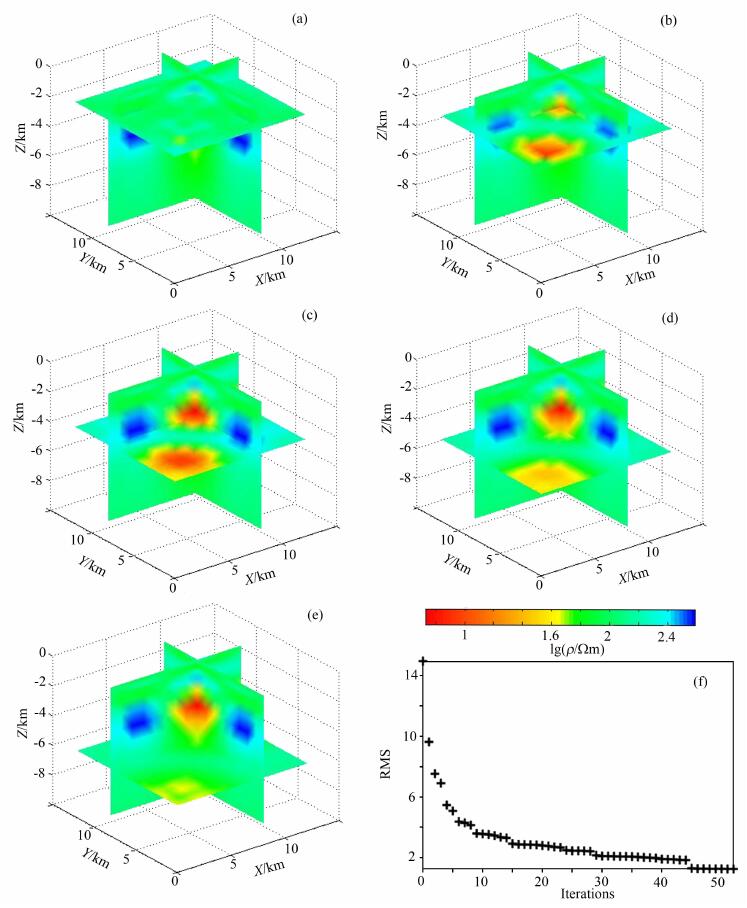
图 4 反演结果及拟合差.(a)-(e)深度分别是1.5 km、2.5 km、3.5 km、4.5 km、5.5 km的水平切片; (f)反演拟合差结果 Fig. 4 Results of inversion and fitting error. (a)-(e) Horizontal sections of different depth with 1.5 km, 2.5 km, 3.5 km, 4.5 km, 5.5 km; (f) Fitting error |
图 4为三维反演结果, 迭代52次后满足终止条件, RMS为1, 主频为2.6GHz的6核12线程计算机运行时间为4858s, 图 4a为地下1.5 km处电阻率水平切片, 图 4b为地下2.5 km处电阻率水平切片, 图 4c为地下3.5 km处电阻率水平切片, 图 4d为地下4.5 km处电阻率水平切片, 图 4e为地下5.5 km处电阻率水平切片, 图 4f为反演拟合差结果.由图可见, 两个低阻异常体和两个高阻异常体均能够较好地分辨出来, 异常体中心电阻率分别为10 Ωm和370 Ωm.
但是, 可以看到异常体上方网格电阻率略有反向变化, 低阻异常体上方网格电阻率较原始模型的高, 而高阻异常体上方网格电阻率较原始模型低, 最大差异小于20%, 主要是因为正则化因子数值较小造成的, 反演结果着重拟合数据, 而轻视了模型光滑度.
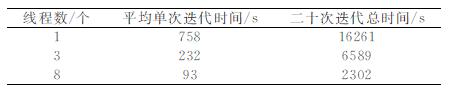
4.1.3 并行计算效率分析由表 1可知, 使用的计算机线程越多, 计算效率越高.应用1个线程时, 每次迭代需要进行6×8次正演和1次流程计算; 应用3个线程时, 每次迭代需要进行6×3次正演和1次流程计算; 应用8个线程时, 每次迭代需要进行6×1次正演和1次流程计算.因此, 反演的并行效率与线程数量呈非线性正比例关系.
|
|
表 1 并行计算效率对比(合成数据反演算例) Table 1 Compare of compute efficiency (Example of synthetic data inversion) |
该算例通过实测数据验证了反演算法的有效性, 并且对比了不同反演算法的结果, 验证了本文算法的实用性.
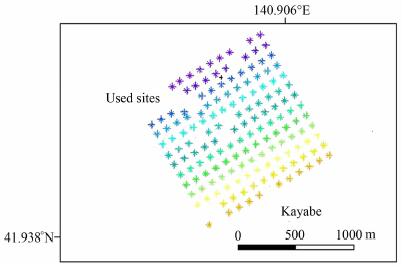
4.2.1 反演数据及参数设计日本KAYABE地区测点位置如图 5所示.
|
图 5 KAYABE测点示意图 Fig. 5 Real stations of KAYABE data |
数据频率范围64~2 Hz, 共6个频点, 网格数为23×23×38(含8个空气层网格), 横向长度10 km, 纵向深度10 km, 初始电阻率为100 Ωm, 正则化因子为0.1, 150个测点位于网格中心, 反演目标拟合差为1, 最大迭代次数为100.
4.2.2 反演结果反演结果如图 6示.

|
图 6 KAYABE反演结果水平切片与拟合差.(a)-(e)深度分别是100、200、300、400、500 m的水平切片; (f)反演拟合差结果 Fig. 6 Results of inversion and fitting error of KAYABE data. (a)-(e) Horizontal sections of different depth with 100, 200, 300, 400 m and 500 m; (f) Fitting error |
全张量阻抗反演经过89次迭代后结束, 最终RMS为2.32, 在CPU主频2.6GHz的2核4线程计算机上计算时间为4h.测区地下500 m深度范围内主要体现为低阻异常.测区地下浅表电阻率分布较为凌乱, 边缘出现小面积高阻异常体, 而50~200m深处, 低阻异常由东向西收敛, 主要表现为西南和东南两个低阻异常体, 至300 m以下, 西南部以及中部的低阻异常体逐渐变小, 并且与东南部低阻异常体分离.
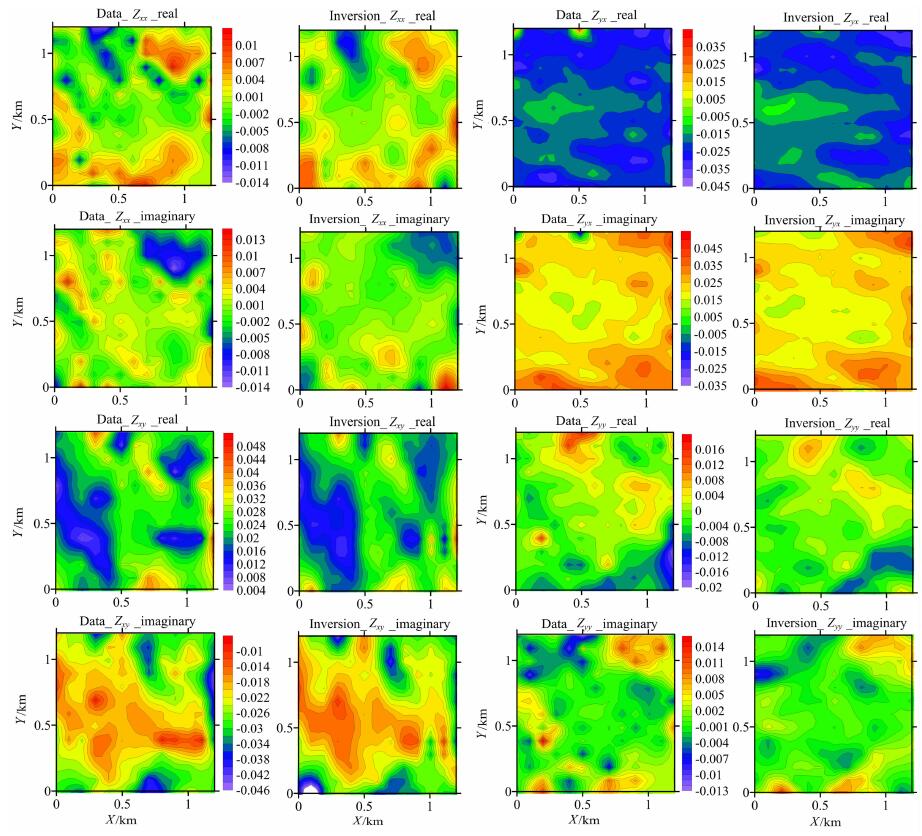
图 7为数据与响应的阻抗对比, 可见, 本文NLCG三维反演的拟合情况较为理想, 该反演使用的预处理因子和模型修改量计算采用了与初始模型不相关的参数, 因此受初始模型的影响较小.
|
图 7 测区实测阻抗数据和反演模型响应对比图(16 Hz).Data表示实测阻抗数据, Inversion表示反演模型响应阻抗数据, real表示阻抗的实部, imaginary表示阻抗的虚部 Fig. 7 Impedance compare of real data and inversion sounding (16 Hz).Data:Impedance of real data; Inversion:Impedance of inversion sounding; real:realpart of impedance; imaginary: image part of impedance |
图 8中NLCG为本文提出的非线性共轭反演方法结果; REBOCC为Weerachai (2006)三维数值域反演方法[12]结果; CG为林昌洪(2010)给出的共轭梯度反演方法结果[13]; RRI为谭捍东等(2003)给出的快速松弛反演方法结果[14].可见, 4种三维反演方法在KAYABE地区实测数据中的应用结果存在相似的地方, 在100~200m深度范围内, 都表现出主体低阻异常特征和周边相对高阻异常特征, 并且本文NLCG方法与REBOCC方法的结果有较高的相似度, 反演结果基本一致.但是, 4种方法的反演结果也存在一定的差异, 特别是对测区中部小范围次高阻异常体的反应存在较大差异.CG反演结果模型最为平滑, 分辨率最低, 这可能因为正则化因子的取值更偏重于模型光滑度; RRI反演结果反应的中部高阻体范围和电阻率值最大.总体上, 4种反演结果有可比性, 能够反应出测区地下低阻介质.

|
图 8 KAYABE实测数据不同反演方法结果对比(深度100 m和200 m水平切片) Fig. 8 Results comparing with different inversion methods using KAYABE data (Horizontal sections with the depth of 100 m and 200 m) |
本文以现有大地电磁场反演理论为基础, 研究大地电磁场反演理论和算法, 在Newman和Alumbaugh (2000)[2]提出的三维非线性共轭梯度算法和Rodi和Mackie (2001)[7]给出的大地电磁场二维NLCG反演预处理方法的基础上实现了大地电磁场NLCG三维反演算法, 改进了反演的预处理方法, 将反演计算对初始模型的依赖性降到最低, 编写了三维反演代码, 并验证了程序的正确性.
(1) 提出了一种简单的代替目标函数二次导数计算的方法, 使用当前迭代电阻率以及数据误差作为预处理因子, 不但能够将每一次迭代或者线性搜索得到的模型改变量引入下一次迭代或线性查找, 而且能够规避为计算Hessian矩阵产生的4次正演计算.
(2) 将OPENMP并行计算方法引入到大地电磁场非线性共轭梯度三维反演中, 采用频点并行计算的方法, 将不同频点数据分配给不同的CPU线程进行并行计算, 很大程度上提高了计算效率, 并且内存消耗较小, 因此, 可以在普通PC上完成计算工作.此外, 由于各频点计算过程中没有关联, 这种并行计算不会产生额外的计算误差, 也不会造成计算失真, 是一种保证计算精度的并行方法.
| [1] | Wannamaker P E, Ward S H, Hohmann G W. Magnetotelluric responses of three-dimensional bodies in layered earths. Geophysics , 1984, 49(9): 1517-1533. DOI:10.1190/1.1441777 |
| [2] | Newman G A, Alumbaugh D L. Three-dimensional magnetotelluric inversion using non-linear conjugate gradients. Geophys. J. Int. , 2000, 140: 410-424. DOI:10.1046/j.1365-246x.2000.00007.x |
| [3] | Smith J T, Booker J R. Rapid inversion of two-and three-dimensional magnetotelluric data. J. Geophys. Res. , 1991, 96(B3): 3905-3922. DOI:10.1029/90JB02416 |
| [4] | Mackie R L, Madden T R. Three-dimensional magnetotelluric inversion using conjugate gradients. Geophys. J. Int. , 1993, 115(1): 215-229. DOI:10.1111/gji.1993.115.issue-1 |
| [5] | Smith J T. Conservative modeling of 3-D electromagnetic fields, Part Ⅰ: Properties and error analysis. Geophysics , 1996, 61(5): 1308-1318. DOI:10.1190/1.1444054 |
| [6] | Smith J T. Conservative modeling of 3-D electromagnetic fields, Part Ⅱ: Biconjugate gradient solution and an accelerator. Geophysics , 1996, 61(5): 1319-1324. DOI:10.1190/1.1444055 |
| [7] | Rodi W L, Mackie R L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion. Geophysics , 2001, 66(1): 174-187. DOI:10.1190/1.1444893 |
| [8] | Tikhonov A N, Arsenin V Y. Solutions of Ill-Posed Problems. New York: John Wiley , 1977. |
| [9] | de Groot-Hedlin C, Constable S C. Occam's inversion to generate smooth, two-dimensional models from magnetotelluric data. Geophysics , 1990, 55(12): 1613-1624. DOI:10.1190/1.1442813 |
| [10] | Fletcher R, Reeves C M. Function minimization by conjugate gradients. Comp. J. , 1964, 7(2): 149-154. DOI:10.1093/comjnl/7.2.149 |
| [11] | Polyak E, Ribiere G. Note sur la convergence des methods conjugate. Rev. Fr. Inr. Rech. Oper. , 1969, 16: 35-43. |
| [12] | Siripunvaraporna W, Egbert G, Lenbury Y, et al. Three-dimensional magnetotelluric inversion: data-space method. Physics of the Earth and Planetary Interiors , 2005, 150(1-3): 3-14. DOI:10.1016/j.pepi.2004.08.023 |
| [13] | 林昌洪.大地电磁张量阻抗三维共轭梯度反演研究.北京:中国地质大学(北京), 2009. Lin C H. Three-dimensional conjugate gradients inversion of magnetotelluric impedance tensor. Beijing: China University of Geosciences (Beijing), 2009. http://cdmd.cnki.com.cn/Article/CDMD-11415-2009075367.htm |
| [14] | 谭捍东, 余钦范, JohnB, 等. 大地电磁法三维快速松弛反演. 地球物理学报 , 2003, 46(6): 850–855. Tan H D, Yu Q F, John B, et al. Three-dimensional rapid relaxation inversion for the magnetotelluric method. Chinese Journal of Geophysics (in Chinese) , 2003, 46(6): 850-855. |
 2013, Vol. 56
2013, Vol. 56