2. 中国石油集团东方地球物理勘探有限责任公司 新兴物探开发处, 河北涿州 072751
2. BGP Inc., China National Petroleum Corporation, Hebei Zhuozhou 072751, China
探地雷达是一种高分辨率、高效率的地球物理探测技术.它广泛应用于水文地质学[1]、工程环境[2]、考古学[3]、浅层地下水调查[4]、冰川学[5]和其他领域的无损耗探测.使用地面探地雷达探测时, 电磁波必须穿透电导率值较大的覆盖层和风化层, 从而抑制了探地雷达信号的传播, 使其测量深度受到了限制.常规取芯填图以及地球物理测井能提供一些岩石质量的信息, 但只对井眼周围有限的范围敏感, 大多数的测井方法仅能测量距井眼几毫米到几米范围的地层, 由于井眼的布局所限, 许多重要的地质特征将被错过[6].
钻孔雷达探测技术的出现, 弥补了地面探地雷达方法和地球物理测井方法的不足.钻孔雷达方法也是建立在地下介质中的雷达波传播的基础上的, 它能在岩石或土壤中穿透一定的距离(在相对导电的岩石中, 探测范围可达10~20m), 频率通常在10~1000 MHz[7].钻孔雷达的测量方式有三种:单孔反射测量、跨孔测量、孔中-地面测量.其中跨孔测量是在一个钻孔中放入发射天线, 并在相邻钻孔中放置接收天线, 采集直达波数据的方法[8].
层析成像方法是常用的跨孔测量数据的解释方法.根据记录数据的不同, 层析成像方法可分为振幅层析成像和走时层析成像两种.其中走时层析成像利用直达波的初至时数据, 通过求解走时方程进行目标体重建.在走时层析成像中, 通常需要进行射线追踪.射线追踪一方面可以用来在正演过程中精确地计算走时, 另一方面也被用来在反演过程中构建包含每个元胞中射线长度的系数矩阵.当地下介质较均匀时, 电磁波可看作沿射线传播, 而当地下存在波速异常较大的非均匀体时, 电磁波在地层中传播时的射线弯曲现象必须加以考虑[9-15].1993年, Ammon和Vidale提出了一种无需进行射线追踪的地震波初至时层析成像方法.该方法用有限差分法近似求解走时程函方程和雅可比矩阵, 并用线性迭代方法进行速度估计, 其主要思想是通过追踪波前代替追踪射线来计算走时[16].此后, 该方法在跨孔雷达走时层析成像中也得到了迅速的发展[17-18].
在Ammon和Vidale给出的局部走时计算方法的基础上, Sethian和Popovici (1999)提出了一种通过在当前波前附近的窄带中选取具有最小波前传播时间来进行波前扩展的方法, 称为快速推进方法(FMM)[19].此后, 为了提高计算走时的精度, Sethian (1999)使用二阶有限差分近似梯度来求解走时程函方程, 并提出了相应的高精度快速推进方法(HAFMM)[20].
在本文中, 我们使用基于HAFMM的正演计算走时的方法以及线性迭代的反演方法[21]进行了跨孔雷达走时层析成像的研究.在此基础上, 分析了单位矩阵算子、一阶差分算子和拉普拉斯算子等三种不同模型参数加权算子对模型的约束和平滑效果; 讨论了HAFMM和FMM对反演精度的影响; 测试了LSQR (最小二乘法)[22], GMRES (极小残量法)[23]和BICGSTAB (双稳定共轭梯度法)[24]等三种矩阵反演算法的反演效果.此外, 我们还对一组采集自鞍山岫岩巨型矿体的实测数据进行了反演, 并将反演结果与用平直射线追踪和弯曲射线追踪走时层析成像所得到的反演结果进行了对比.最后, 对所有的模型重建结果进行了讨论.
2 方法 2.1 迭代线性反演公式在跨孔雷达探测中, 为了获得地下速度模型, 可以使用离散走时层析成像进行反演.我们将慢度(速度的倒数)模型划分为一系列离散的慢度值为常量的慢度元胞, 相应的数据集是有限数目的走时观测值.走时t和慢度s之间的关系可以表示为
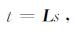
|
(1) |
这里L是系数矩阵, 它由每条射线通过每个慢度元胞时在其中的射线路径长度组成.为了求解方程(1), 通常需要使用射线追踪的方法计算系数矩阵L[9].1993年, Ammon和Vidale提出了一种无需进行射线追踪的方法, 该算法通过对走时方程(1)进行如式(2)所示的函数化描述从而避免了计算系数矩阵L[16].
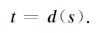
|
(2) |
实际上, 地球物理反问题是病态的.换言之, 地球物理反问题具有多解性.为了求得反演问题的一个解, 我们必须从多个能拟合观测数据的解中, 挑选出一个我们所需要的特定解.因此, 在解方程(2)时, 必须加上一些在观测数据中未包含的先验信息.病态问题中一种常应用的先验信息是假定地球物理模型"最简单", 即在保留实际地球物理模型基本特征不变的情况下, 对地球物理模型的一种简化.由l2范数定义的最简单模型, 有天然的合理性, 因为它保留了模型所有的基本特征.数据空间和模型空间上的l2范数目标函数可分别表示为

|
(3) |

|
(4) |
这里d0和d(s)分别为观测数据矢量和计算数据矢量, s和s0分别是未知的模型参数矢量和初始模型参数矢量, Wd和Wm分别是数据加权矩阵和模型参数加权矩阵[25].
1977年, Tikhonov和Arsenin提出了一种求解病态地球物理反演问题的目标函数的定义, 该方法被称作Tikhonov正则化函数[26]
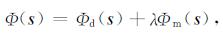
|
(5) |
这里λ是正则化参数, 用来权衡数据和模型失配的比例.求解反演问题即求目标函数Φ(s)的最小值, 可以推导出下面的等式
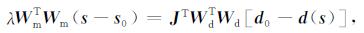
|
(6) |
这里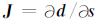
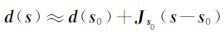
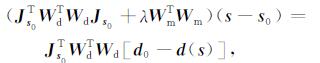
|
(7) |
等式(7)可以写成如方程(8)所示的循环形式
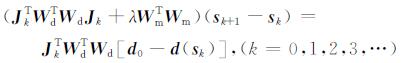
|
(8) |
求解方程(8)时需要进行矩阵与矩阵的相乘, 计算效率比较低.因此, 我们可以通过求解公式(9)的最小二乘解来提高计算效率[27].

|
(9) |
在这里, 公式(9)和公式(8)是等价的, 而且通过计算公式(9)得到的解比求解公式(8)得到的解更加准确.为了求解公式(9), 可以使用一些线性方程解法.本文使用了LSQR, GMRES和BICGSTAB等三种解线性方程的方法来对我们的反演算法进行测试.而d(sk)可以通过用有限差分法求解走时程函方程来计算.
2.2 计算波前走时的FMM算法和HAFMM算法在迭代线性反演的每一步中, 走时数据d(sk)的计算尤为重要.本文使用HAFMM算法和FMM算法通过求解二维走时程函方程来计算d(sk).在高频近似的条件下, 电磁波沿几何射线传播.复杂二维介质中, 电磁波传播时间满足下列程函方程

|
(10) |
这里, t是波前传播时间, s(x, y)表示点(x, y)处波的传播慢度.把二维复杂介质离散成长方形网格单元, 利用前向差分公式, 可以得到(10)式的一阶前向差分近似形式

|
(11) |
利用(11)式所示的一阶差分精度来近似求解程函方程并进行波前扩展的方法称为FMM.为了提高计算走时的精度, 我们用二阶前向差分近似求解(10)式, 得到以下形式

|
(12) |
利用(12)式所示的二阶差分精度来近似求解程函方程并进行波前扩展的方法称为高精度快速推进方法(HAFMM).
对于式(11), 如果ti+1, j和ti, j+1为已知, 那么就可以由式(11)计算出节点(i, j)上的波前传播时间.对于式(12), 如果满足下列两个条件, 则能应用二阶差分近似; 否则它将恢复到一阶近似.
(1) 各个方向上距离节点(i, j)两个离散网格距远的节点的波前传播时间是已知的.
(2) 各个方向上距离节点(i, j)两个离散网格距远的节点的波前传播时间必须比距离节点(i, j)一个离散网格距远的节点的波前传播时间小.
在FMM和HAFMM算法中, 波前从源点开始逐步向外推进, 用上述离散程函方程解法计算与当前波前相邻的节点上的波前传播时间.二维情形的推进过程如图 1所示.在每次推进时, 需要在当前波前附近的窄带(图 1中标记为N的带状区)选取具有最小波前传播时间的节点, 再以该点作为次级源向外扩展波前.

|
图 1 FMM/HAFMM二维波前扩展示意图 Fig. 1 Two-dimensional case of FMM/HAFMM |
在图 1中, 星号代表源点, 活点(标记为M=2)表示已经确定波前传播时间的节点, 近点(标记为M=1)表示计算过但还未确定是波前传播时间的节点, 远点(标记为M=0)表示还未计算波前传播时间的节点.下面给出了FMM和HAFMM算法的流程:
(1) 为所有节点赋足够大的波前传播时间初值, 如ti, j=105;
(2) 将所有节点标记为Mi, j=0;
(3) 在以源点为中心的2×2单元内,
①将源点标记为Mi0, j0=2;
②令源点的波前传播时间为ti0, j0=0, 根据式(11)或(12)计算其他节点上的波前传播时间;
③将计算的各个节点的坐标(i, j)保存到N中, 并标记为Mi, j=1;
(4) 搜索N中具有最小波前传播时间的节点(i, j):
①利用式(11)或(12)更新与之相邻的节点(l, m)中满足Ml, m=1的各个节点的波前传播时间.若相邻节点(l, m)满足Ml, m=0, 则利用式(11)或(12)计算该节点(l, m)上的波前传播时间, 且令Ml, m=1, 并把该节点保存到N中;
②将点(i, j)移出集合N, 并令Mi, j=2;
(5) 若N集合非空, 则跳回到(4);否则, 终止.
2.3 用有限差分法计算雅可比矩阵在基于射线理论的层析成像算法中, 雅可比矩阵的计算是通过射线追踪实现的.而本文的无射线追踪算法是使用有限差分法近似计算雅可比矩阵, 这种近似是基于模型慢度的扰动[18].对于一个离散模型, 雅可比矩阵的元素可以表示如下:

|
(13) |
这里, m和n分别是观测数据和模型参数的个数. di是第i条射线的走时函数, sj是第j个网格的慢度.式(13)使用有限差分近似可写成

|
(14) |
这里δs是扰动量.通过实验研究(这里没有展示), 我们选定每个模型慢度的扰动量δs为0.5%.
2.4 Wd和Wm的选择Wd和Wm中能包含一些可以减少反演问题多解性的先验信息.在实际上, 依据解的定义不同, Wd和Wm有很多种不同的选择.在本文中, Wd选取单位矩阵算子, 即表示数据被均匀加权; 而为了使解稳定, 我们研究了三种类型的Wm:
(1) Wm选取单位矩阵算子.此时式(8)简化成地球物理反演中广泛应用的Levenberg-Marquardt形式[25].
(2) Wm选取一阶差分算子.此时对应着平缓约束.水平一阶差分算子Wmx和垂直一阶差分算子Wmy的形式[28]分别见式(15)和(16)所示:
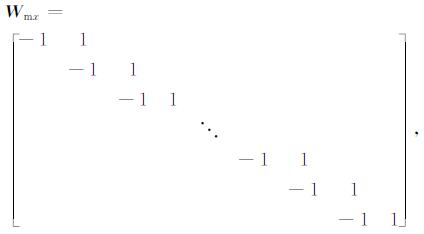
|
(15) |

|
(16) |
二维反演中该算子可以写成一般形式:
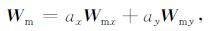
|
(17) |
这里ax和ay为两个常数(0或1).在本文的研究中, Wmx和Wmy的值都选择为1, 这也意味着模型在x和y方向上都进行了加权.
(3) Wm选取二阶差分算子(拉普拉斯算子).此时对应着光滑约束.二维情形下的拉普拉斯算子的形式为:

|
(18) |
使用五点有限差分方法[16], 式(18)可以近似为:
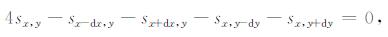
|
(19) |
进而可以利用(19)式构建拉普拉斯算子.
3 HAFMM精确性验证为了验证HAFMM算法在计算走时上的准确性, 我们对三个速度模型进行了实验, 分别使用FMM算法和HAFMM算法计算了每个模型观测点处的走时, 并将之与解析解进行了对比.由于复杂速度模型的解析解很难获得, 我们使用一个连续可微的函数Tα作为走时函数, 相应的速度函数Vα可以由下面的公式获得:
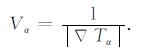
|
(20) |
表 1列出了三个模型所用的走时函数及其相应的速度函数的解析解方程.这些模型被划分为67×67个元胞, 元胞间距为1 m, 其中T1中发射源位于(1, 1)位置, T2中发射源位于(34, 1)位置, T3中发射源位于(34, 34)位置.为了测量计算值T与解析解Tα之间的误差, 本文使用了如下所示的均方根误差定义:

|
(21) |
|
|
表 1 三种走时函数Tα及其相应的速度函数Vα的解析解形式 Table 1 The losed form solution of three types of traveltime functions and their corresponding velocity functions |
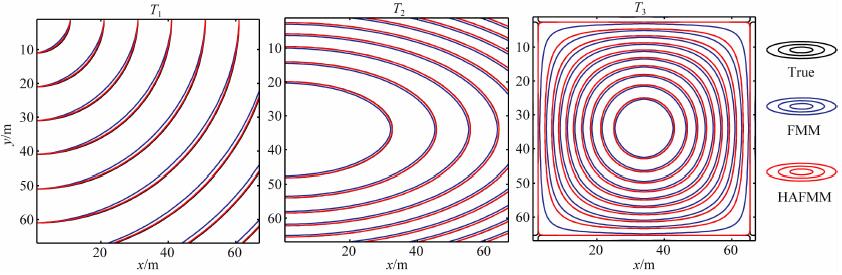
式中n为总的网格数.图 2给出了三个模型分别使用FMM及HAFMM算法计算所得的走时等值线与解析解走时等值线的对比.其中黑线表示走时解析解等值线, 蓝线表示FMM算法计算的走时等值线, 红线表示HAFMM算法计算的走时等值线.表 2为相应的误差对比.从图 2中可以看出, 在三个速度模型中, 红线所代表的用HAFMM算法计算所得的走时等值线几乎与黑线代表的解析解的走时等值线重合, 而蓝线代表的用FMM算法计算所得的走时等值线与前两者形态上大体一致, 但是距两者都有一段的距离.这说明使用FMM和HAFMM算法计算走时是一种切实可行的方法, 并且HAFMM在计算精度上要高于FMM.表 2所示的误差对比也进一步印证了这个结论.
|
图 2 FMM及HAFMM计算的走时等值线与解析解等值线对比 Fig. 2 Contrast of the contour line between the traveltime calculated using FMM/HAFMM and the Analytical solution |
|
|
表 2 V1, V2和V3分别使用FMM和HAFMM计算T1, T2和T3与解析解的误差 Table 2 Error norms between the computed V1, V2 and V3 from T1, T2 and T3 using FMM and HAFMM, respectively |
为了测试本文的反演算法, 我们对三组合成数据和一组野外实测数据进行了反演.在反演过程中, 使用L曲线法[29]选取正则化参数λ值为25.在每次反演迭代过程中, 最耗时的是雅可比矩阵的计算过程.通过对大量模型的反演结果(没有展示在这里)进行分析, 我们发现误差收敛曲线仅仅在前3次迭代过程中有明显下降, 在后续迭代中渐渐趋于平缓.因此, 为了使每次反演迭代都能稳步收敛, 在反演的前3次迭代过程中使用有限差分法计算雅可比矩阵, 3次迭代以后使用Broyden方法[30]加速计算雅可比矩阵, 在不降低分辨率的情况下, 可极大地提高反演速度.为了计算观测数据d0和第k次迭代的计算数据d(sk)之间的误差, 我们继续使用公式(21)所定义的误差准则, 并且分别用d0和d(sk)代替式(21)中的Tα和T.三组合成数据模型大小均为11 m×6 m, 两个钻孔分别在x轴方向的0.5 m和5.5 m处.在左侧钻孔中, 发射天线从0.5m深度处开始布设, 每隔0.25m移动一次, 一共移动41次; 在右侧钻孔中, 接收天线从0.5 m深度处开始布设, 每隔0.25 m移动一次, 每个发射天线位置上对应接收天线移动41次.反演迭代次数固定为20次.
4.1 模型参数加权算子影响测试如图 3a所示, 模型1中背景场速度为0.1 m/ns, 两块长方形的高速异常体和低速异常体速度分别为0.12 m/ns和0.08 m/ns.反演过程中使用HAFMM和LSQR算法, 并分别使用三种类型的Wm进行反演.采用均匀初始模型, 初始模型的速度值是通过用源点和接收点间直射线长度除以相应的射线走时, 之后再求平均值得到的[31].使用该方法得到模型1的初始模型速度值为0.1006 m/ns.三种模型参数加权算子(单位矩阵算子、一阶差分算子和拉普拉斯算子)进行反演所消耗的CPU时间分别为4.86 h, 4.91 h和4.91 h.反演时间较长的原因是每次迭代过程中雅可比矩阵的计算耗时较长.图 3b至 3d分别为相应的反演结果.从图 3b中可以看出, 当Wm选取单位矩阵算子时, 反演结果不失模型1的基本特征, 同时又能使反演问题大大简化, 因而在地球物理反演中得到了广泛的应用; 而图 3c所示的当Wm选取一阶差分算子时的反演结果比图 3b中的反演结果更为平缓, 在地球物理资料反演中有时会更为有用; 当Wm选取拉普拉斯算子时, 图 3d所示的反演结果最为平滑, 异常体形态也最为接近模型1.而在误差对比上, 使用单位矩阵算子反演的误差最小(0.21 ns), 一阶差分算子次之(0.23 ns), 拉普拉斯算子最大(0.25 ns).但是三者的差别并不大.考虑到拉普拉斯算子对目标体的重建结果是最好的, 并且其误差与另两种算子差别不大, 在后面的反演中, 我们采用拉普拉斯算子作为模型参数加权算子.

|
图 3 使用不同模型参数加权算子对模型1进行的重建 (a)模型1(真实模型); (b)单位矩阵算子反演结果; (c)一阶差分算子反演结果; (d)拉普拉斯算子反演结果. Fig. 3 Reconstruction of model 1 using different model parameter weighting operator (a) Model 1 (true model); (b) Result of unit matrix operator; (c) Result of first difference operator; (d) Result of Laplace operator |
在第3节中, 我们已经验证了HAFMM算子在计算走时的精度上要优于FMM算法.那么当将这两种算法应用到本文所提出的反演算法中时, 是否也是HAFMM的反演效果要好于FMM呢?本节将进行HAFMM和FMM的反演效果测试.在图 4a中, 模型2中背景场、高速异常体和低速异常体的速度分别为0.1 m/ns, 0.12 m/ns和0.08 m/ns.反演过程中使用拉普拉斯算子和LSQR算法, 并分别使用FMM和HAFMM进行反演.采用求平均值法得到均匀初始模型速度值为0.1008 m/ns.FMM和HAFMM进行反演所消耗的CPU时间分别为4.29h和4.77h, 相应的反演结果展示在图 4b和 4c中.如图 4b中所示, 当选用FMM时, 图 4b对模型2中两个层状异常体的形态重建得比较好, 但是对两个正方形异常体的形态重建效果不好, 其中高速正方形异常体的范围变大, 低速正方形异常体的范围变小, 并且位置发生了移动; 而图 4c对模型2中两个层状异常体和两个正方形异常体的形态重建的都好于图 4b, 并且两个正方形异常体的位置对应得也很准确.而在误差对比上, 使用HAFMM进行反演的误差(0.33 ns)明显小于FMM的误差(0.43 ns).所以, 综合模型重建效果和误差分析, HAFMM要明显好于FMM, 在后续的反演中, 我们均使用HAFMM计算走时.

|
图 4 使用不同精度的FMM对模型2进行的重建 (a)模型2(真实模型); (b) FMM反演结果; (c) HAFMM反演结果 Fig. 4 Reconstruction of model 2 using FMM with different accuracy (a) Model 2 (true model); (b) Result of FMM; (c) Result of HAFMM. |
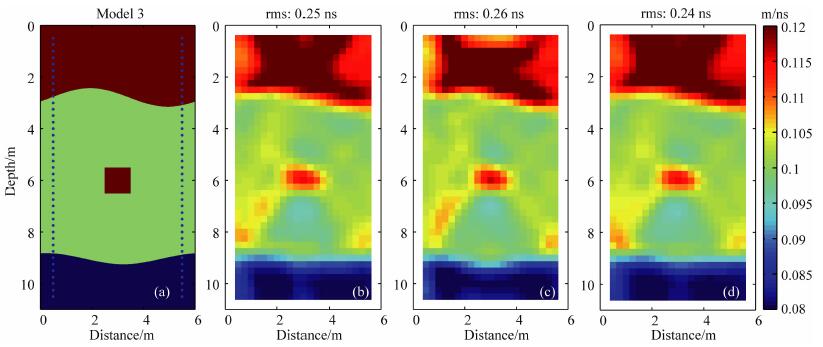
图 5a为地层起伏时的模型.其中, 模型3的上半部为高速异常地层, 速度为0.12 m/ns; 下半部为低速异常地层, 速度为0.08 m/ns; 中间地层速度为0.1 m/ns, 并且其中镶嵌着一个速度和上层地层相同的高速正方形异常体.三个地层间的分界面均为起伏界面.反演过程中使用拉普拉斯算子和HAFMM, 并分别使用LSQR, GMRES和BICGSTAB等三种矩阵反演方法进行反演.采用求平均值法得到均匀初始模型速度值为0.1025 m/ns.三种矩阵反演算法(LSQR, GMRES和BICGSTAB)进行反演所消耗的CPU时间分别为4.84h, 4.84h和4.90h.图 5b, 5c和5d分别为相应的反演结果.从中可以看出, 使用三种矩阵反演算法对模型3中的起伏界面和正方形异常体重建得都比较好, 其中使用LSQR和BICGSTAB进行重建的效果很相似, 都稍好于GMRES的重建效果.而在误差对比上, 使用GMRES进行反演的误差是最大的(0.26 ns), LSQR次之(0.25 ns), BICGSTAB最小(0.24 ns), 但是三者误差差别很小.因此, 对于本文的算法而言, 使用这三种矩阵反演算法均可得到比较好的反演结果.
|
图 5 使用不同矩阵反演方法对模型3进行的重建 (a)模型3(真实模型); (b) align="left"SQR反演结果; (c) GMRES反演结果; (d) BICGSATB反演结果. Fig. 5 Reconstruction of model 3 using different matrix inversion method (a) Model 3(true model); (b) Result of LSQR; (c) Result of GMRES; (d) Result of BICGSTAB |
在前文中我们已经提过, 本文所用的方法的实质是通过追踪波前来代替追踪射线.所以通过对反演后速度模型的波前面等时线图进行分析, 我们也能定性地判断出异常体的位置和形态.图 6为使用本文反演方法分别对三组合成数据反演迭代20次后, 所得到的速度模型各个发射天线的波前面等时线图, 并且异常体及起伏界面的位置已经用黑线画出.

|
图 6 三组合成数据模型的波前等时线图 Fig. 6 Sketch map of wavefront traveltime contour line of the synthetic data model |
在图 6a中, 各发射天线的波前面等时线在垂直方向的连线在7~8 m处向右发生了偏移, 并且在水平方向上从左到右偏移程度越来越大, 这说明在该位置处存在一个高速异常体, 并且该异常体在水平方向上有一定的延伸; 在3~4 m处, 各发射天线的波前面等时线垂直方向的连线向左发生了偏移, 并且在水平方向上从左到右偏移程度越来越大, 这说明在该位置处存在一个低速异常体, 并且该异常体在水平方向上有一定的延伸.这与模型1中异常体的形态和位置有很好的吻合.
在图 6b中, 各发射天线的波前面等时线垂直方向的连线在4 m及7 m处的情况与图 6a中很相似, 说明在这两个位置处分别存在两个低速和高速的并且在水平方向上有延伸的异常体; 在垂直方向的9 m, 水平方向的2m处, 波前面等时线垂直方向的连线向左发生了偏移, 但是在水平方向上从左到右偏移程度没有变化, 这说明该位置处有一个低速异常体, 但是异常体在水平方向上延伸不大; 而在垂直方向的2m, 水平方向的4.5m处, 波前面等时线垂直方向的连线向右发生了偏移, 但是在水平方向上该位置左侧的波前面等时线垂直方向连线并没有发生偏移, 这说明该位置处有一个高速异常体, 并且异常体在水平方向上延伸不大.这也很好地印证了模型2中的异常体形态.
在图 6c中, 各发射天线的波前面等时线在垂直方向的连线的上部和下部分别发生了向右和向左的偏移, 偏移一直持续到反演区域的顶部和底部, 并且在水平方向上从左到右开始发生偏移的位置并不在一条水平线上, 其中上层偏移开始点的位置逐渐下降, 而下层偏移开始点的位置逐渐上升.这说明模型的上部和下部分别为高速和低速的地层, 并且这两个地层与中间地层的分界面为起伏界面, 其中上界面从左到右有下降的趋势, 而下界面从左到右有上升的趋势; 在垂直方向的大约6m, 水平方向的大约3m位置处, 波前面等时线在垂直方向的连线向右发生了偏移, 并且该位置的左侧垂直方向的连线没有发生偏移, 而其右侧垂直方向的连线偏移的程度没有发生变化, 这说明该位置处存在一个高速异常体, 并且在水平方向上延伸不大.
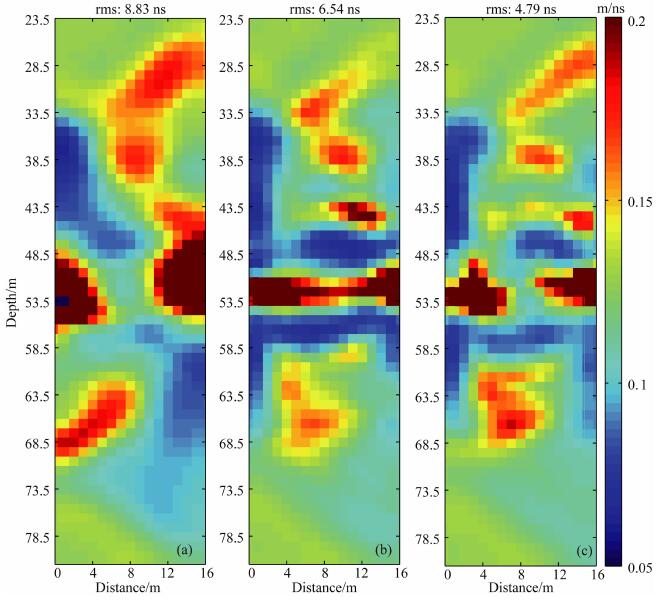
5 实测数据实例为了测试本方案对实测数据的反演效果, 我们对采集于鞍山岫岩"玉皇"巨型玉体地质灾害治理工程工区8号井和13号井之间的雷达波走时数据进行了反演.其中发射天线在左侧的8号井中, 接收天线在右侧的13号井中.发射天线从16.5m深度处开始移动, 每隔1 m移动一次, 共移动39次; 接收天线从29.5m处开始移动, 每隔1 m移动一次, 每个发射天线位置接收天线共移动28次; 并且发射天线每移动一次, 接收天线的起点位置也相应地向下移动1 m.反演过程中采用拉普拉斯算子, HAFMM和BICGSTAB矩阵反演算法.为了对反演结果进行评价, 我们还分别使用基于平直射线追踪的走时层析成像算法(以下简称平直射线算法)和基于弯曲射线追踪的走时层析成像算法(以下简称弯曲射线算法)对实测数据进行了反演.本方案及弯曲射线算法分别在迭代4次和5次后误差达到最小, 而平直射线算法的射线路径是从源点到接收点直连的平直射线, 其反演的系数矩阵是固定的, 只能进行1次迭代.三种算法(平直射线算法、弯曲射线算法及本方案)反演所需要的CPU时间分别为6.76s, 60.86s和6.35h.图 7即为分别使用三种算法进行反演的结果, 从中可以看出, 平直射线算法的反演结果中异常体范围较大, 重建效果不理想, 误差较大(8.83 ns), 这是由于平直射线算法只对速度差异比较小的情况比较适用, 而本文所采用的实例速度差异很大, 造成了平直射线算法的反演结果较差.而弯曲射线算法及本方案对异常体的刻画更加细致, 反演结果比较相似, 并且本方案误差(4.79 ns)还小于弯曲射线算法的误差(6.54 ns), 这是由于当地下异常体情况比较复杂时, 弯曲射线追踪的射线路径容易产生较大的偏差, 而本方案通过用微扰的方式计算雅可比矩阵避免了进行射线追踪, 反演的效果也更好一些.由此可见, 虽然由于计算雅可比矩阵使本方案的计算效率较前两种算法差, 但是在反演精度上本方案则更好一些.
|
图 7 鞍山岫岩"玉皇"巨型玉体工区8号井和13号井间区域重建结果 (a)平直射线追踪层析成像结果; (b)弯曲射线追踪层析成像结果; (c)无射线追踪层析成像结果. Fig. 7 Reconstruction of the area of Xiuyan giant jade between well 8 and well 13 (a) Result of straight ray tracing tomography; (b) Result of curve ray tracing omography; (c) Result of without ray tracing tomography. |
通过对比前面合成数据的反演精度, 我们发现本方案及其他两种反演算法在实测数据中反演的误差比较大.经过分析, 我们认为影响实测数据反演精度的因素有以下几点:
(1) 本文中对实测数据进行采集时使用的是我们自主研制的钻孔雷达采集系统, 与市面上常用的商用探地雷达相比, 所采集数据的质量可能稍有欠缺.
(2) 进行实测数据采集的地区地下异常体比较复杂, 并且两个钻孔的间距比较大(为合成数据两钻孔间隔的3倍多), 电磁波传播距离长, 接收到的信号信噪比较低, 造成提取的走时数据误差较大.
(3) 对实测数据进行采集时, 天线排列所形成的射线覆盖区域是一个梯形区域, 而我们的算法是对包含该梯形区域的一个矩形区域进行反演, 这就使得没有射线覆盖的区域反演误差较大, 进而造成了整体区域误差的变大.
从图 7b和7c的对比中可以看出, 虽然由于一些客观原因造成反演结果的误差较大, 但是基于本方案和弯曲射线算法的反演结果的异常体位置和形态都很相似, 并且本方案的反演误差更低, 这也说明使用本方案能达到甚至优于弯曲射线算法的重建效果.
6 结论(1) 传统的射线追踪层析成像需要计算射线路径和射线路径在每个网格单元内的长度, 而本文所应用的方案通过使用HAFMM计算波前走时和用有限差分法近似计算雅可比矩阵, 从而用追踪波前避免了追踪射线.
(2) 分别使用了三种模型参数加权算子(单位矩阵算子、一阶差分算子以及拉普拉斯算子), 两种精度的FMM (FMM和HAFMM)以及三种矩阵反演算法(LSQR, GMRES和BICGSTAB)对本文提出的方案进行了反演, 重建结果表明, 使用拉普拉斯算子和HAFMM所得到的反演结果最好, 而在矩阵反演方法的选择上, GMRES, LSQR和BICGSTAB反演效果均很好.
(3) 通过对三组合成数据反演后速度模型的波前面等时线图进行分析, 我们可以定性地判断出高速和低速异常体的位置和形态, 并能判断出起伏地层的位置和起伏方向.将之与层析成像结果进行对比, 两者能达到很好的吻合.
(4) 在对实测数据进行重建中, 平直射线追踪层析成像由于其射线路径为平直射线的限制, 反演效果最差, 精度最低; 本方案和弯曲射线追踪层析成像反演结果和精度都比较相似, 并且本方案的反演误差更低, 证明本方案能达到甚至优于弯曲射线算法的重建效果.
(5) 由于仪器、测区地下复杂度、钻孔间隔、天线排列方式等客观条件的影响, 造成本文中实测数据的反演误差较大.在今后的工作中, 我们需要提高野外数据的采集质量, 使用一组高质量的实测走时数据进一步验证本方案的有效性和精确性.
(6) 本算法在雅可比矩阵的计算上耗时很大, 在今后的工作中, 需要进一步优化算法, 提高计算雅可比矩阵的效率, 减少反演所需时间.
| [1] | Beres M Jr, Haeni F P. Application of ground-penetrating-radar methods in hydrogeologic studies. Ground Water , 1991, 29(3): 375-386. DOI:10.1111/gwat.1991.29.issue-3 |
| [2] | Knight R. Ground penetrating radar for environmental applications. Annual Review of Earth and Planetary Sciences , 2001, 29(1): 229-255. DOI:10.1146/annurev.earth.29.1.229 |
| [3] | Conyers L B. Innovative ground-penetrating radar methods for archaeological mapping. Archaeological Prospection , 2006, 13(2): 139-141. DOI:10.1002/(ISSN)1099-0763 |
| [4] | Cardimona S J, Clement W P, Kadinsky C K. Seismic reflection and ground-penetrating radar imaging of a shallow aquifer. Geophysics , 1998, 63(4): 1310-1317. DOI:10.1190/1.1444432 |
| [5] | Hinkel K M, Doolittle J A, Bockheim J G, et al. Detection of subsurface permafrost features with ground-penetrating radar, Barrow, Alaska. Permafrost and Periglacial Processes , 2001, 12(2): 179-190. DOI:10.1002/(ISSN)1099-1530 |
| [6] | 吴俊军.跨孔雷达全波形层析成像反演方法的研究.吉林:吉林大学, 2012. Wu J J. Research on cross-borehole radar tomography using full-waveform inversion method (in Chinese). Jilin: Jilin University, 2012. http://www.geophy.cn/CN/abstract/abstract10335.shtml |
| [7] | 曾昭发, 刘四新, 王者江, 等. 探地雷达方法原理及应用. 北京: 科学出版社, 2006 . Zeng Z F, Liu S X, Wang Z J, et al. Principles and Applications of GPR (in Chinese). Beijing: Science Press, 2006 . |
| [8] | 李玉喜.钻孔雷达层析成像软件系统的研究与开发.吉林:吉林大学, 2010. Li Y X. Borehole radar tomography software system study and development (in Chinese). Jilin: Jilin University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10183-2010110578.htm |
| [9] | Aldridge D F, Oldenburg D W. Two-dimensional tomographic inversion with finite-difference traveltimes. Journal of Seismic Exploration , 1993, 2: 257-274. |
| [10] | Clement W P, Knoll M D. Tomographic inversion of crosshole radar data confidence in results SAGEEP 2000.// Proceedings Environmental and Engineering Geophysical Society. Arlington, Virginia, 2000: 553-562. |
| [11] | Tronicke J, Tweeton D R, Dietrich P, et al. Improved crosshole radar tomography by using direct and reflected arrival times. Journal of Applied Geophysics , 2001, 47(2): 97-105. DOI:10.1016/S0926-9851(01)00050-7 |
| [12] | Musil M, Maurer H R, Green A G. Discrete tomography and joint inversion for loosely connected or unconnected physical properties; application to crosshole seismic and georadar data sets. Geophysical Journal International , 2003, 153(2): 389-402. DOI:10.1046/j.1365-246X.2003.01887.x |
| [13] | Clement W P, Barrash W. Crosshole radar tomography in a fluvial aquifer near Boise, Idaho. Journal of Environmental and Engineering Geophysics , 2006, 11(3): 171-184. DOI:10.2113/JEEG11.3.171 |
| [14] | Giroux B, Gloaguen E, Chouteau M. bh_tomo-a Matlab borehole georadar 2D tomography package. Computers and Geosciences , 2007, 33(1): 126-137. DOI:10.1016/j.cageo.2006.05.014 |
| [15] | Irving J D, Knoll M D, Knight R J. Improving crosshole radar velocity tomograms: a new approach to incorporating high-angle traveltime data. Geophysics , 2007, 72(4). |
| [16] | Ammon C J, Vidale J E. Tomography without rays. Bulletin of the Seismological Society of America , 1993, 83(2): 509-528. |
| [17] | Hanafy S, al Hagrey S A. Ground-penetrating radar tomography for soil-moisture heterogeneity. Geophysics , 2006, 71(1). |
| [18] | Gokturkler G, Balkaya C. Traveltime tomography of crosshole radar data without ray tracing. Journal of Applied Geophysics , 2010, 72(4): 213-224. DOI:10.1016/j.jappgeo.2010.09.004 |
| [19] | Sethian J A, Popovici A M. 3-D traveltime computation using the fast marching method. Geophysics , 1999, 64(2): 516-523. DOI:10.1190/1.1444558 |
| [20] | Sethian J A. Level Sets Methods and Fast Marching Methods. (2nd ed). Cambridge: Cambridge University Press, 1999 . |
| [21] | Pelton W H, Rijo L, Swift C M. Inversion of two-dimensional resistivity and induced-polarization data. Geophysics , 1978, 43(4): 788-803. DOI:10.1190/1.1440854 |
| [22] | Paige C C, Saunders M A. LSQR: an algorithm for sparse linear equations and sparse least squares. ACM Transactions on Mathematical Software , 1982, 8(1): 43-71. DOI:10.1145/355984.355989 |
| [23] | Saad Y, Schultz M H. GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems. SIAM Journal on Scientific and Statistical Computing , 1986, 7(3): 856-869. DOI:10.1137/0907058 |
| [24] | Gerard L G, Diederik R. BICGSTAB (L) for linear equations involving unsymmetric matrices with complex spectrum. Electronic Transactions on Numerical Analysis , 1993, 1: 11-32. |
| [25] | Greenhalgh S A, Bing Z, Green A. Solutions, algorithms and inter-relations for local minimization search geophysical inversion. Journal of Geophysics and Engineering , 2006, 3(2): 101-113. DOI:10.1088/1742-2132/3/2/001 |
| [26] | Tikhonov A N, Arsenin V Y. Solutions of Ill posed problems. New York: Winston, 1977. http://www.ebook3000.com/Solutions-of-Ill-Posed-Problems_69459.html |
| [27] | Lines L R, Treitel S. Tutorial: a review of least-squares inversion and its application to geophysical problems. Geophysical Prospecting , 1984, 32(2): 159-186. DOI:10.1111/gpr.1984.32.issue-2 |
| [28] | 成谷, 张宝金, 马在田. 浅谈反射地震走时层析中的正则化. 地球物理学进展 , 2007, 22(6): 1715–1721. Cheng G, Zhang B J, Ma Z T. Regularization in traveltime tomography for reflection seismic data. Progress in Geophysics (in Chinese) , 2007, 22(6): 1715-1721. |
| [29] | Hansen P C, O'Leart D P. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Computing , 1993, 14(6): 1487-1503. DOI:10.1137/0914086 |
| [30] | Broyden C G. A class of methods for solving nonlinear simultaneous equations. Mathematics of Computation , 1965, 19(92): 577-593. DOI:10.1090/S0025-5718-1965-0198670-6 |
| [31] | Jackson M J, Tweeton D R. MIGRATOM: Geophysical tomography using wavefront migration and fuzzy constraints: U. S. Bureau of Mines, Report of Investigation 9497.1994:35. http://www.cdc.gov/niosh/nioshtic-2/10005134.html |
 2013, Vol. 56
2013, Vol. 56