2. 中国科学院地质与地球物理研究所, 北京 100029;
3. 中国科学院大学, 北京 100049;
4. 中国石油大学(北京)地球物理与信息工程学院, 北京 102249;
5. Abai Kazakh National Pedagogical University, Almaty, Kazakhstan
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. College of Geophysics and Information Engineering, China University of Petroleum, Beijing 102249, China;
5. Abai Kazakh National Pedagogical University, Almaty, Kazakhstan
高斯束的研究已有几十年的历史, 许多物理问题用到高斯束, 如光学、电波、量子力学等.高斯束是弹性波动方程的集中于中心射线邻域的高频渐近解, 是计算非均匀介质地震波场的一种渐近方法, 因而可以用来做地震波场模拟和偏移成像.在传统的几何射线理论中, 射线振幅在焦散区是无界的; 而高斯束在传播过程中沿着中心射线路径始终保持规则, 即使在焦散点处也没有任何奇异性, 因而高斯束叠加方法是射线方法的有力扩展[1-4].
许多学者将高斯束叠加方法应用于地震偏移成像中[5-11].Hill给出了用高斯束表示平面波以及高斯束偏移的具体实现过程[5-6].Alkhalifah[7]及Zhu等[8]分别研究了各向异性介质的高斯束深度偏移. Gray和Bleistein研究了真振幅的高斯束偏移[9]. Gray还研究了共炮点道集的高斯束偏移并讨论了变方位角偏移问题[10].Sun等人研究了高斯束偏移的加速技巧[11].Kirchhoff偏移是将一个输入道投影到整个成像剖面, 与Kirchhoff偏移不同的是, 高斯束偏移首先将一组相邻的输入地震道通过倾斜叠加或束叠加分解, 然后将倾斜叠加的结果投影到一组局限的位置处, 成像位置由特定的射线方向决定[12-13].高斯束偏移方法为这些成像位置提供振幅和相位信息.高斯束偏移方法具有Kirchhoff偏移的优点(如陡倾角成像), 并且能够方便地处理焦散点、多值走时等问题.
高斯束偏移可以分为三个步骤:(1)把地震数据分解为高斯束形式; (2)向下传播高斯束; (3)在成像点处叠加各高斯束的贡献.其中第一步是高斯束偏移的关键, 它决定了偏移的计算量和成像效果.因此, 本文重点研究地震数据的高斯束分解技术.Hill通过倾斜叠加对地震数据进行高斯束分解[5], 不带有稀疏性.Nicolay等把地震数据转化到传播波场, 然后对数据进行分解[14].Nowack和Aki试验了不同的束分解参数对结果的影响[15].Weber将束分解得到的解与精确解进行了比较[16], White等利用束分解技术研究了在界面附近传播的首波[17].Wang等通过逼近狄拉克(Dirac)函数对地震数据进行稀疏高斯束分解, 并指明该方法具有数据规则化功能[18].最近对于地震数据规则化的方法还有傅里叶变换方法以及反泄漏傅里叶方法和加权Radon变换等[19-21].但这些方法主要是基于在频率域进行线性插值, 需要多次正反变换迭代实现, 从而增加了数据重建的计算量.
本文进一步研究了用高斯束稀疏分解表示地震数据.本质上这是一个拟0范数约束优化问题.在求解拟0范数极小化问题的过程中, 我们通过扫描同相轴的方法并使用了一种快速单调下降的梯度优化方法, 减少了迭代次数, 提高了计算效率.本文提出的稀疏优化方法同时具有去噪的功能, 使解得的波形更加稳定.
2 高斯束分解地震波场数据分解问题的一个关键步骤是通过适当的变换技巧对地震数据进行重新表达.在远场假设条件下, 地震波场可以认为是由局部平面波组成, 可以把局部平面波分解为高斯束[5].
频率域的高斯束可以表示为

|
(1) |
其中c为振幅, xc为高斯束中心位置, ωr为常数, ω为波动频率, θc为倾角, w为高斯束半宽.对式(1)做逆傅里叶变换(IFT)可以得到时间-空间域的高斯束函数,
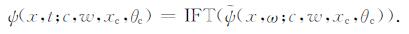
|
(2) |
图 1表示一个束中心的坐标在xc, 半宽为w=150m, 倾角为0°的时间-空间域的高斯束.在束中心的垂直方向上, 随离束中心距离平方的增加, 高斯束的振幅呈指数衰减, 如图 2所示.

|
图 1 一个高斯束 Fig. 1 A single Gaussian beam |

|
图 2 高斯束振幅指数衰减 Fig. 2 Exponential decrease ofa mplitude of Gaussian beam |
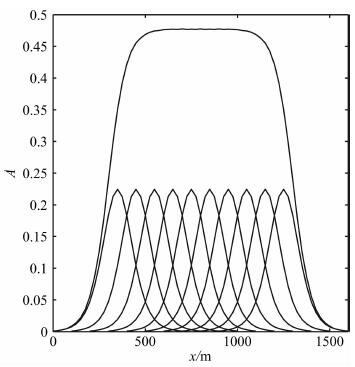
通过几个高斯束的并排叠加, 可以近似地得到局部的平面(一系列平行线), 它们的叠加形式如图 3所示.并且, 通过波形函数与局部平面的褶积可以得到局部平面波.
|
图 3 高斯束叠加形式 Fig. 3 Form of sum of Gaussian beams |
基于上述讨论, 我们可以把地震数据d(x, t)表示为以下形式:
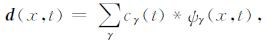
|
(3) |
其中, *为褶积符号, γ表示组成波形函数的参数, 对于任意的γ∈Γ, cγ(t)为一个波形函数, Γ是所有可能γ=(xc, tk, w, θc)的一个集合, tk为波形函数中心在时间轴上的位置, θc为地层倾角, ψγ(x, t)如前面所述为高斯束函数ψ(x, t; c, w, xc, θc).比如, 束中心的坐标xc=350m, 高斯束的半宽w=150m, 倾角θc为0°, 则得到图 1所示的单高斯束函数.
只要得到波形函数cγ(t), 便可以重建地震波场, 地震数据分解问题转化为一个求解最小二乘的问题,

|
(4) |
但上述问题是一个光滑的范数极小化问题, 直接求解并不能导致求得有限个高斯束来表征地震波场.因此, 接下来考虑稀疏优化模型及求解方法.
3 稀疏优化分解算法 3.1 稀疏优化模型表达式(3)可以表示成矩阵形式
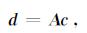
|
(5) |
其中, A为由高斯束函数形成的有限秩算子, c={cγ}(γ∈Γ)为波形向量, d为列向量地震数据.
对地震数据做稀疏高斯束分解, 即要求用尽可能少的波形向量(系数)cγ来表示地震数据, 这相当于求解一个lp范数(p→0)的极小化问题:
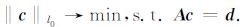
|
(6) |
其中, ‖·‖l0定义为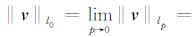


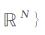
直接求解式(6)是NP-难的问题, 特别是对于大的地震数据量问题更是如此.为达到拟0范数的极小化, 我们做如下考虑:
对于地震数据, 并不是在每个时间点上都有一个波形中心, 也不是每个方向上都有波形.因此, 首先根据所选高斯束的宽度, 确定高斯束中心的距离, 在每个束中心上, 通过扫描同相轴的方法, 得到组成地震数据的局部平面波的位置、长度以及方向, 使得分解过程中的未知量大大减少.
同相轴扫描可以通过对L道地震数据做相干性度量获得:
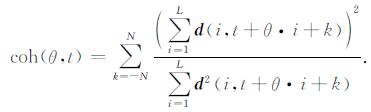
|
(7) |
N为一个时间窗, 选取与相干系数最大值对应"倾角"θ作为该处的反射波同相轴倾角, 为了增加倾角扫描的稳定性, 可以对数据进行插值加密.考虑到地震资料中存在着交叉同相轴的现象, 在利用倾斜叠加拾取倾角时, 拾取两组倾角θ1与θ2, θ1与最大值相对应, θ2与次的大值相对应.在时间轴上, 相邻且同相轴倾角方向相同的多个点组成波形.在实际问题中, 考虑到叠前资料的低信噪比特点, 可以采取地质构造约束来保障可靠地拾取倾角信息.
根据上述讨论, 求解波形向量, 我们可以利用梯度下降方法实现[27].记

|
(8) |
则可以定义一个下降方向

|
(9) |
梯度下降法指的是下面的迭代公式

|
(10) |
其中dl和αl分别为搜索方向和沿搜索方向所走的步长.一种取搜索步长的方法是采用柯西步长, 即下面的公式
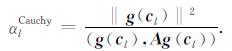
|
(11) |
但柯西公式会导致大步长, 从而使得每次迭代的梯度方向趋于真解比较慢.为了克服该问题, 本文提出了如下的改进措施:
即在计算中, 沿着直线y(cn)=cn-αg(cn)交替极小化两个函数‖g(c)‖和J[c], 使得

|
(12) |
或

|
(13) |
其中, J[c]定义为‖d-Ac‖2.
在实际计算中, 公式(12)和(13)可以交互使用.比如当n为奇数时, 得到
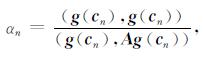
|
(14) |
当n为偶数时, 得到

|
(15) |
公式(12)-(15)是对经典的梯度下降方法(公式(11))的改进方式.经典的梯度下降方法收敛速度慢, 原因是总在一个负梯度方向上搜索下降步长, 而该方向不是最优的.公式(12)和(13)说明我们可以在一个修改的方向上搜索不同的下降步长, 一方面满足梯度的模随着迭代递减, 另一方面使得目标函数充分下降.
4 数值试验 4.1 单同相轴本方法假设地震波为局部平面波, 因此, 首先在单个同相轴情况下, 对传统的梯度下降法、快速单调下降迭代方法和传统的高斯-赛德尔迭代方法进行比较.记d为原始数据, dres为重建数据, 定义相对误差和信噪比分别为
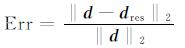
|
和

|
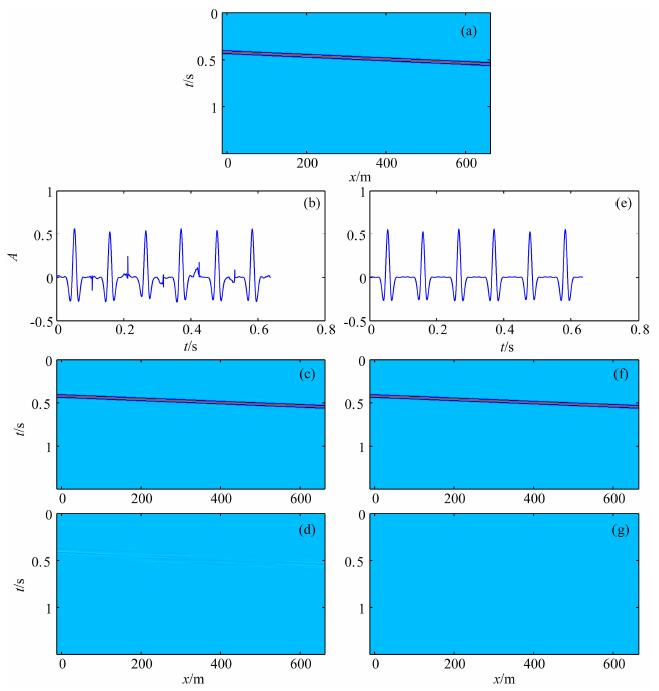
我们取道间距为25 m, 采样间隔为2 ms, 原始数据如图 4a所示, 令高斯束的半宽w=150m, 束中心的间距a=100 m, 则有6个束中心, 每个束中心上扫描得到一个波形, 一共可以得到6个波形.图 4b、4c、4d分别为使用高斯-赛德尔迭代法得到的波形、重建的数据、余量, 迭代次数为20次, 与原始数据对比得到的相对误差为Err=0.04, 信噪比SNR=63.8;图 4e、4f、4g分别为使用快速单调下降迭代法得到的波形、重建的数据、余量.迭代次数为8次, 与原始数据对比得到的相对误差为Err=0.0082, 信噪比SNR=96.0.可以看出快速单调下降迭代方法不仅收敛速度快, 而且具有正则化的功能[28], 得到的波形更稳定.
|
图 4 高斯-赛德尔方法与快速单调下降方法比较 Fig. 4 Gauss-Seidel method versus the fast gradient descent method |
为了验证本文提出的梯度下降方法的快速收敛功能, 我们与传统的梯度下降方法(公式(11))做了对比.如图 5a、5b、5c分别为使用传统的梯度下降迭代法得到的波形、重建的数据、余量结果.迭代次数为16次, 与原始数据对比得到的相对误差为Err=0.0086, 信噪比SNR=95.1.

|
图 5 传统梯度下降方法计算结果 Fig. 5 Computational results using the traditional gradient descent method |
可以看出快速单调下降迭代方法只需传统梯度下降方法1/2的计算量就可以达到相同的收敛效果, 因而对于地震数据分解和重建更为有效.
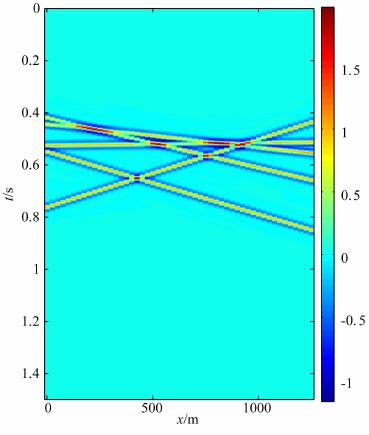
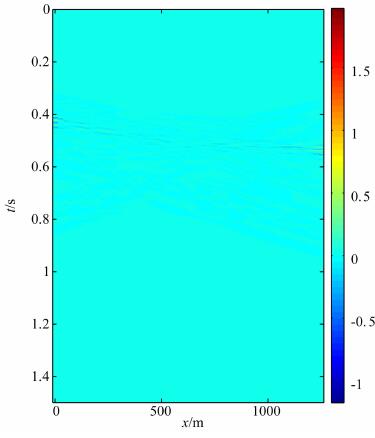
4.2 交叉同相轴存在多个交叉同相轴的复杂情况下, 公式(7)不能完美地把每个波形扫描出来, 只能是先扫描出能量大的波形, 通过计算减去这部分, 然后再扫描能量小的部分, 对于实际数据更是如此.在本次试验中, 道间距为25 m, 采样间隔为2 ms, 原始数据如图 6所示, 令高斯束的半宽w=200 m, 束中心的间距a=150m, 理论上只需要40个波形, 这里通过两次计算, 每次迭代20次, 共使用了108个波形重建地震数据如图 7所示, 原始数据与合成数据的差如图 8所示, 与原始数据对比得到的相对误差为Err=0.059, 信噪比SNR=56.5.模拟结果表明, 本文提出的方法具有良好的地震数据规则化功能, 重建结果可以很好地逼近原始数据, 因此本文的稀疏分解方式是可靠的.

|
图 6 原始地震数据 Fig. 6 The original seismic data |
|
图 7 由高斯束重建的地震数据 Fig. 7 Restoration of seismic data based on Gaussian beams |
|
图 8 原始数据与重建数据的差 Fig. 8 Residual between the original data and the data of restoration |
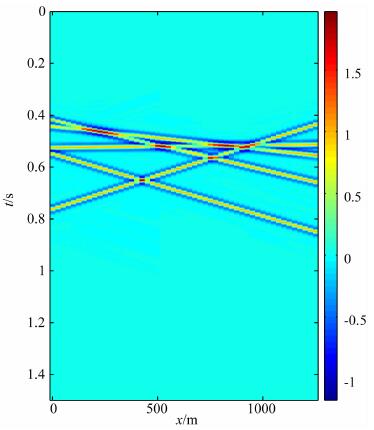
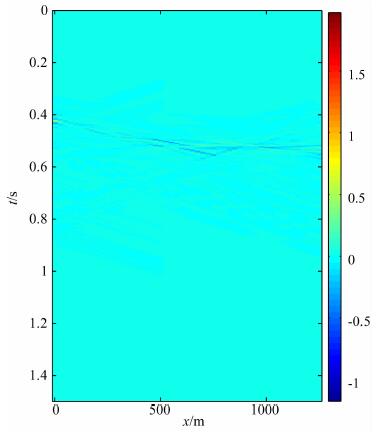
接着我们验证本方法具有插值加密功能.缺道地震数据会引起假频现象, 即扫描得到更多的波形, 这些波形在横向上缺乏连续性, 在联合反演过程中自然被消除(能量极小).对于图 6, 随机抽取若干道, 得到地震数据如图 9所示, 通过该道缺失数据重建的地震数据如图 10所示, 使用了115个波形, 信噪比SNR=47.2, 余量如图 11所示, 相对误差Err=0.094.

|
图 9 随机采样地震数据 Fig. 9 Seismic data of random sampling |
|
图 10 由随机采样数据重建的地震数据 Fig. 10 Restoration of seismic data based on random sampling data |
|
图 11 原始数据与重建数据的差 Fig. 11 Residual between the original data and the data of restoration |
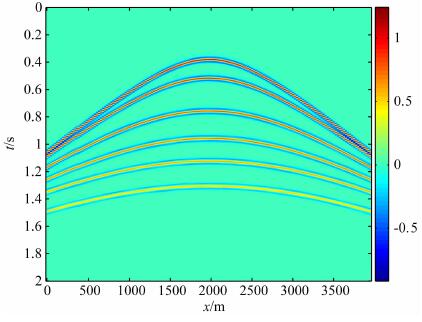
接下来研究高斯束分解方法的噪音去除功能.设点源在一个水平层状介质模型中产生的地震记录, 并加入了一定量的噪音(SNR=8.37), 道间距为25m, 采样间隔为2 ms, 如图 12所示, 令高斯束的半宽w=150m, 束中心的间距a=100m, 使用253个波形重建的地震数据如图 13所示.其中信噪比SNR=44.3, 余量如图 14所示, 相对误差Err=0.11.模拟结果表明本文的稀疏分解方法具有良好的去噪功能, 其原因是随机噪音极少形成同相轴, 更无法形成波形, 在扫描同相轴的过程中被消除.

|
图 12 带有高斯随机噪音的原始地震数据 Fig. 12 The original seismic data with Gaussianr and omnoise |
|
图 13 由带噪音数据重建的地震数据 Fig. 13 Restoration of seismic data based on noisy data |

|
图 14 层状介质数据与重建数据的差 Fig. 14 Residual between the layered media data and the data of restoration |
为进一步验证方法的可靠性, 使用实际数据对方法进行测试.如图 15所示, 为海上地震数据的一部分, 采样间隔为2ms, 道间距为25m, 选取了115道, 图 16是由1367个波形重建的地震数据, 消除了表面的随机噪音, 图 17由实际数据减去重建数据得到, 可以看出, 余量中已经没有明显的同相轴, 能量大小与噪音能量级接近.这说明稀疏高斯束地震数据分解是可行的.

|
图 15 实际海洋地震数据 Fig. 15 Marine seismic data |
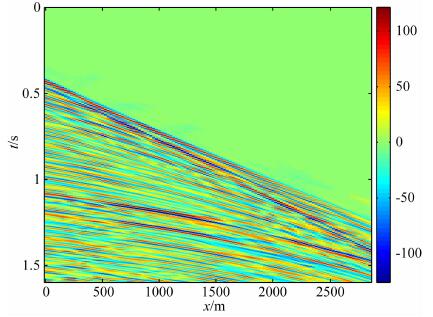
|
图 16 由高斯束重建的海洋地震数据 Fig. 16 Restoration of marine seismic data based on Gaussian beams |
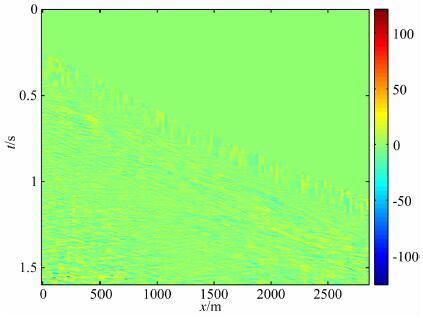
|
图 17 实际数据与重建数据的差 Fig. 17 Residual between the actual data and the data of restoration |
本文提出用高斯束方法分解地震数据, 通过扫描同相轴的方法使分解具有稀疏性, 数值实现上提出了一种快速单调下降的梯度优化方法计算波形向量.在扫描同相轴的过程中, 可以消除部分噪音, 随机噪音无法形成波形, 被排除在外; 对于一些波, 虽然可以形成波形, 它们并非来自地下, 倾角过大, 如直达波, 可以通过控制倾斜范围和波形能量值加以消除.模型和实际数据重建结果表明了方法的可行性和可靠性.通过本方法得到的波形可以用于高斯束偏移成像.
致谢感谢审稿人对文章算法的讨论以及对内容提出的良好建议.
| [1] | Popov M M. A new method of computation of wave fields using Gaussian beams. Wave Motion , 1982, 4(1): 85-97. DOI:10.1016/0165-2125(82)90016-6 |
| [2] | Cerveny V, Psencik I. Gaussian beams in two-dimensional elastic inhomogeneous media. Geophysical Journal International , 1983, 72(2): 417-433. DOI:10.1111/gji.1983.72.issue-2 |
| [3] | Babich V M, Popov M M. Gaussian summation method (review). Radiophysics and Quantum Electronics , 1989, 32(12): 1063-1081. DOI:10.1007/BF01038632 |
| [4] | Klimes L, Pěeňík R I. Optimization of the shape of Gaussian beams of a fixed length. Stud. Geophys. Geod. , 1989, 33(2): 146-163. DOI:10.1007/BF01646581 |
| [5] | Hill N R. Gaussian beam migration. Geophysics , 1990, 55(2): 1416-1428. |
| [6] | Hill N R. Prestack Gaussian-beam depth migration. Geophysics , 2001, 66(4): 1240-1250. DOI:10.1190/1.1487071 |
| [7] | Alkhalifah T. Gaussian beam depth migration for anisotropic media. Geophysics , 1995, 60(5): 1474-1484. DOI:10.1190/1.1443881 |
| [8] | Zhu T, Gray S H, Wang D. Prestack Gaussian-beam depth migration in anisotropic media. Geophysics , 2005, 72(3): 133-138. |
| [9] | Gray S H, Bleistein N. True-amplitude Gaussian-beam migration. Geophysics , 2009, 74(2). |
| [10] | Gray S H. Gaussian beam migration of common-shot records. Geophysics , 2005, 70(4): 71-77. DOI:10.1190/1.1988186 |
| [11] | Sun Y H, Qin F H, Steve C, et al. 3D prestack Kirchhoff beam migration for depth imaging. Geophysics , 2000, 65(5): 1592-1603. DOI:10.1190/1.1444847 |
| [12] | Costa C A, Raz S, Kosloff D. Gaussian beam migration. //59th Ann. Internat. Mtg. Soc. Expl. Geophys., Expanded Abstracts, 1989:1169-1171. |
| [13] | Raz S. Beam stacking: a generalized preprocessing technique. Geophysics , 1987, 52(9): 1199-1210. DOI:10.1190/1.1442383 |
| [14] | Nicolay M T, Richard T, Sergey F, et al. Gaussian beam decomposition for seismic migration. SEG Expanded Abstracts , 2011, 30: 3356-3361. |
| [15] | Nowack R, Aki K. The two-dimensional Gaussian beam synthetic method: testing and application. Journal of Geophysical Research , 1984, 89(B9): 7797-7819. DOI:10.1029/JB089iB09p07797 |
| [16] | Weber M. Computation of body-wave seismograms in absorbing 2-D media using the Gaussian beam method: comparison with exact methods. Geophysical Journal International , 1988, 92(1): 9-24. DOI:10.1111/j.1365-246X.1988.tb01116.x |
| [17] | White B S, Norris A, Bayliss A, et al. Some remarks on the Gaussian beam summation method. Geophysical Journal International , 1987, 89(2): 579-636. DOI:10.1111/j.1365-246X.1987.tb05184.x |
| [18] | Wang Y F, Liu P, Li Z H, et al. Data regularization using Gaussian beams decomposition and sparse norms. Journal of Inverse and Ill-posed Problems , 2013, 21(1): 1-23. DOI:10.1515/jip-2012-0030 |
| [19] | 高建军, 陈小宏, 王芳芳, 等. 不规则地震道数据规则化重建方法研究. 地球物理学进展 , 2011, 26(3): 983–991. Gao J J, Chen X H, Wang F F, et al. Study on regularized reconstruction of uneven seismic traces. Progress in Geophys (in Chinese) , 2011, 26(3): 983-991. |
| [20] | 王维红, 裴江云, 张剑锋. 加权抛物Radon变换叠前地震数据重建. 地球物理学报 , 2007, 50(3): 851–859. Wang W H, Pei J Y, Zhang J F. Prestack seismic data reconstruction using weighted parabolic Radon transform. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 851-859. |
| [21] | 刘喜武, 刘洪, 刘彬. 反假频非均匀地震数据重建方法研究. 地球物理学报 , 2004, 47(2): 299–305. Liu X W, Liu H, Liu B. A study on algorithm for reconstruction of de-alias uneven seismic data. Chinese J. Geophys. (in Chinese) , 2004, 47(2): 299-305. |
| [22] | 曹静杰, 王彦飞, 杨长春. 地震数据压缩重构的正则化与0范数稀疏最优化方法. 地球物理学报 , 2012, 55(2): 596–607. Cao J J, Wang Y F, Yang C C. Seismic data restoration based on compressive sensing using the regularization and zero-norm sparse optimization. Chinese J. Geophys. (in Chinese) , 2012, 55(2): 596-607. |
| [23] | Cao J J, Wang Y F, Zhao J T, et al. A review on restoration of seismic wavefields based on regularization and compressive sensing. Inverse Problems in Science and Engineering , 2011, 19(5): 679-704. DOI:10.1080/17415977.2011.576342 |
| [24] | Wang Y F, Yang C C, Cao J J. On Tikhonov regularization and compressive sensing for seismic signal process. Mathematical Models and Methods in Applied Sciences , 2012, 22(2): 1150008-1. DOI:10.1142/S0218202511500084 |
| [25] | Wang Y F, Cao J J, Yang C C. Recovery of seismic wavefields based on compressive sensing by an l1-norm constrained trust region method and the piecewise random subsampling. Geophysical Journal International , 2011, 187(1): 199-213. DOI:10.1111/gji.2011.187.issue-1 |
| [26] | Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inform. Theory , 2007, 53(12): 4655-4666. DOI:10.1109/TIT.2007.909108 |
| [27] | 王彦飞, 斯捷潘诺娃I E, 提塔连科V N, 等. 地球物理数值反演问题. 北京: 高等教育出版社, 2011 . Wang Y F, Stepanova I E, Strakhov V N, et al. Inverse Problems in Geophysics and Solution Methods (in Chinese). Beijing: Higher Education Press, 2011 . |
| [28] | 王彦飞. 反演问题的计算方法及其应用. 北京: 高等教育出版社, 2007 . Wang Y F. Computational Methods for Inverse Problems and Their Applications (in Chinese). Beijing: Higher Education Press, 2007 . |
 2013, Vol. 56
2013, Vol. 56


