2. 中国科学院大学, 北京 100049;
3. 日本地学数据分析研究所, 东京 184-0012
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Geo-Analysis Institute Co., Ltd. Tokyo 184-0012, Japan
S波速度结构是地球内部物理和动力学研究的重要参数, 能反映地球深部物质成分和属性变化, 对研究壳幔动力学模型及地质演化过程具有重要作用[1].相对于P波而言, S波对地下流体、热物质等的速度变化更敏感[2-3], 能更好地反映地球内部介质的流变状态和热结构, 研究S波速度结构, 将有助于加深对研究区域地下介质物理状态和深部动力学过程的认识.因此, 在地球动力学及地震学研究中, S波速度结构研究日益受到重视.
目前, 从天然地震记录中获取S波速度结构的方法主要有S波走时层析成像[4], 面波层析成像[5-6], 接收函数方法[7-8], S波波形拟合法[9]以及地震背景噪声成像技术[10]等.S波走时层析成像利用S波到时数据, 反演获得三维S波速度结构, 并可结合P波走时层析成像结果, 进一步获得泊松比分布[11].但由于S波到时数据拾取精度较差, 对成像结果有较大影响, 限制了该方法的使用.传统面波层析成像主要用来研究岩石圈板块的厚度及其横向不均匀性, 对地壳、尤其是上地壳的速度结构分辨率较低[6].接收函数法是反演台站下方S波速度结构的有效手段[7, 12], 它从长周期远震体波中分离出接收函数, 通过波形反演拟合接收函数的径向分量, 对观测台站下方介质的S波速度结构进行估计[7], 同时也可以通过偏移叠加获得的接收函数道集(地震剖面图)追踪速度间断面[12].该方法避免了对天然地震震源及其附近结构混响效应等复杂因素的影响, 对S波速度的垂向分布敏感、垂向分辨率高.然而由于接收函数从地震波形记录中分离得到的是PS转换波, 因此该方法对产生PS转换波的界面, 如莫霍面、岩层圈、软流圈分界面比较敏感和有效.近年来发展的地震背景噪音成像技术[10]则采用地震台网连续记录的环境噪音数据, 通过互相关计算提取面波经验格林函数, 可得到较多的路径覆盖和短周期频散信息, 从而可有效提高地壳、特别是上地壳速度结构的分辨率[13].
上述获取S波速度结构的方法各具特色, 有些是利用S波信息直接得到S波速度结构, 如S波走时层析成像、S波波形拟合法; 另一些则是利用其对剪切波的敏感性, 通过P波与S波之间的经验公式转换间接得到S波速度结构, 如面波层析成像、接收函数法等.在间接方法中, P波和S波互相依赖, 无法独立分开反演, 因此, 难以对波速比进行更深入的研究.显然, 不依赖P波直接获得S波速度结构的方法更具优势, 用相互独立的P波、S波速度结构可获取更为真实的泊松比.
空间自相关法[14-18] (Spatial Autocorrelation Method, 简称SPAC法)是从台阵微动信号的垂直分量中提取瑞利波相速度频散曲线的数据处理方法, 通过对瑞利波频散曲线的反演可估算介质S波速度结构.这是目前公认最有效、快捷的确定沉积层S波速度结构的方法之一[19], 这种方法不依赖于P波、可独立获得S波速度结构.该方法以往都用于对圆形观测台阵微动数据的处理, Prieto等[20]将该方法用于处理不规则天然地震台阵背景噪声, 并获得了南加州地区的一维剪切波速度模型, 从而表明该方法用于估算不规则天然地震台阵微动信号同样有效.我们尝试将这种方法应用于首都圈地区北京附近的天然地震台阵微动数据, 为该地区地壳结构、成分研究提供新的S波速度结构模型.本文介绍其数据处理、计算相速度频散曲线以及反演获得S波速度结构的方法.通过与其他地球物理成果的对比, 探讨该方法的可靠性与适用性.
2 基于SPAC法的S波速度结构估算从台阵记录的微动数据中提取面波频散曲线的SPAC法最早由Aki (1957)[14]提出.它基于两点基本假设:(1)微动在时空上符合平稳随机过程; (2)微动所包含的各种成分的波中, 基阶面波占优势.其基本原理叙述如下.
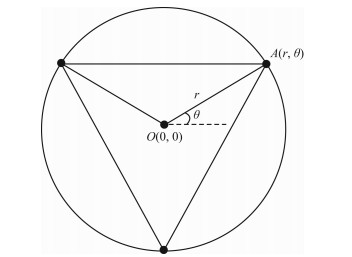
图 1所示圆形台阵的中心O(0, 0)和半径为r的圆周上A(r, θ)点的微动信号垂直分量表达式分别为[17]
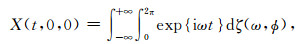
|
(1) |
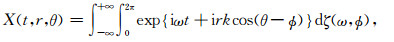
|
(2) |
|
图 1 微动观测台阵示意图 Fig. 1 Sketch of microtremor observation array |
其中ω为角频率, k为波数, φ为微动信号的入射角, ζ(ω, φ)为一个正交随机过程.
定义O、A两点的空间自相关函数S(r, θ)为

|
(3) |
式中, 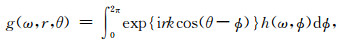
空间协方差函数g(ω, r, θ)的方位平均为
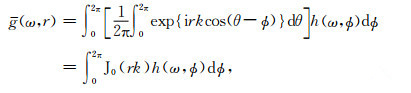
|
(4) |
式中, 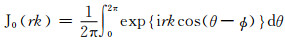
定义空间自相关系数ρ(ω, r)为

|
(5) |
将g(ω, 0, 0)代入g(ω, r, θ), 则有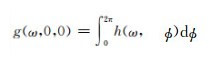
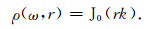
|
(6) |
该式表明, 波的相速度c(ω)可以通过第一类零阶Bessel函数J0和空间自相关系数求得.
Okada等[21]和Chavez-garcia等[22]利用窄带滤波进行谐波分离在时间域计算空间相关系数, 但计算耗时而且精度差.冈田广[23]对此进行了改进, 通过傅里叶变换在频率域计算空间自相关系数, 不但速度快而且精度高.
分别将圆心O点和半径为r的圆周上A(r, θ)点微动信号的傅里叶变换表示为SO(ω)、SA(r, ω), 则这两点的空间自相关系数在频率域有如下关系式[24]:

|
(7) |
其中*代表复数共轭.求得不同ω对应的空间自相关系数, 由(7)式代入(6)式即可得到相速度c(ω), 最终获得相速度频散曲线.
从微动信号中提取瑞利波相速度频散曲线之后, 采用全局寻优算法---分歧型遗传算法(fGA)[25]反演地下介质S波速度结构.分歧型遗传算法具有计算速度快、全局搜索能力强的优点, 在地球物理反演问题中得到广泛应用.进行反演计算之前首先给定初始模型参数(层数n、各层S波速度vS、层厚h), 然后搜索S波速度结构的全局最优解.
3 微动数据及其处理 3.1 台站分布与微动数据的选取选取首都圈地区北京附近作为本文研究区域.该地区是我国地震台网分布较为密集、观测数据质量相对较好的地区, 以往对该区速度结构的地震学及人工地震探测研究结果, 可为本项研究提供建模约束和重要的对比依据.
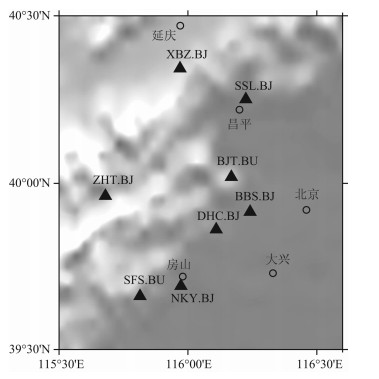
受多期构造运动改造, 首都圈地区形成坳隆相邻、盆山相间、密度不均匀、壳内结构与莫霍面埋深变化较大的地壳分块构造格局[26].为了避免微动观测台阵因跨不同构造单元带来的平均效应, 我们选取图 2所示北京附近的较小范围(39°30′N-40°30′ N, 115°30′E-116°30′E)作为研究区域.该区域内有10个宽频带地震台站, 数据预处理后剔除了2个台站、8个地震台站记录良好用于本文研究, 这些台站基本位于同一构造单元.
|
图 2 研究区台站分布图(三角形示意宽频带地震台站位置) Fig. 2 Distribution of stations in study region (Triangles denote the broadband seismic stations) |
选取2009年7月14日北京时间2h05′1.4″发生在台湾花莲的6.7级地震, 其后的微动信号作为原始微动数据.大地震激发的面波和后续微动信号中长周期成分(低频信号)丰富、能量较强, 有利于反演获得更深的S波速度结构.图 3为该地震的波形记录(BBS.BJ地震台的垂直分量记录).为避开体波, 微动数据从发震时刻之后17 min开始截取, 时长1h.

|
图 3 用于本文研究的地震波形(BBS台站的垂直分量记录) Fig. 3 Seismic waveform used in study region (the vertical component of BBS station records) |
首先对单台微动数据进行预处理, 主要包括重采样、仪器响应校正、去均值、去倾斜分量以及带通滤波等.
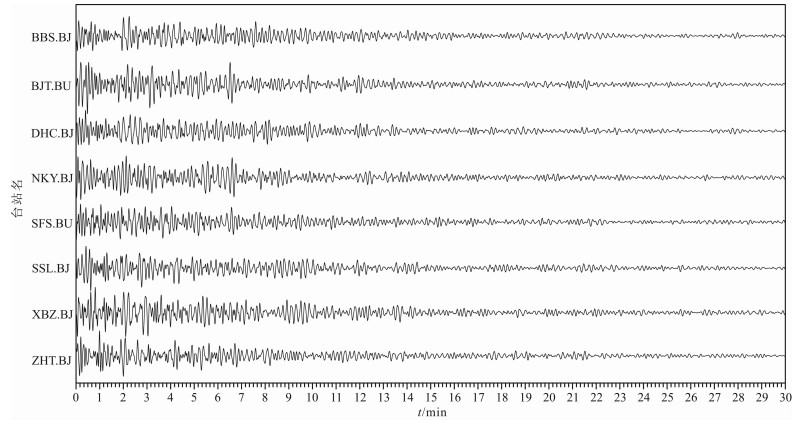
拷自国家地震台网的原始地震数据采样频率有100 Hz和50 Hz两种, 为方便使用首先用20 Hz的采样频率进行统一重采样.为了校正这8个台站因使用不同地震计和数据采集系统所造成的微动信号幅频特性和相频特性的差异, 又对这些台站重采样后的地震数据分别进行了仪器响应校正.对于微动数据中存在的基线漂移等现象, 采用去均值的办法消除.最后对垂直分量微动记录进行0.01~0.5 Hz的带通滤波以提高信噪比.图 4给出预处理之后8个台站30 min微动波形记录.
|
图 4 预处理后的微动波形记录 Fig. 4 Microtremor record after pretreatment |
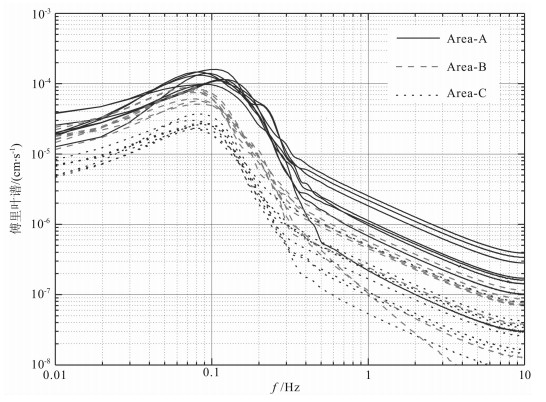
对预处理后的微动信号, 分别选取0~102.4 s、600~702.4 s和1200~1302.4 s三个时段内的微动信号进行频谱分析.结果(图 5)显示, 8个台站的傅里叶谱一致性好, 能量主要集中在0.02~0.4 Hz频率范围(有效频带)内, 不同时段微动信号的傅里叶谱除能量略有差异外, 在有效频带范围内形态相似、能量稳定.从而表明, 所选用的微动信号在时间域和空间域是平稳的.
|
图 5 8个台站微动信号的傅里叶频谱 计算长度为2048个数据, 即2048×0.05=102.4s.Area-A:0~102.4s;Area-B:600~702.4s;Area-C:1200~1302.4s. Fig. 5 Fourier spectrum of eight stations Calculation length is 2048 data, 2048×0.05=102.4s, Area-A:0~102.4s; Area-B:600~702.4s;Area-C:1200~1302.4s. |
相速度频散曲线的求取分如下三步进行.
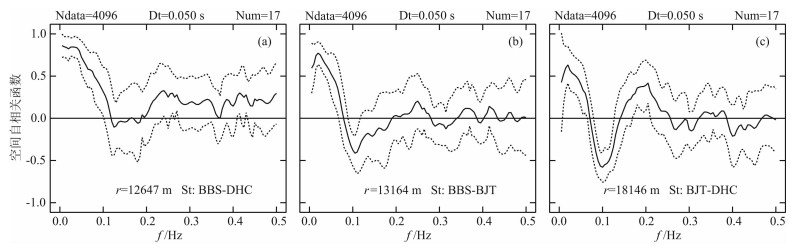
3.3.1 计算空间自相关函数将研究区域内的8个台站进行两两组合, 共得到28个不同台间距的台站对(见表 1).对每个台站对的波形记录在相同时间段内进行空间自相关计算.首先将微动记录分成17个数据段, 每段4096个数据(Num=17, Ndata=4096, 见图 6); 其次对每段数据进行快速傅里叶变换(FFT)求功率谱和互功率谱, 用(7)式计算每段数据的空间自相关函数; 最后将17段数据的空间自相关函数求平均得到该台站对的空间自相关函数, 并计算标准差.部分台站对的空间自相关函数见图 6.
|
图 6 台站对的空间自相关函数 Num=17表示把1个小时的微动信号分成17段; Dt为采样频率; St:BBS-DHC表示两个台站对的台站名; r为台站对的间距.实线为空间自相关函数的平均, 虚线表示在平均值的基础上增加或减少一个标准差. Fig. 6 Spatial autocorrelation function of stations Num denotes 1hour microtremors is divided into 17 segments, Dt is sampling frequency, St: BBS-DHC denotes the two stations′name; r is the distance between two stations, the solid line is the average of spatial autocorrelation function, the dotted line is based on the average increase or decrease one standard deviation. |
|
|
表 1 台站对间距(单位:m) Table 1 Distance between different stations (unit:m) |
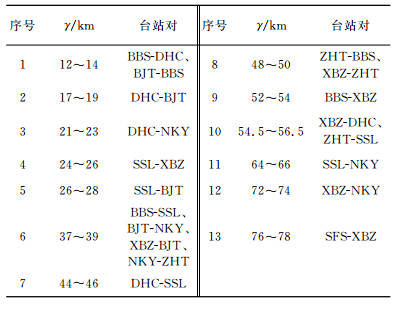
为得到可靠的空间自相关系数, 还需对空间自相关函数进行方位平均.首先将相距2 km以内的台站对归为一类, 对每个类里的空间自相关函数进行方位平均, 得到该类的空间自相关系数ρ(ω, r), 以减少数据离散, 提高结果的可靠性.按此方法, 在剔除了那些两两相关性差的数据后, 由28个台站对的13条(表 2)空间自相关系数曲线可用于本项研究, 图 7给出其中两条.图 7a是图 6(a, b)两条曲线的平均, 图 7b就是图 6c曲线, 因为该类中只有一个台站对.对比图 6和图 7可知, 当有多条空间自相关函数进行平均时, 得到的空间自相关系数的标准差小, 曲线比较光滑.

|
图 7 空间自相关系数 Fig. 7 Spatial autocorrelation coefficient |
|
|
表 2 以2 km间距分类的台站对 Table 2 Classification by 2 km distance between stations |
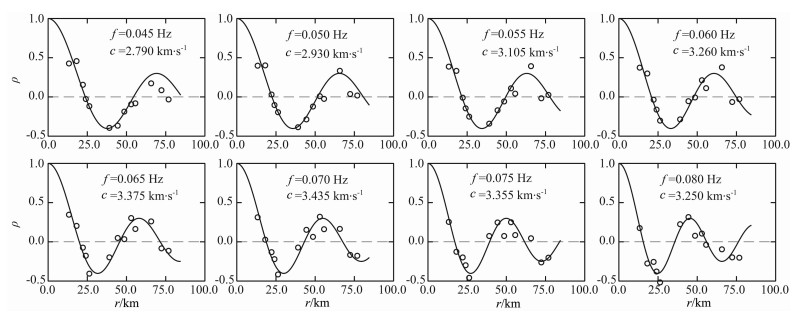
固定频率f, 式(6)变为ρ(r)=J0(rk), 其中k=2πf/c(f), c(f)为相速度.对于每个不同的r, 可得一个ρ(图 7).用第一类零阶Bessel函数拟合r-ρ曲线(图 8), 可得频率f的相速度c(f)[16, 18], 由此获得的相速度频散曲线(图 9).
|
图 8 拟合的Bessel函数 Fig. 8 Bessel function fitting to Fig.7 |

|
图 9 瑞利波频散曲线 Fig. 9 Rayleigh-wave dispersion curve |
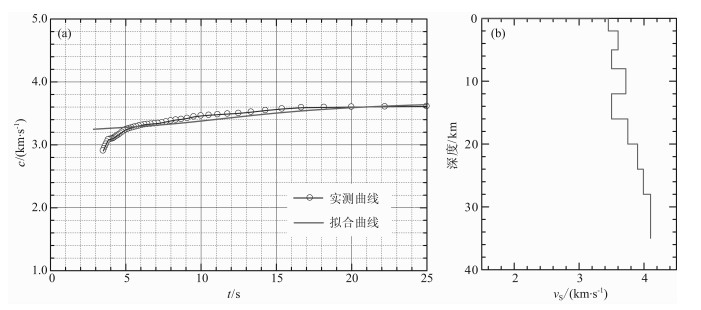
面波频散特性与介质层厚、密度、纵、横波速度有关, 其反演计算实质上是多极值问题的求解.因为面波频散对S波速度比对P波及介质密度更为敏感[27], 所以在本项研究中只反演S波速度.P波速度、介质密度的取值据文献[28]中的经验公式.传统的线性反演方法在很大程度上依赖于初始模型, 近年来发展起来的遗传算法, 引入了类似生物进化过程中适者生存的优化思路, 是随机反演方法中速度较快、全局搜索能力较强的非线性优化方法之一, 较好地解决了多极值反演结果严重依赖于初始模型的问题[29].本文采用分歧型遗传算法[25]对面波频散曲线进行反演计算, 参考以往研究成果[30-31]设置本区初始反演模型, 不断调整模型各层的速度和厚度计算其理论频散曲线, 直到与实测频散曲线达到最佳拟合.反演结果见图 10和表 3.
|
图 10 S波速度结构(a)及频散曲线拟合图(b) Fig. 10 S-wave velocity structure (a) and the fitting curve (b) |
|
|
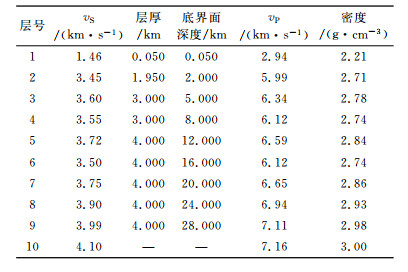
表 3 S波速度结构 Table 3 S-wave velocity structure |
反演获得的S波速度结构, 可看成是图 2中8个台站所覆盖区域(中心约在116°E、40°N)介质S波速度结构的平均值.速度结构大致可分为三层, 第一层(0~8 km), vS=3.45~3.6 km·s-1, 底部发育3 km厚的低速层(vS=3.55 km·s-1).第二层(8~20 km), vS=3.72~3.75 km·s-1, 岩性较为均匀, 中部(12~16 km)发育低速层(vS=3.5 km·s-1).第三层(>20 km), vS≥3.9 km·s-1, 波速随深度平稳增加.
研究区位于太行山与华北盆地的盆山边界, 本文结果显示在2 km深处vS=3.45 km·s-1, 已对应结晶基底, 这与结晶基底埋深较浅(1~2 km)的人工地震探测结果相符[31].延怀盆地接收函数研究结果显示该地区上地壳发育低速层[32], 与本文地壳上部5~8 km处的低速层相当.本文结果揭示的地壳中部(12~16 km)低速层, 以往人工地震探测、接收函数和地震层析成像研究成果中均有显示[32-34], 厚度一般在3~6 km, 延伸几公里至数十公里, 低速层内外速度差异小于5%[33], 也与电磁测深结果中的高导层相对应[35].我国华北太行山以东地区地壳发育局部低速层的地质事实, 被认为与该地区所处俯冲-伸展大地构造环境、地壳内岩石部分熔融和水的存在有关[33-35].因为低速层是流变学意义上的“软弱层”, 岩石强度低, 易导致壳内介质解耦形变进而诱发地震成为“孕震层”, 华北东部地区地震震中分布表现为面状弥散展布特点而并非集中在若干大的活断层上, 与低速层发育有较好对应关系[34].
总体而言, 本文方法获得的S波速度结构基本反映了研究区的地质特征, 可与以往地球物理研究成果相比较.但因为受台站数限制, 本文用于方位平均计算的台站对数量较少, 这会造成用于拟合Bessel函数的数据点离散, 影响结果精度.另外, 本文所用到8个台站中的最小台间距12.6 km, 最大台间距约77 km, 这样的台阵仅能“检测”到周期为4~25s的瑞利波, 反演获得S波速度结构的可靠深度范围估计在2~28 km, 28 km以下难于有效分层.所以, 为获得精细的S波速度结构, 需要密集、规模较大的地震台阵.
5 结语本文尝试利用SPAC法估算地壳S波速度结构.介绍从天然地震台站微动信号中提取瑞利波相速度频散曲线, 反演估算地壳S波速度结构的方法, 并利用北京附近8个台站的微动数据获得了一维S波速度结构.根据S波速度结构特点, 本文把研究区地壳分为三层, 0~8 km为上部地壳, 8~20 km为中部地壳, 20 km以下为下部地壳, 8 km和20 km处是S波速度差异较大的速度分界面.分别在上部地壳底部(5~8 km)和中部地壳(12~16 km)发现S波低速层.这一结果与研究区地质构造特征相符, 也与以往地震学和地球物理研究成果较为吻合.
该方法利用天然地震台网微动地震噪声数据, 获得独立的S波速度结构, 不依赖于P波速度.日益完善的地震台网以及针对特定研究区域布设的流动地震台网, 均可为本方法提供大量高质量的原始微动数据, 使得利用本文方法获得精细三维地壳S波速度结构成为可能, 这对研究地壳的泊松比结构、岩性组成和各向异性极为有用.
致谢中国地震局地球物理研究所“国家数字测震台网数据备份中心”为本项研究提供地震波形数据.非常感谢评审专家的宝贵意见.
| [1] | 王凯, 姚振兴. 中国上地幔剪切波速度结构的初步研究. 地球物理学报 , 1989, 32(1): 36–45. Wang K, Yao Z X. Preliminary study of upper mantle shear velocity structure of China. Chinese J. Geophys. (in Chinese) , 1989, 32(1): 36-45. |
| [2] | Mavko G M. Velocity and attenuation in partially molten rocks. J. Geophys. Res. , 1980, 85(B10): 5173-5189. DOI:10.1029/JB085iB10p05173 |
| [3] | Eberhart-Phillips D, Michael A J. Seismotectonics of the Loma Prieta, California, region determined from three-dimensional VP, VP/VS, and seismicity. J. Geophys. Res. , 1998, 103(B9): 21099-21120. DOI:10.1029/98JB01984 |
| [4] | Zhao D, Hasegawa A, Horiuchi S. Tomographic imaging of P and S wave velocity structure beneath northeastern Japan. J. Geophys. Res. , 1992, 97(B13): 19909-19928. DOI:10.1029/92JB00603 |
| [5] | 朱介寿, 曹家敏, 蔡学林, 等. 东亚及西太平洋边缘海高分辨率面波层析成像. 地球物理学报 , 2002, 45(5): 679–698. Zhu J S, Cao J M, Cai X L, et al. High resolution surface wave tomography in East Asia and West Pacific Marginal Seas. Chinese J. Geophys. (in Chinese) , 2002, 45(5): 679-698. DOI:10.1002/cjg2.v45.5 |
| [6] | Huang Z, Su W, Peng Y, et al. Rayleigh wave tomography of China and adjacent regions. J. Geophys. Res. , 2003, 108(B2): 2073-2073. |
| [7] | Langston C A. Structure under Mount Rainier, Washington, inferred from teleseismic body waves. J. Geophys. Res. , 1979, 84(B9): 4749-4762. DOI:10.1029/JB084iB09p04749 |
| [8] | Owens T J, Zandt G, Taylor S R. Seismic evidence for an ancient rift beneath the Cumberland Plateau, Tennessee: A detailed analysis of broadband teleseismic P waveforms. J. Geophys. Res. , 1984, 89(B9): 7783-7795. DOI:10.1029/JB089iB09p07783 |
| [9] | Hemberger D V, Ingen G R. Upper mantle shear structure. J. Geophys. Res. , 1979, 29(26): 4077-4078. |
| [10] | Bensen G D, Ritzwoller M H, Barmin M P, et al. Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements. Geophys. J. Int. , 2007, 169: 1239-1260. DOI:10.1111/gji.2007.169.issue-3 |
| [11] | 齐诚, 赵大鹏, 陈颙, 等. 首都圈地区地壳P波和S波三维速度结构及其与大地震的关系. 地球物理学报 , 2006, 49(3): 805–815. Qi C, Zhao D P, Chen Y, et al. 3-D P and S wave velocity structures and their relationship to strong earthquakes in the Chinese capital region. Chinese J. Geophys. (in Chinese) , 2006, 49(3): 805-815. |
| [12] | Yuan X, Ni J, Kind R, et al. Lithospheric and upper mantle structure of southern Tibet from a seismological passive source experiment. J. Geophys. Res. , 1997, 102(B12): 27491-27500. DOI:10.1029/97JB02379 |
| [13] | Guo Z, Gao X, Yao H, et al. Midcrustal low-velocity layer beneath the central Himalaya and southern Tibet revealed by ambient noise array tomography. Geochemistry Geophysics Geosystems , 2009, 10(5): Q05007. |
| [14] | Aki K. Space and time spectra of stationary stochastic waves, with special reference to microtremors. Bull. Earthq. Res. Inst. , 1957, 35: 415-456. |
| [15] | Ling S Q. Research on the estimation of phase velocities of surface waves in microtremors (in Japanese). Japan: Hokkaido University, 1994. |
| [16] | Okada H. "The Microtremor Survey Method", Society of Exploration Geophysicists, Geophysical Monographs Series Vol. 12, translated by Koya Suto. Society of Exploration Geophysicists, Tulsa, 2003. |
| [17] | Okada H. Theory of efficient array observations of microtremors with special reference to the SPAC method. Explor. Geophys. , 2006, 59(1): 73-85. |
| [18] | Ohori M, Nobata A, Wakamatsu K. A comparison of ESAC and FK methods of estimating phase velocity using arbitrarily shaped microtremor arrays. Bull. Seism. Soc. Am. , 2002, 92(6): 2323-2332. DOI:10.1785/0119980109 |
| [19] | Satoh T, Kawase H, Matsushima S. Estimation of S-wave velocity structures in and around the Sendai Basin, Japan, using array records of microtremors. Bull. Seism. Soc. Am. , 2001, 91(2): 206-218. DOI:10.1785/0119990148 |
| [20] | Prieto G A, Lawrence J F, Beroza G C. Anelastic Earth structure from thd coherency of the ambient seismic field. J. Geophys. Res. , 2009, 114: B07303. DOI:10.1029/2008JB006067 |
| [21] | Okada H, Sakajili N. Estimation of an S-wave velocity distribution using long-period microtremors. Geophys. Bull., Hokkaido University (in Japanese), 1983, 42: 119-143. |
| [22] | Chávez-García F J, Rodríguez M, Stephenson W R. Subsoil structure using SPAC measurements along a line. Bull. Seism. Soc. Am. , 2006, 96(2): 729-736. DOI:10.1785/0120050141 |
| [23] | 冈田广, 凌甦群.微动利用の地下构造探查に关する最近の研究につぃて.北海道大学大学院研究报告, 1994. Okada H, Ling S Q. About a recent study on the surveying geologic structures by using the Microtremor Survey Method. Report of Hokkaido University (in Japanese), 1994. |
| [24] | Asten M W. On bias and noise in passive seismic data from finite circular array data processed using SPAC methods. Geophysics , 2006, 71(6): V153-V162. DOI:10.1190/1.2345054 |
| [25] | Cho I, Nakanishi I, Ling S Q, et al. Application of Forking Genetic Algorithm fGA to an exploration method using microtremors. Butsuri-Tansa (in Japanese), 1999, 52: 227-246. |
| [26] | 姜文亮, 张景发. 首都圈地区精细地壳结构-基于重力场的反演. 地球物理学报 , 2012, 55(5): 1646–1661. Jiang W L, Zhang J F. Fine crustal structure beneath Capital area of China derived from gravity. Chinese J. Geophys. (in Chinese) , 2012, 55(5): 1646-1661. |
| [27] | Horike M. Inversion of phase velocity of long-period microtremors to the S-wave-velocity structure down to the basement in urbanized areas. J. Phys. Earth. , 1985, 33(2): 59-96. DOI:10.4294/jpe1952.33.59 |
| [28] | Ludwig W J, Nafe J E, Drake C L. Seismic refraction. The Sea , 1970, 4(Part 1): 53-84. |
| [29] | 石耀霖, 金文. 面波频散反演地球内部构造的遗传算法. 地球物理学报 , 1995, 38(2): 189–198. Shi Y L, Jin W. Genetic algorithms inversion of lithospheric structure from surface wave dispersion. Chinese J. Geophys. (in Chinese) , 1995, 38(2): 189-198. |
| [30] | 房立华, 吴建平. 背景噪声频散曲线测定及其在华北地区的应用. 地震学报 , 2009, 31(5): 544–554. Fang L H, Wu J P. Measurement of Rayleigh wave dispersion from ambient seismic noise and its application in North China. Acta Seismologica Sinica (in Chinese) , 2009, 31(5): 544-554. |
| [31] | 嘉世旭, 张先康. 华北不同构造块体地壳结构及其对比研究. 地球物理学报 , 2005, 48(3): 611–620. Jia S X, Zhang X K. Crustal structure and comparison of different tectonic blocks in North China. Chinese J. Geophys. (in Chinese) , 2005, 48(3): 611-620. DOI:10.1002/cjg2.694 |
| [32] | 刘启元, 李顺成, 沈扬, 等. 延怀盆地及其邻区地壳上地幔速度结构的宽频带地震台阵研究. 地球物理学报 , 1997, 40(6): 763–772. Liu Q Y, Li S C, Shen Y, et al. Broadband seismic array study of the crust and upper mantle velocity structure beneath Yanhuai basin and its neighbouring region. Chinese J. Geophys. (in Chinese) , 1997, 40(6): 763-772. |
| [33] | 李松林, 苗琪, 王旭. 华北地区的地壳低速层. 大地测量与地球动力学 , 2011, 31(5): 31–38. Li S L, Miao Q, Wang X. Low velocity layers of the crust in North China. Journal of Geodesy and Geodynamics (in Chinese) , 2011, 31(5): 31-38. |
| [34] | Xu P, Zhao D. Upper-mantle velocity structure beneath the North China Craton: implications for lithospheric thinning. Geophys. J. Int. , 2009, 177(3): 1279-1283. DOI:10.1111/gji.2009.177.issue-3 |
| [35] | 刘国栋, 刘昌铨. 华北北部地区地壳上地幔构造及其与新生代构造活动的关系. 中国科学 , 1982, 12(12): 1132–1140. Liu G D, Liu C Q. Crust-uppermantle structures in northern region of North China and its relationships to Cenozoic tectonic activities. Science China (in Chinese) , 1982, 12(12): 1132-1140. |
 2013, Vol. 56
2013, Vol. 56