固体潮源于月亮和太阳以及其他天体的引力作用[1-3].固体潮的影响可以通过安置在地表的高精度仪器观测出来,如用于地震研究的应变仪[4-5].应变反映了质体内任一点因外力作用引起的形状和尺寸的相对改变,它与地球内部的应力状态密切相关,因此可有效反映地震前后的应力分布和传输.应变固体潮是应变测量时间序列中的最主要的部分,因此从观测资料中有效扣除应变固体潮的影响,并应用于地球内部介质特征和地震的研究具有非常重要的意义.
应变或应力固体潮的理论值通常根据地表的Love数计算获得[1-3],而实际上应变仪是安装在地球内部,因此采用地球内部的Love数来计算理论的应变或应力固体潮则更加符合实际.除此之外,地球内部应力固体潮可用于地震的潮汐触发的研究[6-8],潮汐应力对地震临界状态的影响有可能是导致地震最终发生的力源.尽管地球内部的应力潮汐已经应用于潮汐触发地震的研究[6-8],但具体的关于地球内部应力的计算问题则语焉不详.吴庆鹏曾从点源的角度,根据地球在引潮力作用下的变形讨论了固体潮应力,给出了球谐展开的二阶和三阶的地球内部函数结果;但是并没有给出最终的结果,而是给出了以天体天顶距为参数的公式[9].因此如需获得地球内部任一点的应力在地球地固系下的应力和应变仍需进行进一步的推导和计算;另外目前的观测精度越来越高,球谐展开的四阶项尽管小,但也是需要考虑的.孙文科也曾对地球内部的重力、倾斜固体潮潮汐因子进行了研究,并且给出了北京地下300 km应力潮汐的计算实例,表明应力潮汐的振幅达到103 Pa[10].
为了让读者更加深入详细地了解地球内部应变和应力潮汐的理论和计算问题,以及应力和应变潮汐在地球内部不同区域的变化特征,本文对此进行了详细的介绍与讨论,分析了应变和应力固体潮在地球内部不同深度和不同纬度处的时间变化特征.作为应力固体潮在潮汐触发地震研究中的应用实例,本文也探讨了断层面潮汐应力相位与地震发震时刻的相关性.
2 计算理论 2.1 引潮位及其导数的计算根据引潮位展开表,引潮位可以表示为[2]

|
(1) |
其中,Gnm是大地系数,n是球谐展开的阶数,m是展开的次数,其二阶表达式为[2]
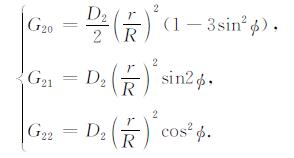
|
(2) |
三阶表达式为
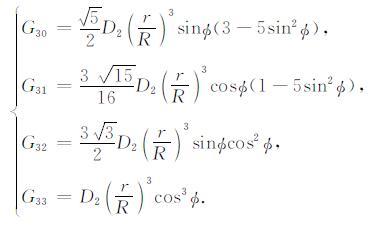
|
(3) |
四阶表达式为
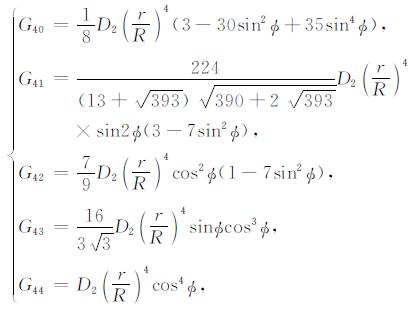
|
(4) |
其中D2称为Doodson常数,r是地球内部一点到地心的距离,R是地球半径,Φ为纬度,Aω是频率为ω的潮波的相对幅度,Δφω是相应的相位改正数(由于有些正弦波要统一表示为余弦函数的形式),m取0、1、2、3和4对应于长周期、周日、半日、1/3日和1/4日,τ是平地方太阴时,它与世界时t和计算点经度的关系如下:
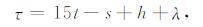
|
(5) |
(1)中的省略号部分是包含s和h等5个天文参数的线性组合,与τ一起,6个天文参数的系数构成Doodson编码[1-2].
需要注意的是,传统的Doodson展开方法和现代引潮位展开方法略有不同,如使大地系数保持不变,则现代方法展开的Aω需要除以一个转换系数(表 1),以便得到正确的结果[11].
|
|
表 1 潮波振幅转换系数 Table 1 Transfer coefficients for amplitudes of tidal constituents |
通常所使用的Love数是研究地表固体潮现象的重要参数,固体潮产生的地表位移的三个分量可以用Love数hn和ln来表示,对于地球内部问题,同样可以采用Love数.我们采用如下的Love数的定义[12]:
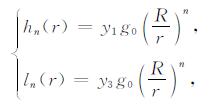
|
(6) |
式中,引潮位的展开系数取为1,而没有选择文献[12]中的Rg0,这种归一化系数的选取并不会改变最终的结果.那么,地球内部或表面任一点的垂直和水平位移为

|
(7) |
其中,U,Vθ和Vλ分别是垂直位移、余纬向和经向的水平位移,Tn是n阶引潮位,θ是计算点的余纬,g0是地表重力(加速度)值,N是截断的阶数,目前通常为4阶.由(2)-(4)可知,引潮位中包含(r/R)n因子,而Love数中含有(R/r)n因子,因此直接用习惯的y1和y3来代替内部Love数则使得这两个因子相互抵消,从而使公式更加简洁,其表达式如下:
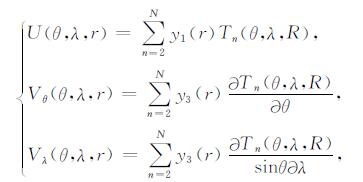
|
(8) |
值得注意的是,文献[10]定义的Love数为
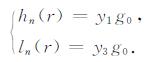
|
(9) |
但是在此Love数定义下计算地表位移时,采用了地表的引潮位,所以位移的表达式与(8)式一致.
根据应变与位移的关系,可得应变张量中6个独立分量的表达式为

|
(10) |
再根据应力与应变的关系:

|
(11) |
即可获得地球内部的潮汐应力,其中μ和λ′是r处的拉梅常数,
从上述的公式可以看出,计算潮汐应力和应变的关键是求得引潮位及其1阶和2阶偏导数,它们可以根据(2)-(5)式推导获得;另外需要计算y1和y3对r的导数,它们是y1、y2、y3和y4以及地球的拉梅常数的函数,其中y1、y2、y3和y4分别表示在引潮力作用下地球内部和表面产生的径向位移、径向应力、水平位移和水平应力,它们的数值结果可以通过求解基于某一地球模型的微分方程组的边值问题获得[2, 10, 13].
2.3 计算步骤综上所述,可以将计算步骤总结如下:
(i)根据固体潮理论求解微分方程组边值问题获得y1、y2、y3和y4随r变化的值,并导出y1和y3对r的导数值;(ii)根据(1)-(5)式求得引潮位(r=R)对Φ和λ的偏导数,其中对λ的偏导数即为对τ的偏导数;(iii)根据(10)和(11)式分别计算获得固体潮应变和应力.
3 计算结果与讨论 3.1 地球内部Love数计算中我们采用了球对称、非自转、弹性和各项同性的PREM地球模型[14],但对此模型进行了修正,对液态的海洋层和地壳最上层进行了平均[15],根据微分方程组的边值问题求解获得了对应于2、3、4阶的y1、y2、y3和y4随r变化的值,以及y1和y3对r的导数值,结果如图 1,Love数可由(6)式获得.

|
图 1 y函数及其导数在地球内部的变化(从左到右三列分别对应于2、3、4阶的结果) Fig. 1 Changes of y-functions and their derivatives in the Earth′s interior |
我们仅给出了从地表到800 km深度处的值,不管是对于应力应变固体潮的研究还是与地震相关的研究,这个深度已经足够.y1~y4都是r的连续函数,而y1和y3对r的导数由于拉梅常数的不连续在间断面处是不连续的.y2~y4都随深度的增大而增大;而y1随着阶数的不同其变化特征也不相同.我们将该结果与文献[10]进行了对比:在地表,本文和文献[10]的h2值分别为0.5988和0.5810,l2值分别为0.0846和0.0903,h2的导数值分别为-0.4229×10-7和-0.3410×10-7(转换到国际单位,下同),l2的导数值分别为-0.8071×10-7和-0.4910×10-7.由以上数值可知,本文和文献[10] h2的结果比较一致,而l2的差异稍大,但本文l2结果与文献[13]的约0.0840比较接近.我们知道,改变最表层的地球模型参数,对地表低阶的Love数影响甚微,但是会明显改变h2和l2的导数值,因为它们与拉梅常数密切相关.对于h3和l3及其导数值以及在地球内部也有类似的结论.
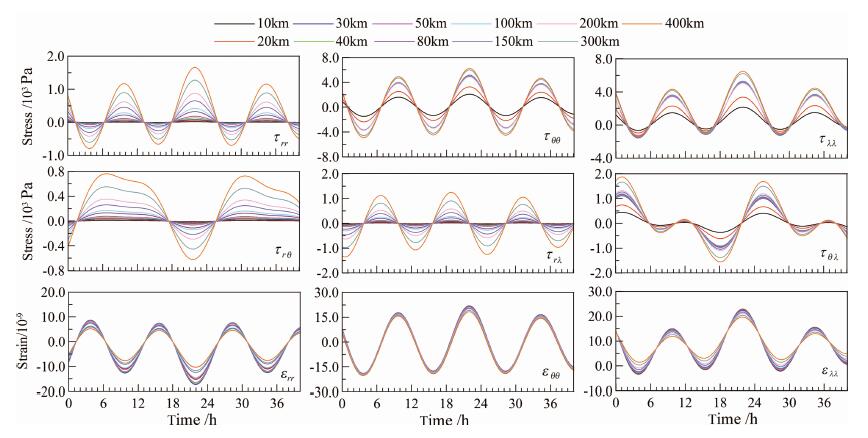
3.2 应力与应变潮汐图 2给出了经度和纬度都为0的地方应力的6个独立分量对应于不同深度、40h内(中间时刻为2013年1月1日0时)的时间变化,其中引潮位展开表采用Xi的结果[16].由图可以看出:深度变化对应力潮汐的影响非常显著,随着深度的增加,应力潮汐的振幅也随之增大.rr、rθ和rλ应力分量在浅层的振幅非常小,只有10 Pa的量级,在地球深部其振幅达到103 Pa;其他分量的振幅在地球浅层达到102 Pa,到地球深部达到103 Pa;除了rθ应力分量外,其他应力分量的潮汐都表现为明显的半日波特征;三个正应力分量的潮汐时间变化在相位上具有较好的一致性.
|
图 2 不同深度处的应力和应变潮汐时间变化 Fig. 2 Time series of tidal stress and tidal strain at different depths |
图 2同时也给出了相对应的应变潮汐的变化,由于剪切应变与剪切应力只相差一个比例系数,因此它们的变化特征一致,所以图中我们只给出了正应变的结果.从图 2可以看出:正应变的振幅都在10-8量级,随着深度的增大,应变潮汐的振幅都有减小的趋势,其中rr分量的正应变潮汐振幅对深度的依赖关系与图 1中的dy1/dr一致,θθ和λλ分量的正应变潮汐振幅对深度的依赖关系也可由图 1中的y1和y3获得.
为了更加清晰地了解深度对应力和应变潮汐的影响,我们对深度从10 km到400 km、间隔10 km处的潮汐曲线在与图 2相同时间段内取其最大值(图中实线)和最小值(图中虚线),最大和最小值的差值反映了潮汐的振幅及变化幅度,结果如图 3所示.从图 3中可以看出,应力的6个分量的潮汐变化幅度都随深度增大而增大,其中θθ、λλ和θλ分量由于地球模型参数在内部边界的不连续而产生不连续的变化,其他3个应力分量潮汐的变化幅度与深度近似呈现线性增大的关系;rr分量的正应变随深度减小,在大约250 km深度处,应变增大,然后又随深度减小;θθ分量正应变分量潮汐的变化幅度随深度变化很小,λλ分量正应变分量潮汐的变化幅度随深度增大逐渐减小.

|
图 3 应力和应变潮汐变化幅度随深度的变化关系 Fig. 3 Changes of magnitudes of tidal stress and tidal strain with respect to depth |
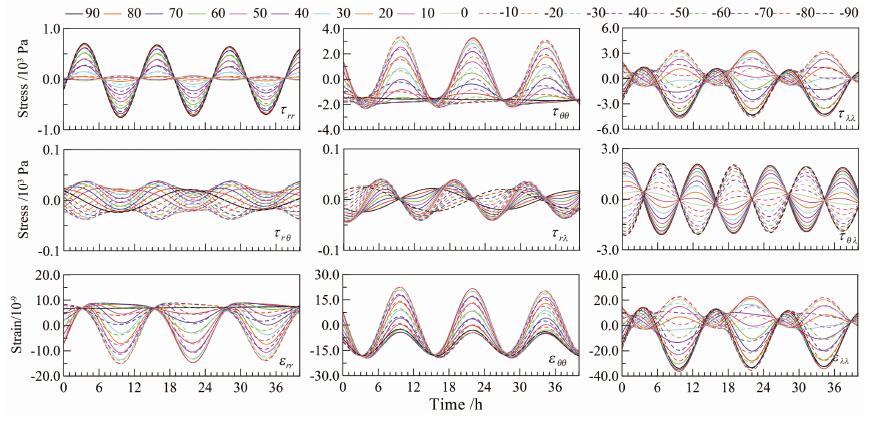
图 4给出了应力潮汐6个独立分量在不同纬度处的时间变化,对于同一纬度,经度的不同只会导致相位的变化,并不会导致振幅的变化,因此我们选择零子午线上纬度从北纬90°到南纬90°,间隔10°,深度为20 km的地点.从图中可以看出:6个应力分量除了在两极外都表现出明显的半日波变化特征,而rθ和rλ应力分量的潮汐在两极表现为周日波特征,θλ分量的潮汐在赤道表现为周日波特征;rθ分量在南北两极的值是有一些差异的,这是因为球谐展开的三阶潮汐项中的周日项是大小相等而符号相反的;rλ分量的潮汐在南北两极是对称的;需要指出的是图中θθ分量在两极处也是半日波特征,只是由于振幅相对其他纬度区域较小,并不是图中显示的长周期特征;其实这些变化特征也不难从大地系数及其导数推断出来.同样地,图 4也给出了3个正应变潮汐随纬度的变化,其变化都比较剧烈,rr分量的正应变潮汐在两极表现为长周期特征,其他的潮汐变化主要表现为半日波特征,正应变潮汐也没有明显的纬度上的对称性.
|
图 4 不同纬度处的应力和应变潮汐时间变化 Fig. 4 Time series of tidal stress and tidal strain at different latitudes |
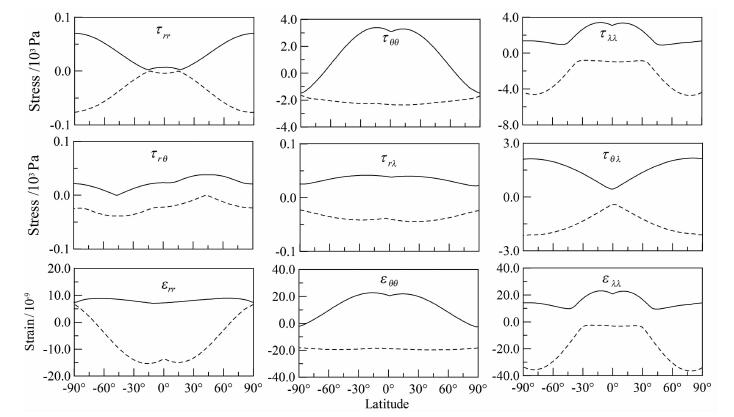
图 5给出了应力和应变潮汐的变化幅度随纬度的变化关系,图中每间隔1°计算一个值.同样地,实线表示最大值,虚线表示最小值.除了应力的rθ分量表现出关于南北纬度的反对称外,其他的应力和应变潮汐的变化幅度都表现为南北纬度的对称特征,但是从图 4可知它们不是严格对称的,只是在变化趋势上具有明显的这一特性,这一结论也可通过仔细观测图 5中的变化曲线得出.通过最大值和最小值的差值我们可以获得应力和应变潮汐在哪一纬度区变化幅度最大,如rr正应力分量潮汐的最大变化幅度出现在两极附近;对于rr正应变,其值在南北纬20°附近.
|
图 5 应力和应变潮汐变化幅度随纬度的变化关系 Fig. 5 Changes of magnitudes of tidal stress and tidal strain with respect to latitude |
作为一个应用实例,我们研究了潮汐触发地震的问题.选取了我国中部地区(纬度范围25°N-40°N,经度范围100°E-106°E)从1976-2010年发生的共101个地震,地震资料从GCMT获得(http://www.globalcmt.org/[2013-01-11]),该资料提供地震发生的时刻、震源三维坐标及断层方位参数,即走向角、倾角和滑动角.由此,我们计算了震源处的潮汐应力,并根据应力的坐标旋转计算了地震断层面上潮汐的正应力、剪应力、应力张量的第一不变量(张量矩阵的迹)和库伦破坏应力的时间序列.
对于距离海洋较近的地区,海潮负荷甚至比固体潮都要大[17],而距离海洋较远的区域,海潮负荷的影响比固体潮小大约一个数量级.为了对海潮负荷如何影响潮汐的振幅与相位有一个具体的认识,以远离海洋的中部地区的汶川地震的震源参数为例,我们首先计算了该地震断层面上的潮汐应力,然后计算离海洋较近的上海台的应力潮汐(采用相同的参数),图 6给出了断层面上的正应力和剪应力潮汐变化曲线,由于上海台(图 6右边一列)的海潮负荷影响较大,因此在表示固体潮和海潮负荷共同影响时,在图的右边采用了不同的虚线标尺.由图可知,对于远离海洋的地区,尽管海潮负荷对潮汐振幅的贡献不大,但是对潮汐的相位还是有较大的影响;而对于离海洋较近的地区,海潮负荷不仅对潮汐振幅而且对潮汐相位都有非常大的影响.因此我们在计算时也加入了海潮负荷的影响.关于如何计算内部的海潮负荷应力和应变潮汐可参考文献[17].

|
图 6 断层面上的应力固体潮及海潮负荷 左边一列(a)为汶川震源处的结果,右边一列(b)为上海台的结果;实线表示固体潮的贡献,虚线表示固体潮与海潮负荷的共同贡献.此处的θ对应于滑动方向. Fig. 6 Tidal stress and ocean tide loading effect on stress on fault plane The left column shows the results at the hypocenter of Wenchuan earthquake.The right column shows the results at Shanghai station.The solid lines represent the solid Earth′s tides and the dash lines represent the sum of solid Earth′s tides and ocean tide loading effects.θ corresponds to slip direction here. |
由断层面上的应力潮汐变化的时间序列,根据发震时刻和文献[8]的方法获得发震时刻的潮汐相位和Schuster统计结果的p值,其中p=e-A/N,A=(Σcosψi)2 +(Σsinψi)2,ψi是某一地震发震时刻的潮汐相位.p值反映了拒绝地震随机发生的零假设的显著性水平,其值越小说明地震的发生越不是随机的.在此,我们选取p < 5%,也就是95%的置信水平,来判定地震发生与断层面上应力潮汐的相关性.
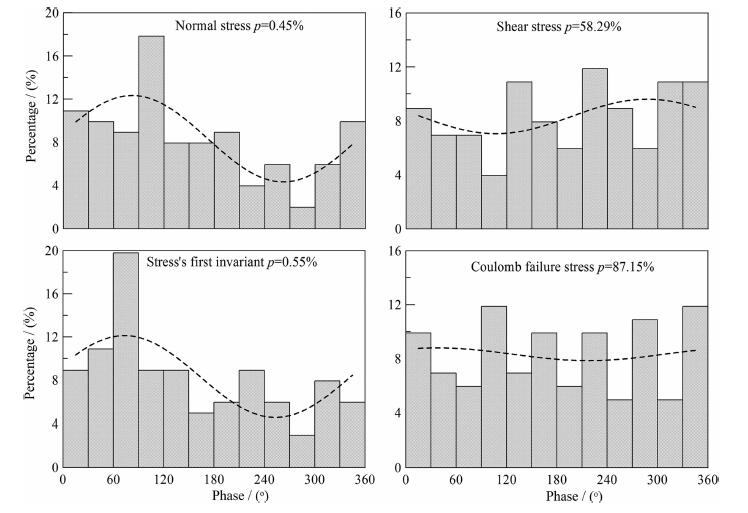
图 7给出了地震发生时刻应力潮汐相位的分布特征,区间间隔为30°,统计了在每个应力潮汐相位区间的地震数目的百分比,图中虚线是拟合的余弦函数,由此函数可以看出发震时刻潮汐相位的分布特征,同时代表相关性大小的p值也在图中给出.由图可以看出,正应力潮汐和应力第一不变量潮汐与地震都具有明显的相关性,其p值分别为0.45%和0.55%;而剪应力潮汐、以及库伦破坏应力潮汐都与地震没有显著的相关性,因为其p值分别为58.29%、87.15%.我们一共采用了101个地震,从统计学的角度来说,样本总量可以认为已经足够,因此该统计结果具有统计学意义.
|
图 7 发震时刻应力潮汐相位分布 Fig. 7 The distributions of the phases of the tidal stresses at the occurrence times |
本文介绍了计算地球内部应力与应变固体潮的理论公式.基于PREM地球模型,采用高精度的引潮位展开表,根据固体潮理论计算了包含直到球谐展开四阶项的地球内部应力和应变固体潮6个独立分量随时间的潮汐变化,分析了不同深度和纬度处的应力和应变的变化特征,结果可为地球内部的应变和应力测量资料的处理提供固体潮改正值.
作为内部应力固体潮应用于潮汐触发地震研究的实例,本文以发生在我国中部地区的101个地震为例,研究了发震时刻与断层面上的应力潮汐相位之间的相关性.我们发现断层面上的正应力潮汐和应力张量的第一不变量潮汐与地震发震时刻具有明显的相关性,这种相关性可以认为是潮汐触发了地震的证据.该应用实例采用了断层面上的应力潮汐相位作为研究对象,而尽管我们所研究的区域距离海洋较远,但是海潮负荷对潮汐相位仍有较大的影响,因此在计算应力潮汐时必须顾及海潮负荷的贡献,否则将导致统计结果的偏差,从而得出不正确的结论.
| [1] | Melchoir P J. The Tides of the Planet Earth. New York: Pergamon Press, 1978 . |
| [2] | 方俊. 固体潮. 北京: 科学出版社, 1985 . Fang J. The Solid Earth's Tides (in Chinese). Beijing: Science Press, 1985 . |
| [3] | 许厚泽. 固体地球潮汐. 武汉: 湖北科学技术出版社, 2010 . Xu H Z. The Solid Earth's Tides (in Chinese). Wuhan: Hubei Science and Technology Press, 2010 . |
| [4] | 蒋骏, 张雁滨, 周翠屏. 我国应变固体潮观测及其长时间序列的调和分析结果. 地壳形变与地震 , 1995, 15(1): 80–85. Jiang J, Zhang Y B, Zhou C P. Strain tide observation and its harmonic analysis results of long series in China. Crustal Deformation and Earthquake (in Chinese) , 1995, 15(1): 80-85. |
| [5] | 周坤根, DucarmeB, 胡延昌. 黄石台ORBES-81型伸缩仪观测结果的调和分析及海潮改正. 地球物理学报 , 1991, 34(4): 474–481. Zhou K G, Ducarme B, Hu Y C. Harmonic analysis and ocean loading correction of observation by ORBES-81 extensometer at Huangshi station. Chinese J. Geophys. (in Chinese) , 1991, 34(4): 474-481. |
| [6] | Métivier L, de Viron O, Conrad C P, et al. Evidence of earthquake triggering by the solid earth tides. Earth and Planetary Science Letters , 2009, 278(3): 370-375. |
| [7] | Tanaka S, Ohtake M, Sato H. Evidence for tidal triggering of earthquakes as revealed from statistical analysis of global data. J. Geophys. Res. , 2002, 107(B10). DOI:10.1029/2001JB001577 |
| [8] | Tsuruoka H, Ohtake M, Sato H. Statistical test of the tidal triggering of earthquakes: Contribution of the ocean tide loading effect. Geophys. J. Int. , 1995, 122(1): 183-194. DOI:10.1111/gji.1995.122.issue-1 |
| [9] | 吴庆鹏. 球状径向不均匀弹性地球模型的固体潮应力. 北京大学学报(自然科学版) , 2001, 37(5): 710–715. Wu Q P. Tidal stress of the radially heterogeneous spherical elastic Earth model. Acta Scientiarum Naturalium Universitatis Pekinensis (in Chinese) , 2001, 37(5): 710-715. |
| [10] | 孙文科. Love函数与地球内部的潮汐形变. 地球物理学报 , 1991, 34(3): 318–328. Sun W K. Love functions and their derivatives and tidal deformation in the interior of the Earth. Chinese J. Geophys. (in Chinese) , 1991, 34(3): 318-328. |
| [11] | 郗钦文. 不同规格化的引潮位展开及其转换. 地球物理学报 , 2007, 50(1): 111–114. Xi Q W. Expansion of tidal generating potential in different normalizations and their conversion. Chinese J. Geophys. (in Chinese) , 2007, 50(1): 111-114. |
| [12] | 郭俊义. 地球物理学基础. 北京: 测绘出版社, 2001 . Guo J Y. Introduction to Geophysics (in Chinese). Beijing: Press of Surveying and Mapping, 2001 . |
| [13] | 徐建桥, 孙和平. SNREI地球对表面负荷和引潮力的形变响应. 地球物理学报 , 2003, 46(3): 328–334. Xu J Q, Sun H P. Deformation response of a SNREI Earth to surface loads and tidal forces. Chinese J. Geophys. (in Chinese) , 2003, 46(3): 328-334. |
| [14] | Dziewonski A M, Anderson D L. Preliminary reference earth model. Phys. Earth Planet. Int. , 1981, 25(4): 297-356. DOI:10.1016/0031-9201(81)90046-7 |
| [15] | 汪汉胜, 许厚泽, 李国营. SNREI地球模型负荷勒夫数数值计算的新进展. 地球物理学报 , 1996, 39(Suppl.): 182–189. Wang H S, Xu H Z, Li G Y. Improvement of computations of load Love numbers of SNREI Earth model. Chinese J. Geophys. (in Chinese) , 1996, 39(Suppl.): 182-189. |
| [16] | Xi Q. The precision of the development of tidal generating potential and some explanatory notes. Bull Inf Marées Terrestres , 1989, 105: 7396-7404. |
| [17] | 周江存, 孙和平, 徐建桥等.海潮负荷对地球内部潮汐应力与应变的影响.地震学报, 2013 (已录用) Zhou J C, Sun H P, Xu J Q, et al. The effect of ocean tide loading on stress and strain in the Earth's interior. Acta Seismologica Sinica (in Chinese), 2013, in press. |
 2013, Vol. 56
2013, Vol. 56


