2. 吉林大学仪器科学与电气工程学院,长春 130026;
3. 吉林大学地球科学学院,长春 130061;
4. 吉林大学地球探测科学与技术学院,长春 130026
2. College of Instrument Science and Electrical Engineering, Jilin University,Changchun 130026,China;
3. College of Earth Sciences, Jilin University, Changchun 130061, China;
4. College of Geo-Exploration Science and Technology, Jilin University, Changchun 130026,China
深部矿产资源勘探过程中,由于勘探深度大,地面接收到的信号经常会被噪声淹没,为提高有效信号的能量,首先需要解决的问题就是如何合理选择震源.目前用于地震勘探的震源主要分为两种:一种为炸药震源,另一种为非炸药震源.炸药震源,以其能量强、频带宽、分辨率高等优点,在野外油气勘探中得到广泛应用,但存在危险、不可控,震源间的一致性差,且当药量增加到一定程度时激发的地震波能量将不再相应增加[1]等问题.常用的非炸药震源有电火花震源、石油勘探用车载液压震源、电磁驱动式可控震源[2].电火花震源适于海上地震勘探.石油勘探用车载液压震源,不适用于矿区复杂地形条件.轻便电磁驱动式可控震源系统,安全、可控且便携,有利于复杂地形地震勘探.但是,单个电磁驱动可控震源的输出力较小,难以获得地下深部信息.为此,通常使用多个震源组合激发方式,但组合震源主要能量方向垂直向下,在对复杂矿区进行勘探时,并不能有效提高地下目标数据的信噪比.为满足深部矿产勘探的需求,相控震源技术逐渐受到人们关注.
相控阵列的思想来自于雷达天线系统[3],利用相控阵列的方向特性,使得能量在某一特定方向汇聚,以达到远距离探测的目的.Arnold[4]首次将相控阵列应用到地震勘探,利用多台车载液压震源,进行了相控震源定向波束的野外试验,验证了相控阵列在地震勘探中应用的可行性.由于复杂地形矿区的地理因素,考虑用轻便的电磁驱动可控震源代替车载液压震源,进行山区作业.基于以上考虑,本文重点对电磁驱动可控震源相控阵列在不同矿区模型的地震响应进行数值模拟研究.
地震波场正演模拟是合理解释地震数据资料的前提,较常用的方法有射线追踪法、波动方程数值解法和积分方程法.射线追踪法是建立在高频近似基础上的一种地震数值模拟方法[5],用几何射线的方法解释波的运动学特征.2004 年,吉林大学可控震源课题组[6-8]用几何射线追踪法对电磁驱动可控震源相控阵列的方向特性进行了分析和模拟,得到基于电磁驱动可控震源的相控阵列,通过合理设置参数,可以在感兴趣的方向上有效提高地震信号的信噪比.基于几何射线追踪法的地震波数值模拟,虽然运算速度快,显示直观,但只反映了地震波的运动学特征,缺乏对地震波动力学特征的描述,且仅适用于简单模型.积分方程法基于Huygens原理,建立在波动方程积分表达式的基础上,计算效率低,主要针对复杂边界区域的求解.本文采用波动方程数值解法.2006年,王忠仁等[9]用有限差分的方法,对相控阵震源在相关前Chirp信号激励下的地震响应进行了数值模拟,引入地震波场边际能量密度的概念,利用地震波场的时间切片技术,对模型空间各个方向上的能量强度进行了定量分析,描述了均匀介质模型下地震波的方向特性.
本文基于电磁驱动可控震源相控技术,采用有限差分方法求解波动方程,仿真计算地下二维空间分别采用单震源、9 单元相控源激励下的波场传播及地面接收位置的地震响应,给出了基于均匀介质、水平层状矿区和不规则矿区三种模型下产生的波场快照和波传播的方向特性图,通过对比,定量得到相控震源在不同介质模型下激发地震波的方向性特点及对目标数据信噪比的改善能力.
2 相控震源波束形成机制相控震源,借鉴相控天线[10]波束定向原理,通过设定阵列[11]各单元起震的绝对时间或相对时间差,以实现各震动单元产生的波场在某个特定方向上的同相叠加,提高了这一方向上的信号能量,合理设置检波器的位置,能有效提高地震记录的信噪比.这一技术已被应用到地震测井等领域[12-14].
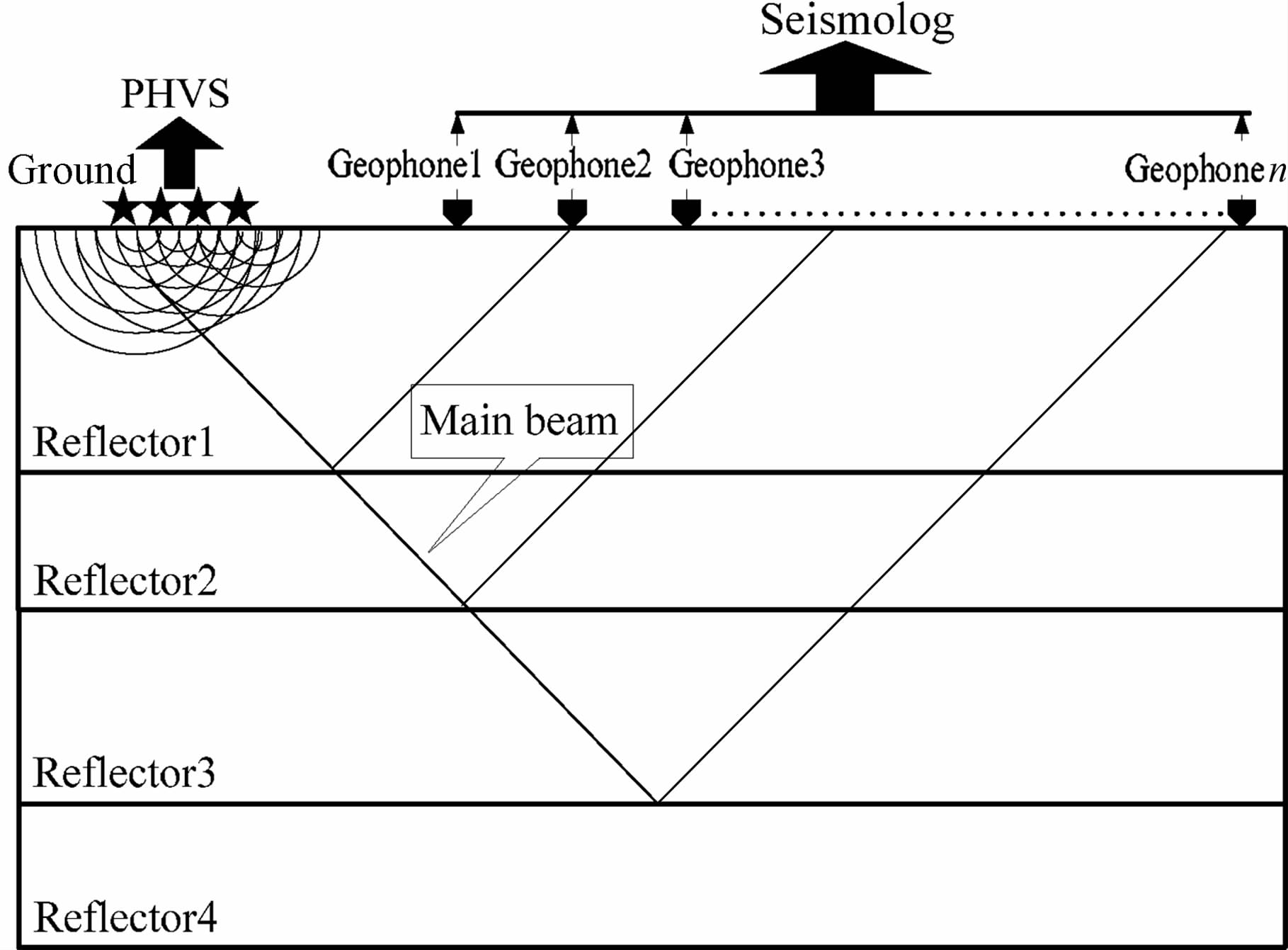
相控震源地震勘探原理如图 1所示.
|
图 1 相控震源系统野外工作原理图 Fig. 1 Principle of Phased-array vibrator system |
在均匀介质中,速度v为常数,图 2中方向角θ定义为地下目标方向与竖直向下方向夹角,且逆时针方向为正方向,则当相控震源相邻激震器间距d和延时参数τ 一定时,有如下公式[15]

|
图 2 $\tau =0.5\text{ms},d=2\text{m},v=2000\text{m}/\text{s}$时王波束万向图 Fig. 2 Main-beam direction graph while $\tau =0.5\text{ms},d=2\text{m},v=2000\text{m}/\text{s}$ |
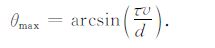
|
(1) |
由公式(1),可以计算地震波主波束在均匀介质中的传播方向,如图 2.
图 2结果说明,相控源激发的地震波在均匀介质中存在方向性,但非均匀介质相控震源波束形态不能确定,需通过求解波动方程获得.
3 相控震源数值模拟方法波动方程数值解法模拟地震响应,主要分为有限差分法[16-17]、有限元法[18-20]和伪谱法[21-22]等.有限元法计算速度慢,占内存大,伪谱法难以消除人工边界.本文采用计算速度快,易于计算机实现的有限差分法.通过有限差分求解波动方程的方法,模拟相控震源在不规则矿区模型中的地震响应.主要方法如下,首先求解相控震源的每个单元形成的地震波场,然后将各相控单元的波场延时叠加,即得到相控震源的地震波场.
在求解每个单元激励的地震波场时,需要构建波动方程,包括初始条件、边界条件以及其它限定条件;波动方程中的震源函数需结合可控震源控制信号特点及可控震源地震勘探原理导出;讨论对波动方程进行数值离散后,差分方程的约束条件和参数选取.
3.1 波动方程数学模型的建立首先讨论相控震源的单个震动单元波场求解.在非均匀介质中,设定波阻抗为常数,则有全声波方程:
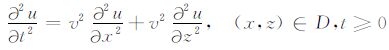
|
(2) |
在模拟区域内,为消除层间多次波,在公式(2)的右侧加入补偿项[23]
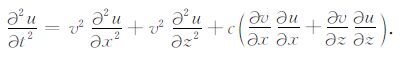
|
(3) |
考虑初始时刻,区域内的波场值为0,地震波的传播速度为0,用方程的形式表示为
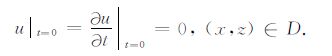
|
(4) |
在区域的边界上,将人工截断边界处理为吸收边界[24],此种边界条件要求震源不能离边界太近.
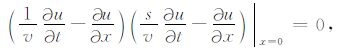
|
(5) |
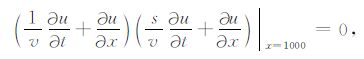
|
(6) |
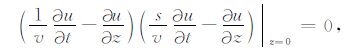
|
(7) |

|
(8) |
另外,对于地面和反射界面,有如下约束方程:

|
(9) |
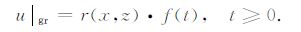
|
(10) |
联立公式(3)—(10)建立波动方程组,求解模拟区域各时刻的波场值.其中,u为网格节点的波场值,D为需求解的区域,g为地面,gr为反射界面,r为界面反射系数,f(t)为震源函数,v为纵波速度,s为常数.
3.2 震源函数上述求解单个震动单元波场过程,需要给出震源函数.震源函数求解与可控震源激励信号及可控震源地震勘探原理密切相关.
电磁驱动式可控震源激励的控制信号X(t)一般采用如公式(11)所示的Chirp信号形式[2]:

|
(11) |
其中,A为扫描信号的幅度,f1,f2 为扫描起始频率和终止频率,t为扫描时间,T为扫描时长.
为加大勘探深度,震源宜采用频率较低的信号,这里以10~100Hz Chirp为例表示,如图 3a.
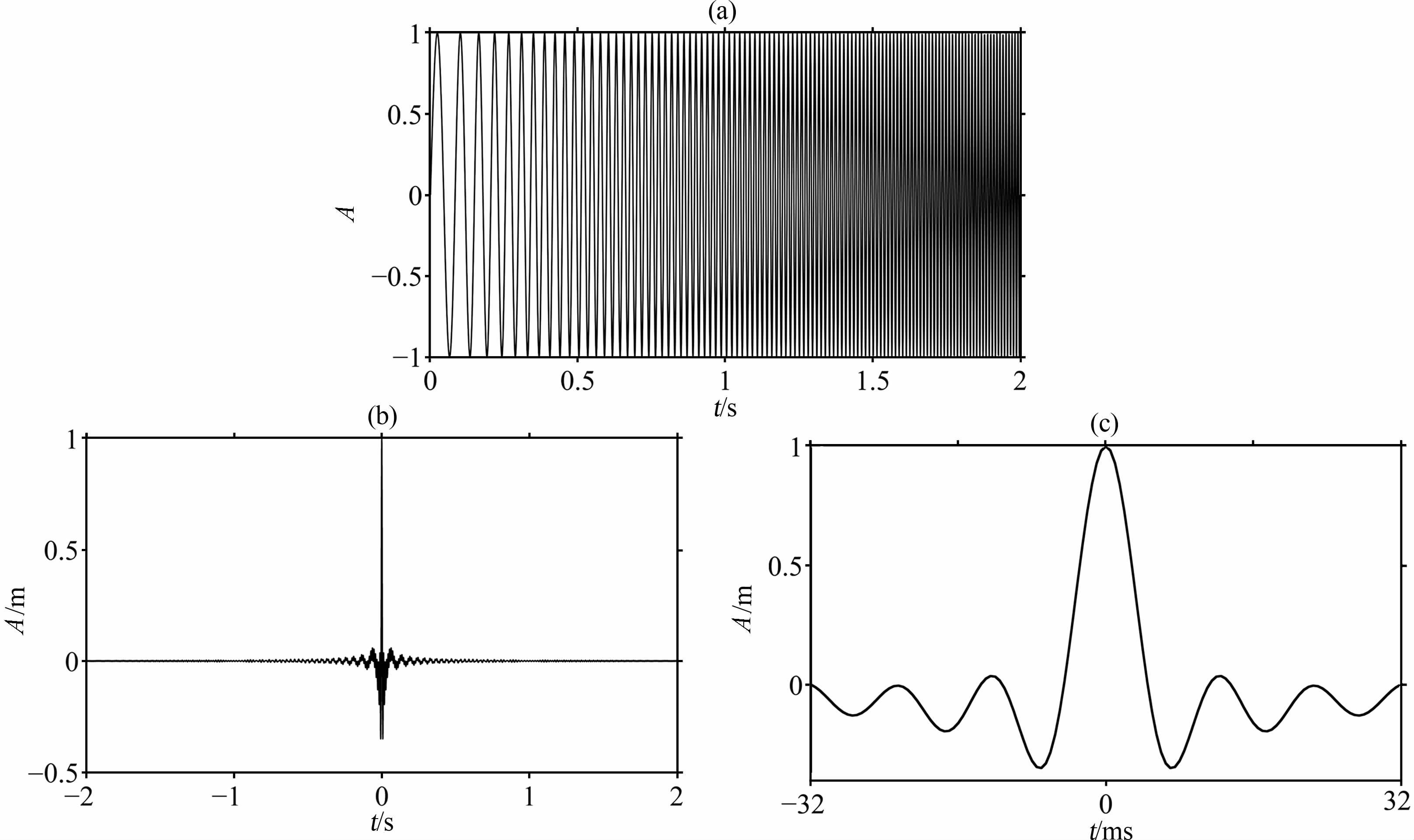
|
图 3 由可控震源控制信号构造震源地震子波 (a) Chrp形式的震源控制信号;(b)控制信号自相关; (c)用于数值模拟的可控震源地震子波. Fig. 3 Signal of source (a) Control signal of source in the form of chirp; (b ) Control signal autocorrelation; (c) Vibroseis wavelet for numerical simulation. |
可控震源与炸药震源工作原理不同.炸药震源工作时,震源信号为冲激信号形式,记为δ(t),当把大地看成一个线性系统,其冲击响应函数用h(t)表示,则检波器接收到的地震信号
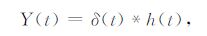
|
(12) |
其中,为卷积运算符号.
而可控震源工作时,震源控制信号X(t)为调频信号,检波器接收到的信号
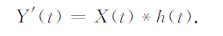
|
(13) |
要得到与炸药震源相似的具有正确到时信息的脉冲形式地震信号,由可控震源地震原理,可控震源地震数据必须经过相关检测处理[25],相关检测后得到的地震数据可表示为
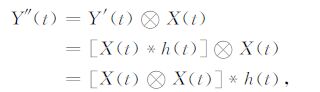
|
(14) |
其中,⊗ 为相关运算符号.X(t)⊗X(t)为X(t)的自相关函数,如图 3b.对比公式(12)和(14),可控震源的等效震源函数应为X(t)⊗ X(t),即控制信号的自相关函数.容易看出自相关函数主要的能量在中心点位置附近,离中心点位置较远部分能量很弱,接近为0.计算表明,在自相关函数中心点左右各取32ms时窗内的能量占整个自相关函数96.4%的能量,为计算方便,本文将波动方程中的震源函数定义为
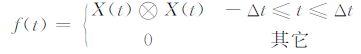
|
(15) |
如图 3c,其中,Δt=32ms.
上面讨论了相控震源的单个单元震源函数的求取过程.针对相控震源的不同震动单元,可在相应位置加入震源函数.
3.3 差分方程的约束条件和参数选取有限差分法是将求解区域网格离散化,对离散后的网格节点进行求解,用有限的节点代替连续的求解区域[26].构造差分一般基于Tailor公式展开,用差商代替微商,构建差分方程,然后对差分方程进行求解.本文采用空间域四阶,时间域二阶的差分格式.
计算中,网格剖分越细,数值解就会越趋近于解析解,但同时也会增大计算量.在模型已知的情况下,如何选择合适的网格步长,既能满足要求,又能提高计算效率,是有限差分法解波动方程需要考虑的首要问题.
对空间域和时间域进行离散时,首先要满足Nyqusit采样定理,考虑3.1 节中构建的模型及震源参数,${{\lambda }_{\min }}=\frac{{{v}_{\min }}}{{{f}_{\max }}}=20\text{m},{{f}_{\max }}=100\text{Hz}$.设空间采样步长dx=dz=dh,空间采样步长为dt,则

|
(16) |
另外,用有限差分法求解波动方程,时间和空间步长都趋近于零时,差分方程的解趋近于微分方程的解,但也要考虑到计算量问题.一般情况下,当差分方程满足稳定性条件时,差分方程就收敛于微分方程.鉴于本文采用的空间域四阶差分,时间域二阶差分,应满足如下稳定性[23]条件:
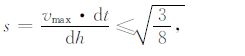
|
即

|
(17) |
根据采样定理及经验,一般时间采样率要求不小于8~10倍的fmax,以及式(16)和(17)的条件约束,模拟中选取空间采样步长dh=4 m,时间采样步长dt=1/1500≈0.00067s.
3.4 相控震源地震波场模拟以上讨论了相控震源的每个单元地震波场的求取过程,根据相控震源原理,将各相控单元的波场延时叠加,即可得到相控震源地震波场.
4 模拟结果针对单震源和相控源,分别给出波场快照、方向特性图,地表检波器信噪比改善等波场模拟结果.
4.1 相控震源参数为展示相控震源具有激发任意方向地震波的能力,相控源选择了0和1.33ms两个延时参数.相控震源采用0 ms延时,实际相当于组合震源工作方式;延时参数1.33ms为任意选择,只用于说明延时参数变化对地震波方向的影响.
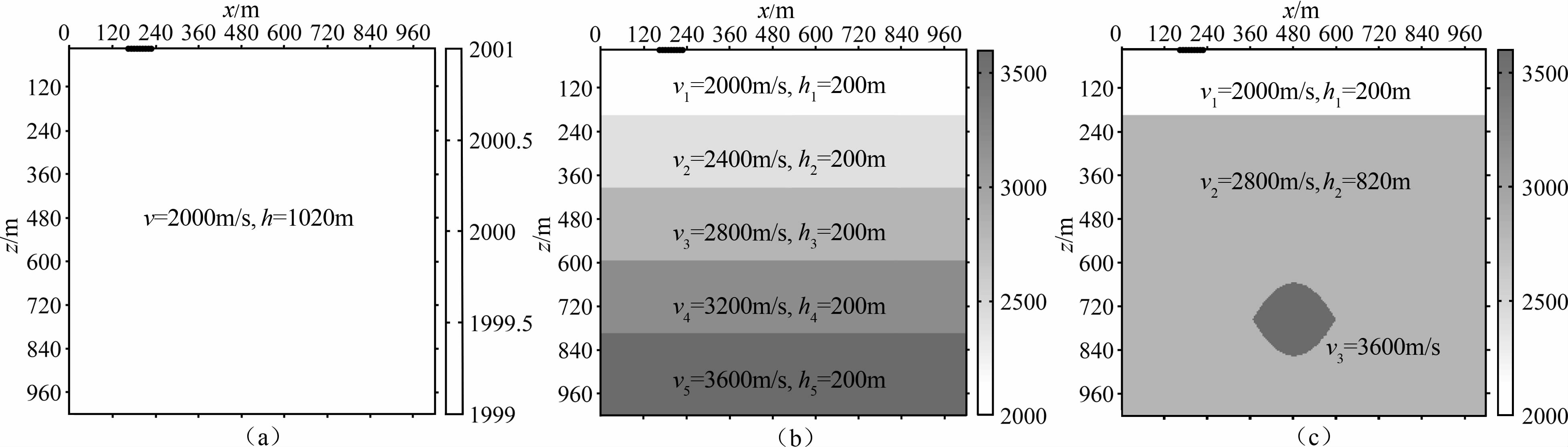
4.2 模型设计三种模型,即均匀介质模型,水平层状矿区模型和不规则矿区模型,如图 4所示,其中黑色圆点标记为震源点位置.
|
图 4 a)均勻介质模型;(b)水平层状矿区模型;(c)不规则矿区模型 Fig. 4 (a) Model of homogeneous media; (b) Model of horizontal layers; (c) Model of irregular mining |
计算区域长1020m,深1020 m,取水平向右为x轴的正方向,竖直向下为z轴正方向,两方向的交叉点取为坐标原点,建立直角坐标系.相控震源各单元炮点坐标分别为(168,20)、(176,20)、(184,20)、(192,20)、(200,20)、(208,20)、(216,20)、(224,20)、(232,20),为作对比,将单震源的炮点设在震源阵列的中间位置,坐标为(200,20).
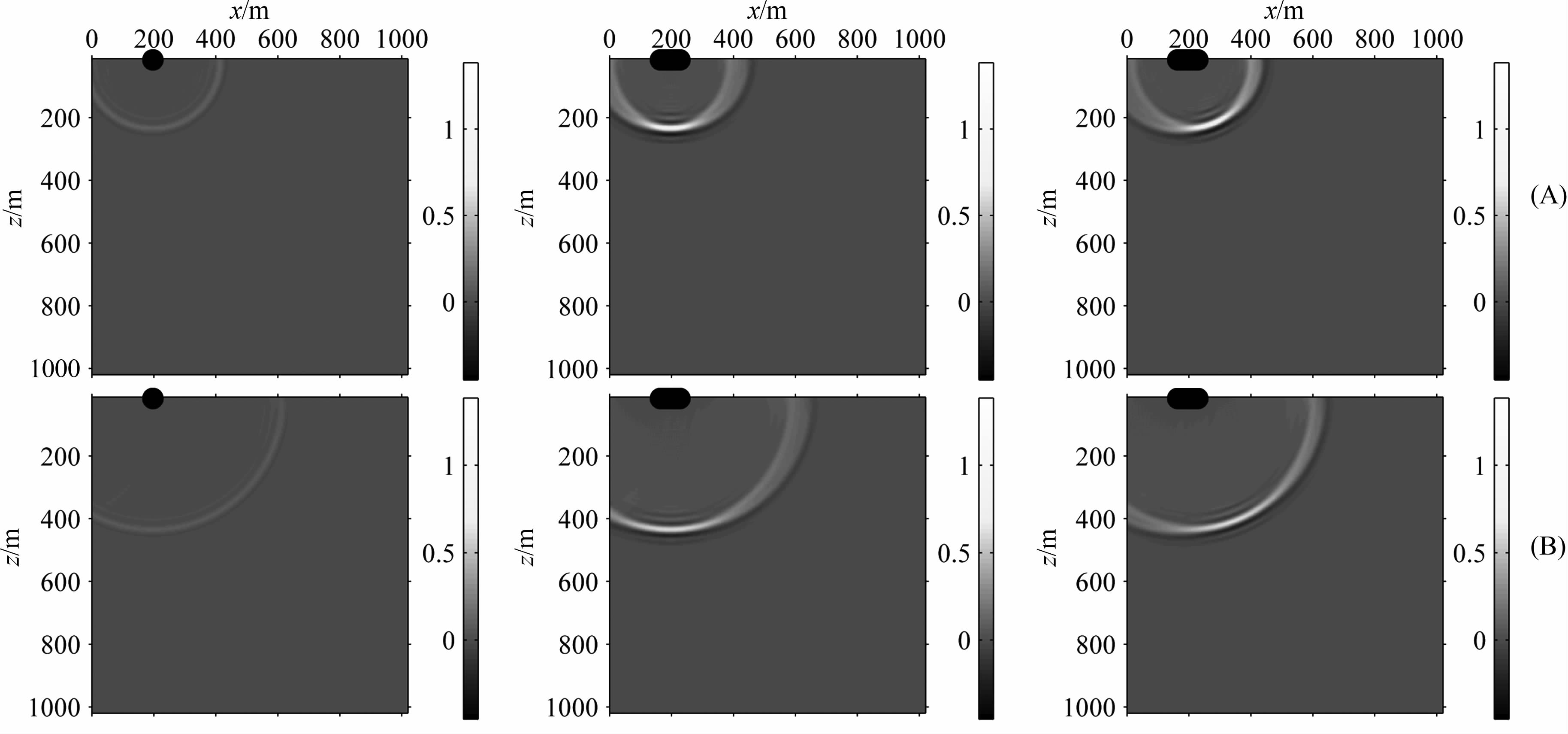
4.3 均匀介质模型模拟结果由图 5可见,均匀介质模型中,单震源产生的地震波不存在方向性;相控源激励的地震波具有明显方向性,延时参数不同,波束方向不同.
|
图 5 单震源、相控源0,1.33 ms延时参数下均勻介质模型的波场快照 (a) 133 ms; (b) 233 ms. Fig. 5 Snapshots of seismic wave of the single vibrator,0 ms and 1.33 ms phased-array vibrator in model of homogeneous media (a)133 ms; (b)233 ms. |
为了描述相控源的方向性,引入方向特性图.方向特性图定义为0~0.7s内每隔6.7ms各网格节点处波场能量值的累加.并且规定地震波主波束方向与x轴正向的夹角为方向特性图中的方向角,记作η.
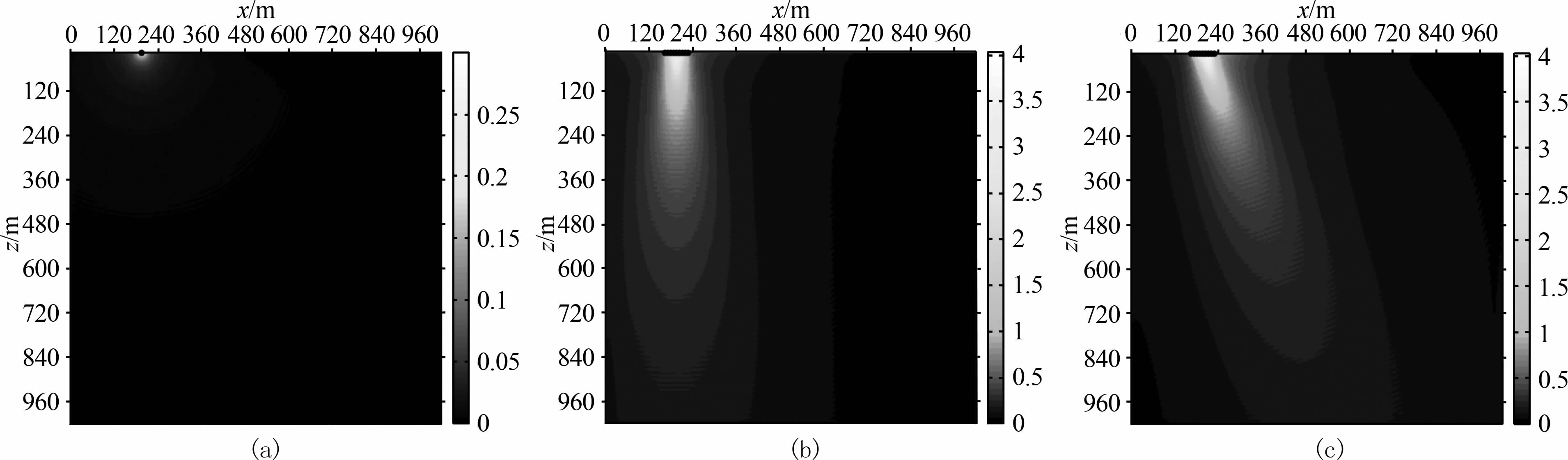
由图 6可见,均匀介质模型中,单震源不能产生定向地震波束;相控源激励下的地震波束有明显的方向性,方向因延时参数的不同而发生变化,0 ms地震震波方向垂直向下,即η 为90°,1.33 ms波束方向η为70.4°;0 ms和1.33 ms相控震源分别提高了90°和70.4°方向上信号的能量.
|
图 6 均勻介质模型方向特性图 (a)单震源;(b) 9单元组合源;(c)9单元相控源. Fig. 6 Directional character of model of homogeneous media (a) Single vibrator; (b) 9-unit vibrator combination; (c) 9-unit vibrator phased-array. |
图 7(a-d)分别为地震波在水平层状矿区模型的不同地层中传播时的波场快照.由图 7可见,单震源产生的地震波不存在方向性;相控源激励下的地震波有了明显的方向性,延时参数不同,方向不同;0ms地震波方向垂直向下,且不同地层中方向不变;1.33ms地震波方向在不同地层中发生偏折;由图 7c见,0ms相控源激励下第一层的反射波与直达波混杂,降低了分辨率,而1.33ms相控源激励下第一层的反射波与直达波能明显分开,提高了分辨率,图 7d中,其它层的反射波也以1.33 ms相控源的能量和分辨率最高.

|
图 7 单震源、相控源0、1.33ms延时参数下(从左至右)水平层状矿区模型波场快照 (A) 133 ms;B) 233 ms;C) 333 ms;D) 367 ms Fig. 7 Snapshots of seismic wave of the single vibrator,0 ms and 1.33 ms phased-array vibrator in model of horizontal layers (A) 133 ms; (B) 233 ms; (C) 333 ms; (D) 367 ms. |
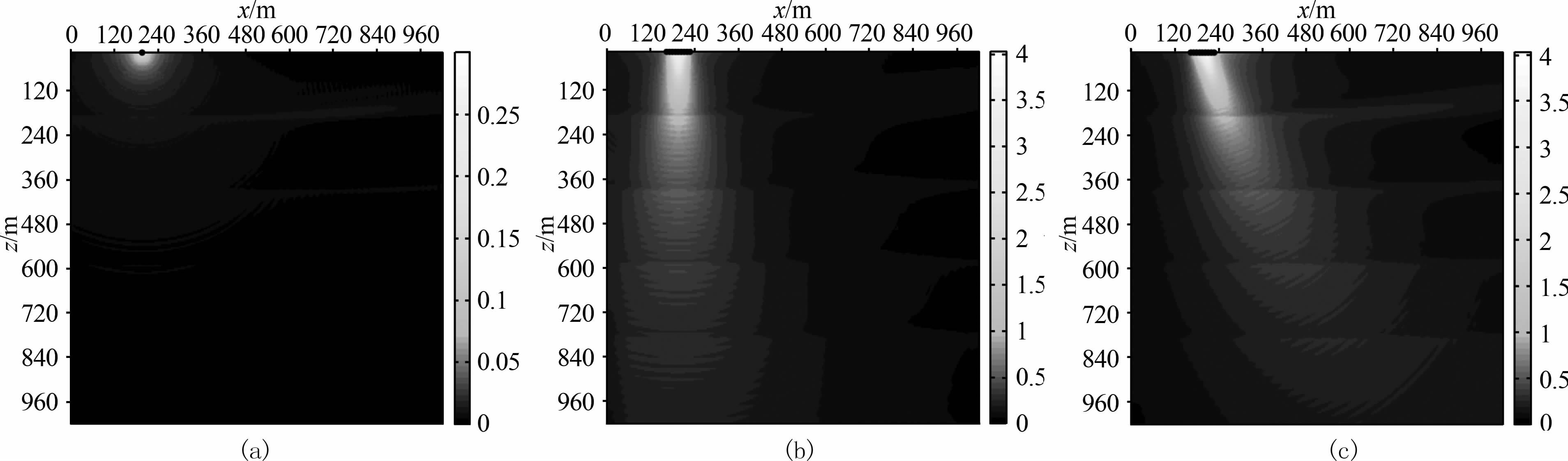
由图 8的方向特性图可见,水平层状矿区模型中,单震源不能产生定向的地震波束;0 ms相控源产生的地震波主波束方向垂直向下,即方向角η为90°;1.33 ms相控源能产生定向的地震波束,但方向随着介质中速度的变化,主波束方向发生偏折,地震波主波束方向角η由70.4°,依次变为68.5°,66.0°,63.7°,61.1°.
|
图 8 水平层状矿区模型方向特性图 (a)单震源;(b) Oms相控源;(c)1. 33 ms相控源. Fig. 8 Directional character of model of horizontal layers (a) Single vibrator; (b) O ms phased-array vibrator; (c) 1. 33 ms phased-array vibrator. |
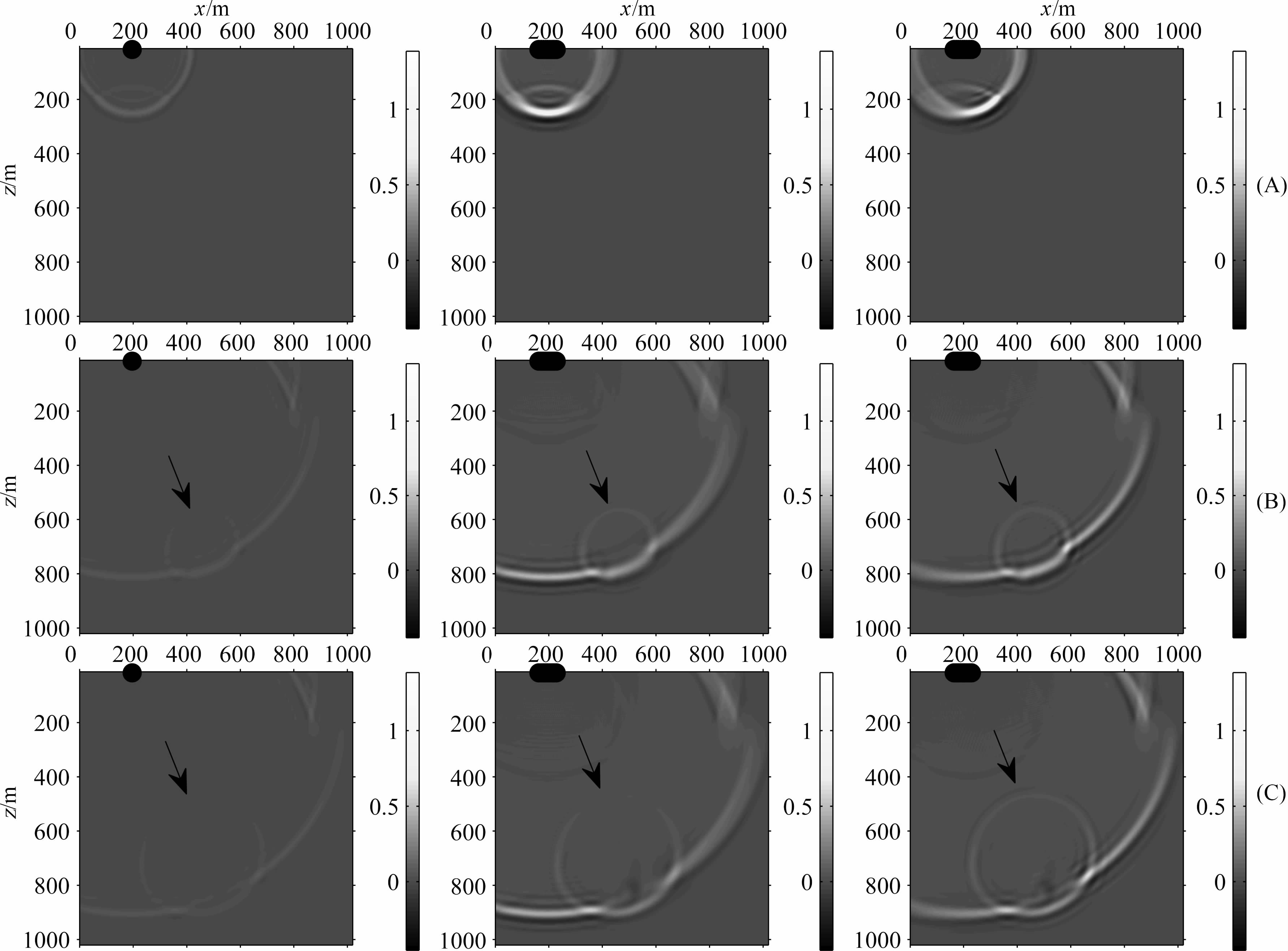
图 9为不规则矿区模型的波场快照.图 9a为地震波穿过第一层介质,进入围岩,图 9b为地震波开始进入不规则矿体,图 9c为地震波下行波波前即将传出不规则矿体.由图 9(b,c)可见,单震源激励下的地震波不存在方向性;相控源激励下的地震波存在方向性,延时参数不同,方向不同;0ms地震波方向垂直向下,且不同地层中方向不变;1.33ms地震波存在方向性,方向在不同地层中发生偏折;由图 9(b,c)可见,不规则矿体上界面处,单震源激励下的地震波能量弱,不能看到明显的反射波,0 ms相控源能看到反射波,但分辨率低,1.33ms相控源反射波能量加强,分辨率高.
|
图 9 单震源、相控源0、1.33ms延时参数下(从左至右)不规则矿区模型波场快照 (A) 133ms;(B) 333 ms; (C) 367 ms. Fig. 9 Snapshots of seismic wave of the single vibrator,Oms and 1. 33ms phased-array vibrator in model of irregular mining (A) 133 ms; (B) 333 ms; (C) 367 ms. |
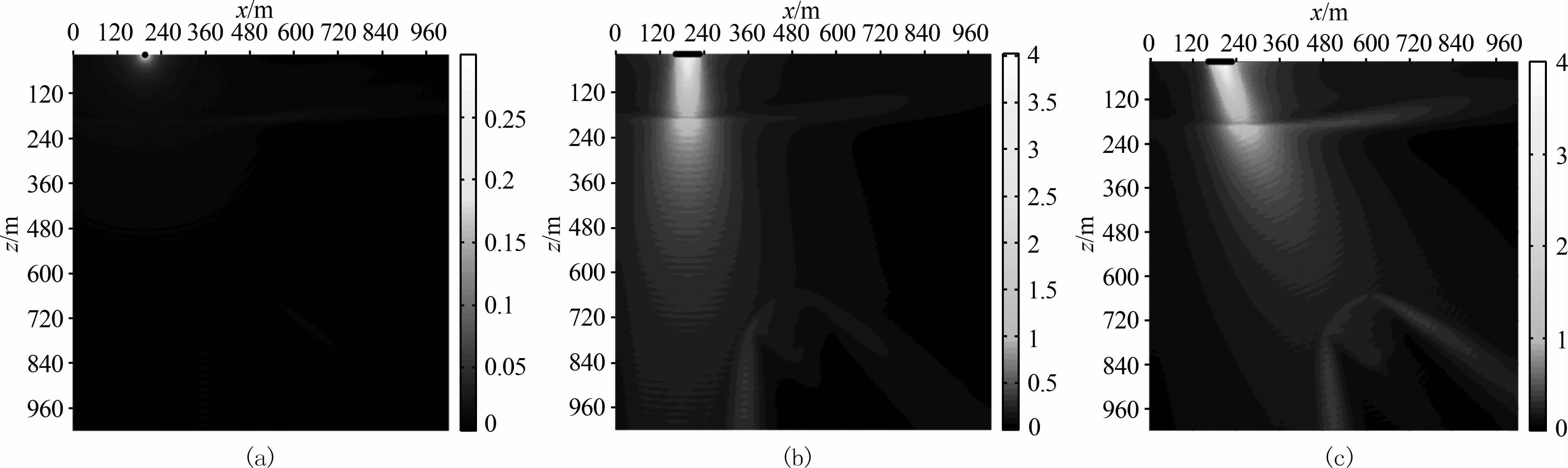
由图 10 的方向特性图可见,不规则矿区模型中,单震源不能产生定向的地震波束;相控源激励下的地震波束有明显的方向性,方向因延时参数的不同而发生变化;0ms相控源产生的地震波束垂直向下,即方向角η为90°,且在不同地层中方向不变;1.33ms相控源产生的定向地震波束方向角η在首层介质内为70.4°,围岩内为65.4°,矿体内为63.1°;相比于单震源,0ms和1.33ms相控源在不规则矿体的分界面处有更高的分辨率,三者中1.33 ms相控源的最高.
|
图 10 不规则矿区模型方向特性图 (a)单震源;(b) 0 ms相控源;(c) 1.33 ms相控源. Fig. 10 Directional character of model of irregular mining (a) Single vibrator; (b) 0 ms phased-array vibrator; (c) 1.33 ms phased-array vibrator. |
在噪声强度相同的情况下,设两个信号S1,S2,则后者相对于前者信噪比的改善[27]为
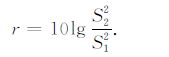
|
(18) |
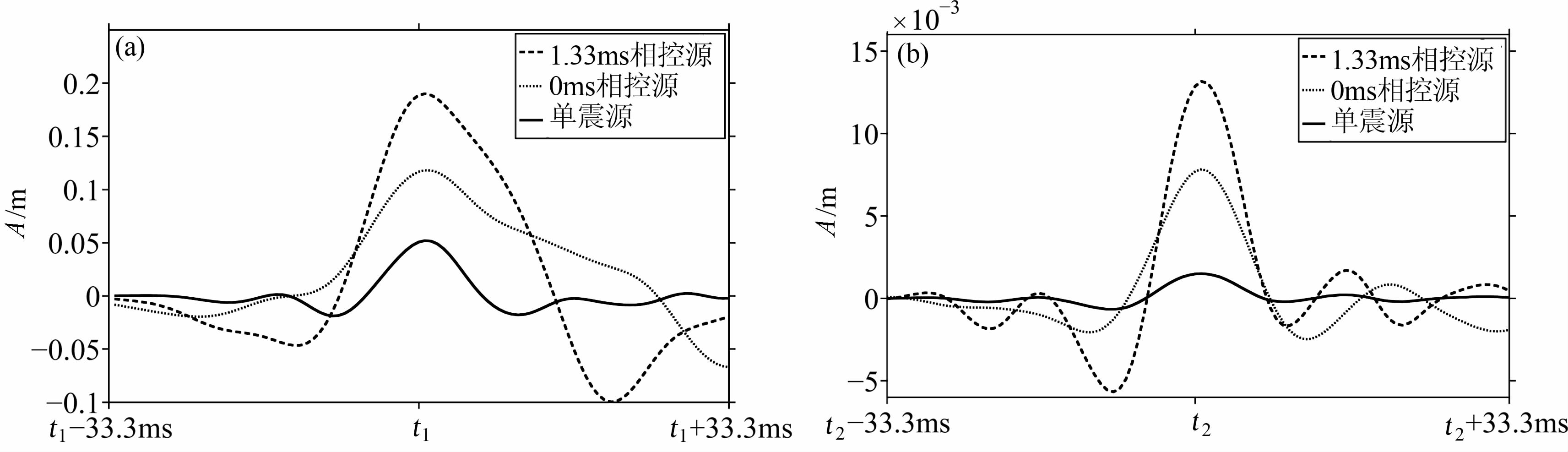
由公式(18)可以定量分析相控源相对单个可控震源在接收点处信噪比的改善能力.需要注意的是,地表检波器排列位置不同,接收数据的信噪比也不相同.图 11a 给出了水平层状矿区模型中,在地面888m 处检波器接收到第一层界面的反射波波形.由公式(18)计算得出,相对于单震源,1.33 ms和0ms相控源信噪比分别改善了14.1dB和10.2dB.
|
图 11 单震源、0、1.33ms相控源激励下检波器分别接收到的反射波 (a) 888 m水平层状矿区模型;(b) 244 m不规则矿区模型 Fig. 11 Reflected wave recorded in the receiving point for the single vibrator,0ms and 1. 33ms phased-array vibrator (a) Model of horizontal layers,888 m; (b) Model of irregular mining,244 m. |
图 11b给出了不规则矿区模型中,地面244 m处检波器接收到的不规则矿体上分界面的反射波波形.相对于单震源,1.33 ms和0 ms相控源信噪比分别改善了18.9dB和14.9dB.
上述结果表明,在本文给出的两种延时参数下,相控源均具有改善信噪比的能力.实际上,由于延时参数直接影响了地震波场在不同方向上的能量分布,可以预期,很多个但不是任一延时参数均能够改善地下目标信噪比.理论上来说,针对某个检波点或检波器排列,是存在一个最优的延时参数,可以令定向地震波照射到地下目标体,使得检波器接收的地下目标数据具有最优信噪比.由于延时参数最优选取是一个较复杂的问题,其涉及内容较多,本文暂不讨论.
5 结 语根据模拟结果,本文得到两个结论.一是相控震源在复杂介质条件下仍然具有激发定向地震波的能力,除0延时参数外,相控震源形成的地震波主波束方向会随介质变化发生偏折;二是不同延时参数下,目标方向的地震波能量分布发生变化,可能存在的多个延时参数均能改善目标数据信噪比,但信噪比改善能力不同.以上结论说明,相控震源技术应用于复杂矿产资源勘探是可行的而且有益的.
同时,我们也清楚地看到,如果能设计合适的延时参数,令地下目标方向上地震波能量最强,可以最大程度改善采集数据质量.有关最优延时参数设计是一个较复杂的问题,理论上存在最优延时参数,但针对复杂模型或实际勘探环境,延时参数选择与多种因素有关,包括相控震源工作参数、地下介质模型及关注的主要目标区域、检波器排列位置等因素,这部分内容研究将作为后续研究工作的重点.另外,相控震源波场模拟,对相控震源地震采集过程的观测系统设计也具有重要指导作用.
| [1] | 张智, 刘财, 邵志刚. 地震勘探中的炸药震源药量理论与实验分析. 地球物理学进展 , 2003, 18(4): 724–728. Zhang Z, Liu C, Shao Z G. Theory and experimentation of the charge sizes in seismic-sources for seismic exploration seismic-sources for seismic exploration. Progress in Geophysics (in Chinese) , 2003, 18(4): 724-728. |
| [2] | 林君. 电磁驱动可控震源地震勘探原理及应用. 北京: 科学出版社, 2004 . Lin J. Seismic Exploration and Application of Vibrator Driven by Electromagnetic (in Chinese). Beijing: Science Press, 2004 . |
| [3] | Garrod A. Digital modules for phase array radar. // IEEE International Radar Conference. Alexandria, VA: IEEE, 1995: 726-731. |
| [4] | Arnold M E. Beam forming with vibrator arrays. Geophysics , 1977, 42(7): 1321-1338. DOI:10.1190/1.1440796 |
| [5] | 裴正林, 牟永光. 地震波传播数值模拟. 地球物理学进展 , 2004, 19(4): 933–941. Pei Z L, Mu Y G. Numerical simulation of seismic wave propagation. Progress in Geophysics (in Chinese), (in Chinese) , 2004, 19(4): 933-941. |
| [6] | 姜弢, 林君, 杨冬, 等. 相控震源定向地震波信号分析. 地球物理学报 , 2008, 51(5): 1551–1556. Jiang T, Lin J, Yang D, et al. Analysis of directional seismic signal based on phased-array vibrator system. Chinese J| Geophys| (in Chinese) , 2008, 51(5): 1551-1556. |
| [7] | 姜弢, 林君, 陈祖斌, 等. 相控震源对水平层状地下介质的高信噪比检测. 仪器仪表学报 , 2006, 27(11): 1369–1372. Jiang T, Lin J, Chen Z B, et al. High signal-to-noise ratio detection of horizontal layer underground medium with phased-array vibroseis. Chinese Journal of Scientific Instrument (in Chinese) , 2006, 27(11): 1369-1372. |
| [8] | 姜弢, 林君, 陈祖斌, 等. 相控震源地震波定向技术. 吉林大学学报(信息科学版) , 2004, 22(3): 181–184. Jiang T, Lin J, Chen Z B, et al. Seismic beam-forming in phased array of vibroseis. Journal of Jilin University (Information Science Edition) (in Chinese) , 2004, 22(3): 181-184. |
| [9] | 王忠仁, 林君, 冯声涯. 地震勘探中相控阵震源的方向特性研究. 地球物理学报 , 2006, 49(4): 1191–1197. Wang Z R, Lin J, Feng S Y. Directivity of phase array vibrators in seismic exploration. Chinese J| Geophys| (in Chinese) , 2006, 49(4): 1191-1197. |
| [10] | Konishi Y. Phased array antennas. IEICE Transactions on Communications , 2003, E86B(3): 954-967. |
| [11] | 朱崇灿. 天线. 武汉: 武汉大学出版社. 1996 . Zhu C C. Antenna (in Chinese). Wuhan: Wuhan University Press (in Chinese). 1996 . |
| [12] | 乔文孝, 车小花, 鞠晓东, 等. 声波测井相控圆弧阵及其辐射指向性. 地球物理学报 , 2008, 51(3): 939–946. Qiao W X, Che X H, Ju X D, et al. Acoustic logging phased arc array and its radiation directivity. Chinese J| Geophys| (in Chinese) , 2008, 51(3): 939-946. |
| [13] | Che X H, Qiao W X. Numerical simulation of an acoustic field generated by a phased arc array in a fluid-filled borehole. Petroleum Science , 2009, 6(3): 225-229. DOI:10.1007/s12182-009-0036-6 |
| [14] | 乔文孝, 杜光升, 陈雪莲. 相控线阵声波辐射器在声波测井中应用的可行性分析. 地球物理学报 , 2002, 45(5): 714–722. Qiao W X, Du G S, Chen X L. Feasibility of application of phased array in acoustic well-logging. Chinese J| Geophys| (in Chinese) , 2002, 45(5): 714-722. |
| [15] | 姜弢. 基于相控震源的地震波定向方法研究. 吉林: 吉林大学仪器科学与电气工程学院 , 2006. Jiang T. Study on seismic beam-forming method based on phased-array vibrator system(in Chinese). Jilin: College of Instrumentation Electrical Engineering (in Chinese) , 2006. |
| [16] | Mohanty R K, Venu G. High accuracy cubic spline finite difference approximation for the solution of one-space dimensional non-linear wave equations. Applied Mathematics and Computation , 2011, 218(8): 4234-4244. DOI:10.1016/j.amc.2011.09.054 |
| [17] | Liu Y, Sen M K. Numerical modeling of wave equation by a truncated high-order finite-difference method. Earthq| Sci| , 2009, 22(2): 205-213. |
| [18] | Phongthanapanich S, Dechaumphai P. An explicit finite volume element method for solving characteristic level set equation on triangular grids. Acta Mechanica Sinica , 2011, 27(6): 911-921. DOI:10.1007/s10409-011-0480-6 |
| [19] | René M. An efficient finite element time-domain formulation for the elastic second-order wave equation: Anon-split complex frequency shifted convolutional PML. Int| J| Numer| Meth| Engng| , 2011, 88(10): 951-973. |
| [20] | Kahkomen S, Glowinski R, Rossi T, et al. Solution of Time-Periodic wave equation using mixed finite elements and controllability techniques. Journal of Computational Acoustics , 2011, 19(4): 335-352. DOI:10.1142/S0218396X11004377 |
| [21] | Carlos S, Escolano J, Garriga A. Semi-empirical boundary conditions for the linearized acoustic Euler equations using Pseudo-Spectral Time-Domain methods. Applied Acoustics , 2011, 72(4): 226-230. DOI:10.1016/j.apacoust.2010.11.002 |
| [22] | 李淅龙. 煤矿井下反射地震勘探技术初步研究与应用. 西安: 西安大学 , 2010. Li X L. The Preliminary Study Andapplication of Reflection Seismic Exploration Technique Applied in Coal Mine Underground(in Chinese). Xi'an: Xi'an University of Science and Technology (in Chinese) , 2010. |
| [23] | 单延明, 吴清岭, 于承业, 等. 复杂地质构造波动方程数值模拟. 物探化探计算技术 , 2002, 24(1): 22–26. Shan Y M, Wu Q L, Yu C Y, et al. Wave equation modeling for complex media. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 2002, 24(1): 22-26. |
| [24] | Reynolds A C. Boundary conditions f or the numerical solution of wave propagation problems. Geophysics , 1978, 43(6): 1099-1110. DOI:10.1190/1.1440881 |
| [25] | 姜弢, 林君, 陈祖斌, 等. 可控震源相控地震的相关检测技术. 仪器仪表学报 , 2005, 26(4): 336–339. Jiang T, Lin J, Chen Z B, et al. The correlation detection method of signals in phased array of vibroseis system. Chinese Journal of Scientific Instrument (in Chinese) , 2005, 26(4): 336-339. |
| [26] | 杨莹. 二维地震波场有限差分法数值模拟研究. 北京: 中国地质大学 , 2009. Yang Y. The research on Two-dimensional Finite-difference seismic wave field numerical simulation(in Chinese). Beijing: China University of Geosciences (in Chinese) , 2009. |
| [27] | 姜弢, 林君, 李桐林, 等. 相控震源对地震信号信噪比的改善研究. 地球物理学报 , 2006, 49(6): 1819–1825. Jiang T, Lin J, Li T L, et al. Boosting signal to noise ratio of seismic signals using the phased-array vibrator system. Chinese J| Geophys| ( in Chinese) (in Chinese) , 2006, 49(6): 1819-1825. |
 2012, Vol. 55
2012, Vol. 55


