岩石热导率是岩石主要的物性参数之一,对地质基础研究(岩石圈热结构、地球内部热传导过程、地球深部热状态、深部岩石的变质作用和热演化历史等)和应用研究(矿山采掘、石油开发和地热能利用)均具有重要的意义.在岩石圈内,热传导是岩石间热传递的最主要方式.岩石圈内的各种地球物理过程(如岩石的流变状态、热结构、大地热流等)都与岩石的热导率紧密相关.
目前取得岩石热导率的方法主要有两种:实验室测量和原位测量.实验室测量一般是在实验室对经过风干(少部分为烘干)的岩芯样品进行测定.这种方法对于低孔隙率的岩石,不会引起大的误差;对高孔隙率的碎屑沉积岩类,则会产生显著的影响.大多数岩石都具有孔隙或裂隙,即使致密的结晶岩类,也有一定程度的孔隙或裂隙.泥岩、页岩、砂岩等岩石的孔隙率可高达20%~30%,对于这些含孔隙的岩石,干试样的热导率与含水试样的热导率存在不同程度的差异[1].忽略岩石孔隙中的水对热导率的影响是实验结果与实际情况不符的主要原因.因此,最理想的热导率测量方法应该在原位进行,现已发展了一系列的原位测量方法,但是原位测量不仅方法复杂,而且一些岩石无法进行原位测量.同时,上述两种方法都必须耗费大量时间.
实际上,孔隙岩石是一种多孔介质[2],并且往往含有水.因此,从岩石的性质出发,建立孔隙岩石的数学模型或经验公式来预测岩石的热导率一直是令人感兴趣的问题[3].前人在这方面已开展大量研究,主要是基于孔隙岩石的特性建立简化多孔介质导热模型,即:(1) 统计模型[4];(2) 局部结构模型[5];(3) 半经验模型[6];(4) 容积平均模型[7];(5) 分形模型[8-9].其中,前四种经典模型无法准确描述多孔介质内孔隙分布情况及结构特征,只能近似地在大尺度范围内描述多孔介质中的热量传导过程,无法揭示真实的热量传递规律和温度场的分布情况,模型的计算结果与实际测量值有较大偏差[10];而分形模型对分析传递过程本身尚未取得有意义的进展,也没能定量化建立导热和结构之间的关系.
针对含湿多孔介质有效热导率的数学模型研究主要有:Bogaty[11]和Hollies[12]对含有不同纤维、孔隙率及饱和度的介质进行了实验,发现织物的有效热导率主要受厚度、孔隙率和饱和度的影响,纤维的排列方式对它的影响不大;Singh 等[13]在Pande等[14-15]模型的基础上,考虑了有效连续介质近似值及其所有可能的相互作用,计算了含湿土壤在不同温度下的有效热导率,其结果与实验值吻合较好;Zhang等[16-18]提出了用多组分体系的随机混合模型预测含湿多孔介质有效热导率的方法,该模型对于孔隙率小于0.6的含湿多孔介质准确度很高,而对于孔隙率大于0.6的含湿多孔介质有一定程度的偏离;Wang等[19]提出了基于三维微观方法来预测有效热导率的随机多孔介质模型;Tiak 等[20]根据傅里叶定律和能量守恒定律提出含湿多孔介质微元体热导率模型;Aurangzeb等[21]采用美国材料实验协会的ASTM 标准测量密度和孔隙率,在保证实验精确度的前提下提出了指数衰减模型.这些模型虽然考虑了多孔介质中液相的存在,便于计算确定热导率.但是,上述方法对孔隙分布情况的处理与自然界的真实情况还有一些差距,得出的经验公式仅在一定程度上可用.
前人的研究表明,应用数值分析方法获得准确的含湿孔隙岩石有效热导率的前提是建立符合实际情况的岩石数值模型.本文在景惠敏对双矿物热导率数值模拟的基础上[22],将其发展至多组分体系,采用随机网格划分和材料指定的方法,建立接近实际情况的岩石模型,用有限元方法进行含湿孔隙岩石有效热导率的三维数值模拟,并将数值模拟所得的大量数据结果进行统计分析,最终获得岩石有效热导率.含湿孔隙岩石采用圆柱体模型,上下表面施加不同的温度,侧面绝热.通过有限元法计算出总热流q,结合上下表面的温度梯度,计算岩石的有效热导率.
2 方法原理 2.1 基本原理含湿孔隙岩石可以看作由矿物、空气和水构成的三组分复合介质,分别用下标m、a、w 标记.本文用孔隙率f和饱和度s来描述其组成.孔隙率f为水和空气所占的岩样体积的体积分数,饱和度s为孔隙中水所占的体积分数.这样,矿物、水和空气的体积分数分别为:1-f、f×s、f×(1-s).
在无热源条件下,对于三维稳态热传导问题[23],其偏微分控制方程为

|
(1) |
边界条件是

|
(2) |
kx、ky、kz是材料分别沿物体三个主方向(x、y、z方向)的热导率,单位为W·m-1·K-1,$\phi $=${\bar{\phi }}$是在Γ1 边界上的给定温度.
对于微分方程(1)和边界条件(2),可推导出变分原理中的泛函表达式
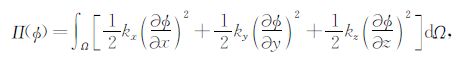
|
(3) |
利用$\delta \prod{\left( \phi \right)}$=0可以建立有限元的求解方程.
将求解域Ω 离散为有限个单元体,单元内各点的温度$\phi $近似地由单元的节点温度${{\phi }_{i}}$插值得到
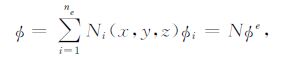
|
(4) |
其中ne是每个单元的节点数;Ni(x,y,z)是C0 型插值函数,具有下述性质:
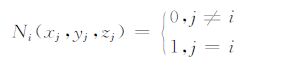
|
(5) |
并且
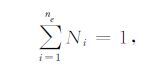
|
(6) |
将(4)式代入有限元离散后的泛函,从$\delta \prod{\left( \phi \right)}$= 0,可以得到稳态热传导问题的有限元求解方程:
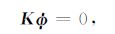
|
(7) |
式中K是热传导矩阵,它是对称矩阵,在引入给定温度条件以后,K是对称正定的;$\phi ={{\left[ {{\phi }_{1}}{{\phi }_{2}}\cdots {{\phi }_{n}} \right]}^{\text{T}}}$是节点温度列阵.矩阵K元素表示如下:
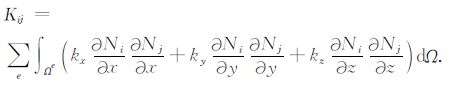
|
(8) |
(8)式中右侧是各单元对热传导矩阵的贡献,可将其改写成单元集成的形式:

|
(9) |
其中
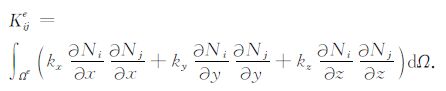
|
(10) |
以上就是三维稳态热传导问题的有限元方程.
三维稳态热传导的傅里叶定律为
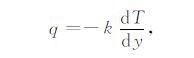
|
(11) |
其中,q表示热流密度.有限元模型的等效热导率为
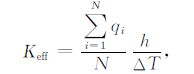
|
(12) |
式中,Keff为模型的等效热导率,qi为节点的热流密度,ΔT为模型上下表面的温度差,h为模型垂直方向的高度,N为节点总数.
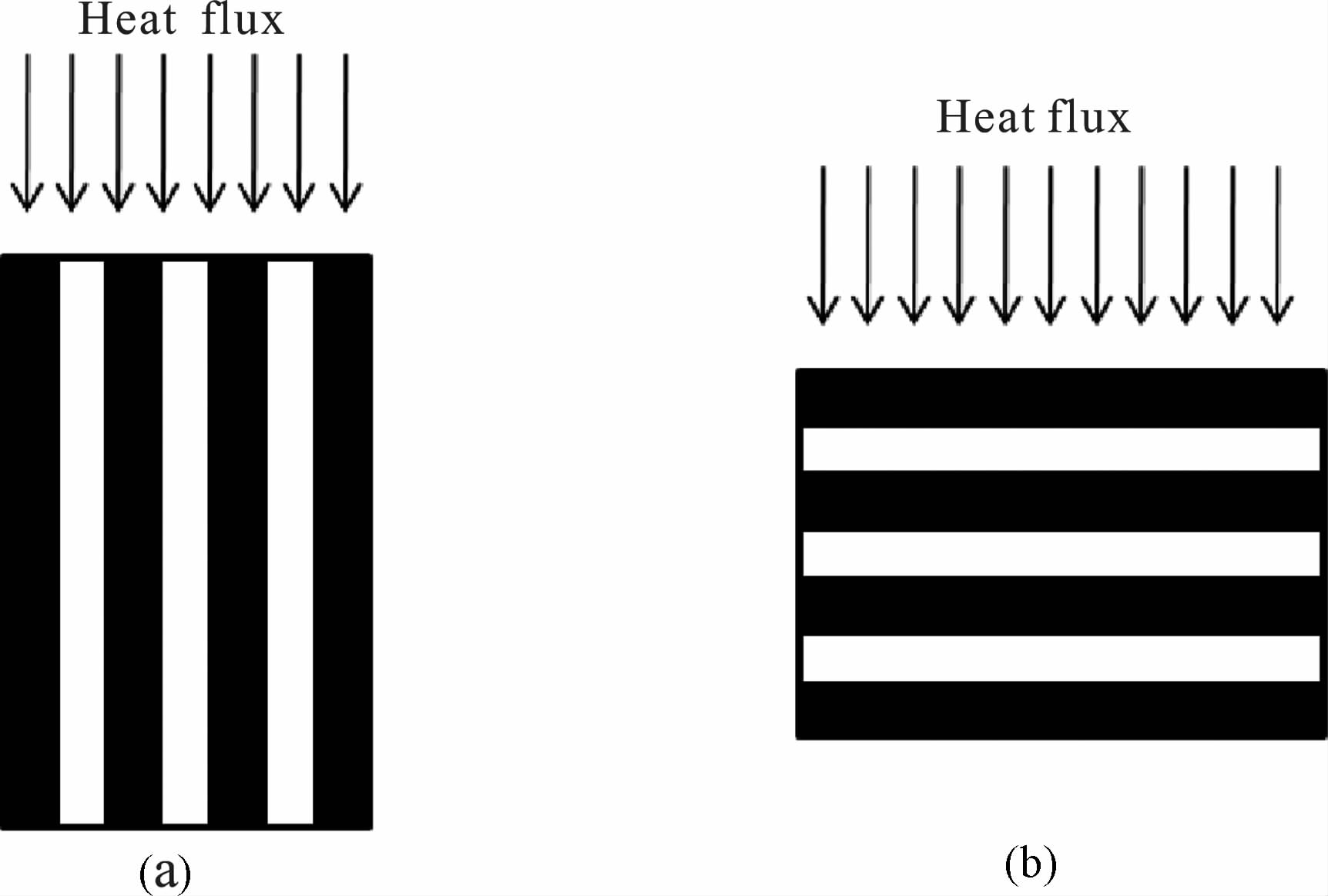
2.2 模型及网格剖分方法本数值分析模型基于四面体网格,并假设由若干网格组成一个矿物颗粒,在给定孔隙率及饱和度的前提下,固液气三相的空间分布完全随机确定.岩石的有效热导率与孔隙的分布有密切关系[24].图 1为岩石中只有一种流体相时,岩石中孔隙分布的极端情况[25].岩石可能包含比例不同的多种矿物,但在初步模拟中我们暂时先假定它们的热导率相差不大,近似视为一种矿物,称为矿物的热导率.如图 1a所示,当热流与孔隙平行时,岩石的有效热导率最大,可表示为
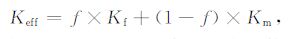
|
(13) |
其中Keff为岩石的有效热导率,Kf 为流体相的热导率,Km 为岩石骨架的热导率,f为孔隙率.当热流与孔隙垂直时(图 1b),岩石的有效热导率最小,可表示为
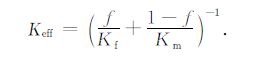
|
(14) |
考虑到固体矿物成分、孔隙率及饱和度完全相同的岩石,由于内部孔隙分布和材料分布的不同,其导热性质会有很大的不同,因此为获得最符合客观实际的含湿孔隙岩石的热导率,模型采用随机剖分单元、随机指定材料属性的方法来模拟岩石内部各种孔隙分布情况下的岩石导热性.基于此,先生成四面体网格,然后由若干网格组成一个颗粒,并按一定混合比例,随机对各个颗粒指定材料性质,模型内部的孔隙分布与每次试验所产生的一个伪随机数相关,在固定孔隙率及饱和度的条件下,每次试验都可以产生不同的孔隙分布,而且孔隙的形状、大小、方向不规则,更接近于真实情况,使数值模拟结果更加客观真实.
本文的网格划分方法可任意控制组成一个颗粒的网格数,并且可以按照研究需要为不同的颗粒赋予相应的材料属性.首先对模型进行四面体网格划分.假设生成的网格总数为maxelem,需要生成的颗
粒数为M,则组成一个颗粒的网格数为n=int(maxelem/M).
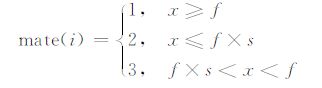
|
(15) |
其中,x为由计算机产生(0~1)之间的随机数,i为单元号,1、2、3为材料编号,依次代表矿物、水、空气.
从第一个节点开始按节点号进行单元拓扑,搜索以此节点为顶点的单元,按单元号从小到大的顺序选定n个单元,并据(15)式赋材料属性mate(i).如果在某次循环中,进行单元拓扑时,搜索到的单元已被赋属性,则跳过继续搜索其它单元;如果以此节点为顶点的单元都已被赋属性,则进行下一个节点的单元拓扑,如此循环M次.如果循环M次后,还有单元未赋属性,则再循环一次.
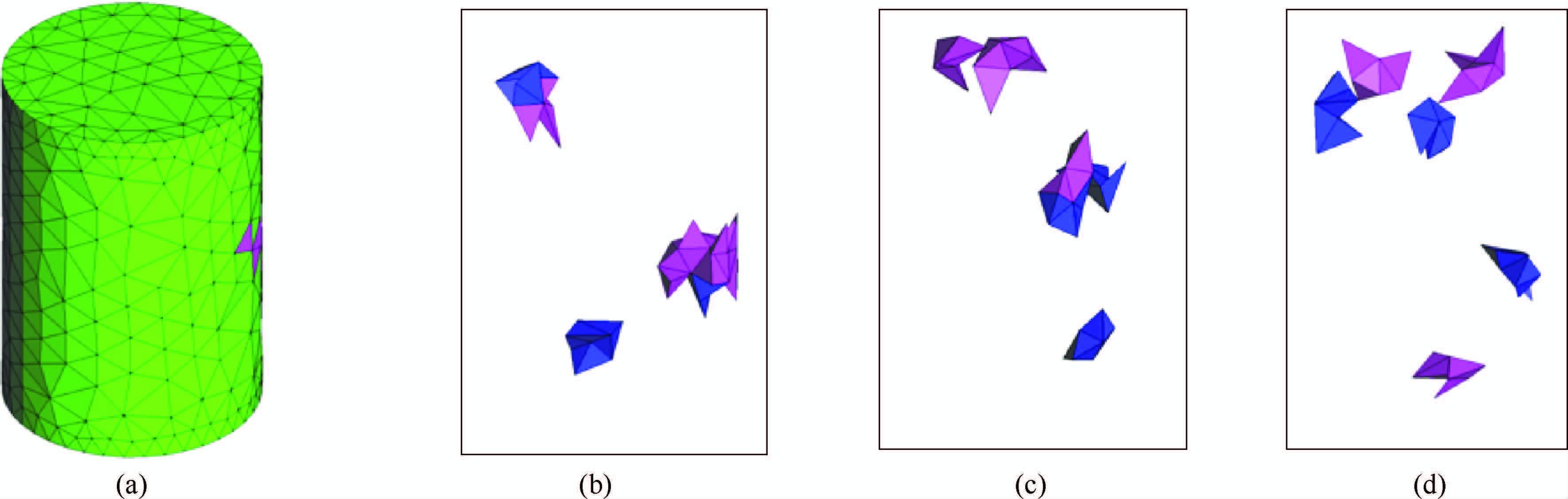
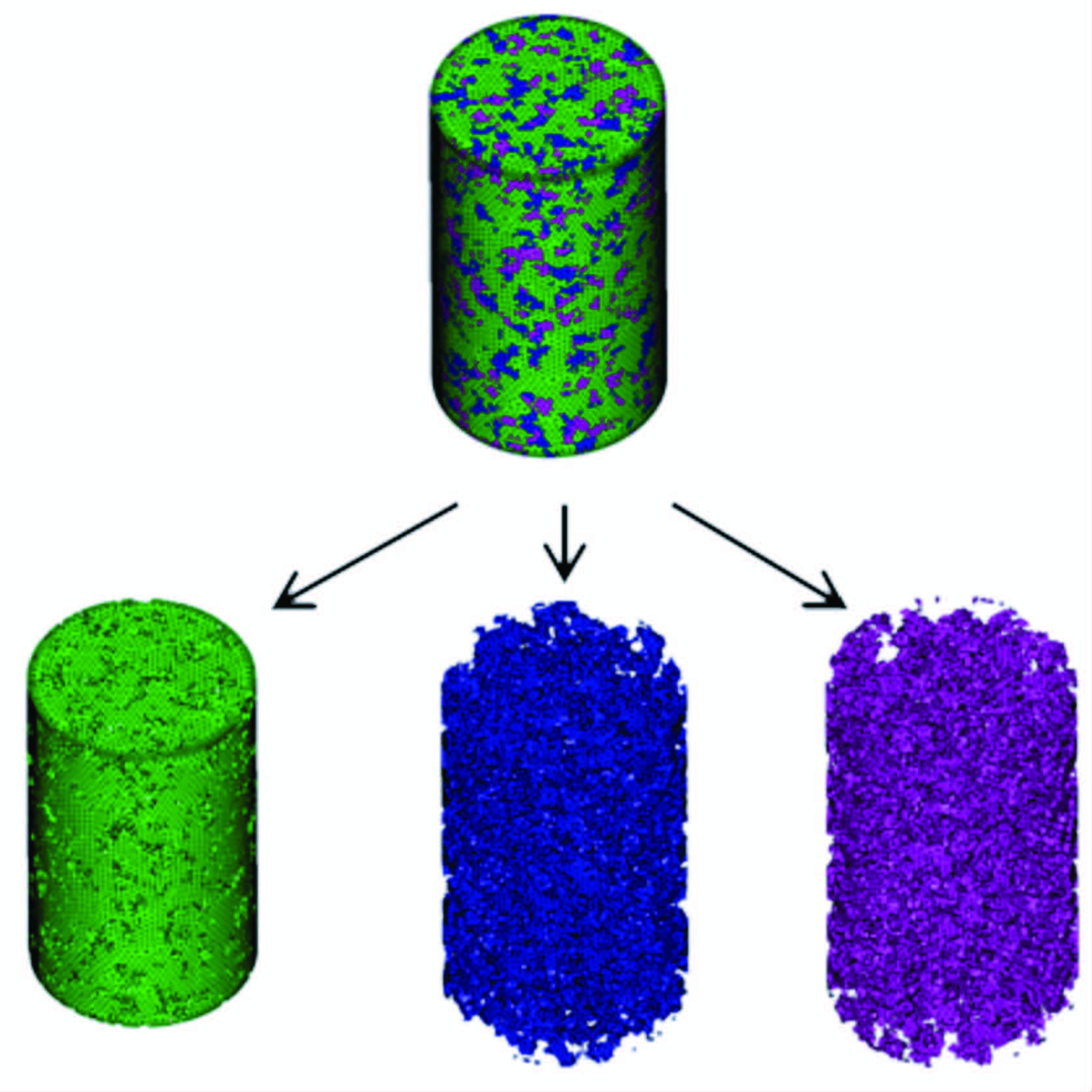
为验证文中采用方法的正确性及合理性,先建立一个网格数量较少的模型(3960个网格),6个网格组成一个颗粒.为清楚显示颗粒的组成及分布情况,此模型的孔隙率设定为0.01、饱和度为0.5,因此代表水、空气的颗粒数都为3 个.限于篇幅,挑选三次随机生成的模型来进行说明,如图 2所示,绿色代表的是矿物,蓝色代表的是水,粉红色代表的是空气.图 2a是某次随机生成的整体模型,图 2b是与之对应的水颗粒、空气颗粒的分布情况,图 2c、图 2d是其它两次随机模型中水颗粒、空气颗粒的分布.图 3为数值模拟中建立的含湿孔隙岩石模型,上侧为岩石整体模型,下侧为矿物、水、空气的分布.
|
图 2 孔隙率很小时部分模型中水、空气的分布 Fig. 2 Distribution of water and air in some models when porosity is very small |
|
图 3 含湿孔隙岩石模型 Fig. 3 Wet porous rock model and the parts |
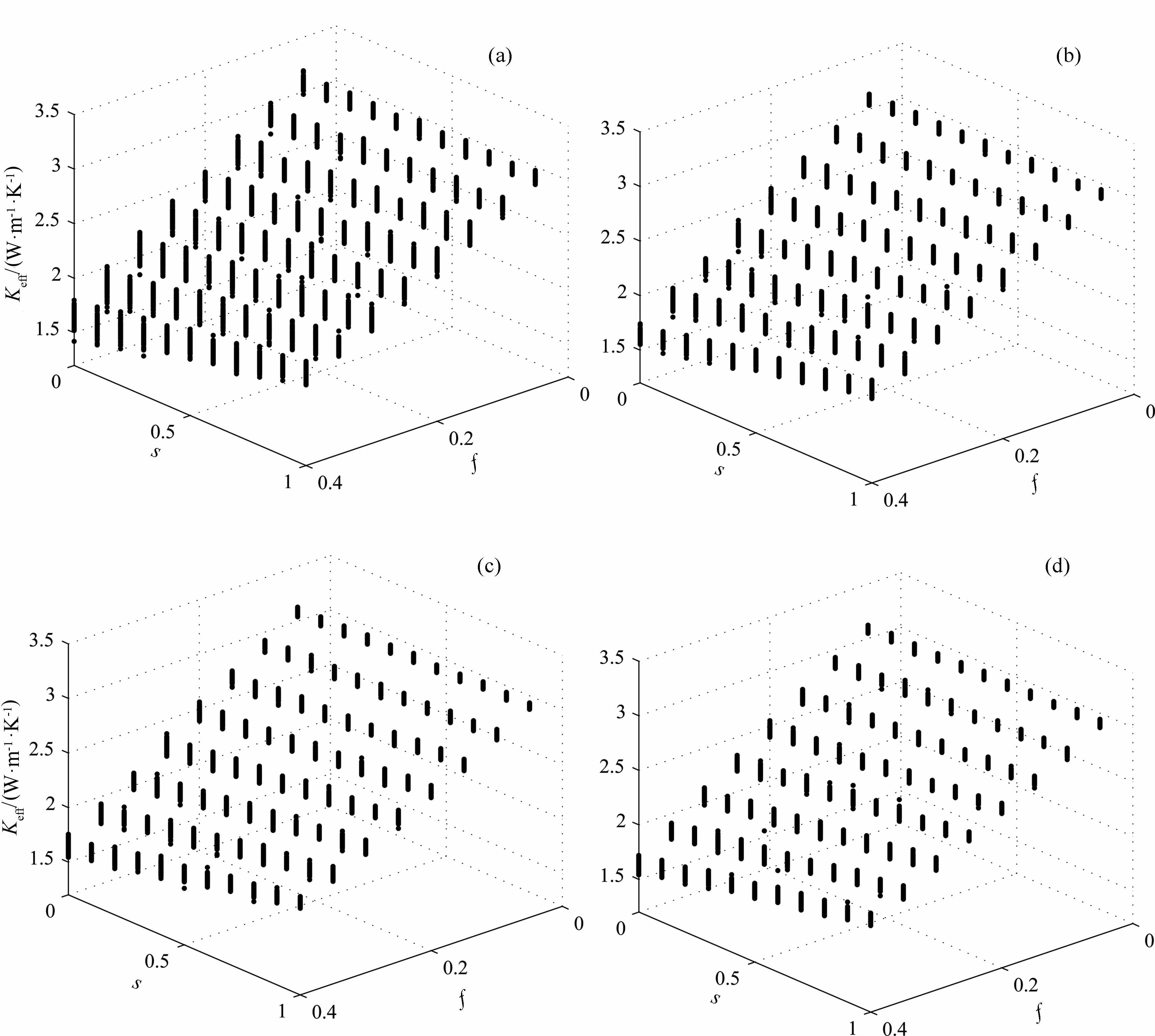
如上所述,孔隙的分布会影响试验数值的分布,因此对于相同的一组输入参数,多次试验的结果会有分散性.所以,单次的计算结果不具有代表性,要用MonteCarlo法生成多个模型进行计算.在每一种固定的孔隙率及饱和度下,随机生成200个模型进行计算,每次试验得到的Keff值均绘出.图 4(a—d)分别是网格为4万、8万、12万、15万时的Keff值分布情况,图中的f轴表示孔隙率,数值依次取0.05、0.1、0.15、0.2、0.25、0.3、0.4;s轴表示饱和度,数值由0 递增至1;Keff轴表示岩石有效热导率.Km、Kw、Ka 的取值分别为3.3、0.6、0.0274 W·m-1·K-1.
|
图 4 (a)4万网格时Keff值分布;(b)8万网格时Keff值分布;(c) 12万网格时Keff值分布;(d) 15万网格时Keff值分布 Fig. 4 (a) Distribution of Keff, 40000 grids; (b) Distribution of Keff, 80000 grids;(c) Distribution of Keff, 120000 grids; (d) Distribution of Keff, 150000 grids |
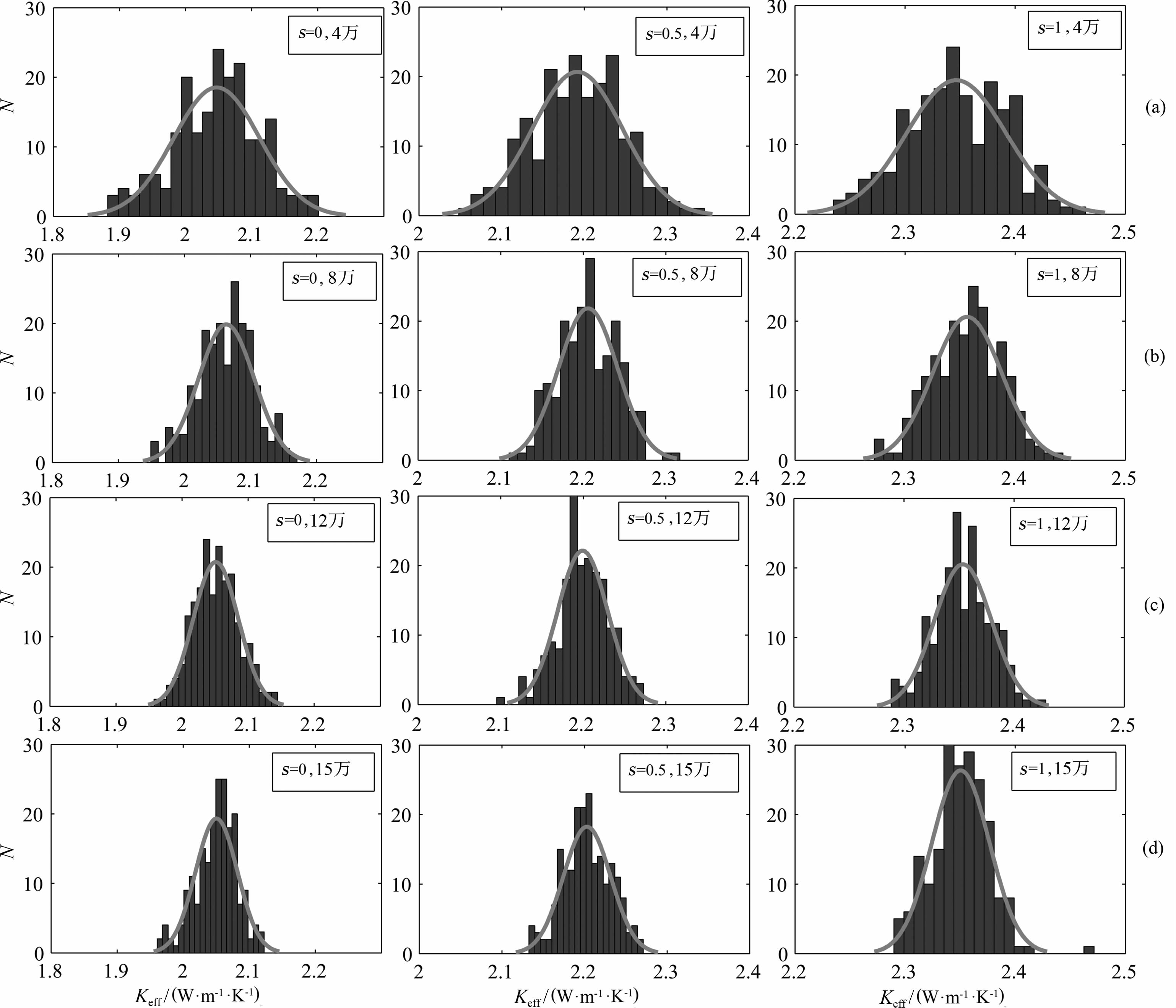
由图 4可见:(1)当孔隙率和饱和度固定时,Keff的分布有起伏(即Keff不同),说明孔隙的分布、结构等对有效热导率有影响;(2)岩石的孔隙率对有效热导率Keff有显著影响,Keff随着孔隙率的增大而减小;(3)网格的数量对计算结果有影响,网格较少时,计算的Keff值起伏较大、分布较分散,网格较多时,计算的Keff值起伏较小,分布相对集中.图 5更好地说明了网格数目对Keff集中程度的影响.
|
图 5 孔隙率为0.3时,不同饱和度及网格数目下的Keff值分布 Fig. 5 Gaussian distribution of Keff when porosity is 0. 3 with different degree of saturation and the number of grids |
图 5只列出了孔隙率为0.3,饱和度分别取0、0.5、1时的Keff值分布图.由于采用了随机网格模型,试验所得数值较为符合高斯分布,高斯分布的均值对应不同比例下的Keff的平均值,图中显示固定孔隙率及饱和度下的数值分布与高斯曲线拟合较好.对比图 5(a—d)四幅图可见:数值试验中在固定孔隙率及饱和度的情况下,网格数越多可以获得相对越集中的数值,峰值越明显.
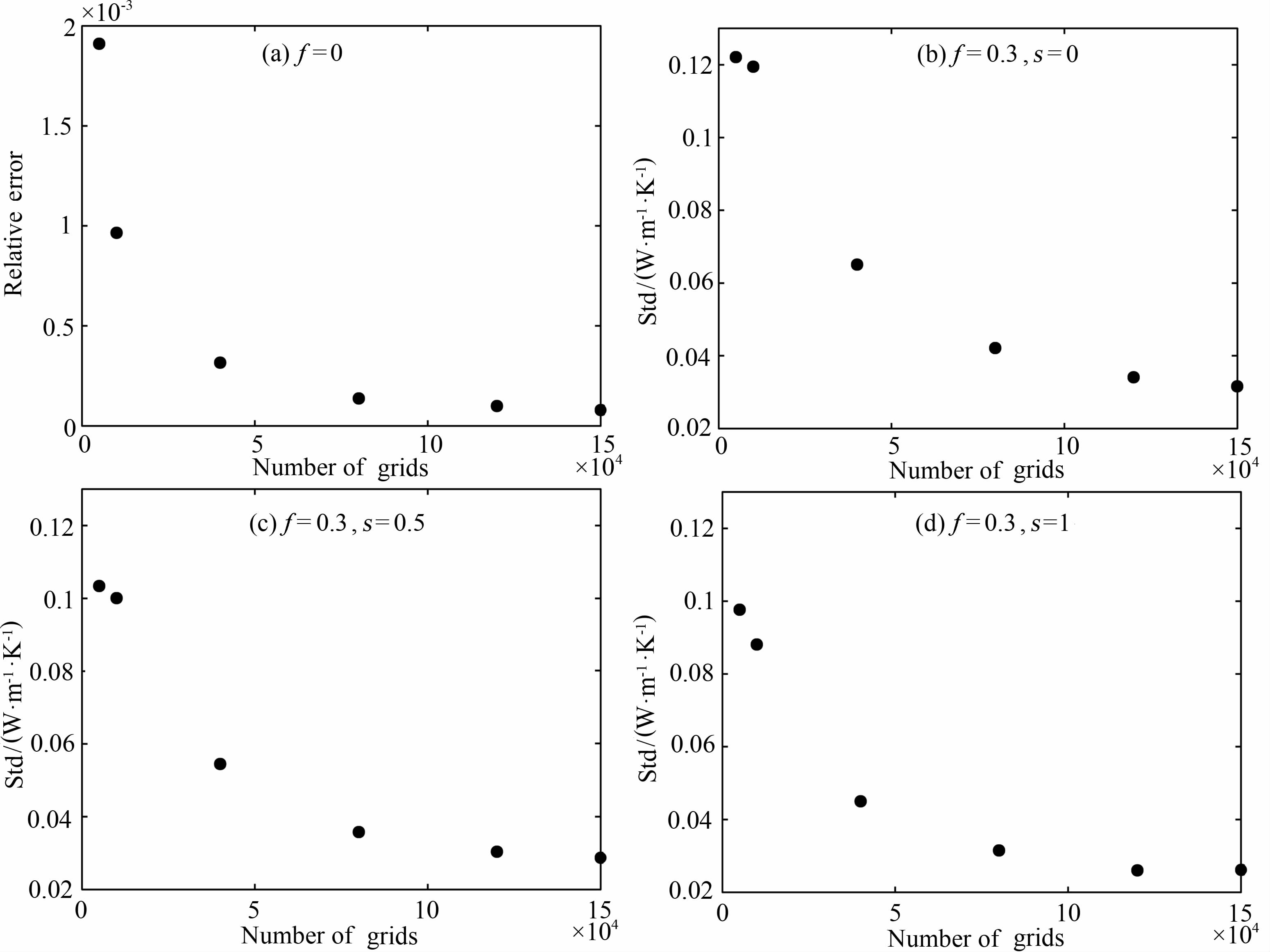
本文采取固定孔隙率和饱和度的方法来分析不同情况下网格数目对误差的影响.图 6a为只含固体矿物时,数值计算结果的相对误差随网格数的变化图,图 6(b—d)是孔隙率为0.3、饱和度分别为0、0.5、1时有效热导率的标准偏差随网格数目的变化图.从图 6a可以看出相对误差随网格数的增多而减小,当网格数目大于10万时,相对误差虽然还有减小的趋势,但变化已相对平缓;网格为15万时,数值计算出的Keff的相对误差为0.007%,这同时也验证了程序的可靠性及正确性.图 6(b—d)中标准偏差的分布显示了类似的趋势:标准偏差随网格数目的增多而减小,即网格数目越多数值计算出的Keff的分散度越小、试验稳定性越好;当网格增多到一定程度时,标准偏差变化趋于平缓.如图所示,网格数目对误差影响的临界值约为1×105.以上分析说明,为保证误差稳定在一定范围内,网格数不能少于1×105,而网格继续增多虽然可以进一步减小误差,但效果已不明显.因此,在数值计算中既为了节省计算时间又保证精度,可以把网格划为10万左右.
|
图 6 误差随网格数目变化的分布图 Fig. 6 Error of Keff versus number of grids |
图 7为网格数为12 万时,孔隙率为0.3、饱和度分别为0、0.5、1 时,颗粒数为500、1000、2000、5000、10000、20000、30000时的标准偏差分布图.图 7(a—c)显示了相同的趋势:标准偏差随颗粒数目的增多而减小;当颗粒数目大于1×104 时,标准偏差随颗粒数目的变化已趋于平缓.以上分析说明,岩石试件体积与矿物颗粒平均体积之比对标准偏差影响的临界值约为1×104.据此可解释对小尺寸试样实际测量时的尺度效应,试件要足够大、或者说包含了足够多的矿物颗粒和孔隙时,测量结果才有代表性.

|
图 7 标准偏差随颗粒数目变化的分布图 Fig. 7 Standard deviation of Keff versus number of grains |
用热导率仪测量试件的热导率时,由于试件尺寸有限,因此不同试件测量结果会有差异.一般由于时间、经费的限制,实际测量数目有限,而数值计算方法,如同图 7所显示的,不但能够得到热导率的平均值,而且能对有限尺寸(包含有限矿物颗粒和孔隙)的试件测量的误差分布有所了解.因此计算方法提供了更多的信息,也为我们提供了消除试件大小尺度效应的途径.
用热导率仪测量试件的热导率时,对试件的尺寸有严格要求.实验试件最大一般为7.85×104 mm3(美国EKO 公司生产的HC-110(190)热导率仪对试件的尺寸要求为直径51~63.5mm,厚度为0~25mm,最大约78.5×104 mm3,精度为5%).据图 7可知,测量含湿孔隙岩石的有效热导率时,为了保证标准偏差稳定在5% 以内,岩石试件的体积与矿物颗粒的体积之比应大于2000.因此,只有当矿物粒径小于4 mm 时,热导率仪的测量误差才可达5%以下.而对于矿物粒径大于4 mm 的岩石来说,试件存在尺度效应,单个试件的测量结果则可能出现较大的偏差,要对大量试件测量和求平均值才能减小误差.而我们的计算方法则不受试件大小或矿物颗粒大小的限制.
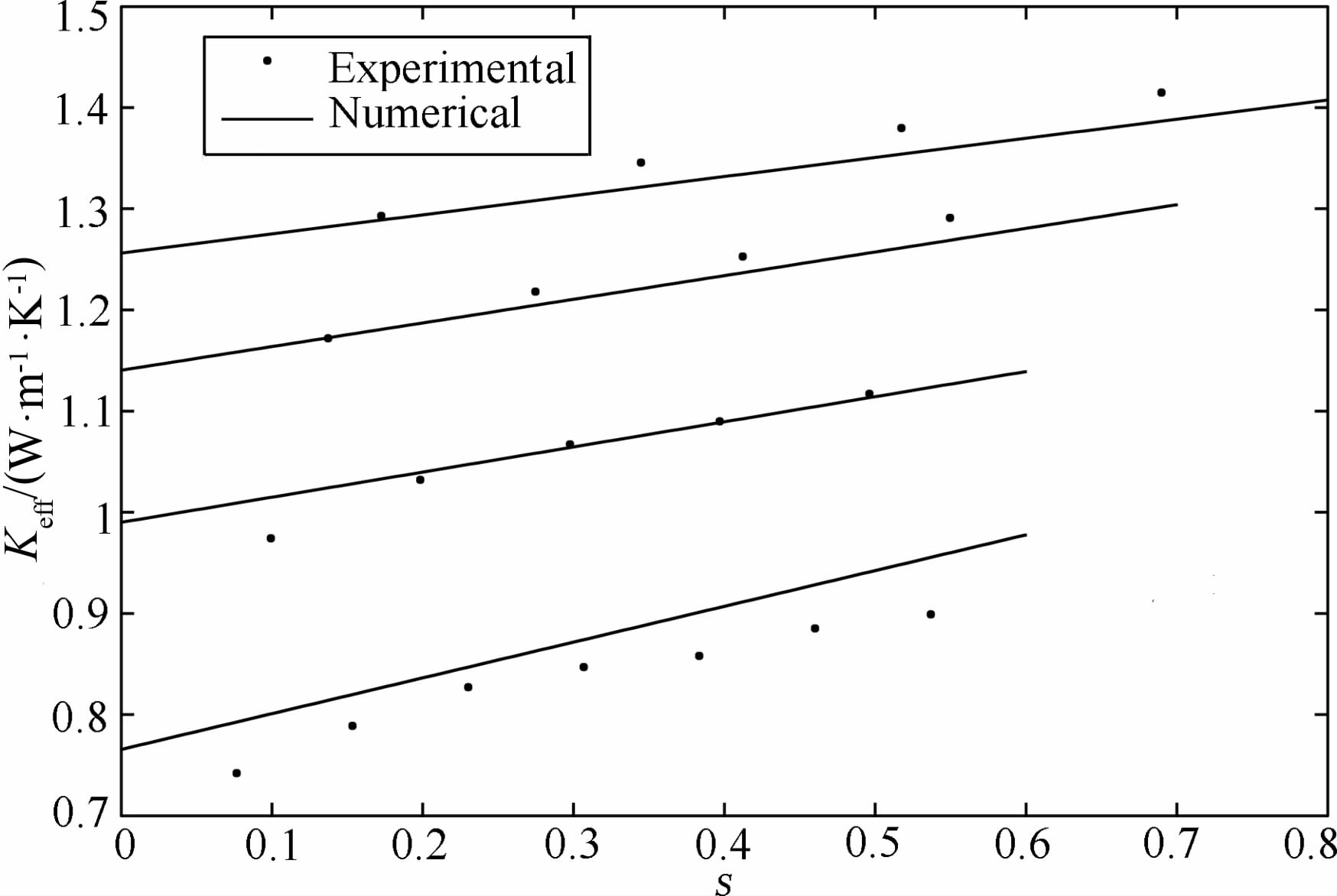
图 8给出了本数值计算结果和实验数据[26]的对比,各组分的热导率Km 、Kw 、Ka按文献分别取1.856、0.574、0.025 W·m-1·K-1.由图可知,本文数值计算的结果和实验数据基本一致,各测点的平均偏差为2.4%,最大偏差为7.37%.这说明本文所述的孔隙岩石模型是合理的,计算方法可行.
|
图 8 数值计算结果和实验数据[26]的对比 Fig. 8 Comparison of the experimental resultssup>[26]and the numerical calculation |
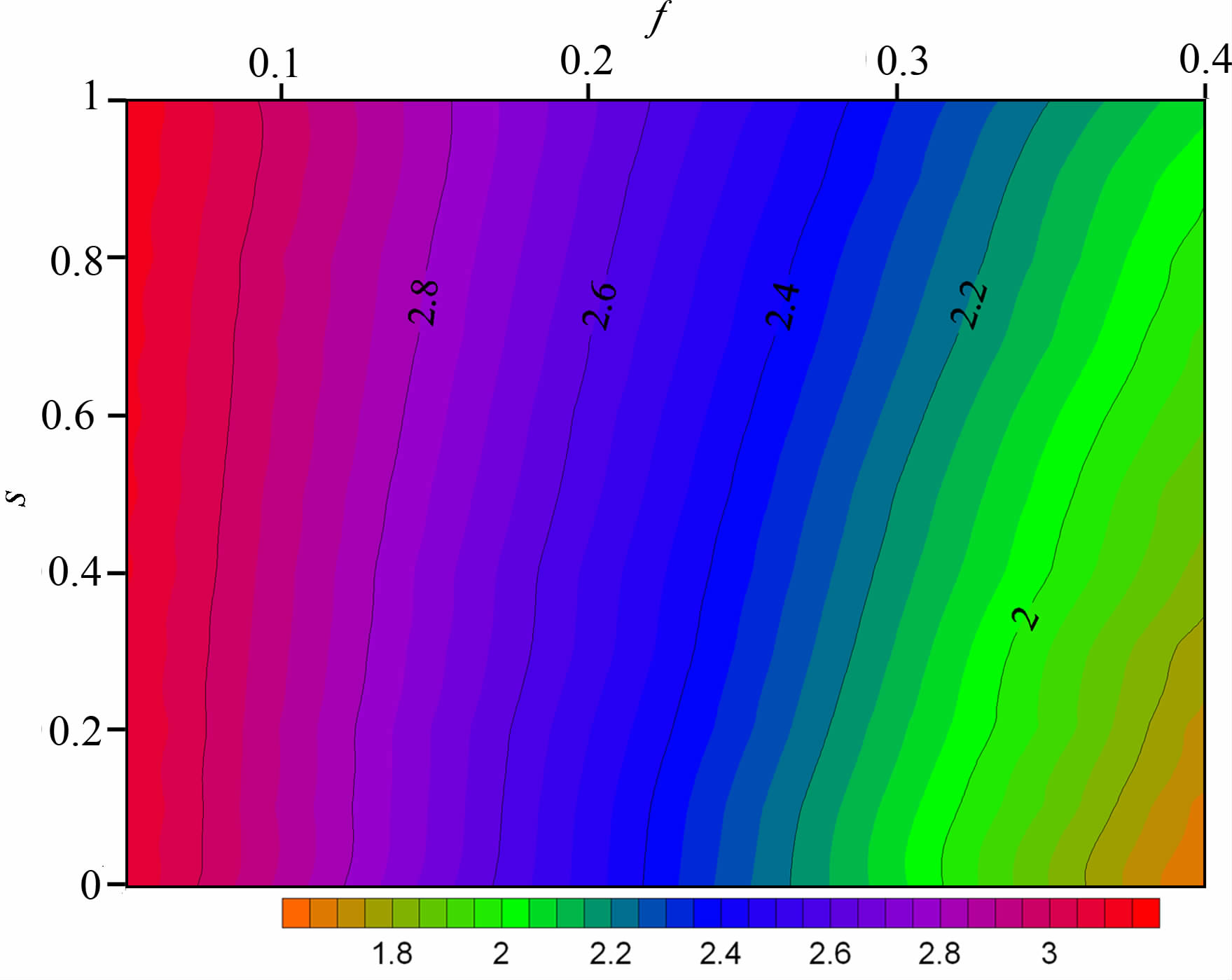
图 9给出了孔隙率、饱和度对有效热导率的影响.整体而言,随着孔隙率的增加,有效热导率逐渐减小;当孔隙率较小时(约小于0.15),饱和度对有效热导率的影响较小,孔隙率对有效热导率的影响特别大;当孔隙率较大时,饱和度对有效热导率的影响趋于明显;孔隙率不变时,有效热导率随饱和度的增大而增大.由图 9可知,在已知模型孔隙率和饱和度的情况下,可直接在图中确定出岩石的有效热导率.模型中矿物、水、空气的热导率分别取3.3、0.6、0.0274 W·m-1·K-1.
|
图 9
孔隙率、饱和度对K |
这样,为快速方便确定岩石的有效热导率,可以模拟计算得到含湿孔隙岩石的孔隙率及饱和度与有效热导率的关系图;固体矿物、水、空气所占比例与有效热导率关系图,然后根据岩石的孔隙率及饱和度、或者是固体矿物、水、空气所占比例,从图中确定出岩石有效热导率的范围.
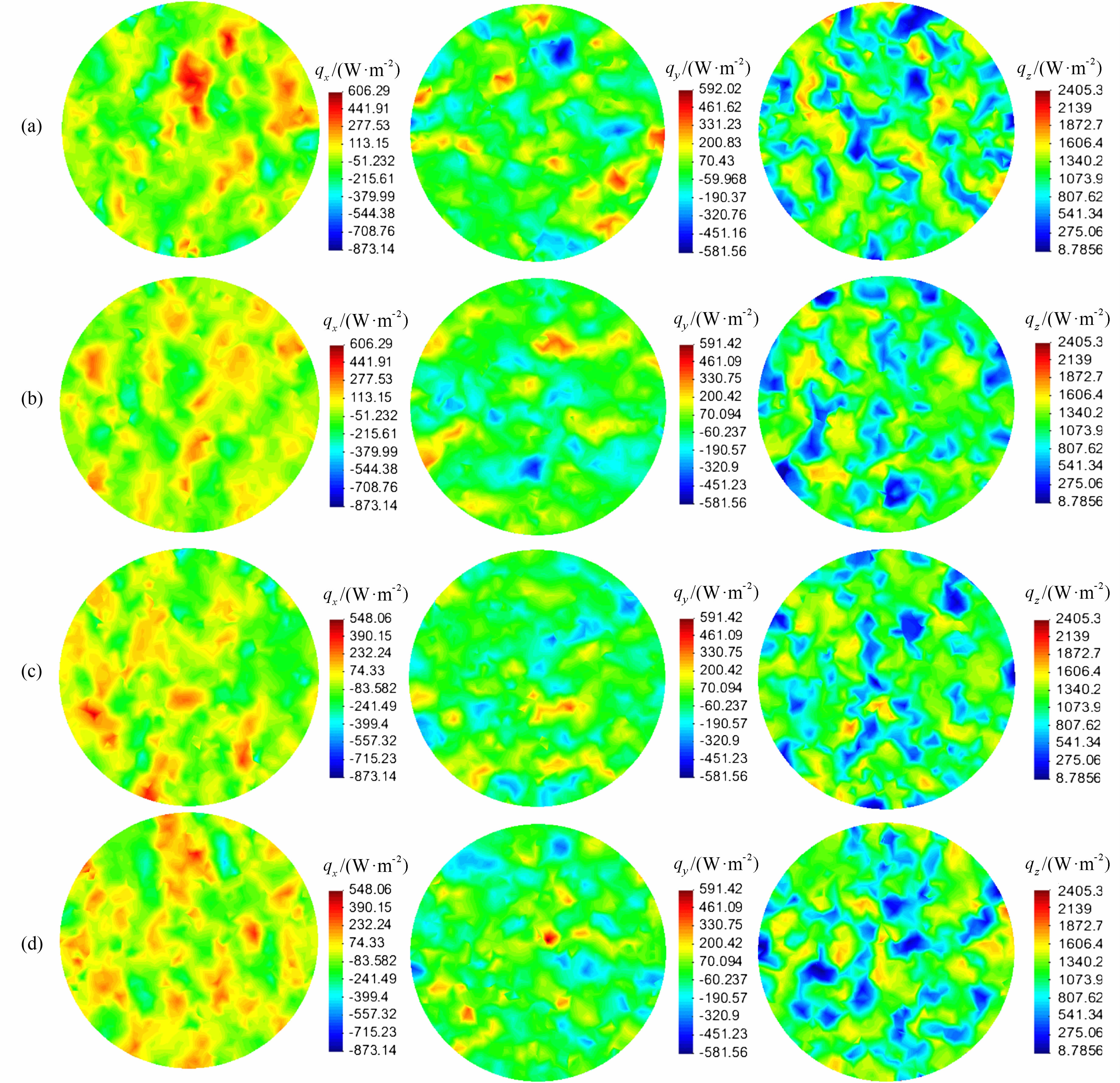
此有限元方法可以较好地模拟含湿孔隙岩石内部的热流情况.图 10(a—d)分别给出四个不同位置(h/5、2h/5、3h/5、4h/5)截面的x、y、z三个方向的热流分布情况,可以看出热流的分布显示出了明显的不均匀性,这说明热流的分布同样受孔隙分布情况的影响.根据能量平衡,流过每个截面的总热流是一个定值,但由于孔隙的存在,导致每个截面的热流分布不均匀.
|
图 10 不同截面的热流分布情况 Fig. 10 Heat flux distribution on different cross sections |
本文应用随机剖分单元、随机指定材料属性的有限元前处理方法,对含湿孔隙岩石的有效热导率进行了数值模拟计算,并与实验数据进行了对比.结果表明:(1)用有限元方法和MonteCarlo方法进行含湿孔隙岩石的热力学性质数值模拟是高效可行的;(2)本数值方法可以应用于各类多孔介质的有效热导率预测上,也可以推广到更为复杂的非均匀多孔介质的研究上,从而进一步认识多孔介质中的传热过程,为工程计算提供指导;(3)数值计算结果表明,孔隙岩石的传热不仅取决于矿物、水、空气本身的热物理特性,而且在很大程度上还与孔隙分布情况和孔隙结构有关,在局部热性质是不均匀的,但整个岩体宏观可以用一个热导率描述;(4)试样尺度会对岩体宏观热导率测量或网格数目对岩体宏观热导率计算造成误差,这种误差随着实测时试件的增大或计算时网格数目的增加而减小;(5)在数值计算中,为了节省计算时间、保证计算精度,可以把网格划为10万左右;(6)通过我们的计算可知,用热导率仪测量岩石试件热导率时,只有当矿物粒径小于4mm 时,才能保证误差在5%以内,当矿物粒径大于4mm时,要对大量试件测量和求平均值才能减小误差.本文仅简单假定孔隙岩石骨架各种矿物的热导率相差不大,可以近似视为一个常数,不过沿用本文的方法,不难实现对组分已知的多种矿物复合孔隙岩石的模拟.
本方法结合CT_LBM 技术[27]可以推广到岩石的力学、电学等其它物理性质的研究,也可以推广到人工复合材料的研究、设计,成为确定复合材料性质的重要手段.本文的方法在常温常压下得到了证实,进一步,如果我们知道各种矿物高压高温下的物性,以及岩石中各种矿物所占的比例,那么也不难计算多矿物岩石在高温高压下的性质.高温高压下实验测试成本更高,以矿物物性测量为基础,计算组分已知的岩石的物性,本文的方法应该有广阔的应用天地.
| [1] | 杨淑贞, 张文仁, 沈显杰. 孔隙岩石热导率的饱水试验研究. 岩石学报 , 1986, 2(4): 83–91. Yang S Z, Zhang W R, Shen X J. Experimental research on the thermal conductivity of water-saturated porous rocks. Acta Petrologica Sinica (in Chinese) , 1986, 2(4): 83-91. |
| [2] | Bear J. Dynamics of Fluids in Porous Media . Beijing: China Architecture and Building Press, 1983 . |
| [3] | 李大心. 国外岩石热导率的研究动向. 地质科技情报 , 1985, 4(2): 12–20. Li D X. Research trends of thermal conductivity of rocks abroad. Geological Science and Technology Information (in Chinese) , 1985, 4(2): 12-20. |
| [4] | Miller M N. Bounds for effective electrical, thermal, and magnetic properties of heterogeneous materials. Mathematical Physics , 1969, 12(10): 1988-2004. |
| [5] | Carbonell R G, Whitaker S. Heat and mass transfer in porous media. //Proceedings of the NATO Advanced Study Institute on Mechanics of Fluids in Porous Media. Newark, USA, 1982; 121-198. |
| [6] | Hadley G R. Thermal conductivity of packed metal powders. Int| J| Heat and Mass Transfer , 1986, 29(6): 909-920. |
| [7] | Kaviany M. Principle of Heat Transfer in Porous Media. New York: Springer-Verlag , 1995. |
| [8] | Katz A J, Thompson A H. Fractal sandstone pores: implications for conductivity and pore formation. Physical Review Letters , 1985, 54(12): 1325-1328. DOI:10.1103/PhysRevLett.54.1325 |
| [9] | Thompson A H, Katz A J, Krohn C E. The microgeometry and transport properties of sedimentary rock. Advances in Physics , 1987, 36(5): 625-694. DOI:10.1080/00018738700101062 |
| [10] | 李小川, 施明恒, 张东辉. 非均匀多孔介质中导热过程. 东南大学学报(自然科学版) , 2005, 35(5): 761–766. Li X C, Shi M H, Zhang D H. Heat conduction process in non-uniform porous media. Journal of Southeast University (Natural Science Edition) (in Chinese) , 2005, 35(5): 761-766. |
| [11] | Bogaty H, Hollies N R S, Milton H M. Some thermal properties of fabrics: Part Ⅰ. The effect of arrangement. Text| Res| , 1957, 27(6): 445-449. |
| [12] | Hollies N R S, Bogarty H. Some thermal properties of fabrics Part Ⅱ. The effect of water content. Text| Res| , 1965, 35(2): 187-190. |
| [13] | Singh A K, Singh R, Chaudhary D R. Heat conduction through moist soils at different temperatures. Pramana , 1988, 31(6): 523-528. DOI:10.1007/BF02847041 |
| [14] | Pande R N, Kumar V, Chaudhary D R. Thermal conduction in a homogeneous two-phase system. Pramana , 1984, 22(1): 63-70. DOI:10.1007/BF02875588 |
| [15] | Pande R N, Chaudhary D R. Thermal conduction through loose and granular two-phase materials at normal pressure. Pramana , 1984, 23(5): 599-605. DOI:10.1007/BF02846682 |
| [16] | Zhang H F, Ge X S, Ye H. Effectiveness of the heat conduction reinforcement of particle filled composites. Modelling Simul| Mater| Sci| Eng| , 2005, 13(3): 401-412. |
| [17] | Zhang H F, Ge X S, Ye H. Randomly mixed model for predicting the effective thermal conductivity of moist porous media. J| Phys| D: Appl| Phys| , 2006, 39(1): 220-226. |
| [18] | Zhang H F, Ge X S, Ye H, et al. Heat conduction and heat storage characteristics of soils. Applied Thermal Engineering , 2007, 27(2-3): 369-373. DOI:10.1016/j.applthermaleng.2006.07.024 |
| [19] | Wang M R, Wang J L, Pan N, et al. Three-dimensional effect on the effective thermal conductivity of porous media. Phys| D: Appl| Phys| , 2007, 40(1): 260-265. |
| [20] | Tiak D, Delkumburewatte G B. The influence of moisture content on the thermal conductivity of a knitted structure. Measurement Science and Technology , 2007, 18(5): 1304-1314. DOI:10.1088/0957-0233/18/5/016 |
| [21] | Aurangzeb, Maqsood A. Modeling of the effective thermal conductivity of consolidated porous media with different Saturants: A test case of Gabbro rocks. International Journal of Thermophysics , 2007, 28(4): 1371-1386. DOI:10.1007/s10765-007-0203-1 |
| [22] | 景惠敏. 数值模拟在地震海啸、港口风浪等地学问题上的应用. 北京: 中国科学院研究生院地球科学学院 , 2011. Jing H M. Numerical simulation applied in evaluation of tsunami and wave hazard in a harbor (in Chinese). Beijing: College of Earth Science, Graduate University of Chinese Academy of Sciences (in Chinese) , 2011. |
| [23] | 王勖成. 有限单元法. 北京: 清华大学出版社, 2003 . Wang X C. Finite Element Method (in Chinese). Beijing: Tsinghua University Press, 2003 . |
| [24] | Bouguerra A. Prediction of effective thermal conductivity of moist wood concrete. J| Phys| D: Appl| Phys| , 1999, 32(12): 1407-1414. |
| [25] | Vermia L S, Shrotriya A K, Singh R, et al. Prediction and measurement of effective thermal conductivity of three phase systems. J| Phys| D: Appl| Phys| , 1991, 24(9): 1515-1526. |
| [26] | Somerton W H. Thermal Properties and Temperature Related Behavior of Rock/Fluid Systems. New York: Elsevier , 1992. |
| [27] | Zhu B J, Cheng H H, Qiao Y C, et al. Porosity and permeability evolution and evaluation in anisotropic porosity multiscale-multiphase-multicomponent structure. Chinese Science Bulletin , 2012, 57(4): 320-327. DOI:10.1007/s11434-011-4874-4 |
 2012, Vol. 55
2012, Vol. 55