2. 安徽省地球物理地球化学勘查技术院, 合肥 230022
2. Anhui Institute of Geophysical and Geochemical Prospecting Techniques, Hefei 230022, China
航空和地面重磁位场观测面通常不是一个水平面,观测面起伏变化使各测点离地下场源远近变化,导致测得的重磁场形态复杂化.因此,需要通过曲化平消除观测面起伏的影响.前人已研究出几种曲化平方法:等效源法[1-16]、傅里叶级数法[17]、Taylor级数法[18-21]、有限元法[22-23]、边界元法[24-25]等.等效源法在观测曲面下方布置一系列点分布等效源[1, 2],使它们在观测曲面产生的场值与观测场值近似等效,通过求解线性方程组,得到等效源的物性参数(密度或磁化强度),再计算这些等效源在水平面上的重磁场.以上等效源多点离散分布,还可以设置为连续分布,如重力场的等效面密度分布及磁场的等效偶极子面分布(偶层)[3, 7-8, 10-16].傅里叶级数法把观测曲面上的重磁场用有限项傅里叶级数表示,该级数的有限个系数由矩阵逆运算得到,再由该级数计算水平面上的重磁场[17].Taylor级数法把观测曲面上的重磁场沿垂向在一水平面上进行Taylor展开,级数的各项系数包含水平面上重磁场的各阶垂向导数,它们由傅里叶逆变换计算,再由该级数迭代求取水平面上的重磁场[18-21].有限元法把重磁场在观测曲面及其以上空间满足的边值问题化为相应的变分问题,通过空间区域剖分、插值、单元分析、总体合成、线性方程组求解,得区域内各节点(包含换算平面各节点)的重磁场值[22-23].边界元法把重磁场在观测曲面及其以上空间满足的边值问题化为关于观测曲面的边界积分方程,通过观测曲面的剖分、插值、单元分析、总体合成、线性方程组求解,得观测曲面上各节点重磁场法向导数值,由包含重磁场及其法向导数的观测曲面积分,数值计算其上方任一水平面各点重磁场[24-25].
等效源法、傅里叶级数法、有限元法、边界元法一般需要解线性方程组,对大数据量的实际资料,由于需要很大的内存和计算时间,使这些方法不实用.Taylor级数法由于高阶导数放大异常高频成分,该法不宜处理较大起伏观测面上的位场.姚长利等[26]由观测曲面上的位场及其垂向一阶导数,用三次样条函数计算该面上的位场垂向二阶导数及垂向三阶导数,再由位场的三阶Taylor展开式进行曲化平换算,其计算速度快,计算结果稳定,但该法不能用于单一的位场资料.刘天佑等[14]、Li等[16]用小波压缩算法对等效源法的积分方程进行压缩与降阶求解,减少了内存量和计算时间,他们分别给出了51×51和64×64数据量的处理算例,但还未见处理更大的数据量.Pilkington等[10]在观测曲面的镜像面上确定等效源,Xia等[11]在观测曲面下方水平面上确定等效源,他们给出了等效源密度分布与观测曲面上重力异常的关系或等效源磁化强度分布与观测曲面上磁异常的关系,通过文献[27]中的迭代公式确定等效源密度或磁化强度,再计算等效源上方任一水平面上的重力异常或磁异常,较以往的等效源法显著地提高了计算速度,但等效源为人为设置的场源.徐世浙等[28]用观测曲面上重磁场值作为其下方一水平面上重磁场的初值,用Fourier变换把该平面上重磁场向上延拓到若干个平面(4~6个),再插值求出观测曲面上理论重磁场,并把它与观测曲面上重磁场的差值作为校正值,迭代计算该水平面上重磁场,这种方法具有较高的计算精度,但对大数据量,插值会大大增加计算时间.
本文不用设置等效源,不用求解方程组,不用插值,把曲化平建立在第一类Fredholm 积分方程基础上,通过较严密的数学推导,研究出一种实用的空间域或波数域迭代求解方法,这也是我们提出的平面向下延拓波数域迭代法[29]向曲面向下延拓的推广.
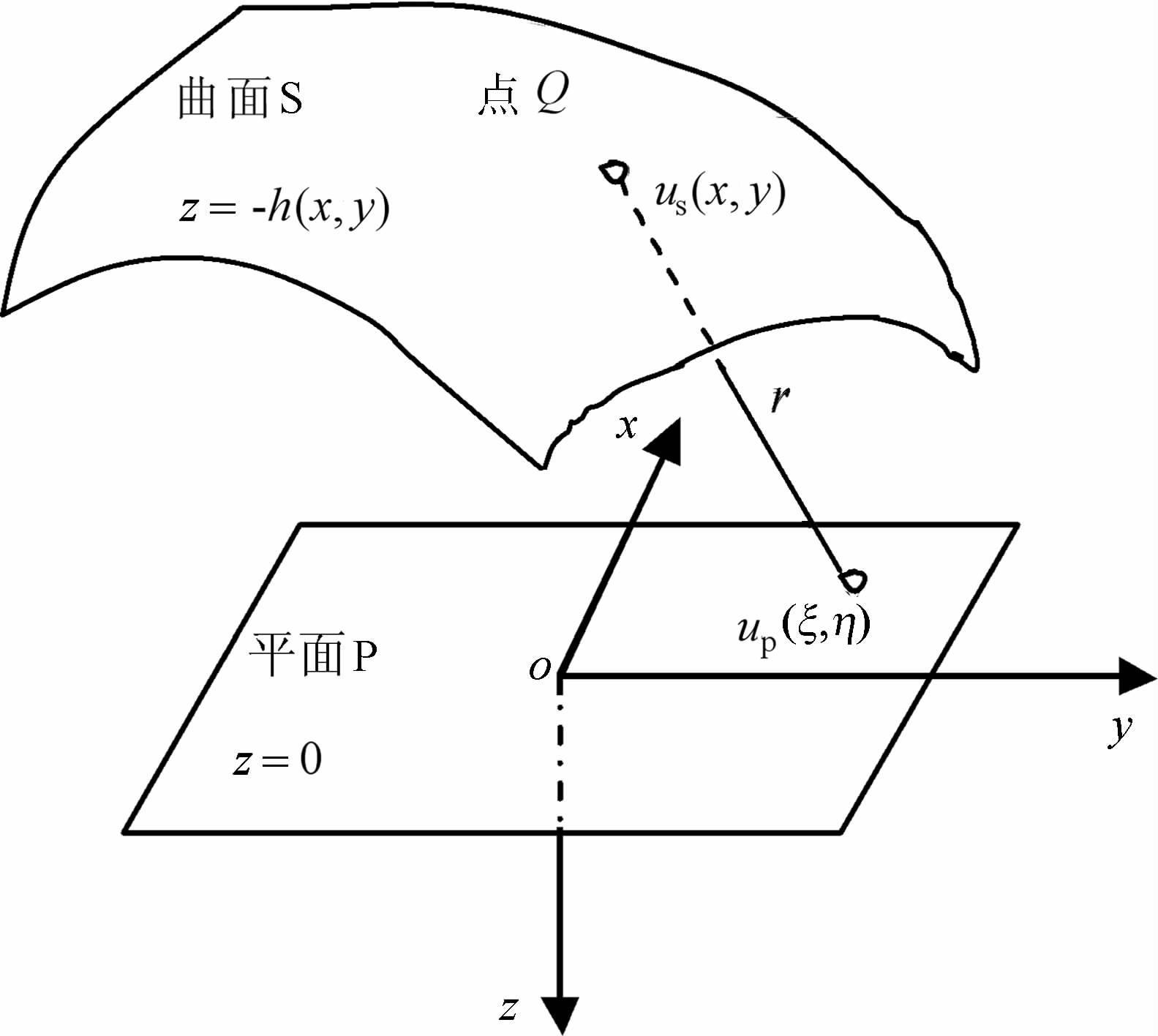
2 位场曲化平的积分方程位场(这里指重力场、磁场、重力场的导数、磁场的导数)观测面为曲面S,取其下方与其邻近的一平面P(图 1),该平面及后文所述平面均为水平面.按右手定则取直角坐标系,oxy平面与平面P 重合,z轴垂直向下.曲面S 的高程为hs(x,y);平面P 的高程为hp;曲面S 关于平面P 的相对高程为h(x,y)(= hs(x,y)- hp),h(x,y)>0 ,则曲面S 的方程为:z=-h(x,y).已知曲面S上的位场:
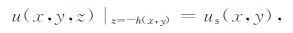
|
(1) |
|
图 1 位场曲化平示意图 Fig. 1 Schematic diagram of potential field continuation from an irregular surface to a plane |
计算平面P上的位场:
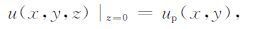
|
(2) |
这种换算称之为位场曲化平(或曲化平,也称位场曲面延拓).这里的曲化平是曲面向下延拓,广义的位场曲化平指由曲面S上的位场换算场源以上空间任一平面的位场,这可由曲面S上的位场换算平面P上的位场,再由平面P 上的位场向上延拓或向下延拓得到.
设平面P的上半空间Ω 无场源,则Ω 内的位场u(x,y,z)满足Laplace方程▽2u=0,当已知平面P上的位场时,可确定Ω 内任一点Q 的位场.把点Q 取在曲面S上,根据无限平面的位场向上延拓公式,得观测曲面S上的位场us(x,y)与平面P 上的位场up(x,y)的关系
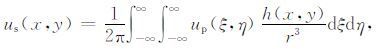
|
(3) |
式中代入积分微元位置点(ξ,η,0)与曲面S 上点Q(x,y,-h(x,y))之间距离r的公式,把us(x,y)与up(x,y)的关系表示为下面的空间域积分表达式:Aup(x,y)=
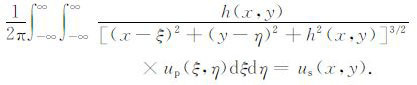
|
(4) |
由曲面S上的位场us(x,y)和相对高程h(x,y)求平面P上的位场up(x,y),式(4)就是位场曲化平的积分方程,它属于第一类Fredholm 积分方程.式中的A是线性积分算子,用它简洁表达其中的积分关系,它表示位场由平面P到曲面S的向上延拓.
3 积分方程的解法 3.1 逐次逼近法的表达形式第一类Fredholm 积分方程(4)可用逐次逼近法[30]求解,即用如下的迭代公式表示为
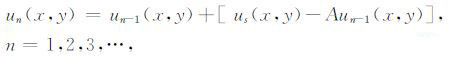
|
(5) |
式中un(x,y)是式(4)中up(x,y)的第n次迭代近似值;平面P上位场的初始迭代值取观测曲面S上的位场,即
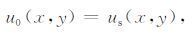
|
(6) |
Aun-1(x,y)是un-1(x,y)自平面P(z=0)至观测曲面S(z=-h(x,y))的向上延拓位场,由式(4),其表达式为

|
(7) |
式(5)的迭代过程一直进行到满足如下迭代终止准则:
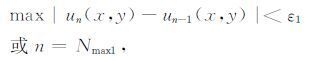
|
(8) |
式中ε1、Nmax1分别是给定的很小正数和最大迭代次数.这样,就得到平面P上位场

|
(9) |
在对积分方程(4)进行上述迭代求解时,需要解决由平面P上位场计算曲面S上位场,即求解平面位场换算曲面位场问题,简称平化曲问题.对平化曲问题,式(7)的计算若采用数值积分法,运算量太大,不实用.为使式(7)的计算切实可行,关键在于减少平化曲问题的计算量,因此,下面将利用Fourier变换,探索式(7)的其它表达式.
3.2 逐次逼近法的关键---位场由平面向上延拓到曲面的实用表达式式(7)中的积分是对空间域变量ξ 和η 的积分,我们尝试把它变成波数域变量kx和ky的积分.为此,对平面P上位场up(x,y)的第n-1次迭代近似值un-1(x,y),其Fourier变换为

|
(10) |
其Fourier逆变换式为
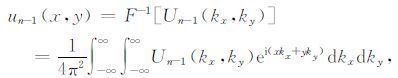
|
(11) |
其中kx、ky分别是x、y方向的波数.把式(7)中un-1(ξ,η)用式(11)代入,并交换积分次序,得
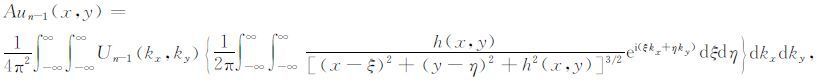
|
(12) |
注意到上式中x、y不随积分变量ξ、η 变化,作变量代换

|
则式(12)大括号中式子化为

|
(13) |
式中
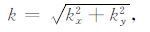
|
(14) |
把式(13)代入式(12),得式(7)的波数域积分表达式Aun-1(x,y)=

|
(15) |
或表达为
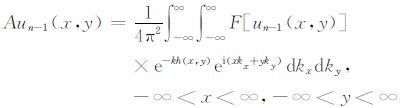
|
(16) |
式(16)是un-1(x,y)自平面P(z=0)至观测曲面S(z=-h(x,y))的向上延拓位场,它是式(7)的另一表达式,但较简洁.
通过考察式(16)中积分及其被积函数的形式,我们还知道,观测曲面S上点Q(x,y,- h(x,y))处的位场Aun-1(x,y)可以按下述方法得到.
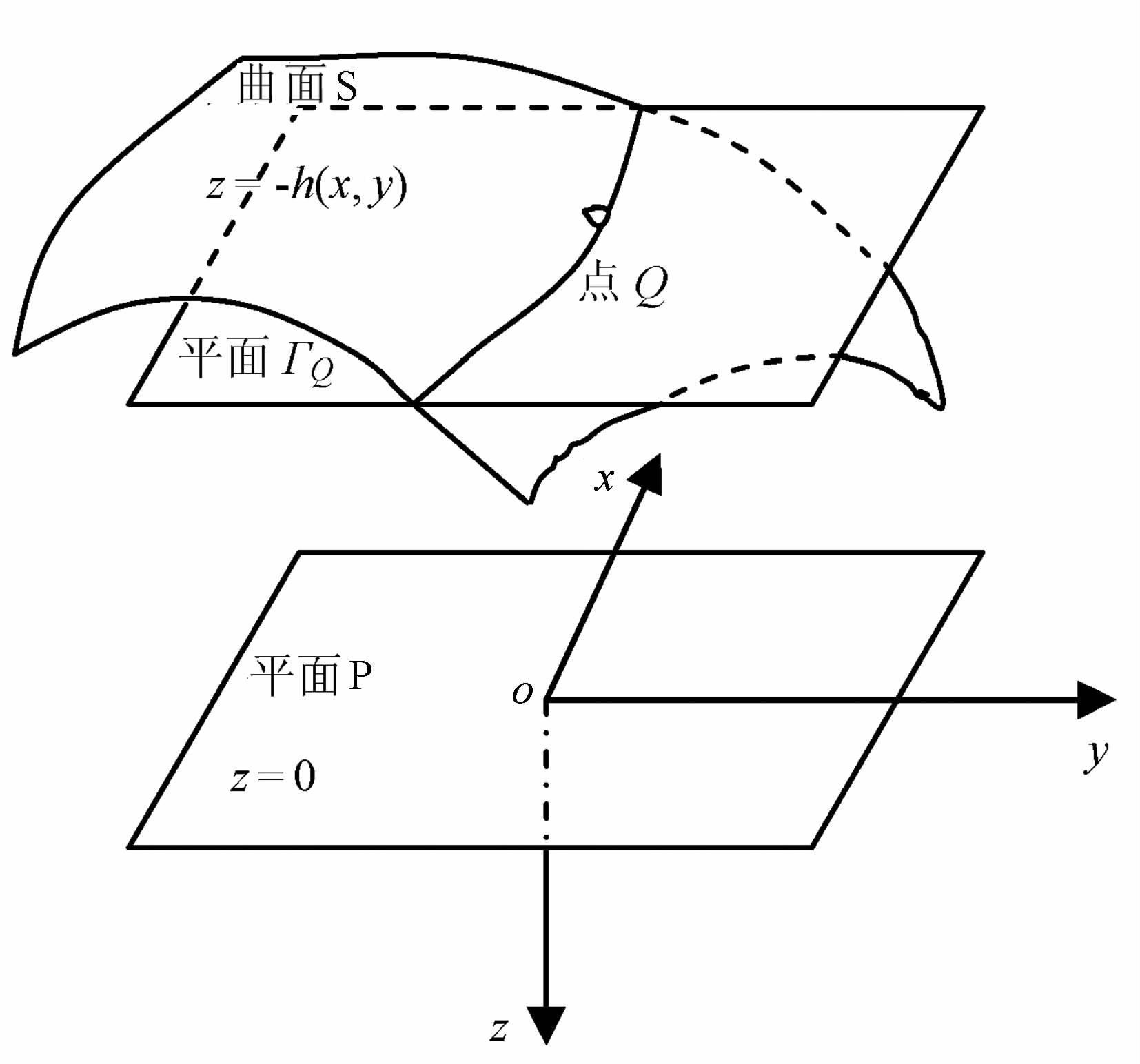
过观测曲面S上任意一点Q(x,y,-h(x,y))作平行于平面P的平面ΓQ(图 2),在波数域中把平面P的位场向上延拓到平面ΓQ,得平面ΓQ上位场波谱
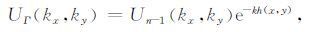
|
(17) |
|
图 2 过观测曲面S上点Q的平面ΓQ Fig. 2 Plane ΓQ through the point Q on S |
对平面ΓQ上位场波谱作Fourier逆变换,得平面ΓQ上位场表达式
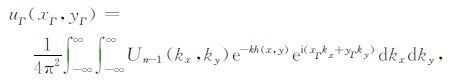
|
(18) |
式中(xΓ,yΓ )为平面ΓQ上任意一点坐标.由于点Q(x,y,-h(x,y))属于平面ΓQ与观测曲面S,把点Q的(x,y)坐标代入式(18),再与式(15)比较,得uΓ(x,y)= Aun-1(x,y),即得观测曲面S 上点Q处位场Aun-1(x,y).
式(16)(或(15))表明,通过波数域中的向上延拓和Fourier逆变换,我们可以实现式(7)的积分计算;若直接用式(16),每计算曲面S 上任意一个点(如点Q)处的位场Aun-1(x,y),要进行一次向上延拓,即需要作一次Fourier逆变换,所以,计算整个曲面S上的位场将花费大量时间.故式(16)也不宜用于平化曲的向上延拓计算.
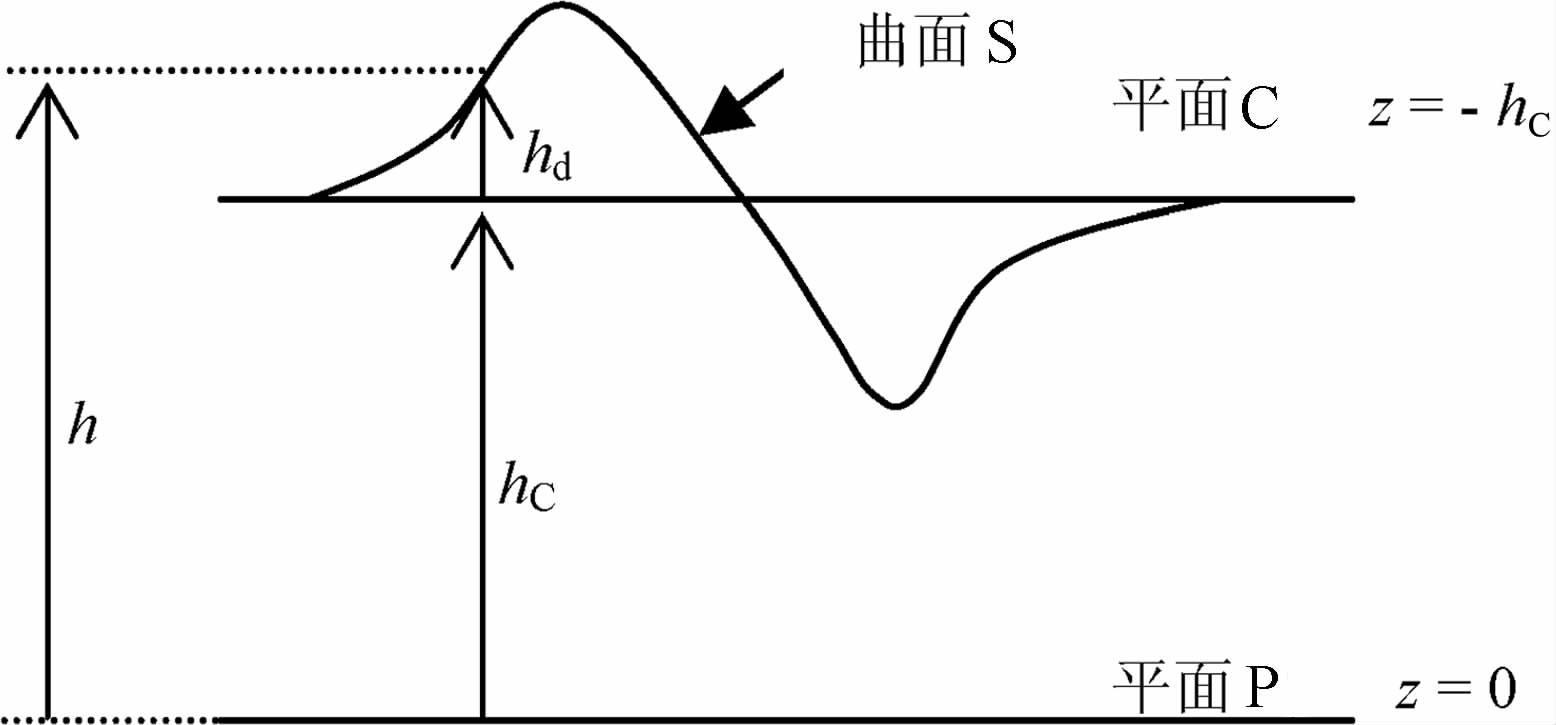
要减少式(16)的计算量,需设法使该式中空间域变量(x,y)的函数h(x,y)能放到积分号外面.为此,将相对高程h(x,y)用其极大值和极小值的平均值

|
(19) |
和其偏差(见图 3)

|
(20) |
|
图 3 h(x,y)的两个部分:hc、和hd(x,y) Fig. 3 Two parts of h(x,y) :hc and hd(x,y) |
表示为

|
(21) |
把式(21)代入式(16)中的实指数函数,并利用Taylor展开式,得
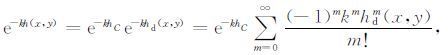
|
(22) |
就式(16)的积分而言,式(22)中函数项级数的自变量为(kx,ky),参变量为(x,y).记hdmax = max|hd(x,y)|,对式(22)级数中各项取绝对值,可得
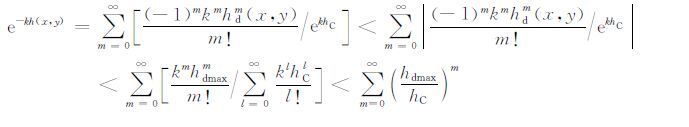
|
(23) |
当条件

|
(24) |
成立时,式(23)最右端的数项级数收敛,根据魏尔斯特拉斯M-判别法,式(22)中的级数绝对且一致收敛.由式(22)级数的一致收敛性及各项关于(kx,ky)的连续性,则该级数可逐项积分(魏尔斯特拉斯M-判别法与函数项级数逐项积分的定理见文献[31]),也就是将式(22)代入式(16),可交换积分与求和的次序,这样就把式(16)化为无穷级数形式
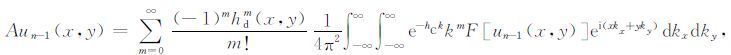
|
(25) |
用Fourier逆变换符号F-1和正变换符号F,把上式简洁地表示为
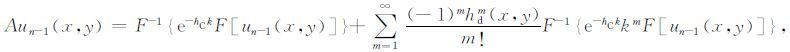
|
(26) |
式(26)是位场un-1(x,y)自平面P 向上延拓到上方曲面S的公式,是式(7)的又一个表达式.式(26)的推导利用了前人关于指数函数Taylor 展开的思路[10-11, 15, 18, 32].
式(26)右边第一项是Aun-1(x,y)的主要部分;第二项是无穷级数,它是由于位场观测面起伏引起的校正项,其第m项中F-1 {e-hCkkmF[un-1(x,y)]}是un-1(x,y)自平面P(z=0)到上方位场观测面中间平面C(z=- hC,见图 3)的延拓后m阶垂向导数场.位场观测面起伏越小,校正项的绝对值越小,需要求和的项数亦越少.通常,取求和项数4~8.
式(26)看上去比式(16)复杂,但对平化曲问题的计算,Fourier变换次数远小于曲面S上计算点的个数,所以其计算效率远高于式(16);此外,式(26)中的向上延拓因子e-hCk压制了垂向m阶导数因子km的放大作用,因此,式(26)为式(7)的计算提供了一个稳定、快速和有效的实用表达式.
3.3 积分方程的迭代解空间域迭代求解由式(6)、(5)、(26)、(8)、(9)实现.
波数域迭代求解按以下方式进行:
对观测曲面S上的位场us(x,y)作Fourier变换

|
(27) |
令平面P上位场的初始迭代值u0(x,y)的Fourier变换

|
(28) |
由式(5)得波数域迭代公式
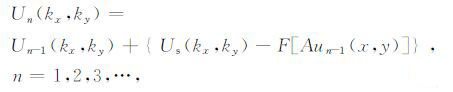
|
(29) |
式中Un(kx,ky)、Un-1 (kx,ky)分别是un(x,y)、un-1(x,y)的Fourier 变换;F[Aun-1 (x,y)]是un-1(x,y)自平面P(z=0)向上延拓到观测曲面S(z=-h(x,y))的位场的Fourier变换,由式(26)两边作Fourier变换,得

|
(30) |
式(30)是位场自平面P 向上延拓到上方曲面S 的波数域表达式.式(29)的迭代过程一直进行到满足如下迭代终止准则:

|
(31) |
式中ε2、Nmax2分别是给定的很小正数和最大迭代次数.这样,就得到平面P上位场
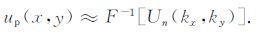
|
(32) |
应当指出,当位场观测面为平面时,式(30)右边只有第一项,式(28)至(32)的迭代求解便成为我们在文献[29]中提出的位场向下延拓波数域迭代法,我们在那里严格地证明了其收敛性,并研究了收敛特性和滤波特性.
在上述迭代求解时,应注意如下几点:
(1) 平面P应位于观测曲面S最低点的下方附近.这因为hdmax/hC<1是式(26)成立的充分条件;平面P距离曲面S最低点越远,hC 越大,(从式(26)可见)越有利于压制垂向m阶导数因子km的放大作用,但我们关于位场向下延拓波数域迭代法滤波特性的研究表明,迭代次数一定时,向下延拓深度越大,干扰放大得越大[29].
(2) 对观测曲面S 上的位场us(x,y)及式(20)中hd(x,y)的实际数据应进行扩边扩点,使其渐变为零,以减少截断引起的吉布斯效应的影响.
(3) 对实际数据通常应进行圆滑或低通滤波,以压制高频干扰;以减少采样引起的混叠效应.
(4) 式(30)或(26)第二项求和取前几项,通常取4~8项,这对应于式(22)中的指数函数Taylor展开到5~9项,由此引起的计算误差可粗略分析.以二度异常为例,设采样点数为N,考虑到波数域采样间隔Δk与空间域采样间隔Δx满足关系ΔkΔx=2π/N,则式(22)中第二个指数函数在第l个波数点的值为
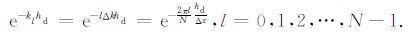
|
上式表明,在指数函数展开项数一定时,展开式在高波数点(即对短波异常)的误差较大;展开式的误差随观测面起伏与点距之比增大而增大.
(5) 式(29)或(5)的迭代次数一般取30~60.由我们在文献[29]中关于位场向下延拓波数域迭代法收敛特性分析可知,随迭代次数增加,收敛区从低波数向高波数扩大,由于位场为有界波谱,计算表明,当取上述迭代次数时,收敛区一般能包含场源位场波谱的波数范围.
4 算 例 4.1 理论模型场源为两个球形矿体(见图 4b),它们的参数是:半径分别为0.3km 和0.5km,球心埋深分别为0.8km 和1.8km,两球心y坐标均为0.0km,球心x坐标分别为-4.5km 和4.5km;剩余密度均为1.0×103 kg/m3;磁化强度均为1.0 A/m,磁倾角均为48°,磁偏角均为0°;北为x坐标正向,东为y坐标正向.矩形网格参数为:线数M=256,每线点数N=256,线距Δx=100m、点距Δy=100m.观测曲面S由4 个峰和4 个谷组成,相对高差取600m(见图 4a),它由下式计算得到

|
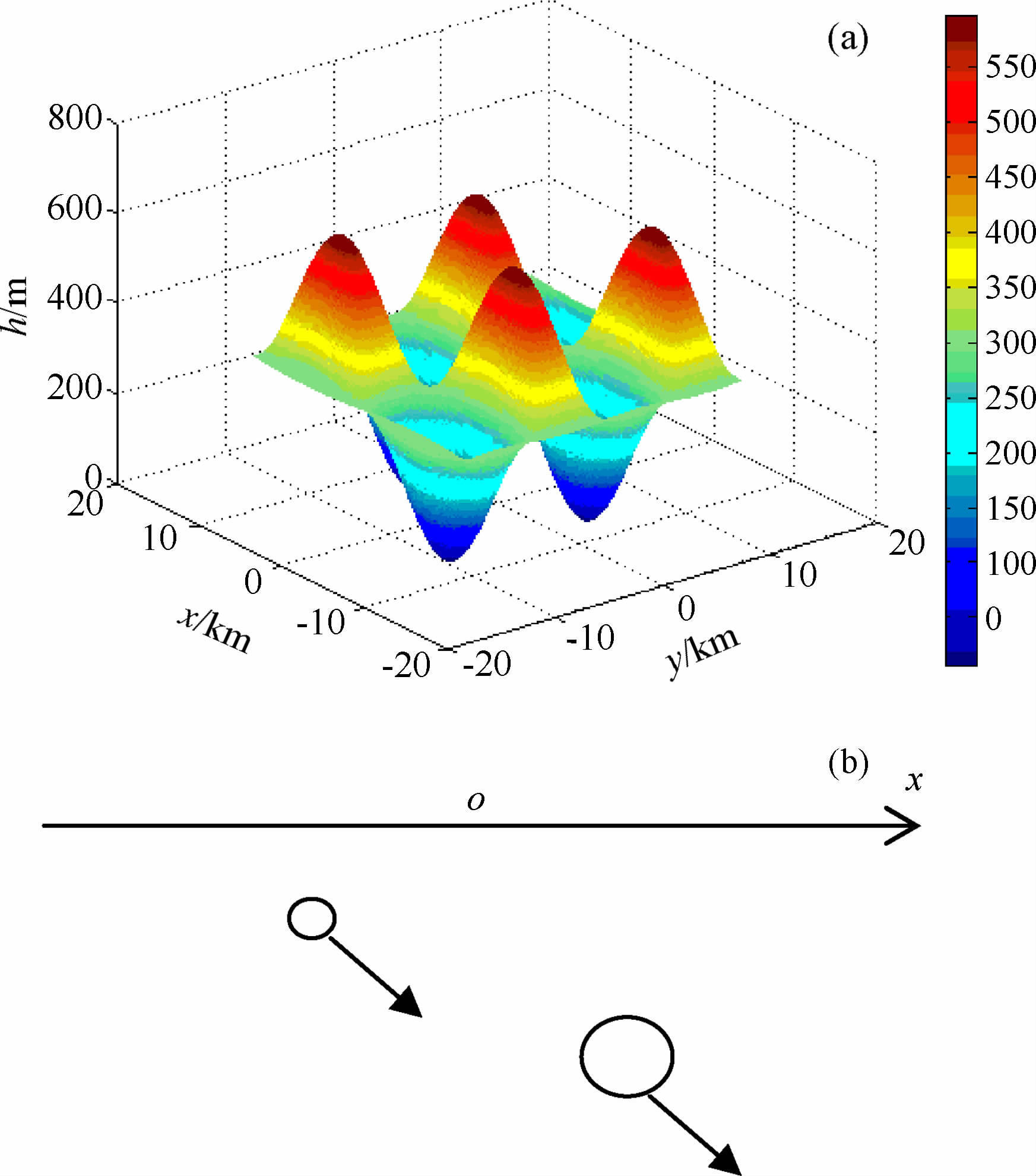
|
图 4 (a)观测曲面S及曲化平平面P; (b)场源 Fig. 4 (a) Observation surface S and reduction plane P; (b) Field sources |
其中参数取a=1m,As=300m.
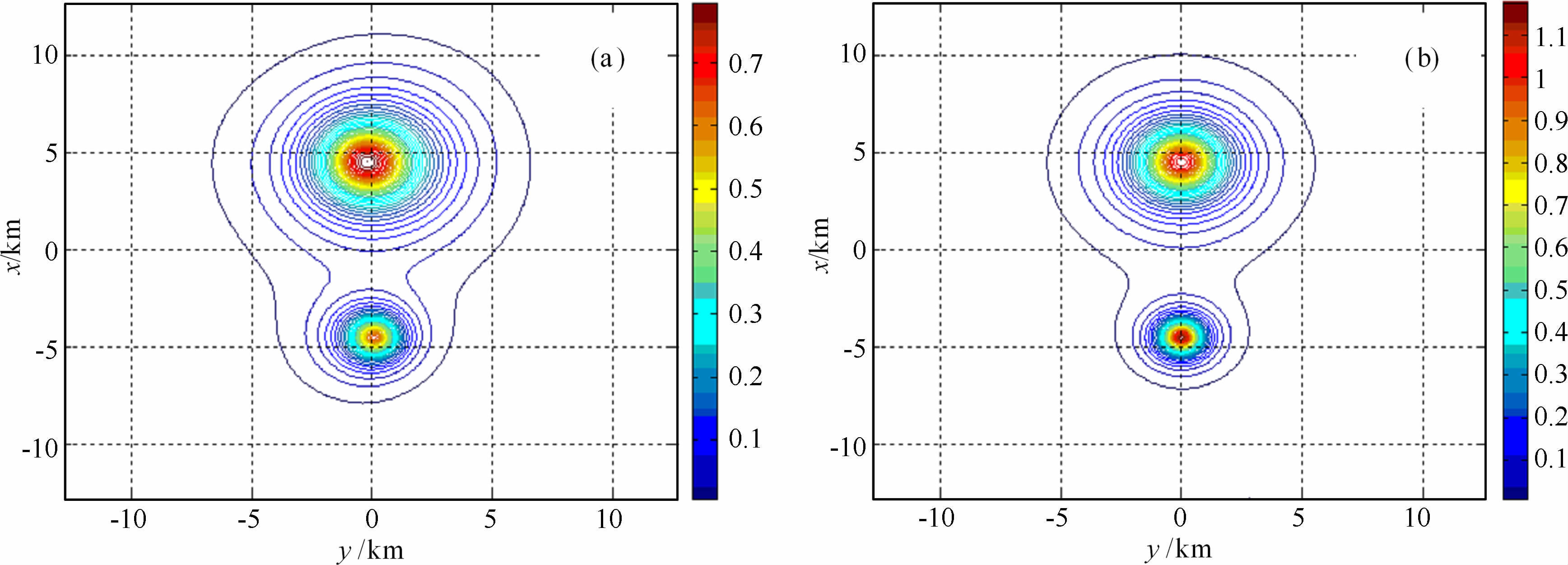
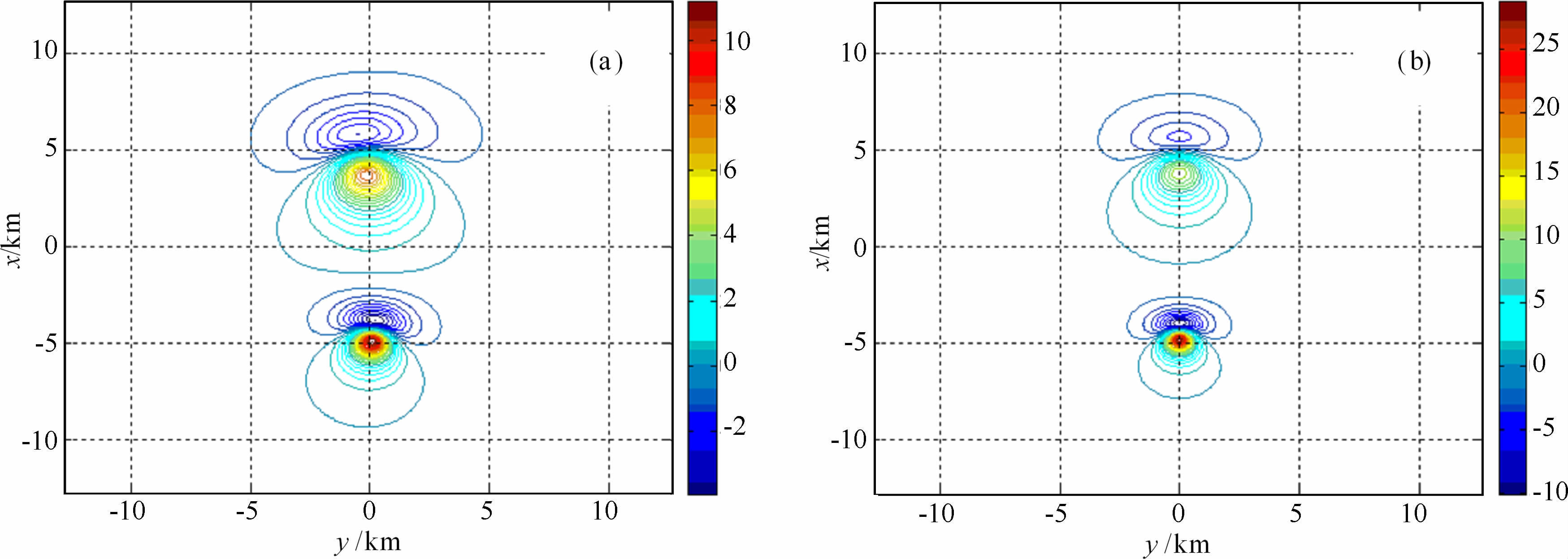
观测曲面S的起伏变化对重力异常Δg(图 5a)和磁异常ΔT(图 6a)的形态、幅值均有影响,如图 6a磁异常ΔT的正负中心因曲面S的影响而偏离正北方向.经过曲化平换算(迭代55次)到水平面P (图 4a中oxy坐标面)上,曲化平重力异常Δg(图 5b)与P 上的理论重力异常Δg(图略)非常接近,均方差rms为0.0008mGal;曲化平磁异常ΔT(图 6b)与P上的理论磁异常ΔT(图略)亦非常接近,均方差rms为0.0019nT.
|
图 5 (a) S上的重力场Ag等值线图;(b) P上的曲化平重力场A犵等值线图 Fig. 5 (a) Contour map for gravity anomaly Ag on S;(b) Contour map for reduction gravity anomaly |
|
图 6 (a) S上的磁异常AT等值线图;(b) P上的曲化平磁异常AT等值线图 Fig. 6 (a) Contour map for magnetic anomaly AT on S; (b) Contour map for reduction magnetic anomaly AT on P |
在不改变算区、观测曲面S 和场源大小的条件下,改变点距大小,研究曲化平计算精度和计算时间(表 1).曲面S起伏600m,S上磁异常ΔT最大值为11.33nT,最小值为- 4.05nT;迭代35次.由表 1可见,随曲面S起伏与点距之比增大,计算精度降低,但曲面S起伏与点距之比较大时,曲化平新方法仍然有较高的计算精度,如曲面S起伏是48倍点距时,均方差为0.0154nT;新方法计算快,且能处理大数据量资料,如数据量为2048×2048 时,使用2.26GHz主频、1.98GB 内存的笔记本电脑,曲化平计算时间仅需16.25min(即975s).
|
|
表 1 曲化平新方法的计算精度、计算时间 Table 1 Calculation precision and calculation time of the continuation method |
安徽省马鞍山市和尚桥铁矿东矿段矿床成因类型属于“玢岩铁矿"系列中的贫磁铁矿床.矿段内共有八个(层)矿体,其主矿体为Ш 号矿体,矿段内矿体总体走向长约1230 m,沿倾向最大延伸780 m,最大厚度59m.
矿石中主要有用组分为铁,全矿段平均品位为24.93%.工业品位弱磁性铁矿石333 类资源量6105.06万吨,平均品位为24.93%;低品位弱磁性铁矿石333 类资源量4723.73 万吨,平均品位为17.12%.
矿区面积约3km2,磁测工作测网密度20m×10m.
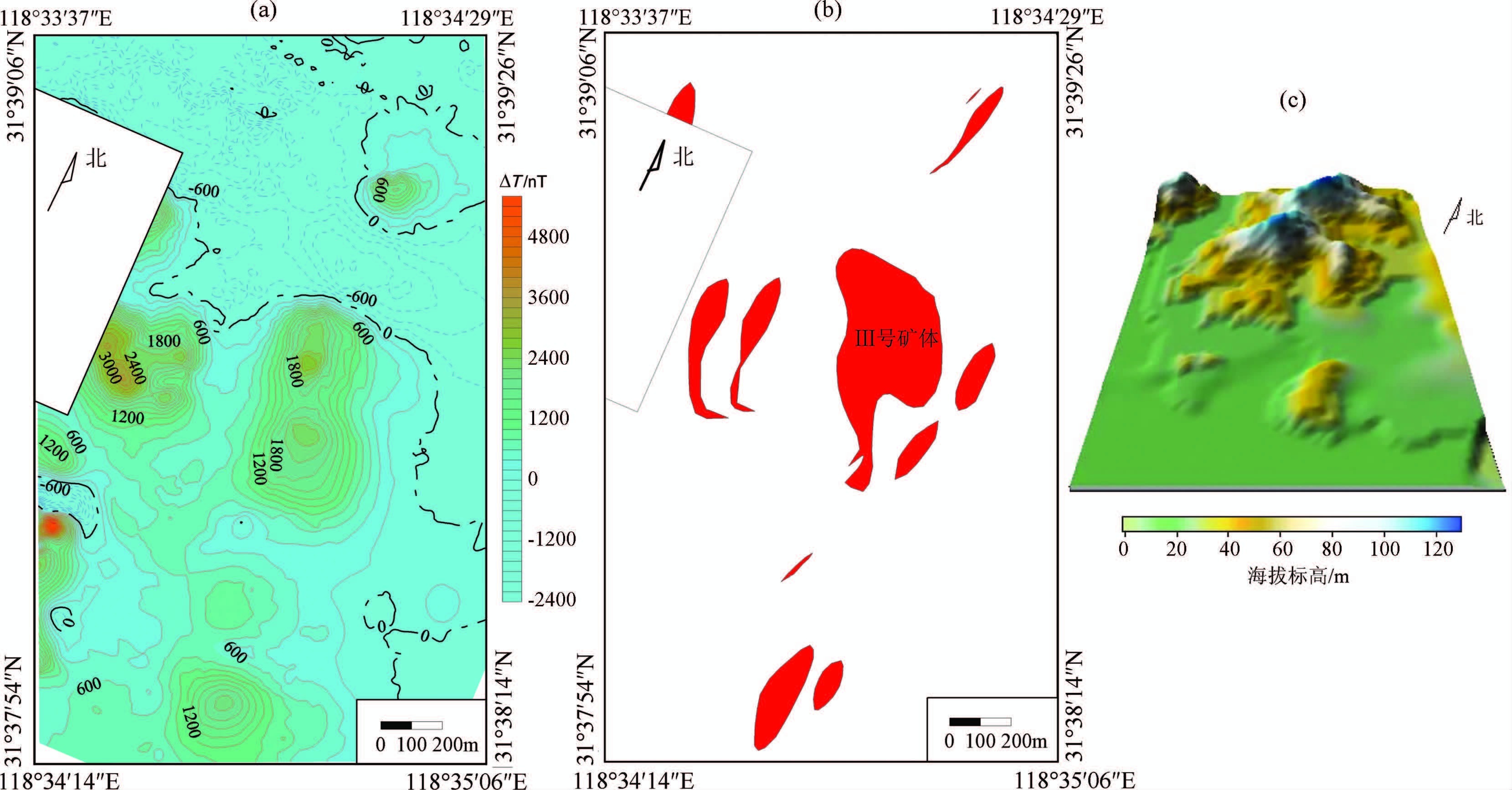
图 7a是矿区高精度地磁异常ΔT平面图.图 7b是矿区-200m 标高的矿体水平断面图.地磁异常分布特征主要反映了矿区主(大)矿体分布的基本轮廓.
|
图 7 (a)地磁异常AT平面图;(b) - 200 m标高矿体水平断面;(c)矿区地形高度图 Fig. 7 (a) Contour map of AT; (b) Ore bodies horizontal section map at -200 m; (c) Mining area topographic map |
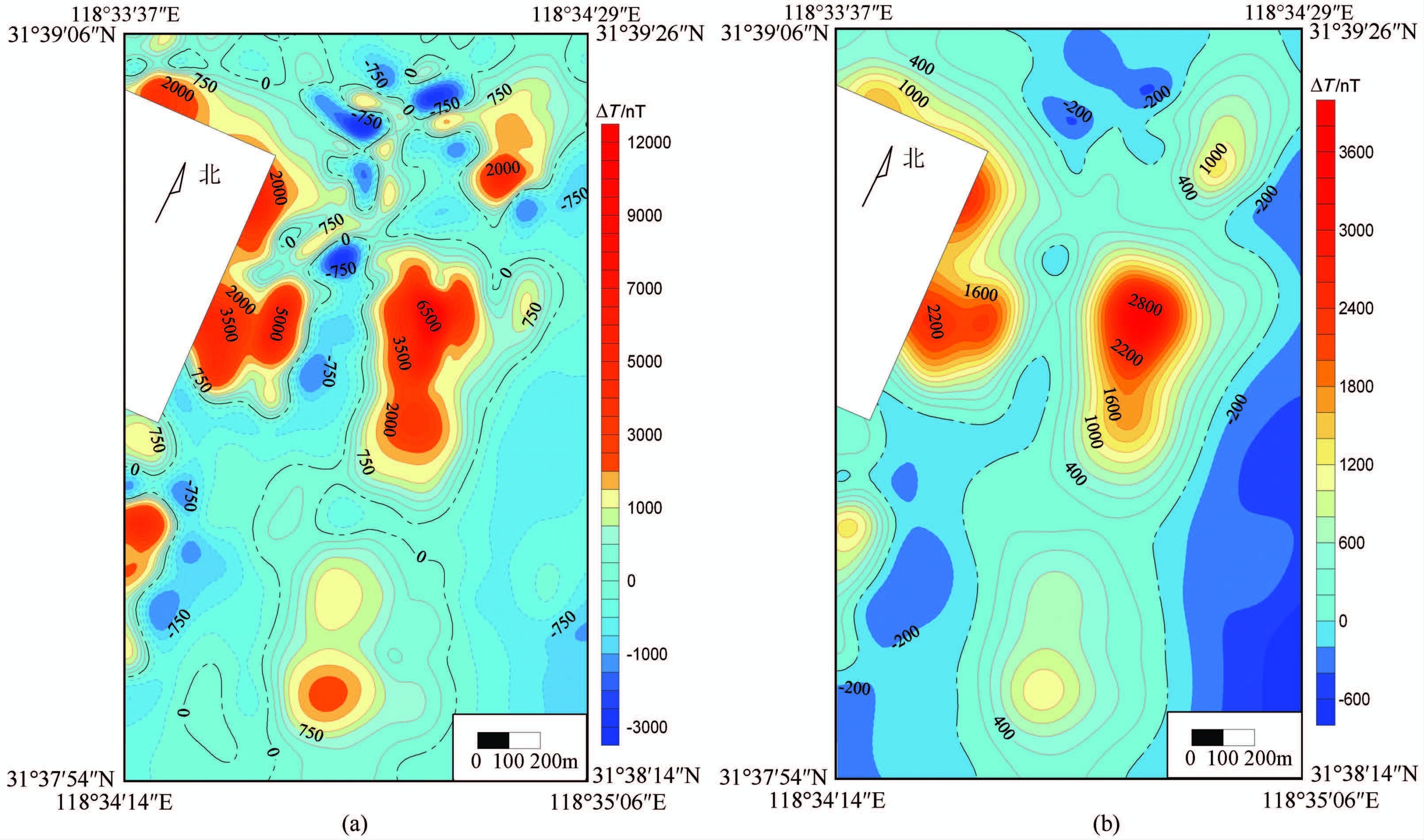
矿区地形起伏不大,最高点高程为130.57 m,最低点高程为12.22 m,地形起伏为118.35 m(图 7c).地磁异常大多分布于低山、丘岗地段.曲化平到两个平面,一是用本文方法将实测的地磁异常换算到矿区的最低点下方平面P(高程hp=0.38 m);用FFT 将曲化平P 面上的地磁异常向上延拓到矿区地面的中间平面C(高程hC=71.40 m);再将两平面的磁异常ΔT进行化极,处理结果分别见图 8a和图 8b.根据矿区详查地质勘探剖面,平面P 和C 均在矿体顶板面以上.
|
图 8 (a)曲化平P面上的地磁化极异常△T┴ ; (b)曲化平C面上的地磁化极异常△T┴ Fig. 8 (a) Contourmap of reduction △T┴ on the plane P; (b) Contourmap of reduction △T┴ on the plane C. |
由于平面C 高度大,埋深浅的矿体异常(矿区最北东端异常)走向更趋于矿体走向;埋藏深的矿体异常叠加在一起,异常范围扩大,小而深的矿体异常消失,异常强度或幅度总体降低.
平面P位置低,无论是埋藏深的还是埋深浅的矿体异常更加清晰,异常边界更接近矿体的实际分布情况,异常强度或幅度总体增大.
5 结论5.1 测曲面S 与其下方水平面P(场源以上)的相对高程(非负函数)、两面上的位场三者之间满足一个积分关系式.对S 到P 的曲化平换算,该关系是一个第一类Fredholm积分方程;对P到S的平化曲换算,是一个空间域的广义积分.
5.2 利用Fourier逆变换式把这个空间域的广义积分化为波数域的广义积分,用指数函数的Taylor展开把波数域的广义积分变为一含有Fourier变换的级数.
5.3 利用逐次逼近法及该级数进行第一类Fredholm 积分方程的迭代求解,实现S到P的曲化平换算.
5.4 这一曲化平方法可在空间域中也可在波数域中进行迭代计算.
5.5 这一曲化平换算精度高、速度快,能克服大的起伏观测面和大数据量的限制.
5.6 理论模型和实际资料都表明这一曲化平方法有好的应用效果.
本文的曲化平方法将可用于曲面位场转换.对曲面上的位场,用上述方法换算出下方平面上的位场,并进行转换,把转换后的位场代入式(26)中的un-1(x,y),由该式算得曲面上转换后的位场.
致谢感谢安徽省国土资源厅何义权教授级高工对本文工作的讨论和建议.
| [1] | Dampney C N G. The equivalent source technique. Geophysics , 1969, 34(1): 39-53. DOI:10.1190/1.1439996 |
| [2] | Emilia D A. Equivalent sources used as an analytic base for processing total magnetic field profiles. Geophysics , 1973, 38(2): 399-348. |
| [3] | Bhattacharyya B K, Chan K C. Reduction of magnetic and gravity data on an arbitrary surface acquired in a region of high topographic relief. Geophysics , 1977, 42(7): 1411-1430. DOI:10.1190/1.1440802 |
| [4] | Nakatsuka T. Reduction of magnetic anomalies to and from an arbitrary surface. Geophysical Exploration , 1981, 34(5): 6-13. |
| [5] | 杜维本. 三维重磁场"曲化平"的一个方法. 地球物理学报 , 1982, 25(1): 73–83. Du W B. A new method of reducing from an arbitrary surface into a plane for the three dimensional magnetic and gravity field. Chinese J. Geophys. (in Chinese) , 1982, 25(1): 73-83. |
| [6] | 陈钟琦. 等效偶层法位场曲面延拓的原理和计算方法. 地球物理学报 , 1983, 26(1): 70–79. Chen Z Q. Principle and computational method of curved surface's continuation of potential field for equivalently dipolar layer's method. Chinese J. Geophys. (in Chinese) , 1983, 26(1): 70-79. |
| [7] | Hansen R O, Miyazaki Y. Continuation of potential fields between arbitrary surfaces. Geophysics , 1984, 49(6): 787-795. DOI:10.1190/1.1441707 |
| [8] | 侯重初, 蔡宗熹, 刘奎俊. 从偶层位出发建立曲面上的位场转换解释系统. 地球物理学报 , 1985, 28(4): 410–418. Hou C C, Cai Z X, Liu K J. Interpretation system of potential field transformation on an uneven surface from the potential of double layer. Chinese J. Geophys. (in Chinese) , 1985, 28(4): 410-418. |
| [9] | 管志宁, 安玉林, 陈维雄. 曲线与曲面上磁场向上延拓和分量转换. 地球物理学报 , 1985, 28(4): 419–428. Guan Z N, An Y L, Chen W X. Upward continuation and transformation of component of magnetic field on an undulating observed profile or surface. Chinese J. Geophys. (in Chinese) , 1985, 28(4): 419-428. |
| [10] | Pilkington M, Urquhart W E S. Reduction of potential field data to a horizontal plane. Geophysics , 1990, 55(5): 549-555. DOI:10.1190/1.1442866 |
| [11] | Xia J H, Sprowl D R, Adkins-Heljeson D. Correction of topographic distortion in potential-field data: a fast and accurate approach. Geophysics , 1993, 58(4): 515-523. DOI:10.1190/1.1443434 |
| [12] | Ivan M. Upward continuation of potential fields from a polyhedral surface. Geophysical Prospecting , 1994, 42(5): 391-404. DOI:10.1111/gpr.1994.42.issue-5 |
| [13] | Meurers B, Pail R. Potential-field continuation between irregular surfaces-Remarks on the method by Xia et al. Geophysics , 1998, 63(1): 104-108. DOI:10.1190/1.1444301 |
| [14] | 刘天佑, 杨宇山, 李媛媛, 等. 大型积分方程降阶解法与重力资料曲面延拓. 地球物理学报 , 2007, 50(1): 290–296. Liu T Y, Yang Y S, Li Y Y, et al. The order-depression solution for large-scale integral equation and its application in the reduction of gravity data to a horizontal plane. Chinese J. Geophys. (in Chinese) , 2007, 50(1): 290-296. |
| [15] | 王万银, 刘金兰, 邱之云, 等. 频率域偶层位曲面位场处理和转换方法研究. 地球物理学报 , 2009, 52(10): 2652–2665. Wang W Y, Liu J L, Qiu Z Y, et al. The research of the frequency domain dipole layer method for the processing and transformation of potential field on curved surface. Chinese J. Geophys. (in Chinese) , 2009, 52(10): 2652-2665. |
| [16] | Li Y G, Oldenburg D W. Rapid construction of equivalent sources using wavelets. Geophysics , 2010, 75(3): L51-L59. DOI:10.1190/1.3378764 |
| [17] | Handerson R G, Cordell L. Reduction of unevenly spaced potential field data to a horizontal plane by means of finite harmonic series. Geophysics , 1971, 36(5): 856-866. DOI:10.1190/1.1440220 |
| [18] | Guspi F. Frequency-domain reduction of potential field measurements to a horizontal plane. Geoexploration , 1987, 24(2): 87-98. DOI:10.1016/0016-7142(87)90083-4 |
| [19] | 杨再朝. 应用迭代法进行位场的曲化平. 石油地球物理勘探 , 1989, 24(2): 200–207. Yang Z C. The datuming of gravitational potential fields with the use of iteration method. Oil Geophysical Prospecting (in Chinese) , 1989, 24(2): 200-207. |
| [20] | 侯俊胜, 管志宁, 张自力. 综合利用位场及其梯度的频率域曲化平方法. 物探化探计算技术 , 1995, 17(4): 60–66. Hou J S, Guan Z N, Zhang Z L. Method of frequency domain for reduction to aplane using the potential field and its gradients. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1995, 17(4): 60-66. |
| [21] | 刘金兰, 王万银, 于长春. 逐步逼近曲化平方法研究. 地球物理学报 , 2007, 50(5): 1551–1557. Liu J L, Wang W Y, Yu C C. Reduction of potential field data to a horizontal plane by a successive approximation procedure. Chinese J. Geophys. (in Chinese) , 2007, 50(5): 1551-1557. |
| [22] | 程振炎. 重磁场的有限元法曲化平. 物探与化探 , 1981, 5(3): 153–158. Cheng Z Y. Reduction of magnetic and gravity data to a horizontal plane by using finite element method. Geophysical & Geochemical Exploration (in Chinese) , 1981, 5(3): 153-158. |
| [23] | 徐世浙. 有限元法及其在物探中的应用简介. 物探与化探计算技术 , 1982, 4(2-3): 86–103. Xu S Z. Brief introduction on the finite element method and its application in geophysical exploration. Geophysical & Geochemical Exploration (in Chinese) , 1982, 4(2-3): 86-103. |
| [24] | 徐世浙, 楼云菊. 起伏地形二维位场上延与换算的边界单元法. 物探与化探计算技术 , 1987, 7(3): 195–199. Xu S Z, Lou Y J. Application of the boundary element method to the continuation upward and transformation of 2-D potential field on relief topography. Geophysical & Geochemical Exploration (in Chinese) , 1987, 7(3): 195-199. |
| [25] | 黄永亨. 边界元法计算曲化平精度的改进. 物探化探计算技术 , 1990, 12(3): 259–261. Huang Y H. A supplemental opinion for solving the problem of terrain correction by the boundary element method. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1990, 12(3): 259-261. |
| [26] | 姚长利, 黄卫宁, 管志宁. 综合利用位场及其垂直梯度的快速样条曲化平方法. 石油地球物理勘探 , 1997, 32(2): 229–236. Yao C L, Huang W N, Guan Z N. Fast splines conversion of curved-surface potential field and vertical gradient data into horizontal-plane data. Oil Geophysical Prospecting (in Chinese) , 1997, 32(2): 229-236. |
| [27] | Bott M H P. The use of rapid digital computing methods for direct gravity interpretation of sedimentary basins. Geophysical Journal of the Royal Astronomical Society , 1960, 3(1): 63-67. DOI:10.1111/gji.1960.3.issue-1 |
| [28] | 徐世浙, 余海龙. 位场曲化平的插值-迭代法. 地球物理学报 , 2007, 50(6): 1811–1815. Xu S Z, Yu H L. The interpolation-iteration method for potential field continuation from undulating surface to plane. Chinese J. Geophys. (in Chinese) , 2007, 50(6): 1811-1815. |
| [29] | 刘东甲, 洪天求, 贾志海, 等. 位场向下延拓的波数域迭代法及其收敛性. 地球物理学报 , 2009, 52(6): 1599–1605. Liu D J, Hong T Q, Jia Z H, et al. Wave number domain iteration method for downward continuation of potential fields and its convergence. Chinese J. Geophys. (in Chinese) , 2009, 52(6): 1599-1605. |
| [30] | 沈以淡. 积分方程(第二版). 北京: 北京理工大学出版社, 2002 : 127 -130. Shen Y D. The Integral Equation, Second Edition (in Chinese). Beijing: Beijing Institute of Technology Press, 2002 : 127 -130. |
| [31] | Asmar N H. Partial Differential Equations with Fourier Series and Boundary Value Problems, Second Edition. New Jersey: Prentice Hall, 2005 : 85 -93. |
| [32] | Parker R L. The rapid calculation of potential anomalies. Geophys. J. Roy. Astr. Soc. , 1973, 31(4): 447-455. DOI:10.1111/j.1365-246X.1973.tb06513.x |
 2012, Vol. 55
2012, Vol. 55


