对弹性波在弹性介质分界面上的反射和透射大多是利用平面波来讨论的[1].目前在石油和天然气勘探领域,主要是利用纵波,所以这里主要讨论纵波在弹性介质中的传播.地震AVO(振幅随偏移距变化)研究的理论基础主要是基于平面波理论的Zoeppritz方程,该方法简单又易于求解,但仅适合研究小角度的AVO 情况[2-6].
随着采集技术的提高和长排列的引入,地震反射达到和超过临界角的记录变得非常普遍.最近三参数(纵、横波速度、密度)反演也揭示要想得到精确的密度必须要有广角反射.当波传过速度差别不大的地层时,相位作为一个局部波形相对振幅而言能更好地反映这种差别,在近临界角或超临界角处会发生相移.
常规的AVO 反演主要是基于平面波分析和Zoeppritz方程的线性近似求解.这些近似是以较小的入射角、较少的参数变化为前提的.平面波反射系数是不适用于近临界角的[7-10].Zoppritz方程的线性近似公式在大角度处开始出现问题,在临界角处已不适用,即使精确的Zoppritz方程也是用平面波对现实世界的一个近似.研究结果表明,在近临界角处柱面波模拟结果相对于平面波模拟结果更接近于实际地震数据[11-13],在临界角处与平面波计算的振幅跳跃不同的是,柱面波与实际数据在临界角处振幅是渐变的.这就提出了球面波的AVO 响应是什么特征,受哪些因素影响? 本次研究借用Hasse(2006)[14]对球面波进行一个柱面近似,假定质点的位移平行于反射P波的射线方向,垂直于SV 波,研究了第Ⅰ类和第Ⅲ类AVO 的反射P 波反射系数变化趋势,通过数值模拟,分析了球面波的地震响应特征,并总结了球面波形成机理与平面波形成机理的差异,最后,用实际数据进行模拟对所得认识做了验证.
2 球面波AVO 理论基础AVO 研究的基本模型是完全弹性各向同性双层介质的单界面模型,上层介质纵波速度为α1,横波速度为β1,密度为ρ1,下层介质纵波速度为α2,横波速度为β2,密度为ρ2.对于平面波的反射、透射系数通过线性近似的Zoeppritz方程来计算[15-16].为求解球面波反射系数,取位移位函数φ 和ψ,则质点的位移U满足
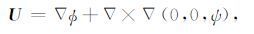
|
(1) |
点震源激发的入射球面P波位移位φinc 如(2)式

|
(2) |
这里R是距离震源的距离,满足R=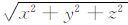
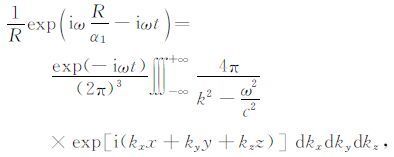
|
(3) |
其中kx、ky、kz分别为x、y、z方向的波数,k2 =kx2+ky2+kz2.式(3)右端被积函数为一平面简谐波,分母可视为一加权系数,积分为对平面简谐波的加权叠加.对式(3)进一步演算,得到球面波理论中的韦尔积分公式
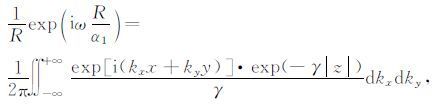
|
(4) |
式中,
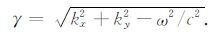
|
如果这个界面是水平的、各向同性的,或者至少是横向各向同性的,这时可假定柱对称,这时P-SV波与SH 波是解耦的,问题简化到二维空间,韦尔积分可简化为索墨菲尔德积分,表达式φinc 是相对于柱面的,可以通过所有同方位的面波的积分来表示.定义
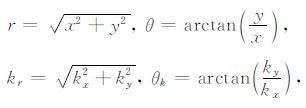
|
则
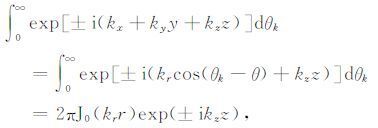
|
这里J0(krr)为零阶贝塞尔函数.
根据Aki和Richards(1980)[17]描述,这些柱面波出现在索墨菲尔德积分中,可写为
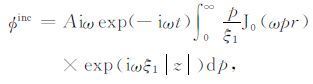
|
(5) |
这里已从波数转到慢度,kr/ω 是水平慢度p,kz/ω是垂直慢度ξ (P波)或者η (SV 波),常数A代表入射波的振幅.
从对称的角度考虑,反射和透射波的位函数也可以按照柱面波来表示:
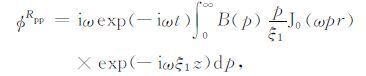
|
(6) |
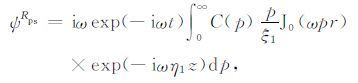
|
(7) |
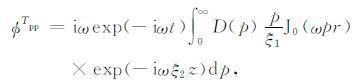
|
(8) |

|
(9) |
根据界面处位移与应力边界条件方程,可生成求解B(p)、C(p)、D(p)、E(p)的方程组.在柱坐标系下求解方程(1),可得出非零位移分量ur,uz.在界面处应力分量必须是连续的,

|
(10) |

|
(11) |
这里λ 和μ 是拉梅常数.首先对φinc,φRpp,ψRps 运算,来得到ur(1),uz(1),τzr(1)和τzz(1),然后类似地求解下一层.反射和透射参数与界面位置无关,因此通常定义界面在z=0处.设ur(1)(z=0)=ur(2)(z=0),其它位移和应力分量也类似.这四个方程的每一个都可以写成单个的积分,对于每一个p值,被积函数都应为0.这就形成了四个关于A、B、C、D和E的线性方程.
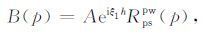
|
(12) |
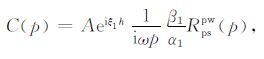
|
(13) |
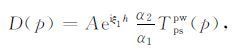
|
(14) |
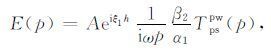
|
(15) |
这里αi,βi分别是第i层的P波速度和S波速度.把这些表达式代入方程(1)到(6),可得出反射波位移位的显式表达式,可以看出它们是类似平面波反射系数的积分.
反射P波的位函数通过(16)式计算,
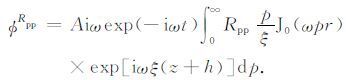
|
(16) |
根据位移方程(1)和方程(16)给定的反射P 波位函数可进一步计算出质点的位移U,再根据由Zoeppritz方程计算的质点位移反射系数可计算出弹性界面的反射系数[14, 18],计算过程中,以最大质点位移位单位反射系数进行标准化,来得到反射PP波反射系数.方程(16)给出的是某一时间的单频响应,在计算完所有目的区间的频率之后,通过傅里叶逆变换,即可以求出时间域的道集[12],其相应的正交道可通过希尔伯特变换来求取.这样,根据这两个道集即可求出球面波的反射系数与相位.
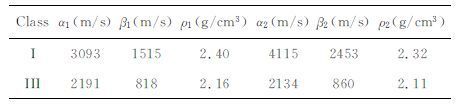
3 模型分析我们以一个两层气砂油藏模型[19]为研究对象.界面深度分别为500m、1000m、1500m、2500m,第Ⅰ类AVO 介质及第Ⅲ类AVO 介质参数如表 1所示.
|
|
表 1 两层模型的弹性参数 Table 1 Elastic parameters of the two-layer model |
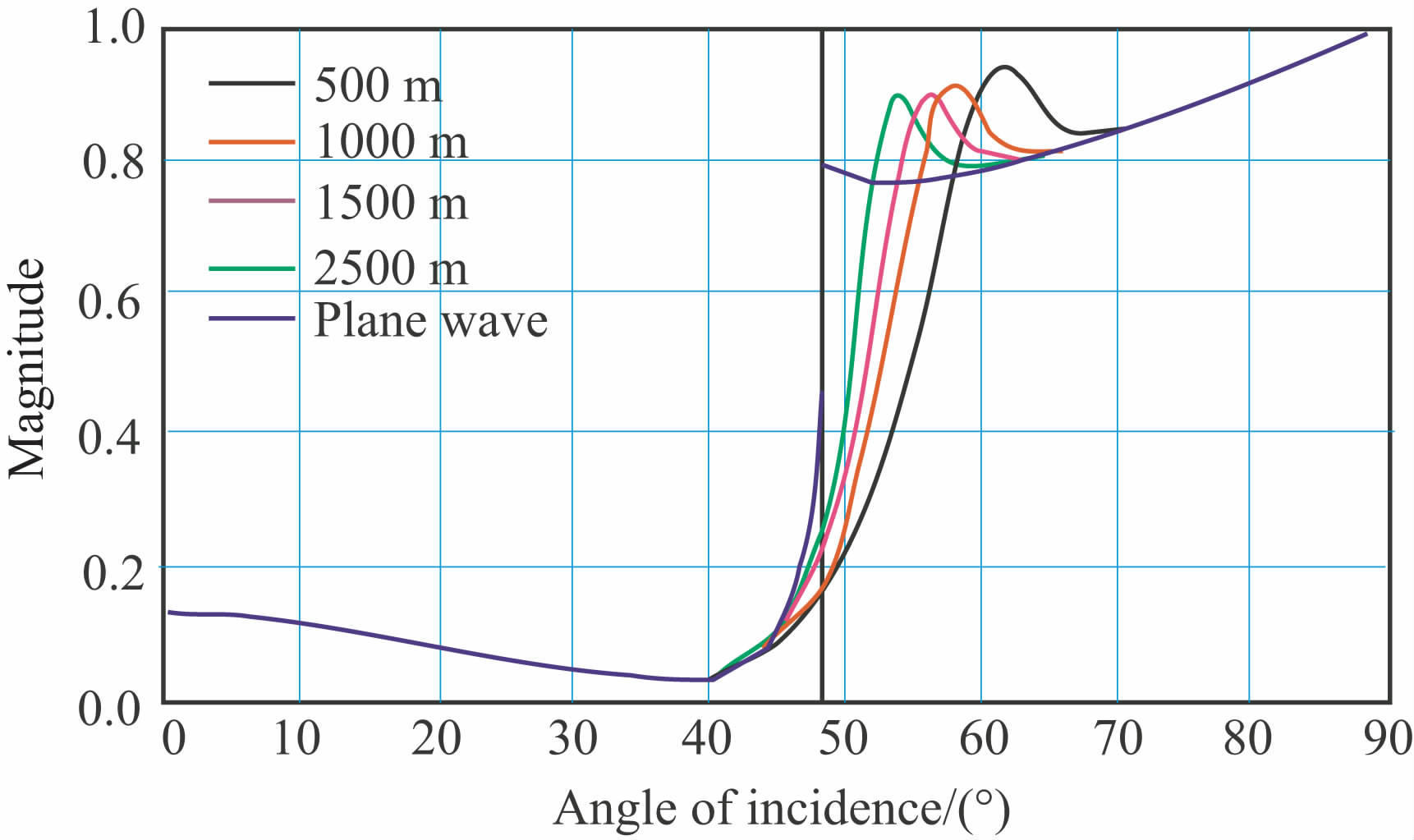
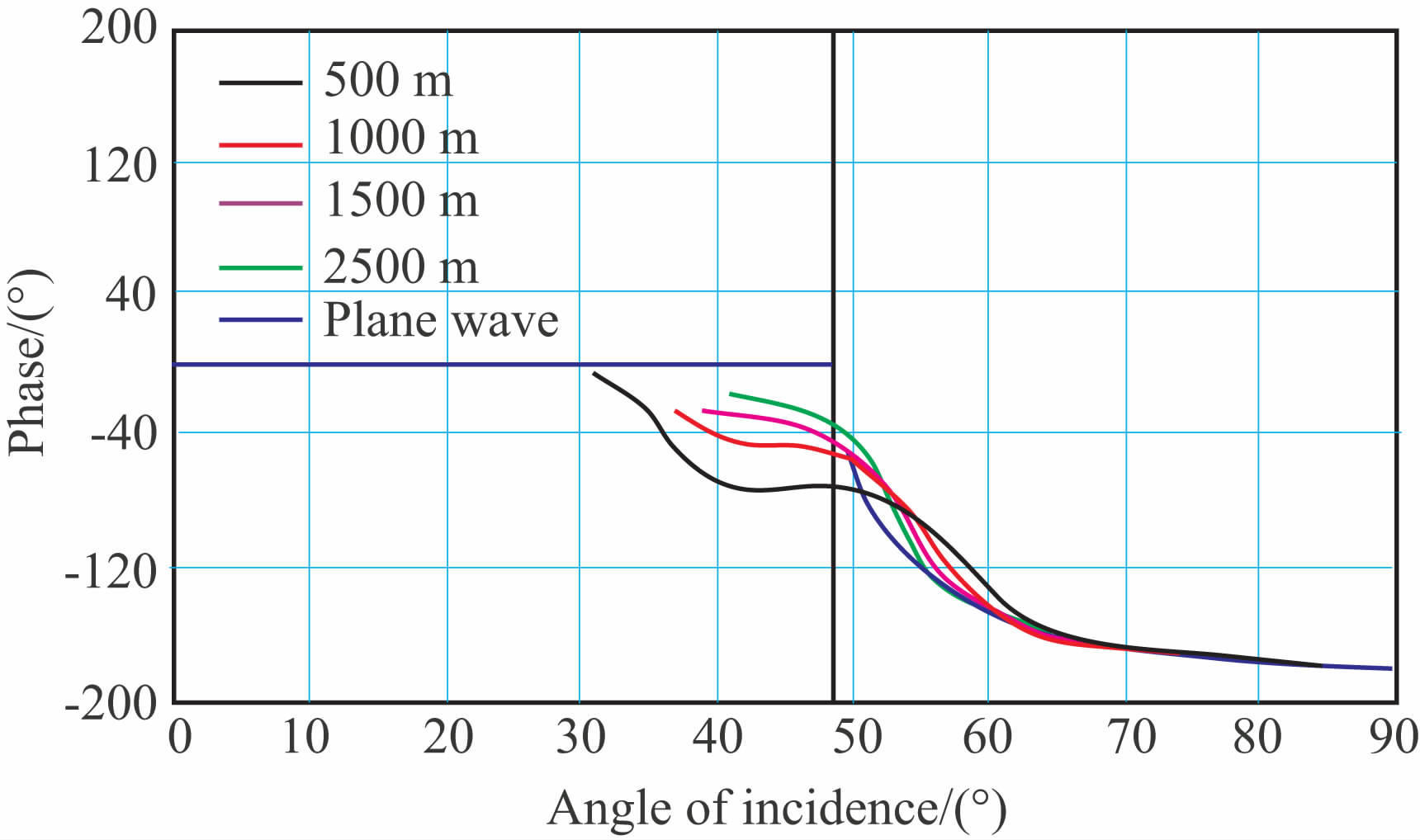
图 1为第Ⅰ类AVO 介质不同深度时基于球面波的P波AVO 变化曲线与基于平面波的Zoeppritz方程计算的P波AVO 变化曲线的对比图,图 2 为相应的相位变化曲线.从图中可以看出,基于平面波的Zoeppritz方程计算的反射系数(蓝色),在临界角处产生一个突变,相位在小于临界角时为零相位,超临界角后,逐渐变为负相位;而球面波AVO 反射系数在临界角附近变化相对平缓,随着界面深度逐渐增加,球面波AVO 曲线也逐渐接近平面波AVO 趋势,球面波的相位也有同样趋势,随着界面深度的变化,相位逐渐接近于平面波相位曲线.这一现象主要是由于在临界角处首波出现引起的变化,而平面波只是球面波高频近似,它的菲涅耳带收缩为一个点,临界角处反射系数的梯度相对较高.球面波AVO不仅是入射角的函数,而且与界面深度、波的传播距离有一定关系,由于实际地震震源激发的是球面波,因此,对于浅层大偏移距的AVO 现象球面波AVO的描述比平面波AVO 的描述更精确.
|
图 1 第Ⅰ类球面波AVO和平面波AVO(反射P波)变化曲线 Fig. 1 Variation curves of spherical wave and plane wave AVO-class Ⅰ (PP reflection) |
|
图 2 第Ⅰ类球面波和平面波相位变化曲线 Fig. 2 Variation curves of spherical wave and plane wave phase-class Ⅰ (PP reflection) |
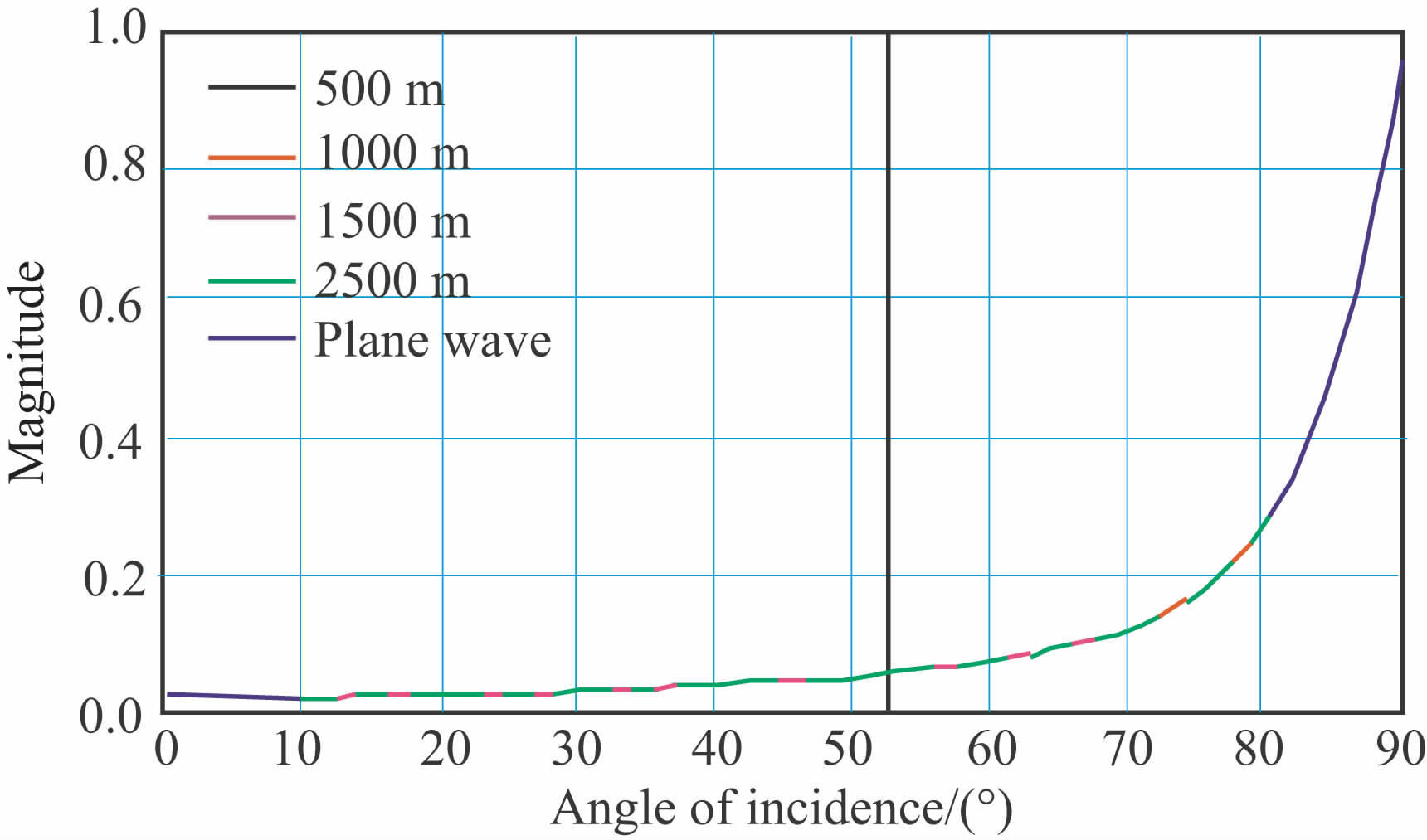
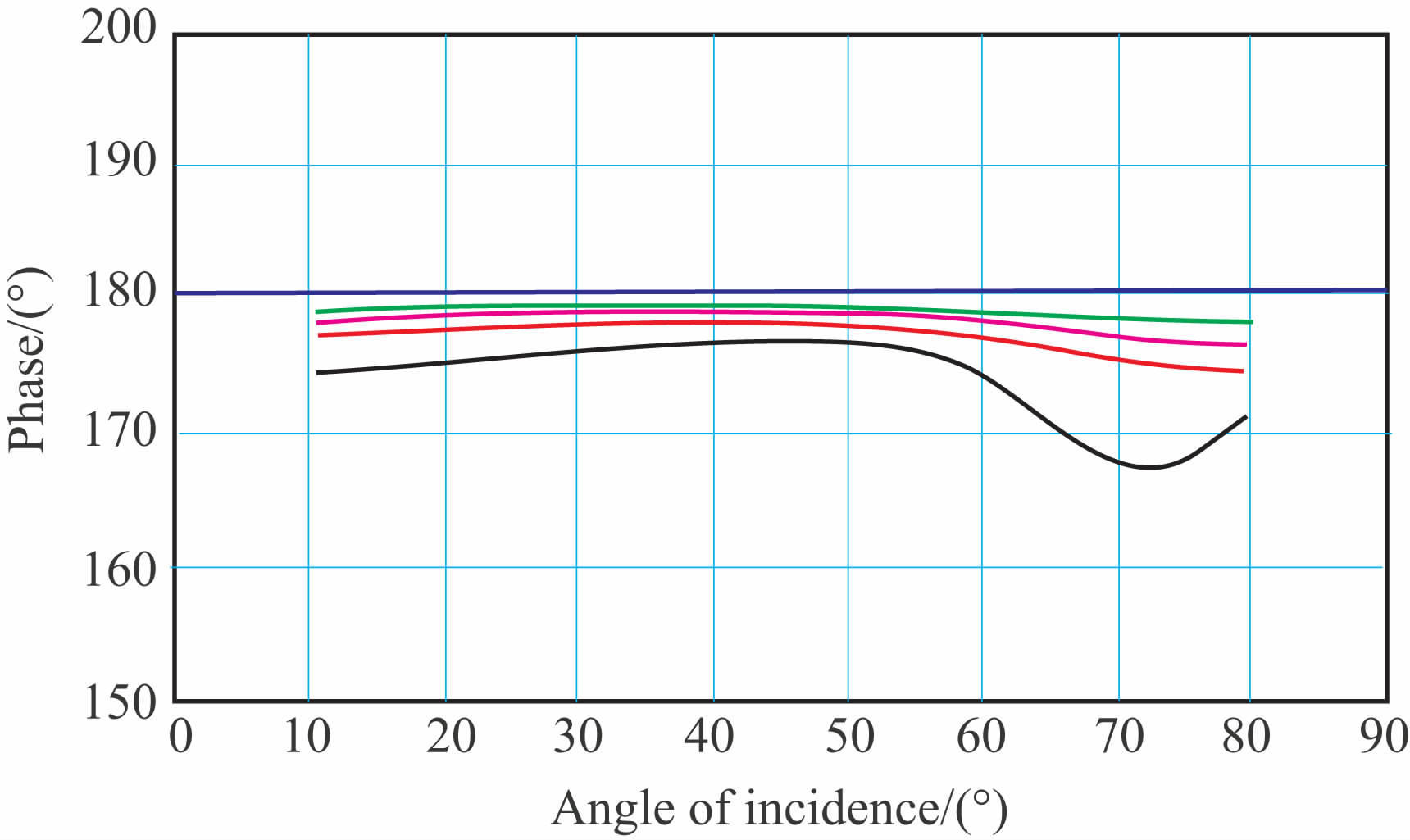
图 3为第Ⅲ类AVO 介质不同深度时球面波AVO 变化曲线与基于平面波的Zoeppritz方程的AVO 曲线的对比图,图 4 为相应的相位变化曲线.从图中可以看出,基于平面波的Zoeppritz方程计算的反射系数与球面波AVO 反射系数是一致的,这是由于上层介质P 波速度高于下层介质的P 波速度,不存在临界角的问题,为增加对比的合理性,消除了球面扩散引起的损失,对于第Ⅲ类AVO 而言,反射系数不存在深度的影响.但是,由于球面波与平面波传播机理的差异,在相位上仍是有一些轻微的差异,但随着界面深度的增加,相同入射角时球面波的相位逐渐接近于基于平面反射的相位.
|
图 3 第Ⅲ类球面波AVO和平面波 AVO(反射P波)变化曲线 Fig. 3 Variation curves of spherical wave and plane wave AVO-class Ⅲ (PP reflection) |
|
图 4 第Ⅲ类球面波和平面波相位变化曲线 Fig. 4 Variation curves of spherical wave and plane wave phase-class Ⅲ (PP reflection) |
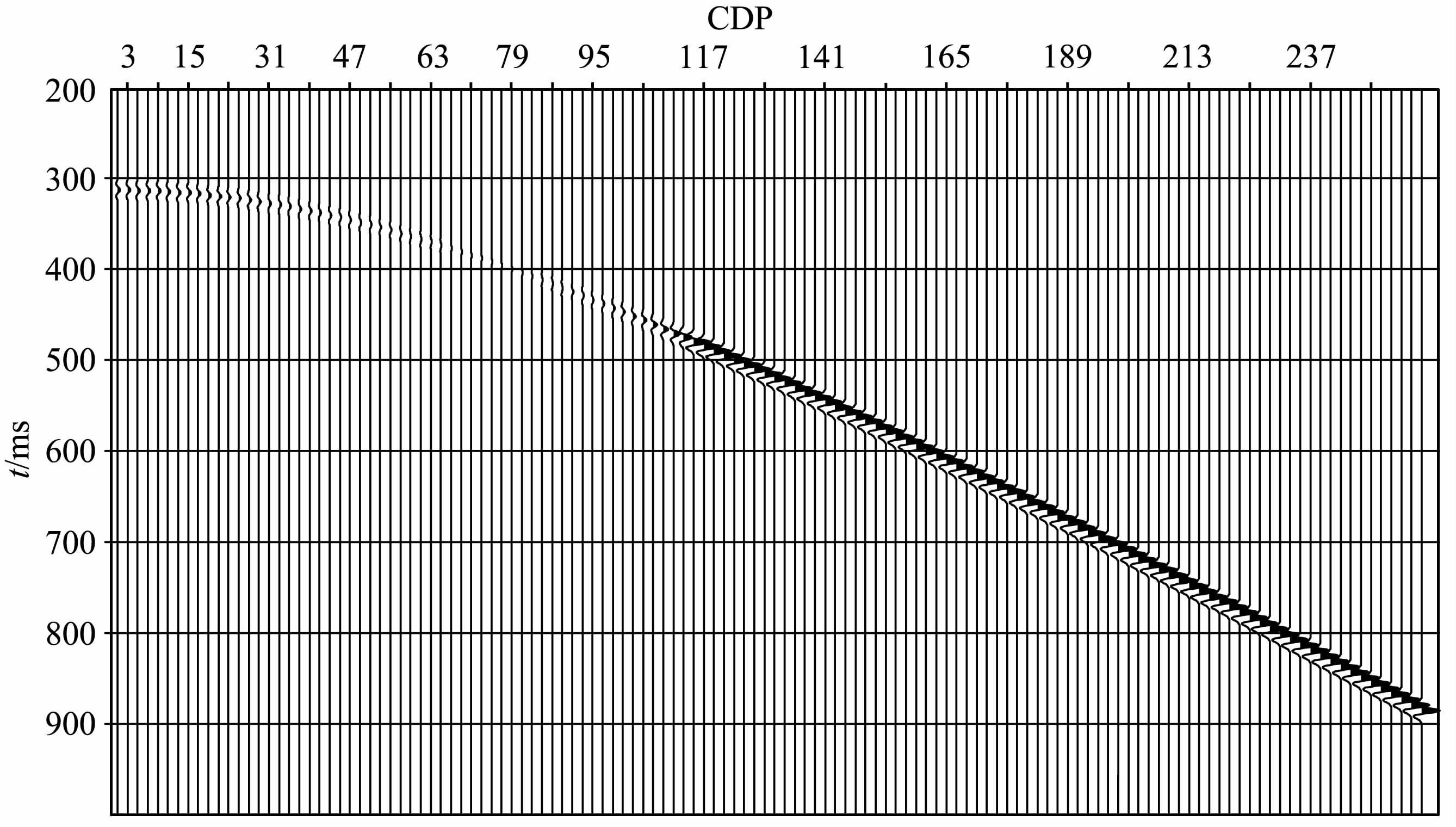
我们通过8阶精度交错网格差分算法模拟P波点震源在介质中的传播[20-21],模型参数如表 1所示,界面深度在500 m 处.第Ⅰ类AVO 介质模拟的P波反射记录如图 6所示,由于排列长度的限制,最大入射角为71°.采用同样的观测系统和模型参数,用基于平面波理论Zoeppritz方程计算射线与Ricker子波进行褶积运算,炮集记录如图 5所示.
|
图 5 界面在500 m处时第Ⅰ类AVO褶积结果 Fig. 5 Convolution results of AVO-class Ⅰ with interface at 500 m |
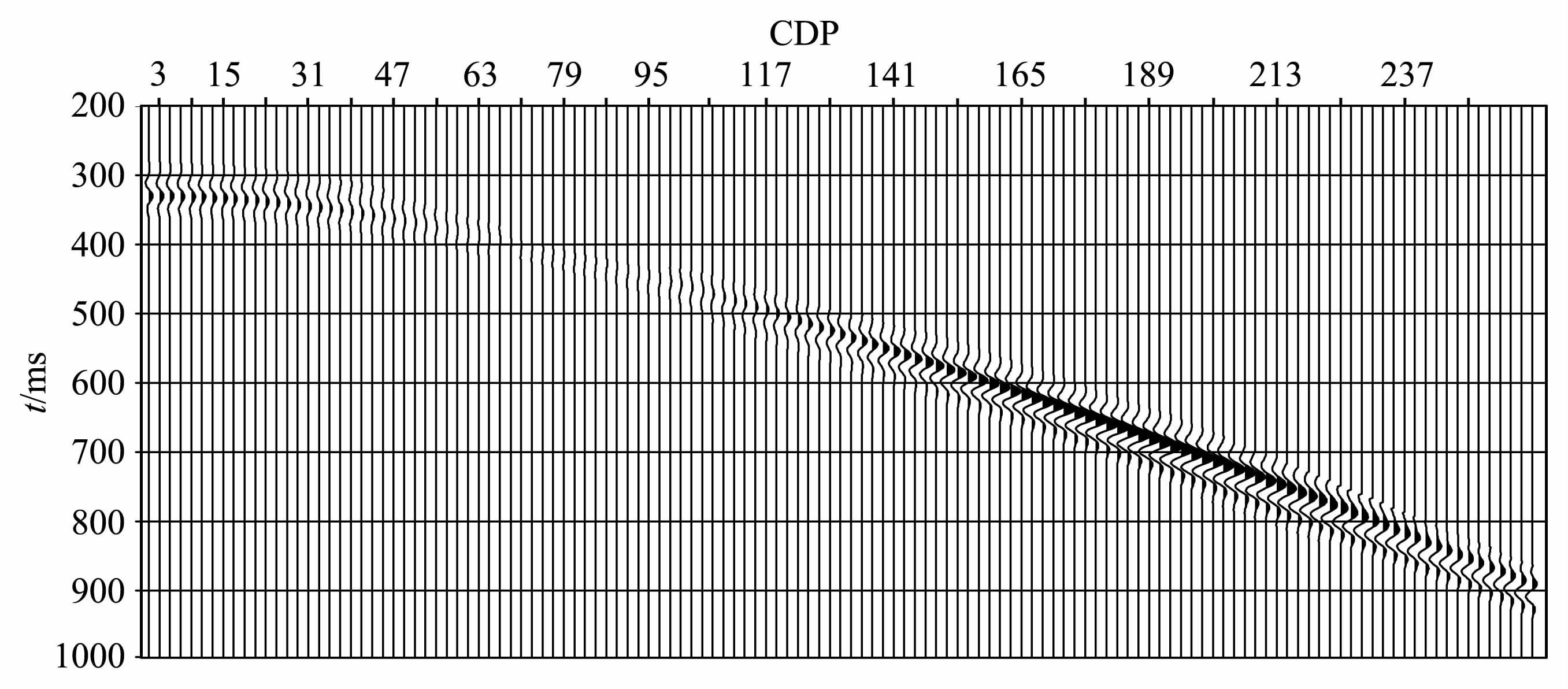
|
图 6 界面在500 m处时第Ⅰ类AVO模拟结果 Fig. 6 Modeling result of AVO-class Ⅰ with interface at 500 m |
按基于平面波的Zoeppritz方程计算,如图 1中的振幅曲线(蓝色)及图 2中相位曲线(蓝色),振幅在小于临界角(49°)时随入射角增大呈减小趋势,临界角处产生突变,相位在第114道处发生相移,振幅在第84道处开始增大,在第114道处振幅突变,而后呈先减小后增大趋势,模拟结果如图 5,与分析是吻合的,差异只是由于模拟角度的限制,在大偏移距处未出现振幅减小后再明显增大的情形.而基于球面波的模拟结果如图 6所示,可以看出,反射P波相位是在第58道处产生的相移,第110道处相位已达到-80°,振幅在第84道处开始增大,在188道处达到一个局部极值,然后逐渐减小,与图 1及图 2中的黑色曲线描述的趋势一致,只是由于排列长度的限制,图 6中最大入射角为71°,而未再出现图 1中所示那样振幅又一次增大的过程.两种模拟结果对比可以发现,在临界角处,无论振幅变化还是相位变化都存在不小的差异.这主要是由于模型参数中下层介质P波速度高于上层介质P 波速度,使得临界角存在,从而引起折射波的产生,在超临界角处折射波从反射波分离出来.另一方面,平面P波的波前垂直于波的传播方向,而球面波的波前是点源为轴的同心球面.球面波的反射主要来自第一菲涅耳带内的相长干涉,也就是说球面反射包括一些相邻慢度的积分效应.而平面波只是一个高频近似,因此它的菲涅耳带收缩到一点.在临界角处反射系数的梯度相对较高,这正是为什么平面波不能在临界角附近应用的理论解释.实际地震波场是球面波的,平面波只是对球面波的一个近似,因此球面波描述AVO现象更加合理,图 6 基于球面波理论的计算结果也更加接近实际地震记录.
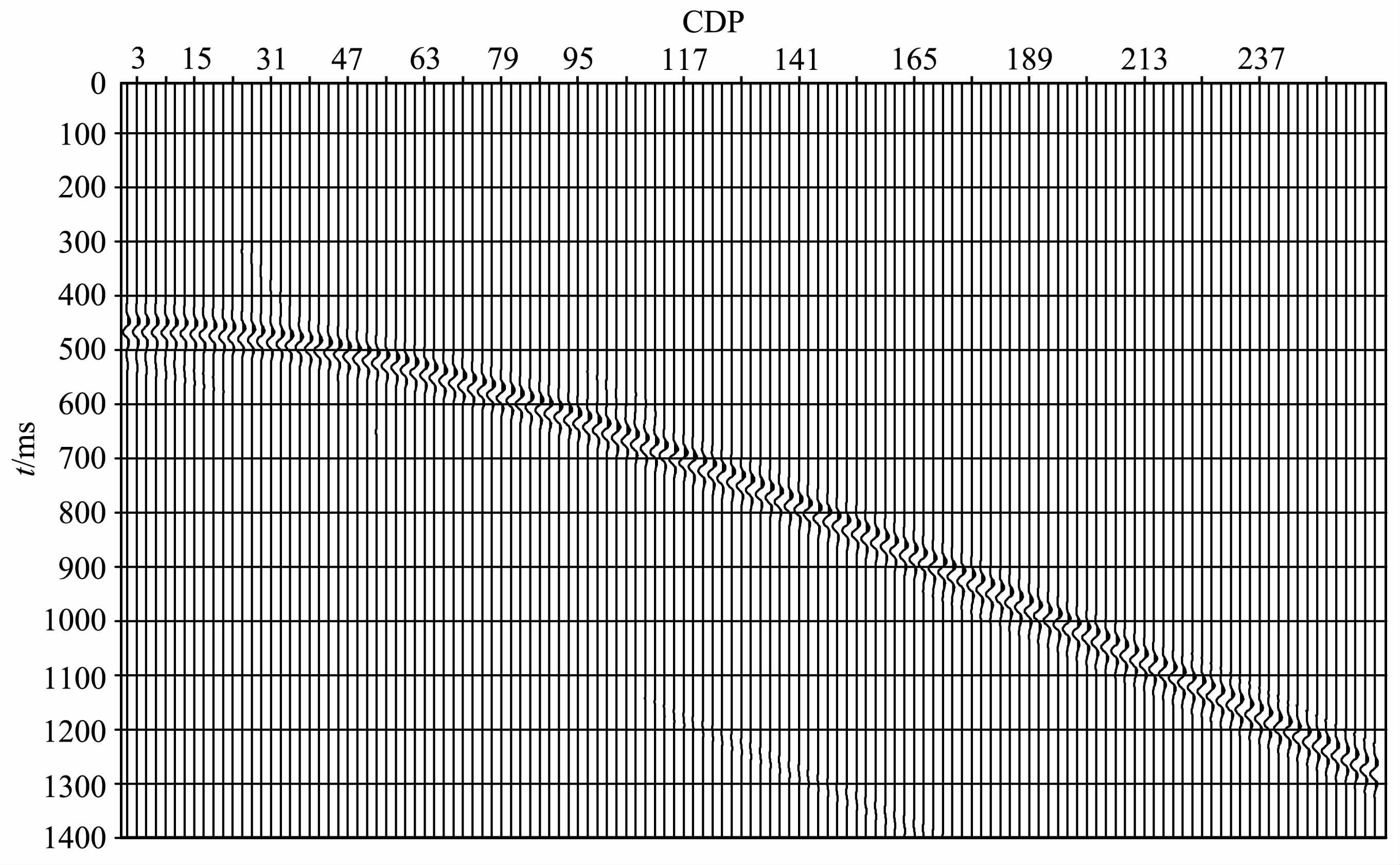
图 7为第Ⅲ类AVO 球面波反射P 的模拟结果,图中可以看出,振幅随偏移距的增加缓慢增加,而未产生如图 6中的急剧变化,这是由于,第一,由于排列长度的限制,最大入射角为71°,从图 3可以看出,振幅还未达到增大的角度;第二,该模型参数中P波速度与模型Ⅰ相反,不存在临界角,不会产生折射波.但是,相位还是有些微弱的变化,在120道处比较接近-180°,随角度的增加相位有轻微的变化,而不是图 4中蓝色Zoeppritz方程描述的那样一直是-180°相位,这个相位的变化是由球面波与平面波传播机理不同引起的.对于第Ⅲ类AVO 模型,基于平面波的振幅与基于球面波的振幅是无差异的,相位相差也非常小,褶积结果也与图 7是基本类似的.
|
图 7 界面在500 m处时第Ⅲ类AVO模拟结果 Fig. 7 Modeling result of AVO-class Ⅲ with interface at 500 m |
也就是说,球面波和平面波传播机理的不同,在存在临界角的数据上会引起这种振幅和相位的明显差异,对于第Ⅱ类、第Ⅳ 类AVO 是否会出现球面波与平面波模拟结果的不同与模型界面处临界角的存在与否直接相关.
4 实际资料分析实际地震勘探中,也常常遇到不同类型的气藏,尤其是对于第Ⅰ类AVO 的数据,在叠前反演中很难得到准确的速度、密度等参数,原因又解释不清楚.这里选用新疆维吾尔自治区鄯善县境内吐哈油田的一口探井数据为例进行分析,实际气层埋深3800m,界面顶底弹性参数如表 2所示.
|
|
表 2 实际气层界面两侧弹性参数 Table 2 Elastic parameters of actual gas interface |
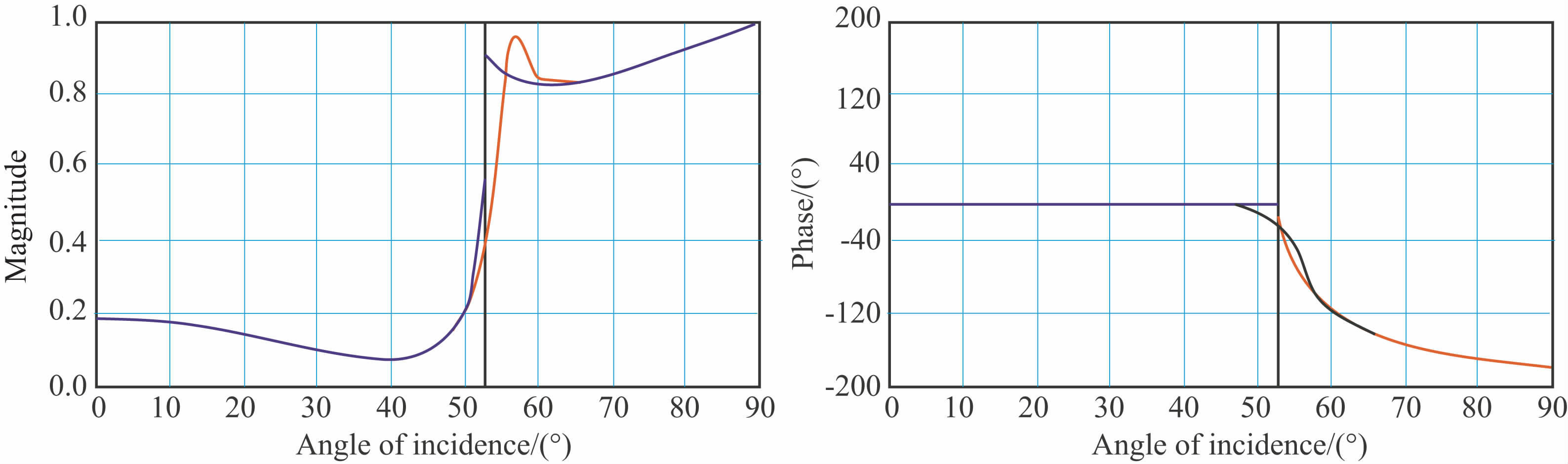
针对表 2中的数据,首先用基于平面波理论的Zeoppritz方程和基于球面波理论的方程分别计算其振幅和相位情况,如图 8 所示.从计算结果中可知,振幅极小值出现在6637m 偏移距处,模型临界角为52.7°,对应的偏移距为9976m,基于平面波的振幅局部极大值刚好在临界角处出现;而基于球面波理论的振幅极大值出现在入射角57.0°,偏移距为11700m 处.对于相位的变化,球面波理论的计算结果与平面波理论计算结果差别相对较小,差别在于球面波理论计算结果相位是在临界角前就开始逐渐变化,平面波理论的计算结果是在临界角处急剧变化.
|
图 8 球面波AVO绝对反射系数及相位与平面波AVO对比 Fig. 8 Comparison of PP absolute reflection coefficient and phase between spherical wave and plane wave |
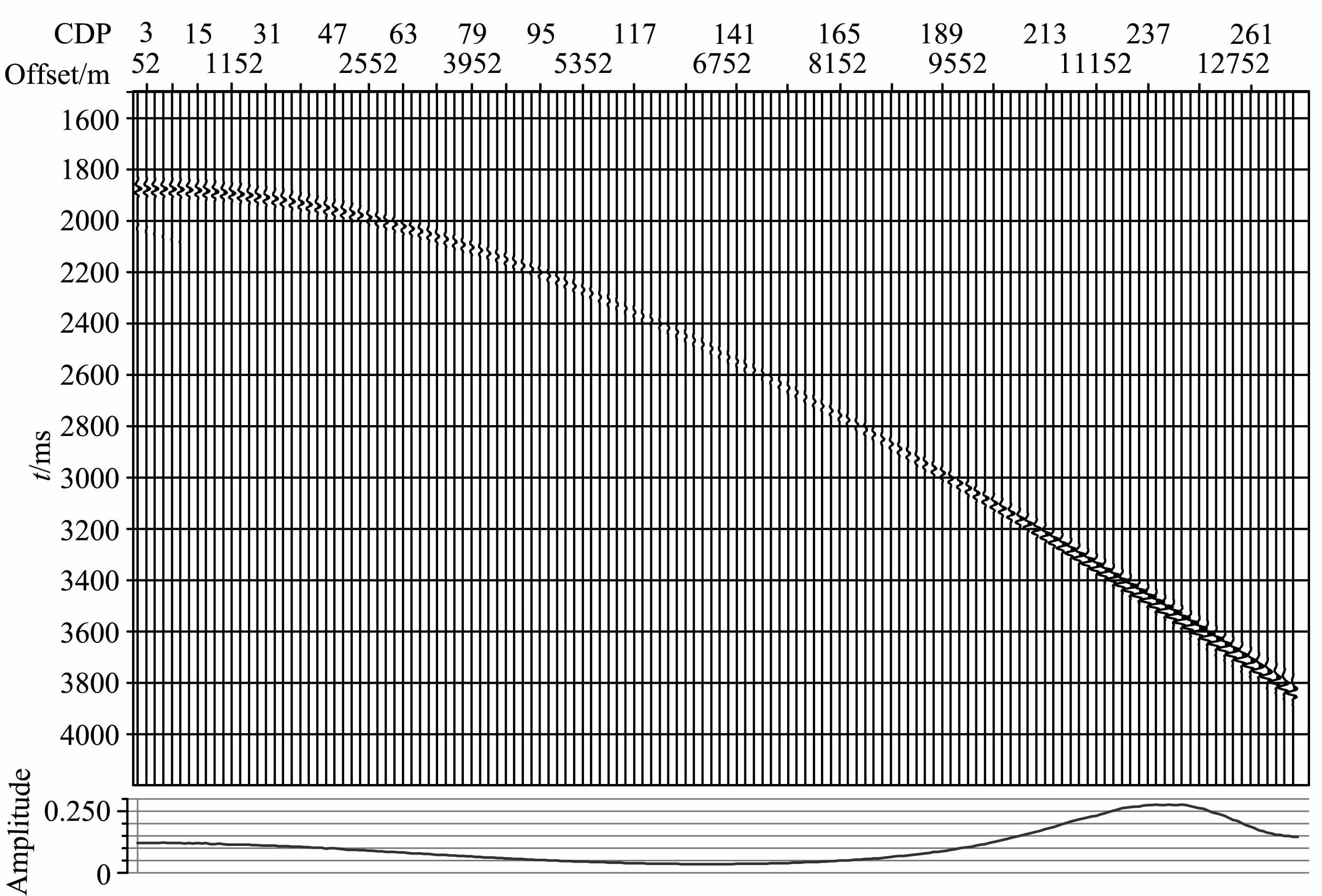
同样,采用8阶精度交错网格差分算法模拟球面P波点震源在介质中的传播,模型参数如表 2所示,界面深度在3800m 处,排列长度为13500m,模拟结果如图 9所示.针对模拟结果拾取振幅极大值,曲线如图 9下所示,可以明显地看出,振幅极小值出现在偏移距为6377 m 处,极大值出现在偏移距为11700m 处,与实际地震数据吻合较好,因此对于第Ⅰ类AVO 情形,在大偏移距处,基于平面波理论的Zoeppritz计算结果通常是有误差的.实际地震资料处理时,往往大偏移距数据会出现波形畸变[22],通常会作为无效信息或者因影响叠加效果而切除掉,因此有时地下实际存在气藏,而叠加剖面上没有振幅异常的显示,另一方面,常规的叠前反演是基于平面波理论Zoeppritz方程近似式的,这些近似式对于大偏移距或者说大入射角的地震数据本身就是不很精确的,这两方面的原因共同造成了对第Ⅰ类AVO现象的数据叠前反演结果不是很理想.
|
图 9 球面波模拟炮集记录及振幅变化曲线 Fig. 9 Gather record and amplitude curve of spherical wave modeling |
通过对球面波AVO 与平面波AVO 的对比分析,及对模型数据和实际数据模拟结果的定量对比分析,结果表明,基于平面波理论的反射系数只与弹性界面两侧的纵、横波速度及密度有关,而基于球面波理论的反射系数还与界面深度有关,在深度变大时,球面波计算结果接近于平面波.对于浅层的第Ⅰ类AVO 现象,基于平面波的Zoeppritz方程计算的振幅及相位在近临界角和超临界角处误差是比较大的.
对于类似第Ⅰ类AVO 的参数模型,由于临界角的存在,使得折射波出现,这是引起平面波AVO与球面波AVO 差别的主要原因,因此,对于大偏移距的道集,基于球面的AVO 分析解释更加合理.对于第Ⅲ类AVO 的参数模型,从计算结果和模拟结果均可以看出,反射系数基本是一致的,但由于形成机理的差异,使得相位上还是有一定差异.
致谢本文在完成过程中得到了中国石油大学(华东)孙成禹教授的悉心帮助和指导,在此表示衷心感谢,同时对李智勇工程师在论文图件绘制中给予的帮助表示衷心感谢.
| [1] | 徐基祥, 吴律. 弹性波理论研究——关于球面波首项(I). 石油物探 , 1997, 35(1): 1–12. Xu J X, Wu L. The theoretical study of the elastic wave-on the first term of spherical wave. Geophysical Prospecting for Petroleum (in Chinese) , 1997, 35(1): 1-12. |
| [2] | Aki K, Richards P G. Quantitative Seismology-Theory and Method . Beijing: Petroleum Industry Press, 1987 . |
| [3] | 孙成禹. 地震波理论与方法. 东营: 中国石油大学出版社, 2007 : 31 -58. Sun C Y. Theory and Methods of Seismic Waves (in Chinese). Dongying: China University of Petroleum Press, 2007 : 31 -58. |
| [4] | 孙鹏远, 孙建国, 卢秀丽. P-SV波AVO方法研究进展. 地球物理学进展 , 2003, 18(4): 602–607. Sun P Y, Sun J G, Lu X L. Progress in research on the method of P-SV wave AVO. Progress in Geophysics (in Chinese) , 2003, 18(4): 602-607. |
| [5] | 陆基孟. 地震勘探原理. 东营: 石油大学出版社, 1996 : 155 -186. Lu J M. Principle of Seismic Exploration (in Chinese). Dongying: China University of Petroleum Press, 1996 : 155 -186. |
| [6] | 阴可, 杨慧珠. 各向异性介质中的AVO. 地球物理学报 , 1998, 41(3): 382–391. Yin K, Yang H Z. AVO in anisotropic media. Chinese J. Geophys. (in Chinese) , 1998, 41(3): 382-391. |
| [7] | Ursenbach C P, Haase A B. Efficient spherical-wave AVO modeling. The Leading Edge , 2007, 26(12): 1584-1589. DOI:10.1190/1.2821946 |
| [8] | 周竹生, 刘喜亮, 熊孝雨. 弹性介质中瑞雷面波有限差分法正演模拟. 地球物理学报 , 2007, 50(2): 567–573. Zhou Z S, Liu X L, Xiong X Y. Finite-difference modelling of Rayleigh surface wave in elastic media. Chinese J. Geophys. (in Chinese) , 2007, 50(2): 567-573. |
| [9] | 何涛, 史謌, 邹长春, 等. 砂岩储层AVO特征影响因素的不确定性研究. 地球物理学报 , 2011, 54(6): 1584–1591. He T, Shi G, Zou C C, et al. The uncertainty analysis of the key factors that affect the AVO attributes in sandstone reservoir. Chinese J. Geophys. (in Chinese) , 2011, 54(6): 1584-1591. |
| [10] | 宋建国, 王艳香, 乔玉雷, 等. AVO技术进展. 地球物理学进展 , 2008, 23(2): 508–514. Song J G, Wang Y X, Qiao Y L, et al. Advances in AVO technique. Progress in Geophysics (in Chinese) , 2008, 23(2): 508-514. |
| [11] | Haase A B. Spherical AVO modeling of converted waves in isotropic media. 74th Annual International Meeting, SEG, Expanded Abstracts , 2004, 23: 263. |
| [12] | 黄饶, 陈小宏, 李景叶. 基于球面波的地震记录合成方法及AVO分析. 中国石油大学学报(自然科学版) , 2009, 33(3): 49–52. Huang R, Chen X H, Li J Y. Seismogram synthesis method based on spherical wave and AVO analysis. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese) , 2009, 33(3): 49-52. |
| [13] | Winterstein D F, Hanten J B. Supercritical reflections observed in P-wave and S-wave data. Geophysics , 1985, 50(2): 185-195. DOI:10.1190/1.1441908 |
| [14] | Hasse A B, Ursenbach C P. Spherical-wave AVO modeling in elastic and anelastic media. CREWES Research Report , 2006, 18: 1-18. |
| [15] | 印兴耀, 赵剑, 张繁昌, 等. 球面波叠前地震记录的合成方法. 中国石油大学学报 (自然科学版) , 2006, 30(1): 26–32. Yin X Y, Zhao J, Zhang F C, et al. Method of generating prestack synthetic seismograms of spherical wave. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese) , 2006, 30(1): 26-32. |
| [16] | 孙成禹. 球面波分解理论及其倾斜叠加方法的实现. 石油地球物理勘探 , 2000, 35(6): 723–729. Sun C Y. Theory of spherical wave decomposition and realization of dip stack. Oil Geophysical Prospecting (in Chinese) , 2000, 35(6): 723-729. |
| [17] | Aki K, Richards P G. Quantitative seismology-theory and method: Volume 1. San Francisco: W. H. Freeman and Company. 1980 . |
| [18] | Hasse A B, Geo-X Systems L T D. Plane wave, spherical waves and angle-dependent P-wave reflectivity in elastic VTI-models. 72th Annual International Meeting, SEG, Expanded Abstracts, 2002. |
| [19] | 孙夕平, 赵良武. 地震振幅解释. 北京: 石油工业出版社, 2002 : 70 -74. Sun X P, Zhao L W. Quantitative Seismic Interpretation (in Chinese). Beijing: Petroleum Industry Press, 2002 : 70 -74. |
| [20] | 李胜军, 王福焕, 雍学善, 等. 塔中地区碳酸盐岩溶洞地震响应机理及影响因素. 新疆石油地质 , 2011, 32(3): 305–307. Li S J, Wang F H, Yong X S, et al. Seismic response mechanism of carbonate caverns and influence factors in Tazhong area. Xinjiang Petroleum Geology (in Chinese) , 2011, 32(3): 305-307. |
| [21] | 李胜军, 孙成禹, 高建虎, 等. 地震波数值模拟中的频散压制方法分析. 石油物探 , 2008, 49(5): 444–448. Li S J, Sun C Y, Gao J H, et al. Analysis of dispersion suppression in wave equation numerical simulation. Geophysical Prospecting for Petroleum (in Chinese) , 2008, 49(5): 444-448. |
| [22] | 周义军, 蒲仁海, 曾令帮. 叠前储层描述技术在岩性气藏勘探中的研究与应用. 地球物理学进展 , 2011, 26(1): 229–234. Zhou Y J, Pu R H, Zeng L B. Application research on prestack seismic reservoir characterization. Progress in Geophysics (in Chinese) , 2011, 26(1): 229-234. |
 2012, Vol. 55
2012, Vol. 55