地球物理学报  2012, Vol. 55 Issue (10): 3370-3378   PDF    
引用本文
孙成禹, 张立. 任意方向震源二维兰姆问题的一个精确解. 地球物理学报, 2012, 55(10): 3370-3378, doi: 10.6038/j.issn.0001-5733.2012.10.019.  
SUN C Y, ZHANG L. An exact solution for 2-D Lamb problem of arbitrary direction source. Chinese J. Geophys. (in Chinese), 2012, 55(10): 3370-3378, doi: 10.6038/j.issn.0001-5733.2012.10.019.  
任意方向震源二维兰姆问题的一个精确解
孙成禹 , 张立     
中国石油大学地球科学与技术学院, 青岛 266555
收稿日期 2012-02-14, 2012-06-26 收修定稿
基金项目: 国家科技重大专项(2011ZX05006-002);国家973课题(2013CB228604)和中央高校基本科研业务费专项资金(09CX04009A)联合资助.
作者简介: 孙成禹，男，1968年生，博士，教授，从事地震波传播理论的教学与科研工作.E-mail:suncy@upc.edu.cn.
摘要: 均匀弹性半空间表面或内部震源产生的地震波场的解析解属于Lamb问题,采用Cagniard-deHoop方法,对与水平面呈任意夹角的表面线源,求解了其作用于弹性半空间时的拉普拉斯-傅里叶双积分变换解.以δ-脉冲函数为例,给出了任意方向作用力下波场的构成,并定量解出了P波、S波、首波和Rayleigh波等各波的位移表达式,分析了不同作用方向下各波位移的相对大小.建立数值模型并进行数值模拟,模拟结果验证了理论研究的正确性.研究成果为近地表地震波场的研究提供了理论依据.
关键词: Lamb问题      Cagniard-de Hoop方法      震源问题      自由表面     
An exact solution for 2-D Lamb problem of arbitrary direction source
SUN Cheng-Yu, ZHANG Li     
School of Geosciences, China University of Petroleum, Qingdao 266555, China
Abstract: The analytic solution of seismic wave field caused by surface or inner seismic source in homogeneous elastic half-space belongs to Lamb problems. With the Cagniard-deHoop method, we developed a Laplace-Fourier double integral transformed solution for a surface line source which is in arbitrary angle with horizontal plane on elastic half-space. Some quantitative relations of displacements of P-wave, S-wave, head wave and Rayleigh wave under (-impulse are shown, and the relationship between amplitudes is analyzed. A digital model is built and the results of wave equation modeling are used to verify the accuracy of the theoretical achievements. Due to the particularity of near surface, the achievement on arbitrary direction source provides theoretical foundation to wave filed analysis..
Key words: Lamb problem      Cagniard-deHoop method      Source problem      Free surface     
1 引言

在弹性固体波传播领域具有持久影响的贡献之一就是Lamb在1904年发表的经典性论文[1]，该论文主要研究了作用在弹性半空间无限体表面的一条线或一点处、内部的一条线或一点处等四种冲击载荷条件下弹性波传播问题的解析解.Cagniard[2]在Lamb的思路上提出求解了该问题的一般方法，后经deHoop[3]作了进一步改进，因此该方法被称作Cagniard-deHoop方法.此后Pekeris[4]和Chao[5]分别用该方法具体分析了竖向力和水平力作用下的解.Johnson[6]也用Cagniard-deHoop方法求得了点源作用的Lamb问题的解，并给出了与“源点"和“接收点"坐标相关的解的导数形式.王可成和王贻荪[7]推导出了半空间竖向集中力产生的表面位移的表达式.郑建龙[8]运用叠加原理，依据全空间基本解导出了半空间内部集中点源的基本解.刘凯欣(2004)和刘广裕(2007)[9-10]采用Cagniard-deHoop 方法，对Pekeris的部分积分法加以改进，给出了脉冲载荷作用于弹性半空间的垂直点源问题的一个代数形式的精确解，并采用积分变换方法，求得了区域脉冲载荷下一个二维Lamb问题的代数形式的精确解.本文在前人研究的基础上，采用Cagniard-deHoop方法，求得了与水平面呈任意夹角的表面线源作用于弹性半空间时质点位移的积分变换解，给出了任意方向震源作用下P 波、S 波、首波和Rayleigh 波等各波位移的解析解，并将理论研究结果与数值解进行了对比分析.结果表明，本文所得解析解在特殊情况下的退化解与他人的结果一致，与数值模拟结果吻合较好，验证了其正确性.鉴于近地表波场的复杂性和工程中实际激发问题的多样性，本研究结论在地震勘探、近地表波场分析和工程检测中都具有一般性和普遍意义，可为相应研究提供理论支持.

2 问题的数学描述及其双积分变换

如图 1 所示，一作用力σ0F(t)沿y轴均匀分布，该作用力与xoy面夹角为α，于t=0时突然起始作用.我们将研究导出此力作用下半空间z≥0区域在t>0 时波场的构成.问题的控制方程和边值条件为:

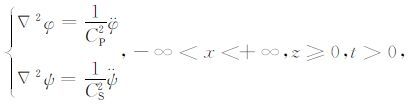
(1)

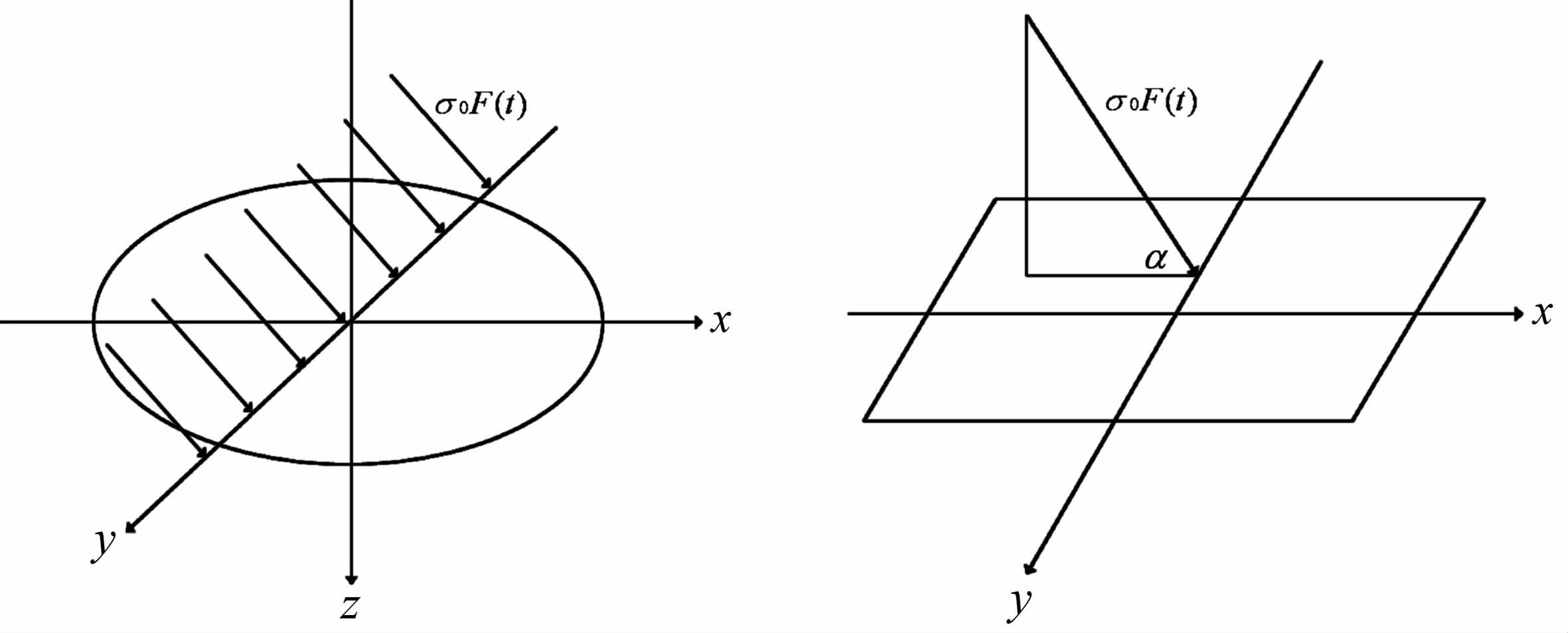
图 1 作用力分布图 Fig. 1 Sketch map of stress distribution

(2)

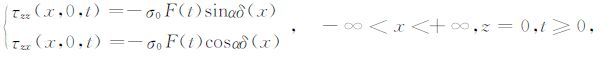
(3)

(4)

式中，φ 和ψ 为该力引起波动的标量势和矢量势函数，x和t分别是空间和时间变量，l为离开震源的距离，τzz和τzx为正应力和切应力分量，CP 和CS 分别表示介质中P波和S波的传播速度，δ(x)为空间Dirac函数.变量上方的点号(·)和双点号(··)分别表示该量对时间的一阶和二阶导数，公式(4)中的省略号表示φ 和ψ 的高阶导数.

对方程(1)的时间变量t取拉普拉斯变换，用“-"表示，变换后对应变量为p；对空间变量x取傅里叶变换，用~ 表示，变换后对应变量为ω.同时考虑初值条件，可得:

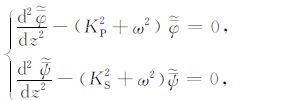
(5)

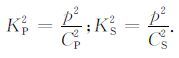
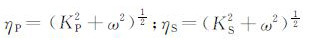
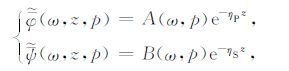
其中.令 ，取其正实根，结合辐射条件，可知该方程的通解具有以下形式:

(6)

其中系数A和B可以根据边界条件来确定.为此，利用弹性介质中的本构关系和柯西方程，将边界条件(3)表示成势函数的形式，并对其取拉普拉斯-傅里叶双积分变换，得到:

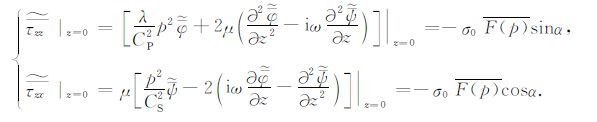
(7)

将式(6)代入式(7)，化简得到:

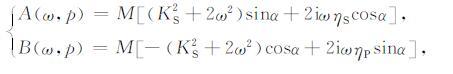
(8)

其中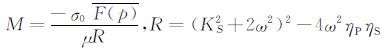， 为ω 的函数.将式(8)代入拉普拉斯-傅里叶域波动方程位移势解的表达式(6)，并根据位移函数与位移势函数的关系，可得:

(9)

其中，$\widetilde{\overline{{{u}_{x}}}}$和$\widetilde{\overline{{{u}_{z}}}}$ 分别为拉普拉斯-傅里叶域内在x和z方向上的位移函数.

3 位移函数的积分变换解

为求式(9)的拉普拉斯-傅里叶逆变换解，采用Cagniard-deHoop的方法.为此引入变量ζ，令ζ =ω/KP，则dω = KPdζ，将其代入ηP 和ηS 的表达式，可得:

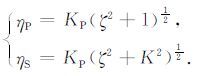
(10)

其中K=CP/CS，将上述关系代入逆变换积分(9)，并对变量ω 取傅里叶逆变换，可以得到拉普拉斯域内位移函数的解具有如下形式:

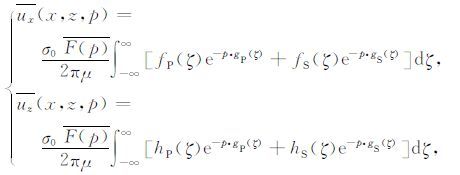
(11)

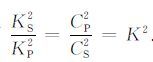
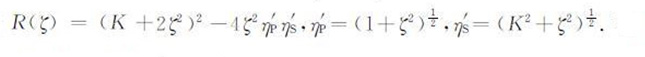
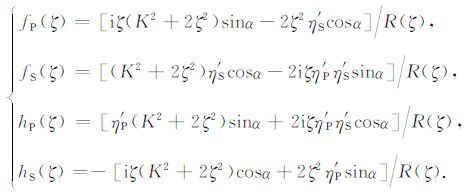
其中考虑到了令容易得到:

(12)

以及

(13)

由式(13)可得

(14)

在以上关系中带下标P和下标S的量分别表示与P波和S波有关的项.

为将式(11)表示成某函数的拉普拉斯变换的形式，在ζ 的复平面上讨论被积函数的性质[11].函数fP(ζ)，fS(ζ)，hP(ζ)和hS(ζ)在ζ 平面上有两组支点:ζ=±i和ζ=±iK；在ζ=±iζR 处有简单极点，其中ζR 为R(ζ)=0的根，此极点即Rayleigh极点.而函数gP(ζ)和gS(ζ)只有两组支点:ζ =±i和ζ =±iK.如图 2a，根据柯西积分定理，可以将积分路线-∞ <ζ< ∞ 变换到下半平面的C1-C3-C4 -C2.当.ζ. ￫ ∞ 时，被积函数中的指数项沿着曲线C1 和C2 的积分为零，因此积分路线变为曲线C3 -C4.下面以式(11)-(14)中与P 波有关的量为例，讨论问题的解.

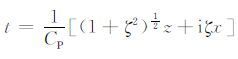
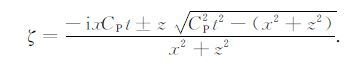
显然，gP(ζ)具有时间t的量纲，为此令gP(ζ)=t，t为正实数，则，由此得到

(15)

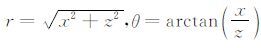
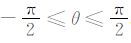
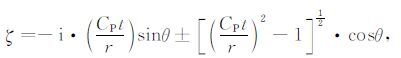
引入极坐标，令，由于仅考虑下半空间，故其变化范围分别是0 ≤r< ∞ 和.考虑到介质的均一性，在此处仅讨论x≥0的范围.此时.式(15)变为

(16)

显然，当t为正实数时，ζ 为一双曲线，其渐近线为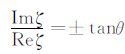.如图 2b所示，在下半平面，双曲线的顶点位于ζ =-isinθ，它不与支线相交，在顶点处，$t=\frac{r}{{{C}_{P}}}$.

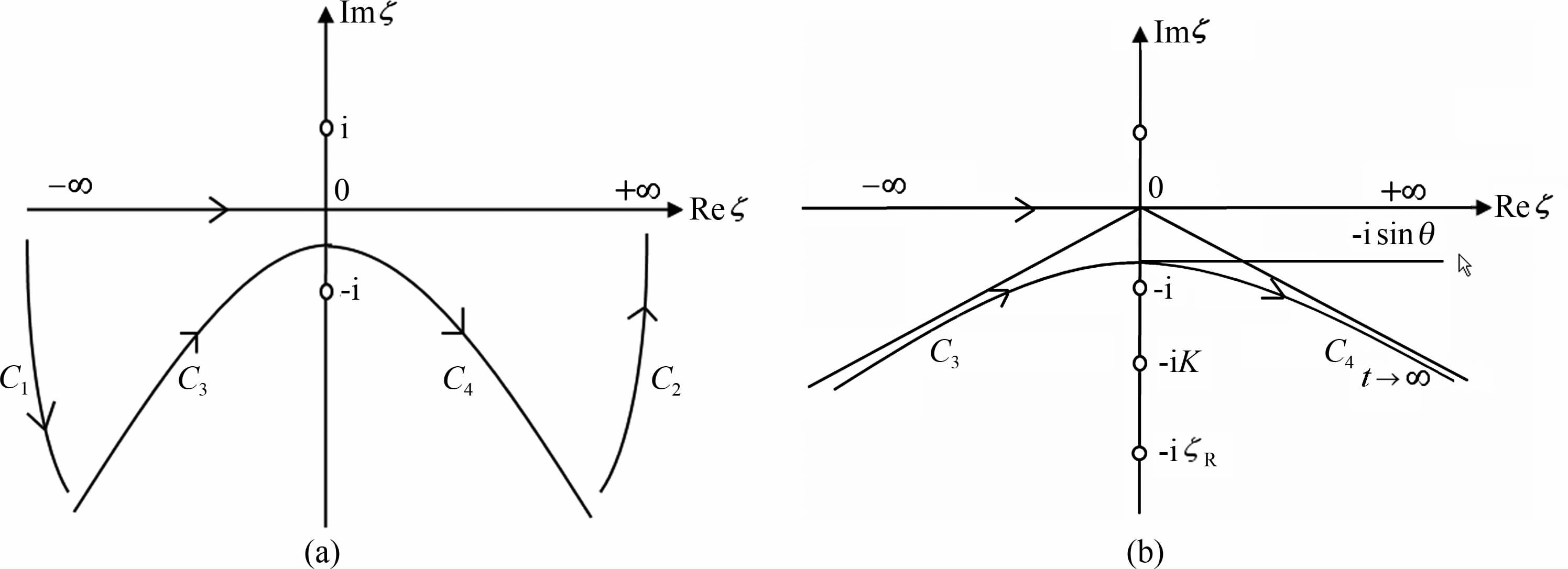
图 2 ζ 平面上的积分路线 Fig. 2 Singularities, branch lines and integral path sin the ζ plane

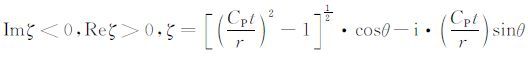
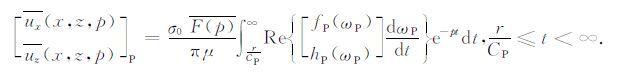
容易证明:gP，fP 和hP 在第三象限中的值与其在第四象限的值互为共轭，故沿C3-C4 的积分等于其沿着C4 积分实部的2倍.在C4 区域，，为t的函数，将其用ωP(t)表示，即ζ =ωP(t)，有

(17)

同理，对式(11)-(14)中与S波有关的量求解，可以获得相应的位移解.合并可得与P波、S波和首波有关的位移分量的拉普拉斯变换表达式为:

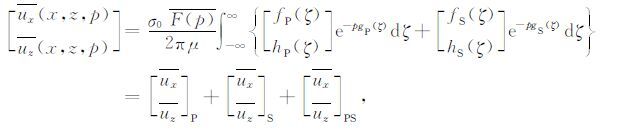
(18)

其中

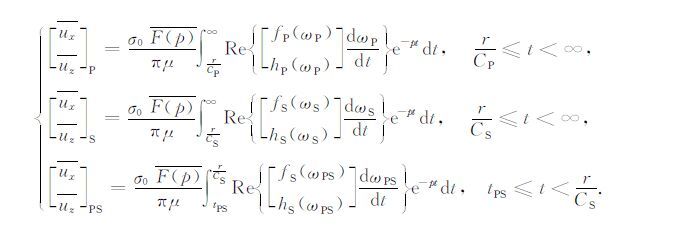
(19)

式中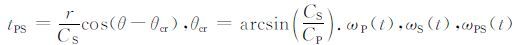，的表达式分别为

(20)

4 自由表面上各波的位移解

考虑到介质的均匀性和各向同性，以及问题在y轴方向的无限性，可以使用柱坐标系讨论波的传播.将xoz平面内位移分解为径向分量和切向分量，从而得到各波在拉普拉斯域的位移表达式.其中P波的位移函数为:

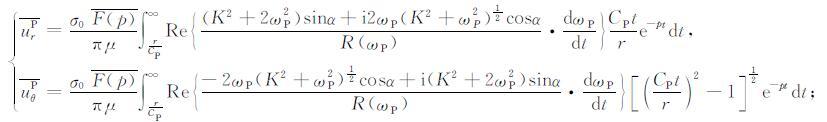
(21)

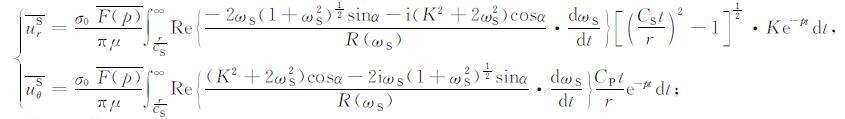
(22)

首波的位移函数为:

(23)

由公式(21)-(23)，对于任意的F(t)均可获得各波分量位移解的表达式.在均匀半空间内任意一点上的位移ur，uθ 的积分，可以分为三部分，即与P 波相应的位移urP和uθP ，与S波相应的位移urS和uθS ，与首波相应的位移分量urPS和uθPS .

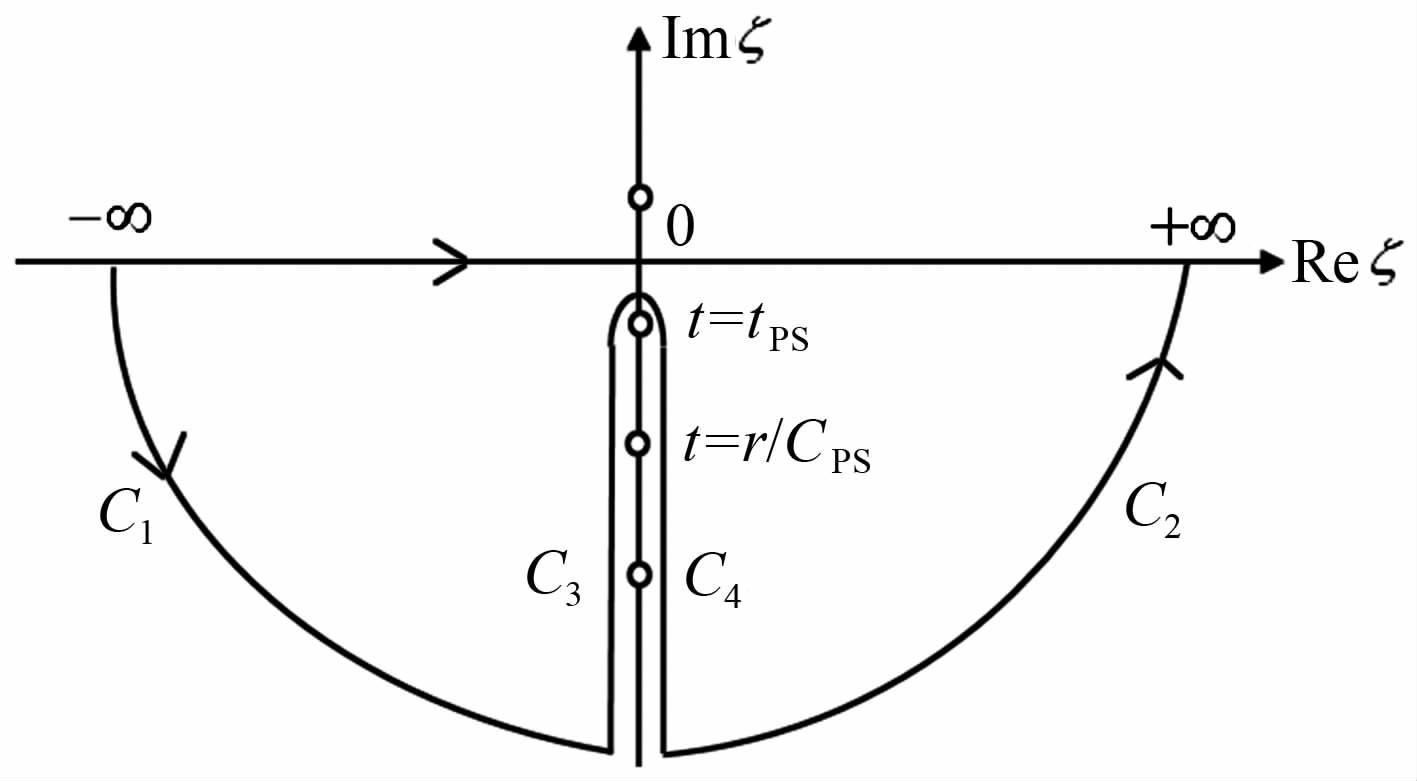
值得注意的是，被积函数中存在极点，即Rayleigh极点，因此积分时会产生与Rayleigh波相对应的位移.以自由表面上z=0，x≥0的区域为例，有0≤r< ∞，θ=$\frac{\pi }{2}$.对积分路线进行变换，将θ =$\frac{\pi }{2}$代入ζ =ωP(t)，ζ=ωS(t)和ζ=ωPS(t)中，积分路线变为ζ平面上沿负虚轴的直线，如图 3所示.

图 3 ζ 平面上的积分路线 Fig. 3 Integral path sin the ζ plane

由前面讨论可知，积分路径C1 和C2 对积分的贡献为零.积分时遇到极点ζ =-iζR 产生的积分主值就是与Rayleigh波相应的位移部分，用urR和uθR表示.根据留数定理得到

(24)

取其拉普拉斯逆变换，得到:

(25)

特殊地，若F(t)=δ(t)，则在自由表面上，Rayleigh波的位移函数为

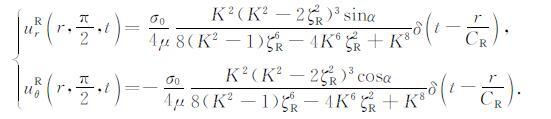
(26)

显然，这就是以速度CR 沿自由表面r方向传播的Rayleigh波.当F(t)=δ(t)时，对公式(21)-(23)应用拉普拉斯逆变换，得到在自由表面上其它波动类型的位移分别为:

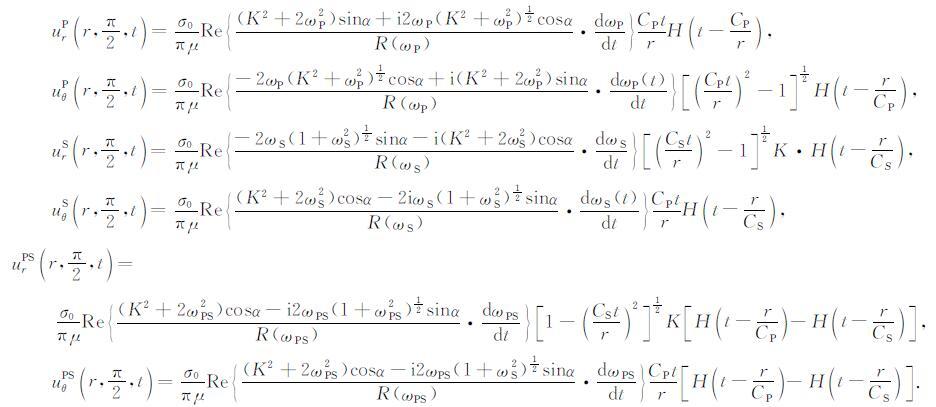
(27)

此为δ-脉冲压力作用下的位移解，对于其他压力函数作用下的位移，可通过压力函数与脉冲响应的卷积得到.这样，任意方向震源在自由表面上的位移就包括P 波、S波、首波和Rayleigh 波四部分.P 波、S 波和Rayleigh波顺序到达，首波存在于P波和S波之间.综合式(26)和式(27)各式，可得在自由表面总位移的表达式为

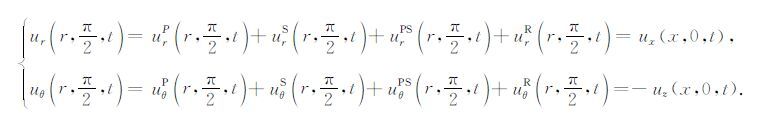
(28)

特殊地，当α=90°时，为垂向作用力.式(26)和式(27)各式得到进一步简化，可以得到与Forrestal(1966)[12]相同的表达式.

5 算例分析 5.1 δ-脉冲压力下自由表面的位移解析解

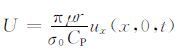
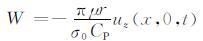
以脉冲压力F(t)=δ(t)作用于泊松体介质为例，图 4给出了压力脉冲沿不同角度α 作用时自由表面上的位移解析解结果.图中为归一化的水平位移振幅，为归一化的垂直位移振幅.P 表示P 波，初至时间为$\frac{{{C}_{P}}t}{r}$=1；S表示S波，初至时间为$\frac{{{C}_{P}}t}{r}$=1.732；首波介于P 波和S 波之间；R 表示Rayleigh 波，该波为位于ζR =1.885处的尖脉冲.

图 4 (a)α=0°时的位移；(b)α=30°时的位移；(c)α=45°时的位移；(d)α=90°时的位移 Fig. 4 (a) Displacements at a = 0°； (b) Displacements at a = 30°；(c) Displacements at a = 45°； (d) Displacements at a = 90°

从图中可以看出:初至P 波的水平位移随α 的增大先增大后减小，而其垂直位移则随α的增大单调减小.初至S波的水平位移和垂直位移随α 的增大单调减小.首波在P 之后S 波之前到达，连接P波和S波的波前面.α=0°时水平位移Rayleigh波能量最强，垂直位移P波能量最强.α=90°时水平位移P波能量最强，Rayleigh波次之；垂直位移Rayleigh波能量最强.其他角度情况下，水平和垂直位移均以Rayleigh波为优势波.当α=90°时，得到了与前人一致的计算结果(刘凯欣(2004)[9]，Forrestal(1966)[12]).

5.2 自由表面位移的数值解分析

图 5为一均匀泊松体半空间速度模型，模型大小为1000m×500m, P 波速度为800m/s.在自由边界条件下进行弹性波动方程有限差分数值模拟.炮点坐标为(500 m, 1 m)，震源的方向垂直向下(α=90°)，在自由表面处接收.以下各图中P 表示P波，S表示S波，PS表示首波，R 表示Rayleigh波.

图 5 均匀半空间速度模型 Fig. 5 Homogenous half-space velocity model

图 6a和图 6b分别为地表排列接收到的位移水平分量和垂直分量在500ms时刻的波场快照，从中可以清晰地显示出P 波、S波、首波和Rayleigh波.图 7为从模拟记录中提取的t=500ms时刻地表各质点的位移曲线.可以看出:水平位移中P 波能量最强，垂直位移中Rayleigh 波能量最强.该结果与上一小节的理论结果相符.

图 6 地表接收的弹性波模拟记录及波场快照 (a)水平分量在500ms时刻的波场快照；(b)垂直分量在500ms时刻的波场快照. Fig. 6 Elastic wave snapshots at surface (a) Horizontal components； (b) Vertical components.
图 7 t=500ms时各质点的振动情况 (a)水平分量；(b)垂直分量. Fig. 7 Displacements at 500 ms (a) Horizontal components； (b) Vertical components.

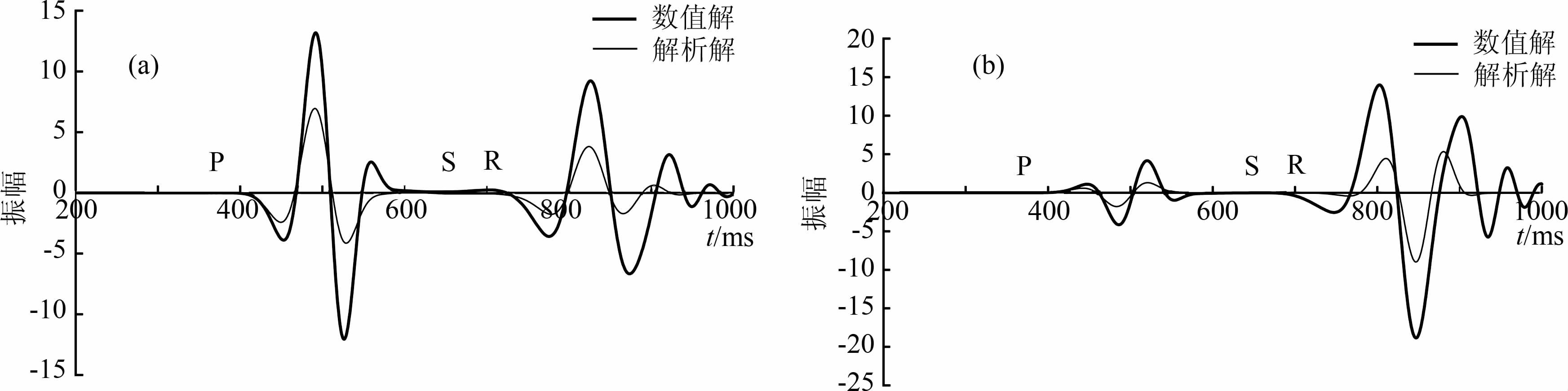
图 8 中的实线为数值模拟记录中地震波传播300m 后，即在x=800m 处质点位移随时间的变化曲线.虚线为以数值解震源子波作为输入，根据上一小节的解析解计算得出的质点位移曲线.对比可见，两者波形吻合较好，各波振幅相对关系基本一致.说明了本研究结论的正确性.

图 8 x=800处质点的振动情况(粗线:数值解；细线:解析解) (a)水平分量；(b)垂直分量. Fig. 8 Displacements at x = 800 m (thick line: digital result； thin line: analytical result) (a) Horizontal components； (b) Vertical components.
6 结论

本文在前人研究的基础上，对任意方向作用于弹性半空间自由表面的震源，采用Cagniard-deHoop方法，求解了其拉普拉斯-傅里叶双积分变换解，分析了解的组成.给出了δ-脉冲压力作用下自由表面上P 波、S 波、首波和Rayleigh 波各成分的代数形式解，并将理论研究结果与数值模拟结果进行了对比分析，得出了以下几点结论:

(1) 本文所得解析解在α=90°下的退化解与前人的计算结果一致，即其中在水平位移中P 波能最强，Rayleigh 波次之；在垂直位移中Rayleigh 波能量最强.此时的数值模拟结果也与解析解相吻合，这都验证了研究结果的正确性.

(2) 当0°<α<90°时，随着角度α 的增大，初至P波的水平位移先增大后减小，而其垂直位移则单调减小；初至S波的水平位移和垂直位移单调减小.当0°<α<90°时水平位移和垂直位移中均以Rayleigh波为优势波.

(3) 本文只给出了δ-脉冲压力作用下自由表面上各波位移的解析解.对于其他类型荷载作用下的波场位移，可以通过压力函数与脉冲响应的卷积得到.

参考文献
[1] Lamb H. On the propagation of tremors over the surface of an elastic solid. Philosophical Transactions of the Royal Society (London) , 1904, 203: 1-42. DOI:10.1098/rsta.1904.0013
[2] Cagniard L. Reflexion et Refraction des Ondes Sismiques Progressives. Paris: Cauthiers-Villars, 1939; translated into English and revised by Flinn E A, Dix C H. Reflection and Refraction of Progressive Seismic Waves. New York: McGraw-Hill, 1962.
[3] deHoop A T. A modification of Cagniard's method for solving seismic pulse problem. Applied Science Research , 1960, 8(1): 349-356. DOI:10.1007/BF02920068
[4] Pekeris C L. The seismic buried pulse. Proceedings of the National Academy of Sciences , 1955, 41(9): 629-639. DOI:10.1073/pnas.41.9.629
[5] Chao C C. Dynamical response of an elastic half-space to tangential surface loadings. ASME Journal of Applied Mechanics , 1960, 27(3): 559-567. DOI:10.1115/1.3644041
[6] Johnson L R. Green's function for Lamb's problem. Geophysics Journal of Royal Astronomy Society , 1974, 37(1): 99-131. DOI:10.1111/j.1365-246X.1974.tb02446.x
[7] 王可成, 王贻荪. 弹性半空间内的突加竖向集中力所产生的表面位移. 固体力学学报 , 1983, 4(3): 427–434. Wang K C, Wang Y S. Surface displacement of an elastic half-space due to a vertically buried point-source load. Chinese Journal of Solid Mechanics (in Chinese) , 1983, 4(3): 427-434.
[8] 郑建龙. 弹性半空间动力问题的基本解. 固体力学学报 , 1988, 9(1): 76–81. Zheng J L. Fundamental solutions of elastic half-space for dynamic problems. Chinese Journal of Solid Mechanics (in Chinese) , 1988, 9(1): 76-81.
[9] 刘凯欣, 刘广裕. 垂直点源问题的一个精确解. 科学通报 , 2004, 49(5): 419–423. Liu K X, Liu G Y. An exact solution for a normal point source problem. Chinese Science Bulletin (in Chinese) , 2004, 49(5): 419-423.
[10] 刘广裕, 刘凯欣. 区域脉冲载荷下二维Lamb问题的精确求解. 固体力学学报 , 2007, 20(3): 341–346. Liu G Y, Liu K X. Exact solution for a two-dimensional Lamb's problem due to a strip impulse loading. Acta Mechanica Solida Sinica (in Chinese) , 2007, 20(3): 341-346.
[11] 何樵登, 韩立国, 朱建伟, 等. 地震波理论. 长春: 吉林大学出版社, 2005 : 91 -94. He Q D, Han L G, Zhu J W, et al. Theory of Seismic Waves (in Chinese). Changchun: Jilin University Press, 2005 : 91 -94.
[12] Forrestal M J, Fugelso L E, Neidharllt G L. Response of a half-space to transient loads. //Proceedings of Engineering Mechanics Division Specially Conference. The American Society of Civil Engineers, 1966: SN 1-SN 6.