2. 中国科学院研究生院, 北京 100049;
3. 桂林理工大学地球科学学院, 广西地质工程中心区重点实验室, 桂林 541004
2. Graduate School of Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of Geological Engineering Centre of Guangxi Province, College of Earth Sciences, Guilin University of Technology, Guilin 541004, China
地震波走时的计算在地球物理学中起着极其重要的作用[1-6].例如,确定震中位置时,较古老的方法是,以所有地震台观测到的走时的剩余值最小为准则来求解;Kirchhoff偏移需要计算Green 函数,而Green函数描述了观测点与地下介质内部点之间的走时[7-8];走时反演和层析成像更是直接利用地表观测到的走时数据来直接反演地下的速度分布,进而构建地下的岩性结构[9-11].传统的计算走时的方法为射线方法,其原理是沿程函方程的特征方向,即射线方向求解走时,经插值计算后得到地下规则网格点上的地震波走时.但是,对于复杂构造的地质模型,这种古典射线方法将遇到焦散面及阴影区等问题[8, 12-13].Vidale[14-15]基于扩张波前的思想开创性地提出一种用有限差分方法来近似程函方程,但该方法采用扩张矩形来追踪波前,在一定的速度分布情况下,计算出的走时并不是最小,且在处理强速度界面时会出现不稳定现象.Qin等[16]改进了Vidale的方法,尽可能沿扩张的波前面来计算走时,方法和Vidale基本相同,但他考虑到了因果关系,首先寻求上一个近似波前面的走时全局极小点,然后向外扩张;但该方法计算机实现较困难,大部分时间要用于寻找全局极值,效率不高.VanTrier 等[17]将迎风有限差分法引入解程函方程,大大的提高了差分格式的稳定性.Sethian等[18-21]提出了一种称之为快速推进的方法(Fast marching method, FMM),该方法利用迎风差分格式求解局部程函方程,采用窄带延拓重建走时波前,利用堆选排技术保存走时,将最小走时放在堆的顶部.该方法显著缩短了寻找极小值的时间,计算量由波前扩展法的O(N3)减少到O(N·logN)(logN由堆的排序算法产生),其中N是节点数.近年来,很多学者对快速推进法进行了推广和应用[22-29].最近,Zhao等[30]提出了一种称之为快速扫描的方法(Fastsweepingmethod, FSM)用于求解一阶双曲型偏微分方程,并指出该方法的计算量为O(N),且证明了该算法的单调性和稳定性.实际上快速扫描法和快速推进法都是求解相同的离散方程,且都是基于因果关系沿程函方程的特征方向求解,但前者更强健且对高阶方程更灵活,效率也一般较后者高[31-32].
前面提到的计算地震波走时的方法基本都是基于水平地表的.然而,在我国随着东部平原地带大规模油气勘探工作已接近尾声,目前的油气勘探重点已转移到了西部、西南部地区.与东部地区不同,西部地区剧烈的地形起伏给地震勘探工作提出了严峻的挑战,传统的基于平缓构造勘探的地震数据采集、处理和解释方法在这类复杂地表地区已不再适用[33-34].研究复杂地表条件下地震波走时的计算问题,对于在这些地区进行反射地震偏移成像、走时层析反演均有非常重要的意义.到目前为止,绝大多数的可以处理起伏地表的地震波走时计算方法都是基于非规则网格的[19, 23, 25, 35-40].然而,一般的,无论是在网格剖分阶段还是走时计算阶段,基于不规则网格的方法都比基于规则网格的方法需要更多的计算量.另外,目前常用的很多地震波场数值模拟方法都是基于规则网格的[33, 41-48],这使得在这些网格上的走时计算变得愈加重要,因为基于以上的正演结果进行Kirchhoff偏移时需要这些走时信息.因此,基于规则网格剖分的起伏地表下的走时计算具有重要意义.最近,Sun 等[49]提出了一种在规则网格上求解起伏地表下地震波走时的方法,该方法的关键是在起伏地表附近采用非均一的网格间距且通过引入地表点、地表上点、界面点、界面下点等概念使其适于用FMM 求解.我们也发展了一种求解起伏地表下地震波走时的方法[50-52].首先,借助于贴体网格和坐标变换,把笛卡尔坐标系中的程函方程变换到曲线坐标系中,推导出了曲线坐标系的程函方程,然后采用Lax-Friedrichs快速扫描法求解曲线坐标系的程函方程.数值实例表明该方法准确、高效.由于地表起伏,导致与之拟合的贴体网格在空间上的展布呈各向异性,本文就探究这种各向异性的强弱对坐标变换法求解地震波初至走时所产生的影响.
本文首先简要回顾一下我们的方法,然后通过数值实例来探究贴体网格展布的各向异性对我们方法所产生的影响.
2 曲线坐标系的程函方程及其Lax-Friedrichs快速扫描求解方法 2.1 曲线坐标系中的程函方程笛卡尔坐标系各向同性介质中的程函方程为
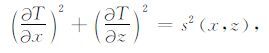
|
(1) |
这一方程给出了射线经过慢度为s(x,z)介质中的点(x,z)时的走时T(x,z).
利用关系式(A2a-b),方程(1)可变换为
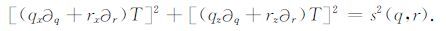
|
(2) |
其中,q,r表示曲线坐标系(的坐标);qx表示∂q(x,z)/∂x,qz,rx,rz的意义也类似,这些导数叫做度量导数(详细可参见附录A).利用方程(A4)来替换上式中的度量导数qx,qz,rx,rz,则程函方程(2)可进一步变换为

|
(3) |
此方程即为曲线坐标系中的程函方程,是Hamilton-Jacobi方程中常见的一种.上述方程可记为下列更为紧凑的形式
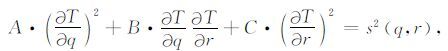
|
(4) |
其中,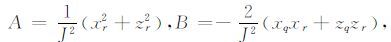


作为求解Hamilton-Jacobi方程的一种迭代方法,快速扫描法近年来得到了迅速发展.Tsai等[59]将其应用到一类基于均一网格上的Godunov 型Hamiltonians的Hamilton-Jacobi方程的求解当中.Kao等[60]提出了一种基于Lax-Friedrichs型数值哈密尔顿的(Gauss-Seidel)G-S扫描型算法.它可以求解任意的静态Hamilton-Jacobi方程,这种方法简单易行、收敛速度快.与基于Godunov数值哈密尔顿的方法不同的是,基于Lax-Friedrichs数值哈密尔顿的方法需要加一些边界条件.本文中采用Lax-Friedrichs快速扫描法(Kao等[60])来求解曲线坐标系的程函方程.首先把曲线坐标系的程函方程整理成Lax-Friedrichs型哈密尔顿算子的形式,然后给出用Lax-Friedrichs快速扫描法求解的离散格式和求解步骤.
2.2.1 Lax-Friedrichs型哈密尔顿算子
对曲线坐标系中的矩形区域[qmin,q max] ×[rmin,r max] 进行均匀剖分,网格点记为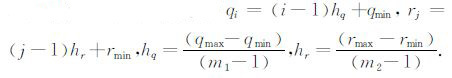
曲线坐标系中的程函方程(4)是一种特殊的静态Hamilton-Jacobi方程,它可以写做如下的形式:
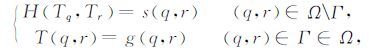
|
(5) |
其中

|
为哈密尔顿算子,A,B,C的意义与前述相同;s(q,r)是慢度,g(q,r)表示震源点的初始值,Ω 为计算区域,Γ为震源点.
用Lax-Friedrichs格式来离散哈密尔顿算子H(Tq ,T r):
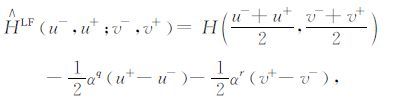
|
(6) |
其中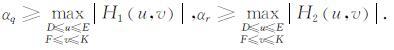

|
(7) |
这里不写Ti+1,j,Ti-1,j的上标是因为它们的上标与扫描方向有关.对于二维情形,我们有四个扫描方向:
(1)从左下角向右上角,即i=1∶m1,j=1∶m2;(2)从右下角向左上角,即i= m1∶1,j=1∶m2;
(3)从左上角向右下角,即i=1∶m1,j= m2∶1;(4)从右上角向左下角,即i= m1∶1,j= m2∶1.
以从左下角向右上角方向扫描,即i=1∶m1,j=1∶m2 为例,我们有

|
(8) |
需要指出的是以上的更新公式不涉及任何非线性求逆,因此本文的求解方法很容易实现.
2.2.2 计算边界条件由于利用Lax-Friedrichs数值哈密尔顿计算一个网格点的解时需要它周围所有相邻点的信息,因此我们必须仔细地确定那些超出计算区域的网格点的值.为此,采用Kao等[60]提出的方法处理计算边界,他们结合外推、最大和最小策略计算那些超出计算区域的网格点的值.二维问题的边界条件为

|
(9) |
总结Gauss-Seidel 型Lax-Friedrichs 扫描算法,它主要包含初始化、交替扫描和实施计算边界条件这三个步骤.具体如下:
(1) 初始化.在震源Γ 上的网格点或邻近的网格点,赋精确值或插值,并且每次迭代过程中这些值固定不变.其它网格点上的初值设为一个较大的值(远大于所有计算点最终能算出的走时值),这些点上的走时在后续计算时会被更新.
(2) 交替扫描.在第n+1次迭代时,除了那些赋精确值或插值的网格点,按照(11)式计算Ti,jn+1在所有网格点(qi,rj),1≤i≤m1,1≤j≤m2 的值,并且只有当它小于以前的值Ti,jn时才更新Ti,jn+1.值得注意的是,这个过程需要按交替扫描方向进行,即在二维情形需要四个不同的扫描方向.一般来说,d维情形需要2d次交替扫描.
(3) 实施计算边界条件.每次扫描之后,按照(9)式实施计算边界条件,不同的边界只需作一些细微的修改.
(4) 收敛准则.如果‖Tn+1 -Tn‖L1 ≤δ,算法收敛并终止,这里δ 是一个给定的收敛阀值.
3 贴体网格的各向异性对起伏地表走时计算的影响为了研究由于地表地形起伏而产生的贴体网格各向异性对曲线坐标系的程函方程求解地震波初至走时的影响,首先,考虑对相同的起伏地表模型进行不同精度的贴体网格剖分.这是因为,疏网格的剖分较密网格剖分中网格扭曲剧烈,因此,网格各向异性也较后者强.第二,研究在相同的模型和相同的网格剖分精度下,震源置于不同位置时对走时计算的影响.采用规则的贴体网格对模拟区域进行剖分,在地表处网格要与地表地形吻合,因此扭曲较为严重,而随着远离地表,网格逐渐接近于矩形,因此震源位于不同深度即震源位于各向异性不同的贴体网格上.最后,对地表起伏不同程度的模型进行研究.地形起伏不同的模型产生的贴体网格的各向异性也不同,因此对一组不同起伏程度的地表地形模型进行研究具有重要意义.考虑到以上三点,我们设计了一组起伏程度不同的模型进行研究.模型大小为[-1km, 1km]2,模型表面是由一个山丘和两个凹陷组合成的地表起伏模型.它的高程可以用下面的余弦函数来表示
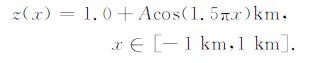
|
(10) |
其中,A为余弦函数的振幅,A取值不同表示地表地形起伏的剧烈程度不同,分别取A为0.1、0.15、0.2、0.25来进行研究.用四种不同精度的网格(100×100,200×200,400×400,800×800)分别离散该模型,受篇幅的限制,只给出当A为0.2 时模型的贴体网格(100×100)剖分图(图 1).可以看出,在地表地形处,贴体网格发生扭曲,随着地表地形起伏逐渐剧烈,贴体网格扭曲逐渐剧烈;随着远离地表地形,贴体网格的形状逐渐接近于矩形,各向异性程度减弱.为了考查震源在不同各向异性的贴体网格上时对计算的影响,我们将震源置于6个不同的深度处(α= -0.9,-0.5,-0.1,0.3km, 0.7,1.0km),震源点的坐标为(-0.2km, α).由于点源的走时场在震源点存在奇异性,因此通常将包含震源点一个区域内点的值初始化为精确值[31, 61-62].在本文的算例中,我们把以震源为圆心,半径为0.12km 的区域内的点的初值赋为精确值.

|
图 1 地表地形为z(x)=1.0+0.2cos(1.5πx)km 的模型结构化网格剖分 Fig. 1 The surface-fitting grids of the 100 X 100 mesh for the model whose surface is described by the function z(x)=1.0 + 0.2cos(1.5nx)km |
为了便于和解析解比较,假设所有模型中介质都是均匀的,速度均为2000m/s.一般的,复杂地表下的走时很难计算出其解析解,但在地表地形可以用解析式表示的情况下,其解析解是可以求解的.对于不同地形的均匀介质模型,按照附录B 的方法计算出其相应的解析解并和本文计算的数值解对比来考查贴体网格各向异性对起伏地表的程函方程求解地震波初至走时的影响.分别计算L1 和L∞ 误差,L1 误差表示的是全部(模型)计算网格上的平均误差,因此其体现的是数值解在整个模型空间的精度;而L∞ 误差是全部计算网格上的最大误差,因此其反映的是某单点的效应[63],易受奇异点的影响.L1、L∞ 误差和收敛阶数α的定义如下[64]:
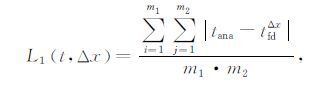
|
(11) |

|
(12) |
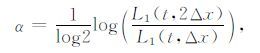
|
(13) |
其中,tana 表示按照附录A 的方法计算的解析解,tfdΔx 表示基于曲线坐标系的程函方程用Lax-Friedrichs快速扫描法计算的数值解,Δx表示网格间距.
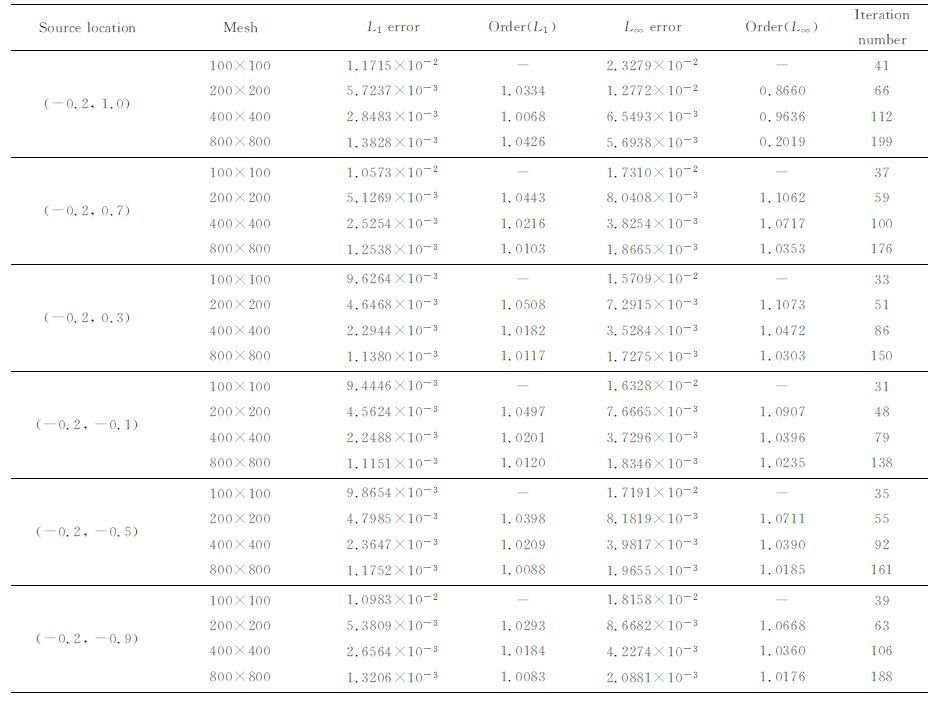
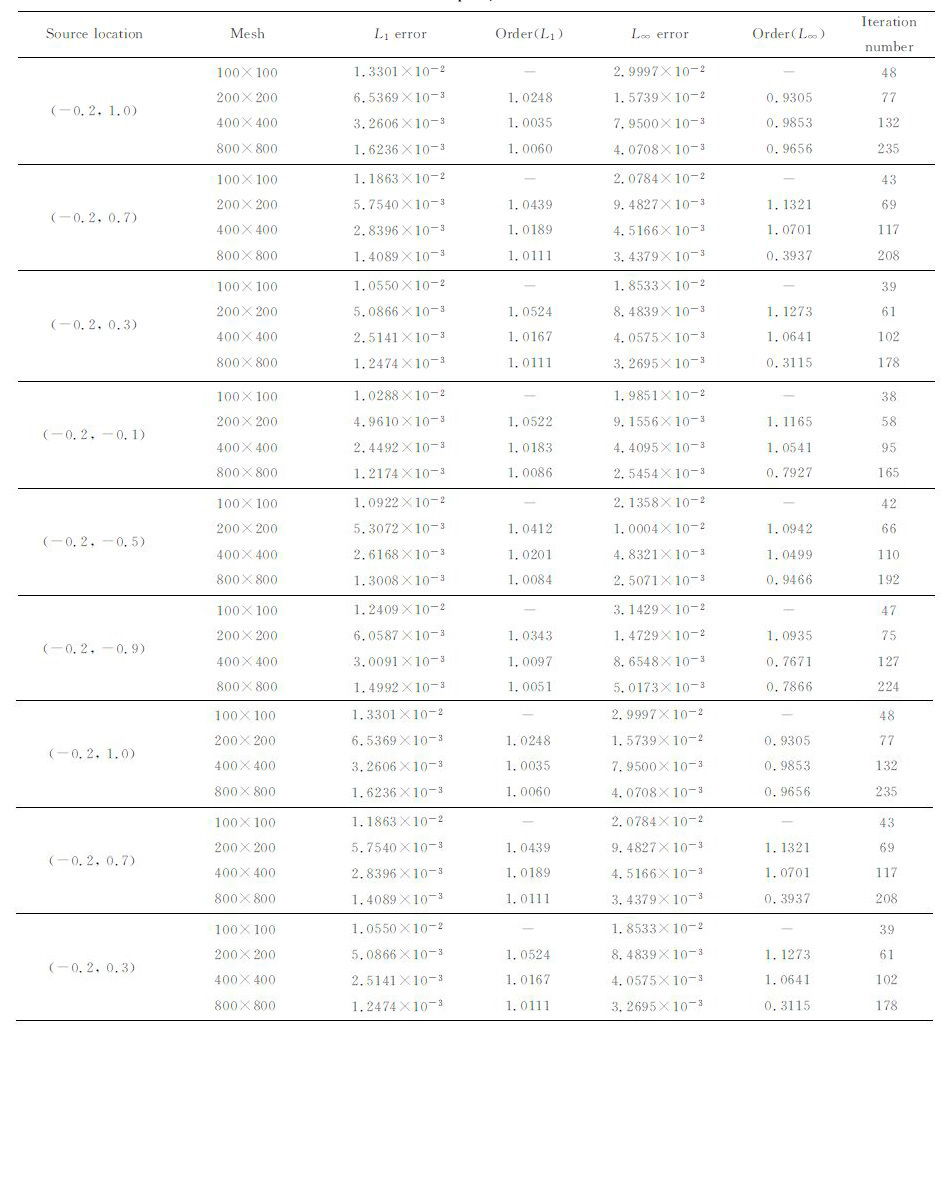
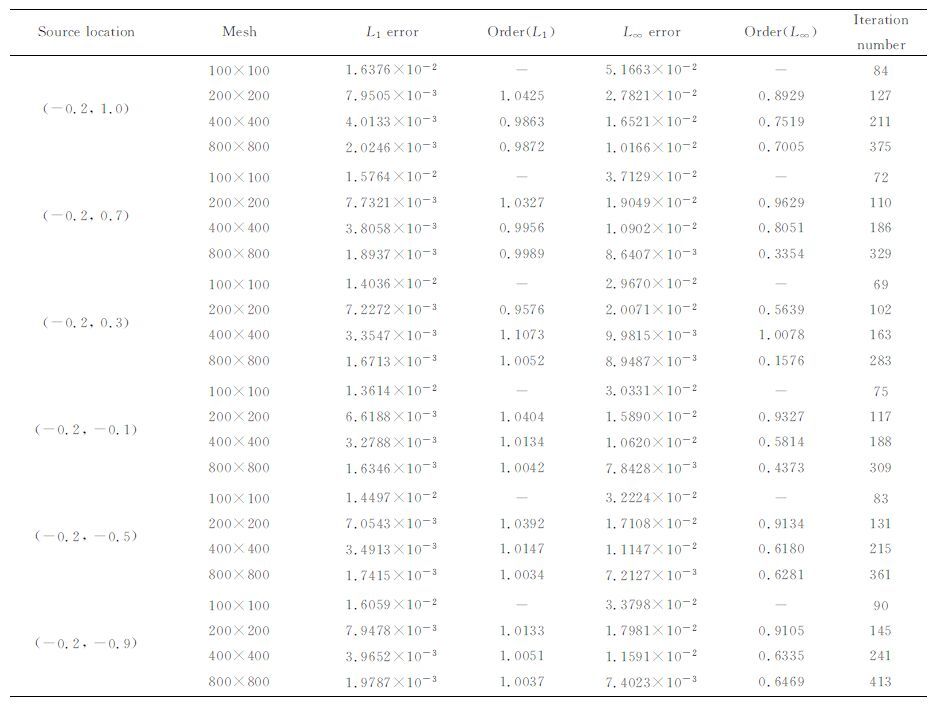
3.1 对相同的模型进行不同精度的网格剖分对走时计算的影响把相对于不同程度的地形起伏,不同的震源深度,不同精度的网格剖分,共计96 个模型的数值解与解析解一一仔细对比,结果见附录C.这里仅以余弦函数的振幅A为0.2,震源坐标为(-0.2km, 1.0km)的模型为例来分析不同精度的网格剖分对走时计算的影响.
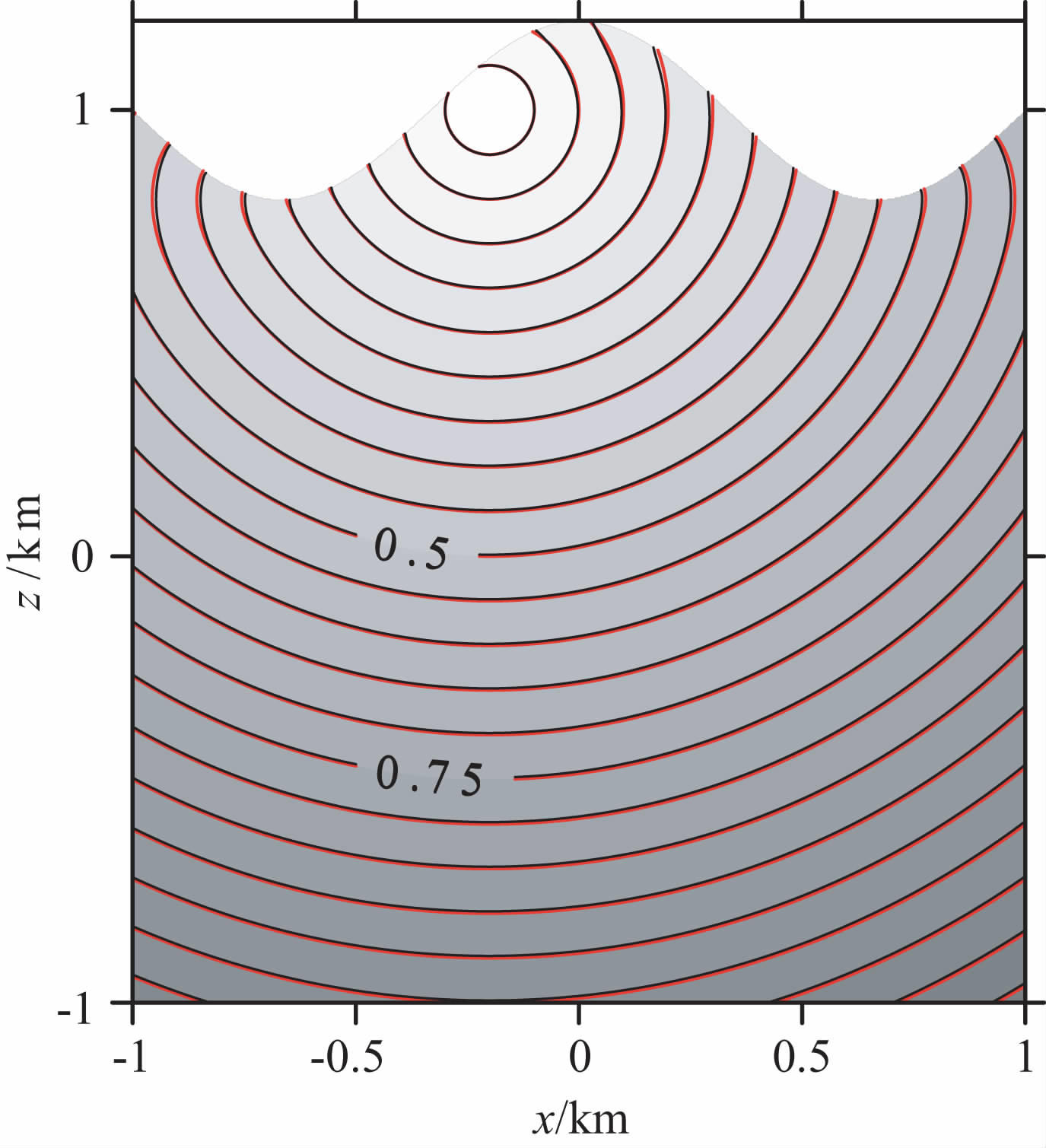
图 2为800×800的剖分网格上的走时等值线图.图 3描述了相对于不同精度的剖分网格,计算误差和计算效率的分布情况.如图 3a所示,随着网格的加密,贴体网格各向异性减小,误差也随着减小,我们计算相应的收敛阶数,得到相对于四种精度的网格剖分,α 依次为1.0327,0.9956,0.9989,这与本文方法的一阶精度的结论是一致的.图 3b为相对于不同精度的网格剖分,计算结果收敛所需要的迭代次数,由图可见,随着剖分精度的提高,迭代次数也随之增多,这是由求解起伏地表的程函方程时所采用的Lax-Friedrichs快速扫描法不是迎风格式的性质所导致的,虽然其能保证结果的收敛,但是随着网格剖分精度的逐渐提高,迭代次数也将随着增大.因此,发展迎风格式的求解方法,对坐标变换法求解地震波走时具有重要意义.
|
图 2 振幅为0.2km 的余弦型起伏地表模型震源坐标为(-0.2km, 1.0km)时的初至波走时等值线图 红线虚线表示解析解,黑线实线表示数值解,走时等值线的单位为s. Fig. 2 Traveltime contours (in seconds) for themodelwhose surface is a cosine curve-like feature The source is at (-0.2 km, 1.0 km).The black and red lines denote the numerical and analytical solutions, respectively. |

|
图 3 不同精度的网格剖分振幅为0.2km 的余弦型起伏地表模型时计算误差(a)和所需迭代次数(b)的分布图 横坐标1,2,3,4表示的剖分网格分别为100×100,200×200,400×400,800×800. Fig. 3 L1 errors and iteration numbers for the model whose surface is a cosine curve-like feature under grid refinement. The x coordinates 1,2,3,4 denote the meshes which discretize the model are 100X100,200X200,400X400,800X800,respectively. |
我们也仅以余弦函数的振幅A为0.2,剖分网格为800×800的模型为例来探讨震源位于不同深度时对走时计算的影响.
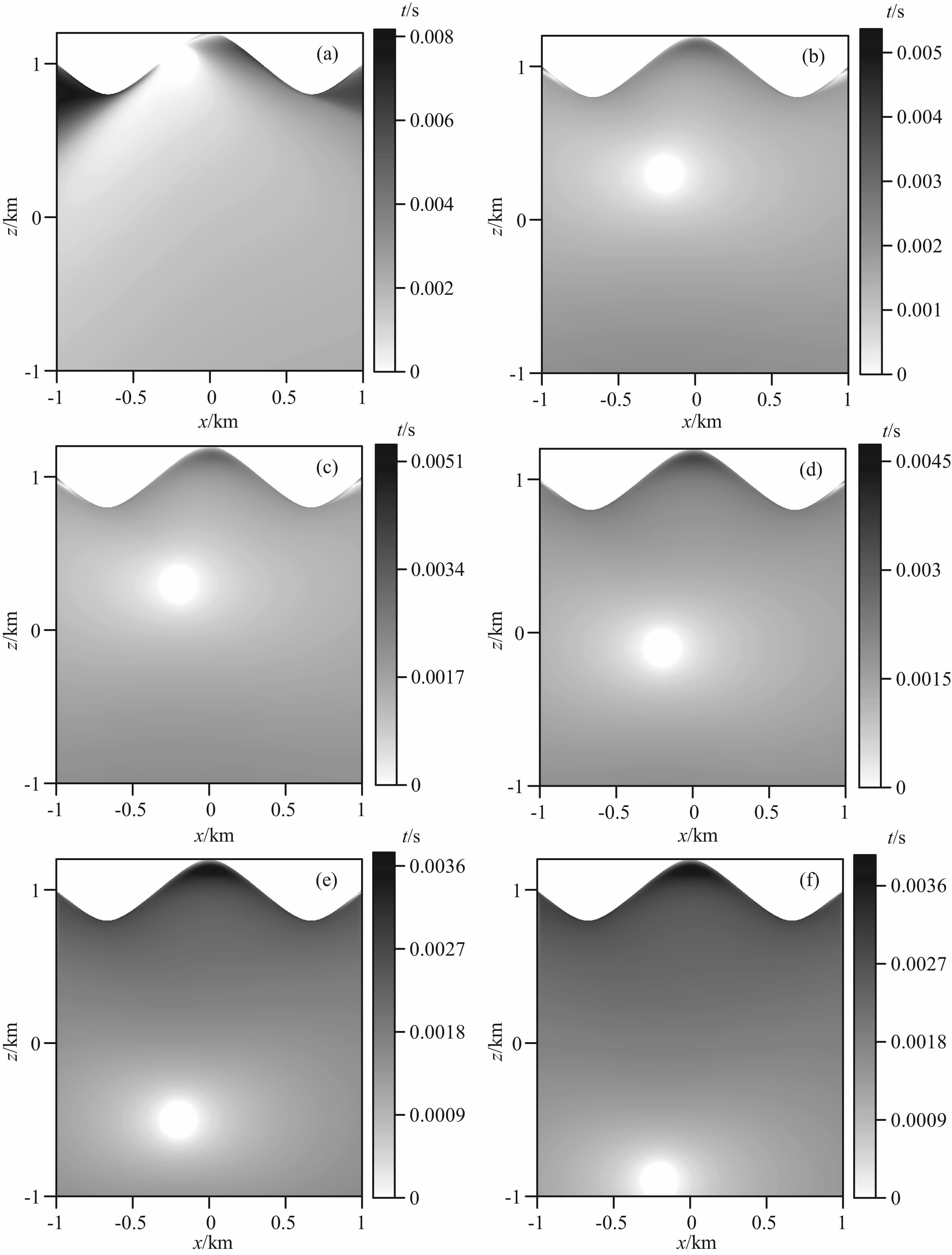
图 4为震源位于不同深度时所对应的走时等值线,图 5为相应的绝对误差分布.由图可见,数值解与解析解拟合的很好,误差在网格扭曲较严重(网格各向异性较强)的地方较大.图 6为相应的L1 误差(图 6a)和迭代次数(图 6b)分布图.如图 6a所示,震源位于模型的顶部和底部时的误差较震源位于中部时的大,这主要是由于误差随着距离逐渐累积的缘故,传播距离增大,误差随之增大;其次,震源点(起始点)附近误差的大小也对整个计算空间误差的大小有重要影响,在相同的区域内,当震源点附近贴体网格扭曲较严重,各向异性较强时其初始误差就大,而当震源点附近贴体网格各向异性较弱时其初始误差较小,当传播相同的距离时,误差逐渐累积且前者的误差会增值的较快,这也是本例中当震源位于点(-0.2km, 0.7km)时的误差比点(-0.2km, -0.5km)时的误差大的缘故.震源位于点(-0.2km, 1.0km)时的误差与位于点(-0.2km, -0.9km)时的相当,因为在前者中,虽然震源位于地表附近,网格各向异性较后者明显强,但由于在初始化时将震源点半径为0.12km 区域的初至都附为精确值,因此在前者中地表附近的初始误差就小,这基本抵消了(由于网格各向异性较强)其误差累积速率较快的效应.当然这与震源初始化时半径的大小有很大关系,当半径减小直至点源时误差就会比较客观,这也表明当震源位于地表附近时以合适的半径来初始化是很有必要的[50, 52].迭代次数(图 6b)的分布情况与误差的分布是一致的,这主要是由于较大误差需要较多次迭代才能收敛的缘故.

|
图 4 振幅为0.2km 的余弦型起伏地表模型当震源位于不同深度时走时等值线图 (a)(-0.2km, 1.0km);(b)(-0.2km, 0.7km);(c)(-0.2km, 0.3km),(d)(-0.2km, -0.1km);(e)(-0.2km, -0.5km);(f)(-0.2km, -0.9km).红线虚线表示解析解,黑线实线表示数值解,走时等值线的单位为s. Fig. 4 Traveltime contours (in seconds) on the 800X800 mesh for the modelwhose topography amplitude is 0.2 km with different source depths (a) ( - 0.2 km, 1.0 km) ; (b) ( - 0.2 km, 0.7 km) ; (c) (- 0.2 km, 0.3 km) ; (d) (- 0.2 km, -0.1km); (e) (- 0.2 km, -0.5 km); (f) ( - 0.2 km, -0.9 km),respectively.The black and red lines denote the numerical and analytical solutions, respectively. |
|
图 5 振幅为0.2km 的余弦型地表起伏模型(800×800)当震源位于不同深度时绝对误差分布图 (a)(-0.2km, 1.0km);(b)(-0.2km, 0.7km);(c)(-0.2km, 0.3km);(d)(-0.2km, -0.1km);(e)(-0.2km, -0.5km);(f)(-0.2km, -0.9km). Fig. 5 Absolute differences, or errors, (in seconds) between travel times calculated by the numerical and the analytical solutions on the 800X800 mesh for the model whose topography amplitude is 0.2 km with different source depths (a) (- 0.2 km, 1.0 km) ; (b) (- 0.2 km, 0.7 km) ; (c) (- 0.2 km, 0.3 km) ; (d) (- 0.2 km, -0.1 km);(e) ( - 0.2 km, -0.5 km) ; (f) ( - 0.2 km, -0.9 km). |

|
图 6 振幅为0.2km 的余弦型地表起伏模型当震源位于不同深度时计算误差(a)和所需迭代次数(b)分布图 Fig. 6 Li errors (a) and iteration numbers (b) for the model whose topography amplitudeis 0.2 km with different source depths |
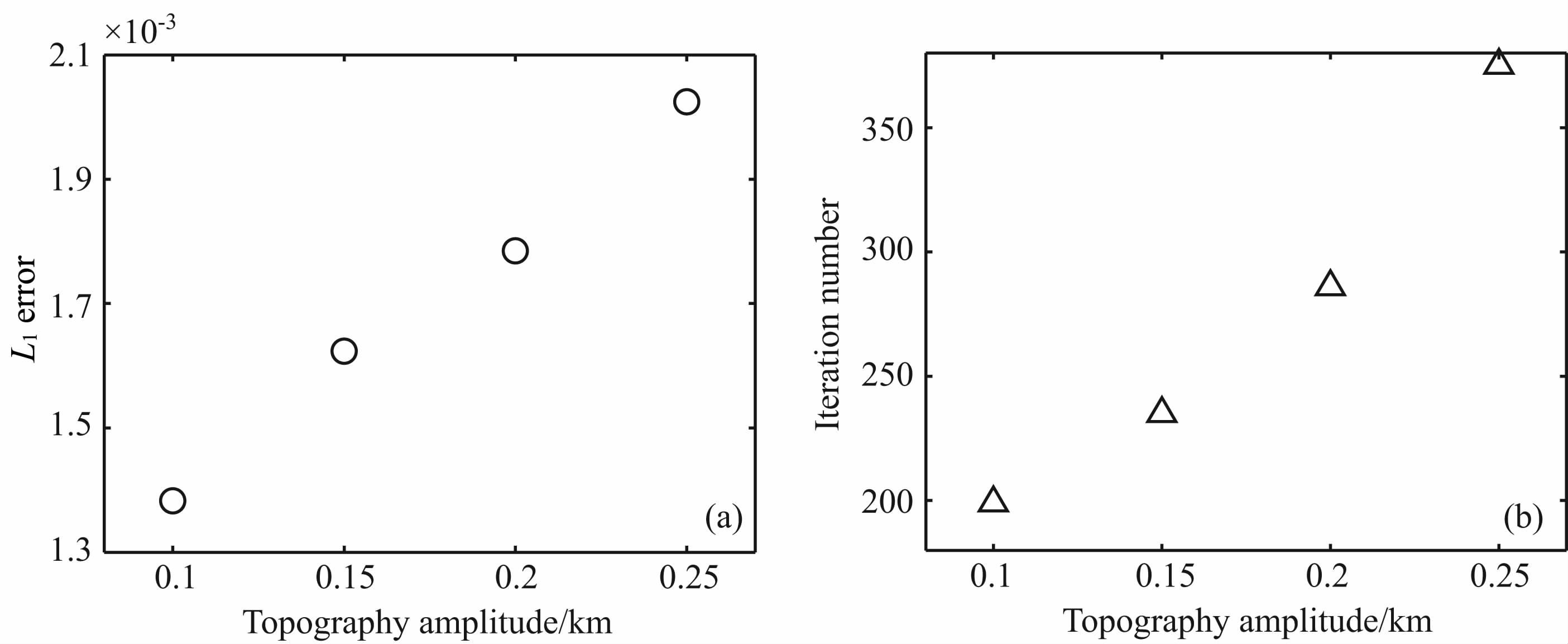
以震源位于点(-0.2km, 1.0km),剖分网格为800×800的模型为例来分析地表起伏不同程度对走时计算的影响.图 7 为地形起伏不同程度的模型所对应的L1 误差(图 7a)和迭代次数的(图 7b)的分布图.由图 7a可知,随着地形起伏逐渐剧烈,贴体网格各向异性增强,L1 误差增大.迭代次数的变化规律与误差的变化是一致的.
|
图 7 地表地形起伏不同程度时计算误差(a)和所需迭代次数(b)分布图 Fig. 7 L1 errors and iteration numbers for the models with different topography amplitudes |
综合图 3、6、7及表C1、C2、C3、C4的结果,我们可以看出,对于本文的计算实例,误差对网格密度的变化最敏感,而随震源深度和地形起伏程度的变化次之.
4 结论笔者近来提出了一种求解起伏地表下地震初至波走时的新方法.首先,借助于贴体网格,把笛卡尔坐标系中的程函方程变换到曲线坐标系中,然后,采用Lax-Friedrichs快速扫描算法求解曲线坐标系的程函方程.由于地表起伏,导致与之拟合的贴体网格在空间上的展布呈各向异性,本文主要研究由于不同的网格密度、不同的震源深度及地形起伏程度引起的各向异性的强弱对坐标变换法求解地震初至波的走时的影响.研究表明,随着贴体网格的各向异性增强,用坐标变换法求解地表起伏区域的走时计算误差增大,且计算效率降低,这对于该方法的实际应用具有重要指导意义.
附录A:笛卡尔坐标和曲线坐标的转换对于复杂地表的介质,离散网格边界需与起伏的地表吻合以避免人为的产生误差.这种网格被称作贴体网格[53-54],且广泛应用于数值模拟中[33, 41-46, 55-56].贴体网格可以通过由计算空间到物理空间的坐标变换获得[53-54](图 A1).通过坐标变换曲线坐标系的q,r映射到物理空间的笛卡尔坐标系,这两个坐标系中垂直轴都取向上方向为正.

|
图 A1 计算域和物理域映射示意图 Fig. A1 Mapping between computational and physical space in two dimensions |
贴体网格生成之后,笛卡尔坐标系中的网格点与曲线坐标系中的网格点就一一对应,即
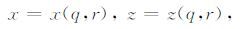
|
(A1) |
由链锁规则,我们有

|
(A2a) |
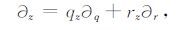
|
(A2b) |
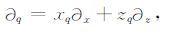
|
(A3a) |
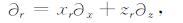
|
(A3b) |
这里qx表示∂q(x,z)/∂x,qz,rx,rz的意义也类似.这些导数叫做度量导数,把(A2a, b)式分别代入式(A3a, b),经过化简,可得
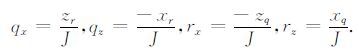
|
(A4) |
J是变换的雅克比,它可以表示为J=xqzr-xrzq,详细的推导过程请参见文献[46].
附录B:复杂地表下均匀介质模型中的精确走时计算策略一般的,复杂地表下的走时很难用解析的方法进行刻画,但在地表地形可以用解析式表示的情况下,其解析解还是可以求解的.在此,我们探讨本文模型的解析解的求解.
以地表地形振幅为0.2km 的余弦曲线模型为例来介绍其精确走时的求解.首先,讨论震源在点(-0.2km, 1.0km)的情形,对于其它情形后续再讨论.求解的难点是如何确定从震源到区域内其它点的射线的最短路径.根据从震源‘S'到模型内其它点的射线路径的形态,求解区域可以被剖分为三部分,如图 B1 显示的两个灰色区域和白色区域的部分.对于白色区域内的点,从震源到该点的最短射线路径均为直线,因此其走时很容易求得.对于两个灰色区域,以左上角的灰色区域为例来介绍,右上角的区域可类似计算.对于灰色区域内的一点‘B'(弧$\overset\frown{DM}$下方,线段DE上方),过该点做一条直线与$\overset\frown{DM}$相切,切点为‘C'(在$\overset\frown{DC}$上),那么此时从震源‘S'到点‘B'的最短射线路径为SD+DC+CB(易被证明,在此从略),向量SD和CB的长度可以通过两点间距离公式求得,而DC的长度可以通过弧长公式计算得出.进而可以求出其相应的走时.同理,可以计算出此区域内其它点的走时.
由于弧$\overset\frown{MD}$和$\overset\frown{NG}$为严格的凹曲线,因此对于这两段弧上的点,最短射线路径只包括两部分,即一根线段和一段圆弧.以点‘A'为例,从震源点‘S'到该点的最短射线路径为SD+$\overset\frown{DA}$,它的长度可以通过前面介绍的方法求得.
当震源位于点(-0.2km, 0.7km)(Fig.B1b)或(-0.2km, 0.3km)(Fig.B1c)上时,解析解的求解同上面介绍的情形类似;当震源位于点(-0.2km, -0.1km)(Fig.B1d)上时,只有右上角一小部分区域内的点需要按照上述的方法特别处理;当震源位于点(-0.2km, -0.5km)(Fig.B1e)或(-0.2km, -0.9km)(Fig.B1f)上时,解析解变得较为简单,即为两点间的距离与速度的商.
综上所述,我们就可以求得该模型中的初至波精确走时.对于其它模型的情况可以类似求解,这里从略.

|
图 B1 本文中的起伏地表模型走时计算策略 ‘S'表示震源,SE、SF分别切余弦曲线于点‘D'、‘G';‘A'表示地表曲线上一点,‘B'表示曲线下一点;CB切余弦曲线于点‘C';曲线交左右边界分别于点‘M'、‘N'. Fig. B1 The strategy for computing analytical solutions of travel times for the irregular surface models of this paper ‘S' denotes the source for this model; SE and SF are two vectors which are tangent to the cosine curve (irregular surface) at points ‘D' and ‘G',respectively; ‘A' denotes a point on the surface curve, while ‘B'denotes a point beneath the surface; CB is tangent to the cosine curve at point ‘ C' ; the cosine curve intersects the left and right boundaries at points ‘M' and ‘N',respectively. |
|
|
表 C1 振幅为0.1km的余弦型地表起伏模型当震源位于不同深度,不同精度的网格剖分时的误差和迭代次数分布 Table C1 Errors and convergence order for the model whose topography amplitude is 0.1 km with the source located at different depths, the unit for the source location is km |
|
|
表 C2 振幅为0.15km的余弦型地表起伏模型当震源位于不同深度,不同精度的网格剖分时的误差和迭代次数分布 Table C2 Errors and convergence order for the model whose topography amplitude is 0.15 km with the source located at different depths, the unit for the source location is km |
|
|
表 C3 振幅为0.2km的余弦型地表起伏模型当震源位于不同深度,不同精度的网格剖分时的误差和迭代次数分布 Table C3 Errors and convergence order for the model whose topography amplitude is 0.2 km with the source located at different depths,the unit for the source location is km |
|
|
表 C4 振幅为0.25km的余弦型地表起伏模型当震源位于不同深度,不同精度的网格剖分时的误差和迭代次数分布 Table C4 Errors and convergence order for the model whose topography amplitude is 0.25 km with the source located at different depths, the unit for the source location is km |
本研究工作得到了中国科学院地质与地球物理研究所张中杰研究员的悉心指导和帮助.Alexander Vladimirsky 和 Jianliang Qian 两位博士对本研究工作提供了许多建设性的意见.笔者在此表示衷心的感谢.
| [1] | Aki K, Richards P G. Quantitative Seismology. Univ Science Books, 2002. |
| [2] | Hole J. Nonlinear high-resolution three-dimensional seismic travel time tomography. Journal of Geophysical Research , 1992, 97(B5): 6553-6562. DOI:10.1029/92JB00235 |
| [3] | Chen Y, Badal J, Hu J. Love and Rayleigh wave tomography of the Qinghai-Tibet Plateau and surrounding areas. Pure and Applied Geophysics , 2010, 167(10): 1-33. |
| [4] | Zelt C, Smith R. Seismic traveltime inversion for 2-D crustal velocity structure. Geophysical Journal International , 1992, 108(1): 16-34. DOI:10.1111/gji.1992.108.issue-1 |
| [5] | Zhang Z, Wang G, Teng J, et al. CDP mapping to obtain the fine structure of the crust and upper mantle from seismic sounding data: an example for the southeastern China. Physics of the Earth and Planetary Interiors , 2000, 122(1-2): 133-146. DOI:10.1016/S0031-9201(00)00191-6 |
| [6] | 张中杰, 秦义龙, 陈赟, 等. 由宽角反射地震资料重建壳幔反射结构的相似性剖面. 地球物理学报 , 2004, 47(3): 469–474. Zhang Z J, Qin Y L, Chen Y, et al. Reconstruction of the semblance section for the crust and mantle reflection structure by wide-angle reflection seismic data. Chinese J. Geophys. (in Chinese) , 2004, 47(3): 469-474. |
| [7] | 朱金明, 王丽燕. 地震波走时的有限差分法计算. 地球物理学报 , 1992, 35(1): 86–92. Zhu Z M and Wang L Y. Finite difference calculation of seismic travel times. Chinese J. Geophys. (in Chinese) , 1992, 35(1): 86-92. |
| [8] | Cerveny V, Molotkov I A, Psencik I. Ray Methods in Seismology. Univ. of Karlova Press. 1977 . |
| [9] | Zhang Z, Badal J, Li Y, et al. Crust-upper mantle seismic velocity structure across Southeastern China. Tectonophysics , 2005, 395(1-2): 137-157. DOI:10.1016/j.tecto.2004.08.008 |
| [10] | Zhang Z, Li Y, Lu D, et al. Velocity and anisotropy structure of the crust in the Dabieshan orogenic belt from wide-angle seismic data. Physics of the Earth and Planetary Interiors , 2000, 122(1-2): 115-131. DOI:10.1016/S0031-9201(00)00190-4 |
| [11] | Zhang Z, Wang Y, Chen Y, et al. Crustal structure across Longmenshan fault belt from passive source seismic profiling. Geophys. Res. Lett., 2009, 36. http://cn.bing.com/academic/profile?id=2049749807&encoded=0&v=paper_preview&mkt=zh-cn |
| [12] | Xu T, Xu G, Gao E, et al. Block modeling and segmentally iterative ray tracing in complex 3D media. Geophysics , 2006, 71: T41-T51. DOI:10.1190/1.2192948 |
| [13] | Xu T, Zhang Z, Gao E, et al. Segmentally iterative ray tracing in complex 2D and 3D heterogeneous block models. Bulletin of the Seismological Society of America , 100(2): 841-850. DOI:10.1785/0120090155 |
| [14] | Vidale J E. Finite-difference calculation of travel times. Bulletin of the Seismological Society of America , 1988, 78(6): 2062-2076. |
| [15] | Vidale J E. Finite-difference calculation of traveltimes in three dimensions. Geophysics , 1990, 55(5): 521-526. DOI:10.1190/1.1442863 |
| [16] | Qin F, Luo Y, Olsen K B, et al. Finite-difference solution of the eikonal equation along expanding wavefronts. Geophysics , 1992, 57: 478-487. DOI:10.1190/1.1443263 |
| [17] | Van Trier J, Symes W W. Upwind finite-difference calculation of traveltimes. Geophysics , 1991, 56(6): 812-821. DOI:10.1190/1.1443099 |
| [18] | Sethian J. Evolution, implementation, and application of level set and fast marching methods for advancing fronts. Journal of Computational Physics , 2001, 169(2): 503-555. DOI:10.1006/jcph.2000.6657 |
| [19] | Sethian J A. Fast marching methods. SIAM review , 1999, 41(2): 199-235. DOI:10.1137/S0036144598347059 |
| [20] | Sethian J A, Popovici A M. Three dimensional traveltimes computation using the Fast Marching Method. Geophysics , 1999, 64(2): 516-523. DOI:10.1190/1.1444558 |
| [21] | Sethian J A. A fast marching level set method for monotonically advancing fronts. Proceedings of the National Academy of Sciences of the United States of America , 1996, 93(4): 1591-1595. DOI:10.1073/pnas.93.4.1591 |
| [22] | Alkhalifah T, Fomel S. Implementing the fast marching eikonal solver: spherical versus Cartesian coordinates. Geophys. Prospect. , 2001, 49: 165-178. DOI:10.1046/j.1365-2478.2001.00245.x |
| [23] | Fomel S. A variational formulation of the fast marching eikonal solver. SEP-95: Stanford Exploration Project , 1997: 127-147. |
| [24] | Kim S. 3-D eikonal solvers: First-arrival traveltimes. Geophysics , 2002, 67(4): 1225-1231. DOI:10.1190/1.1500384 |
| [25] | Rawlinson N, Sambridge M. Wave front evolution in strongly heterogeneous layered media using the fast marching method. Geophysical Journal International , 2004, 156(3): 631-647. DOI:10.1111/gji.2004.156.issue-3 |
| [26] | Rawlinson N, Sambridge M. Multiple reflection and transmission phases in complex layered media using a multistage fast marching method. Geophysics , 2004, 69(5): 1338. DOI:10.1190/1.1801950 |
| [27] | Rawlinson N, Sambridge M. The fast marching method: an effective tool for tomographic imaging and tracking multiple phases in complex layered media. Exploration Geophysics , 2005, 36(4): 341-350. DOI:10.1071/EG05341 |
| [28] | 孙章庆, 孙建国, 韩复兴. 复杂地表条件下基于线性插值和窄带技术的地震波走时计算. 地球物理学报 , 2009, 52(11): 2846–2853. Sun Z Q, Sun J G, Han F X. Travehimes computation using linear interpoiation and narrow band technique under complex topographical conditions. Chinese J.Geophys. (in Chinese) , 2009, 52(11): 2846-2853. |
| [29] | De Kool M, Rawlinson N, Sambridge M. A practical grid-based method for tracking multiple refraction and reflection phases in three-dimensional heterogeneous media. Geophysical Journal International , 2006, 167(1): 253-270. DOI:10.1111/gji.2006.167.issue-1 |
| [30] | Zhao H. A fast sweeping method for eikonal equations. Mathematics of Computation , 2005, 74(250): 603-628. |
| [31] | Zhang Y T, Zhao H K, Qian J. High order fast sweeping methods for static Hamilton-Jacobi equations. Journal of Scientific Computing , 2006, 29(1): 25-56. DOI:10.1007/s10915-005-9014-3 |
| [32] | 兰海强, 张智, 徐涛, 等. 地震波走时场模拟的快速推进法和快速扫描法比较研究. 地球物理学进展 , 2012, 待刊. Lan H Q, Zhang Z, Xu T, et al. A comparative study on the fast marching and fast sweeping methods in the calculation of first-arrival traveltime field. Progress in Geophys. (in Chinese) , 2012, 待刊. |
| [33] | Lan H, Zhang Z. Three-dimensional wave-field simulation in heterogeneous transversely isotropic medium with irregular free surface. Bulletin of the Seismological Society of America , 2011, 101(3): 1354-1370. DOI:10.1785/0120100194 |
| [34] | 阎世信, 刘怀山, 姚雪根. 山地地球物理勘探技术. 北京: 石油工业出版社, 2000 . Yan S X, Liu H S and Yao X G. Geophysical Exploration Technology in the Mountainous Area (in Chinese). Beijing: Petroleum Industry Press, 2000 . |
| [35] | Kao C Y, Osher S, Qian J. Legendre-transform-based fast sweeping methods for static Hamilton-Jacobi equations on triangulated meshes. Journal of Computational Physics , 2008, 227(24): 10209-10225. DOI:10.1016/j.jcp.2008.08.016 |
| [36] | Kimmel R, Sethian J A. Computing geodesic paths on manifolds. Proceedings of the National Academy of Sciences of the United States of America , 1998, 95(15): 8431-7435. DOI:10.1073/pnas.95.15.8431 |
| [37] | Lelièvre P G, Farquharson C G, Hurich C A. Computing first-arrival seismic traveltimes on unstructured 3-D tetrahedral grids using the Fast Marching Method. Geophysical Journal International , 184(2): 885-896. DOI:10.1111/gji.2011.184.issue-2 |
| [38] | Qian J, Zhang Y T, Zhao H K. A fast sweeping method for static convex Hamilton-Jacobi equations. Journal of Scientific Computing , 2007, 31(1): 237-271. |
| [39] | Qian J, Zhang Y T, Zhao H K. Fast sweeping methods for Eikonal equations on triangular meshes. SIAM Journal on Numerical Analysis , 2008, 45(1): 83-107. |
| [40] | Sethian J A, Vladimirsky A. Fast methods for the Eikonal and related Hamilton-Jacobi equations on unstructured meshes. Proceedings of the National Academy of Sciences of the United States of America , 2000, 97(11): 5699. DOI:10.1073/pnas.090060097 |
| [41] | Appelo D, Petersson N. A stable finite difference method for the elastic wave equation on complex geometries with free surfaces. Communications in Computational Physics , 2009, 5(1): 84-107. |
| [42] | 孙章庆, 孙建国, 张东良. 二维起伏地表条件下坐标变换法直流电场数值模拟. 吉林大学学报: 地球科学版 , 2009, 39(3): 528–534. Sun Z Q, Sun J G, Zhang D L. 2D DC electric field numerical modeling including surface topography using coordinate transformation method. Journal of Jilin University: Earth Science Edition (in Chinese) , 2009, 39(3): 528-534. |
| [43] | Hestholm S, Ruud B. 2-D finite-difference elastic wave modeling including surface topography. Geophys. Prosp. , 1994, 42: 371-390. DOI:10.1111/gpr.1994.42.issue-5 |
| [44] | Lan H, Zhang Z. Seismic wavefield modeling in media with fluid-filled fractures and surface topography. Applied Geophysics , 2012, 9(3): 301-312. DOI:10.1007/s11770-012-0341-5 |
| [45] | Tessmer E, Kosloff D. 3-D elastic modeling with surface topography by a Chebychev spectral method. Geophysics , 1994, 59: 464. DOI:10.1190/1.1443608 |
| [46] | 兰海强, 刘佳, 白志明. VTI介质起伏地表地震波场模拟. 地球物理学报 , 2011, 54(8): 2072–2084. Lan H Q, Liu J, Bai Z M. Wave-field simulation in VTI media with irregular free surface. Chinese J.Geophys. (in Chinese) , 2011, 54(8): 2072-2084. |
| [47] | 孙建国. 复杂地表条件下地球物理场数值模拟方法评述. 世界地质 , 2007, 26(3): 345–362. Sun J G. Methods for numerical modeling of geophysical fields under complex topographicaI conditions:a critical review. Global Geology (in Chinese) , 2007, 26(3): 345-362. |
| [48] | Lan H, Zhang Z. Comparative study of the free-surface boundary condition in two-dimensional finite-difference elastic wave field simulation. Journal of Geophysics and Engineering , 2011, 8: 275-286. DOI:10.1088/1742-2132/8/2/012 |
| [49] | Sun J, Sun Z, Han F. A finite difference scheme for solving the eikonal equation including surface topography. Geophysics , 2011, 76(4): T5-T63. |
| [50] | Lan H, Zhang Z. Topography-dependent eikonal equation and its solver for calculating first-arrival travel times with an irregular surface. Geophysical Journal International,2012a,in review. http://cn.bing.com/academic/profile?id=2012988286&encoded=0&v=paper_preview&mkt=zh-cn |
| [51] | 刘一峰, 兰海强. 曲线坐标系程函方程的求解方法研究. 地球 物理学报 , 2012, 55(6): 2014–2026. Liu Y F, Lan H Q. Study on the numerical solutions of the eikonal equation in curvilinear coordinate system. Chinese J.Geophys. (in Chinese) , 2012, 55(6): 2014-2026. |
| [52] | Lan H, Zhang Z. A high order fast sweeping scheme for calculating first-arrival travel times with an irregular surface. Bull. Seismol. Soc. Am., 2012b, in review. |
| [53] | Hvid S L. Three dimensional algebraic grid generation . Technical University of Denmark, 1994. |
| [54] | Thompson J, Warsi Z, Mastin C. Numerical grid generation: foundations and applications. 1985, North-holland Amsterdam. http://cn.bing.com/academic/profile?id=1542333376&encoded=0&v=paper_preview&mkt=zh-cn |
| [55] | Hestholm S, Ruud B. 3-D finite-difference elastic wave modeling including surface topography. Geophysics , 1998, 63: 613-622. DOI:10.1190/1.1444360 |
| [56] | Tessmer E, Kosloff D, Behle A. Elastic wave propagation simulation in the presence of surface topography. Geophys. J. Int. , 1992, 108(2): 621-632. DOI:10.1111/gji.1992.108.issue-2 |
| [57] | Alton K, Mitchell I M. Fast marching methods for stationary Hamilton-Jacobi equations with axis-aligned anisotropy. SIAM J. Numer. Anal , 2008, 47: 363-385. |
| [58] | Sethian J A, Vladimirsky A. Ordered upwind methods for static Hamilton-Jacobi equations. Proceedings of the National Academy of Sciences , 2001, 98(20): 11069. DOI:10.1073/pnas.201222998 |
| [59] | Tsai Y H R, Cheng L T, Osher S, et al. Fast sweeping algorithms for a class of Hamilton-Jacobi equations. SIAM Journal on Numerical Analysis , 2004: 673-694. |
| [60] | Kao C Y, Osher S, Qian J. Lax-Friedrichs sweeping scheme for static Hamilton-Jacobi equations* 1. Journal of Computational Physics , 2004, 196(1): 367-391. DOI:10.1016/j.jcp.2003.11.007 |
| [61] | Sethian J A. Level Set Methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science. Cambridge University Press. 1999 . |
| [62] | Luo S, Qian J. Factored singularities and high-order Lax-Friedrichs sweeping schemes for point-source traveltimes and amplitudes. J. Comput. Phys. , 2011, 230: 4742-4755. DOI:10.1016/j.jcp.2011.02.043 |
| [63] | Lin C T and Tadmor E. L1-stability and error estimates for approximate Hamilton-Jacobi solutions. Numer. Math. , 2001, 87: 701-735. DOI:10.1007/PL00005430 |
| [64] | Qian J, Symes W W. Finite-difference quasi-P traveltimes for anisotropic media. Geophysics , 2002, 67: 147-155. DOI:10.1190/1.1451438 |
 2012, Vol. 55
2012, Vol. 55