2. 中国科学院计算地球动力学重点实验室,北京 100049
2. Key Laboratory of Computational Geodynamics, Chinese Academy of Sciences, Beijing 100049, China
在计算地震引起的同震与震后形变过程中,地球一般被简化为平面半空间模型或者球对称模型,但实际地球是一个三维不均匀球体:东亚地区的S波速度结构展现出很强的横向扰动[1];P 波速度场与球对称模型相比大约存在1%的横向偏差[2-3];等等;上述结论都是利用经典射线理论计算获得,如果利用更高精度的有限频率波理论计算,横向扰动的幅度将在此基础上扩大30% 左右[4].鉴于此,在很多高精度计算领域必须考虑实际地球横向不均匀结构的影响,因而有必要发展基于三维不均匀地球模型的形变理论.另一方面,随着GPS,卫星重力等大地测量技术的发展,大地测量观测精度目前已经达到非常高的水准,利用大地测量观测技术已可探测地球内部三维不均匀结构的变化,并已经积累了大量的优质观测资料,这些高精度观测资料期待基于三维不均匀地球模型的形变理论对其进行更精确的解释.
震源模拟的方法很多,其中影响最大的是位错理论.地震学家基于不同的地球模型和不同的位错类型建立了各种各样的位错理论.由于简洁的计算公式和快捷的计算速度,基于平面半空间地球模型的平面位错理论[5-7]被广泛应用于计算地球对地震、火山的响应,以及反演地震断层模型.然而,由于平面半空间位错理论没有考虑地球曲率、成层结构以及横向不均匀结构等影响,该理论的有效性仅局限于震源周围地区(如100km 以内),且计算精度有限.基于球对称、非旋转、完全弹性和各向同性地球模型的弹性球体位错理论[8-13]以及基于粘弹性地球模型的震后形变理论[14-15]反复表明,地球曲率以及成层结构对地震形变的影响非常大:对于震源深度为20km 的位错,地球成层结构对垂直形变的影响在全地球的平均值达到同震信号的25%左右,且震源深度越深,影响越大[16].
也有不少学者致力于以更接近实际地球的三维不均匀球形地球模型为基础推导地震形变计算公式.Pollitz[17]以横向不均匀粘弹性地球模型为基础建立了一个震后形变理论,研究地震产生的震后位移与震后应变.他首先基于粘弹性自由震荡理论推导出以球对称地球模型为基础的地震位错引起的震后形变计算公式,然后依据震荡模耦合理论计算地球的非对称结构对震后形变的响应.由于Pollitz的理论[17]是以自由震荡理论为基础建立的,有其固有的局限性,即当地球模型的结构相对复杂化后,自由振荡模的数目就会大幅度增加,甚至变为无限,从而出现难以克服的数值困难,因此该理论不适合研究实际三维不均匀地球对地震的响应.为克服Pollitz的理论中出现的困难,Fu & Sun[18]以Sun的球体位错理论[8]以及Molodenskiy的扰动方法[19-21]为基础提出一个建立在位错格林函数基础上的新算法,用来计算地球的横向不均匀结构对同震重力变化的影响,但该算法公式推导过程复杂,给出的计算公式不够简洁,阅读起来相对困难.
本文重建了Fu & Sun[18]的计算公式,改正了Fu & Sun[18]中存在的符号错误,可用来高精度计算地球表面各类重力仪器观测到的同震重力变化.同时,本文扩展了Fu & Sun理论的应用范围,给出了计算地球外部空间固定点同震重力变化计算公式,可用来高精度解释GRACE 卫星观测到的2008年汶川Mw8.0地震、2010 年智利Mw8.8 地震以及2011年日本Mw9.0 地震等伴随的同震重力变化[22-23].本文给出的计算公式完全在复数域推导完成,推导过程与计算公式相对简洁,计算精度更高.这个新算法适合研究实际地球内部中长波长横向不均匀结构对同震重力变化的响应,特别适合对空间重力卫星观测数据进行高精度解释.另外,本文给出的计算公式只需简单修改即可直来计算同震位移.
2 球对称地球模型中位错产生的同震重力变化本文以球对称、非旋转、完全弹性和各项同性(SNREI)地球模型[24]为基础开始研究,这个地球模型中含密度参数ρ(r),重力参数g(r),拉梅参数λ(r)和μ(r),其中变量r指的是相对于地心的距离.地球由于内力或者外力作用而产生的弹性形变可由平衡方程,应力应变关系以及泊松方程来表达[25-27].
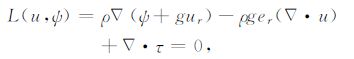
|
(1) |
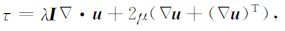
|
(2) |

|
(3) |
式中,u是位移矢量,ψ(r)指重力位变化,τ 是应力张量,I 是一致性张量,G是牛顿重力常数.为了避免操作过大的数值,我们把地球假设为一个无量纲的单位球进行公式推导:把地心处λ 和ρ 的值设定为弹性参数和密度的单位,地表的重力值g0 设定为重力的单位,地球半径a设定为长度的单位.于是,地球形变和位场变化可以展开成一系列球函数的叠加[26].
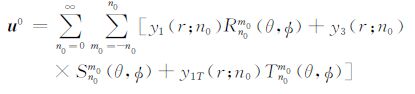
|
(4) |
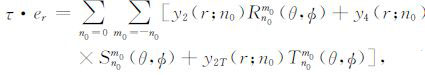
|
(5) |
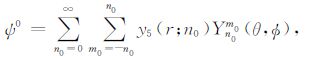
|
(6) |
式中,完全正规化球函数在复数域可表示为

|
(7) |

|
(8) |
这里,Pm0n0(cosθ)代表缔合拉格朗日多项式,θ 代表地球的余纬.变量y1(r;n0)和y3(r;n0)分别代表垂直方向和水平方向的球形解位移分量,变量y2(r;n0)和y4(r;n0)分别代表垂直方向和水平方向的球形解应力分量,y1T(r;n0)和y2T(r;n0)代表对应的环形解分量,y5(r;n0)代表位场变化.上下标0 标明是基于SNREI地球模型的形变,与接下来以三维不均匀地球模型为基础的形变场与位场变化相区分.在方程(4)-(6)中,球面矢量函数表述如下:
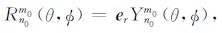
|
(9) |
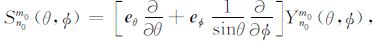
|
(10) |
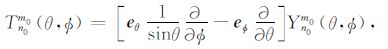
|
(11) |
在这些方程中,er,eθ 和e$\phi $ 是球坐标系的单位矢量.为了方便,我们依照Takeuchi& Saito[26]定义:

|
(12) |
把(4)-(6)和(12)代入方程(1)-(3)可得到一阶偏微分方程组
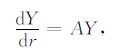
|
(13) |
式中,Y= (y1,…,y6)t,A是依赖于半径r,调和级数n和地球模型的系数矩阵.A的直接表达式可从参考文献[27]中找到.无量纲的表达式可从参考文献[8]中找到.在一定的边界条件下对六阶线性方程组(13)进行积分就可以得到它们的解,关于积分的详细讨论见参考文献[8, 26].
为了研究地震位错引起的同震重力变化,我们依据Sun等[12]的研究思路定义点源位错模型(图 1):在直角坐标系(e1,e2,e3 )中,径向距离rs 的地方有一个无限小的位错面dS,其滑动矢量v,法线矢量n,滑动角λd,倾角δ.单位矢量e1 和e2 分别位于赤道面上经度为$\phi $ =0和π/2所对应的方向,e3 位于极轴上.两个面的相对运动(位错)定义为(U/2)-(-U/2)=U.因此,震源的位移矢量Uv和法线矢量n可表示为

|
图 1 位于坐标系(e1,e2,e3)中的位错模型.滑动矢量v,法线矢量n滑动角λd和 倾角δ位错面之间的相对运动定义为(U/2)-(-U/2)=卩(参照Sun等[12]]) Fig. 1 A dislocation model expressed using slip vector v,normal n,slip angle λd and dip angle δ in the coordinate system of(e1,e2,e3). Relative movement of the two fault sides is defined as (U/2) - ( - U/2) =U (after Sun et al.,[2006]) |
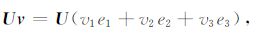
|
(14) |
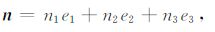
|
(15) |
对于张裂位错,滑动方向与法线方向一致:v=n.为了公式展开的简便,我们把震源的位置设定在北极.任意位置的位错产生的形变可以通过坐标转换的方式得到.
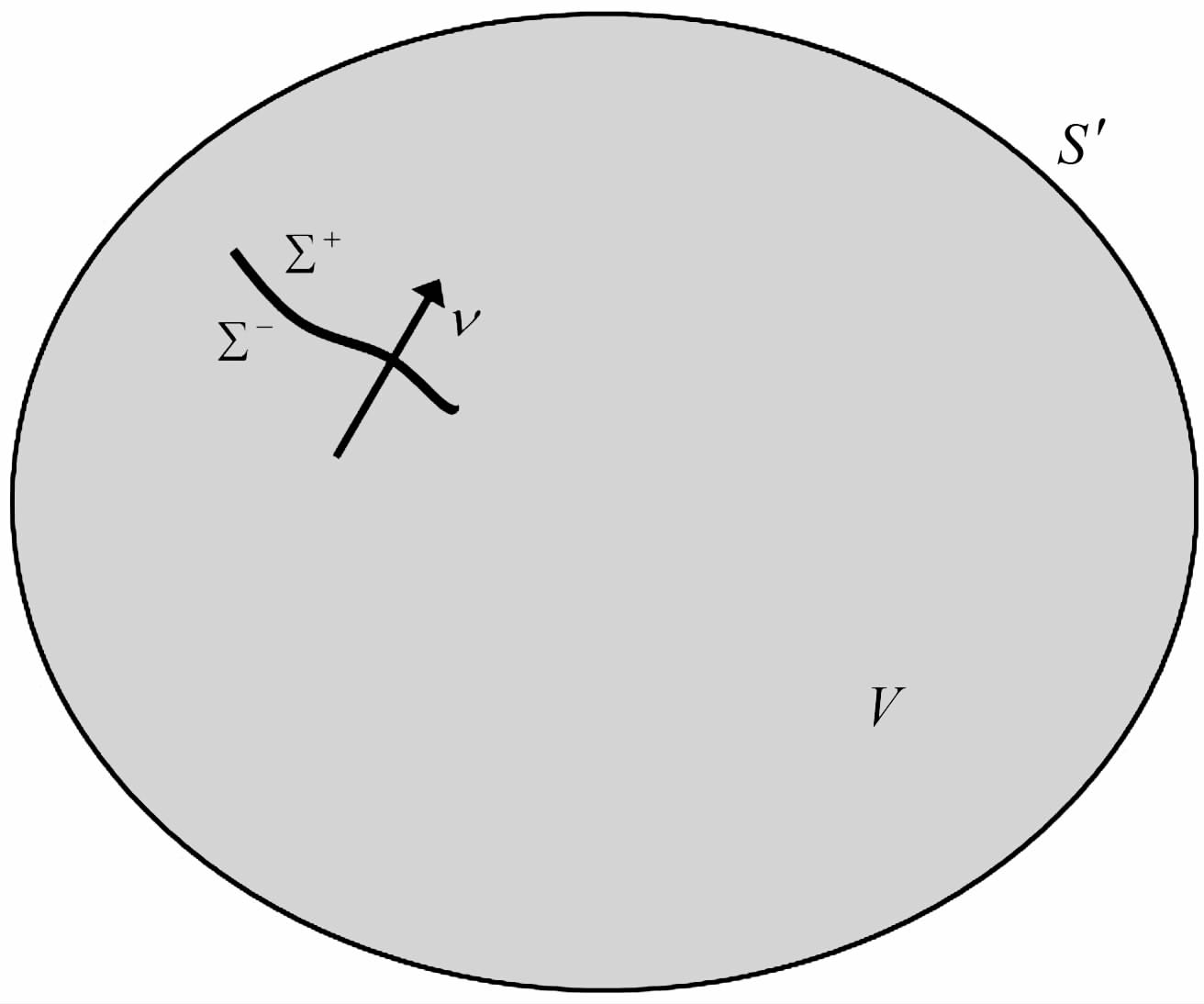
平衡方程(1)在完全弹性的连续介质中成立.但是,如果地球内部震源处产生位错,连续介质破裂,则该处的位移场不连续,平衡方程(1)在整个地球内部就不再满足,此时对于震源的处理相对困难.为解决这一难题,如图 2所示,我们可以把位错面即破裂面看成地球内部两个相连的内表面Σ+ 和Σ-,则地球的表面就可以认为由外表面S′ 和内表面Σ++Σ-共同组成,在外表面与内表面内部即S′+Σ++Σ- 围绕的空间内介质连续,其内部介质满足平衡方程(1).该思想的详细论述见Aki& Richards撰写的经典文献《定量地震学》[28]第三章第一节,并在Sun等的球体位错理论[13]中得到良好的应用.又因为震源(双力偶)可用内部边界来替代并可表示为震源函数,地球内部位错问题就可转化为外部力源问题,从而可用潮汐或者载荷问题同样的思路求解.于是,在地球外表面r=1处自由边界条件
|
图 2 体积为V,外表面为S′的连续介质内部存在一个位错面Σ .位错面Σ 沿法线方向n的位移可能不连续,在外表面与内表面内部即S′+Σ++Σ- 围绕的空间内部介质连续 Fig. 2 A dislocation Σ berried in a continuous medium with volumeV and external surface S′。The displacement along the normal direction of the dislocation Σ is not continuous.However,the medium between the external and internal surfaces S′+Σ++Σ- is continuous |

|
(16) |
和内表面r=rs 处源函数
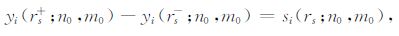
|
(17) |
的控制下,方程组(13)可求解.式中rs±=rs±ε,ε是一个无限小的正函数.源函数si(rs;n0,m0)的表达式见参考文献[26].
Sun[8]第一次利用数值积分法计算了球对称地球模型中地震引起的同震重力变化.本文参照Sun[8]的研究思路进行研究:方程组(13)的积分分成两步完成:从地心积到地表的普通积分和从震源积到地表的特殊积分.两个积分之和在地表满足自由边界条件(16),从而决定最终解.
3 地球横向不均匀结构对重力变化的影响相对于球对称地球模型,实际地球存在较小的横向扰动δρ(r,θ,$\phi $),δλ(r,θ,$\phi $)和δμ(r,θ,$\phi $),由于这些微扰的存在,我们不能把基于三维不均匀地球模型的形变场像(4)-(6)一样直接展开.但是,我们可利用扰动方法计算地球的横向不均匀结构对重力场的贡献,具体地说,我们可依照Molodenskiy的方法[19]把基于三维不均匀地球模型的形变场(u,ψ)展开成拉格朗日多项式,又因为地球的非球对称结构相对较小,对(u,ψ)一阶近似展开就足够满足计算精度[20-21, 29-30].
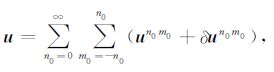
|
(18) |

|
(19) |
式中:
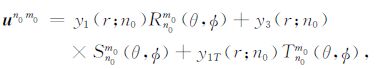
|
(20) |

|
(21) |
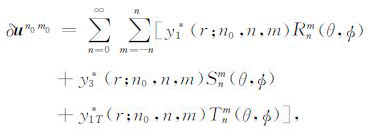
|
(22) |

|
(23) |
与yi(r;n0)有关的项是球对称解即基于球对称地球模型的球形解和环形解.与yi*(r;n0,n,m)有关的项是扰动解即地球横向不均匀结构的响应.一旦yi*(r;n0,n,m)系数全部得到,即可利用(22)-(23)直接计算位移和位场变化的扰动解(δun0m0 ,δψn0m0)进而计算地球的横向不均匀结构对同震重力变化的响应.
依据Molodenskiy 的潮汐理论[19-20],我们利用Betti互换定律以及扰动方法推导出yi*(r;n0,n,m)的完整表达式.yi*(r;n0,n,m)表达式的具体推导过程比较复杂,其详细表达式见附录A.
对于三维不均匀地球模型而言,用地震波速度模型和密度模型来表达比较方便.因此我们把弹性参数λ 和μ 转换成变量${V_{\rm{p}}} = \sqrt {\left( {\lambda + 2\mu } \right)/\rho } ,{V_{\rm{s}}} = \sqrt {\mu /\rho } $和密度ρ.这里Vp,Vs和ρ代表球对称地球模型的值,δVp 和δVs 代表小的横向非对称增量.同时定义$\alpha = \frac{{\delta {V_{\rm{p}}}}}{{{V_{\rm{p}}}}},\beta = \frac{{\delta {V_{\rm{s}}}}}{{{V_{\rm{s}}}}}$和$\gamma = \frac{{\delta \rho }}{\rho }$.于是δλ 和δμ 可表达为:
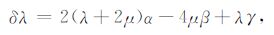
|
(24) |

|
(25) |
因此yi*(r;n0,n,m)可表达为
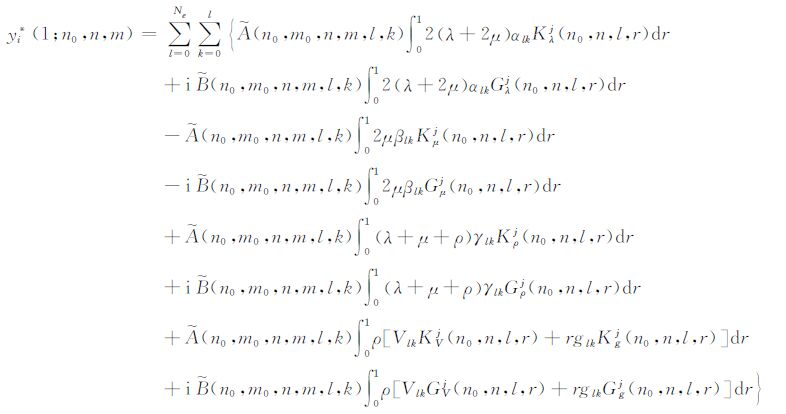
|
(26) |
式中,λ,μ和ρ 表示球对称地球模型中深度r处的弹性参数和密度.当j=1,2,3,4时,利用方程(26)就可分别得到y1*(1;n0,n,m),y3* (1;n0,n,m),y5*(1;n0,n,m)和y1T*(1;n0,n,m).最后,把方程(26)代入方程(22)和(23)就可得到地球的横向增量δλ,δμ 和δρ 对地表形变和位场变化的影响.方程(26)中各参数的详细表达式见附录B 和附录C,j确定边界条件,其选取原则见附录A 中方程(A27).
由于所谓的三角关系[31],即n,n0 和l组成的三角必须满足∣n0 -l∣<n<n0+l;m,m0 和K组成的三角必须满足m=m0 +K,于是可得到如下形变地球表面同震重力变化表达式:

|
(27) |
式中m=m0 +K.剔出垂直形变对重力场的贡献可得到空间固定点同震重力变化计算公式:
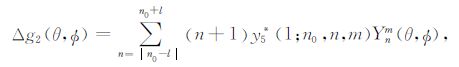
|
(28) |
位错引起的同震重力变化δg可用九个特殊解的组合来表达[8]:

|
(29) |
方程△gij相对于i和j是对称的,即
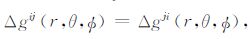
|
(30) |
因此独立位错源△gij的个数减少为六个.为了方便,我们选择图 3所示的六个点震源进行研究:一个垂直走滑位错△g12,两个垂直倾滑位错△g31 和△g32,三个相互垂直面内的张裂位错△g11,△g22 和△g33.任意地震震源可用这六个特殊震源的组合表达.

|
图 3 六个特殊震源.从左到右:垂直走滑位错△g12,垂直倾滑位错△g32,垂直面上的张裂位错△g22,水平面上的张裂位错△g33,垂直走滑位错△g31和另一个垂直面上的张裂位错△g11 Fig. 3 Six special seismic sources. From left to right: a vertical strike slip △g12,a vertical dip slip △g32,a tensile fracturing on a vertical plane △g22,a tensile fracturing on a horizontal plane △g33,a vertical dip slip △g31 and a tensile fracturing on avertical plane△g11 |
对于位错问题,三维响应可分为两个部分:震源的响应和地球横向不均匀结构的响应.前者可应用球体位错理论计算得到[13]:依据三维不均匀地球模型震源处弹性参数(μ+δμ,λ+δλ)和球对称地球模型震源处弹性参数(μ,λ),把它们分别带入震源函数,然后利用球体位错理论分别计算同震重力变化,二者之差即是震源的三维响应.此处的计算是利用球对称地球位错理论,地球模型中只有震源处的弹性参数有所变化.后者则可利用前面章节描述的扰动方法求解.如附录A 所述,表达地表形变扰动量的球谐系数可以通过对Fj(δρ,δλ,δμ)的积分得到,Fj(δρ,δλ,δμ)的核函数依赖于三维不均匀地球模型,球对称解和辅助解,可通过准解析的方式计算得到.因此,如果已知三维地球结构模型和球对称解就可以计算地球横向不均匀结构对同震重力变化的影响.
基于球对称地球模型,Sun等[13]给出了计算垂直走滑位错产生的地表同震垂直位移和位场变化的计算公式:

|
(31) |
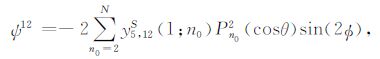
|
(32) |
式中N表示截断阶数.对应的同震重力变化(球对称解)为

|
(33) |
式中,上下标12标示震源的类型:此处12代表垂直走滑位错.方程(31-33)表述基于球对称地球模型的球对称解.上述方程(31-33)是非正规化的,可把方程(33)转化成复数域正规化形式

|
(34) |
式中,m0 =2;yi,12(1;n0)是正规化系数,正规化因子cn0m0由方程(2.8)确定.依据前面章节的讨论,地球横向不均匀结构引起的地表重力变化扰动解可表达为
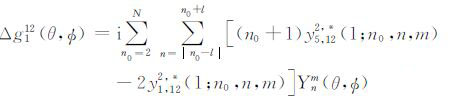
|
(35) |
式中,m= m0 +K.我们可利用球体位错理论[13]计算出的球对称解作为本计算的输入函数,然后利用附录A 给出的方程(A35)和(A28)计算yi,122,* (1;n0,n,m).最后可剔出垂直位移对重力场的贡献而得到空间固定点扰动重力变化:

|
(36) |
与垂直走滑位错△g12 的讨论相同,我们可分别得到垂直倾滑位错△g32,垂直平面上的张裂位错△g22,以及水平平面上的张裂位错△g33 的扰动解(见附录D).另外两个特殊震源△g31 和△g11 可用△g32 和δg22 的公式进行计算,但坐标需要旋转.例如,由于球对称地球模型的对称性,球对称解△gL31可以通过对△gL32旋转π/2得到:
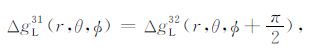
|
(37) |
这个方程意味着球对称解△gL31 与△gL32 不独立.因此,对地球坐标旋转π/2就可利用和计算△g32 完全相同的方案计算△g31.同样也可利用计算△g22 的方案计算△g11.
4.3 极轴上的倾斜位错根据Sun & Okubo[9],任意位错的滑动矢量v和法线矢量n可用断层面的倾斜角λd 和滑动角表达.

|
(38) |
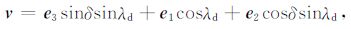
|
(39) |
如果滑动矢量v与位错面平行(剪切问题),我们有
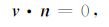
|
(40) |
对于剪切问题,滑动矢量v与法线矢量n的组合可表达为

|
(41) |
于是,任意剪切位错的解可表达为
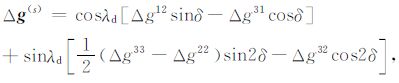
|
(42) |
在三维不均匀地球模型中△g13 与△g32 的解相互独立.如果v与位错面垂直,则可得到张裂位错表达式

|
(43) |
于是滑动矢量v与法线矢量n的组合变为
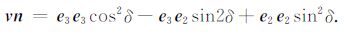
|
(44) |
最后任意张裂位错的解可表达为:

|
(45) |
上面的推导中我们假设地震因子g0UdS/a3 =1,因此得到的结果是无量纲的数值.对于实际的物理问题,我们必须在最终的结果上(如方程42 和45)乘上地震因子g0UdS/a3.其中a=6371km,g0为地表重力值,U为位错量,dS为位错面.
4.4 任意位置的倾斜位错上述讨论都是把震源设定在北极展开,任意位置的位错产生的重力变化可通过选择适当的坐标系统并通过坐标转换得到.具体地说,我们可选择震源作为坐标系统原点(图 4),所有方程以及三维不均匀地球模型均在此坐标系统下展开并进行计算.然后可通过如下三角公式实现新坐标与地理坐标之间的转换(图 5).
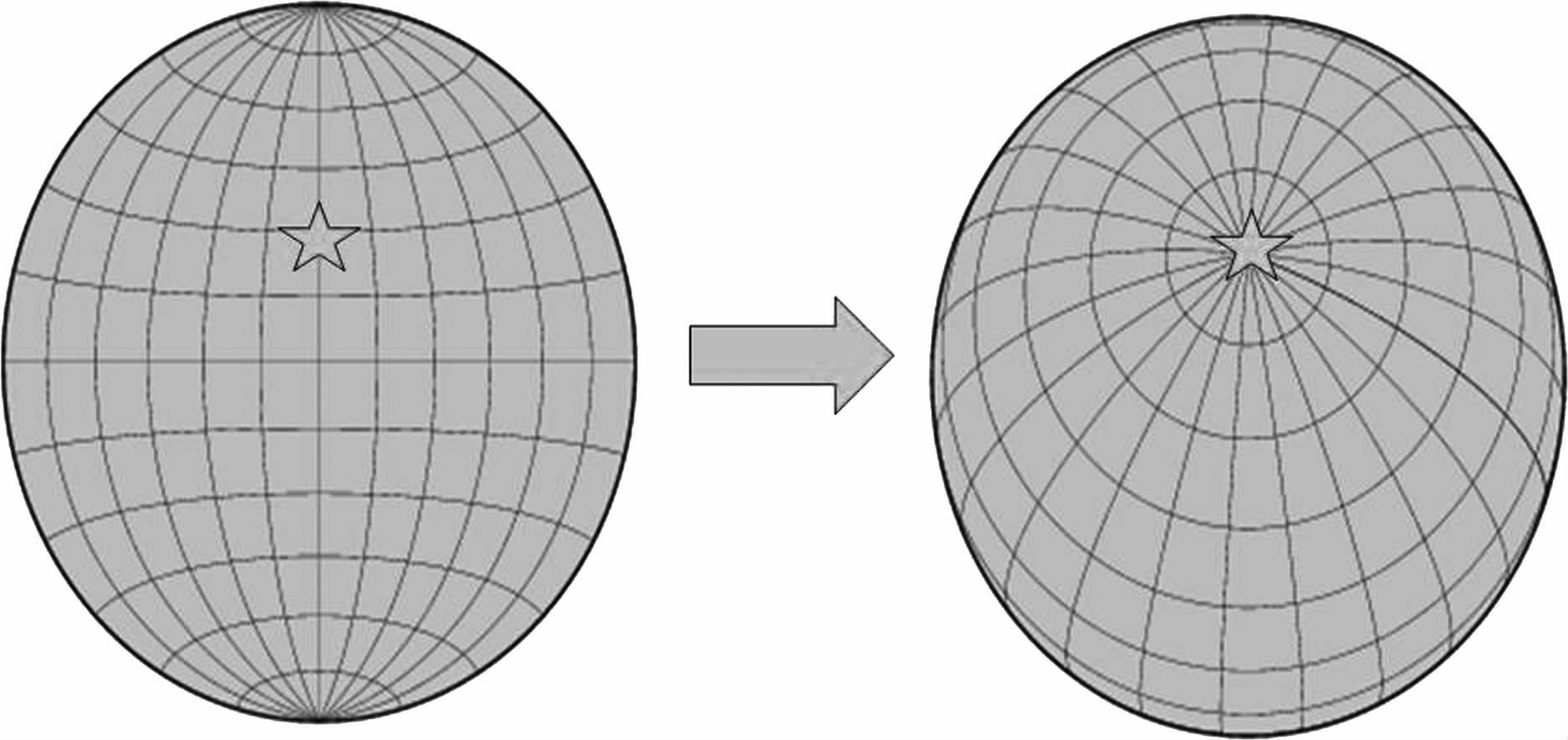
|
图 4 从传统的地理坐标系转换到新的转换坐标系.在转换坐标系中震源位于坐标远点.左:地理坐标系;右:转换坐标系 Fig. 4 Sketchof the coordinate system transformation from a conventional geographical system to a new one with the epicenter as the origin: Left-Geographical coordinate system; Right-transformed coordinate system |

|
图 5 北极,位错点与观测点之间的球面三角关系 Fig. 5 Spherical triangular relation between the north polar, ob^^ervation point and dislocation source |

|
(46) |
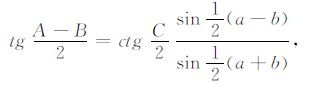
|
(47) |

|
(48) |
最后把计算得到的同震重力变化转回到传统的地理坐标即可.
5 三维不均匀球形地球模型本节讨论三维不均匀球形地球模型.Zhao[2]给出了一个全球三维P 波速度分布模型,该模型依据地震波资料反演得到,其水平分辨率为5°,垂向分别率为15~330km.在上地幔,大陆区域的分辨率比海洋区域高;但是在下地幔,除了南极地区以外空间分辨率都比较好.依据Zhao的模型[2]可知,相对于着名的球对称地球模型PREM[32],全球P波速度场存在大约为1%的扰动.Zhao的全球P 波速度分布模型是本研究的基础模型.
虽然三维S波速度模型和密度结构模型也可通过不同的方式和数据独立反演获得[33-34],但其空间解析度通常都比三维P 波速度模型低,因此本文利用Karato[35]给出的ρ,Vp 和Vs 之间的经验关系式推导S波速度模型和密度模型.Karato[35]依据岩石试验结果给出了地幔中lnρ/lnVs 和lnρ/lnVp 的比率关系,我们可利用该关系式,依据P 波速度模型推导出S波速度模型和密度模型,这样得到的模型和P波速度模型具有相同的空间解析度.得到的S 波速度模型与PREM 相比具有约2%的扰动,密度模型大约具有0.5%的扰动.另外,我们依据密度模型推导出三维重力和位场分布模型.上述模型构成了完整的三维地球模型,我们可依据其计算同震重力变化扰动解即地球的横向不均匀结构对同震重力变化的响应.
6 数值结果本节给出三个假定的点源位错(垂直走滑位错△g12,垂直倾滑位错△g32 和水平平面上的张裂位错△g33)在地表以及空间固定点产生的同震重力变化数值结果,其他类型地震产生的同震重力变化可利用相似的方法得到.我们设定位错源位于日本南部(30°N,135°E),该点周围地区地球内部结构横向变化比较剧烈,适合研究地球内部结构横向不均匀变化对同震重力变化的影响.研究区域限定为纬度15°-45°;经度115°-155°.各项震源参数见表 1.计算中设定地震参数g0UdS/a3 =1,因而计算结果是无量纲数值.因为同震重力变化扰动解的计算量随震源深度的减少而急剧增加,本文以震源深度为637km 的深震震源为基础进行详细讨论,浅源地震引起的同震重力变化留待下一篇文章讨论.
|
|
表 1 假定点震源各项参数 Table 1 Parameters of the sumed seismic source |
球体位错理论[13]给出了计算位错引起的地表和空间固定点同震重力变化计算公式和计算方法,我们可直接利用Sun 等[13]的算法计算基于球对称地球模型的同震重力变化即球对称解.我们首先计算三个震源引起的地表固定点非扰动同震重力变化(垂直走滑位错△g12,垂直倾滑位错△g32 和水平平面上的张裂位错△g33 的球对称解),其结果见图 6的左半部分.保留球对称解是为了与扰动解进行比较.图 6中,6a指垂直走滑点源位错△g12 产生的同震重力变化,其球对称解呈现四象限分布特征.6c指垂直倾滑点源位错△g32 的解,其球对称解沿断层线分成两个部分,一半重力增加,一半减少,呈现出反对称特征.水平面上的张裂位错△g33 产生的非扰动同震重力变化则呈现同心圆分布特征,震中距越大,同震重力变化越小(6e).其中,张裂位错△g33 产生的同震重力变化最大.本文中,因为我们假设g0UdS/a3 =1,所有的球对称解都是无量纲的数值,对于实际物理问题,我们需要在得到的结果上乘上地震因子${{\hat g}_0}\hat U{\rm{d\hat S/}}{{\hat a}^3}$,其中${\hat a}$=6371km,${{\hat g}_0}$ 为地表重力值,${\hat U}$为位错量,${\rm{d\hat S}}$为位错面.如果深度为637km 的地方发生一个地震,其地震矩为M0=3.19×1022N· m,则图中重力变化的单位为1×10-8m·s-2.
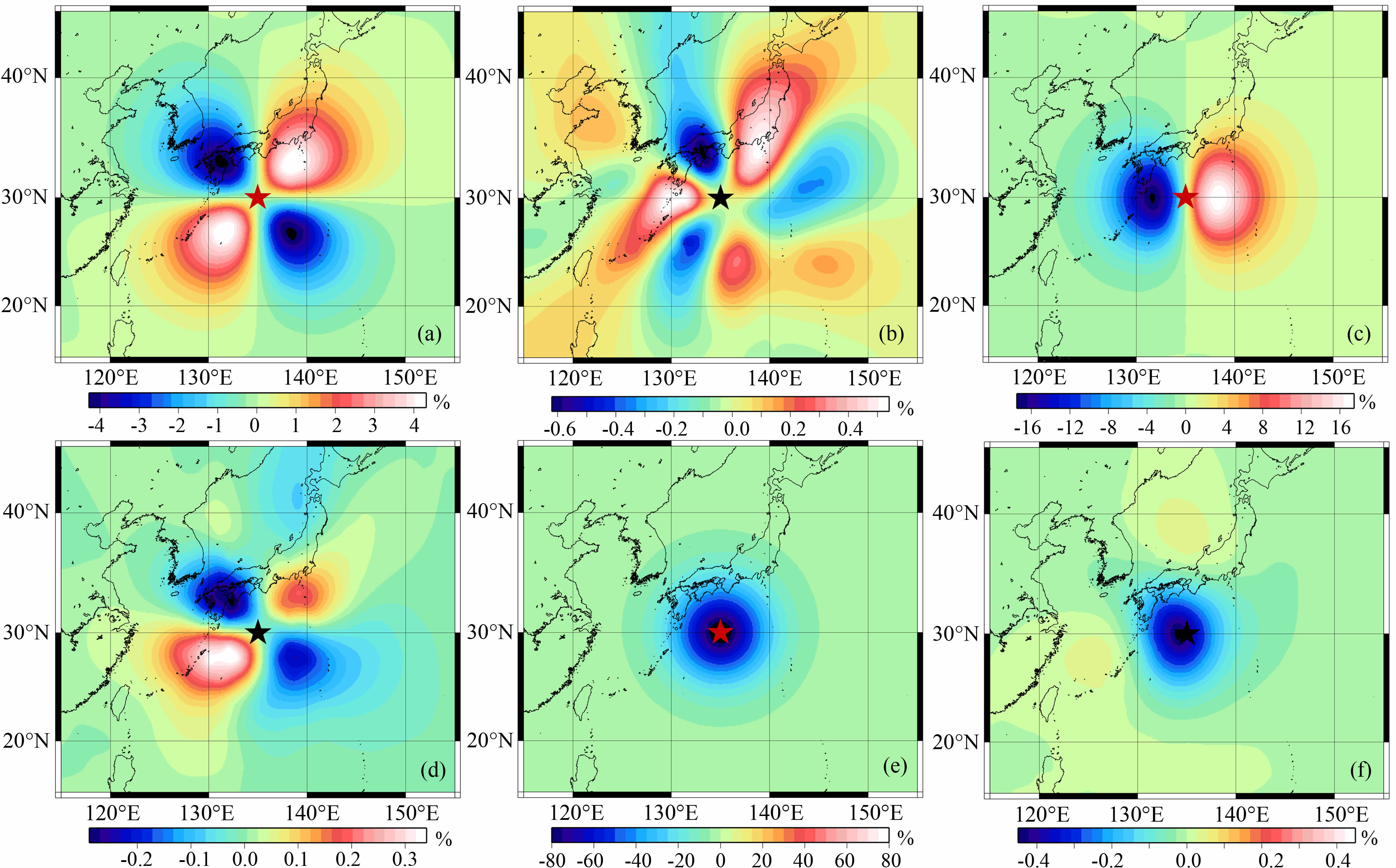
|
图 6 垂直走滑位错,垂直倾滑位错和水平面内的张裂位错产生的地表固定点同震重力变化(球对称解和扰动解)(a)、(b)垂直走滑位错的解;(c)、(d)垂直倾滑位错的解;(e)、(f)水平面内张裂位错的解.(a)、(c)、(e)基于球对称地球模型(PREM)的 球对称解;b)、(d)、(f)三维响应即地球横向不均匀结构对同震重力变化的影响.颜色代表重力变化的大小;星号代表震中位置.因为我 们假设g0UdS/a3 = 1,球对称解为无量纲的数值.扰动解用相对于球对称解最大值的比值来表达 Fig. 6 The unperturbed and perturbed co-seismic gravity changes on deformed earth surface caused by a vertical strike slip,a vertical dip slip and a horizontal opening (a) and (b) Results of vertical strike slip; (c) and (d) Results of vertical dip slip; (e) and (f) Results of horizontal opening; (a),(c) and (e) : The gravity changes on a layered earth model (PREM) ; (b), (d) and (f) : The perturbed gravity changes caused by the lateral inhomogeneous structures (3- D effect). Color represents the magnitudes of gravity changes. Star denotes the epicenter. The unperturbed solutionsare dimensionless because we assume g0UdS/a3 = 1 . The perturbed solutions are expressed as percentages by the ratio with respect to the maximum value of the unperturbed solutions. |
依据小节5描述的三维不均匀地球模型,我们计算上述三个点源地震位错产生的同震重力变化扰动解即地球横向不均匀结构对同震重力变化的影响(三维响应).扰动解的数值结果见图 6.扰动解用相对于球对称解最大值的比值来表达,用百分数表示.例如,因为垂直走滑位错产生的最大同震重力变化的球对称解为4.2(无量纲),所有对应的扰动解都除4.2,然后以百分比的形式表示在图 6中.由于三维地球模型分布的复杂性,绕动解是无规则分布的.因此,我们不能用格林函数的方式[13]来表达扰动解,而只能分别全图表达.
经过与球对称解比较后(图 6),我们分别得到三个点源位错产生的扰动解的相对大小.垂直走滑位错△g12 产生的同震重力变化的扰动解大约占球对称解的0.6% (6b).相似的,垂直倾滑位错△g32和水平张裂位错△g33 的扰动解分别占球对称解的0.2~0.3%(6d)和0.3~0.4% (6f).换句话说,地表固定点的同震重力变化的最大扰动量即地球横向不均匀结构对同震重力变化的影响与震源类型有关,总体上在球对称解的0.5% 左右变动.
同样可研究空间固定点同震重力变化.图 7给出垂直倾滑位错△g32 和水平面的张裂位错△g33 产生的空间固定点同震重力变化,包括球对称解和扰动解(三维响应).比较图 6和图 7发现,空间固定点的三维响应比地表固定点的三维响应稍小,但处在同一个量级上.空间固定点上垂直倾滑位错和水平面张裂位错的三维响应大约分别为非扰动解的0.2%和0.3%.

|
图 7 垂直倾滑位错和水平面张裂位错产生的空间固定点处同震重力变化(球对称解和扰动解).其它讨论同图 6 Fig. 7 The unperturbed and perturbed co-seismic gravity changes on space-fixed point caused by a vertical dip slip and a horizontal opening. Discussions are as in Fig. 6 |
这一节分别讨论三个地球模型对同震重力变化的影响即P 波速度模型,S波速度模型和密度模型的3-D响应.因为位场模型和重力模型是三维密度模型的衍生品,本小节密度的影响包含位模型和重力模型的影响.图 8 基于垂直倾滑位错源给出3 个地球参数在地表固定点的三维响应.结果显示三个模型的三维响应的空间分布完全不同,其中S波速度模型的影响最大,大约是其他模型的3~5倍.
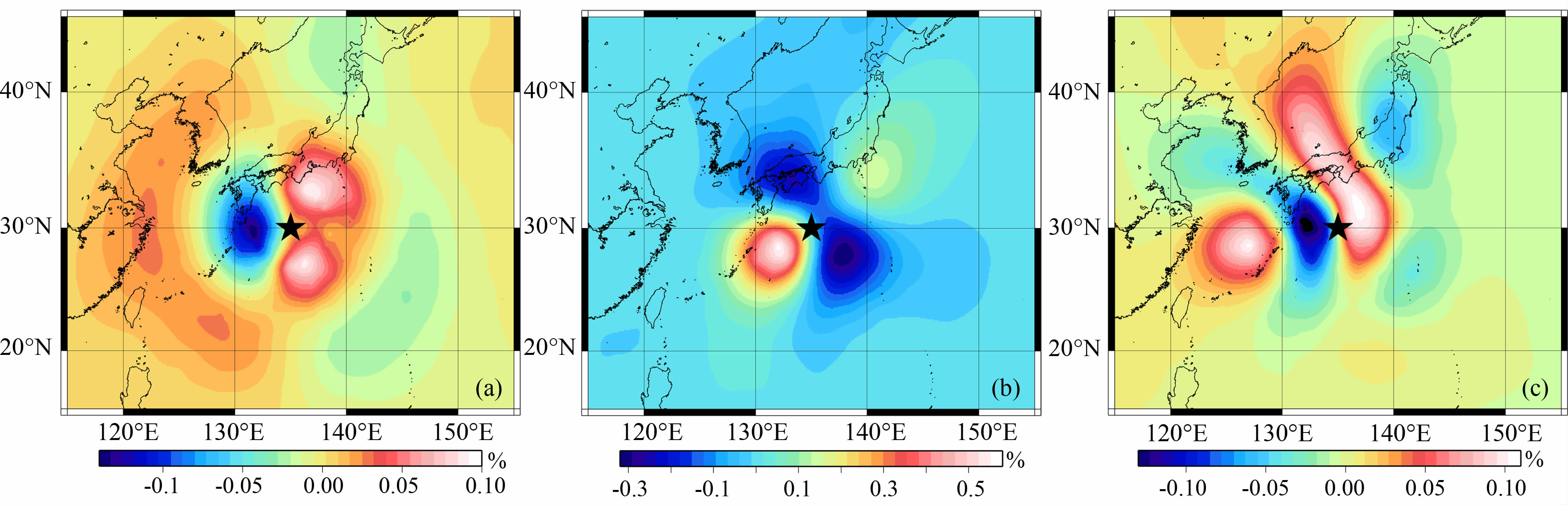
|
图 8 P波速度模型,S波速度模型和密度模型的三维响应(垂直倾滑位错在地表产生的同震重力变化扰动解).左:P波 速度模型的响应;中:S波速度模型的响应;右:密度模型(含位场模型和重力模型)的响应.颜色代表重力变化的大小,星号代表震源,计算结果用相对于球对成解最大值的比值来表达 Fig. 8 The contribution of P-wave velocity, S-wave velocity and density models for perturbed gravity changes on deformed earth surface for a vertical dip slip. Left: contributions of P-wave velocity model; Middle: contributions of S-wave velocity model; Right: the contributions of density model (including potential and gravity models). Color represents the magnitudes of gravity changes. Star denotes the epicenter. The solutions are expressed as percentages by the ratio with respect to the maximum value of the unperturbed solutions |
依据小节2我们知道同震重力变化扰动解由两个部分组成:地球模型的响应和震源的响应,二者可分别用对平衡方程和震源函数的变分或者扰动得到.实际上,震源的响应可利用基于球对称地球模型的位错理论[13]计算得到:只需把三维不均匀地球模型和球对称地球模型中震源处的弹性参数分别带入震源函数,得到两套震源函数值,然后把二者分别带入球体位错理论进行计算,其差值就是震源函数的响应.根据Fu & Sun[18]的讨论,六个特殊震源中,有三个震源存在震源响应(垂直走滑位错,两个垂直面上的张裂位错),另外三个震源的震源响应为零(两个垂直倾滑位错,一个水平面上的张裂位错).图9给出了震源以及地球横向不均匀结构对垂直走滑位错产生的地表同震重力变化的影响.比较可知震源的响应和地球模型的响应处于同一量级.虽然二者都依赖于震源位置,震源的响应对位置的依赖显然更加敏感.
7 结 论依据扰动理论[19-21, 29]和球对称地球位错理论[13],本文给出一个新算法,研究三维不均匀地球模型中地震位错产生的同震重力变化.计算内容包括形变地球表面和空间固定点同震重力变化,其结果可分别用来解释地表重力观测和卫星重力观测数据.具体地说,我们首先计算了球对称地球模型中位错引起的同震重力变化(球对称解),并在其基础上研究地球的横向不均匀结构对地表或者空间固定点同震重力变化的贡献(三维响应).三维响应和球对称解之和即为三维不均匀地球模型中地震引起的同震重力变化.本文中三维响应被刻意分成两个部分:三维地球模型的响应和震源的响应,二者可分别利用对平衡方程的变分以及对震源函数的变分得到.
本文给出了三维不均匀地球模型中六个特殊点位错产生的同震重力变化计算公式:一个垂直走滑位错,两个相互垂直的垂直倾滑位错,一个水平面的上的开裂位错和两个垂直面上的开裂位错.基于这些计算公式,本文还给出了计算任意位置任意类型点位错产生的同震重力变化计算总公式.相较于Fu & Sun[18],本文给出的公式相对简洁.
一套完整的三维不均匀地球模型由三个参数组成:三维P 波速度模型,S 波速度模型和密度模型(包括附加的重力模型和位场模型).因为三维P 波速度模型一般比其他两个模型的精度高,本文依据三维P 波速度模型[2],利用Karato 岩石经验关系式[35],推导出三维S 波速度模型和密度模型,本文同时以密度模型为基础推导出三维重力模型和位场模型.最后,本文依据上述三维地球模型和日本南部的理论点源位错(经纬度:30°N,135°E,深度:637km)进行了理论计算.结果显示最大三维响应随震源的类型而改变,总体上大约为球对称的0.5%左右,三个参数当中S波速度模型影响最大.在三维响应当中,震源响应和地球横向不均匀构造的响应大体上处于同一量级,皆不可忽略.
附录A yi*(r;n0,n,m)的表达式及其推导过程依据Molodenskiy 的潮汐理论[19-20] 以及Takeuchi& Saito 的表达方式[26],我们利用Betti互换定律以及扰动方法可导出勒夫数的偏导数.具体地说,对平衡方程式(1)进行变分可得到
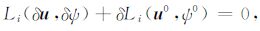
|
(A1) |
式中(δu,δψ)指方程(22)-(23)定义的扰动解即地球横向不均匀结构的影响,(u0,ψ0)为球对称解即初始球对称地球模型对应的解,引数i=1,2,3指解析坐标的三个分量.为了解析计算扰动解(δu,δψ),我们定义辅助解(uj,ψj),它满足如下平衡方程和泊松方程:

|
(A2) |

|
(A3) |
(uj,ψj)为辅助解,是基于球对称地球模型的球对称解,具体值由边界条件确定.辅助解是外部力源如潮汐、剪切力、载荷或者其他力源导致的球对称地球的形变解.方程(A1)乘上辅助解uij,(A2)乘上-δiu,两者相加,三个方向i(i=1,2,3)求和,最后全地球积分,可得如下方程式:
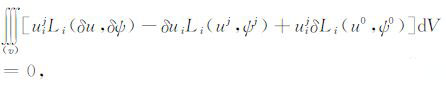
|
(A4) |
式中应用爱因斯坦求和符号,体积v是指整个单位球(r=1)的体积.
方程(A4)可表达为
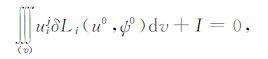
|
(A5) |
其中,
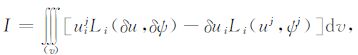
|
(A6) |
方程(1)和(2)是自洽的,所以可使用互换定理进行处理.本文利用互换定理和偏微分,公式(A6)可表达为如下面积分和体积分之和[19]:

|
(A7) |
式中
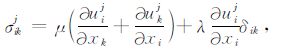
|
(A8) |

|
(A9) |
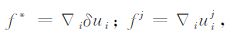
|
(A10) |

|
(A11) |
因为初始边界和扰动边界上零应力边界条件我们得到
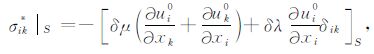
|
(A12) |
于是,应用格林公式和泊松方程(3),方程(A7)变为

|
(A13) |
因为一个常数的导数为零,即
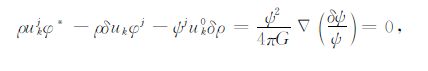
|
(A14) |
我们得到
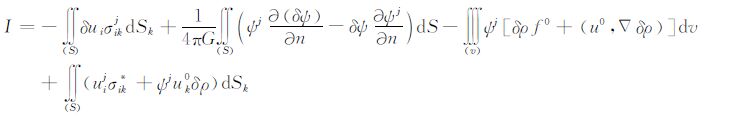
|
(A15) |
把式中前两项展开成球函数,保持其它项不变,积分I变为
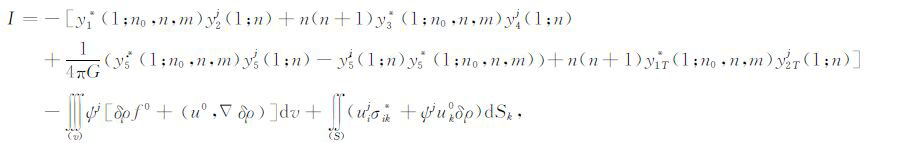
|
(A16) |
式中

|
(A17) |
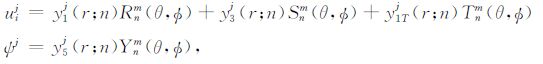
|
(A18) |
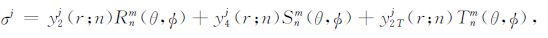
|
(A19) |
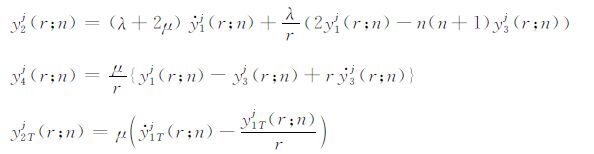
|
(A20) |
依照参考文献[34],我们定义

|
(A21) |
因为方程(A16)中不存在任何扰动解变量,所以积分式I可表达为勒夫数偏导数的函数,从而可求方程(A7)中的球谐系数.换句话说,方程(A7)中的系数可用一组球谐函数表达,这组球谐函数可用辅助解、球对称解以及地球横向不均匀结构模型的函数对整个地球的体积分来表达.于是,把公式(A16)带入方程(A5)可得到
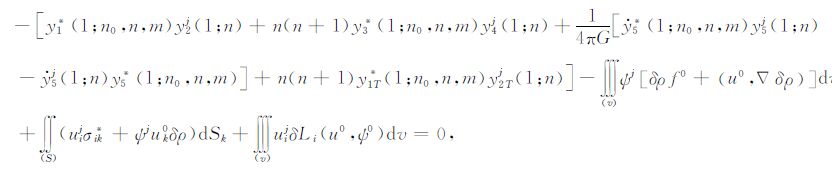
|
(A22) |
利用自由边界y6j(1)=0,以及如下关系
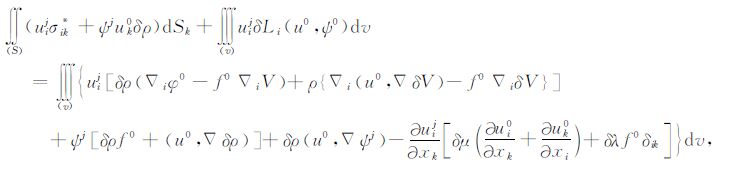
|
(A23) |
方程(A22)变为
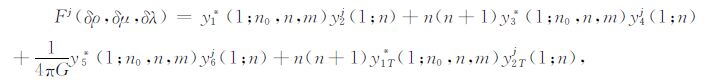
|
(A24) |
这个关系式具体显示了球对称解、三维地球模型、扰动解以及辅助解之间的联系,其中:
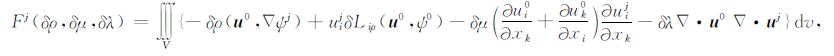
|
(A25) |
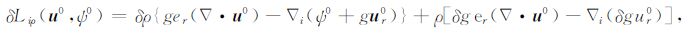
|
(A26) |
在这些方程中,δg是三维地球内部密度的横向扰动而产生的附加重力场,(u0,▽ψj)是内积符号.
假设辅助解由如下边界条件确定:
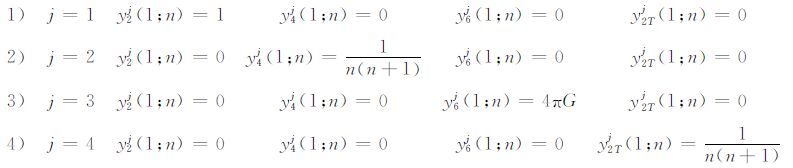
|
(A27) |
通过对角变量的积分就可分别得到

|
(A28) |
如果预先计算出球对称解和辅助解,依据三维地球模型就可计算Fj(δρ,δμ,δλ).换句话说,当我们用方程(A27)给出的边界条件定义辅助解,就可以分别算出方程(A28)中等号右边的系数y1*(1;n0,n,m)、y3*(1;n0,n,m)、y5* (1;n0,n,m)和y1T*(1;n0,n,m),然后把这些系数带入方程(22)和(23),就可得到地球的横向不均匀结构对同震位移以及位场变化的影响,进而可计算地球的横向不均匀结构对重力变化的影响.因为地震问题的时间尺度比地幔动力过程的时间尺度小很多,可把三维不均匀地球看成一个准静态的平衡球体[26],从而可忽略地球内部初始应力的影响.于是,Fj(δρ,δλ,δμ)可解藕成如下三个部分:
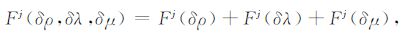
|
(A29) |
它们分别对应δλ,δμ 和δρ 的响应.为了把Fj(δρ,δλ,δμ)展开成球谐函数的形式,我们首先把三维弹性参数模型δλ 和δμ、密度模型δρ、位模型δV以及重力模型δg展开成如下形式:

|
(A30) |

|
(A31) |
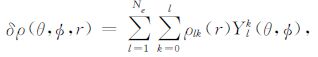
|
(A32) |

|
(A33) |
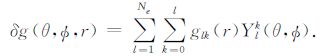
|
(A34) |
方程(A30)-(A34)中,Ne 是指地球模型的最大阶数.Fj(δρ)包含密度模型δρ、附加的位模型δV以及重力模型δg的响应,它们同样可以展开成球谐函数形式.
于是,Fj(δρ,δλ,δμ)可表达成如下形式:
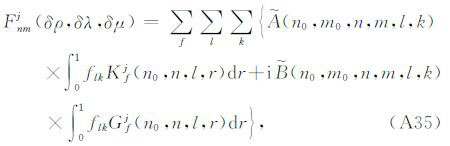
|
(A35) |
式中,f为三维不均匀密度模型(δρ、δV和δg),或者弹性参数模型(δλ 和δμ).核函数K和G的详细表达式见附录C,系数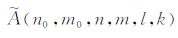
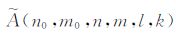
需要注意的是,方程(A27)给出的边界条件是通常表达式,该表达式在一些特别情况下并不满足,此时需要特别考虑.具体地说,当n=0和n=1时,方程(A27)给出的边界条件超定,此时不能用方程(A28)计算系数y1*(1;n0,n,m),y3* (1;n0,n,m),y5*(1;n0,n,m)和y1T*(1;n0,n,m).
对于特例n=0,因为辅助解(uj,ψj)能够满足方程(A27)中j= 1 给出的边界条件,所以y1*(1;n0,0,0)可借(A27)定义的助辅助解确定.但是,由于零阶情况下球函数是一个常数,其导数为0,此时系数y3*(1;n0,n,m)和y1T*(1;n0,n,m)没有实际物理意义.同时,由于地球变形前后总体质量不变,自由空间零阶位δψ 也必须为零.因此可直接得到:

|
(A36) |
对于n=1,因为辅助解(uj,ψj)必须满足一致性关系[25]:

|
(A37) |
方程(A27)定义的辅助解(uj,ψj)与方程(4.2)矛盾,所以也需要特别处理.例如,对于j=1 这种情况,方程(A27)给出的边界条件是y2j(1;1)= 1,y4>j(1;1)=0,y6j(1;1)=0,它们不满足方程(A37),这意味着方程(A27)定义的辅助解超定.为了克服这个困难,我们不利用方程(A27)分别求系数y1*(1;n0,1,m)和y5* (1;n0,1,m),而是假设y4j(1;1)=0,借助方程(A37),可求得g(1)y1*(1;n0,1,m)-y5*(1;n0,1,m)的值.又因为坐标原点定义为地球质心,地球外部的1阶位不存在,所以可直接得到y5*(1;n0,1,m)=0,进而可求得y1 *(1;n0,1,m)的值.同时,假设y2j(1;1)= 0,可利用相同的方法和思路得到y3*(1;n0,1,m).1阶环形解描述的是地球的章动的影响,本文考虑的是地震形变,地球章动的影响可不予考虑,因而可得到y1T*(1;n0,1,m)=0.
关于n= 0,1 情况下的球对称解的讨论见文献[25, 36].
附录B:三个球函数乘积的球面积分地球表面的形变可转化为对整个地球的体积分,该体积分的核函数为三维地球模型、球对称解以及所谓的辅助解(或者它们的导数)的乘积的积分[21, 29].应用球谐函数表达法,这些体积分可分解为一系列径向函数和球面函数积分的乘积.径向积分通常只能从地心数值地积到地表,面积分则由三个球函数及其导数的乘积组成,可数值计算,亦可解析处理.其解析计算公式计算速度快,精度高,在本文中非常重要.
依照Wang[29],单位球面上一个基本类型的球面积分可表达为
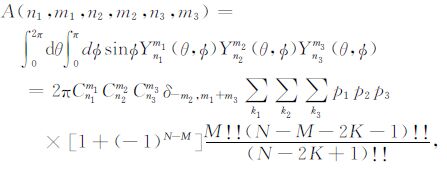
|
(B1) |
式中,Cnm由方程(8)定义,
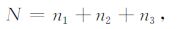
|
(B2) |
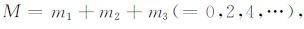
|
(B3) |

|
(B4) |

|
(B5) |

|
(B6) |
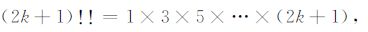
|
(B7) |

|
(B8) |
其中求和符号ks(s=1,2,3)从0求和至(ns-ms)/2.
另一个类型的面积分可表达为

|
(B9) |
式中

|
(B10) |
同样依照Wang[29]可得到
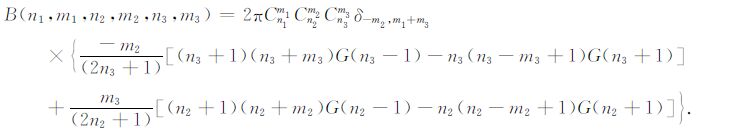
|
(B11) |
这里,G(n3 -1)=G(n1,m1,n2,m2,n3 -1,m3),如此类推.
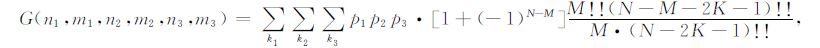
|
(B12) |
这些公式中m1,m2 和m3 非负.
如果三个球谐函数中的一个表达式为复共轭形式
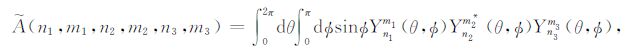
|
(B13) |

|
(B14) |
我们可得到
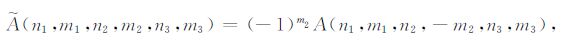
|
(B15) |
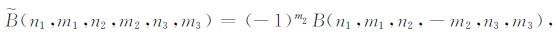
|
(B16) |
在利用扰动方法计算扰动解的过程中,应用方程(B15-B16)是非常方便的.
附录C:Fj(δρ,δλ,δμ)的详细表达式依照Wang[29],扰动解即球对称解(球对称、各向同性、完全弹性地球模型表面因外力产生的形变)的偏导数可用如下积分表达:
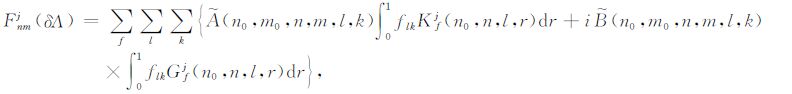
|
(C1) |
这里,δΛ 代表δρ,δλ 或者δμ.flK表示对应的三维不均匀地球模型展开系数(密度和弹性参数).核函数K和G详细表达为

|
(C2) |
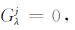
|
(C3) |
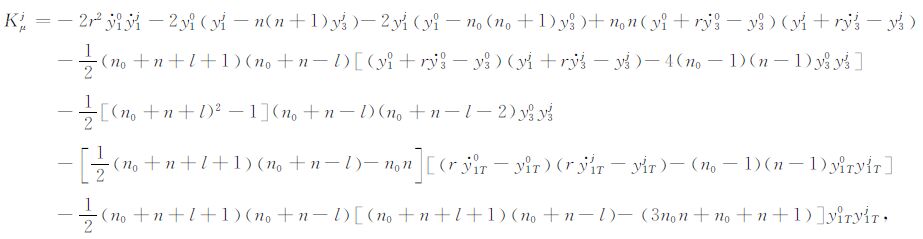
|
(C4) |
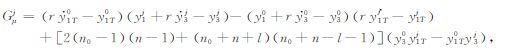
|
(C5) |
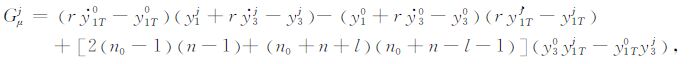
|
(C6) |
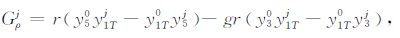
|
(C7) |
上面方程中符号·表示相对于r的偏导.y0(r;n0)和yj(r;n)分别简单表达为y0 和yj.
另外,我们也可进一步考虑位和重力横向不均匀扰动对形变场的响应:
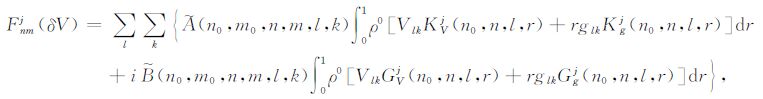
|
(C8) |
式中
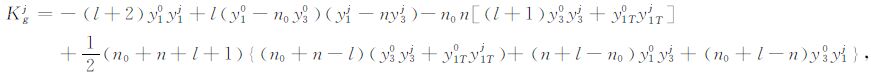
|
(C9) |

|
(C10) |

|
(C11) |
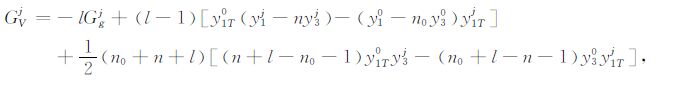
|
(C12) |
(1)垂直倾滑位错δu32
依照Sun等[13],球对称地球模型中一个垂直倾滑点源位错在地球表面产生的垂直位移和位场变化可表达为

|
(D1) |

|
(D2) |
其中N表示截断阶数,上下缀32表示震源类型(垂直倾滑位错).对应产生的重力变化可表达为:
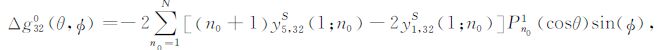
|
(D3) |
方程(D1~3)给出了球对称地球模型中位错引起的重力变化即球对称解.把方程(D3)转化为复数域正规化形式则为:
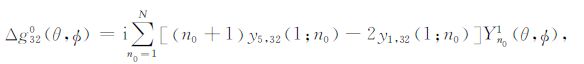
|
(D4) |
于是,相应的地球表面的扰动解则可表达为

|
(D5) |
式中m=m0 +k.该扰动解即为三维地球横向不均匀结构对同震重力变化的影响.yi,32(r;n0)为球对称解,可利用球体位错理论[13]直接计算得到;yi,321,* (1;n0,n,m)为扰动解,可利用方程(A35)和(A28)计算得到.其他讨论与δu12 同.
最后,剔出垂直位移对重力场的贡献,我们可得到空间固定点重力变化扰动解表达式:
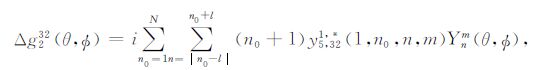
|
(D6) |
(2)垂直面上的开裂位错δu22
依照Sun等[13],球对称地球模型中一个垂直面上的张性开裂位错产生的地球表面上的垂直位移和位场变化可表达为

|
(D7) |
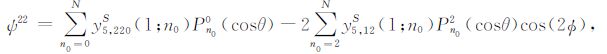
|
(D8) |
式中N为截断阶数,上下标22代表震源类型.方程(D7~8)给出的是球对称解.需要注意的是,此时作为输入的球对称解是yi,220S(r;n0)和yi,12S(1;n0).于是同震重力变化可表达为

|
(D9) |
我们把方程(D9)转化为复数域正规化形式:

|
(D10) |
于是,依照小结4中的讨论,对应的地表扰动解即地球横向不均匀结构的响应可表达为:
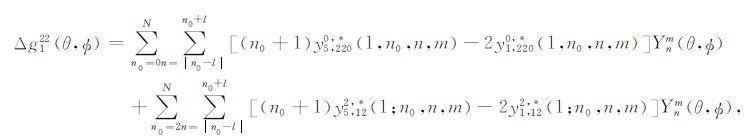
|
(D11) |
式中,m= m0 +k.作为输入的球对称解yi,220(1;n0)和yi,12(1;n0)可利用球体位错理论[13]计算得到.其他讨论与δu12 同.最后,剔出垂直位移对重力场的贡献可得到空间固定点的重力变化扰动解:
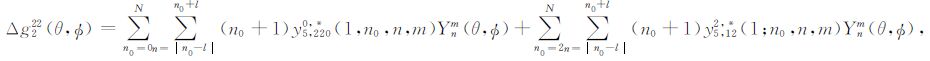
|
(D12) |
(3)水平面上的张裂位错δu33
依照Sun等[13],球对称地球模型中一个水平面上的张裂位错在地球表面产生的垂直位移和位场变化可表达为:

|
(D13) |

|
(D14) |
式中N表示截至阶数.上下缀33表示震源的类型,相应的重力变化可表达为:

|
(D15) |
方程(D15)表示球对称地球模型中重力变化的非扰动解即球对称解.把方程(D15)转化为复数域正规化形式:
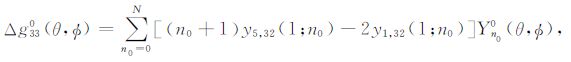
|
(D16) |
于是,依照小节4中的讨论,对应的地球表面上的扰动解即地球横向不均匀结构对同震重力变化的影响可表达为:

|
(D17) |
式中,m=m0 +k.同样,作为输入的非扰动解yi,33(r;n0)可利用球体位错理论[13]计算得到;yi,330,* (1;n0,n,m)可利用方程(A35)和(A28)计算得到.其他讨论与δu12 同.
最后,剔出垂直位移对重力场的影响可得到空间固定点重力变化扰动解:
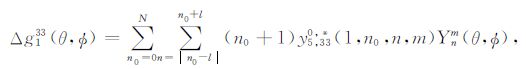
|
(D18) |
感谢R.Wang博士无私提供其博士论文以及用于计算三个球函数乘积积分的计算代码,也感谢D.Zhao博士提供其三维P 波速度模型.感谢匿名审稿者严格的审阅与中肯的修改意见.
| [1] | Friederich W. The S-velocity structure of the east Asian mantle from inversion of shear and surface waveforms. Geophysical Journal International , 2003, 153: 88-102. DOI:10.1046/j.1365-246X.2003.01869.x |
| [2] | Zhao D. Seismic structure and origin of hotspots and mantle plumes. Earth and Planetary Science Letters , 2001, 192: 251-265. DOI:10.1016/S0012-821X(01)00465-4 |
| [3] | Zhao D. Multiscale seismic tomography and mantle dynamics. Gonewana Research , 2009, 15: 297-323. DOI:10.1016/j.gr.2008.07.003 |
| [4] | Montelli R, Nolet G, Dahlen F A, et al. Finite-frequency tomography reveals various plumes in the mantle. Science , 2004, 303: 338-343. DOI:10.1126/science.1092485 |
| [5] | Maruyama T. Statical elastic dislocations in an infinite and semi-infinite medium. Bulletin of the Earthquake Research Institute. University of Tokyo , 1964, 42: 289-368. |
| [6] | Okada Y. Surface deformation due to shear and tensile faults in a half-space. Bulletin of the Seismological Society of America , 1985, 75: 1135-1154. |
| [7] | Okubo S. Potential and gravity changes due to shear and tensile faults in a half-space. Journal of Geophysical Research-Solid Earth , 1992, 97: 7137-7144. DOI:10.1029/92JB00178 |
| [8] | Sun W. Potential and gravity changes caused by dislocations in spherically symmetric earth models. Bulletin of the Earthquake Research Institute, University of Tokyo , 1992, 67: 89-238. |
| [9] | Sun W, Okubo S. Surface potential and gravity changes due to internal dislocations in a spherical earth-I. Theory for a point dislocation. Geophysical Journal International , 1993, 114: 569-592. DOI:10.1111/gji.1993.114.issue-3 |
| [10] | Sun W, Okubo S. Surface potential and gravity changes due to internal dislocations in a spherical earth-П. Application to a finite fault. Geophysical Journal International , 1998, 132: 79-88. |
| [11] | Sun W, Okubo S and Vanicek P. Global displacement caused by dislocations in a realistic earth model. Journal of Geophysical Research-Solid Earth , 1996, 101: 8561-8577. DOI:10.1029/95JB03536 |
| [12] | Sun W, Okubo S and Fu G. Green's functions of co-seismic strain changes and investigation of effect of earth's spherical curvature and radial heterogeneity. Geophysical Journal International , 2006, 167: 1273-1291. DOI:10.1111/gji.2006.167.issue-3 |
| [13] | Sun W, Okubo S, Fu G, et al. General formulations of global co-seismic deformations caused by an arbitrary dislocation in a spherically symmetric earth model-applicable to deformed earth surface and space-fixed point. Geophysical Journal International , 2009, 177: 817-833. DOI:10.1111/gji.2009.177.issue-3 |
| [14] | Tanaka Y, Okuno J and Okubo S. A new method for the computation of global viscoelastic post-seismic deformation in a realistic earth model (I)-vertical displacement and gravity variation. Geophysical Journal International , 2006, 164: 273-289. DOI:10.1111/gji.2006.164.issue-2 |
| [15] | Tanaka Y, Okuno J and Okubo S. A new method for the computation of global viscoelastic post-seismic deformation in a realistic earth model (II)-Horizontal displacement. Geophysical Journal International , 2007, 170: 1031-1052. DOI:10.1111/gji.2007.170.issue-3 |
| [16] | Sun W, Okubo S. Effect of earth's spherical curvature and radial heterogeneity in dislocation studies-for a point dislocation. Geophysical Research Letters , 2002, 29(12): 46. |
| [17] | Pollitz F F. Post-seismic relaxation theory on a laterally heterogeneous viscoelastic model. Geophysical Journal International , 2003, 155: 57-78. DOI:10.1046/j.1365-246X.2003.01980.x |
| [18] | Fu G, Sun W. Surface coseismic gravity changes caused by dislocations in a 3-D heterogeneous earth. Geophysical Journal International , 2008, 172: 479-503. DOI:10.1111/gji.2008.172.issue-2 |
| [19] | Molodenskiy S M. The influence of horizontal inhomogeneities in the Mantle on the amplitude of tidal oscillations. Physics of the Solid Earth , 1977, 13(2): 77-80. |
| [20] | Molodenskiy S M. The effect of lateral heterogeneities upon the tides. BIM| Fevrier , 1980, 80: 4833-4850. |
| [21] | Molodenskiy S M, Kramer M V. The influence of large-scale horizontal inhomogeneities in the Mantle on earth tides. Earth Physics , 1980, 16(1): 1-11. |
| [22] | 周新, 孙文科, 付广裕. 重力卫星GRACE检测出2010年智利Mw8|8地震的同震重力变化. 地球物理学报 , 2011, 54(7): 1745–1749. Zhou X, Sun W and Fu G. Gravity satellite GRACE detects coseismic gravity changes caused by 2010 Chile Mw8.8 earthquake. Chinese Journal Geophysical (in Chinese) , 2011, 54(7): 1745-1749. |
| [23] | 王武星, 石耀霖, 顾国华, 等. GRACE卫星观测到的与汶川Ms8|0地震有关的重力变化. 地球物理学报 , 2010, 53(8): 1767–1777. Wang W, Shi Y, Gu G, et al. Gravity changes associated with the Ms8.0 Wenchuan earthquake detected by GRACE. Chinese Journal Geophysica (in Chinese) , 2010, 53(8): 1767-1777. |
| [24] | Dahlen F A. The normal modes of a rotating, elliptical earth. Geophysical Journal Royal Astronomical Society , 1968, 16: 329-367. DOI:10.1111/gji.1968.16.issue-4 |
| [25] | Farrell W E. Deformation of the earth by surface loads. Reviews of Geophysics and Space Physics , 1972, 10: 761-797. DOI:10.1029/RG010i003p00761 |
| [26] | Takeuchi H, Saito M. Seismic surface waves. Academic Press Inc., 1972. |
| [27] | Alterman Z, Jarosch H, Pekeris C L. Oscillation of the earth. Proceedings of the Royal Society of London. Ser. A , 1959, 252: 80-95. DOI:10.1098/rspa.1959.0138 |
| [28] | Aki K, Richards P G. Quantitative seismology. Freeman, 1980. |
| [29] | Wang R. Tidal deformations on a rotating, spherically asymmetric, visco-elastic and laterally heterogeneous earth. European University Studies, Earth Sciences, Bd. 5, 1991. |
| [30] | Fu G, Sun W. Effects of lateral inhomogeneity in a spherical earth on gravity earth tides. Journal of Geophysical Research-Solid Earth , 2007, 112: B06409. |
| [31] | Jones M N. Spherical harmonics and tensors for classical field theory. Research studies LTD, England, 1985. |
| [32] | Dziewonski A M, Anderson D L. Preliminary reference earth model. Physics of the Earth and Planetary Interiors , 1981, 25: 297-356. DOI:10.1016/0031-9201(81)90046-7 |
| [33] | 王新胜, 方剑, 许厚泽. 华北克拉通岩石圈三维密度结构. 地球物理学报 , 2012, 55(4): 1154–1160. Wang X., Fang J, Hsu H. Density structure of the lithosphere beneath North China Craton. Chinese Journal Geophysica (in Chinese) , 2012, 55(4): 1154-1160. |
| [34] | Peng H, Hu J, Yang H, et al. An effective technique to constrain the non-uniqueness of receiver function inversion. Chinese Journal Geophysical , 2012, 55(4): 1168-1178. |
| [35] | Karato S I. Importance of inelasticity in the interpretation of seismic tomography. Geophysical Research Letters , 1993, 20: 1623-1626. DOI:10.1029/93GL01767 |
| [36] | Okubo S, Endo T. Static spheroidal deformation of degree 1-consistency relation, stress solution and partials. Geophysical Journal Royal Astronomical Society , 1986, 86: 91-102. DOI:10.1111/j.1365-246X.1986.tb01074.x |
 2012, Vol. 55
2012, Vol. 55


