2. Modeling and Imaging Laboratory,University of California,Santa Cruz,U.S.A. 95064
2. Modeling and imaging laboratory,University of California,Santa Cruz,U.S.A. 95064
地震反射波数据是用于获得地下地层构造与油气藏情况的重要工具.随着地震勘探处理技术的发展,叠前深度偏移技术、逆时偏移技术等偏移成像技术迅速地发展起来,同时计算能力的增长使得越来越多的地震数据被用于偏移成像过程中以获得更加精确的成像结果.海量地震数据的出现使得对地震数据压缩的研究具有重要的现实意义.
按照有无信息损失的标准,地震数据压缩方法可以分为有损压缩和无损压缩.本文讨论的压缩方法属于有损压缩方法,这类方法通过一定的变换方法分解地震数据并保留分解后系数中的大分量而达到压缩的目的.因此,在这类压缩过程中,选取合适的变换方法来稀疏地表示地震数据显得尤为重要[1-2].
一类用于数据压缩的变换方法为新兴发展起来的小波变换,它用在图像压缩、语音处理、地球物理信号分析等多个领域,并得到成功而广泛的应用[3],同时研究结果也显现出其在地震数据压缩方面的潜力[4-7].近年来,为了更好地表示图像中沿边缘(alongedge)的特性,许多具有方向特性的类小波变换被研究和发展,包括Curvelet 变换[8-9]、Bandelet变换[10-11]、Shearlet变换[12-14]等.Candes与Demanet证明了作为一种多尺度、多方向的各向异性变换方法,Curvelets可以有效并稀疏地表示波传播算子[15],Curvelet变换也被迅速地应用于地震数据处理[16-19] 中.Douma 等2007 年[20] 提出基于Curvelet变换的2.5 维共偏移距映射时间偏移(common-offset2.5D maptime-migration).Felix等2007 年[21]将压缩感知(compressedsensing)理论与Curvelet变换结合提出压缩波场延拓理论,通过在模域(modaldomain)减少传播算子的维数以及解决相应的最优化问题计算波场的延拓.与各向同性小波变换不同,利用Curvelet变换进行数据分解可以获得数据中的局部斜率信息.然而,Curvelet变换冗余度很大并且仅能最优稀疏表示数据中具有二阶可微奇异性(C2-singularity)的分段连续目标.Fomel与Liu 提出了Seislet变换以便更加直接有效地提取与表示地震波场信息[22].
另一类变换方法为离散余弦变换[23-24].相比小波变换,这类变换方法可以更好地表示振荡特性[1].一方面,通过引入光滑窗口可以进一步构成局部余弦基[25-26],这可以避免因直接使用长方形窗口截取数据而产生的高频大幅值系数;另一方面,通过最优基算法也可以获得自适应局部余弦基,从而更加有效地分解和表示数据[27].吴如山等将局部余弦基变换应用于地震数据分解以及单程波算子分解和传播,并结合局部扰动理论与局部背景参考速度提出了小波束(Beamlet)偏移方法[28-29];毛剑等发展了局部指数标架方法以获得单一的方向性,并进一步应用于方向照明分析[30-31].然而对这些方法的研究均是在频率域内进行的,为了进一步获得时间-频率域的局部化性质,王永忠等将自适应局部余弦基应用于地震数据压缩并讨论了压缩后的数据对偏移成像过程的影响[2],在近期的研究中吴如山等进一步提出了基于时间-空间局部化性质的Dreamlet变换方法并证明Dreamlet原子是定义在观测平面的物理小波(Physicalwavelet)[32],初步的研究工作将这种方法应用于地震偏移成像过程的研究[33-35].时间域局部化性质的引入使得Dreamlet变换对地震数据的表示相对于在频率域使用Beamlet方法更为稀疏;同时,与Curvelet变换相比,Dreamlet变换在能提供局部斜率信息的同时也具有较小的冗余度.
地震数据在时间-空间域的分布需要满足因果关系,同时在频率-波数域也需要满足频散关系.因此,仅简单地应用小波变换或者离散余弦变换分解地震数据不能体现数据本身的特性.Dreamlet的时间-空间-频率-波数域的局域化性质为表示地震数据自身的特性提供了很大的便利.本文从这一特性出发,研究利用该变换方法进行地震数据压缩的方法,并且根据地震数据的特性提出多尺度Dreamlet变换以更加有效地表示地震数据.实验结果表明Dreamlet与多尺度Dreamlet方法可以在实现高压缩比的同时保留地震数据中的大部分重要信息.通过与Curvelet、Beamlet等方法的对比,Dreamlet与多尺度Dreamlet方法在相同的条件下可以获得更高的压缩比.同时使用压缩后的重建数据进行偏移成像的实验也表明,在高压缩比的情况下,多尺度Dreamlet方法可以保留成像结果中的重要结构信息.因此,基于Dreamlet的地震数据压缩可以进一步与偏移成像研究结合实现高效而准确的偏移成像算法.本文的研究基于二维地震数据,可以被进一步推广到三维地震数据.
2 Dreamlet变换 2.1 局部余弦基、局部指数标架与Dreamlet原子与其对地震数据的分解在空间域,局部余弦基的定义为
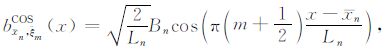
|
(1) |
其中,xn为空间域起始位置,m为对应的波数域指数(局部波数${{\bar \xi }_m} = \pi \left( {m + \frac{1}{2}} \right)/{L_n}$,并且m=0,1,2,…M,Ln=xn+1 -xn为区间长度,Bn为在区间[xn-ε,xn+1 +ε′]上紧支撑的钟形窗函数.
局部余弦基由调制的谐函数构成并且是一组正交基,因此十分适用于分解波场.研究表明,使用局部余弦基表示地震数据具有很好的稀疏性,同时利用局部余弦基获得的小波域单程波传播算子(LCB单程波偏移算子)也是一种高效而且精准的传播算子.然而,与局部余弦基对应的小波束沿深度方向(z轴)并不具有单一的传播方向性,为了构造具有单一传播方向性的小波束,毛剑等更进一步发展与讨论了具有冗余度为2 的局部指数标架.与局部余弦基类似,局部指数标架可以写为
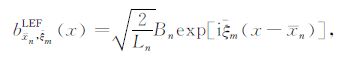
|
(2) |
其中${{\bar \xi }_m} = \pi \left( {m + \frac{1}{2}} \right)/{L_n}$,m=-M…0,1,2,…M.
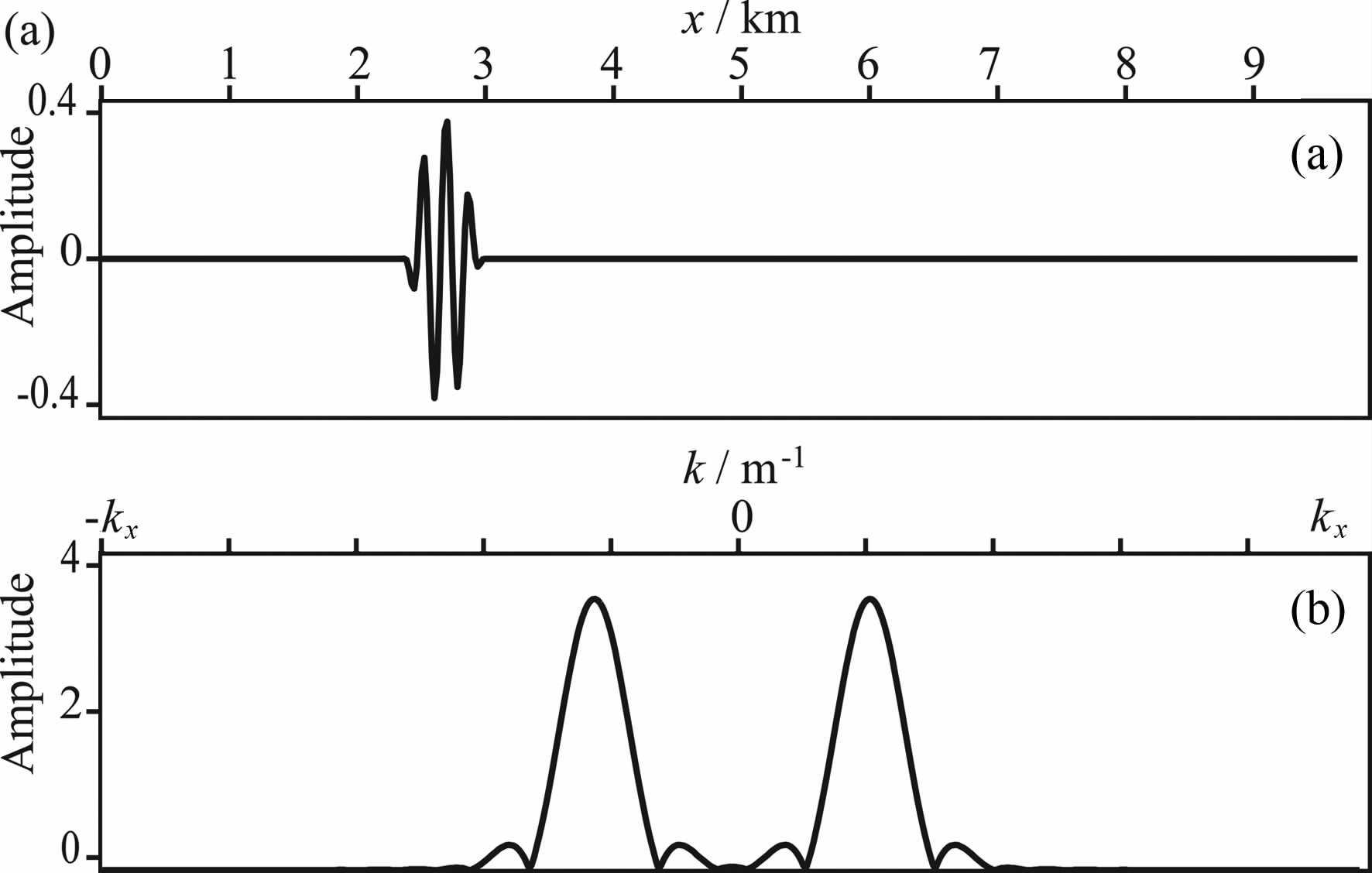
局部余弦基与局部指数标架均可以构成空间域的Beamlet原子bxξ(x).同时,时间域Drumbeat原子gtω(t)的定义与在bxξ(x)空间域的定义类似.图 1给出了由局部余弦基获得的一个原子样本.
Dreamlet原子由空间域Beamlet原子bxξ(x)与时间域Drumbeat原子gtω(t)的张量积构成:
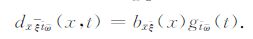
|
(3) |
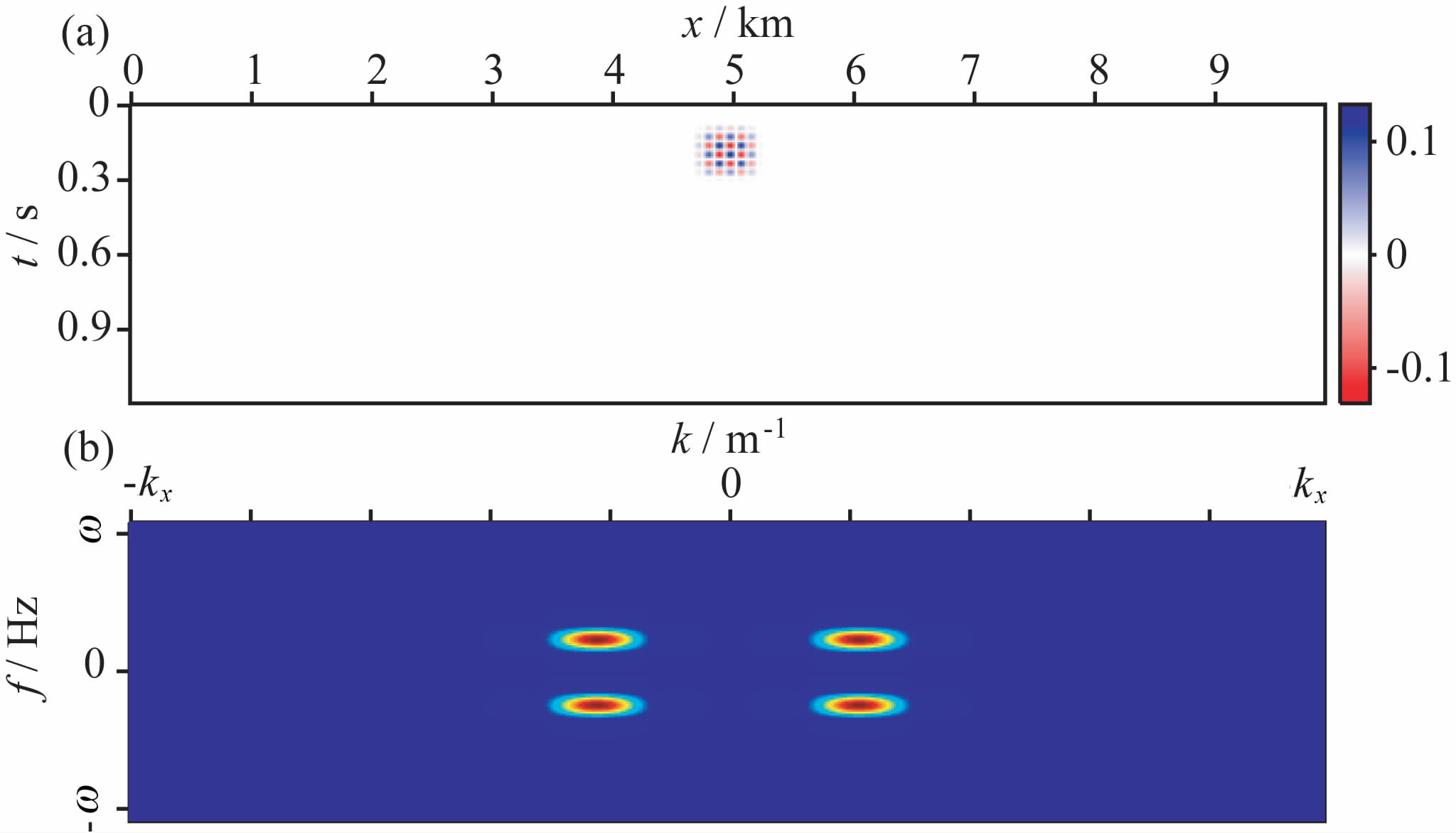
图 2 给出了由局部余弦基获得的一个Dreamlet原子样本.从图中可以看出,Dreamlet原子具有时间-空间的局域化性质;同时,由局部余弦基得到的Beamlet、Drumbeat原子均在对应的变换域中存在2个对称瓣,由此构造出的Dreamlet原子在频率-波数域中具有4个对称波瓣.使用局部指数标架作为Beamlet与Drumbeat原子可以获得在频率-波数域中仅有一个波瓣的Dreamlet原子.
|
图 1 由局部余弦基获得的一个Beamlet原子 (a)在空间域原子的形态;(b)在波数域原子的形态 Fig. 1 A single Beamlet atom obtained by Local Cosine Basis (a) An atom obtained by Local Cosine Basis in space domain; (b) An atom obtained by Local Cosine Basis in wavenumber domain. |
|
图 2 由两个局部余弦基原子张量积获得的 一个 Dreamlet 原子 (a)在空间-时间域原子的形态;(b)在波数-频率域原子的形态 Fig. 2 A single Dreamlet atom obtained by tensor product of Local Cosine Basis (a) An atom in space and time domain;(b) An atom in wavenumber and frequency domain. |
假设地震数据为u(x,t),它可以被局部时间-频率-空间-波数域Dreamlet原子表示为
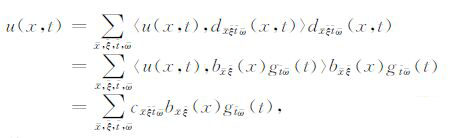
|
(4) |
其中〈,〉表示内积,cxξtω 为分解得到的系数.
2.2 多尺度Dreamlet变换与其对地震数据的分解用Beamlet进行地震数据分解与传播算子的研究通常是在频率域进行并且建立在固定区间长度Ln的基础上的.Dreamlet变换使得对数据分解和传播算子的研究可以直接在时间-空间域进行,Wang等[2]的研究表明通过改变区间长度可以更加有效地表示地震数据.一种改变区间长度的方法为使用二维自适应局部余弦基变换分解地震数据.这种方法通过使用最优基算法计算得到对应于被分解数据的局部余弦四叉树,因此对应的局部余弦基将图像平面划分为不同大小的正方形.利用自适应局部余弦基变换表示具有振荡特性的数据比直接使用局部余弦基具有更为稀疏的特性,然而这种方法仍需要将地震数据当作图像数据来进行处理.另一种改变区间长度的方法为根据地震数据不同频率的频散关系来调节区间长度,这是本文所要研究的内容.
假设v是地表附近的速度,θ 为波传播方向与垂直方向的夹角,ξ,ζ 分别为水平、垂直波数,则波数K与频率ω 应该满足如下频散关系:
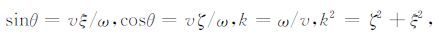
|
(5) |
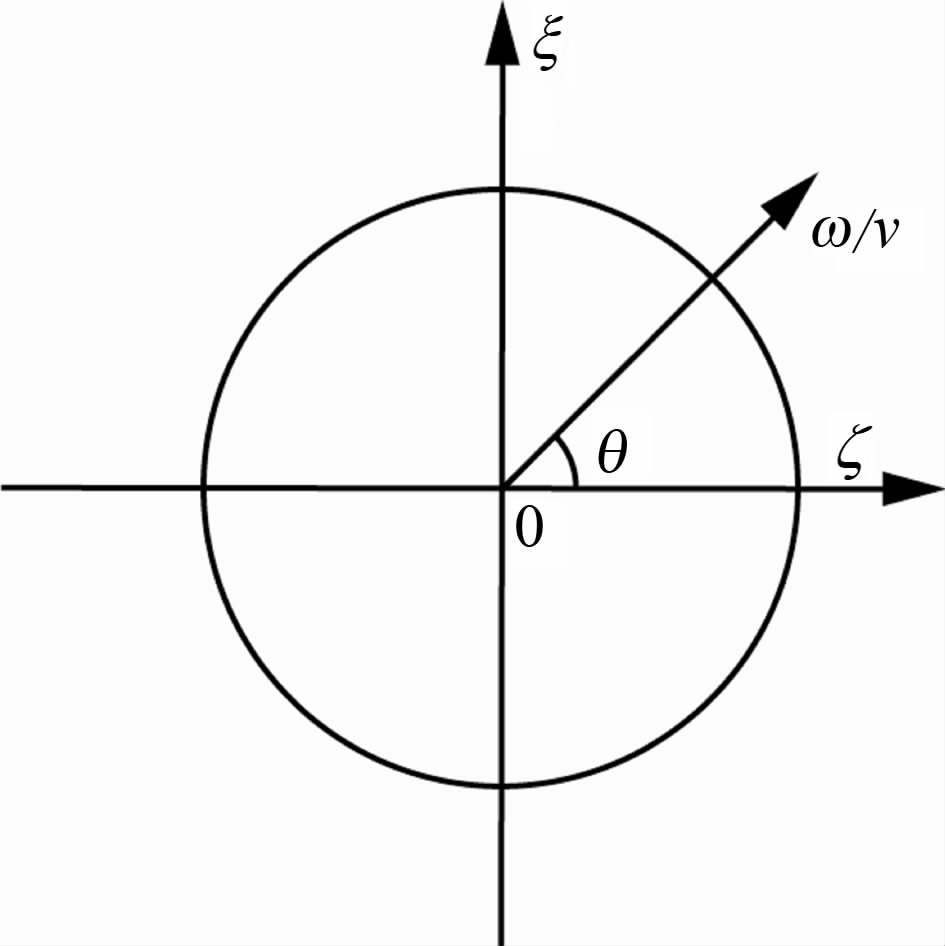
如图 3所示.
|
图 3 色散关系示意图 Fig. 3 Dispersion relationship |
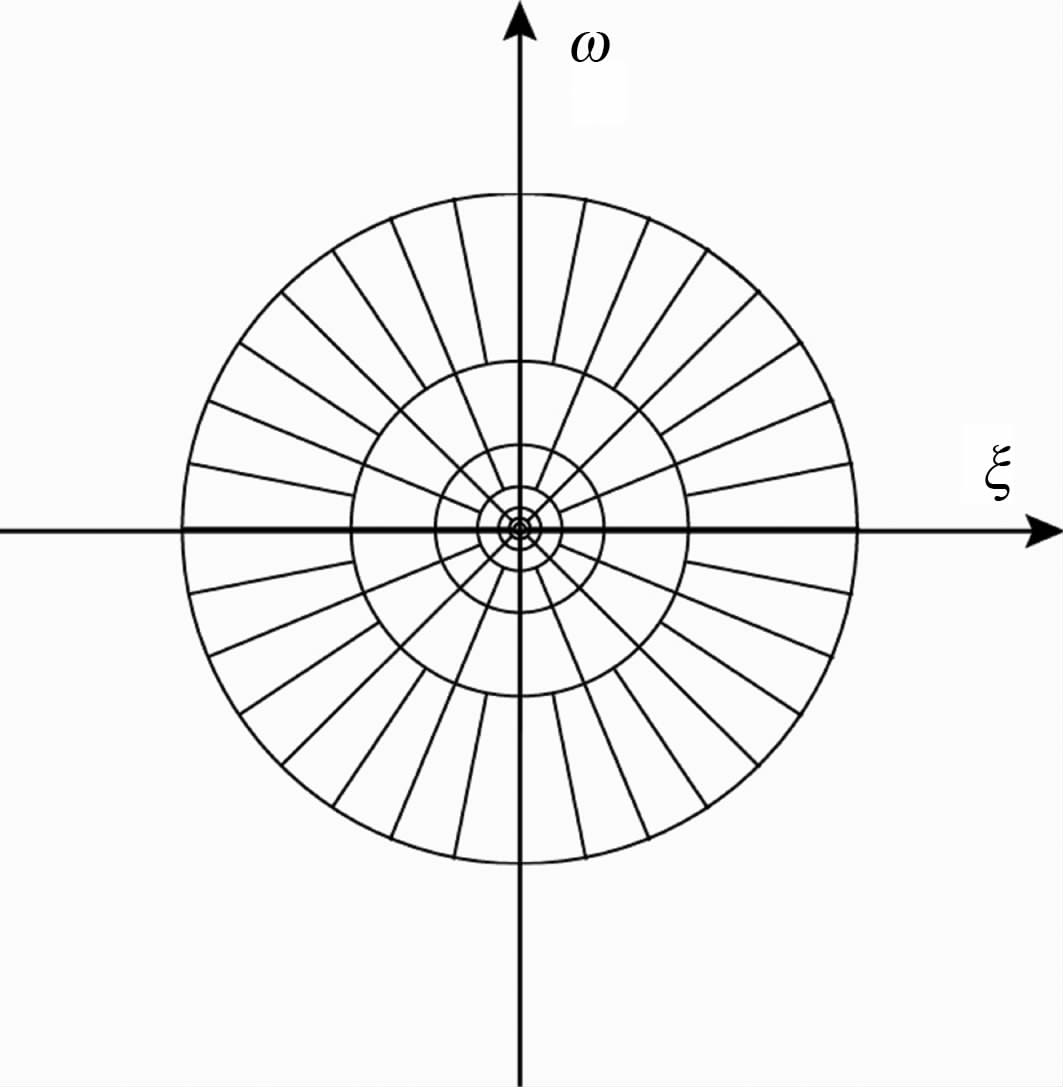
仅将地震数据当作时间-空间域的图像进行处理无法顾及频率域与波数域之间的关系式.如图 4所示为Curvelet变换分解地震数据时对应的频率-波数域的划分,当ω 趋近于零时将无法解释ξ 的取值,因此在频率-波数域中Curvelet变换的角度θ 也不能与满足关系式的波传播方向对应.在Dreamlet变换中,首先对地震数据进行Drumbeat变换,使时间域的数据由中心时间为t、中心频率为ω 的Drumbeat原子表示,然后再通过确定空间区间长度获得Beamlet原子而最终完成Dreamlet变换.因此在每个中心频率处,若根据关系式令空间区间长度Lx取值正比于对应的波长长度λ ,则空间区间长度Lx可以写为
|
图 4 Curvelet 变换对频率波数域的划分 Fig. 4 Curvelet transform in frequency-wavenumber domain |
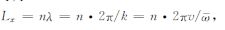
|
(6) |
其中,n取值为任意正整数.此时,频散关系的引入使在对应的频率范围只有空间宽度在一定波长范围的Dreamlet原子被用于分解地震数据,即在不同频段使用不同长度的空间窗分解地震数据.在低频处选择较长的空间窗分析数据;在高频处选择较短的空间窗分析数据.这使得在保留局部余弦/指数变换的时间-空间域的局部变化性质的同时,引入了多尺度分析并将其用于地震数据的分解.与二维自适应局部余弦基变换不同,多尺度Dreamlet变换基于地震数据在频率-波数域内的联系,而不是将地震数据作为简单的图像处理.
3 地震数据压缩算法
地震数据经过Dreamlet变换后,对于每个局部时间和局部空间位置,系数中的大分量主要集中在每个局部频率-波数
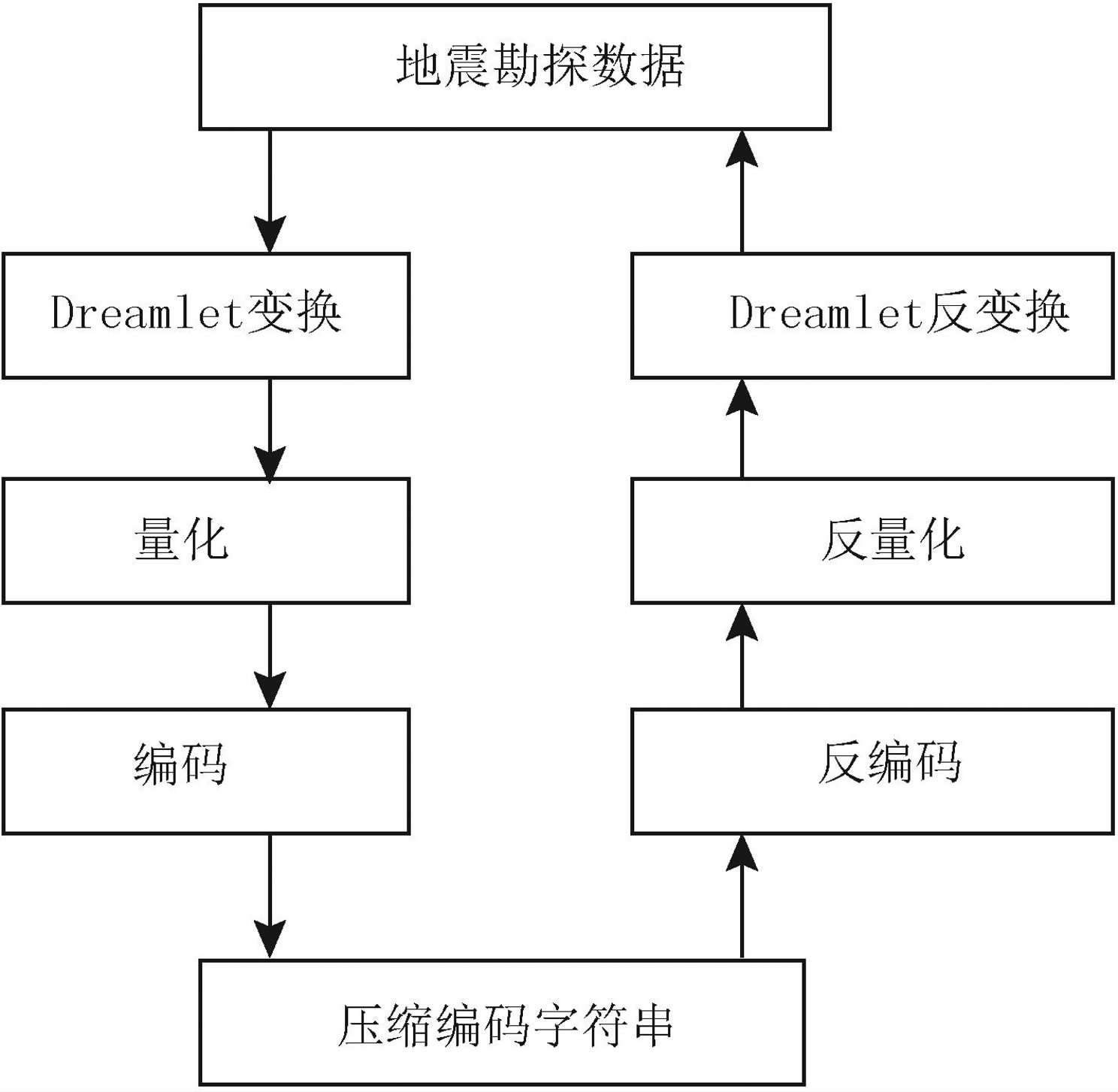
数据压缩与解压缩的过程如图 5所示.
|
图 5 地震数据的压缩/解压算法 Fig. 5 Procedure of seismic data compression/ decompression |
(1)分解:使用Dreamlet变换或者多尺度Dreamlet变换分解地震数据.
(2)取阈值及量化:通常,量化是将一组连续的实数值影射成一组离散的数值,量化可以分为标量量化和矢量量化两种方法.本文使用归一化标量量化.假设T为阈值,c为分解数据后得到的系数,Q为量化权值.则量化过程可以写为

|
(7) |
反量化过程为
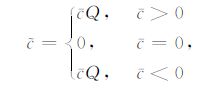
|
(8) |
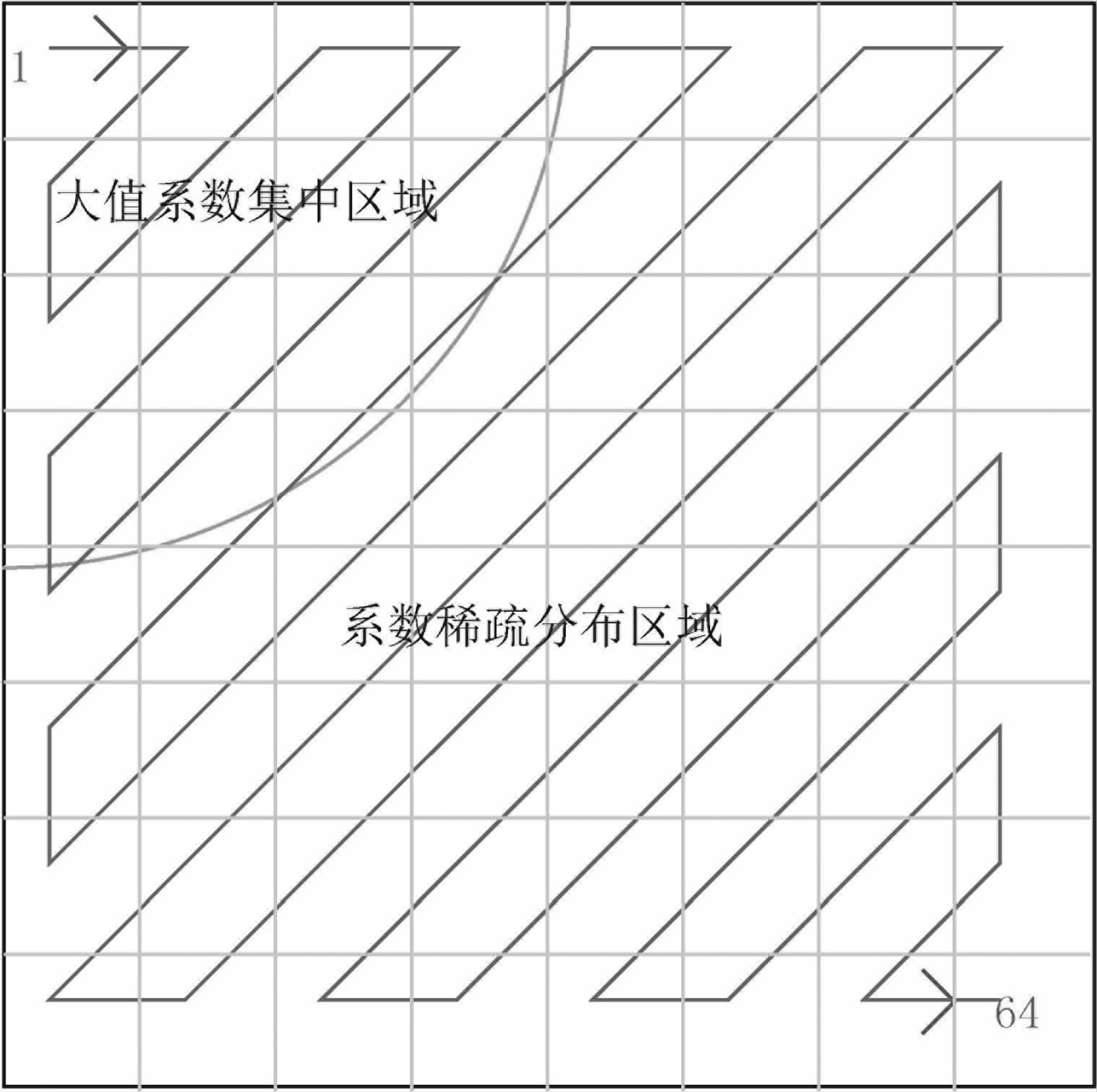
3)编码:与JPEG 标准[24]类似,本文选用游程编码算法.通过Z字形的顺序扫描并存储零系数的个数与非零系数的数值.Z字形顺序扫描序列如图 6所示.
|
图 6 用于扫描一个8×8的(t-ω,x-ζ)块的Z字形秩序 Fig. 6 An 8×8 zig-zag sequence |
为了衡量压缩算法对数据质量的影响,压缩比可以被用来作为衡量压缩算法的标准.压缩比定义为

|
(9) |
同时,地震数据最终将被处理并被用于偏移成像.本文将使用偏移成像结果作为衡量压缩算法的另一个标准.
本文在进行快速局部余弦变换时使用零延拓来处理边界;为了更好地保留地震数据中的弱信号,在使用各种压缩变换方法前对数据进行了同样的振幅增益操作,并且在数据重建后消除了增益的作用;对地震数据及重构数据均使用基于局部余弦基的小波束偏移方法进行偏移成像.
4.1 2D SEG-EAGE 叠后数据算例
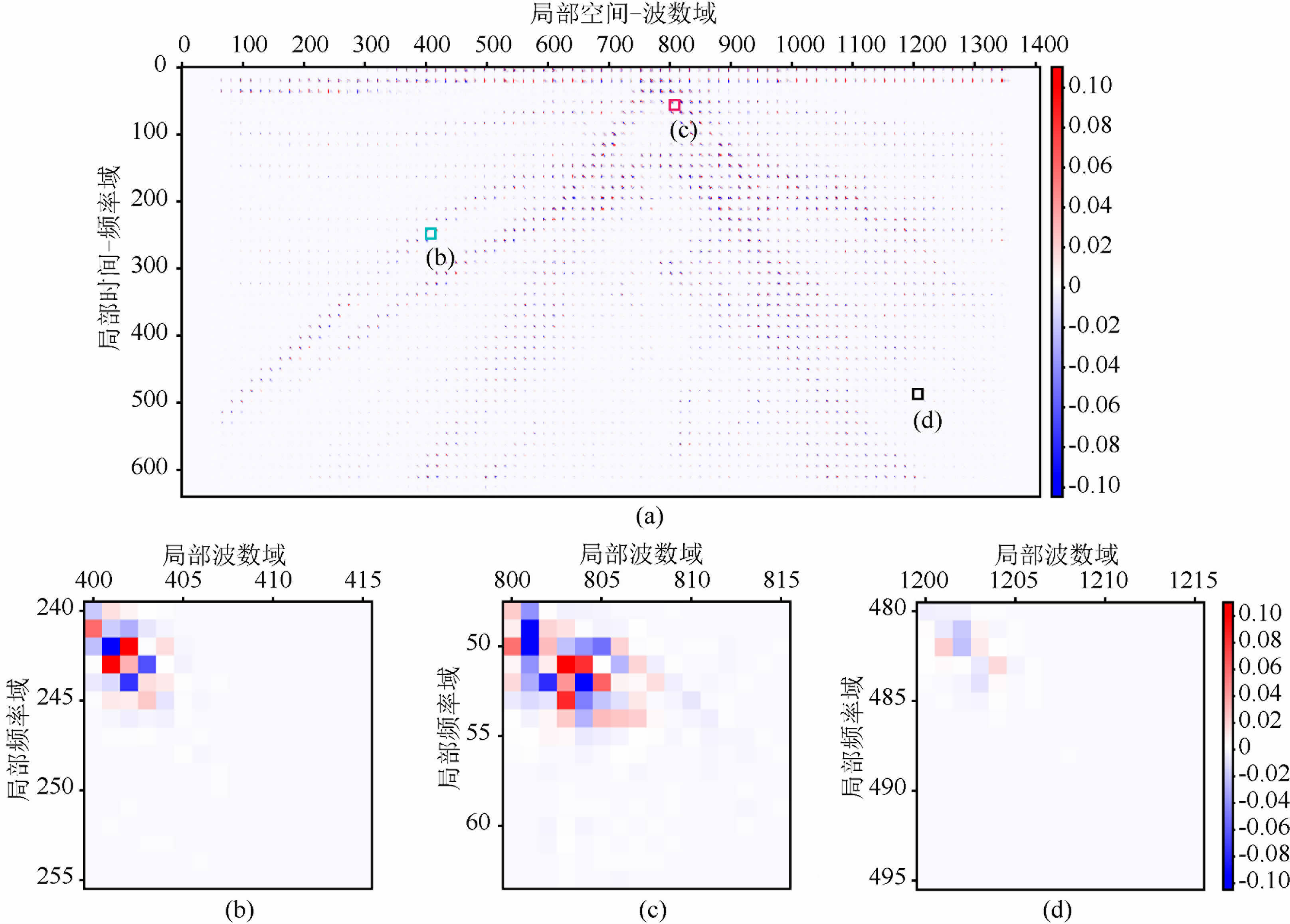
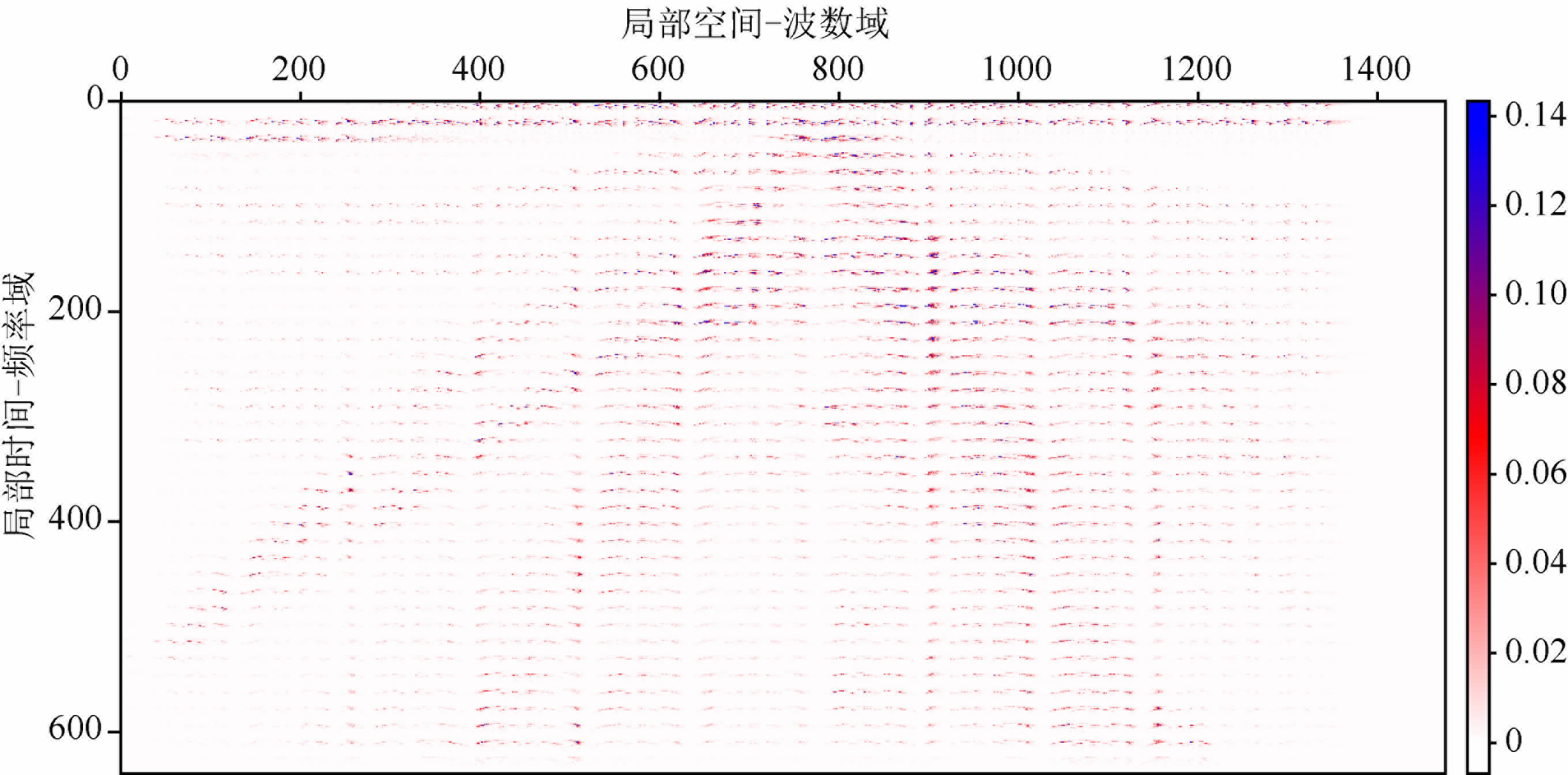
图 7为SEG-EAGE 盐丘模型对应的叠后地震数据.图 8、图 9 分别为使用由局部余弦基构成的Dreamlet分解与多尺度Dreamlet分解获得的系数.图 8a与图 9中纵轴表示局部时间和局部频率两个维度,顺序存储对应于每个局部时间的所有局部频率分量(其中快维为局部频率维,慢维为局部时间维);横轴表示局部空间位置和局部波数两个维度,顺序存储对应于每个局部空间位置的所有局部波数分量(其中快维为局部波数维,慢维为局部空间位置维).因此每个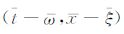
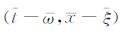

|
图 7 2D SEGEAGE 叠后地震数据 Fig. 7 2D SEG-EAGE salt model poststack data |
|
图 8 Dreamlet变换分解得到的系数矩阵 (a)Dreamlet系数矩阵。(b)-(d)对应于系数矩阵中蓝、红、黑方框的不同(t-ω,x-ξ)块。 Fig. 8 Coefficient matrix obtained by Dreamlet transform (a)Coefficientmatrix.(b)-(d)different(t-ω,x-ξ)blocks corresponding to the blue, red, black squares in the coefficient matrix. |
|
图 9 多尺度Dreamlet变换分解得到的系数矩阵 Fig. 9 Coefficient matrix obtained by multiscale Dreamlet transform |
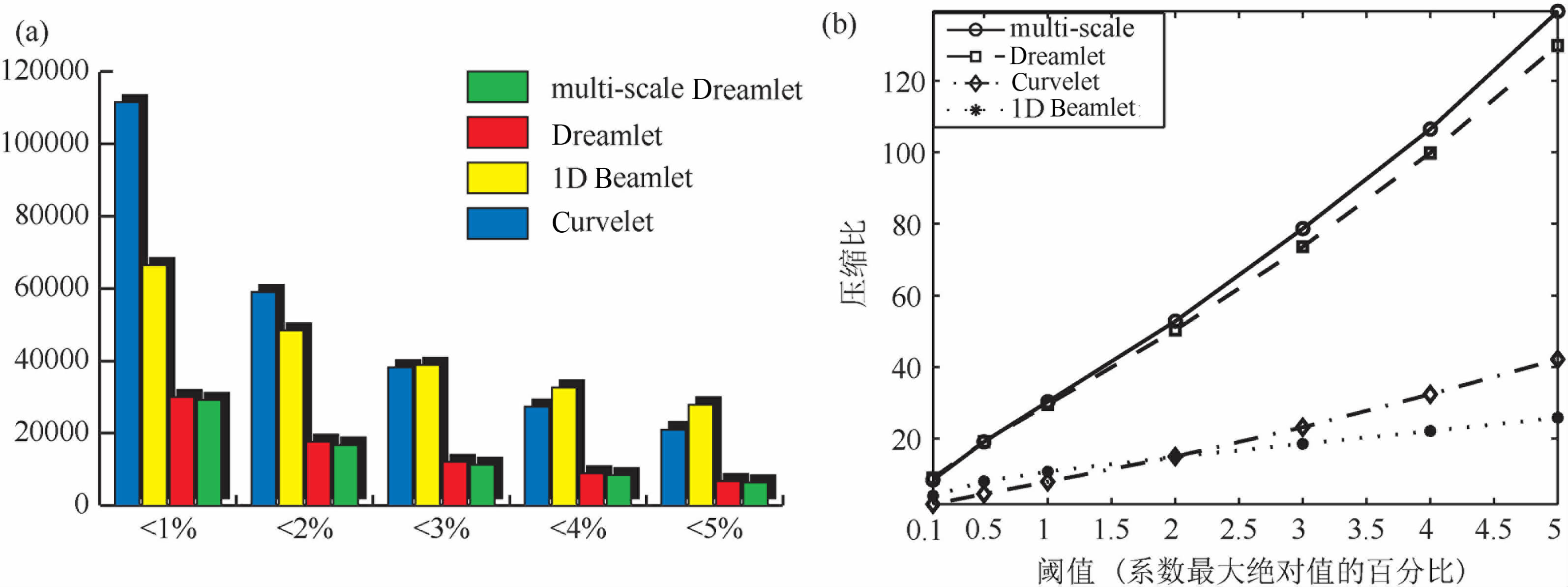
将阈值定义为分解系数中绝对值最大值的0.5%~5%,图 10 为使用Curvelet变换、频率域Beamlet 小波束变换、Dreamlet 变换与多尺度Dreamlet变换得到的系数分布范围以及相应的压缩比曲线.Curvelet变换由于具有2.8 的冗余度而不能得到很高的压缩比,相应的,由局部余弦基构成的Dreamlet变换和多尺度Dreamlet变换均具有很高的压缩比.图 11为在阈值条件为对应最大系数绝对值的2%时使用Dreamlet与多尺度Dreamlet变换压缩后得到的重构数据,此时压缩比分别达到50.32∶1与51.81∶1.
|
图 10 系数分布以及相应的压缩比曲线 (a)不同变换方法得到的系数分布;(b)不同方法获得的压缩比曲线。 Fig. 10 Coefficient distrubition and compression ratio obtained by Dreamlet, multi-scale Dreamlet, Curvelet, 1D Beamlet method (a)Coefficient distrubition;(b)Compression ratios. |

|
图 11 在阈值条件为对应最大系数绝对值的2%时使用Dreamlet与多尺度Dreamlet变换压缩后得到的重构数据 (a)Dreamlet变换压缩后得到的重构数据;(b)多尺度Dreamlet变换压缩后得到的重构数据 Fig. 11 Reconstruction results after compression with threshold taking value as 2% of the maximal coefficient after decomposition (a)Dreamlet method;(b)Multi-scale Dreamlet method |
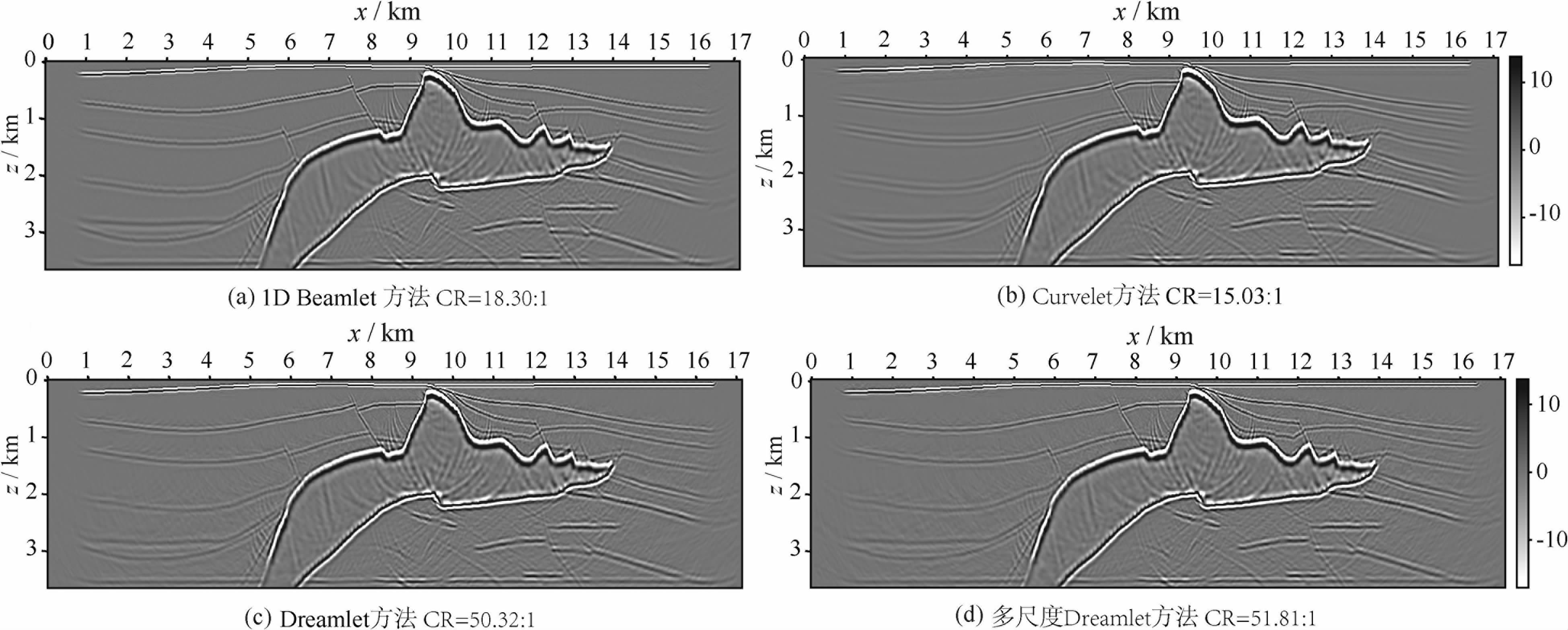
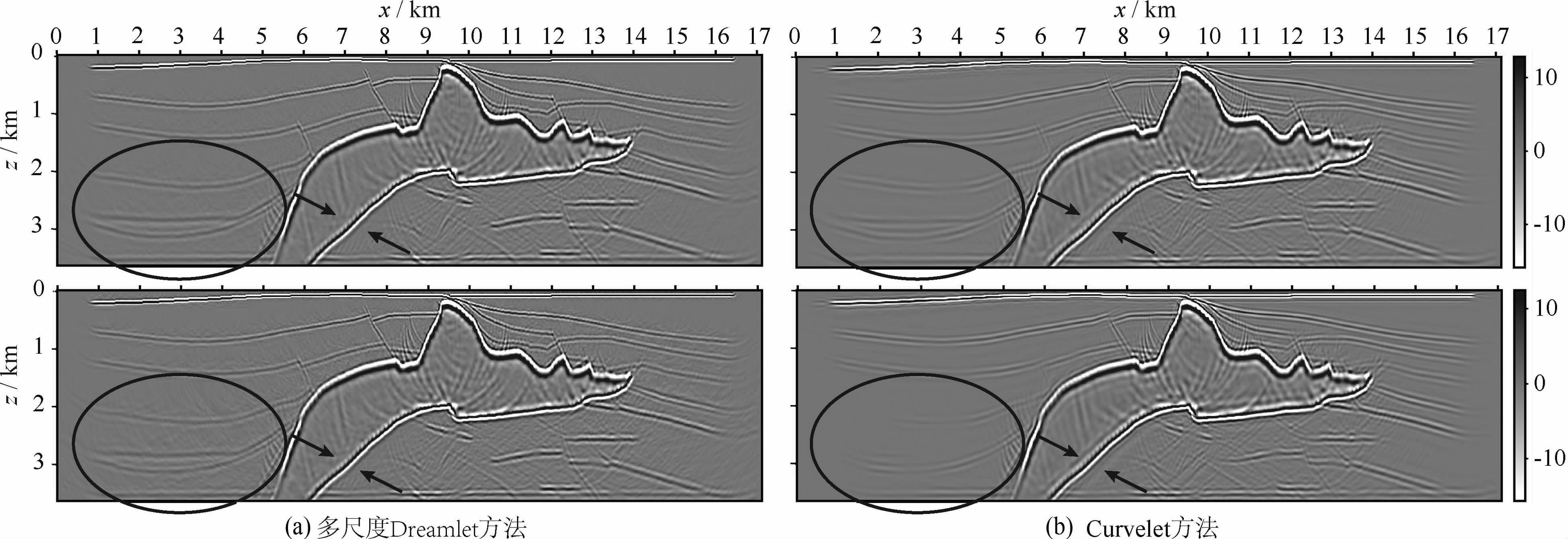
此外,利用压缩后重建数据进行偏移成像所得到的成像结果也是衡量地震数据压缩的一个重要标准.作为对比,图 12 为使用原始数据进行偏移成像得到的结果.图 13a-13d分别为在给定阈值条件下使用频率域Beamlet变换、Curvelet变换、Dreamlet变换和多尺度Dreamlet变换进行数据压缩后,使用基于局部余弦基的小波束偏移方法偏移重建数据获得的成像结果.在相同阈值条件下,Curvelet变换、Beamlet变换、Dreamlet变换和多尺度Dreamlet变换的压缩比分别为15.03∶1、18.30∶1、50.32∶1和51.81∶1.从图 13中可以看出,在成像结果中盐丘周围的反射层信息都被很好的保留,即使用重建数据均可以获得较高质量的成像结果,然而显然使用多尺度Dreamlet变换可以在获得相似高质量偏移结果的同时具有更大的压缩比优势.图 14为压缩比分别为30∶1 与50∶1 时,使用Curvelet 方法与多尺度Dreamlet方法得到的成像结果.如图中所示,当压缩比同样为50∶1时,在黑色圆圈所示区域Curvelet方法得到的成像结果已经开始丢失盐丘左部的反射层信息,同时在黑色箭头所指区域,Curvelet方法得到的成像结果也引入了一定的假象,而在这些区域多尺度Dreamlet方法仍然可以获得高质量的成像结果.

|
图 12 使用基于局部余弦基的小波束偏移方法得到的原始数据偏移成像结果 Fig. 12 Depth migration result of original data set using LCB Beamlet migration method |
|
图 13 在阈值条件为对应最大系数绝对值的2%时使用不同变换方法得到的重建数据获得的成像结果,基于局部余弦基的小波束偏移方法被用于获得偏移成像结果。 (a)1DBeamlet变换方法,压缩比为18.30∶1;(b)Curvelet变换方法,压缩比为15.03∶1;(c)Dreamlet变换方法,压缩比为50.32∶1;(d)多尺度Dreamlet变换方法,压缩比为51.81∶1. Fig. 13 Depth migration results of different decomposition under same thresholds, and the threshold takes value as 2% of the maximal coefficient after decomposition. LCB Beamlet migration method is used to get the imaging results (a)1D Beamlet method,CR=18.30∶1;(b)Curvelet method, CR=15.03∶1;(c)Deamlet method,CR=50.32∶1;(d)Multi-scale Deamlet method,CR=51.81∶1. |
|
图 14 使用多尺度Dreamlet压缩方法(a)与Curvelet压缩方法(b)得到的重建数据获得的成像结果,基于局部余弦基的小波束偏移方法被用于获得偏移成像结果 第一行为压缩比30 : 1,第二行为压缩比50 : 1.黑色椭圆与箭头指出多尺度Dreamlet方法结果优于Curvelet方法结果的地方 Fig. 14 Depth migration results of different decomposition under different CR. LCB Beamlet migration method is used to get the imaging results From the left column to the right column,the decomposition methods are mult--scale transform,Curvelet transform,respectively. From the first row to the last row,the CRs are 30 : 1 and 50 : 1,respectively. Black circles and arrows show the difference between the results of multi-scale Dreamlet method and Curvelet method |
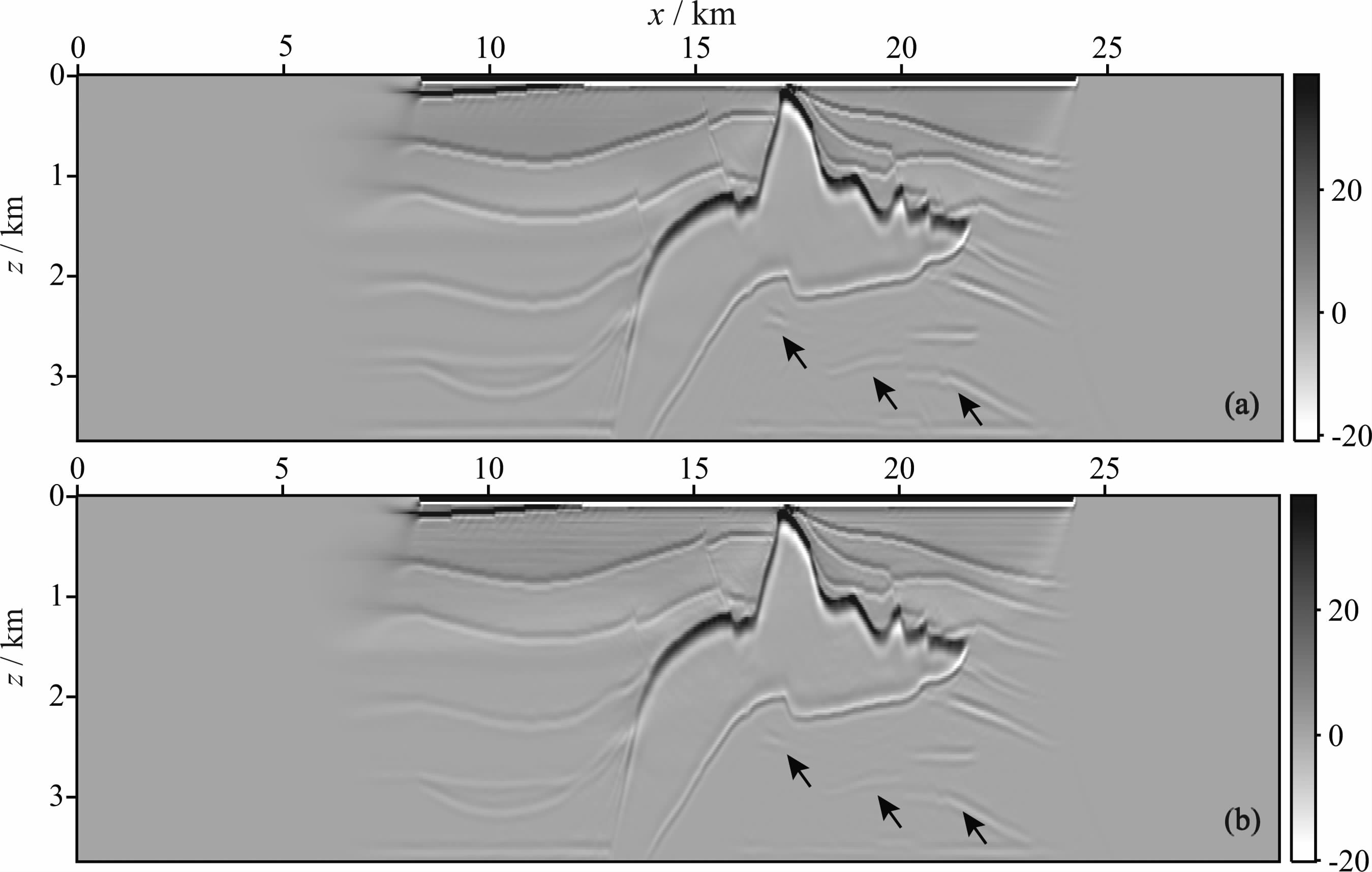
为了进一步表明Dreamlet方法的有效性,我们将Dreamlet压缩方法应用于2DSEG-EAGE叠前数据.该数据具有325个炮集,每炮具有176个接收器.图 15为使用原始数据得到的偏移成像结果.图 16为使用不同压缩比的重建数据偏移成像得到的结果.从图中可以看出,在压缩比为21.04∶1 的情况下,偏移重建数据得到的成像结果与图 15中使用原始数据得到的偏移成像结果基本没有差别;在压缩比为70.64∶1的情况下,虽然高阈值的选取使得更多的分解系数被舍弃从而在最终成像结果中浅层开始出现一定的水平层n假象,但是如图中黑色箭头所示使用重建数据仍然可以得到清晰的盐丘下反射层的像.

|
图 15 使用基于局部余弦基的小波束偏移方法得到的原始数据偏移成像结果 Fig. 15 Depth migration result of original data set using LCB Beamlet migration method |
|
图 16 6由Dreamlet压缩方法重建数据得到的偏移成像结果,基于局部余弦基的小波束偏移方法被用于获得偏移成像结果 (a)数据压缩比为21.04 Q得到的成像结果;(b)数据压缩比为70.64 Q得到的成像结果. Fig. 16 Depth migration results under different CR using Dreamlet method. LCB Beamlet migration method is used to get the imaging results (a) CR=21.04:1;(b) CR= 70.64 1 |
本文研究了基于Dreamlet变换的地震数据压缩方法,同时考虑地震数据中蕴含的频散关系而进一步提出了多尺度Dreamlet变换.通过与Curvelet等方法的对比,Dreamlet类方法显示了其对地震数据的更为稀疏的表达,同时地震数据特性的引入,也使得在高压缩比情况下,多尺度Dreamlet方法仍能保持地震数据中的重要信息,这对高效而精确的偏移成像研究都是非常重要的.
| [1] | Averbuch A Z, Meyer F, Stromberg J O, et al. Low bit-rate efficient compression for seismic data. IEEE Transactions on Image Processing , 2001, 10(12): 1801-1814. DOI:10.1109/83.974565 |
| [2] | Wang Y Z, Wu R S. Seismic data compression by an adaptive local cosine/sine transform and its effects on migration. Geophysical Prospecting , 2000, 48(6): 1009-1031. DOI:10.1046/j.1365-2478.2000.00224.x |
| [3] | Mallat S. A Wavelet Tour of Signal Processing: The Sparse Way. New York: Acedemic Press Inc, 2009 . |
| [4] | 朱光明, 高静怀, 王玉贵. 小波变换及其在一维滤波中的应用. 石油物探 , 1993, 32(1): 1–10. Zhu G M, Gao J H, Wang Y G. Wavelet transform and its application to 1-D filtering. Geophysical Prospecting for Petrole (in Chinese) , 1993, 32(1): 1-10. |
| [5] | 高静怀, 汪文秉, 朱光明, 等. 地震资料处理中小波函数的选取研究. 地球物理学报 , 1996, 39(3): 392–400. Gao J H, Wang W B, Zhu G M, et al. On the choice of wavelet functions for seismic data processing. Chinese J. Geophys (in Chinese) , 1996, 39(3): 392-400. |
| [6] | Villasenor J D, Ergas R A, Donoho P L. Seismic data compression using high-dimensional wavelet transforms. Proceedings of the Data Compression Conference , 1996: 396-405. |
| [7] | Vassiliou A, Wickerhauser M V. Comparison of wavelet image coding schemes for seismic data compression. Wavelet Application in Signal and Image Processing V , 1997, 3169: 118-126. DOI:10.1117/12.279684 |
| [8] | Candes E J, Donoho D L. New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities. Communications on Pure and Applied Mathematics , 2004, 57(2): 219-266. DOI:10.1002/cpa.v57:2 |
| [9] | Candes E, Demanet L, Donoho D, et al. Fast discrete curvelet transforms. Multiscale Modeling & Simulation , 2006, 5(3): 861-899. |
| [10] | Le Pennec E, Mallat S. Bandelet image approximation and compression. Multiscale Modeling & Simulation , 2005, 4(3): 992-1039. |
| [11] | Le Pennec E, Mallat S. Sparse geometric image representations with bandelets. IEEE Transactions on Image Processing , 2005, 14(4): 423-438. DOI:10.1109/TIP.2005.843753 |
| [12] | Guo K H, Labate D. Sparse shearlet representation of Fourier integral operators. Electronic Research Announcements in Mathematical Sciences , 2007, 14: 7-19. |
| [13] | Guo K, Labate D. Optimally sparse multidimensional representation using shearlets. Siam Journal on Mathematical Analysis , 2007, 39(1): 298-318. DOI:10.1137/060649781 |
| [14] | Guo K, Labate D. Analysis and detection of surface discontinuities using the 3D continuous shearlet transform. Applied and Computational Harmonic Analysis , 2011, 30(2): 231-242. DOI:10.1016/j.acha.2010.08.004 |
| [15] | Candes E J, Demanet L. The curvelet representation of wave propagators is optimally sparse. Communications on Pure and Applied Mathematics , 2005, 58(11): 1472-1528. DOI:10.1002/(ISSN)1097-0312 |
| [16] | Hennenfent G, Herrmann F J. Seismic denoising with nonuniformly sampled curvelets. Computing in Science & Engineering , 2006, 8(3): 16-25. |
| [17] | Herrmann F J, Wang D L, Hennenfent G, et al. Curvelet-based seismic data processing: A multiscale and nonlinear approach. Geophysics , 2008, 73(1): A1-A5. DOI:10.1190/1.2799517 |
| [18] | Herrmann F J, Brown C R, Erlangga Y A, et al. Curvelet-based migration preconditioning and scaling. Geophysics , 2009, 74(1): A41-A46. |
| [19] | Chauris H, Nguyen T. Seismic demigration/migration in the curvelet domain. Geophysics , 2008, 73(2): S35-S46. DOI:10.1190/1.2831933 |
| [20] | Douma H, de Hoop M V. Leading-order seismic imaging using curvelets. Geophysics , 2007, 72(6): S231-S248. DOI:10.1190/1.2785047 |
| [21] | Lin T T Y, Herrmann F. Compressed wavefield extrapolation. Geophysics , 2007, 72(5): SM77-SM93. DOI:10.1190/1.2750716 |
| [22] | Fomel S, Liu Y. Seislet transform and seislet frame. Geophysics , 2010, 75(3): V25-V38. DOI:10.1190/1.3380591 |
| [23] | Coifman R, Meyer Y. Remarques sur l'analyse de Fourier a fenetre. Comptes Rendus de L Academie Des Sciences , 1991, 32: 259-261. |
| [24] | Wallace G K. The JPEG still picture compression standard. Communications of the Acm , 1991, 34(4): 30-44. DOI:10.1145/103085.103089 |
| [25] | Pascal A, Guido W, Wicherhauser M V. Local Sine and Cosine Bases of Coifman and Meyer and the Construction of Smooth Wavelets. Wavelets: A Tutourial in Theory and Applications, 1992. |
| [26] | Averbuch A, Aharoni G, Coifman R, et al. Local cosine transform—a method for the reduction of the blocking effect in JPEG. Journal of Mathematical Imaging and Vision , 1996, 3(1): 7-38. |
| [27] | Coifman R R, Wickerhauser M V. Entropy-based algorithms for best basis selection. IEEE Transactions on Information Theory , 1992, 38(2): 713-718. DOI:10.1109/18.119732 |
| [28] | Wu R S, Wang Y Z, Gao J H. Beamlet migration based on local perturbation theory. Expanded abstracts, SEG 70th Annual Meeting , 2000: 1008-1011. |
| [29] | Wu R S, Wang Y Z, Luo M Q. Beamlet migration using local cosine basis. Geophysics , 2008, 73(5): S207-S217. DOI:10.1190/1.2969776 |
| [30] | Mao J, Wu R S, Gao J H. Directional illumination analysis using the local exponential frame. Geophysics , 2010, 75(4): S163-S174. DOI:10.1190/1.3454361 |
| [31] | 毛剑, 吴如山, 高静怀, 等. 局部指数标架小波束在复杂介质方向照明分析中的应用. 地球物理学报 , 2010, 53(12): 2955–2963. Mao J, Wu R S, Gao J H, et al. Directional illumination analysis for complex medium using local exponential frame beamlet. Chinese J. Geophys2010 (in Chinese) , 2010, 53(12): 2955-2963. |
| [32] | Wu R S, Geng Y, Wu B Y. Physical wavelet defined on an observation plane and the dreamlet. Expanded abstracts, SEG 81th Annual Meeting , 2011, 30: 3835-3839. |
| [33] | Wu R S, Wu B Y, Geng Y. Seismic wave propagation and imaging using time-space wavelets. Expanded abstracts, SEG 78th Annual International Meeting , 2008: 2983-2987. |
| [34] | Wu R S, Wu B Y, Geng Y. Imaging in copressed domain using Dreamlets. Expanded Abstracts: Annual International Meeting, Beijing SEG, 2009. |
| [35] | Wu B Y, Wu R S, Gao J H. Sourve-receiver prestack depth migration using dreamlets. Expanded Abstracts, SEG 81th Annual Meeting , 2011, 30: 3377-3381. |
 2012, Vol. 55
2012, Vol. 55


