2. 中国科学院研究生院, 北京 100049;
3. CNES/GRGS, Toulouse, France 31401;
4. 华中科技大学地球物理研究所,武汉 430074
2. Graduate School of Chinese Academy of Sciences, Beijing 100049, China;
3. CNES/GRGS, Toulouse 31401, France;
4. Institute of Geophysics, Huazhong University of Science and Technology, Wuhan 430074, China
陆地水变化是全球水循环的重要组成部分,是降雨、蒸发、径流和地下水等活动过程的综合反映.因此对陆地水变化开展研究有助于更好地研究干旱、洪水和地下水变化等现象.亚马逊流域作为世界上最大的流域,有着十分明显的陆地水变化,在全球气候变化中占有十分重要的地位.由于传统的气象和水文观测资料(如降雨资料、土壤湿度数据、地表径流数据和地下水测井资料等)的空间分辨率不高,无法很好地获得陆地水变化信息.而以实测资料为基础结合相关物理规律的气候模型仍存在很大的不确定性,在对干旱、洪水等异常气候的定量研究方面仍显不足[1].
GRACE (Gravity Recovery and ClimateExperiment)卫星自2002年3月发射至今,对全球重力场变化进行了近十年的连续观测[2].GRACE卫星重力技术目前已经广泛应用于研究陆地水变化[3-4]、南极和格陵兰岛冰盖变化[5-6]以及全球海平面变化等[7-8].Wahr等[9]利用模拟数据较早地研究了GRACE 数据获取陆地水变化的基本理论和方法.在此基础上,Swenson 等[10] 进一步研究了GRACE 提取区域陆地水变化的方法.Tapley等[11]和Wahr等[3]利用实测GRACE 资料研究了亚马逊流域陆地水的季节变化特征.随着GRACE 观测资料的积累,很多学者又进一步研究了陆地水的年际变化特征.Rodell等[4]和Tiwari等[12]利用GRACE资料和水文模式数据,发现了印度北部由于地下水抽取导致的陆地水变化.Chen 等[1, 13]的研究发现,利用GRACE 资料可以有效地监测到亚马逊流域2005年的干旱和2009 年的洪水.在2010 年,亚马逊流域又经历了十分严重的干旱[14],那么GRACE是否可以有效地监测到此次干旱?
本文利用GRACE 卫星重力数据进一步研究了亚马逊流域2002年8月至2010年12月的陆地水变化,并与三个水文模式和降雨资料进行了比较分析,最后对GRACE 估计陆地水变化的精度进行了分析.
2 数据处理 2.1 GRACE数据处理我们采用美国德克萨斯大学空间研究中心CSR (Centerfor Space Research, University of Texasat Austin)提供的2002年8月至2010年12月共100 个月的GRACElevel-2 (Release-4)数据计算了亚马逊流域的陆地水变化.该数据为60阶正则化球谐系数,并扣除了非潮汐大气、高频海洋信号、各种潮汐、固体潮和固体极潮的影响[15].受GRACE 卫星轨道设计和观测精度的制约,原始数据中的高阶球谐系数存在较大噪声,同时还存在南北方向的“条带"误差.为此,我们采取如下处理步骤:从球谐系数中,扣除该段时间的平均值;加回了卫星激光测距(SLR)观测的C20项[16]和Swenson等[17]计算的地心改正项;采用了Swenson 等[18]提出的滑动窗口方法分别去除同一次的奇数阶和偶数阶球谐系数的相关性,减少“条带"误差的影响,具体细节可参考Duan等[19]的文章;使用400km 高斯平滑来降低高阶球谐系数的噪声[20];球谐系数最终可转化为1°×1°的全球分布的等效水柱高变化[9].
区域陆地水总量变化为流域内等效水柱高变化和流域面积的乘积.我们采用Oki和Sud[21]提供的流域数据得到亚马逊流域的范围.参考Swenson等[10]的方法,利用下式可得到流域内等效水柱高变化:
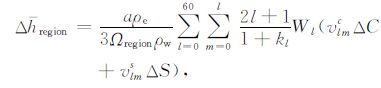
|
(1) |
其中a为地球半径,ρe 和ρw 为地球平均密度(取5517kg/m3)和水的密度(取1000kg/m3),Ωregion为流域对应的角面积,Wl为l阶对应的高斯平滑系数,ΔC和ΔS为GRACE 提供的大地水准面变化的球谐系数,vlmc和vlms为区域核函数v(θ,λ)展开的球谐系数,kl为负荷勒夫数.
区域核函数用下式表示:
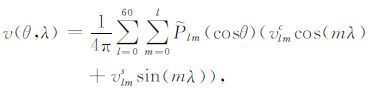
|
(3) |
其中$\tilde{P}$lm(cosθ)为正则化勒让德函数,θ和λ 为余纬和经度.
受地壳均衡调整(GIA)的影响,大地水准面存在长期变化趋势.这部分影响利用Paulson 地壳均衡模型进行了扣除[22].
为了估计GRACE 观测误差,我们采用了Wahr等[23]提出的方法,即扣除球谐系数的周年和半年变化,将剩余残差作为每个球谐系数的误差,并利用误差传播定律得到误差的全球分布.在此基础上,我们利用核函数进一步得到了流域内的GRACE 观测误差.影响GRACE 估计陆地水变化精度的因素除了GRACE 观测误差外,还包括:球谐系数的截断误差、去“条带"和高斯平滑引起的误差.在估计区域陆地水变化时,周边区域的陆地水信号会“泄露"到研究区域内,同时研究区域内的信号也可能因为高斯平滑而有所改变[24].为了更好地利用GRACE 估计亚马逊流域的真实陆地水变化,我们采用GLDAS水文模式数据估计了以上因素导致的信号变化.Klees等[24]的方法是利用模式数据在不同时刻估计不同的尺度因子,这导致GRACE 结果过分依赖于水文模式.我们则采取了以下方法,通过估计单一尺度因子,减小对GLDAS水文模式的依赖.具体步骤为:(1)将GLDAS水文模式的网格数据进行球谐展开,并截取至60 阶;(2)对得到的球谐系数进行与GRACE 数据一样的数据处理,即去“条带"、高斯平滑和使用核函数,得到区域陆地水变化的时间序列;(3)计算GLDAS 原始网格数据中该区域内的陆地水变化时间序列,假设第(2)步得到的时间序列乘以一个尺度因子后,与原始时间序列的残差平方和最小,计算得到该尺度因子;(4)对GRACE 估计的区域陆地水变化时间序列乘以该尺度因子,作为最终估计.利用该方法计算得到亚马逊流域的尺度因子为1.168,即对GRACE 得到的结果乘以该因子,作为最终的估计值.
2.2 水文模式数据处理 2.2.1 GLDAS水文模式GLDAS水文模式是由美国宇航局哥达航空中心(Goddard Space Flight Center, NASA)和美国国家环境预报中心(NCEP,National Centers of Environmental Prediction)共同建立的全球水文模式[25].该模式通过陆地表面建模和数据同化技术,输出陆地表面各项参数(如土壤湿度和温度、蒸发量等).本文采用了基于Noah 陆地表面模型的GLDAS 水文模式(以下简称GLDAS_Noah 模式)[26].该模式利用降雨观测值和太阳辐射等作为输入参数,其空间分辨率为1°×1°,每月一值.我们采用了GLDAS_Noah 模式提供的土壤湿度(0~0.1m、0.1~0.4 m、0.4~1 m 和1~2 m)计算了亚马逊流域的陆地水变化.
2.2.2 NCEP再分析水文模式NCEP/DOE AMIP-IIReanalysis (R-2)是由美国国家环境预报中心(NCEP)和美国能源部(DOE)在NCEP/NCAR 再分析数据基础上建立的水文模式(以下简称NCEP水文模式)[27-28].数据每月一值,为全球分布的高斯格网数据.该模式的土壤湿度数据分两层,包括了0~10cm 和10~200cm的土壤水.本文采用该模式的土壤湿度数据计算亚马逊流域的陆地水变化.
2.2.3 CPC 水文模式CPC 水文模式是由美国国家海洋和大气管理局(NOAA)气象预报中心(Climate Prediction Center)提供的陆地同化数据集[29].该模式输出结果的空间分辨率为0.5°×0.5°,每月一值.本文采用CPC模式输出的土壤湿度数据(0~1.6m)计算亚马逊流域的陆地水变化.
2.2.4 水文模式处理方法为了比较水文模式与GRACE 观测结果,我们需要对水文模式进行与GRACE 相同的数据处理过程.我们对三个水文模式的格网数据做球谐展开,并截取前60阶;进行去“条带"和高斯平滑处理;采用核函数和尺度因子的方法获得亚马逊流域的陆地水变化时间序列.
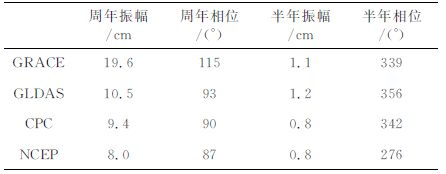
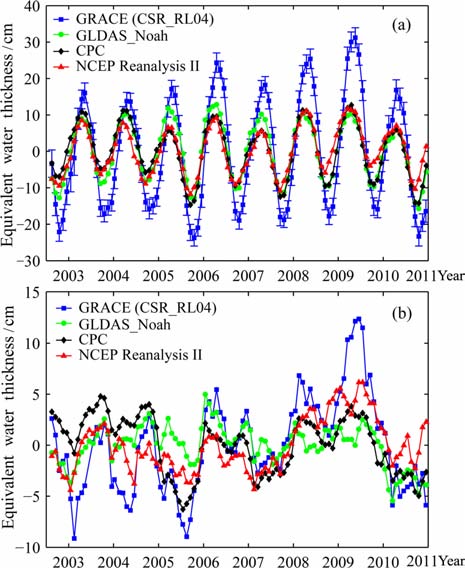
3 计算结果与讨论 3.1 GRACE与水文模式结果分析图 1a结果显示,GRACE 观测的亚马逊流域陆地水变化等效水柱高和三个水文模式的结果均表现出明显的季节性变化,但GRACE 结果的周年振幅明显大于三个水文模式的结果.这是由于水文模式只提供了表层土壤水数据,没有包括深层土壤水和地下水数据,此外地表湖泊和湿地对陆地水的影响也没有考虑,而GRACE 观测的为综合各因素后的陆地水变化,因此GRACE 的振幅大于水文模式的结果.图 1a中还表示出了GRACE 观测误差.如表 1所示,三个水文模式的周年相位符合得很好,最大值出现在3月底4 月初;GRACE 观测的陆地水变化最大值出现在4月底,与水文模式存在20天左右的相位差.GRACE 与三个水文模式的半年振幅符合得较好,但NCEP 水文模式的半年相位则与GRACE 和其他水文模式结果存在显著差别.
|
图 1 (a) GRACE(蓝色)、GLDAS(绿色)、CPC(黑色)和NCEP(红色)得到的亚马逊流域陆地水变化的等效水柱高;(b) GRACE(蓝色)、GLDAS(绿色)、CPC(黑色)和NCEP(红色)得到的亚马逊流域陆地水年际变化的等效水柱高 Fig. 1 (a) Equivalent water thickness of terrestrial water storage (TWS) changes in the Amazon basin from GRACE (blue),GLDAS (green),CPC (black) and NCEP (red) ; (b) Equivalent water thickness of interannual TWS changes m the Amazon basin from GRACE (blue),GLD AS (green),CPC (black) andNCEP (red) |
|
|
表 1 亚马逊流域陆地水变化等效水柱高的周年和半年项的振幅、相位 Table 1 Annual and semiannual amplitude and phase of equivalent water thickness of TWS changes in the Amazon basin |
我们将周年和半年信号扣除,得到亚马逊流域陆地水等效水柱高的年际变化时间序列,如图 1b所示.需要说明的是,由于GRACE 数据中存在S2 潮汐混频问题,我们从GRACE 的时间序列中扣除了161天的S2项周期信号[30].经计算,从GRACE 的时间序列中扣除的S2项的振幅为0.5cm.如图 1b所示,GRACE 结果的年际变化最为明显.GRACE观测到2002-2003年和2005年亚马逊流域陆地水明显减少,这与Chen等[1, 13]的结果一致.自2007年开始,陆地水呈逐年增加的趋势,2009 年6 月陆地水总量达到最大值.扣除季节影响后,2009 年6 月的陆地水增加了772±181km3.但随后,自2009年6月至2010年12 月,亚马逊流域陆地水又急剧减少,陆地水总量变化达到1139±262km3,这相当于全球海平面上升3.2±0.7 mm 所需水量.在2010年,GRACE 观测到2005年以来亚马逊流域最为严重的干旱.
与GRACE 观测结果相比,水文模式的年际变化相对较小.在2005年亚马逊干旱期,只有CPC 模式表现出较为明显的陆地水减少,这与GRACE 的观测结果相符合.从2007到2009年,CPC 和NCEP模式均表现出明显的陆地水增加趋势,但趋势没有GRACE 结果明显.从2009年下半年至2010年,三个水文模式均表现出陆地水减少的趋势,即亚马逊流域经历了2005年以来最明显的干旱.总体来说,三个水文模式没有很好地表现亚马逊流域的陆地水年际变化特征,而GRACE 卫星重力结果则很好地反映了该地区的陆地水年际变化特征.
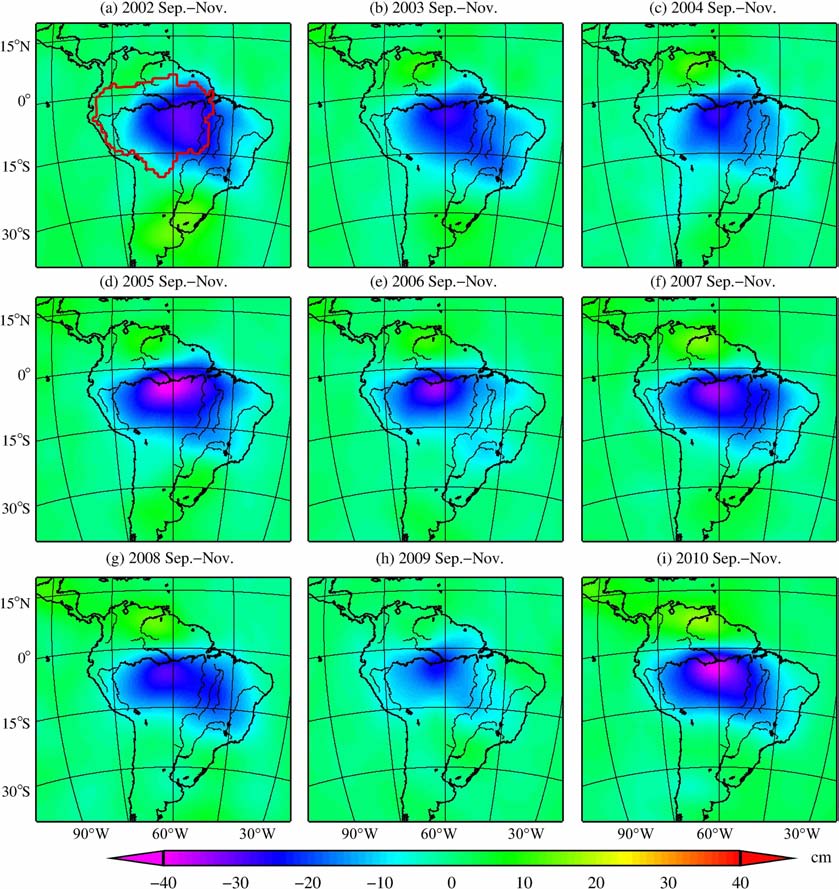
为了更好地显示亚马逊流域在2010年经历的干旱,我们利用GRACE 数据计算了每年亚马逊流域陆地水最少的三个月(9-11 月)的平均等效水柱高.如图 2所示,亚马逊流域的陆地水在2005年和2010年的旱季较其他年份同期相比,减少十分明显;且干旱主要发生在亚马逊流域的中游.图 2a还表示出了亚马逊流域的范围.
|
图 2 2002-2010年GRACE观测到的亚马逊流域9月、10月和11月陆地水变化等效水柱高的平均值 Fig. 2 GRACE-averaged September, October and November equivalent water thickness of TWS changes in the Amazon basin from 2002 to 2010 |

|
图 3 亚马逊流域2010年10月陆地水变化等效水柱高较2002-2009年同期10月份均值之差 (a) GRACE;b) GLDAS_Noah;c) CPC;d) NCEP Reanalysis II . Fig. 3 Differences of October equivalent water thickness of TWS changes in the Amazon basin in 2010 relative to mean October TWS changes of other years in the period 2002-2009 |
由于10月份是亚马逊流域陆地水最少的月份,我们进一步计算了2010 年10 月份陆地水变化与2002-2009年同期均值之差.如图 3 所示,与往年同期相比,GRACE、GLDAS 模式和CPC 模式的结果在2010年10月表现出十分明显的陆地水减少;而NCEP水文模式则没有很好地表现出这种变化.此外,GLDAS和CPC 模式结果的地理分布较为相似,但与GRACE 的结果存在明显差异.产生这种差异的可能原因包括以下两方面:由于水文模式只提供了表层土壤水对陆地水变化的贡献,忽略了深层土壤水、地下水、地表湖泊和湿地等的影响,因此导致了与GRACE 结果的差异;此外,GRACE 包含的观测误差和数据处理产生的误差也会导致GRACE与水文模式之间的差异.经计算,GRACE 观测到的2010年10月的陆地水较往年同期减少了290km3.
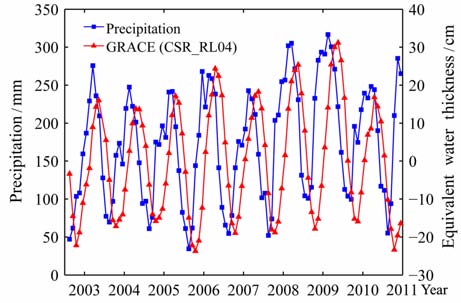
3.2 与降雨资料的比较为了进一步研究亚马逊流域的陆地水变化,我们分析了NCEP提供的该区域的降雨资料.如图 4所示,降雨资料与陆地水变化时间序列在年际尺度上有很好的一致性.亚马逊流域在2005年8月份的降雨较其他年份的同期有显著减少;2007年至2009年,流域内的降雨呈逐年增加的趋势;2010 年的降雨则较前两年有明显减少.以上结果与GRACE 观测到的陆地水变化十分一致.
|
图 4 亚马逊流域每月平均降雨量与GRACE得到的陆地水变化的对比(2002-8-201012) Fig. 4 Comparison between average monthly precipitation and GRACE t derived TWS changes in the Amazon basin (2002-8-2010-12) |
|
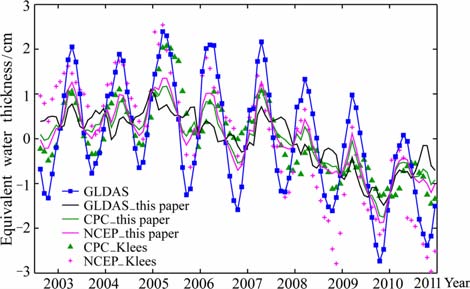
图 5 利用GLDAS模拟的亚马逊流域 GRACE后处理误差的等效水柱高 Fig. 5 Equivalent water thickness of GRACE post-process errors in the Amazon basin simulated by the GLDAS model |
陆地水是降雨、蒸发、径流和地下水等共同作用的结果.通过图 4我们可以发现,降雨是亚马逊流域陆地水年际变化的重要因素.此外,GRACE 观测的该地区陆地水变化较降雨变化滞后约2 个月左右.这主要是因为GRACE 观测的某月的陆地水包括了留在流域内的该月之前的降雨部分,因此出现了陆地水变化较降雨滞后的现象.
3.3 GRACE 结果的精度分析影响GRACE 估计陆地水变化精度的因素包括GRACE 观测误差和GRACE 处理过程中产生的误差.
首先讨论GRACE 观测误差的影响.我们采用了Wahr等[23]提出的方法,利用球谐系数扣除周年和半年信号后的残差计算GRACE 观测误差.在球谐系数中,除周年和半年信号,还有可能存在其他的周期信号、年际信号和趋势信号(如亚马逊流域的年际水文信号、冰后回弹效应等),因此该方法把这部分信号也作为误差处理,高估了GRACE 观测误差的影响.由于无法获得GRACE 球谐系数的方差协方差矩阵,对球谐系数的误差传播规律不够了解,Wahr等[23]提出的方法目前仍广泛采用.亚马逊流域的每月陆地水变化的GRACE 观测误差结果以误差棒的形式显示于图 1a.2002年8月至2010年12月,亚马逊流域的GRACE 观测误差等效水柱高的平均值为2.6cm.Chen 等[1]利用GRACE 在赤道地区(20°S-20°N)海洋上的残差估计的亚马逊流域的GRACE 观测误差的等效水柱高为2.4cm, 与本文的结果较为一致.
除GRACE 观测误差外,GRACE 处理过程中也会产生误差:如球谐系数的截断误差、去“条带"引起的误差、高斯平滑的影响以及在研究区域问题时的“泄露"误差.我们将这些因素的综合影响称为GRACE 后处理误差.本文采用了尺度因子来减少GRACE 后处理误差的影响.
为了进一步分析GRACE 后处理误差对亚马逊流域陆地水变化估计的影响,我们利用GLDAS 水文模式进行了模拟研究.我们将该水文模式球谐展开至60阶,进行去“条带"和高斯平滑处理,使用核函数得到流域内的时间序列,并与区域内水文模式模拟的真实结果进行比较,得到GRACE 后处理误差的影响.我们利用GLDAS、CPC 和NCEP三个水文模式,分别采用Klees等[24]的方法和本文的方法对后处理误差进行了改正,改正前后的GRACE 后处理误差如图 5 所示.需要说明的是,由于是利用GLDAS水文模式进行模拟,因此当采用Klees的方法和GLDAS模式计算改正时,后处理误差为零.如图 5所示,我们可以发现:
(1) 使用尺度因子前,GRACE 后处理误差表现出明显的季节变化特征.在陆地水变化较大的月份,GRACE 后处理误差也较大,反之亦然.后处理误差的均方差为1.3cm, 周年振幅达到1.5cm, 占GRACE 周年振幅结果的8%;
(2) 当采用Klees提出的方法时,利用CPC 和NCEP模式数据进行改正后,得到的后处理误差的均方差为0.8cm 和1.3cm.这说明Klees方法对先验水文模式数据的依赖性较强,当采用的模式数据不合适时(如模拟实验采用的NCEP模式),不能有效地降低后处理误差.这与Klees 等[24]的结论一致.因此,采用Klees方法的重要前提是,必须有较为可靠的先验模型.本文以及Chen等[1, 13]的结果均表明,利用水文模式得到的亚马逊流域陆地水变化结果明显较真实值偏小,因此Klees方法不能较好地扣除该地区的GRACE 后处理误差;
(3) 当采用本文的方法时,利用GLDAS、CPC和NCEP三种模式数据进行改正后,得到的后处理误差的均方差分别为0.6cm、0.7cm 和0.8cm.这说明该方法对先验模型的依赖性不高,且可以有效地降低亚马逊流域的GRACE 后处理误差.以上模拟实验结果表明,针对亚马逊流域水文模式数据可靠性不高的特点,本文采用的单一尺度因子方法可以有效地降低GRACE 后处理误差.
4 结论本文利用GRACE 卫星重力数据研究了2002年8月至2010年12月亚马逊流域的陆地水变化,并与三个水文模式和降雨资料进行了比较分析,得到如下结论:
(1) 亚马逊流域陆地水变化表现出明显的季节性变化.GRACE 观测的季节性变化大于水文模式的结果;
(2) 年际尺度上,GRACE 观测到2002-2003年和2005年亚马逊流域发生的明显干旱现象;2007年至2009年,陆地水又呈逐年增加的趋势,2009年6月陆地水总量达到最大值772±181km3;自2009年6月至2010年12月,陆地水又急剧减少.扣除季节影响后,从2009年6月最大值到2010年12月之间的亚马逊流域陆地水总量减少了1139±262km3,这相当于全球海平面上升3.2±0.7 mm 所需水量.三个水文模式的年际变化特征没有GRACE观测结果明显,但在2010年均表现出十分明显的陆地水减少,这与GRACE 结果符合得较好;
(3) 亚马逊流域的降雨资料与GRACE 观测资料有很好的一致性,在2005年和2010年的干旱期,亚马逊流域的降雨显著减少.这说明降雨是影响亚马逊流域陆地水变化的重要因素;
(4) 本文采用的尺度因子方法有效地降低了GRACE 后处理误差的影响.
致谢文中的水文模式和降雨数据下载自美国国家海洋和大气管理局网站http://www.esrl.noaa.gov/psd.文中图件由GMT[31]软件生成.感谢中国科学院中法联合博士培养项目对本文第一作者的资助.
| [1] | Chen J L, Wilson C R, Tapley B D, et al. 2005 drought event in the Amazon River basin as measured by GRACE and estimated by climate models. J| Geophys| Res| , 2009, 114: B05404. |
| [2] | Tapley B D, Bettadpur S, Watkins M, et al. The gravity recovery and climate experiment: Mission overview and early results. Geophys| Res| Lett| , 2004, 31(9): L09607. |
| [3] | Wahr J, Swenson S, Zlotnicki V, et al. Time-variable gravity from GRACE: First results. Geophys| Res| Lett| , 2004, 31(11): L11501. |
| [4] | Rodell M, Velicogna I, Famiglietti J S. Satellite-based estimates of groundwater depletion in India. Nature , 2009, 460(7258): 999-1002. DOI:10.1038/nature08238 |
| [5] | Velicogna I, Wahr J. Measurements of time-variable gravity show mass loss in Antarctica. Science , 2006, 311(5768): 1754-1756. DOI:10.1126/science.1123785 |
| [6] | Velicogna I, Wahr J. Acceleration of Greenland ice mass loss in spring 2004. Nature , 2006, 443(7109): 329-331. DOI:10.1038/nature05168 |
| [7] | Chambers D P, Wahr J, Nerem R S. Preliminary observations of global ocean mass variations with GRACE. Geophys| Res| Lett| , 2004, 31(13): L13310. |
| [8] | Lombard A, Garcia D, Ramillien G, et al. Estimation of steric sea level variations from combined GRACE and Jason-1 data. Earth Planet| Sci| Lett| , 2007, 254(1-2): 194-202. |
| [9] | Wahr J, Molenaar M, Bryan F. Time variability of the Earth's gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J| Geophys| Res| , 1998, 103(B12): 30205-30229. |
| [10] | Swenson S, Wahr J. Methods for inferring regional surface-mass anomalies from Gravity Recovery and Climate Experiment (GRACE) measurements of time-variable gravity. J| Geophys| Res| , 2002, 107(B9): 2193. |
| [11] | Tapley B D, Bettadpur S, Ries J C, et al. GRACE measurements of mass variability in the Earth system. Science , 2004, 305(5683): 503-505. DOI:10.1126/science.1099192 |
| [12] | Tiwari V M, Wahr J, Swenson S. Dwindling groundwater resources in northern India, from satellite gravity observations. Geophys| Res| Lett| , 2009, 36: L18401. |
| [13] | Chen J, Wilson C R, Tapley B D. The 2009 exceptional Amazon flood and interannual terrestrial water storage change observed by GRACE. Water Resour| Res| , 2010, 46(12): W12526. |
| [14] | Lewis S L, Brando P M, Phillips O L, et al. The 2010 Amazon drought. Science , 2011, 331(6017): 554-554. DOI:10.1126/science.1200807 |
| [15] | Bettadpur S. UTCSR Level-2 gravity field product user handbook, GRACE 327-734, Center for Space Research. The Universtiy of Texas at Austin, Austin , 2007. |
| [16] | Cheng M K, Tapley B D. Variations in the Earth's oblateness during the past 28 years. J| Geophys| Res| , 2004, 109(B9): B09402. |
| [17] | Swenson S, Chambers D, Wahr J. Estimating geocenter variations from a combination of GRACE and ocean model output. J| Geophys| Res| , 2008, 113(B8): B08410. |
| [18] | Swenson S, Wahr J. Post-processing removal of correlated errors in GRACE data. Geophys| Res| Lett| , 2006, 33(8): L08402. |
| [19] | Duan X J, Guo J Y, Shum C K, et al. On the postprocessing removal of correlated errors in GRACE temporal gravity field solutions. J| Geod| , 2009, 83(11): 1095-1106. |
| [20] | Jekeli C. Alternative methods to smooth the Earth's gravity field, Rep. 327, Dep. of Geod, Department of Geodetic Science and Surveying. The Ohio State University, Columbus , 1981. |
| [21] | Oki T, Sud Y C. Design of total runoff integrating pathways (TRIP)-A global river channel network. Earth Interact| , 1998, 2(1): 1-37. |
| [22] | Paulson A, Zhong S J, Wahr J. Inference of mantle viscosity from GRACE and relative sea level data. Geophys| J| Int| , 2007, 171(2): 497-508. |
| [23] | Wahr J, Swenson S, Velicogna I. Accuracy of GRACE mass estimates. Geophys| Res| Lett| , 2006, 33(6): L06401. |
| [24] | Klees R, Zapreeva E A, Winsemius H C, et al. The bias in GRACE estimates of continental water storage variations. Hydrol| Earth Syst| Sci| , 2006, 3(6): 3557-3594. |
| [25] | Rodell M, Houser P R, Jambor U, et al. The global land data assimilation system. Bull| Amer| Meteor| Soc| , 2004, 85(3): 381-394. |
| [26] | Ek M, Mitchell K, Lin Y, et al. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J| Geophys| Res| , 2003, 108(D22): 8851. |
| [27] | Kalnay E C, Kanamitsu M, Kistler R, et al. The NCEP/NCAR 40-year reanalysis project. Bull| Amer| Meteor| Soc| , 1996, 77(3): 437-471. |
| [28] | Kanamitsu M, Ebisuzaki W, Woollen J, et al. NCEP-DOE AMIP-II REANALYSIS(R-2). Bull| Amer| Meteor| Soc| , 2002, 83(11): 1631-1643. |
| [29] | Fan Y, van den Dool H. Climate Prediction Center global monthly soil moisture data set at 0.5? resolution for 1948 to present. J| Geophys| Res| , 2004, 109(D10): D10102. |
| [30] | Knudsen P. Ocean tides in GRACE monthly averaged gravity fields. Space Sci| Rev| , 2003, 108(1): 261-270. |
| [31] | Wessel P, Smith W H F. Free software helps map and display data. Eos Trans| AGU , 1991, 72(41): 441-446. |
 2012, Vol. 55
2012, Vol. 55