2. 油气资源研究重点实验室, 中国科学院地质与地球物理研究所, 北京 100029;
3. 中国科学院研究生院, 北京 100049
2. Key Laboratory of Petroleum Resources Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. Graduate University, Chinese Academy of Sciences, Beijing 100049, China
在地震勘探中由于采集成本、坏道、噪声、地形等诸多因素的影响,采集的数据常常不满足采样定理,会影响多次波消除、偏移等处理的效果[1-2],因此在数据处理过程中常常需要对地震数据进行重构.地震数据重构主要有三大类方法.最常用的方法是基于变换的方法,这类方法基于信号在变换域的特征进行数据重构,计算结果比较稳健,因此得到广泛的应用.常用的变换有傅里叶变换[3-5],Radon变换,局部Radon变换[6]等.第二类方法是预测滤波方法,基于分频预测的思想,用低频的信息预测高频信息.这类方法主要有F-X 域预测滤波[7],F-K 域预测滤波[8-9]和T-X 域预测滤波[10].第三类方法是基于波动方程的方法,利用波传播的物理性质重构地震波场[11-12],这类方法由于需要速度信息且计算量大,因此没有得到广泛的应用.
地震数据重构问题可以变为一个稀疏优化问题.文献[13]中采用curvelet变换作为稀疏变换,利用压缩传感的理论对随机欠采样的地震数据进行重构.采用的迭代阈值法需要多次迭代,计算效率比较低;而随机欠采样方式不能够有效控制采样间隔,因此需要进一步改进.本文将地震数据重建问题变为一个稀疏优化问题,并构造0范数的逼近函数作为目标函数,利用curvelet变换的紧框架性,采用投影梯度法解,同时本文运用作者近期提出的一种能够控制最大采样间隔并且保持采样随机性的分段随机采样方式.数值试验表明基于0范数逼近的投影梯度法的计算效率比现有的稀疏优化解法有很大的提高;分段随机采样能够有效地控制采样间隔并且保持采样的随机性,比随机欠采样有更好的重构效果.
本文结构如下:第二节阐明了地震数据重构问题的数学模型;第三节简单介绍所采用的稀疏变换;第四节回顾了稀疏优化算法并详细介绍了0范数逼近方法和梯度迭代技巧;第五节探讨采样方式并提出新的采样方式;第六节的数值模拟表明分段随机采样比随机欠采样能够更好地改进重构效果;0范数逼近方法可以显著地提高计算效率,其CPU计算时间大约是通常采用的迭代阈值法(IST)和谱投影法(SPGL1)的三分之一.
2 地震数据重构的数学模型地震数据采集可以表示为如下数学模型:

|
(1) |
其中f∈RN为原始波场数据,R为采样矩阵,y∈RM(M<N)为采集的波场数据.由于采集数据的不完整性,因此R是一个欠定矩阵.地震数据重构由采集的数据y和采样算子R重构完整的数据f.由于M<N,因此存在无穷多的f满足公式(1).因此地震数据重构是一个不适定的反问题[1].
方程(1)可以通过优化问题

|
(2) |
来求解,其中‖·‖2 是向量的2范数.由于问题(1)的不适定性,必须采用正则化方法求解,其中最经典的方法是Tikhonov正则化[14-15],即解

|
(3) |
该优化问题的最优解为f= (RTR+αI)-1y,其中I为单位矩阵,α是正则参数.此外,正则化方法还包括迭代正则化、自适应正则化、截断的奇异值分解、共轭梯度法等方法[14-16].
若存在某个变换C使得x=Cf是稀疏的,则可以先解方程RC-1x=y,求出稀疏的解x,然后再求出f=C-1x.此时问题(1)变为约束极小化问题

|
(4) |
其中零范数‖·‖0 表示向量的非零元素个数,记RC-1=A.问题(4)需要穷举所有的组合才能找到最优解[1, 17].在一定的条件下,可以利用1 范数优化问题求解欠定矩阵的稀疏解[17].这种基于数据的稀疏性,由欠采样数据重构完整数据的问题就是压缩传感问题.压缩传感主要由三部分组成:稀疏变换、采样方法和求解方法.这三部分共同影响重构的结果.本文基于压缩传感的理论进行地震数据重构,下面简要地介绍采用的稀疏变换.
3 稀疏变换稀疏变换是压缩传感的重要组成部分.变换域中的数据越稀疏,需要的采样个数就越少,而且重构效果越好.地震数据处理中最常用的变换有傅里叶变换、Radon变换、小波变换以及Gabor变换.但是这些变换不能直接用于压缩曲线形状的地震记录,因此Candes提出了curvelet变换[18].这种多尺度、多方向、各向异性的变换在局部窗内用线段逼近曲线,因此能够很好地压缩曲线形状的记录.连续的curvelet变换可以表示为
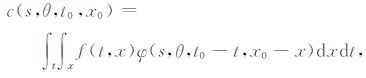
|
(5) |
其中f(t,x)为T-X 域的数据,函数φ(s,θ,t,x)是变换的核函数,其中s为尺度,θ为角度或倾角,t0,x0 为T-X 域的位置参数.该变换将数据分解成不同的尺度和角度,其离散形式记为c= Ψf,其中c为curvelet系数,Ψ 为算子的离散形式,f为T-X域数据的离散形式.由于离散curvelet变换是一个紧的框架,因此ΨH 为Ψ 的广义逆.
4 稀疏优化方法基于稀疏变换的地震数据重构问题需要解一个稀疏优化问题,对于线性系统的稀疏解法研究已经有了很多成果.下面首先总结常见的稀疏解法,然后介绍在地震数据重构中得到应用的稀疏解法,在4.2节提出了地震数据重构的0范数逼近算法.
4.1 稀疏解法介绍最常见的稀疏解法是基于1范数的方法.主要有内点法、迭代重赋权1范数方法、投影梯度类法等等.除此之外,匹配追踪类方法是著名的贪婪类方法,包括匹配追踪、正交匹配追踪和匹配追踪的其他变形,这类方法不适合大规模问题和解非精确稀疏的情况.第三类方法是阈值法[19],该方法简单易行,能够解大规模问题,但是需要多次迭代.此外还有同伦法和最小角度回归方法,该类方法适合维数较小且解为精确稀疏的情形,迭代重赋权最小二乘法通过在迭代过程中调节解的权重得到稀疏解.
若信号在某个变换域是稀疏的,则在一定条件下可以利用1范数优化问题求出问题的稀疏解[17],即解以下问题:
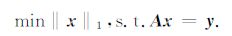
|
(6) |
问题(6)可以变为线性规划问题,并用内点法等方法[1, 20]求解.若采集数据含有加法噪声n,即y=Ax+n,则问题(4)变为

|
(7) |
问题(7)可以变为二阶锥优化问题求解.其无约束优化形式为
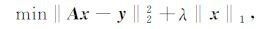
|
(8) |
其中λ 为拉格朗日乘子.问题(8)可以用内点法、投影梯度法及同伦算法等方法求解[21-22].
文献[23]提出一种解不适定问题的lp-lq模型:

|
(9) |
该模型给出了解优化问题的一个统一框架,可以求解一般的反问题.基于变换的地震数据重构问题的先验条件是解的稀疏性.当p=2,q→1时,问题(9)可以求出稀疏解.文献[24]进一步提出了1 范数信赖域解法.在q=0的情形,文献[25]提出基于0范数的稀疏分解法.
对于线性问题求稀疏解有许多方法,但是由于地震数据量大,目前只有基于梯度的方法被用到地震数据重构中.文献[26]利用傅里叶变换作为稀疏变换,并采用迭代重赋权最小二乘法(IRLS)求解.
Hennenfent等对问题(8)采用迭代软阈值法(IST)求解[13].该方法的迭代方式为:若xk为当前迭代点,则下一个迭代点为xk+1 =Tλ(xk+AT(y-Axk)),其中Tλ(x)=sgn(x)·max(0,x- λ).该迭代方式简单,参数设定容易,但是不能保证解的稀疏性且可能收敛到局部解.
问题(7)也可以采用投影梯度法来求解,Ewout等提出了一种谱投影梯度法(SPGL1)[27].该方法利用Pareto曲线φ(τ)= ‖rτ‖2(其中rτ =y-Axτ),将以下两个优化问题联系起来

|
(10) |

|
(11) |
令xτ 为(LSτ)的最优解,Pareto曲线是关于τ的连续可微凸函数.当τ取合适的值时,(BPσ)和(LSτ)有相同的解,因此可以通过解(LSτ)得到(BPσ)的最优解.对于(LSτ)采用投影梯度法求出解xτ,然后通过Pareto曲线来更新τ,通过解新的(LSτ)问题逐渐逼近(BPσ)的准确解.在求解(LSτ)问题时,利用对偶间隙作为停机准则,每次迭代将负梯度方向投影到1范数球上,然后采用非单调梯度法求步长,该方法能够保证解的快速收敛性[28].
不难发现谱投影梯度法中的参数τ 的求解方法实质上是利用了反问题研究领域中的后验选取正则参数的偏差准则,并且该参数τ 可以用高阶收敛算法求得[15, 29].
以上三种方法具有相同的收敛性[30],但是地震数据处理需要更加快速稳定的解法.因此,研究大规模问题的稳定高效的快速计算方法对于地震数据处理有重要意义.
下面提出一种地震数据重构的快速方法.该算法构造简单,参数设置比较容易,而且在相同重构效果情况下,其计算时间大约是谱投影梯度法和迭代阈值法的三分之一.数值模拟证明了算法的高效性.
4.2 0范数逼近算法按照lp-lq的正则化思想,当q→0时可以根据问题(9)求出稀疏解.因此我们研究0 范数优化问题:

|
(12) |
大多数方法采用1范数作为0范数的逼近,然后解1范数优化问题.我们知道1范数是0范数的最好的凸逼近形式,这是一种近似转化的方法.下面我们构造非凸函数作为0范数的逼近.为此我们构造满足以下性质的函数fσ(x):(1)对于固定的σ,fσ(x)在x的一个合适的邻域内是连续的凸函数;(2)当σ 趋向于0时,函数逼近于0范数:

|
(13) |
通过研究发现函数

|
(14) |
和
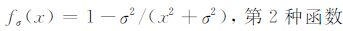
|
(15) |
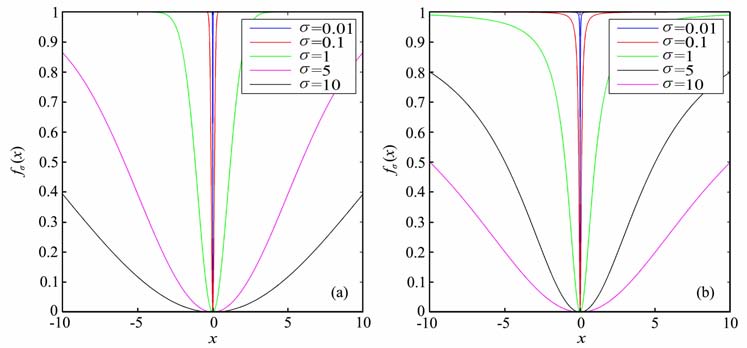
满足上述两个性质.图 1给出了一维情形下这两个函数的图像.
|
图 1 第一种函数fσ(x) = 1 - exp(-x2/2σ2)(a)和第二种函数 fσ= 1 - σ2/(x2+σ2) (b) Fig. 1 (a) Case 1 funcation: fσ= 1 - exp(-x2/2σ2); (b) Case2 function: fσ= 1-σ2/(x2+σ2) |
这两种函数是非凸的,而且随着参数σ 变小,逐渐逼近0范数.因此对于问题(12),我们可以构造连续函数来作为目标函数,然后求其极小值.这样问题(12)就变为

|
(16) |
由于目标函数是σ的函数,σ越小,函数越逼近0范数,由于函数的非凸性,对一个小的σ 值,直接求解问题(16)很难获得全局最优解.但是对于较大的σ值,函数$\sum\limits_{i=1}^{N}{{{f}_{\sigma }}\left( {{x}_{i}} \right)}$是光滑的,容易求出全局最优解,因此可以通过针对逐渐下降的σ 序列来解(16),用上次的近似解作为下一次迭代的初始解,并逐渐降低σ .这样就可以防止迭代得到局部最优解.该方法本质上是一种逼近的投影梯度法.对于上述两种函数,该方法具有相同的效果.
(1) 给出内部循环次数L,外部循环次数J,步长ω,初始解x0(x0 为Ax=y的2范数解),初始的σ 值,并令l=0,j=0,x=x0;
(2) 求出当前迭代点x的梯度$g=\nabla \left( \sum\limits_{i=1}^{M}{\left( 1-{{f}_{\sigma }}\left( {{x}_{i}} \right) \right)} \right)$,更新迭代点:x:=x-ωg(ω 为迭代步长,需要线搜索计算);
(3) 将x投影到可行集Z = {x|Ax =y}上,即x:=x-AT(AAT)-1(Ax-y);
(4) 令l:=l+1,如果l<L,转第(2)步;否则,令σ =σ/2,j=j+1,l=0,转步2;
(5) 判断停机准则:如果j>J,则停机,输出解${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}}$;否则,转步(2),继续迭代.
由于本文的curvelet变换是正交的,因此矩阵A的广义逆的求取比较方便,x:=x-AT(AAT)-1(Ax-y)可以很容易求出,因此大大地提高了计算效率.该算法结合了正则化和最优化技巧,因此具有稳定的收敛性.关于梯度算法的正则性和收敛性的理论性结果见文献[14, 25].
5 分段随机采样在地震勘探中,观测系统的设计对地震数据处理有一定的影响.在相同采样个数下,如何设计好的采样方式是值得研究的方向.本节给出一种分段随机采样方法,该采样方法能够保持随机性和控制采样间隔,因此能够改进数据重构的效果.
采样方式是压缩传感的重要组成部分,采样方法关系到重构的效果.虽然在其他领域已经有各种采样方法[31],但是由于地震采集只能在地表放置检波器接收地震信号,因此采样方法受到很大的限制.目前的欠采样方法主要分为规则欠采样和随机欠采样[24].规则欠采样在测线上等间隔地放置检波器,但是采样间隔大于完整采样所要求的间隔.规则欠采样如图 2所示.

|
图 2 规则欠采样方式 Fig. 2 Schematic of regular sub-sampling |
其中的黄点代表放置了检波器,白点表示没有放置检波器.这种规则欠采样在F-K 域会产生严重的相干假频.
随机欠采样在测线上随机的放置检波器,其采样间隔不能得到控制.随机欠采样如图 3所示.

|
图 3 随机欠采样方式 Fig. 3 Schematic of random sub-sampling |
随机欠采样在F-K域产生的噪声分布在整个频率域,可以看做随机噪声,因此可将波场重构看作去噪问题[13].由于随机欠采样会产生大的采样间隔,当这些间隔大于curvelet的某个尺度时,重构结果就会丢失原始信息,因此需要提出新的采样方法来克服随机欠采样的缺点.
Hennenfent引进一种jittered采样方法[32].这种采样方法先等间隔的选取点,然后以这些点为中心随机的扰动.jittered 采样能够控制采样间隔而且具有随机性,但是该采样方法缺乏灵活性,只能取完整采样个数的整数分之一.
针对上述三种采样方法的缺点,本文详细描述文献[24]给出的一种分段采样方法.对于随机欠采样来说,每个点被采样到的概率是相等的,假设Nyquist采样个数为N,实际采样个数为K,则采样比例为K/N.该采样方法不能够控制最大间隔,其最大间隔为N-K,当采样间隔大于curvelet的某个尺度时,则在这个尺度内的采样为零,因此重构的数据必然会丢失原始信息.分段随机采样首先将这N点均匀的分成M段,每段的长度为N/M,在每段内按照一定的比例随机的采样,这种采样方式下,其最大采样间隔为2(N/M)(1-K/N),但是这种概率出现的极小.因此这种分段随机采样方法能够有效地减小采样间隔,同时保持了采样的随机性.
分段随机采样的具体的操作如下:(1)将所有的采样个数N划分为M段(M<K),每段长度N/M小于curvelet的尺度Q.(2)在每段上随机的取K/M个点,每段的采样点的总和等于所有的采样点数K.当划分的段数M足够多时,这种方法既能够有效地控制最大采样间隔又能够保持采样的随机性,因此能够得到好的重构效果.
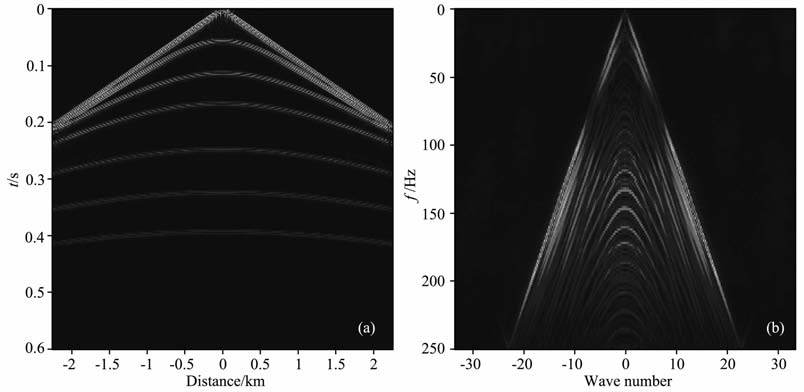
6 数值试验 6.1 分段随机采样的数值模拟为了证明新的分段随机采样的效果,本文对模拟的炮记录进行数值试验.图 4是一个水平层状介质的地震炮记录及其频谱,空间采样间隔为15 m, 时间采样间隔为2ms, 该数据含有直线形状的直达波和双曲线形状的反射波.图 5a是规则欠采样数据,其采样个数为图 4a采样个数的1/3,图 5b 产生严重的相干假频.图 6a是随机欠采样数据,和图 5a有相同的采样个数,图 6b是图 6a的频谱.图 7a是图 6a的重构数据,其信噪比为7.1606,图 7b是图 7a的频谱.信噪比公式为
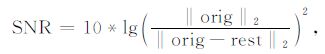
|
(17) |

|
图 4 原始数据(a)及其频谱(b) Fig. 4 (a) The original data; (b) Frequency spectrum of (a) |

|
图 5 规则欠米样的数据(a)及其频谱(b) Fig. 5 (a) Data of regular sub-sampling; (b) Frequency spectrum of (a) |

|
图 6 随机欠采样数据(a)及其频谱(b) Fig. 6 (a) Data of random sub-sampling; (b) Frequency spectrum of (a) |
|
图 7 随机欠米样的重构数据(a)及其频谱(b) Fig. 7 (a) Restoration of random sub-sampling; (b) Frequency spectrum of (a) |
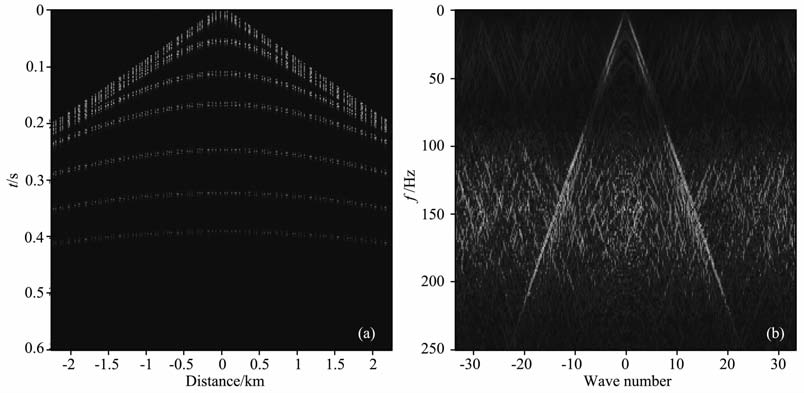
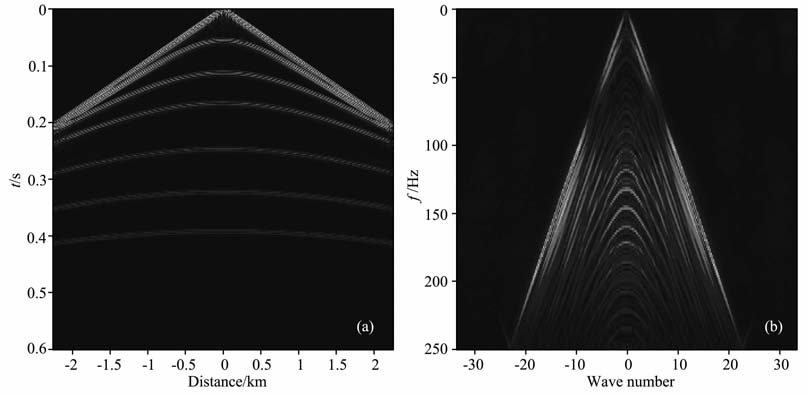
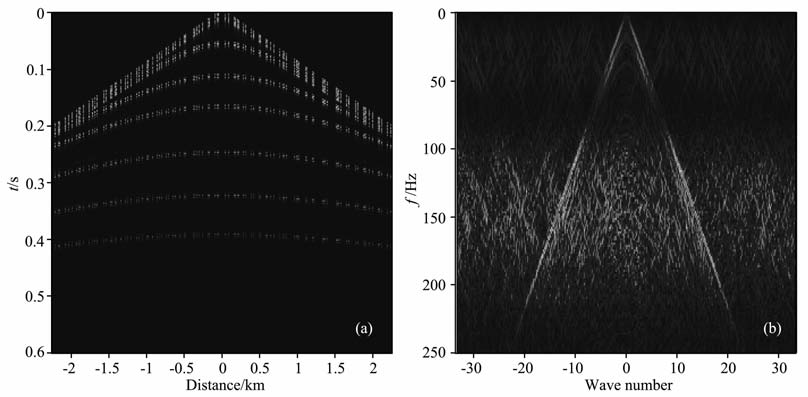
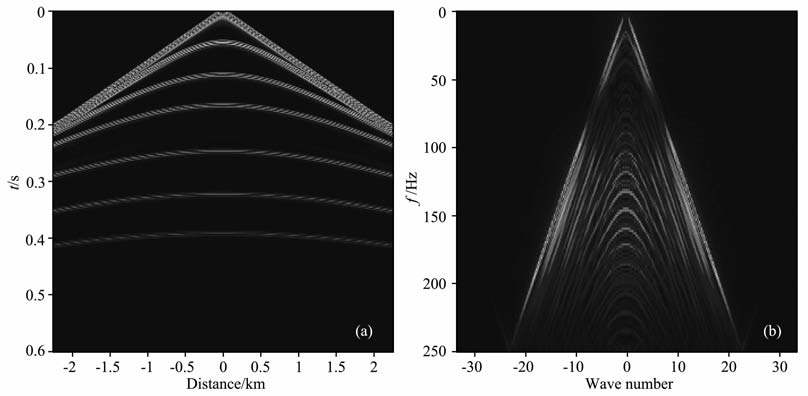
其中orig为完整的记录,rest为重构的记录.图 8是jittered采样数据及其频谱,图 8a和图 5a的采样个数相同.图 9表示图 8a的重构数据及其频谱,重构结果的信噪比为9.3008.图 10表示分段采样数据及其频谱,图 10a和图 5a具有同样的采样个数.图 11是分段采样的重构数据及其频谱,重构结果的信噪比为9.8417.经过多次试验,随机欠采样重构的信噪比在7.5 左右;jittered 随机欠采样的信噪比在9.2左右;分段采样重构的信噪比在9.8左右.因此分段随机采样的重构效果有明显的改进.
|
图 8 jittered采样数据(a)及其频谱(b) Fig. 8 (a) Data of jittered sampling; (b) Frequency spectrum of (a) |
|
图 9 jittered采样的重构数据(a)及其频谱(b) Fig. 9 (a) Restoration of jittered sampling; (b) Frequency spectrum of (a) |
|
图 10 分段随机采样数据U)及其频谱(b) Fig. 10 (a) Data of piecewise random sampling; (b) Frequency spectrum of (a) |
|
图 11 分段随机米样的重构数据U)及其频谱(b) Fig. 11 (a) Restoration of piecewise random sampling; (b) Frequency spectrum of (a) |
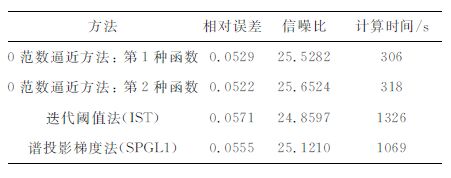
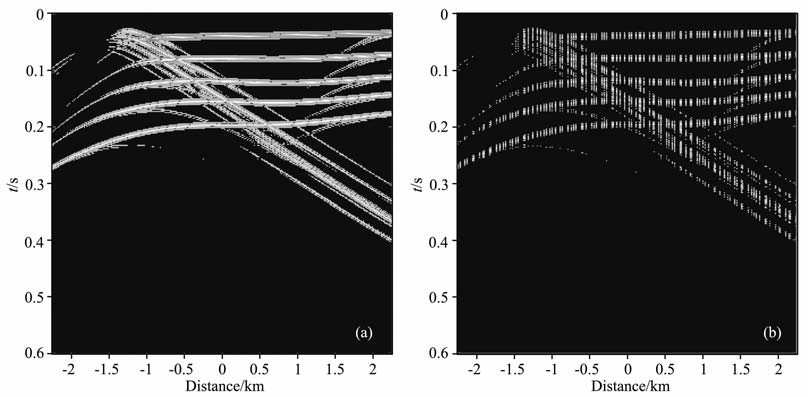
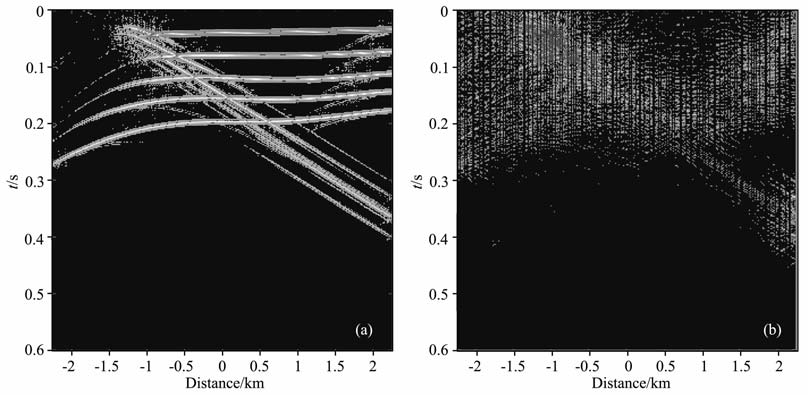
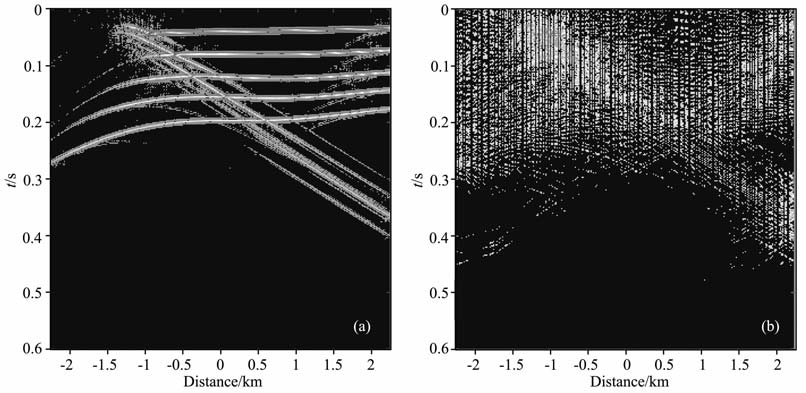
下面给出0范数逼近方法的数值模拟.图 12a中的地震数据的空间采样间隔为15m, 共有300道,时间采样间隔为2ms, 采样时间为0.6s, 图 12b是已知的采样数据,采样个数为图 12a的一半.图 13a是第1种函数fσ(x)=1-exp(-x2/2σ2)时0范数逼近算法的重构数据,信噪比为25.5282,计算时间为306s, 图 13b是图 13a与原始数据的误差.图 14a是第2种函数fσ(x)=1-σ2/(x2 +σ2)时0范数逼近算法的重构结果,信噪比为25.6524,计算时间为318s, 图 14b是图 14a与原始数据的误差.图 15a是迭代阈值法(IST)的重构数据,信噪比为24.8597,计算时间为1326s, 图 15b 是图 15a与原始数据的误差.图 16a 是谱投影梯度法(SPGL1)的重构数据,信噪比为25.1210,计算时间为1069s, 图 16b 是图 16a与原始数据的误差.表 1列出了以上三种方法重构的CPU 计算时间、相对误差以及信噪比.综上可见,0 范数逼近算法的计算时间明显减少,约为迭代阈值法和谱投影梯度法的三分之一;因此0范数逼近方法更适合地震数据重构.
|
图 12 原始数据(a)和采样数据(b) Fig. 12 (a) 丁he original data; (b) 丁he sampled data |
|
图 13 基于函数1的0范数逼近算法的重构数据(a)及其与原始数据的误差(b) Fig. 13 (a) Restoration of zero-norm approximate method based on case 1 function; (b) Difference between the original data and (a) |
|
图 14 基于函数2的0范数逼近算法的重构数据(a)及其与原始数据的误差(b) Fig. 14 (a) Restoration of zero-norm approximate method based on case 2 function; (b) Difference between the original data and (a) |

|
图 15 迭代阈值法(1ST)的重构数据(a)及其与原始数据的误差(b) Fig. 15 (a) Restoration of 1ST method; (b) Difference between the original data and (a) |

|
图 16 谱投影梯度法(SPGL1)的重构结果(a)及其与原始数据的误差(b) Fig. 16 (a) Restoration of the SPGL1 method; (b) Difference between the original data and (a) |
|
|
表 1 三种算法重构结果的比较 Table 1 The restoration results comparison of the above three methods |
本文采用curvelet变换作为稀疏变换,将地震数据重构问题变为稀疏优化问题,提出了一种基于0范数逼近的投影梯度法求解地震数据重构问题;并且利用最近提出的分段随机采样方式来改进重构的效果.数值模拟显示,在相同重构结果情况下,基于0范数逼近的投影梯度算法的计算时间是谱投影梯度法和迭代阈值法的三分之一,因此具有更快的计算效率.分段随机采样能够控制采样间隔和保持采样的随机性,因此比随机欠采样方式更适合地震数据重构.
稀疏优化技术在地震数据处理中具有广阔的应用前景,比如时频分析、去噪、多次波消除和偏移等等.高精度反褶积问题[33]是时间域的插值,因此可以利用压缩传感的理论解高精度反褶积问题,进行时间域的信息重构.
稀疏变换直接影响重构的结果,变换后的数据越稀疏,越有利于数据恢复;快速高效的求解方法是稀疏优化的核心;好的采样方式在保证质量的前提下,能够节约采样时间和成本;三者都是值得研究的重要方向.
基于稀疏重构的正则化方法和最优化方法是当前的研究热点.稀疏优化解法目前主要集中在基于1范数的解法,真正的基于0范数的快速稳定方法会有更好的数值结果.
致谢感谢评审人提出的宝贵意见,使得本文的研究内容有了很大的充实.
| [1] | Wang Y F, Yang C C, Cao J J. On Tikhonov regularization and compressive sensing for seismic signal processing. Mathematical Models and Methods in Applied Sciences , 2012, 22(2). DOI:10.1142/S0218202511500084 |
| [2] | Cao J J, Wang Y F, Zhao J T, et al. A review on restoration of seismic wavefields based on regularization and compressive sensing. Inverse Problems in Science and Engineering , 2011, 19(5): 679-704. DOI:10.1080/17415977.2011.576342 |
| [3] | Sacchi M D, Ulrych T J. Estimation of the discrete Fourier transform, a linear inversion approach. Geophysics , 1996, 61(4): 1128-1136. DOI:10.1190/1.1444033 |
| [4] | Duijndam A J W, Schonewille M A, Hindriks C O H. Reconstruction of band-limited signals, irregularly sampled along one spatial direction. Geophysics , 1999, 64(2): 524-538. DOI:10.1190/1.1444559 |
| [5] | Liu B. Multi-dimensional reconstruction of seismic data. Alberta: University of Alberta, 2004. |
| [6] | Sacchi M D, Verschuur D J, Zwartjes P M. Data reconstruction by generalized deconvolution. 74th Annual International Meeting, SEG, Expanded Abstracts, 2004: 1989-1992. |
| [7] | Spitz S. Seismic trace interpolation in the F-X domain. Geophysics , 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [8] | Gülünary N. Seismic trace interpolation in the Fourier transform domain. Geophysics , 2003, 68(1): 355-369. DOI:10.1190/1.1543221 |
| [9] | Claerbout J F. Earth Soundings Analysis: Processing Versus Inversion. Blackwell Science, 1992. |
| [10] | Crawley S. Seismic trace interpolation with nonstationary prediction-error filters. Stanford: Stanford University, 2000. |
| [11] | Ronen J. Wave-equation trace interpolation. Geophysics , 1987, 52(7): 973-984. DOI:10.1190/1.1442366 |
| [12] | Stolt R H. Seismic data mapping and reconstruction. Geophysics , 2002, 67(3): 890-908. DOI:10.1190/1.1484532 |
| [13] | Hennenfent G, Herrmann F J. Random sampling: New insights into the reconstruction of coarsely-sampled wavefields. SEG, Expanded Abstracts , 2007, 26: 2575-2579. |
| [14] | 王彦飞. 反问题的计算方法及其应用. 北京: 高等教育出版社, 2007 . Wang Y F. Computational Methods for Inverse Problems and Their Applications (in Chinese). Beijing: Higher Education Press, 2007 . |
| [15] | 肖庭延, 于慎根, 王彦飞. 反问题的数值解法. 北京: 科学出版社, 2003 . Xiao T Y, Yu S G, Wang Y F. Numerical Methods for the Solution of Inverse Problems (in Chinese). Beijing: Science Press, 2003 . |
| [16] | 袁亚湘, 孙文瑜. 最优化理论与方法. 北京: 科学出版社, 1997 . Yuan Y X, Sun W Y. Theory and Methods for Optimization (in Chinese). Beijing: Science Press, 1997 . |
| [17] | Candes E J. Compressive sampling. //Proceedings of International Congress of Mathematicians. Madrid: European Mathematical Society Publishing House, 2006: 33-52. |
| [18] | Candes E J, Donoho D L. Curvelets: A surprisingly effective nonadaptive representation of objects with edges.//Cohen A, Rabut C, Schumaker L L, eds. Curves and Surfaces Fitting: Saint-Malo 1999. Nashville: Vanderbilt University Press, 2000: 105-120. |
| [19] | Herrity K K, Gilbert A C, Troop J A. Sparse approximation via iterative thresholding. //Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Proceeding, 2006: 624-627. |
| [20] | Wang Y F, Fan S F, Feng X. Retrieval of the aerosol particle size distribution function by incorporating a priori information. Journal of Aerosol Science , 2007, 38(8): 885-901. DOI:10.1016/j.jaerosci.2007.06.005 |
| [21] | Wang Y F. Seismic impedance inversion using l1-norm regularization and gradient descent methods. J. Inv. Ill-Posed Problems , 2011, 18(7): 823-838. |
| [22] | Wang Y F, Ma S Q, Yang H, et al. On the effective inversion by imposing a priori information for retrieval of land surface parameters. Science in China D , 2009, 52(4): 540-549. DOI:10.1007/s11430-009-0036-9 |
| [23] | Wang Y F, Cao J J, Yuan Y X, et al. Regularizing active set method for nonnegatively constrained ill-posed multichannel image restoration problem. Applied Optics , 2009, 48(7): 1389-1401. DOI:10.1364/AO.48.001389 |
| [24] | Wang Y F, Cao J J, Yang C C. Recovery of seismic wavefields based on compressive sensing by an l1-norm constrained trust region method and the piecewise random subsampling. Geophysical Journal International , 2011, 187(1): 199-213. DOI:10.1111/gji.2011.187.issue-1 |
| [25] | Mohimani H, Babaie-Zadeh M, Jutten C. A fast approach for overcomplete sparse decomposition based on smoothed l0 norm. IEEE Transactions on Signal Processing , 2009, 57(1): 289-301. DOI:10.1109/TSP.2008.2007606 |
| [26] | Zwartjes P M, Sacchi M D. Fourier reconstruction of nonuniformly sampled, aliased seismic data. Geophysics , 2007, 72(1): V21-V32. DOI:10.1190/1.2399442 |
| [27] | van den Berg E, Friedlander M P. Probing the pareto frontier for basis pursuit solutions. SIAM J. Sci. Comput. , 2008, 31(2): 890-912. |
| [28] | Wang Y F, Yang C C. Accelerating migration deconvolution using a nonmonotone gradient method. Geophysics , 2010, 75(4): S131-S137. DOI:10.1190/1.3457923 |
| [29] | Wang Y F, Xiao T Y. Fast realization algorithms for determining regularization parameters in linear inverse problems. Inverse Problems , 2001, 17(2): 281-291. DOI:10.1088/0266-5611/17/2/308 |
| [30] | Hennenfent G, van den Berg E, Friedlander M P, et al. New insights into one-norm solvers from the Pareto curve. Geophysics , 2008, 73(4): A23-A26. DOI:10.1190/1.2944169 |
| [31] | Lustig M, Donoho D L, Pauly J M. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine , 2007, 58(6): 1182-1195. DOI:10.1002/(ISSN)1522-2594 |
| [32] | Hennenfent G, Herrmann F J. Simply denoise: wavefield reconstruction via jittered undersampling. Geophysics , 2008, 73(3): V19-V28. DOI:10.1190/1.2841038 |
| [33] | Taylor H L, Banks S C, McCoy J F. Deconvolution with the l1 norm. Geophysics , 1979, 44(1): 39-52. DOI:10.1190/1.1440921 |
 2012, Vol. 55
2012, Vol. 55