2. 中国科学院地质与地球物理研究所, 北京 100029
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
AVO 分析是地震资料处理和解释中的重要手段之一,它能够提供有关构造和岩性较为准确的信息.在地震勘探的很多工作都已逐渐由各向同性介质的假设转到各向异性介质的事实的前提下,各向异性的AVO 研究也得到了蓬勃的发展,目前针对各向异性介质的无论是PP波还是PS波的AVO 分析都是研究的热点内容.在各向异性介质中,横向各向同性(TI)介质根据其对称轴的方向不同可以分为垂直横向各向同性(VTI)介质,水平横向各向同性(HTI)和倾斜横向各向同性(TTI)介质.当地层为倾斜薄层或各向同性介质中嵌入了并行的倾斜断裂情况都应将其考虑为TTI介质.TTI介质能更真实地反应地层的地质特征,是众多地球物理学家研究的重点内容.Thomsen[1]在对VTI介质的研究中引入了Thomsen各向异性参数,这些参数的定义建立了弹性系数与裂隙特性关系的桥梁.利用地面地震反射属性来反演Thomsen参数,进一步获取裂隙的物理特性,这对裂隙型储层的勘探开发意思重大.Grechka等[2]研究了单斜介质中利用NMO 速度进行类Thomsen 各向异性参数反演,Bakulin[3]研究了HTI、正交、单斜介质中用反射地震数据进行裂隙参数估计.何樵登[4],周辉[5],张文生[6]等都把最优化理论充分运用到了各向异性参数的反演理论中.轩义华[7]做了TTI介质中NMO 非双曲时差反演各向异性参数的研究;卢明辉等研究了在正交各向异性介质中使用P 波走时进行Thomsen参数反演[8];雍杨研究了TI介质中的多波AVA 各向异性参数反演[9].Banik[10],Thomsen[11]和Rüger[12-14]得出了VTI,HTI介质的反射系数,Rüger的结果也可以应用于正交介质.Donati[15],Alvarez 等[16]及Nefedkina和Buzlukov[17]研究了各向同性介质PS波反射系数的近似解.Ivan PŚencčík 和VaclavVavryčuk[18]给出了弱各向异性介质中的PP 波反射-透射系数通用表达式;Vavryčuk[19],Jílek[20]和Artola等[21]进一步研究了任意各向异性,弱阻抗差、弱各向异性介质的PS 波反射-透射系数.JyotiBehura和IlyaTsvankin[22]完整地给出了TTI介质中PS波正入射反射系数及AVO 梯度表达式,为TI介质中AVO 研究提供了坚实的理论基础.
针对更具有实际意义的TTI介质,用最优化理论,从AVO 信息出发反演各向异性参数的研究属于这一领域的前沿.本文首先介绍了TTI介质的PP波、PS波的反射系数相关理论;接着构造了TTI介质模型,根据所述理论获取模拟地震波记录.随后,建立了TTI介质中PP波、PS波反演Thomsen参数及对称轴倾角、方位角的目标函数,选用遗传算法进行反演;并结合理论模拟数据的反演分析了介质参数的精度.
2 方法原理 2.1 TTI介质PP波、PS波反射系数两个弱的任意各向异性弹性介质分界面处的近似PP波反射系数公式由Vavryčuk和PŚencčík(1998)推导出[18]:
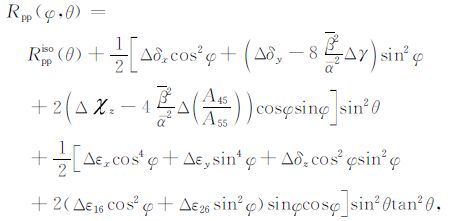
|
(1) |
其中φ、θ 为入射波的方位角和入射角,ρ、α、β 为相应介质的密度和纵横波速度,Rppiso(θ)为分隔两个弱差别的各向同性介质的分界面处的反射系数[23],且有:
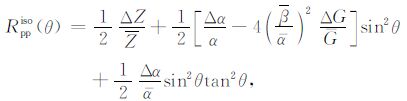
|
(2) |
式中,波阻抗Z和剪切模量G分别为:

|
(3) |
(1) 式中除了背景介质密度及纵横波波速等参数的均值和差值及入射波角度θ、φ 之外,反射系数还取决于其他的8个弱各向异性WA(weakanisotropy)参数差.它们描述了弱各向异性介质的P 波相速度和偏振.WA 参数表征的是各向异性介质性质对各向同性背景的偏离,WA 参数一共有15个,用弹性系数表示分别是:
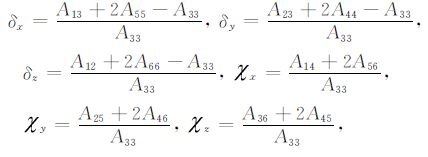
|
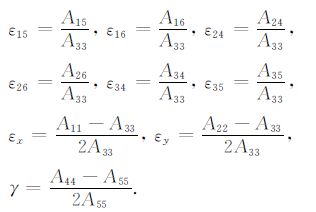
|
(4) |
如果介质是各向同性介质,则所有的WA 参数都变为零;为TI介质时部分WA 参数退化为零或Thomsen参数,未退化的参数根据公式(4)由弹性系数求取.本文涉及的TTI介质模型都是由Thomsen参数直接定义的,使用VTI介质中Thomsen 参数与弹性系数关系及TI介质中弹性系数矩阵旋转原理可以建立TTI介质弹性系数与Thomsen参数的互换关系[7].
通用的PS波反射系数可以写成[20]
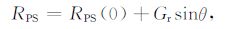
|
(5) |
其中RPS(0)是正入射反射系数,在AVO 分析中也叫截距,Gr 为AVO 梯度.对于各向同性介质入射,TTI介质反射的情形,将PSV 和PSH 作为整体研究的PS波正入射反射系数为[22]

|
(6a) |
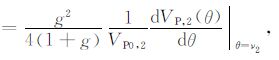
|
(6b) |
其中,g是介质纵横波速度比α/β.(6a)式是关于Thomsen参数的近似线性公式,υ2 指反射半空间对称轴倾角.(6b)式中的VP,2是反射半空间P 波相速度,正入射时的PS 波反射系数与θ=υ2(入射角等于反射半空间对称轴倾角)时的P 波相速度梯度值成比例.本文中对于TTI介质PS波反射系数的计算使用(6a)式,与(6b)式中的相速度计算结果差别不大[22].JyotiBehura同时给出了ISO/TTI(各向同性入射TTI 介质反射)分界面上的PS1、PS2 到PSV、PSH 波的退化关系及PSV、PSH 波AVO 梯度Gr 的解析式[22].
2.2 目标函数的建立遗传算法反演TTI介质各向异性参数与对称轴信息的实质是寻求适当的参数组合p(ε,δ,γ,υ,φ),使其所确定的模型的反射系数与实测的反射系数或振幅拟合.因此,PS波反演的目标函数可以确立为

|
(7) |
其中i为地震记录的道序号,θ(i)为该道转换波对应的P波入射角.PP波反演的目标函数为
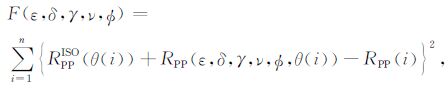
|
(8) |
θ(i)为该道的P波入射角,对称轴倾角和方位角两个参数使用角度的正弦值sinν,sinφ,其余参数使用绝对值,即将所有参数都做归一化处理.本文中,为减少待反演参数个数,提高反演精度,直接给出上下层介质的纵横波速度和密度.计算过程中起始的随机种子数为1000组,每个参数的搜索步长都是0.001.本文使用的遗传算法的计算程序是来自COLORADO的NationalAtmosphericResearch Center发布的遗传算法工具包PIKAIA1.2版本.
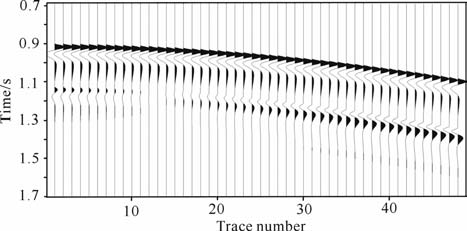
3 理论模拟数据和反演测试 3.1 理论模型和反演结果模型参数如表 1所示.计算PP、PS反射波走时及ISO/TTI界面处的PP、PS 波反射系数值,将反射系数与给定的主频为30Hz的最小相位子波褶积合成地震记录,结果见图 1.采用单边放炮,48 道接收,道间距20 m, 界面深度为900 m, 首道偏移距40m.
|
|
表 1 USO/TTK反射界面上下层介质参数 Table 1 The coefficients of the upper and lower media around the ISO/TTI interface |
|
图 1 ISO/TTI模型PP、PS反射波合成地震记录 Fig. 1 PP and PS reflection wave synthetic seismogram of the ISO/TTI model |
该模型PP、PS波反射系数分别使用(1)式和(5)式求取.通过(1)式计算PP 波反射系数时需要给定反射层TTI介质的弹性系数矩阵.由VTI介质中的Thomsen参数与弹性系数之间的关系计算出相应的VTI介质的弹性系数,再根据TI介质中的坐标系旋转公式求取反射层TTI介质对应的弹性系数矩阵.(5)式中的梯度Gr 使用JyotiBehura给出的GPSV项.表 2是根据(7)式和(8)式使用遗传算法反演出的反射层TTI介质Thomsen参数与对称轴倾角、方位角结果.
|
|
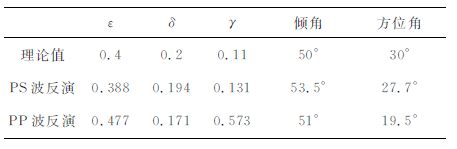
表 2 各向异性参数遗传算法反演结果 Table 2 Genetic algorithm inversion results of anistropic parameters |
分析表 2 中的反演结果可以发现,通过反射PP、PS波反射系数反演的TTI介质各向异性参数结果具有一定的准确性.PP波反演出的各向异性参数与对称轴角度信息的准确性明显低于通过PS波反演的结果.PP 波和PS波反演出的对称轴倾角较准确,对称轴方位角误差较大.
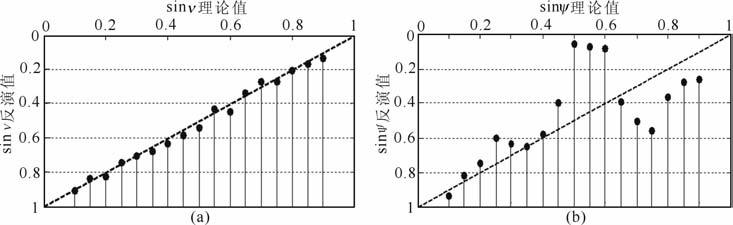
对分别改变反射层对称轴倾角、方位角,其余参数不变的正演记录使用PS 波进行反演,所得的对称轴倾角、方位角结果如图 2所示.从图 2中可以看出,对称轴倾角反演结果的精度较高,稳定性较好,精确度和稳定性远远大于方位角的反演结果.这主要是因为在已给出的反射系数解析解中倾角对反射系数值影响较大,且函数值在自变量变化范围内产生的变化方向较单一,相比之下,在方位角的反演过程中容易陷入局部极值的陷阱.图 3 和图 4 为表 1中模型变化反射层TTI介质对称轴倾角和方位角得到的正演结果.从图中可以看出反射PS 波的振幅随对称轴倾角改变发生了明显的变化,而在方位角发生变化时反射波振幅变化不明显.
|
图 2 改变反射层TTI介质对称轴倾角 (a)和方位角(b)得到的反演结果 Fig. 2 Inversion results by changing the symmetry dip angle (a) and azimuth angle (b) in the reflection TTI media |
|
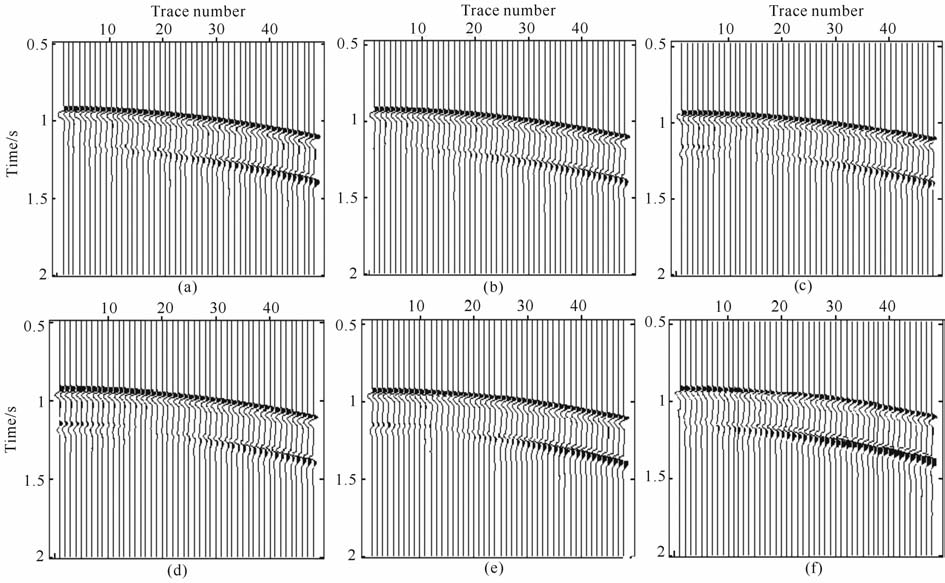
图 3 反射波振幅随反射层TTI介质对称轴倾角的变化 倾角(a) 0%(b) 10%(c) 30°(d) 50。;(f)70%(f) 90° Fig. 3 The changing of reflection amplitude along with the symmetry dip angle in the reflection TTI media |
|
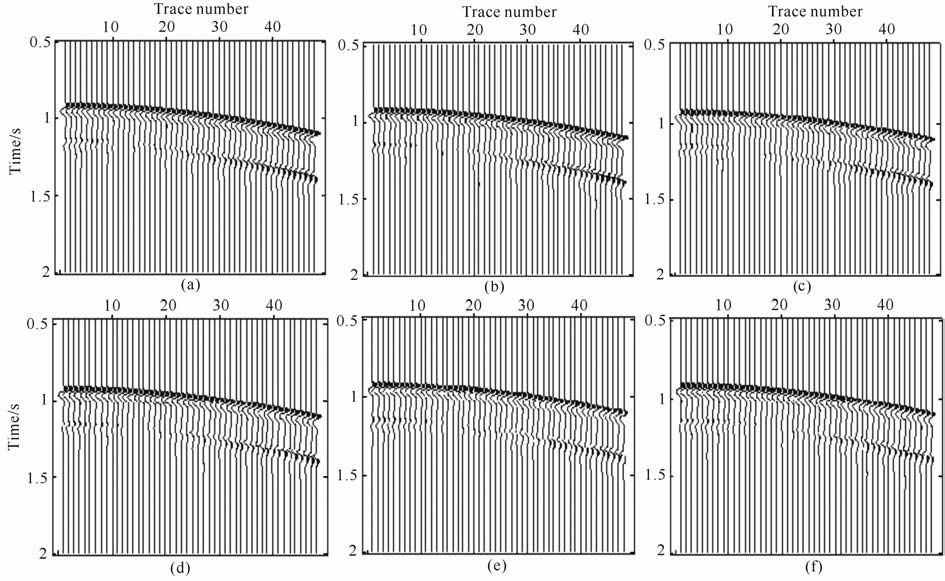
图 4 反射波振幅随反射层TTI介质对称轴方位角的变化 方位角(a) 0。;b) 10°(c) 30。50。;e) 70° ⑴ 90° Fig. 4 The changing of reflection amplitude along with the symmetry azimuth angle in the reflection TTI media |
在以上模型反射波反射系数计算过程中,PP 波反射系数的计算采用的是弱各向异性介质PP 波反射系数通用公式.它给出的是任意各向异性介质中反射系数与弱各向异性参数之间的关系.需要建立Thomsen参数、弹性系数及WA 参数三者之间的互换关系.本文中,虽然都采用相同的反演方法,但是利用PP波反射系数反演的结果误差较大,这证明PP波反射系数对各向异性参数、倾角和方位角的敏感程度比PS波差.同时,从图 3和图 4我们可以看出,对于表 2中的ISO/TTI反射界面模型,使用(1)式所得的PP波反射系数对各向异性参数的依赖程度较低,变化反射层对称轴倾角、方位角时,PP 波振幅未见明显变化,因此对于PP 波的反射系数,使用(1)式给出的解析解,不太适合用来反演各向异性参数.在Thomsen给出的各向异性参数物理意义中,γ表示的是SH 波水平速度和垂向速度的差别.但从(1)式中可见,横波分裂因子γ 也与PP 波反射系数有关.从表 2可知,PP 波反射系数未能成功反演出参数γ,PP波反射系数对参数γ 不敏感.
4 PS波AVO 分析当模型复杂或未知参数增加时,TTI介质参数的反演会陷入严重的多极值非线性反问题中,因此在实际应用中一般采用AVO 分析的方法简化TTI介质的反演.
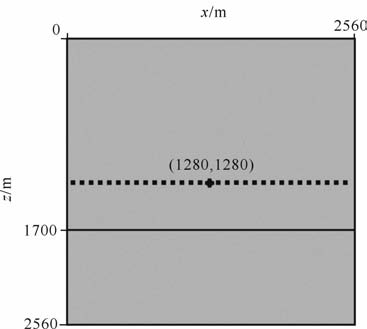
首先介绍如何从反射波振幅出发提取(5)式中的正入射反射系数与AVO 梯度.建立一个TTI/ISO 水平界面的地质模型,如图 5 所示.其中,震源和检波点都位于1280 m 深的平面上,震源使用垂直力源,子波类型是主频为40Hz的衰减正弦波.1700m 处是TTI介质与各向同性介质的水平分界面,表 3中给出了上下层介质的相关参数.利用伪谱法进行波动方程的数值模拟,所得的二维三分量地震记录见图 6.为方便起见,选取从x坐标1280 m处开始的单边记录显示.
|
图 5 TTI/ISO的水平界面模型 Fig. 5 TTI/ISO horizontal reflection interface model |
|
|
表 3 TTK/IISO水平界面模型上下层介质参数 Table 3 The coefficients of the upper and lower media around the TTI /ISO horizontal interface |

|
图 6 TTI/ISO水平界面模型二维三分量地震记录 (a)x分量;(b)y分量;(c) z分量. Fig. 6 The 2D three components seismogram of a TTI/ISO horizontal interface model (a)x component; (b) y component; (c) z component. |
分析图 6中的地震记录,从上至下依次为:直达P波(DqP),直达SH 波(DqSH),直达SV 波(DqSV),反射PP波(RqP),反射的PSH 波(RqPSH)和PSV(RqPSV),反射SH-SH 波(RqSH),反射SV-SV 波(RqSV).由于该模型TTI介质中横波速度差异不大(γ 值较小),同时反射界面深度较浅,故两种PS反射波在时间上很接近.由于SV 波和SH 波相速度随入射角变化很大,导致反射波走时交叉.由于在正演过程中仅仅采用了普通各向同性介质条件下的吸收边界条件,对TTI介质波场没有起到很好的吸收效果,在x和z分量记录上有一定程度的侧边界反射.
从图 6中的地震记录可以看出,地震波频散和波形畸变的现象较为严重.在实际资料的AVO 分析中,除反射系数外,影响地震波振幅的因素很多,包括各种衰减与扩散,震源、检波器组合,动较拉伸,薄层调谐,激发接收条件,各种噪音及仪器因素等等.此时,进行反射系数反演获取准确的反射系数很困难,直接利用遗传算法反演的结果显然并不可信.(5)式中的PS 波AVO 梯度可以通过拾取反射PS波振幅与P 波入射角正弦值的散点图来判断,从RPSV(sini)和RPSH (sini)图中的线性趋势来识别各向异性信息.图 7所示的是图 5中模型的上层TTI介质对称轴倾角变化时拾取的PSV 波振幅与入射角正弦值的散点图,其中转换波入射角的确定暂未考虑入射层介质各向异性的影响,直接使用各向同性介质中的转换波入射角确定方法(假设在弱各向异性介质中误差不大).
从图 7中可以看出,在以每道转换波所对应的P波入射角正弦值为横坐标,该道PSV 波振幅为纵坐标的二维散点图中,散点近似分布在一条直线上,由(5)式可知,如果纵坐标使用的是PSV 波的精确反射系数值,则该直线的斜率应该是PSV 波AVO梯度值,同时该直线的截距是P 波正入射时的PS波反射.图 7中随着对称轴倾角的增大,散点近似直线斜率增大,体现了TTI 介质中对称轴倾角对AVO 梯度的影响.在一阶摄动理论中,只有上下层介质中有不为零的弹性系数ΔA34和ΔA35时,水平界面上法相入射的P波才会产生S波反射[20],与各向同性、VTI、HTI介质不同,TTI介质中的这两个参数非零.上述的散点图中PS 波非零的截距可以揭示界面两侧TTI介质的存在.

|
图 7 TTI介质取不同对称轴倾角时拾取的振幅和人射角正弦值的散点图 倾角(a) 30°(b) 50°(c) 70°. Fig. 7 The scatter diagram of amplitede and sine value of incident angle when the TTI media have a diffrent symmetry dip angle |
从TTI介质中PP波、PS波反射系数解析解出发,建立Thomsen参数和TTI介质对称轴倾角、方位角的目标函数,可以用非线性反演的方法来反演介质的各向异性参数.数值计算表明使用遗传算法进行各向异性参数的反演可以取得较好的效果,反演结果具有一定的稳定性与精确度.通过与PP 波反射系数反演的各向异性参数相对比,PS波的反演结果精确度较差.TTI介质中PS 波反射系数对各向异性参数更敏感,各向异性介质PP 波反射系数通用解不适合用于Thomsen参数反演.反演可同时获得TTI介质对称轴倾角和方位角的信息,模型正演表明,相对于对称轴方位角,反射系数对对称轴倾角更敏感,反演所得的对称轴倾角精确度更高,稳定性更好.对于更复杂的TTI/TTI界面或其他反射界面的情况,待反演参数更多时,可能需要多波联合反演或AVO 梯度与正入射反射系数联合反演.
拾取了反射PS波振幅与P 波入射角正弦值的散点图后,可以通过散点所在直线的斜率与截距判断PS波AVO 梯度与正入射PS波反射.
致谢感谢郝奇博士提供的TTI介质伪谱法全波正演程序.
| [1] | Thomsen L. Weak elastic anisotropy. Geophysics , 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [2] | Grechka V, Tsvankin I. 3-D moveout velocity analysis and parameter estimation for orthorhombic media. Geophysics , 1999, 64(1): 820-837. |
| [3] | Bakulin A. Estimation of azimuthal anisortopy and fracture parameters frommulitiazimuthal walkaway VSP in the presence of lateral heterogeneity. 70th Ann Int SEG Mtg , 2000: 1405-1408. |
| [4] | 何樵登, 陶春辉. 用遗传算法反演裂隙各向异性介质. 石油物探 , 1995, 34(3): 46–50. He Q D, Tao C H. Inversing fractured anisotropic media through a genetic algorithm. Geophysical Prospecting for Petroleum (in Chinese) , 1995, 34(3): 46-50. |
| [5] | 周辉, 何樵登. 非线性各向异性波形反演方法. 石油地球物理勘探 , 1995, 30(6): 725–735. Zhou H, He Q D. Nonlinear waveform inversion in anisotropic medium. Oil Geophys. Prosp. (in Chinese) , 1995, 30(6): 725-735. |
| [6] | 张文生, 何樵登, 吴飞. 用遗传算法反演各向异性介质弹性参数. 物化探计算技术 , 1998, 20(4): 293–299. Zhang W S, He Q D, Wu F. Inversion of elastic parameter in transversely isotropic media using genetic algorithms. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1998, 20(4): 293-299. |
| [7] | 轩义华. 倾斜横向各向同性介质(TT1)参数反演方法研究. 长春: 吉林大学, 2007. Xuan Y H. Research on inversion method in transversely isotropic media with a tilted symmetry axis (in Chinese). Changchun: Jilin University, 2007. |
| [8] | 卢明辉, 唐建候, 杨慧珠, 等. 正交各向异性介质P波走时分析Thomsen参数反演. 地球物理学报 , 2005, 48(5): 1167–1171. Lu M H, Tang J H, Yang H Z, et al. P-wave traveltime analysis and Thomsen parameters inversion in orthorhombic media. Chinese J. Geophys. (in Chinese) , 2005, 48(5): 1167-1171. |
| [9] | 雍杨. 横向各向同性介质多波振幅特征及参数反演方法研究. 成都: 成都理工大学, 2003. Yong Y. The study of multiwave amplitude equation and inversion method in transverse isotropic medium(in Chinese). Chengdu: Chengdu University of Technology, 2003. |
| [10] | Banik N C. An effective anisotropy parameter in transversely isotropic media. Geophysics , 1987, 52(12): 1654-1664. DOI:10.1190/1.1442282 |
| [11] | Thomsen L. Weak anisotropic reflections. //Castagna J P, Backus M M. Offset Dependent Reflectivity. SEG, Tulsa, 1993. |
| [12] | Rüger A. Reflection coefficients and azimuthal AVO analysis in anisotropic media. Center for Wave Phenomena, Colorado School of Mines, Golden, Colorado. 1996. |
| [13] | Rüger A. P-wave reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry. Geophysics , 1997, 62(3): 713-722. DOI:10.1190/1.1444181 |
| [14] | Rüger A. Variation of P-wave reflectivity with offset and azimuth in anisotropic media. Geophysics , 1998, 63(3): 935-947. DOI:10.1190/1.1444405 |
| [15] | Donati S M, Matin N W. Making AVO analysis for converted waves a practical issue. 68th Annual Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 1998, 17: 2060-2063. |
| [16] | Alvarez K, Donati M, Aldana M. AVO analysis for converted waves. 69th Annual Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 1999: 876-879. |
| [17] | Nefedkina T, Buzlukov V. Seismic dynamic inversion using multiwave AVO data. 69th Annual Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 1999, 18: 888-891. |
| [18] | PŜencčík I, Vavryčcuk V. Weak contrast PP wave displacement R/T coefficients in weakly anisotropic elastic media. Pure Appl. Geophys. , 1998, 151(2-4): 699-718. |
| [19] | Vavrycuk V. Weak-contrast reflection/transmission coefficients in weakly anisotropic elastic media: P-wave incidence. Geophys. J. Int. , 1999, 138(2): 553-562. DOI:10.1046/j.1365-246X.1999.00890.x |
| [20] | Jílek P. Converted PS-wave reflection coefficients in weakly anisotropic media. CWP Annual Project Review, 2000, CWP-340, 275-299. |
| [21] | Artola F V A, Leiderman R, Fontoura S A B, et al. Zero-offset C-wave reectivity in horizontally layered media: 73rd Annual Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 2003: 761-764. |
| [22] | Behura J, Tsvankin I. Small-angle AVO response of PS-waves in tilted TI media. Geophysics , 2006, 71(5): 69-79. |
| [23] | Aki K, Richards P G. Quantitative Seismology. Francisco: W. H. Freeman, 1980. |
 2012, Vol. 55
2012, Vol. 55