2. 东北林业大学数学系, 哈尔滨 150040;
3. 长江工程地球物理勘测武汉有限公司, 武汉 430000
2. Department of Mathematics, Northeast Forestry University, Harbin 150040, China;
3. Changjiang Engineering Geophysical Exploration & Testing Co., Ltd, Wuhan 430000, China
混凝土是目前水利水电工程中最主要的结构材料之一.由于设计、施工质量控制不严、自然灾害或结构老化等原因,混凝土结构在使用过程中不可避免地存在如裂缝、蜂窝、孔洞、磨损和侵蚀等损伤,危及整个结构的安全,混凝土无损探测已成为水利水电工程中广泛关注的问题[1-2].
探地雷达(Ground Penetrating Radar)简称GPR,是一种对地下或物体内不可见的目标或界面进行定位的电磁探测技术[3].所谓探地雷达资料反演成像实际上就是通过接收到的电磁波数据计算所探测物体的内部参数的构成,这个过程在数学上称之为反演.在已知物体内部的参数分布(例如介电常数或电导率)去模拟电磁波的传播,这个过程称之为正演.目前,电磁波的正演模拟已经相对比较成熟,常用的方法有FDTD(时域有限差分)、有限元、伪普法等等.而反演成像是一个非常困难的问题(通常情况下反问题要比正文题困难),最早人们通过最小二乘求解,但反演成像是一个不适定问题,即解不连续依赖接收数据,所以必须对原目标函数即最小二乘加上正则化项来克服问题本身的不适定性.有关不适定问题的解法请参考文献[4].
目前关于探地雷达资料反演成像的方法很多.张安学等[5]研究了一种利用交叉测线对地下目标进行成像的方法;底青云等[6]用有限元方法研究了有耗介质时域GPR 速度与介电常数的联合反演;Song等[7]研究了三维层状介质的目标重构问题.但他们的工作都是在频域积分方程的Born近似的意义下进行的,绕开了对Maxwell方程进行数值反演求解这个较为困难的问题,其主要问题是要对背景介质进行理想的假设,实际电导率的影响被忽略等,对许多复杂的工程探测问题并不适用.Cai等[8]研究了利用二维Maxwell方程进行电磁波速度反演问题,证明了波动方程反演的结果要好于射线追逐雷达成像,但计算量增加了几个数量级;Hansen等[9]对水平界面的GPR 反演格式进行了研究;Meincke[10]研究了有耗土壤中的GPR 反演问题;Cui等[11]利用高阶Born近似研究了地下物体低频探测的反演方法;J.R.Ernst等[12]研究了跨孔雷达数据的全波形反演,用共轭梯度法实现了介电常数与电导率的同时反演,虽然所使用的反演理论和方法较为经典,但其结果充分说明了全波形数值反演方法相较于射线方法的优越性.我们也在探地雷达全波形数值反演的大范围收敛方法方面做了一些工作[13-14].
但是探地雷达的数据处理和解释工作,与对空雷达理论系统、地震勘探信号处理、以及日渐成熟的硬件技术相比较时,会发现其还远未达到系统、成熟的阶段.比如,对地面单发单收的探地雷达而言,目前还不能依靠雷达测试数据给出诸如目标位置、目标性质和大小尺寸等混凝土无损检测最为关心的数量指标的精确估计,这种状况严重制约了探地雷达技术对混凝土无损探测的发展.与资源地球物理勘探相比,混凝土探测属于小尺度探测问题.其特点是探测对象的边界条件复杂、目标体的几何尺度很小、探测精度和分辨率要求高、介质的均匀性极差等.对于复杂的探测问题,用基于射线理论的雷达波层析成像,和基于Born 或Rytov 弱散射近似假定的波形反演都已无能为力,因为这些方法采用首次到达波或早期到达波来反演参数,这造成了数据量不够,得到的反演结果不准确,必须发展可视性强、识别精度高的数值反演成像方法.
本文以时域Maxwell方程为基本模型[15],结合更加符合实际情况的PML(完全匹配层)边界条件[16],用FDTD(时域有限差分)方法模拟电磁波在混凝土缺陷中的波场作用过程与响应特征.针对传统Gauss-Newton法容易陷入局部极值困扰这个问题,采用同伦优化算法和阻尼高斯牛顿法结合探地雷达资料实现介电常数的反演成像,其中同伦优化算法可以扩大算法的收敛范围,在初值选取较差的情况下仍然能够得到满意的结果.在本文中,我们首先构造一个同伦函数,然后采用同伦优化方法[17]计算观测数据与非线性算子所构成的最小二乘的全局最优解,目的是通过探地雷达的观测数据识别混凝土构件内部缺陷,在未知真实模型的情况下,给出初始模型,同伦优化算法(外层迭代)结合阻尼高斯牛顿方法(内层迭代)可以得到全局极小解.数值实验验证了该反演成像方法能够更加准确、直观地反映混凝土的内部结构.
2 电磁波正演模拟GPR 是一种电磁波类探测方法.与探空或通讯雷达技术相类似,探地雷达也是利用高频电磁脉冲波的反射来探测目的体及地质现象的.探地雷达系统将高频电磁波以宽频带短脉冲形式由发射天线向被探测物发射,该雷达脉冲在传播过程中,遇到不同电性介质交界面时,部分雷达波的能量被反射回来,由接收天线接收.探地雷达测得的是来自探测物不同介质交界面的反射波,地质雷达通过记录反射波到达时间t、反射波的幅度等来研究被探测介质的分布和特性.GPR具体的工作原理请参考文献[18].
电磁波在混凝土介质中的波场作用过程与响应特征可以由时域Maxwell方程近似给出:
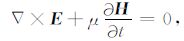
|
(1) |

|
(2) |
其中E和H分别是电场与磁场,ε是介电常数,σ是电导率,μ 是磁导率,sr 是激励源.Maxwell方程的正演过程可以采用FDTD 方法求解,利用高效的PML 吸收边界条件最大限度地克服在边界处反射带来的影响.展开方程(1)和(2)后可得电磁场6个分量的方程组:
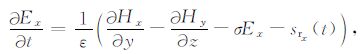
|
(3) |
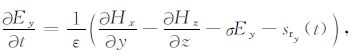
|
(4) |
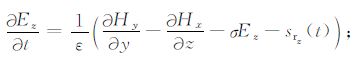
|
(5) |

|
(6) |
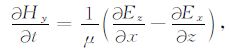
|
(7) |
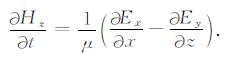
|
(8) |
在2D 问题中即电场和磁场均与z无关时,方程组就形成相互独立的两组方程,其中的一组电场只有Ez分量,这类电磁波称作横磁波用TM 表示,本文的探地雷达2D 正演模拟采用TM 型电磁波求解,TM 波的方程组为
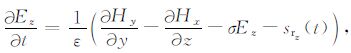
|
(9) |

|
(10) |
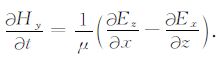
|
(11) |
由上面的方程组可以看出,TM 波只有Ez,Hx和Hy三个分量.将Hx、Hy消元,得到
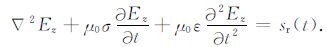
|
(12) |
反演无疑是无损检测最核心的理论问题之一.反演方法就其利用的数据来分,有利用振幅的反演方法,例如求介质衰减系数的计算机层析成像;利用走时的反演方法,例如求介质速度的层析成像;利用波形(同时利用振幅、相位、走时)的反演方法.按是否线性化来分有线性反演方法和非线性反演方法.基于GPR 的混凝土无损检测可以抽象为麦克斯韦方程和波形的非线性反演方法[19-21],该方法的优点是能最大程度地利用接收数据所携带的信息直观地反映地下介质状况.本节从二维麦克斯韦方程组出发推导出介电常数的反演公式[22-23].反演的步骤是:建立初始猜测模型,利用电磁波时间域有限差分法模拟正演数据,用正演数据与观测数据之间的最小二乘建立目标函数,Maxwell方程反问题是高度非线性的、严重不适定的,所以目标函数必须使用Tikhonov正则化,同时采用同伦优化方法结合阻尼高斯牛顿法[24]的策略,将同伦算法应用到混凝土无损检测反问题上,构建一个新的同伦函数,其中阻尼高斯牛顿法可以克服传统牛顿法计算Hessian矩阵的困难,同伦方法可以克服一般迭代法经常陷入局部极值的缺点.
3.1 同伦优化方法传统的牛顿法是局部收敛算法,当选取的初值距离真实值差距较大时,算法失效.也就是说当我们对探测的区域不了解的时候,所选取的混凝土初值模型离混凝土真实模型差距较大,所得到的反演结果无法真实反映混凝土的内部结构的介电常数.而同伦优化算法作为一种大范围收敛算法,可以保证在较差的初值情况下,仍然能够得到满意的反演结果.将方程(12)写成离散的形式[25],可以看出介电常数与混凝土表面的观测数据Eobs之间呈非线性关系:

|
(13) |
其中F是基于Maxwell方程的非线性算子,m是所要识别的参数(介电常数),Eobs是混凝土表面处接收的探地雷达资料.我们感兴趣的混凝土无损探测问题可以转化为最小二乘问题:
给定Φ:X⊆Rn→R,求m* ∈X⊆Rn→R使得

|
(14) |
希望找到最优的介电常数m* 分布,使得最小二乘泛函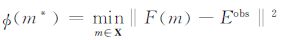
同伦方法的基本思想就是对所考虑的问题引入参数λ∈ [0,1],构造一簇映像H,当λ为某一特定值(例如λ=1时),H就是映像Φ,而当λ=0时,得出的是方程Φ0 =0,它的解m0已知.确切地说,就是构造一簇映像H∶Rn+1→R代替单个映像Φ1,使H满足条件
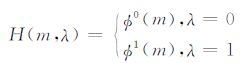
|
(15) |
其中λ 是同伦参数,Δi,i=0,1,…,L-1是同伦算法的步长,满足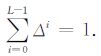

|
(16) |
其中Φ0 = ‖W(m-mref)‖2,Φ1 = ‖F(m)-Eobs‖2.
mref是先验信息,即一般情况下均匀的混凝土介电常数.现在问题转变成为求解同伦方程H(m,λ)=0,用某种数值迭代法从m0(迭代初值即最初的介电常数猜测值)出发跟踪同伦曲线,直到λ=1,就可以最终求出方程(3)的解,从而获得了一种大范围收敛方法.
同伦优化算法的流程如下:
① 给定初值m0= mref,即函数Φ0 的最小范数解,Δi>0,i=0,1,…,L-1,λ0 =0;
② 当i=1,…,L,令λi=λi-1 +Δi-1,在第i步以mi-1 为初值,利用局部极小迭代方法得到mi;
③ 以mi为第i+1步的初值,重复第2步,直至满足停止准则,最终迭代解m* = mL.
同伦算法最大的优势在于增大局部迭代算法的收敛区域,但是在执行的过程中同伦曲线往往会发生停滞不前、回旋或分叉等不收敛现象.为了使算法收敛到真实解,对每一个同伦参数的迭代解扰动,然后采用增大解的容许集的方法.
由算法的计算过程可知,在第i步迭代时,以mi-1 为初值可以得到mi.为了增加算法收敛的可能性,我们将算法修正,在第i步迭代前,将mi-1 做一个扰动.扰动函数为φ:m→mδ.以mi-1 和mi-1δ为第i步迭代的初值,可以得到两个迭代解mi与mδi,然后以此为初值继续进行迭代.显然,解的容许集中的元素呈指数递增,在第i步迭代后解的个数为2i-1.面对如此大的计算量,需要将容许集进行限定,定义容许集中元素的个数为num{X},则我们限定num{X}≤Cmax,Cmax ∈ Z+.当容许集中的元素超过Cmax 时,取使同伦函数最小的Cmax 个解,其他的舍掉.在最后一步(即第L步)迭代后,得到Cmax 个解,将其带入同伦函数比较,使同伦函数取得最小值的解为全局最优解.
修正之后的同伦优化算法:
① 给定初值m0= mref,即函数Φ0 的最小范数解,Δi>0,i=0,1,…,L-1,λ0 =0;
② 当i=1,…,L,令λi=λi-1+Δi-1,在第i步对mi-1 进行扰动,以mi-1 和mδi-1 为第i步迭代的初值,利用阻尼高斯牛顿方法得到mi和miδ,然后以此为初值继续进行迭代;
③ 选取合适的Cmax,当num{X}≤Cmax,Cmax ∈Z+ 时,选取同伦函数值最小的Cmax 个解,返回第2步;
④ 在迭代的最后一步,选取使同伦函数取得最小值的解为全局最优解或迭代过程中满足停止准则,则迭代停止.
3.2 阻尼高斯牛顿法在同伦算法的第i步,即λ =λi时,需要解决同伦函数的优化问题
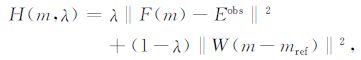
|
(17) |
取同伦函数(17)关于m的导数,可以得到
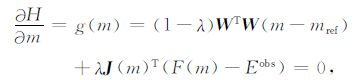
|
(18) |
令参数

|
(19) |
参数β 在这里起到了正则化参数的作用.g(m)是方程(17)的梯度,j(m)是敏感度矩阵,

|
(20) |
如果得到方程(19)的解,就相当于得到方程(17)的解.为了避免牛顿法求解的主要困难即需要计算F对于m的二阶Fréchet导数,将F线性化

|
(21) |
其中R(m,δm)=ο(δm2).于是根据方程(19)和(21)可以得到Gauss-Newton方程
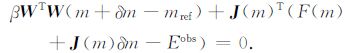
|
(22) |
则目标泛函的极小化问题可以通过下面的迭代格式求解,在第k步

|
(23) |
令mk+1 = mk+δm,则方程(23)可写成
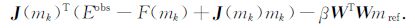
|
(24) |
因此在第k步的解就是
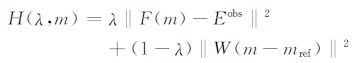
|
(25) |
的最小范数解.
以上讨论的是给定同伦参数情况下的阻尼高斯牛顿算法.下面介绍如何在内层迭代中自适应选取正则化参数β、迭代的终止准则及内层迭代算法的具体流程.
3.3 GCV函数及反演算法广义交叉校验(GCV)方法[26-27]是先验无偏风险估计(UPRE)方法[28]的一种变形,它的主要作用是可以在白噪声方差未知的基础上,通过GCV 函数给出自适应的正则化参数β,并且能够区分实验本身的噪声及线性化过程中的非线性项.令

|
(26) |
并令r(β)=jm(β),m(β)是方程(26)的解.给出GCV函数[26-27]
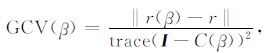
|
(27) |
其中C(β)=J(JTJ+βWTW)-1JT,I是单位阵.找到能够使GCV 函数取得最小值的β,作为第k+1步迭代的参数,记为βk+1.
基于GCV 函数的阻尼高斯牛顿算法:
选择初始模型m0和参考模型mref,当k=1,2,… 时,
① 计算J(mk)和r(mk);
② 在同伦优化的第i步,即λ=λi,令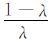

|
并结合GCV 函数给出正则化参数βk+1;
③ 以β =βk+1 为下一次迭代的正则化参数,计算
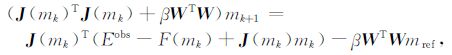
|
然后继续循环;
④ 如果停止准则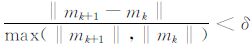
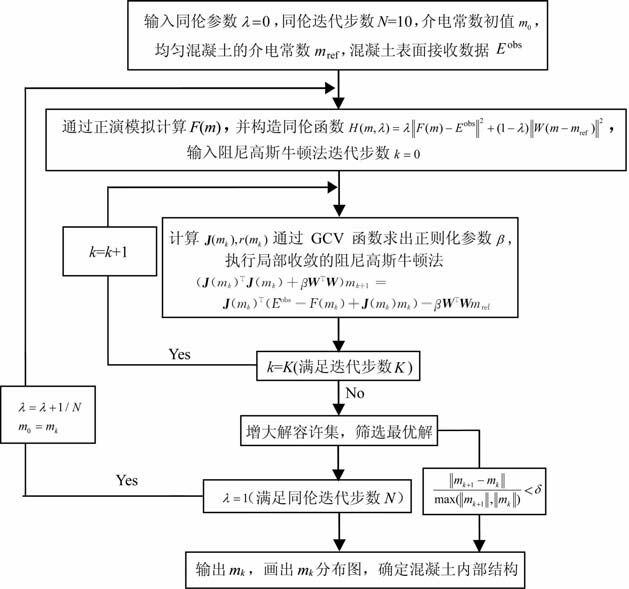
处理流程图如图 1,其中的参数:外层同伦迭代步数N,内层阻尼高斯牛顿法迭代步数K,可以根据精度的要求适当修改.
|
图 1 算法流程图 Fig. 1 The flowchart of algorithm |
我们通过三个数值实验来验证本文提出的方法可以有效地反映混凝土的内部结构,前两个实验采用人工模拟的数据分别进行二维和三维空间反演成像,最后一个实验处理实际资料,所有的计算都是在HPxw6400workstation(CPU 双核2.66,内存4GHz)上完成.
4.1 实验1:混凝土含圆形空洞模型
模型为混凝土中含有圆形空洞,反演区域Ω=25m×6.5m,空间步长Δx=Δy=Δl=2.5cm,时间t=80ns,时间步长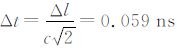
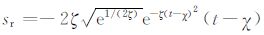
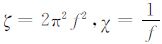
|
|
表 1 实验1混凝土模型参数说明 Table 1 Description of concrete model parameter in Experiment 1 |
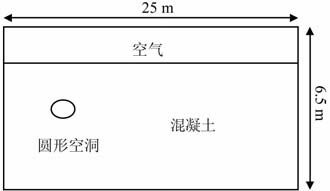
|
图 2 实验1混凝土结构示意图 Fig. 2 The sketch map of concrete structure in Experiment 1 |
通过GPR 剖面图 3b可以看到,基本可以确定空洞垂直方向的位置,但宽度及内部介质的属性还无法判断.对于同一个迭代初值,采用同伦高斯牛顿法与传统高斯牛顿法分别求解,反演成像结果见图 4b和4c.通过对图 4a与4b的比较,反演结果的空洞形状要比真实模型大,这是因为反演过程中在两种介质的分界面有一个渐进的过程,所以反演成像结果能够比较准确地刻画空洞的位置、大小、以及缺陷的属性.但是传统的高斯牛顿法无法有效地反映混凝土空洞,这是由于传统的高斯牛顿法收敛域较小,容易陷入局部极值的困扰,而同伦方法可以扩大收敛域,在初值较差时仍能够得到较好的结果.下面的算例中反演算法都采用同伦高斯牛顿方法.

|
图 3 混凝土模型(a)和GPR剖面图(b) Fig. 3 (a) Concrete model and (b) GPR protile |
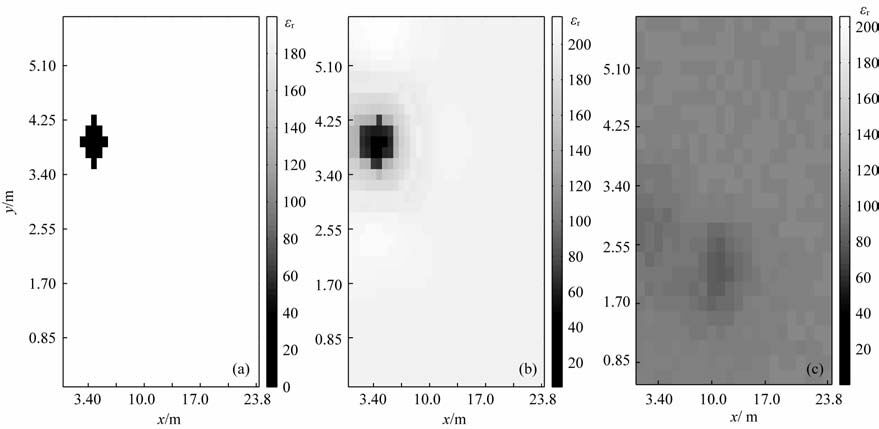
|
图 4 混凝土含空洞模型(a),同伦高斯牛顿反演成像结果(b)和高斯牛顿法反演成像结果(c) Fig. 4 Concrete model with cavity (a),homotopy Gauss-Newton (b),and Gauss-Newton inversion imaging results (c) |
这个实验研究内部参数及结构更加复杂的混凝土模型.模型为三维区域Ω=25m×6.5m×6.5m,空间和时间的长度、步长以及震源与4.1 节实验相同.所要反演的混凝土模型参数说明见表 2,结构示意图见图 5.沿着与y轴垂直的方向,我们做35 条测线,图 6a和6b分别为y=4.5m 处的真实模型剖面图及GPR 剖面图.通过对GPR 剖面图 6b 的观察,可以确定混凝土内部有3个异常体,其位置、大小及属性用同伦高斯牛顿法进行反演成像,反演成像结果见图 7.图 7 所显示的结果为x=12.5 m,y=4.5m处的剖面图,其中图 7a是真实的混凝土结构,图 7b是反演成像的结果.
|
|
表 2 实验2混凝土模型参数说明 Table 2 Description of concrete model parameterin Experiment 2 |

|
图 5 实验2混凝土结构示意图 Fig. 5 The sketch map of concrete structure m Experiment 2 |

|
图 6 真实模型在y = 4.5 m处剖面图(a)和y = 4.5 m处GPR剖面图(b) Fig. 6 (a) True model profile at y = 4. 5 m and (b) GPR profile at y = 4. 5 m |
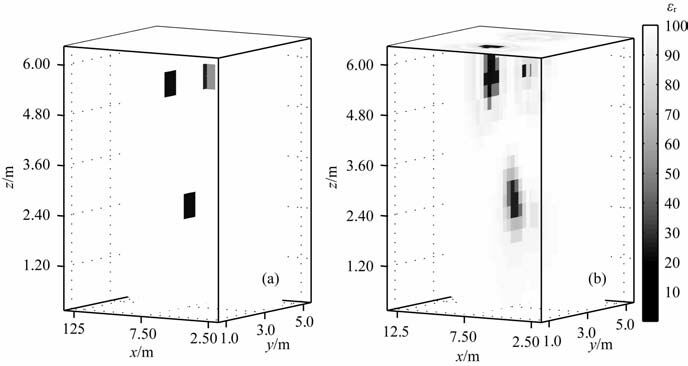
|
图 7 真实模型在x = 12.5 m,y = 4.5 m处剖面图(a)和反演成像结果在x = 12.5 m,y = 4.5 m处GPR剖面图(b) Fig. 7 (a) True model profile at x = 12. 5 m,y=4. 5 m and (b) inversion imaging results at x = 12. 5 m,y=4. 5 m |
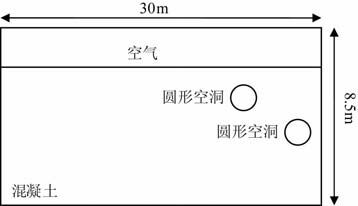
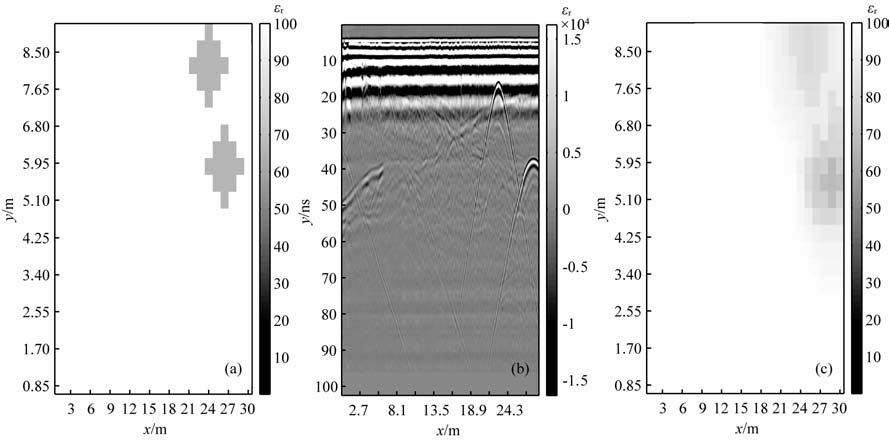
实际资料由长江工程地球物理勘测武汉有限公司提供,模型为二维区域Ω=30m×8.5m,空间和时间的长度、步长以及震源与4.1节实验相同.实际的混凝土模型参数说明见表 3,结构示意图见图 8,GPR 剖面图及反演成像结果见图 9.通过对图 9c的观察,反演结果基本可以反映混凝土内部的缺陷位置及大小,但是在属性上略有偏差.
|
|
表 3 实验3混凝土模型参数说明 Table 3 Description of concrete model parameter in Experiment 3 |
|
图 8 实验3混凝土结构示意图 Fig. 8 The sketch map of concrete structure in Experiment 3 |
|
图 9 真实模型(a),GPR剖面图(b)和反演成像结果(c) Fig. 9 (a)True model,(b)GPR proiile and (c)inversion imaging result |
本文从麦克斯韦方程组出发,在电磁波理论基础上给出了适用于探地雷达数据的混凝土无损探测反演成像方法.该方法分为两个部分,其中作为外层迭代的同伦优化算法能够增大收敛域,使算法大范围收敛;而快速收敛的阻尼高斯牛顿法用于局部迭代,克服了传统牛顿法需要计算Hessian 矩阵这一主要困难.数值模拟实验给出了三种不同混凝土结构的反演成像结果,无论是衰减情况比较严重的空洞,还是反射情况比较严重的金属,这种反演成像方法能比较准确地刻画混凝土中的异常体.它克服了以往只能通过观察接收数据,凭经验判断缺陷位置的情况,导致结果与实际情况误差较大.对于实际资料,如果混凝土内部结构比较简单,即只有若干个空洞或金属,并且异物的间距比较大时,反演成像能够较准确地反映内部结构.但是如果混凝土内部结构比较复杂,即有很多断层及裂缝等,并且缺陷之间的距离很近,这时由于初值的选取以及去噪等问题使得反演成像结果误差较大,所以反演成像方法还有很多需要改进的地方.这种反演成像方法虽然能够比较准确地确定异常体的位置、大小及属性,但是由于每一次反演都要调用多次正演的结果,它的计算量非常大,所以在PC 机上的分辨率还比较低.随着硬件设备的提高,这种算法的应用性也将大大提高.该方法不仅具有分辨能力高、抗噪能力强的特点,而且收敛的速度也较快,有很强的适用性,因此在混凝土无损探测领域内有很好的应用前景.
致谢作者衷心感谢长江工程地球物理勘测武汉有限公司在硬件及数据处理方面提供大力支持,同时也非常感谢英国Edinburgh大学的Antonis Giannopoul博士、美国Emory大学的Eldad Haber教授在数值计算方面提供的帮助.
| [1] | 罗骐先. 水工混凝土缺陷检测和处理. 北京: 中国水利水电出版社, 1997 . Luo Q X. Detection and Process for Defect of Hydraulic Engineering Concrete (in Chinese). Beijing: China Water Power Press, 1997 . |
| [2] | 王继成, 许锡宾, 赵明阶. 水工砼结构损伤诊断技术研究综述. 重庆交通学院学报 , 2004, 23(4): 19–29. Wang J C, Xu X B, Zhao M J. Research review of diagnosis on the damage of hydraulic concrete. Journal of Chongqing Jiaotong University (in Chinese) , 2004, 23(4): 19-29. |
| [3] | 黄卡玛, 赵翔. 电磁场中的逆问题及应用. 北京: 科学出版社, 2005 . Huang K M, Zhao X. Inverse Problems in Electromagnetic Field and Application (in Chinese). Beijing: Science Press, 2005 . |
| [4] | Engl H W, Hank M, Neubauer A. Regularization of Inverse Problems. Netherlands: Kluwer Academic Publishers Group , 1996. |
| [5] | 张安学, 蒋延生, 汪文秉. 探地雷达交叉测线目标搜索和成象方法的研究. 电波科学学报 , 2002, 17(1): 59–63. Zhang A X, Jiang Y S, Wang W B. Object detection and imaging method using cross-line date in GPR system. Chinese Journal of Radio Science (in Chinese) , 2002, 17(1): 59-63. |
| [6] | Di Q Y, Zhang M G, Wang M Y. Time-domain inversion of GPR data containing attenuation resulting from conductive losses. Geophysics , 2006, 71(5): k103-k109. DOI:10.1190/1.2335518 |
| [7] | Song L P, Liu Q H, Li F H, et al. Reconstruction of three-dimensional objects in layered media: Numerical experiments. IEEE Trans. on Antennas and Propagation , 2005, 53(4): 1556-1561. |
| [8] | Cai W Y, Qin F H, Schuster G T. Electromagnetic velocity inversion using 2-D Maxwell's equations. Geophysics , 1996, 61(4): 1007-1021. DOI:10.1190/1.1444023 |
| [9] | Hansen T B, Johansen P M. Inversion scheme for ground penetrating radar that takes into account the planar air-soil interface. IEEE Trans. on Geoscience and Remote Sensing , 2000, 38(1): 496-506. |
| [10] | Meincke P. Linear GPR Inversion for lossy soil and a planar air-soil interface. IEEE Trans. on Geoscience and Remote Sensing , 2001, 39(12): 2713-2721. |
| [11] | Cui T J, Qin Y, Wang G L, et al. Low-frequency detection of two-dimensional buried objects using high-order extended Born approximations. Inverse Problems , 2004, 20(6): 41-62. DOI:10.1088/0266-5611/20/6/S04 |
| [12] | Ernst J R, Maurer H, Green A G, et al. Full-waveform inversion of crosshole radar data based on 2-D finite-difference time-domain solutions of Maxwell's equations. IEEE Trans. on Geoscience and Remote Sensing , 2007, 45(9): 2807-2828. |
| [13] | Li Z, Han B. An adaptive algorithm for solving inverse problems of Maxwell's equations. Journal of Computational Information Systems , 2007, 3(5): 2177-2182. |
| [14] | Li Z, Han B. A parameter differential regularization algorithm for solving inverse problems of GPR. Journal of Computational Information Systems , 2008, 4(1): 407-412. |
| [15] | 王秉中. 计算电磁学. 北京: 科学出版社, 2002 . Wang B Z. Computational Electromagnetism (in Chinese). Beijing: Science Press, 2002 . |
| [16] | Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics , 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [17] | Dunlavy D M, O'Leary D P, Klimov D, et al. HOPE: A Homotopy optimization method for protein structure prediction. Journal of Computational Biology , 2005, 12(10): 1275-1288. DOI:10.1089/cmb.2005.12.1275 |
| [18] | 粟毅, 黄春琳, 雷文太. 探地雷达理论与应用. 北京: 科学出版社, 2002 . Su Y, Huang C L, Lei W T. GPR Theory and Application (in Chinese). Beijing: Science Press, 2002 . |
| [19] | Zhdanov M S, Tolstaya E. Minimum support nonlinear parametrization in the solution of a 3D magnetotelluric inverse problem. Inverse Problems , 2004, 20(3): 937-952. DOI:10.1088/0266-5611/20/3/017 |
| [20] | Lesselier D, Chew W C. Special section on electromagnetic characterization of buried obstacles. Inverse Problems , 2004, 20(6): S1-S256. DOI:10.1088/0266-5611/20/6/S01 |
| [21] | Dmitry B A. Three-dimensional electromagnetic modelling and inversion from theory to application. Surveys in Geophysics , 2005, 26(6): 767-799. DOI:10.1007/s10712-005-1836-x |
| [22] | 王兆磊, 周辉, 李国发. 用地质雷达数据资料反演二维地下介质的方法. 地球物理学报 , 2007, 50(3): 897–904. Wang Z L, Zhou H, Li G F. Inversion of ground-penetrating radar data for 2D electric parameters. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 897-904. |
| [23] | Baboolal S, Bharuthram R. Two-scale numerical solution of the electromagnetic two-fluid plasma-Maxwell equations: shock and soliton simulation. Mathematics and Computer Simulation , 2007, 76(1-3): 3-7. DOI:10.1016/j.matcom.2007.01.004 |
| [24] | Haber E, Oldenburg D. A GCV based method for nonlinear ill-posed problems. Computational Geosciences , 2000, 4(1): 41-63. DOI:10.1023/A:1011599530422 |
| [25] | 丁亮, 韩波, 刘家琦. Maxwell方程反演的小波多尺度方法. 应用数学和力学 , 2009, 30(8): 1–9. Ding L, Han B, Liu J Q. Wavelet multiscale method for the inversion of Maxwell's equation. Applied Mathematics and Mechanics (in Chinese) , 2009, 30(8): 1-9. |
| [26] | Wahba G. Practical approximate solutions to linear operator equations when the data are noisy. SIAM Journal on Numerical Analysis , 1977, 14(4): 651-667. DOI:10.1137/0714044 |
| [27] | Wahba G. Spline Models for Observational Data. Philadelphia: SIAM , 1990. |
| [28] | Vogel C R. Computational Methods for Inverse Problems. Philadelphia: SIAM , 2002. |
 2012, Vol. 55
2012, Vol. 55





