2. Istituto Nazionale di Oceanografia e di Geofisica Sperimentale (OGS), Borgo Grotta Gigante 42c, 34010 Sgonico, Trieste, Italy;
3. 中国石油大学(华东)地球科学与技术学院, 青岛 266555
2. Istituto Nazionale di Oceanografia e di Geofisica Sperimentale (OGS), Borgo Grotta Gigante 42c, 34010 Sgonico, Trieste, Italy;
3. School of Geosciences, China University of Petroleum (East China), Qingdao 266555, China
近年来,中国天然气供应的需求急剧增加,地震法已成为主要的天然气探测手段[1-2].为达到提高气层检测精度、逐步实现定量识别的目的,开展深入研究以探索含气、水两相流体非饱和岩石中的地震波传播与响应规律的工作势在必行.
早期针对含流体多孔介质中的弹性波传播规律的研究,在理论上主要基于宏观均匀性假设[3-4],近似认为流体与固体均匀分布于岩石内部的每一个力学微元中,每一个力学单元内部仅含有一个流体相与一个固体相,而介质内部的所有力学微元都是相同的、均一的.这样的做法明显忽略了岩石内部的局部非均匀性,在实际应用中也被发现明显低估了地震频段内(几十到几百赫兹)岩石内部的波速频散与能量衰减现象[5].
基于宏观均一的Biot理论,White等(1975)首次引入了岩石内部小尺度非均匀性的概念[6],考虑了含水岩石内部局部分布的气泡对地震波传播的影响.在实际岩石中,局部气体集中形成的气泡在地震波的挤压作用下会发生耗散性的振动,即局部流体流动效应.在低频端,局部流体流动的充分发生会造成地震波能量的大量损失,并使得岩石变得松弛;而在高频弹性波的激励下,由于流体在单个振荡周期内不能完成完整的局部荡动,岩石会呈现出比较“硬"的等效状态.
近年来国内外学者从理论、模拟、实验与反演多个角度研究了含非饱和流体孔隙介质的波传播现象[7-13].学界对相关问题形成的一个基本认识是,局部流体流动是导致孔隙岩石中地震波频散与衰减的决定性因素.然而,至今为止,文献中还没有出现一个能够被各种研究与产业部门普遍接受的描述局域流的基础理论与定量技术[5].
在前人基于黏弹性与BISQ 理论的研究中,由于引入了一些不具有明确物理意义或不易于直接实现的参数(如各类松弛时间[14]、黏弹性系数[15]或特征喷射流长度[16]等),使这些理论虽然在进行岩石波动现象描述中非常有效,但其数学基础与物理内涵却难以实现或验证,这类方法在实际工程中很难得到推广.
在基于精细模型的数值模拟与地震响应分析的相关研究中,需要建立过于详细的岩石模型并设置边界条件,这类方法虽然能较准确地给出实际岩石中的地震波响应,但由于在实际工程中缺乏足够的先验信息以及相关方法本身建模的复杂度与计算消耗,因此无法在工程中很好实现.
Pride等(2004)曾采用一种双重孔隙介质模型描述多种复杂岩石结构中的地震波传播与衰减现象[17],并得到了与前人认识有较好一致性的数值预测结果,但相关研究仍然存在如下缺点:(1)过于复杂的方程组,使得相关理论在现场的实际应用中非常困难;(2)方程中引入了过多的参数,不利于理论的实验验证与实际应用;(3)在动力学方程组的推导过程中采用了统计热力学关系,使得方程的一些核心参数在计算过程中仅能通过频率域的关系式进行上、下限的估算,而无法实现更精确的定量预测.
基于以上考虑,本文的研究旨在针对非均匀含流体岩石,推导一种格式尽可能简洁、物理参数尽可能少、各参量均具备物理可实现性的波传播方程,以期满足实际科学研究与工业生产的需要.在处理非饱和岩石中的波传播问题时,本文立足于之前的研究基础,即含一类流体、两种骨架的双孔介质中的Biot-Rayleigh方程组[18],将这一方程的导出过程进行了拓展.针对一类骨架、两类流体的新情况,重新从力学最基本的Hamilton 原理进行了推导,以描述在地震波激励下由于气泡存在所引起的岩石内部的“球状"局部胀缩运动.
2 研究基础在前期研究中,我们针对岩石内部仅含一类流体、但含两类骨架的双重孔隙结构(见图 1),提出的Biot-Rayleigh方程组如下所示:
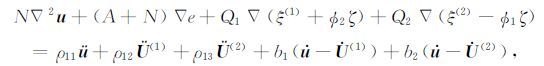
|
(1a) |
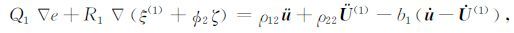
|
(1b) |

|
(1c) |
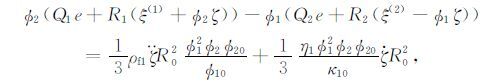
|
(1d) |

|
图 1 仅饱和水的非均匀砂岩中的 双重孔隙结构示意图(一种流体,两类骨架) Fig. 1 Schematic diagram of double-porosity structure in a full water-saturated heterogeneous sandstone ( type of fluid and 2 types of solid skeletons ) |
其中A、N、Q1、R1、Q2 与R2 表示双孔介质中的6个Biot弹性参数,这些基础的弹性参数可以由岩石骨架的弹性模量、流体的体积模量、孔隙度、固体基质的弹性模量等基础的岩石物理参数进行显式的计算与估测;ρ11、ρ12、ρ13、ρ22 与ρ33 表示双孔介质中的五个密度参数,在对岩石内部的单个岩石颗粒采用球状近似假设的前提下,这五个密度参数也可以根据岩石中固体颗粒的密度、孔隙流体的密度、孔隙度以及不同孔隙结构的组分比率进行显式的计算与估测.相关变量u、e等的含义将在本文第4 部分详细阐述.
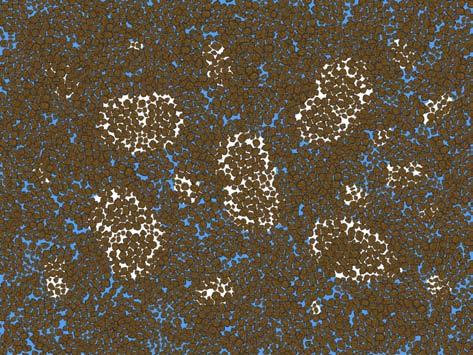
为描述含气水非饱和岩石中的地震波传播与频散规律,需要考虑一种岩石骨架、两类孔隙流体渗入的情况(见图 2),将一类孔抽象为嵌入体,将另一类孔抽象为背景相,嵌入体与背景相之间的固体骨架完全一致,两者之间的主要差别来自于孔隙空间内部的孔隙水与孔隙气在密度、弹性模量与黏滞性方面的差异.基于以上考虑,可以将气水非饱和岩石近似看作另一类双重孔隙介质模型,岩石内部赋含一类气孔、一类水孔,形成“双孔".本文第4 节将给出论证,此情况下波传播方程仍可用(1)式描述,但相关参数需重新定义.
|
图 2 非饱和砂岩中的双重孔隙结构示意图 (两种流体,一类骨架) Fig. 2 Schematic diagram of double-porosity structure in a partially-saturated sandstone (2 types of fluid and 1 type of solid skeleton) |
若采用双重孔隙介质模型近似描述非饱和岩石内部的气、水非均匀分布状态,需满足以下假设条件,否则预测结果的可靠性会受到影响.
假设一:两种组分必须满足传统孔隙介质理论对单孔介质的基础假定.双重孔隙介质内部基质与嵌入体两类组分,每种都可近似看作单一孔隙结构,且满足Biot-Gassmann理论对单孔双相介质的基本假定.
假设二:气、水相对体积比率的限制.岩石内部两类组分在体积比率上有较大差距,其中体积比率高的组分作为背景相,体积比率低(一般不超过30%)的组分作为嵌入体.满足该假设,可以避免由岩石内部组分的空间分布引起的弹性波的空间弥散.
假设三:宏观平均近似假设.一些研究对强非均匀性复合介质采用分区建方程的模式进行波场特征分析[19-20],很难应用于生产工程.为建立更简洁的数学方案,即使岩石内部含一定程度的非均匀体,仍采用宏观平均近似的思路进行处理是必要的(这一思路应用于弹性模量与波传播问题的先例,可参见等效介质理论[21]).岩石内部的局部非均匀性,在本构关系与振动方程引入考虑,以达到用近似简练的数学表述式描述复杂非均匀体的力学现象的目的.
假设四:最小力学微元假设.采用宏观平均近似,必须设定合理的力学体元,即特征单元体.从连续介质力学的角度出发,假设特征单元体尺寸远小于弹性波波长.如此可忽略单元体内的微观结构,在一个单元体内建立多元联立方程,以描述两种或两种以上的孔隙、流体及固体等组分的耦合力学行为.
假设五:均一球形嵌入体(气泡)假设.从经典力学入手研究气泡在地震波激励下的局部振荡效应,需定量计算气泡涨缩运动的动能,鉴于实际气泡的大小形状各异,采用一般的力学方法不能解决问题.本文对岩石内单个气泡采用球状近似,且认为岩石内嵌入的所有气泡具有相同尺寸(半径R0).
假设六:忽略嵌入体内部流体的局部振荡动能.本文将采用Rayleigh 提出的气泡周期性振荡理论[22]描述流体局部流动,忽略气泡内部所具备的微弱振荡动能.
假设七:忽略相邻气泡在胀缩振动中可能发生的相互作用.必须忽略相邻气泡在胀缩运动中可能发生的相互作用,否则会引入相关效应,导致系统动能函数异常复杂,使经典力学手段无法适用.依据在于:①气泡局部振荡振幅非常微弱,沿气泡中心的径向往外,周围液体的振荡幅度在很短距离内即趋于零,因此相邻气泡只要距离不是很近,相互作用非常微弱;②联系到假设二,在嵌入体体积率较低的情况下,相邻嵌入体间发生作用的可能性小;③联系到一些非均匀体散射理论(如Sato的一次散射理论[23])、固体复合材料的等效介质理论(如由Eshelby原理引出的诸多自洽模型[24])、仅考虑一次阶散射的Kuster-Toksöz理论[25]等,目前采用经典力学原理解决复合材料静力学或动力学问题的做法中,普遍仅考虑了单个嵌入体的一阶散射或者一次加载,忽略了嵌入体之间的相互作用及耦合关系.
假设八:忽略气、水界面表面张力对局域流的影响.在地震波激励下,液体内部气泡的局部胀缩运动会受到气、液分界面的表面张力影响,即气泡涨缩不仅伴随着周围液体动能的周期变化,还伴随着气泡表面自由能的变化以及分界面处的摩擦损耗.本文忽略了此部分的影响.
4 理论推导 4.1 势能函数如前所述,孔隙介质理论一般采用宏观平均近似的办法来描述流、固复合介质,在这种平均近似下,如果基于经典力学(哈密顿原理)的方法来分析问题,则每一个力学体元内部将同时含有复合介质的各种组分,单个力学体元的尺寸远大于局部非均匀体结构的平均尺寸,但远低于地震波长.
由于在这种近似假设下,每一个力学微元内部同时可含有复合材料的各种组分,因此,若储层岩石中含有一种固体基质与两类孔隙流体(气、水),则可近似认为,在岩石内部的每一个点(每一个力学微元)上,同时存在着固体、气与水三种成分相互发生动力学耦合作用.
基于以上考虑,在地震波的激励下,岩石内部的弹性应变势能函数W是固体应变(固体应变共含三个独立分量,对应于三个主应变)与两类流体应变(每类流体各含一个独立分量,对应于流体的体应变)的函数,因此,W可用固体应变矩阵的三个独立不变量与两类流体的体应变采用如下形式进行表述:
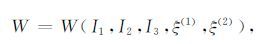
|
(2) |
其中,
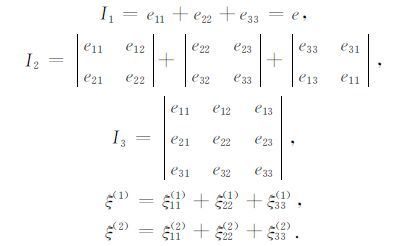
|
此处,
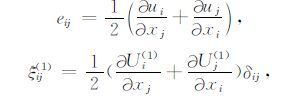
|
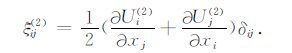
|
其中,

|
分别表示三种组分的空间矢量位移.下标1、2、3 表示矢量空间的三个方向,x1,x2 与x3 分别表示三个方向的坐标.
采用任意一种幂级数对(2)式进行展开,可得到一个无穷序列,在一般线弹性的研究范畴内,一般将该序列近似到二阶,同时将所有一阶与零阶项的系数置零.如Biot在1962年的工作中,曾对单孔双相介质进行了二阶展开,其中,相互独立的二阶弹性常数共有4个.
对于双孔双相介质,(2)式的幂级数展开后,相互独立的二阶项共有六个[26-27],为与前人工作中弹性常数的表述形式保持一致,且为了利于与同行的交流与推广应用,这里我们仍然沿用了非常类似于Biot理论的弹性常数定义形式,将(2)式的二阶展开形式写为

|
(3) |
其中A,N,Q1,R1,Q2,R2 为双重孔隙介质中6个独立的Biot弹性常数.
在纵波的周期性压缩与拉张作用下,若气泡膨胀,则气泡内的流体被拉张,而气泡外的流体被压缩,若气泡收缩,则气泡内的流体被压缩,而气泡外的流体被拉张,因此,在局域流的周期性振荡效应中,以气水界面为边界,若气体被拉张,则水被压缩,反之亦然.这里引入一个流体的体变形增量ζ 来描述地震波激励过程中所产生的这一种局域性的流体变形增量,(3)式可变为如下形式

|
(4) |
其中,在周期性胀缩运动中的每一个瞬时状态下,流体的守恒可以通过$\phi $1($\phi $2ζ)+$\phi $2(-$\phi $1ζ)= 0 来满足,$\phi $1 和$\phi $2 表示两类孔隙的绝对孔隙度.
4.2 动能函数与耗散函数由(4)式的结果可知,基于双重孔隙介质模型,一类骨架、两种流体与两类骨架、一种流体的势能函数具有几乎完全一致的数学表述形式,但式中的各个弹性常数需要重新定义,这些内容将在4.4中详细说明.
一类骨架、两种流体的动能函数在数学形式上可写为
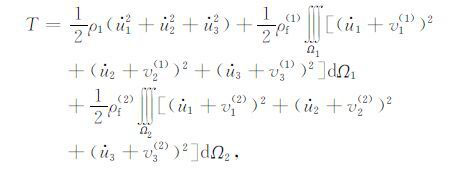
|
(5) |
其中ρ1 = (1-$\phi $)ρs、$\phi $ 表示岩石中总的孔隙度、ρs 表示固体密度.$\phi $ =$\phi $1 +$\phi $2 =ν1$\phi $10 +ν2$\phi $20,ν1 与ν2 分别表示两种流体所占据的骨架占总骨架的体积比率,$\phi $10 与$\phi $20 分别表示两个区域内部的局部孔隙度,如岩石内部仅含有一种骨架,但却饱和有两种流体,则$\phi $10 =$\phi $20.ρ(i)f (i=1,2)是第i种流体的密度.Ωi是第i种流体占据的总的孔隙体积.这里动能是两种流体相对固体的相对运动速度矢量[v1(1) ,v2(1) ,v3(1)]与[v1(2) ,v2(2) ,v3(2)]的函数.
基于球状嵌入体假设,波传播方向上的动能函数与球状流体径向上的动能函数是近似解耦的[18],因此,经过简单的变量替换,可以把动能函数写为流体绝对振动速度的函数:
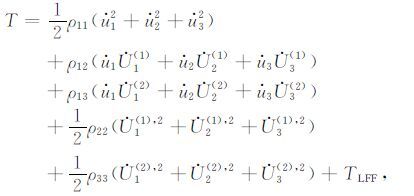
|
(6) |
其中ρ11、ρ22、ρ33、ρ12 与ρ13 是五个密度参数,TLFF 是局域流振荡动能函数.
这里可以观察到,(6)式同样与两类骨架、一种流体的动能函数在数学形式上完全一致,只是所有相关的密度常数需要重新定义.
本文比前期研究[26-31]最大的改进在于,采用了经典力学的方法来描述局部流体流动,而之前的工作多采用了热力学的办法,因此当前的方法得到的表述式较为简洁,参数较少,物理可实现性更强.
基于Rayleigh提出的气泡振荡动能函数,将相关的方程与推导过程推广到孔隙介质中,则气泡局部振动的动能函数可写为
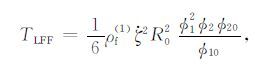
|
(7) |
其中ρf1 表示背景相流体的密度,文中将i=1默认为背景相,R0 表示嵌入体(气泡)半径.
耗散函数一般描述物体运动时各组分之间的摩擦力,基于Biot理论及其在复合介质中的一些延展性成果[32],含两种流体的岩石中的耗散函数在波传播方向上可以写为如下形式:
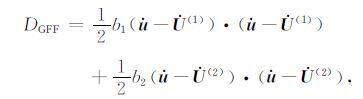
|
(8) |
其中bi(i=1,2)分别表示两种流体饱和区域中各自的耗散系数.
式(8)主要描述岩石振动时固体与流体在波传播方向上的摩擦效应,对于局域流体流动所引起的耗散,可以采用与局域流动能函数类似的推导过程,经过球面积分得到
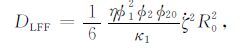
|
(9) |
其中κ1 表示主骨架(背景相)中的渗透率,η 表示背景相中的流体黏度.
4.3 带耗散的拉格朗日方程采用动能函数与势能函数,基于哈密顿原理可以直接推导地震波传播的动力学方程组,其中拉格朗日能量密度可以用下式表述:
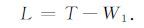
|
(10) |
更具一般性的、带耗散的拉格朗日方程具有如下的表述形式:
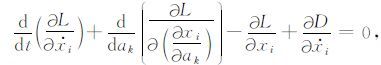
|
(11) |
绝大多数复杂介质中的波传播动力学方程组都可以基于这一方程进行导出.此处xi表示广义坐标.
分别采用ui、Ui(1)、Ui(2)与ζ 作为广义坐标,代入方程(11),即可导出(1)式,一类骨架、两种流体的波传播方程与两类骨架、一种流体的波传播方程在数学上可以采用完全一致的表述形式,但所有的相关参数必须重新定义.
4.4 弹性系数与密度系数为定量给出波动方程中各弹性系数与岩石及流体基本性质之间的显式关系,一般采用虚拟实验的方法进行理论推导[33].前期的研究曾对两类骨架、一种流体的双孔方程中的弹性常数进行了理论分析[18],其中对含两类不同骨架的复合孔隙结构,需要引入一个新的变量β,描述两类骨架的压缩性比例,这一变量β 可以用下式进行近似确定:
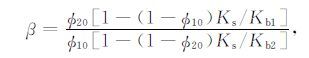
|
(12) |
其中Kb1 与Kb2 分别表示两类骨架的体积模量.
(1) 然而,对于仅含一类骨架却渗入有气、水两种流体的非饱和岩石,含气区与含水区具有相同的结构,变量β 的影响可以近似忽略,即取β=1,这就得到了第一条弹性参数与岩石基本参数的联系.
(2) 忽略流体在剪切方向上对岩石整体受力的影响,即含流体岩石的剪切模量与干岩石的剪切模量相等.
(3) 将含两种流体的岩石用一个橡胶皮套包裹,然后将包裹岩石的皮套置于静水压环境下,且允许流体从中流出,此时岩石内部固、水、气三相的应力应变复合本构关系可再导出一条联系.
(4) 将非饱和岩石置于统一的静水压流体环境中,固、水、气三相都只受到静水压作用,则此时可导出另外三条先验性联系.
与一些方法得不到显式表达式不同[30],基于以上6条先验性联系,可定量导出6 个弹性常数关于岩石流体基本参量的显式表达式:
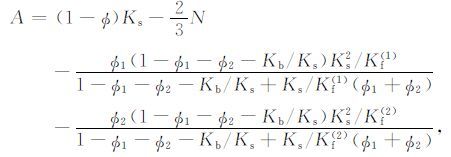
|
(13a) |

|
(13b) |
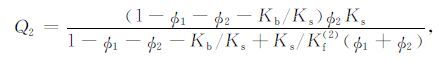
|
(13c) |
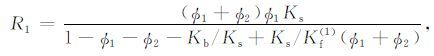
|
(13d) |
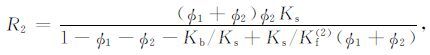
|
(13e) |
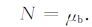
|
(13f) |
一类骨架、两种流体的双孔方程的密度参数的定义与两类骨架、一种流体的情况略有差异.首先,可采用孔隙介质理论通用的密度关系式如下:
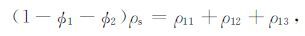
|
(14a) |
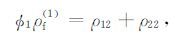
|
(14b) |

|
(14c) |
其次,引用Berryman 关于浸润在流体中的球状颗粒假设[21],可估算岩石弯曲度α,然后对气、水、固三相介质的密度参数进行定量估算:
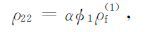
|
(15a) |
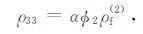
|
(15b) |

|
(15c) |
此外,含气区与含水区的耗散系数仍可沿用Biot1956年的定义进行分别计算,这里不再赘述.
5 数值结果 5.1 与前人理论的对比与分析为检查拓展到非饱和岩石状况的Biot-Rayleigh理论的合理性,选取一个具体案例进行了纵波速度与能量衰减的预测,基于相同的岩石参数,将预测结果与White(1975)[6]与Johnson(2001)[34]的预测结果进行了对比分析.岩石参数包括[35]:基质体积模量35GPa,骨架体积模量7GPa,骨架剪切模量9GPa,水体积模量2.25GPa,空气体积模量0.1 MPa,水黏度0.001Pa·s,空气黏度0.00001Pa·s,基质平均密度2.65g/cm3,水密度0.99g/cm3,空气密度0.1g/cm3,孔隙度为0.15,渗透率为0.1×1012m2,平均气泡尺寸0.25m,本例中空气饱和度设为0.95.
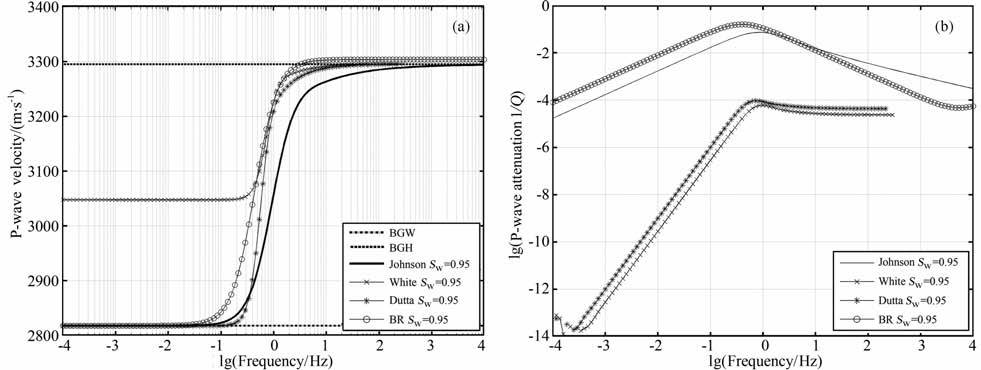
图 3给出了三种理论预测的对比结果.在图 3a中,两条直线BGW 与BGH 分别给出了Biot-Gassmann-Wood边界(指两类流体在力学上并联后作为等效流体,再代入Gassmann 方程,以估算岩石整体模量)与Biot-Gassmann-Hill边界(指两类流体分别代入Gassmann方程估算两个岩石模量,再采用Hill平均估算整体模量).从三种理论预测曲线来看,White理论(1975)低估了地震波速度在低频极限与高频极限间的频散比例,且在低频极限下,White理论不能与BGW 边界(2817.2m/s)吻合,与其他理论相比,White理论明显低估地震波在非饱和岩石中的能量衰减(如图 3b所示),这些问题在Dutta等的结果[7]中也有报告.
|
图 3 Biot-Raylegh理论Johnson理论与White理论纵波速度与衰减的预测结果 (a)三种理论纵波速度预测结果对比;(b)三种理论纵波衰减预测结果对比. Fig. 3 Predicted P-wave velocities and attenuation by Biot-Rayleigh theory,Johnson theory and White theory (a) Comparison of predicted P-wave velocities by the 3 theories; (b) Comparison of predicted P-wave attenuation by the 3 theories. |
在图 3a中,Johnson 与BR 理论的速度预测结果在低频极限下与BGW 边界吻合.在高频极限下,White与Johnson 理论的预测结果与BGH 边界(3295.7m/s)吻合较好,而Biot-Rayleigh曲线同样会逼近BGH边界,但略有超出,这一情况与本文中β 的定义有关.在本文计算中,取β=1,因此在高频极限下两类组分趋向于弹性力学的串联关系.在高频极限下,局部流体流动在单个地震波周期内不能完全进行,岩石呈较“硬"状态,并且地震波散射问题的影响也更显著,因此,具体哪种理论更合适高频还有待深入探索.
与Johnson的预测结果相比,BR 预测结果中纵波速度频散曲线的“台阶"以及纵波衰减曲线的峰值更靠近频率轴的左端.如图 3a所示,在Johnson 速度频散曲线中,频散最早发生在10-1Hz附近,并在102.2Hz达到上限,在Biot-Rayleiph速度曲线中,频散最早发生在10-1.6Hz,在100.9Hz达到上限.如图 3b所示,Biot-Rayleigh理论预测的衰减峰值出现在10-0.67Hz,高于Johnson的峰值预测结果.
5.2 川中须家河组中低孔砂岩:饱和度与孔隙度对纵波速度与衰减的影响针对川中含气储层低孔隙度、低渗透率砂岩普遍存在的现状,进行了变孔隙度含气砂岩中的地震波频散与衰减规律的分析.基于Biot-Rayleigh方程组(1)式,将平面波解析解代入波传播方程组,求解一元三次方程,取实部最大值为快纵波相速度,并可计算对应的衰减逆品质因子.在求解气饱和度高(超过60 %)与气饱和度低(低于60%)的两种情况时,分别采用了“气包水"(水砂作为嵌入体)与“水包气"(气砂作为嵌入体)的两种不同模式.但是,在气饱和度处于40 %~60 %时,实际岩石中的气水分布的几何情况将起决定性作用,这种几何分布所导致的空间弥散使得相关饱和度下的波速预测变得非常困难,本方法仍不能很好的解决这一问题,基于宏观平均近似所给出的预测结果在这种情况下可靠性并不高.
分别对3块岩石样本进行了宽频带纵波的相速度与衰减逆品质因子的定量预测.计算采用的基本岩石物理参数包括:石英体积模量39GPa,砂岩固结系数15,水体积模量2.51GPa,气体积模量1.44×105Pa,水黏度0.001Pa·s,气黏度0.000022Pa·s,砂岩颗粒平均密度2.69g/cm3,水密度1.04g/cm3,气密度0.01g/cm3,平均气泡尺寸1 mm.此外,样本1的孔隙度为0.11,渗透率0.5×1015m2;样本2的孔隙度为0.0757,渗透率0.021×1015m2;样本3的孔隙度为0.0439,渗透率0.004×1015m2.
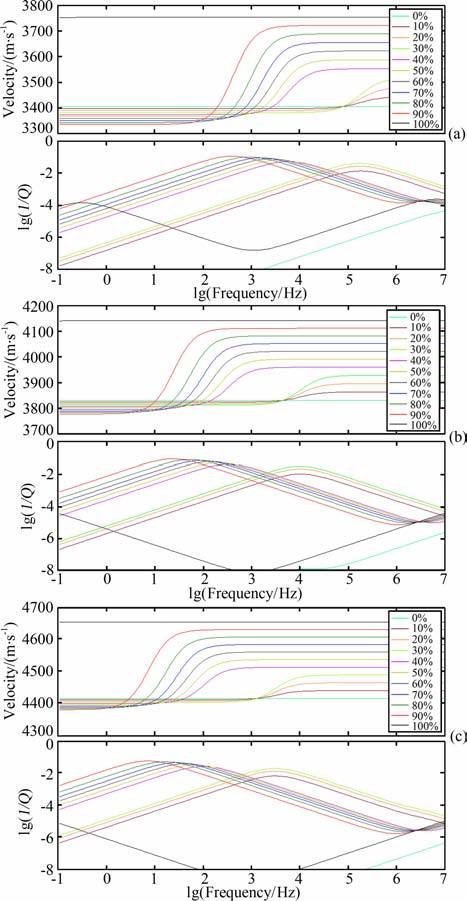
如图 4所示,针对三块不同孔隙度的砂岩给出了相应的预测结果.(1)地震纵波在声波频段(kHz)以上对含气饱和度敏感,纵波速度随气饱和度的增加呈逐步下降趋势,这意味着纵波速度在高频段对气饱和度有较为精细的指示作用;(2)纵波速度在地震频段内,对储层是否含气非常敏感,因为即使在饱和水岩石中掺入非常微量的气,岩石中的纵波速度也会发生剧烈的下降,这也印证了亮点技术与纵波法在气层检测中的一些应用状况与经验认识;(3)在地震频段内,纵波速度对含气饱和度并不敏感,随着含气饱和度的变化,纵波速度集中于很窄的变化范围内,这意味着如果仅采用勘探频段内的纵波速度进行含气饱和度的定量预测,无疑是非常困难的;(4)与纵波速度相比,在地震频段内,纵波衰减无疑能够很好的指示含气饱和度,纵波衰减随气饱和度的变化呈渐变趋势,纵波的品质因子最低为21,这意味着非均匀分布的气泡的局部振荡,造成了地震波在低频段(101~102Hz)的强烈衰减现象;(5)随着孔隙度的降低,纵波速度的曲线在整体上呈现逐步上升的趋势,对孔隙度为0.0439的砂岩,纵波速度最高能达到4659m/s; (6)随着孔隙度的降低,在地震频段内,含气饱和度对纵波频散与衰减的影响更为显著.
|
图 4 变孔隙度砂岩中的地震波频散与衰减 (a)样本1, 孔隙度0.ll;(b)样本2,孔隙度0. 0757;(c)样本3,孔隙度0. 0439. Fig. 4 The seismic wave dispersion and attenuation as a function of porosity in sandstone, in which 0%~ 100 % denotes water saturation in rocks (a) Sample 1, porosity 0. 11; (b) Sample 2,porosity 0. 0757;(c) Sample 3,porosity 0. 0439. |
若孔隙度降低,地震波频散的“台阶"与地震波衰减的峰值会向低频段移动,对于孔隙度为0.0439的含气砂岩,纵波频散台阶的主体已经出现在地震勘探频段(101~102Hz)内,这意味着对于分布普遍的低孔低渗的砂岩储层,低频段的地震波频散与衰减现象将会非常显著
5.3 南海深水区陵水组优质砂岩:CH4 与CO4 对砂岩纵波速度与衰减的影响及其AVO 响应特征以南海深水区渐新统陵水组长石岩屑质石英砂岩为例,调查不同流体对岩石地震波响应特征的影响.陵水组砂岩主要为低成分成熟度的岩屑长石砂岩与长石岩屑砂岩,砂岩粒度中等偏细,大多数为颗粒支撑的接触式胶结[36].砂岩的孔隙类型多样,后期的溶蚀作用对成藏起到了关键作用,这里的储层砂岩的孔隙度一般在15%以上,在地震剖面上会形成明显的低速带.
南海深水区构造运动频繁,火成岩局部发育,气藏普遍含一定比率的CO2.二氧化碳的临界点为31 ℃、7.4 MPa,甲烷的临界点为-82.7 ℃、4.6 MPa.若环境温度高于临界点温度、环境压力高于临界点压力,则气体以超临界状态存在.超临界流体是处于临界温度和临界压力以上,介于气体和液体之间的流体.由于它兼有气体和液体的双重特性,即密度接近液体,黏度又与气体相似,扩散系数为液体的10~100倍,因而具有很强的溶解能力和良好的流动、输运性质.超过临界点的气体,虽然其密度接近于液体,但其物理性质与液体仍有明显差别,特别是体积模量很低.
由于甲烷的临界点很低,因此,埋深超过470m的煤层当中的甲烷就呈超临界状态了,二氧化碳的临界点相对较高,但考虑到陵水组(180 ℃ 以上,围压100 MPa左右,孔隙压50 MPa以上)的具体环境,二氧化碳主要以超临界状态存在,相对而言,水的临界点(374 ℃)很高,一般在储层呈液态.
对超临界状态流体,一般可采用vanderWaals公式计算二氧化碳与甲烷的物理参数,也可以采用实验测量的方法得到.
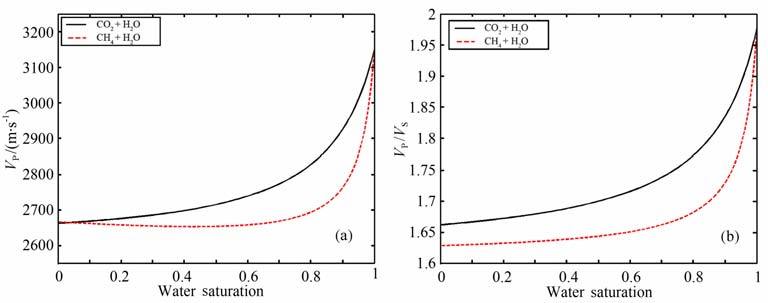
图 5a给出了含二氧化碳、水的砂岩与含二氧化碳、甲烷的砂岩的纵波速度对比结果.在各个含水饱和度下,含二氧化碳的砂岩的纵波速度普遍高于含甲烷的砂岩;二氧化碳与甲烷相比,它的“勾"形曲线从饱和气向饱和水的变化趋势更接近于“线性"的渐变的情况.图 5b给出了含二氧化碳与含甲烷两种情况下,砂岩的纵横波速度比对比图.目前,本理论给出的横波预测结果依赖于密度,横波速度随饱和度的变化关系主要呈线性,含二氧化碳砂岩的横波速度低于含甲烷砂岩的横波速度.
|
图 5 含二氧化碳、水的砂岩与含甲烷、水的砂岩的预测结果对比 (a)015%孔隙度砂岩纵波速度随水饱和度的变化关系;(b) 15%孔隙度砂岩纵、横波速度比随水饱和度变化关系. Fig. 5 Comparison of the predicted results in CO2-H2O saturated sandstone and CH4-H2O saturated sandstone (a) The variations of P-wave velocity as a function of water saturation in a sandstone (porosity 0.15) ;b) The variations of P- and S-wave velocity ratio as a function of water saturation in a sandstone (porosity 0. 15). |
基于前述的岩石物理理论建模,考虑陵水组可能存在的实际岩性情况,分别对盖层为泥岩的含甲烷砂岩储层与盖层为泥岩的含二氧化碳砂岩储层的AVO 特征进行了模拟.模拟中采用如图 5所示的纵波速度、横波速度的预测结果.盖层的泥岩参数较难确定,在缺乏井数据和地质先验信息的情况下,采用前人的观测结果进行给定.考虑埋深3000 m 左右的岩层,其实际泥岩压实情况较好,砂岩处于未完全固结状态,采用了混合粘土的前人观测结果[37]:纵波速度3400m/s,横波速度1600m/s.
分别针对泥与甲烷砂、泥与二氧化碳砂两种情况,对砂岩储层的AVO 特征进行了模拟,模拟结果见图 6所示,其中甲烷与二氧化碳的饱和度给定为70%.
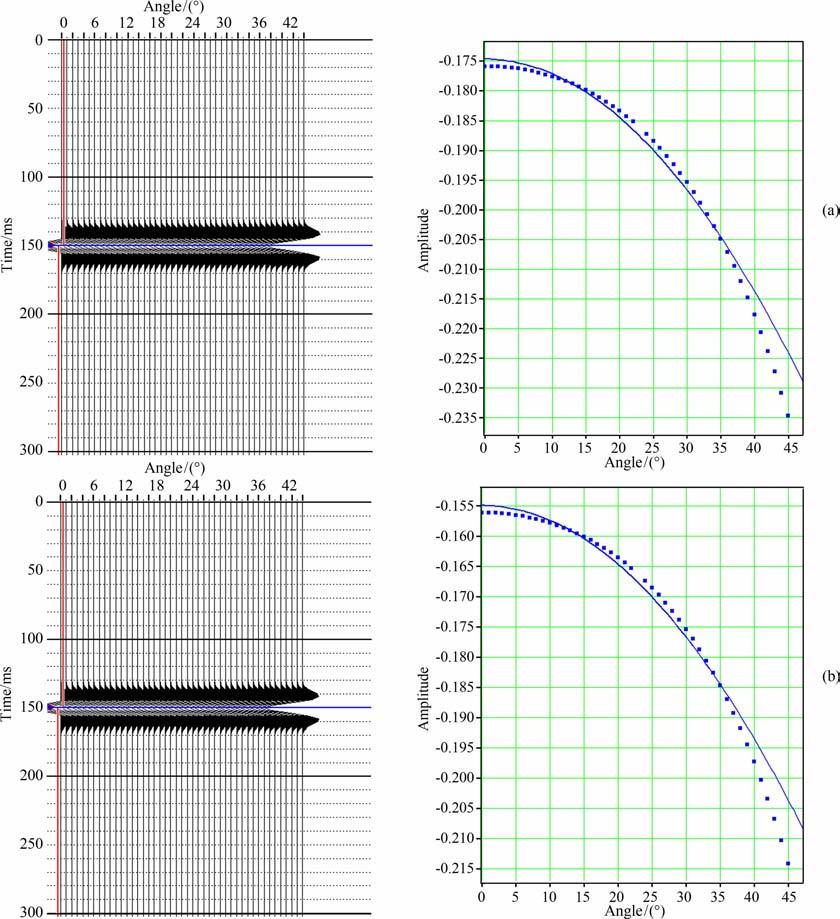
|
图 6 含二氧化碳、水的砂岩与含甲烷、水的砂岩的AVO特征对比 (a)孔隙度15%,含甲烷(70%)(三类AVO特征);(b)孔隙度15%,含二氧化碳(70%)(二类〜三类AVO特征). Fig. 6 Comparison of the simulated AVO curves in CO2-H2O saturated sandstone and CH4-H2O saturated sandstone. (a) 70%-CH4 and 30%-H2O (Class III);(b) 70%-CO2 and 30%-H2O (Class II toClass III). |
对于含甲烷砂岩、上层为泥岩的情况,其AVO特征是近道波谷强,远道波谷更强.对于含二氧化碳砂岩、上层为泥岩的情况,其AVO 特征与含甲烷情况接近,但近道波谷略弱.含甲烷与含二氧化碳的砂岩储层,其AVO 响应特征都接近于第三类,差异不明显,与之相比,含水砂岩一般不表现出明显的AVO 特征或近似表现为第一类AVO 特征.因此,基于叠前的AVO 特征直接区别含气砂岩与含水砂岩是可行的,但无法区分南海深水区砂岩储层中的二氧化碳与甲烷.
5.4 北海高孔砂岩:与宽频带岩石物理实验结果的对比分析为验证本文理论成果的适用性,采用了Batzle等于2006年发表的宽频带非饱和岩石波速观测数据[38],并与本文理论预测的结果进行对比分析.该高孔砂岩来自北海,主要成分为石英,孔隙度为0.35,固结程度好,渗透率达到8.7×1012m2.设置气泡的平均尺寸为5 mm,所得到的实验结果与理论预测结果的对比如图 7所示,结果显示:分别针对地震频段、声波频段与超声波频段的理论结果很好地预测了地震波速度在不同频段内、不同饱和度下的分布趋势与变化规律.低频段的实验观测结果全部分布于地震频段内的理论预测值以下,高频段的实验观测结果则全部分布于超声频段内的理论预测值以上.随着含气饱和度下降、含水饱和度上升,纵波速度的整体变化趋势在理论预测与实验观测两方面完全吻合.
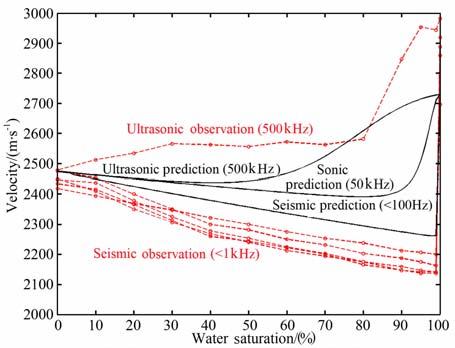
|
图 7 非饱和砂岩多尺度地震波频散规律预测与实验观测对比 Fig. 7 Comparison of the theoretical predictions and experimental measurements of multi-scale seismic wave dispersion in a partially-saturated sandstone |
然而理论预测结果仍低估了低水饱和度范围内砂岩中地震波速度从低频往超声段的频散比例,造成这种情况的原因之一在于本研究中仅考虑了两种不相混溶流体非饱和所造成的频散现象,而忽略了岩石孔隙结构非均匀性所可能导致的另一部分频散[18, 26, 30].当然,应力应变法的宽频带实验观测技术[30, 38]也可能存在高估波速频散的可能性.目前,多频段下理论与实验所得到的趋势基本一致.
6 结 论本文基于双重孔隙介质模型,推导了非饱和岩石中的Biot-Rayleigh方程组,并对方程组中的所有弹性常数进行了重新定义,从而将一种流体、两类骨架的双孔介质波动理论推广到两种流体、一类骨架的特殊情况.
基于相同的岩石参数,与White、Johnson 的两种理论进行了对比.结果显示:Biot-Rayleigh 理论预测的纵波速度在低频极限下与Biot-Gassmann-Wood 边界吻合,在高频极限下纵波速度略高于Biot-Gassmann-Hill边界.与Johnson 理论的预测结果相比,Biot-Rayleigh预测的纵波频散与衰减峰出现的频段更低,且在地震频段给出了更高的衰减预测值.
针对川中地区的中低孔砂岩储层,调查了非饱和岩石中孔隙度与饱和度对纵波速度与衰减的影响.结果显示:纵波速度在声波频段(kHz)以上对含气饱和度敏感,在地震频段内,纵波速度对储层的含气性非常敏感,但对含气饱和度的指示性不强;地震频段的衰减随气饱和度的变化呈渐变趋势;伴随着孔隙度降低,若砂岩中的非饱和情况仍然存在,则地震频段的纵波频散与衰减现象更为显著.
针对南海深水区的优质砂岩储层进行的二氧化碳与甲烷的对比建模分析显示:含二氧化碳与水的砂岩,与含甲烷与水的砂岩,纵波速度随水饱和度的变化规律相近,这主要是由于储层环境下二氧化碳呈超流体状态,其体积模量很低而密度很高.基于泥岩盖层与砂岩储层的合成记录制作及AVO 特征分析显示,含二氧化碳砂岩与含甲烷砂岩主要呈第三类AVO 响应特征,即采用常规的叠前分析技术很难对其鉴别.
针对北海的某实际高孔砂岩样本,采用宽频带岩石物理实验数据与本文理论预测结果进行了对比分析,结果显示:非饱和砂岩中,多频段的纵波观测结果在趋势上与规律上,与理论预测得到的认识一致;但理论预测结果低估了低含水饱和度范围内砂岩地震波速度从低频段往超声段的频散比例,这是由于在本文的非饱和研究中,还未能同时引入对孔隙结构非均匀性的考虑.
本文的讨论主要涉及纵波激励所诱发的局域流体流动问题,对于横波激励可能导致的另一型局域流荡动,由于加载与振动的模式完全不同(见图 8),从基础力学模型的角度必须重新考虑.前人的实验研究[38]已经显示,含流体岩石中的横波也会发生相对较弱的地震波频散,所有横波局域流的相关现象及物理模型仍有待深入研究.
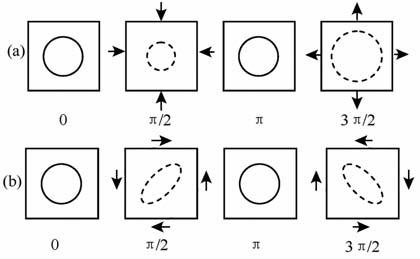
|
图 8 双孔结构中的两种局域流振荡模式示意图 (a)双孔结构中球状嵌人体的压缩波局域流振荡模式;(b)双孔结构中球状嵌人体的剪切波局域流的近似振荡模式. Fig. 8 Schematic diagram of the two oscillation mode of local fluid flow in double-porosity structure (a) The oscillation mode of local fluid flow for compressive waves in a spherical inclusion in double-porosity structure; (b) The oscillation mode of local fluid flow for shear waves rn a spherical rnclusion rn double-porosity structure. |
感谢CSIRO 的Tobias Muller研究员与MiroslavBrajanovski博士、中国科学院声学所的王秀明研究员与作者进行了有益讨论.
| [1] | 杨慧珠, 巴晶, 唐建侯, 等. 油气勘探中常规地球物理勘探方法的发展. 石油地球物理勘探 , 2006, 41(2): 231–236. Yang H Z, Ba J, Tang J H, et al. Development of conventional geophysical methods in oil/gas exploration. Oil Geophysical Prospecting (in Chinese) , 2006, 41(2): 231-236. |
| [2] | 地震勘探技术成为油气勘探主角. 中国科技信息, doi: CNKI:SUN:XXJK.0.2007-18-003. The technology of seismic exploration has become the protagonist in oil-gas exploration industry. China Science and Technology Information, doi: CNKI:SUN:XXJK.0.2007-18-003. |
| [3] | Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid: I. Low-frequency range. J. Acoust. Soc. Am. , 1956, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [4] | Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid: II. Higher frequency range. J. Acoust. Soc. Am. , 1956, 28(2): 179-191. DOI:10.1121/1.1908241 |
| [5] | Muller T M, Gurevich B, Lebedev M. Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks-A review. Geophysics , 2010, 75(5): 75A164. |
| [6] | White J E. Computed seismic speeds and attenuation in rocks with partial gas saturation. Geophysics , 1975, 40(2): 224-232. DOI:10.1190/1.1440520 |
| [7] | Dutta N C, Seriff A J. On White's model of attenuation in rocks with partial gas saturation. Geophysics , 1979, 44(11): 1806-1812. DOI:10.1190/1.1440940 |
| [8] | Gurevich B, Zyrianov V B, Lopatnikov S L. Seismic attenuation in finely layered porous rocks: Effects of fluid flow and scattering. Geophysics , 1997, 62(1): 319-324. DOI:10.1190/1.1444133 |
| [9] | Shapiro S A, Müller T M. Seismic signatures of permeability in heterogeneous porous media. Geophysics , 1999, 64(1): 99-103. DOI:10.1190/1.1444536 |
| [10] | Carcione J M, Picotti S. P-wave seismic attenuation by slow wave diffusion: Effects of inhomogeneous rock properties. Geophysics , 2006, 71(3): 01-08. |
| [11] | 聂建新, 杨顶辉, 杨慧珠. 基于非饱和多孔隙介质BISQ模型的储层参数反演. 地球物理学报 , 2004, 47(6): 1101–1105. Nie J X, Yang D H, Yang H Z. Inversion of reservoir parameters based on the BISQ model in partially saturated porous media. Chinese J. Geophys. (in Chinese) , 2004, 47(6): 1101-1105. |
| [12] | 刘炯, 马坚伟, 杨慧珠. White球状Patchy模型中纵波传播研究. 地球物理学报 , 2010, 53(4): 954–962. Liu J, Ma J W, Yang H Z. Research on P-wave's propagation in White's sphere model with patchy saturation. Chinese J. Geophys. (in Chinese) , 2010, 53(4): 954-962. |
| [13] | Nie J X, Ba J, Yang D H, et al. BISQ model based on Kelvin-Voigt viscoelastic frame in partially saturated porous medium. Applied Geophysics, (in Press). |
| [14] | Carcione J M, Morency C, Santos J E. Computational poroelasticity-A review. Geophysics , 2010, 75(5): 75A229-75A243. DOI:10.1190/1.3474602 |
| [15] | 巴晶, 卢明辉, 胡彬, 等. 黏弹双相介质中的松弛骨架模型. 地球物理学报 , 2008, 51(5): 1527–1537. Ba J, Lu M H, Hu B, et al. The skeleton-relaxed model for poroviscoelastic media. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1527-1537. |
| [16] | Dvorkin J, Nur A. Dynamic poroelasticity: A unified model with the Squirt and the Biot mechanisms. Geophysics , 1993, 58(4): 524-533. DOI:10.1190/1.1443435 |
| [17] | Pride S R, Berryman J G, Harris J M. Seismic attenuation due to wave-induced flow. J. Geophys. Res. , 2004, 109: B01201. DOI:10.1029/2003JB002639. |
| [18] | Ba J, Carcione J M, Nie J X. Biot-Rayleigh theory of wave propagation in double-porosity media. J. Geohpys. Res. , 2011, 116: B06202. DOI:10.1029/2010JB008185. |
| [19] | Liu J, Ba J, Ma J W, et al. An analysis of seismic attenuation in random porous media. Science China Physics, Mechanics & Astronomy , 2010, 53(4): 628-637. |
| [20] | Carcione J M, Helle H B, Pham N H. White's model for wave propagation in partially saturated rocks: Comparison with poroelastic numerical experiments. Geophysics , 2003, 68(4): 1389-1398. DOI:10.1190/1.1598132 |
| [21] | Berryman J G. Thoery of elastic properties of composite-materials. Appl. Phys. Lett. , 1979, 35(11): 856-858. DOI:10.1063/1.90982 |
| [22] | Rayleigh L. On the pressure developed in a liquid during the collapse of a spherical cavity. Phil. Mag. , 1917, 34: 94-98. DOI:10.1080/14786440808635681 |
| [23] | Sato H, Fehler M. Seismic Wave Propagation and Scattering in the Heterogeneous Earth. New York: 1998 . |
| [24] | Eshelby J D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. London, Ser. A , 1957, 241(1226): 376-396. DOI:10.1098/rspa.1957.0133 |
| [25] | Kuster G T, Toksöz M N. Velocity and attenuation of seismic waves in two-phase media: I. Theoretical formulations. Geophysics , 1974, 39(5): 587-606. DOI:10.1190/1.1440450 |
| [26] | Ba J, Nie J X, Cao H, et al. Mesoscopic fluid flow simulation in double-porosity rocks. Geophys. Res. Lett. , 2008, 35: L04303. DOI:10.1029/2007GL032429. |
| [27] | Ba J, Yang H Z, Xie G Q. AGILD seismic modelling for double-porosity media. PIERS 2008 in Hangzhou. Cambridge: The Electromagnetics Academy. 2008. |
| [28] | Ba J, Cao H, Yao F C, et al. Double-porosity rock model and squirt flow in the laboratory frequency band. Applied Geophysics , 2008, 5(4): 261-276. DOI:10.1007/s11770-008-0036-0 |
| [29] | Ba J, Cao H, Yao F C. Pore heterogeneity induces double-porosity in Guang'an sandstone. //CPS/SEG Beijing. Beijing: Society of Petroleum Geophysics, 2009. |
| [30] | 巴晶. 双重孔隙介质波传播理论与地震响应实验分析. 中国科学G辑 , 2010, 40(11): 1398–1409. Ba J. Wave propagation theory in double-porosity medium and experimental analysis on seismic responses. Scientia Sinica Physica, Mechanica & Astronomica (in Chinese) , 2010, 40(11): 1398-1409. |
| [31] | Ba J, Cao H, Yao F C. Velocity dispersion of P waves in sandstone and carbonate: Double-porosity and local fluid flow theory. SEG Expanded Abstracts, Denver, US, 2010. |
| [32] | Berryman J G, Wang H F. Double porosity modelling in elastic wave propagation for reservoir characterization.//SPIE Conference on Mathematical Methods in Geophysical Imaging V. San Diego California: SPIE Press, 1998. |
| [33] | Johnson D L. Recent developments in the acoustic properties of porous media. //Sette D. Frontiers in Physical Acoustics XCIII. New York: North Holland Elsevier. 1987:255-290. |
| [34] | Johnson D L. Theory of frequency dependent acoustics in patchy saturated porous media. J. Acoust. Soc. Am. , 2001, 110(2): 682-694. DOI:10.1121/1.1381021 |
| [35] | Toms J, Müller T M, Ciz R, et al. Comparative review of theoretical models for elastic wave attenuation and dispersion in partially saturated rocks. Soil Dynamics and Earthquake Engineering , 2006, 26(6-7): 548-565. DOI:10.1016/j.soildyn.2006.01.008 |
| [36] | 陈国俊, 吕成福, 王琪, 等. 珠江口盆地深水区白云凹陷储层孔隙特征及影响因素. 石油学报 , 2010, 31(4): 566–572. Chen G J, Lü C F, Wang Q, et al. Characteristics of pore evolution and its controlling factors of Baiyun Sag in deepwater area of Pearl River Mouth Basin. Acta Petrolei Sinica (in Chinese) , 2010, 31(4): 566-572. |
| [37] | Tosaya C A. Acoustical properties of clay-bearing rocks . United States: Stanford University, 1982. |
| [38] | Batzle M L, Han D H, Hofmann R. Fluid mobility and frequency-dependent seismic velocity-direct measurements. Geophysics , 2006, 71(1): N1-N9. |
 2012, Vol. 55
2012, Vol. 55

