随着低轨重力卫星CHAMP (CHAllenging Minisatellite Payload)、GRACE (Gravity Recovery And Climate Experiment)及GOCE (Gravity field and steady-state Ocean Circulation Explorer)的发射及相关数据释放,卫星重力反演已成为当前大地测量的热门研究之一.仅ICGEM (International Centre of Global Earth Models at GFZ)所公布的采用CHAMP 或GRACE 卫星数据反演的地球重力场模型就多达37个,确定这些模型的方法主要包括动力学法[1~4]、能量守恒法[5, 6]、加速度法[7, 8]、短弧长积分法[9~11]及天体力学法[12~14].其中国际主要研究机构GFZ(Geo Forschungs Zentrum Potsdam)或CSR(Center for Space Research)均采用动力学一步法反演了EIGEN[2, 3]或GGM[4]系列重力场模型,该方法基于牛顿运动方程,将低轨卫星轨道与地球重力场参数联合起来统一求解.有学者[13]认为在重力场参数估计中可以不加入原始的GPS 相位或伪距观测值,而是直接利用所确定好的低轨卫星几何轨道及其完全的方差-协方差信息来求解重力场参数,该思路从统计意义上来说与动力学一步法是一致的,而且降低了参数估计问题的复杂性,这可称为二步法求解,事实上很多学者[5~14]都是采用这种思路来解算地球重力场的.动力学法观测方程的系数阵可通过变分方程求解,变分方程中初始历元的参数敏感矩阵一般设为零矩阵,文献[15]认为这从扰动理论上来说也许是成立的,但违背了数学规律或天体力学的物理定律,为此我们最好能避免变分方程的解算.另外GRACE 卫星星间观测值蕴含着丰富的地球重力场信息,但现有动力学法仍无法充分提取这些信息,利用GRACE 卫星数据恢复的地球重力场模型没有达到发射前的模拟精度[16, 17],这除了有对GRACE 原始数据的处理不当、初始模型的精度不高、观测数据的参数化问题等以外,采取不恰当的重力反演方法是主要原因,因此研究新的重力反演方法已迫在眉睫.
由于现有低轨重力卫星能采集高密集的轨道或星间观测数据,采用短弧长的计算方法反演地球重力场已成为可能[18].短弧长积分法的思想最早被用于轨道确定的问题[9],文献[10]将该方法应用于CHAMP卫星真实数据的处理,并采用1年的CHAMP卫星数据恢复了ITG-CHAMP01 模型.随后文献[11]在短弧长积分法的基础上进行梯度改正,并将该方法用于GRACE 卫星星间距离数据解算地球重力场模型,确定了ITG-GRACE02、ITG-GRACE03及ITG-GRACE2010系列模型,其中ITG-GRACE2010模型的外符合精度优于动力学法所确定的EIGEN或GGM 系列模型.短弧长积分法不需要解算变分方程,并且通过对力模型梯度改正降低了轨道误差对重力场解算的影响,从理论上来说优于动力学法.鉴于国内在短弧长积分法方面的工作较少,本文给出了采用短弧长积分法确定地球重力场模型的观测方程,并对力模型进行梯度改正,通过模拟及实际GRACE 数据计算表明,短弧长积分法的精度优于动力学法.
2 短弧长积分法根据牛顿运动方程可推导短弧长积分法[9~11]在某一历元的观测方程为
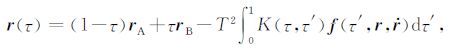
|
(1) |
其中,τ∈ [0, 1]为归一化的时间变量,r(τ)为卫星轨道向量,rA、rB 分别为弧段边界的轨道向量,T为弧段的时间长度,f(τ′,r,${\mathit{\boldsymbol{\dot{r}}}}$)为卫星所受的各种摄动力模型,摄动力模型中保守力与卫星速度无关,非保守力与卫星速度有关,但可用加速度计测得,因此摄动力模型可基本认为与速度无关,f(τ′,r,${\mathit{\boldsymbol{\dot{r}}}}$)可简写为f(τ′,r),积分核函数K(τ,τ′)的表达式为
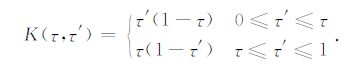
|
(2) |
将整个弧段的观测方程采用矩阵形式表达,式(1)可简化为
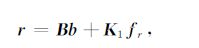
|
(3) |
其中,K1 为力模型积分的系数阵,令N为弧段历元个数,其他矩阵分别表示为
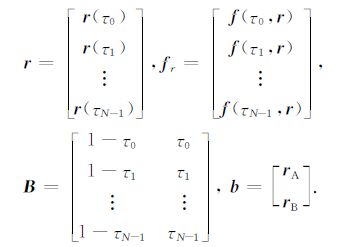
|
(4) |
假设卫星几何定轨、动力学定轨或约化动力学定轨所获得轨道向量为rg(τ),将其代入式(1)得

|
(5) |
将式(1)减去式(5)得
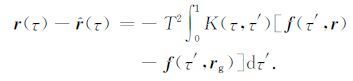
|
(6) |
由于实际测量的卫星轨道存在一定的误差,导致力模型的求解也存在误差,故将力模型在所测卫星轨道处进行Taylor线性展开得
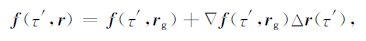
|
(7) |
其中,$\nabla $f(τ′,rg)为力梯度模型,Δr(τ′)为卫星轨道改正向量.将式(7)代入式(6)得
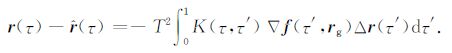
|
(8) |
将(8)式化简为整个弧段的矩阵表达式,

|
(9) |
其中,各矩阵的表达式为

|
(10) |
将式(9)左右两端减去轨道向量rg, 并整理得
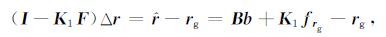
|
(11) |
其中,I为N×N单位矩阵,矩阵(I-K1F)为可逆矩阵,得
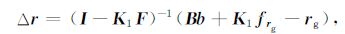
|
(12) |
(12) 式即为由力梯度模型改正所导出的卫星轨道改正向量,从而有参考轨道向量为

|
(13) |
将卫星轨道向量在(13)式参考轨道向量处线性展开,并同时考虑到位系数、边界轨道改正向量及加速度偏差的求解得
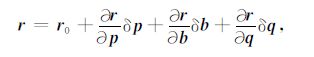
|
(14) |
其中,δp为位系数改正向量,δb为边界轨道改正向量,δq为加速度偏差改正向量,未知参数的系数阵分别表示为
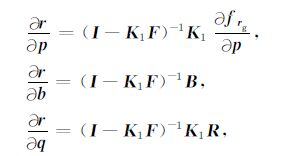
|
(15) |
其中,R为由加速度计参考框架转换到惯性系的旋转矩阵.式(14)即为短弧长积分法观测方程,若将式(13)中右边第二项及式(15)中的(I-K1F)-1 矩阵去掉,即为不加梯度改正的短弧长积分法观测方程,加了梯度改正的观测方程使得参考轨道向量及未知参数的系数阵求解更准确.由于(I-K1F)-1 的行列数等于弧段历元个数N,因此弧段长度不宜设置过长,一般为0.5h.
对于GRACE 卫星,在某一历元处的星间距离ρ 与卫星轨道存在如下关系式:
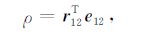
|
(16) |
其中,r12 =r2-r1 为两颗卫星轨道向量之差,e12 =r12/ρ 为星间单位向量.将式(16)在卫星轨道处Taylor线性展开得
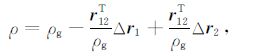
|
(17) |
其中,ρg = ‖rg12‖ 是利用卫星轨道所解算的星间距离,Δr1、Δr2 分别为两颗卫星的轨道扰动向量.将基于轨道扰动的观测方程式(14)代入(17)式,即得到基于星间距离扰动的观测方程.
为了估计梯度改正对轨道的影响,假设GRACE卫星所测轨道误差为±3cm, 采用0.5h的积分弧段(10s间隔),以2008-01-01前0.5小时的力模型梯度为参考值(各分量的量级约为10-8~10-6),利用式(8)计算了力模型梯度改正对轨道积分的影响,在惯性系下的三个分量如图 1 所示,可得在三个方向的量级最大为7.1cm, 说明梯度改正的影响要大于所测轨道本身的误差,随着弧段的延长影响更大,因此梯度改正不容忽视.本文的梯度改正思想与文献[19, 20]中轨道扰动的线性方程在本质上是一致的,区别仅在于本文是采用Fredholm 的方程形式,而文献[19, 20]采用Volterra的方程形式,Fredholm方程不需要速度分量,而Volterra 方程需要速度分量.

|
图 1 梯度改正对轨道积分的影响 Fig. 1 The influence of gradient correction to orbit integration |
在短弧长积分法的观测方程中,系数矩阵K1涉及到数值积分的计算.令A=K1fr,用式(2)代入式(1),并将整个弧段的积分转化为相邻历元积分累加,得第k个历元的系数阵A(τk)可分解如下:
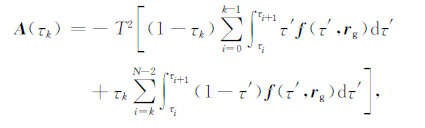
|
(18) |
将(18)式中的时间变量归一化,令Δτ =τi+1 -τi=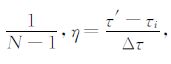
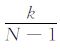
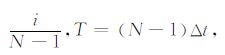

|
(19) |
其中,ωij为多项式拟合系数,具体计算可参考文献[20].用式(19)代入式(18)将积分离散化,得
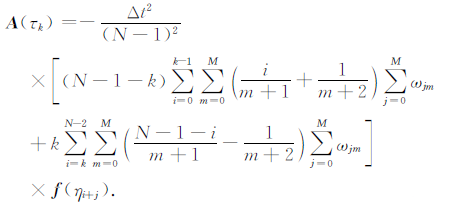
|
(20) |
将(20)式转化为矩阵形式,即为式(3)的表达式.可以看出,系数矩阵K1 的各历元计算可以累加,且只要弧段长度确定,K1 即保持不变,简化了计算过程,该方法有效代替了动力学法中变分方程的数值积分计算.
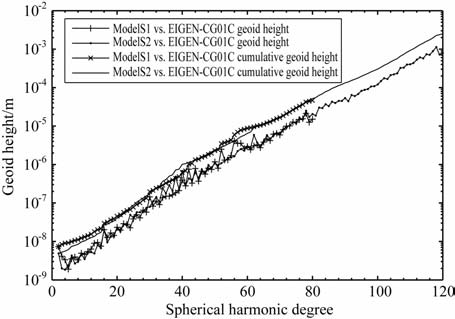
4 应用模拟数据反演地球重力场本节将采用模拟的GRACE 卫星轨道及星间距离数据对短弧长积分法进行仿真计算.采用文献[20]所述的GRACE 卫星初始历元轨道根数,并将其转化为惯性系下的初始状态向量,选择积分步长为10s, 考虑卫星只受中心引力及非球形引力的作用,选择120阶次的EIGEN-CG01C 模型为参考重力场模型,采用8阶Runge-Kutta积分、12阶的Adams及Cowell隐式积分的联合并行积分方法,可积分GRACE 双星1个月的轨道,并利用各历元的轨道计算其星间距离.对模拟的轨道及星间距离不加入任何随机误差,采用上述短弧长积分法列立观测方程,并利用预条件共轭梯度法求解法方程,可解算出对应的球谐位系数.当只采用轨道观测数据时,可解算80阶次的地球重力场模型ModelS1,当采用轨道与星间距离联立求解时,可解算120 阶次的地球重力场模型ModelS2.将这2组模型分别与参考模型EIGEN-CG01C 的位系数作差比较,得到2 组模型的大地水准面差距误差及累计误差,如图 2所示.比较可得ModelS1模型在80阶次的大地水准面差距误差及累计误差分别为1.50×10-5m 及4.65×10-5m, ModelS2 模型在120 阶次的大地水准面差距误差及累计误差分别为7.93×10-4m 及2.50×10-3m, 这充分说明了利用短弧长积分法反演地球重力场的有效性和可靠性.
|
图 2 两组模型的大地水准面精度 Fig. 2 Geoid accuracy of two models |
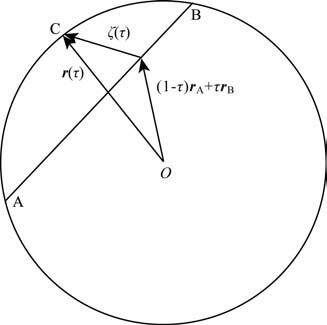
短弧长积分法与动力学法的原理是有差别的,动力学法基于卫星初始状态向量、先验地球重力场模型及其他力模型对非线性卫星运动方程进行线性化,并采用迭代方法求解,为了吸收力模型误差,求解时考虑了多种经验参数,如加速度计的偏差、尺度、漂移,K 波段的偏差、斜率、漂移等参数,最后为了控制力模型误差,也为了能覆盖GRACE 卫星至少一半的共振周期,选择弧段长度为1天或1.5天[2~4];而短弧长积分法是将牛顿运动方程转化为基于卫星边界轨道向量、球谐位系数及某些力模型参数的线性方程,且只估计了加速度计的偏差参数,其轨道观测方程的矢量图如图 3所示,其中(1-τ)rA +τrB为参考轨道,这是线性方程的主项,而ζ(τ)=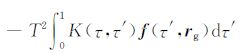
|
图 3 卫星轨道观测方程 Fig. 3 Observational equations of satellite orbits |
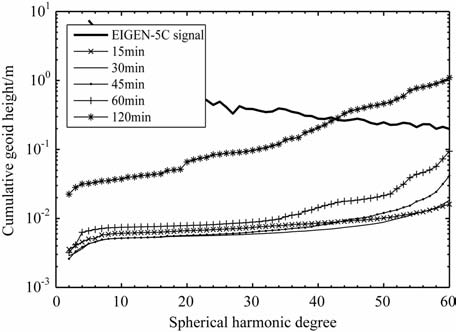
为进一步说明弧段长度的选择问题,直接采用美国喷气推进实验室(Jet Propulsion Laboratory, JPL)所提供的2008-01-01~2008-01-31 的1 个月GRACE 卫星数据进行重力场模型的解算.首先应对卫星轨道、星间距离、加速度及姿态观测数据进行预处理,包括数据粗差探测、数据内插、数据间断处理、坐标系转换等.观测数据预处理完后,将位系数作为全局未知数,弧段边界轨道改正向量、星间距离有偏改正及加速度计偏差改正(加速度计尺度采用JPL 所提供的参考值)作为局部未知数,选取历元间隔为10s, 考虑卫星受地球中心引力、非球形引力、日月引力、固体潮、海潮、极潮、大气与海洋的非潮汐变形影响及非保守力影响,采用最小二乘准则求解地球重力场模型.将位系数按以次为主的顺序排列,列出各弧段的观测方程,消去局部参数矩阵,得到各弧段的法方程矩阵,将各弧段法方程累加,并将累加的法矩阵块对角部分的逆阵作为预条件矩阵,利用预条件共轭梯度法解算法方程.采用星间距离数据时,考虑到初始状态向量的改正,同时为了降低局部法矩阵的病态性,并提高低阶位系数的解算精度,我们将卫星轨道与星间距离联合列立法方程,轨道与距离的权比采用文献[19]的要求.分别采用弧段长度为15min, 30min, 45min, 60min, 120min, 反演了5组60阶次的地球重力场模型,选择ICGEM 常用的模型EIGEN-5C 为参考模型,并将这5组模型分别与参考模型的位系数作差比较,得到这5 组模型相对于参考模型的累计大地水准面差距误差,如图 4所示,可以看出30min弧段反演模型的精度是最高的,随着弧段的延长,反演模型的精度显著降低.
|
图 4 不同弧长反演的模型精度对比 Fig. 4 PA comparison of model accuracy with different arc |
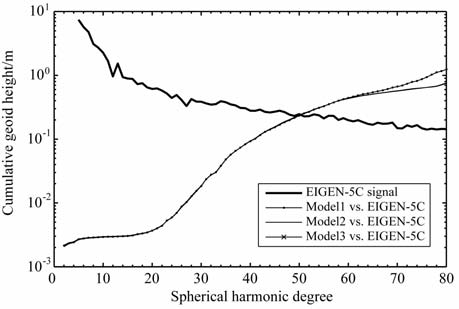
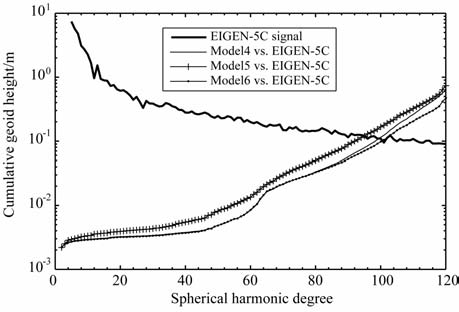
为了突出短弧长积分法的优越性,分别采用动力学法(选择EGM96 为初始模型)、不加梯度改正的短弧长积分法及加了梯度改正的短弧长积分法,弧段长度均选择为30min, 基于GRACE 卫星轨道数据恢复了三组80 阶次的地球重力场模型(Model1、Model2及Model3),基于GRACE 卫星轨道及星间距离数据恢复了三组120阶次的地球重力场模型(Model4、Model5及Model6),并将这6组模型分别与参考模型EIGEN-5C 的位系数作差比较,得到这6组模型相对于参考模型的累计大地水准面差距误差,如图 5~图 6所示,通过比较得出以下结论:
|
图 5 三组模型大地水准面误差 Fig. 5 Geoid errors of three models |
|
图 6 三组模型的大地水准面误差 Fig. 6 Geoid errors of three models |
(1) 基于卫星轨道数据反演地球重力场时,三种方法的精度相近,动力学法在60 阶以后精度略低,加了梯度改正较不加梯度改正的短弧长积分法精度几乎没有提高,这是由于轨道误差本身比较大(约3cm),力模型的梯度改正对从轨道扰动中提取重力场信息并没有多大改善.
(2) 基于卫星轨道及星间距离数据反演地球重力场时,不加梯度改正的短弧长积分法精度最低,加了梯度改正的短弧长积分法精度最高,该方法的整体精度较不加梯度改正的短弧长积分法提高近一倍,动力学法精度优于不加梯度改正的短弧长积分法,并且其在前80阶次与加了梯度改正的短弧长积分法精度相当,80阶次以后的精度要低于加了梯度改正的短弧长积分法,三种方法在120 阶次的大地水准面差距累计误差分别为63.20cm、73.57cm、46.96cm.以上结果表明力模型梯度改正减小了轨道误差对力模型的影响,进而减小了轨道误差对星间距离扰动的影响,从而更能有效提取星间距离中所蕴含的重力场信息.
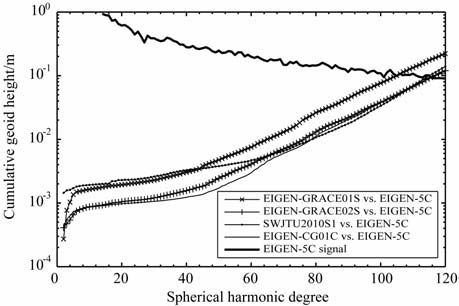
7 SWJTU2010S1模型解算第6节采用GRACE 卫星1个月数据反演地球重力场的整体精度均较低,在120 阶次的大地水准面差距累计误差的最好精度为46.96cm.为了提高重力场反演的精度,本节采用GRACE 卫星在2008-01-01~2008-08-01近200 天的轨道及星间距离数据基于梯度改正的短弧长积分法反演了120阶次的地球重力场模型SWJTU2010S1,具体反演步骤与第5 节一致.为了验证该模型的精度,将EIGEN-GRACE01S、EIGEN-GRACE02S、EIGEN-CG01C及SWJTU2010S1 模型分别与参考模型EIGEN-05C 的位系数作差比较,得到各模型的大地水准面差距累计误差,如图 7所示.比较可得,SWJTU2010S1在120阶次的大地水准面差距误差及累计误差分别为5.11cm 及14.00cm, 该模型在44 阶以前精度低于EIGEN-GRACE01S模型,44阶以后精度高于EIGEN-GRACE01S模型;在67阶以前精度低于EIGEN-GRACE02S 模型,67~108 阶精度高于EIGEN-GRACE02S 模型,108 阶以后精度低于EIGEN-GRACE02S模型;在79 阶以前精度低于EIGEN-CG01C 模型,79~110阶精度高于EIGEN-CG01C 模型,110 阶以后精度低于EIGEN-CG01C模型.总体来说,SWJTU2010S1模型在低阶位系数精度较低,高阶位系数精度较高,整体精度优于EIGEN-GRACE01S 及EIGEN-GRACE02S 模型,而低于EIGEN-CG01C 模型.同时计算该四组模型在区域为:纬度-90°~90°,经度-180°~180°,间隔为1°的网格点的大地水准面差距及重力异常,并与EIGEN-5C 模型的计算值作差比较,精度统计如表 1所示,进一步反映了SWJTU2010S1模型的精度.以上反映的是模型的内符合精度检核,为了更准确地验证模型的精度,采用美国GPS水准网(5379个点)及欧洲GPS水准网(188个点)对模型进行外符合精度检验,如表 2所示.可得这些模型的系统偏差都较大,达1 m 或0.5 m 左右,从标准差来看这四组模型的外符合精度比较与内符合精度基本一致.
|
图 7 SWJTU2010S1模型的内符合检核 Fig. 7 Internal validation of the model SWJTU2010S1 |
|
|
表 1 四组模型与参考模型的大地水准面差距及重力异常比较 Table 1 A comparison of geoid height and gravity anomaly between four models and the reference model |
|
|
表 2 四组模型的外符合精度比较(m) Table 2 A comparison of external precision of four modeSs (m) |
短弧长积分法观测方程中不包含有速度分量,为线性方程,不需要先验地球重力场模型,也不需要进行多次迭代计算,采用移动窗口的多项式内插公式来代替动力学法中变分方程的数值积分计算,计算速度快于动力学法.当采用轨道数据计算地球重力场模型时,不需要对力模型进行梯度改正,但当采用星间距离或距离变率数据解算地球重力场模型时,采用梯度改正模型可以大幅度提高地球重力场模型的解算精度.利用该方法解算的模型SWJTU2010S1在分辨率为167km(半波长)的大地水准面整体精度为14.00cm.对于未来采用激光测距的GRACEFollow-on卫星来说,轨道与星间距离精度的差距更明显,采用梯度改正的短弧长积分法解算地球重力场模型是比较理想的方法.
致谢感谢德国波恩大学Mayer-GürrTorsten博士给予的帮助及JPL所提供的GRACE卫星数据.
| [1] | Visser P N A M, van den Ijssel J, Koop R, et al. Exploring gravity field determination from orbit perturbations of the European Gravity Mission GOCE. Journal of Geodesy , 2001, 75(2-3): 89-98. DOI:10.1007/s001900000155 |
| [2] | Reigber C, Schmidt R, Flechtner F, et al. An earth gravity field model complete to degree and order 150 from GRACE: EIGEN-GRACE02S. Journal of Geodynamics , 2005, 39(1): 1-10. DOI:10.1016/j.jog.2004.07.001 |
| [3] | F?rste C, Schmidt R, Stubenvoll R, et al. The GeoForschungs Zentrum Potsdam/Groupe de Recherche de Gèodésie Spatiale satellite-only and combined gravity field models: EIGEN-GL04S1 and EIGEN-GL04C. Journal of Geodesy , 2008, 82(6): 331-346. DOI:10.1007/s00190-007-0183-8 |
| [4] | Tapley B, Ries J, Bettadpur S, et al. GGM02-An improved Earth gravity field model from GRACE. Journal of Geodesy , 2005, 79(8): 467-478. DOI:10.1007/s00190-005-0480-z |
| [5] | Jekeli C. The determination of gravitational potential differences from satellite-to-satellite tracking. Celestial Mechanics and Dynamical Astronomy , 1999, 75(2): 85-101. DOI:10.1023/A:1008313405488 |
| [6] | Han S C. Efficient global gravity determination from satellite-to-satellite tracking. Ohio: School of the Ohio State University , 2003. |
| [7] | 徐天河, 杨元喜. 利用CHAMP卫星几何法轨道恢复地球重力场模型. 地球物理学报 , 2005, 48(2): 288–293. Xu T H, Yang Y X. CHAMP gravity field recovery using kinematic orbits. Chinese J. Geophys. (in Chinese) , 2005, 48(2): 288-293. |
| [8] | Ditmar P, Kuznetsov V, van Eck van der Sluijs A A, et al. 'DEOS_CHAMP-01C_70’: a model of the Earth's gravity field computed from accelerations of the CHAMP satellite. Journal of Geodesy , 2006, 79(10-11): 586-601. DOI:10.1007/s00190-005-0008-6 |
| [9] | Schneider M. A General Method of Orbit Determination, Report 1279. Hants: Royal Aircraft Establishment , 1968. |
| [10] | Mayer-Gürr T, Ilk K H, Eicher A, et al. ITG-CHAMP01: a CHAMP gravity field model from short kinematic arcs over a one-year observation period. Journal of Geodesy , 2005, 78(7-8): 462-480. DOI:10.1007/s00190-004-0413-2 |
| [11] | Mayer-Gürr T. Gravitationsfeldbestimmung aus der Analyse kurzer Bahnboegen am Beispiel der Satellitenmissionen CHAMP und GRACE. Bonn: Institute fuer Theoretische Geodaesi der Universitaet Bonn , 2006. |
| [12] | Prange L, J?ggi A, Dach R, et al. AIUB-CHAMP02S: The influence of GNSS model changes on gravity field recovery using spaceborne GPS. Advances in Space Research , 2010, 45(2): 215-224. DOI:10.1016/j.asr.2009.09.020 |
| [13] | Beutler G, J?ggi A, Mervart L, et al. The celestial mechanics approach: theoretical foundations. Journal of Geodesy. , 2010, 84(10): 605-624. DOI:10.1007/s00190-010-0401-7 |
| [14] | Beutler G, J?ggi A, Mervart L, et al. The celestial mechanics approach: application to data of the GRACE mission. Journal of Geodesy , 2010, 84(11): 661-681. DOI:10.1007/S00190-010-0402-6 |
| [15] | Xu P L. Zero initial partial derivatives of satellite orbits with respect to force parameters violate the physics of motion of celestial bodies. Science in China Series D: Earth Sciences , 2009, 52(4): 562-566. DOI:10.1007/s11430-009-0049-4 |
| [16] | Flechtner F. More accurate and faster available CHAMP and GRACE gravity fields for the user community. In: System Earth Via Geodetic-Geophysical Space Techniques, Advanced Technologies in Earth Sciences. Berlin Heidelberg: Springer-Verlag, 2010. 3~13 |
| [17] | Flechtner F, Dahle C, Neumayer K H, et al. The release 04 CHAMP and GRACE EIGEN gravity field models. In: System Earth Via Geodetic-Geophysical Space Techniques, Advanced Technologies in Earth Sciences. Berlin Heidelberg: Springer-Verlag, 2010. 41~58 |
| [18] | Ilk K H, L?cher A, Mayer-Gürr T. Do we need new gravity field recovery techniques for the new gravity field satellites? In: Xu P L, Liu J N, Dermanis A eds. VI Hotine-Marussi Symposium on Theoretical and Computational Geodesy. Berlin: Springer, 2008. 3~8 |
| [19] | Xu P L. Position and velocity perturbations for the determination of geopotential from space geodetic measurements. Celestial Mech. Dyn. Astr. , 2008, 100(3): 231-249. DOI:10.1007/s10569-008-9117-x |
| [20] | 游为, 沈云中, 范东明, 等. 基于卫星轨道扰动理论的重力反演算法. 地球物理学报 , 2010, 53(11): 2574–2581. You W, Shen Y Z, Fan D M, et al. The algorithm of Earth's gravitational field recovery based on satellite's orbital perturbation theory. Chinese J. Geophys. (in Chinese) , 2010, 53(11): 2574-2581. |
| [21] | Rowlands D D, Ray R D, Chinn D S, et al. Short-arc analysis of intersatellite tracking data in a gravity mapping mission. Journal of Geodesy , 2002, 76(6-7): 307-316. DOI:10.1007/s00190-002-0255-8 |
 2011, Vol. 54
2011, Vol. 54