2. 中国科学院研究生院, 北京 100049
2. Graduate School of Chinese Academy of Sciences, Beijing 100049, China
Kirchhoff积分偏移被认为是地震叠前成像最灵活有效的方法之一,相对于其他偏移方法,它不仅对观测系统的适应能力强,而且计算效率较高.该方法最早产生于Hagedoorn“绕射最大凸度曲线"的概念[1];之后Schneider、Berryhill和Berkhout在绕射求和偏移的基础上添加倾斜因子、球面扩散因子和子波整形因子,从而形成了Kirchhoff偏移法的数学基础[2-4].Kirchhoff偏移的关键在于走时的计算.Taner和Koehler在均匀层状介质模型中,对走时进行了Taylor展开,建立了弯曲射线理论[5];之后,刘洋提出了反射波时距方程的分式表达式[6].在VTI介质走时计算方面,Hake等导出了其四阶近似NMO 方程[7],但数值计算稳定性欠缺;进而,Tsvankin等在Hake的基础上采用分式逼近的方法得到了多参数约定的四阶VTI介质走时方程[8],但参数反演困难;随后,Alkhalifah等引入了非椭圆各向异性参数,并给出了方便参数扫描的VTI介质走时分式表达式[9];Sun 提出了适用于各向同性介质的优化六阶NMO 方程[10];之后,Sun 又提出了针对VTI介质的NMO 方程修正项[11];最近,刘洪等基于象征理论提出了适用于横向速度变化的非对称走时Kirchhoff叠前时间偏移(KPSTM)[12,13],进而又将其推广到了深度偏移[14].
射线追踪计算的走时,需要平滑速度场,且计算量较大,而基于弯曲射线理论的Kirchhoff偏移[15],是一种综合了时间偏移的速度和深度偏移精度的方法[1],但较多的走时计算项限制了走时计算效率的提高.而正交多项式是对函数进行高精度逼近的有效方法,Werner用Hermite正交多项式求解了高斯函数的高阶导数作为具有多重循环波形的精确表示[16];Zhang等对单平方根算子的Taylor展开使用了截断的Chebyshev 多项式,并进行了全局优化,从而提高了对单平方根算子的逼近精度[17].本文首先在数学上证实了Chebyshev 正交多项式适合做高阶多项式的保精度约简,并给出了Chebyshev正交多项式的约简系数表,进而将模拟退火法分段优化后的二阶式应用于Kirchhoff偏移的走时计算,修改后的方法不仅在大炮检距范围内获得与原高阶展开基本一样的精度,而且减少了计算量,同时分别在均匀介质、VTI介质以及实际地震资料中得到验证.
2 基于Chebyshev 多项式弯曲射线偏移走时系数计算方法对称走时弯曲射线Kirchhoff叠前时间偏移的走时计算如下:

|
(1) |
本文截取到x6 项,各项对应的系数为[5]:
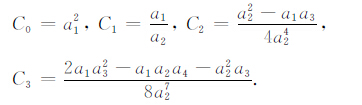
|
(2) |
其中
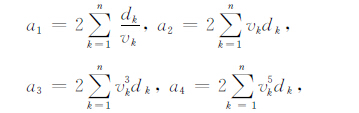
|
(3) |
化简各系数可以看出,常规方法只是弯曲射线方法的二阶近似,随着阶次的增加,高阶项越多地考虑了射线偏折,所以适合更大的炮检距.基于VTI介质,Hake给出了四阶多项式走时计算式[7,18]:

|
(4) |
Alkhalifah等提出了VTI介质四阶分式表达式[9]:

|
(5) |
其中,vnmo 为NMO 速度,η 是非椭圆等效各向异性参数,且有,
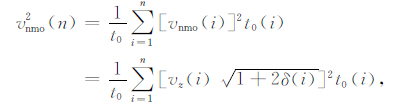
|
(6) |
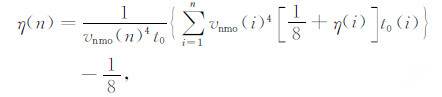
|
(7) |
其中,vz(i)为介质第i层的垂向速度;ε,δ 为Thomsen各向异性参数[19];t0(i)为第i层射线双程垂直走时.值得注意的是,Hake的三项Taylor展开,仅在小炮检距范围内准确[7],且在浅层和大偏移距处存在数值计算的不稳定性,偏移时应予注意.
Chebyshev正交多项式可以将函数在[-1,+1]上关于

|
(8) |

|
(9) |
再设
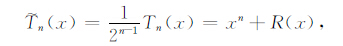
|
(10) |
将(10)式带入(8)式有:
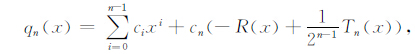
|
(11) |
令
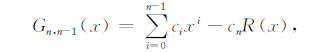
|
(12) |
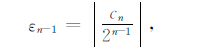
|
(13) |
若

|
(14) |
则有
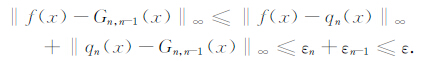
|
(15) |
这时可用Gn,n-1(x)来逼近f(x)[20],在精度满足的条件下,多次进行上述操作就可以实现降阶(上述推导的数学依据见附录A).这样对于(1)式的Taylor展开,我们先将其规整到Chebyshev正交多项式的有效范围内,设x=bm,m为降阶转换系数,b∈ [-1,+1],则有:
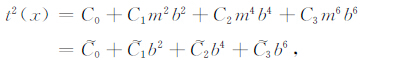
|
(16) |
之后,利用Chebyshev正交多项式将(16)式修改成如下形式:
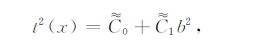
|
(17) |
其中,
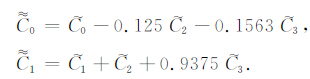
|
(18) |
而对于VTI介质的Hake的四阶走时表达式,修改后的二阶走时式为
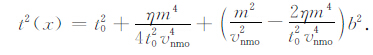
|
(19) |
修改后的系数公式减少了走时计算量,形式与常规方法一样只展开到二次项,但是修改后的新系数并没有舍弃原高阶项的系数,而是高阶系数的组合,所以相对常规方法更适合大炮检距.转换系数m是方法的关键,它影响二阶式与高阶式之间的残差分布范围;利用模拟退火法来优化m值,可以实现在某一指定范围内二者最佳逼近,并将误差控制在指定范围之外,从而使二阶走时表与高阶走时表在大炮检距范围内获得相当的精度.但是在炮检距过大时,高阶项所占的比重加大,造成两种方法走时差变大,要求逐步缩小拟合范围才可以满足精度要求.表 1 给出了用Chebyshev 正交多项式对多项式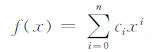
|
|
表 1 Chebyshev 正交多项式约简系数表 Table 1 Reduction coefficients by Chebyshev orthogonal polynomial |
基于上述的走时公式,我们采用与射线弯曲效应相适应的权函数[21-23]
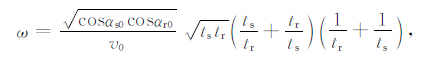
|
(20) |
其中,αs0 和αr0 分别是地表入射射线和出射射线与纵轴夹角,v0 是地表速度,ts 和tr 分别是炮点和检波点到成像点走时.
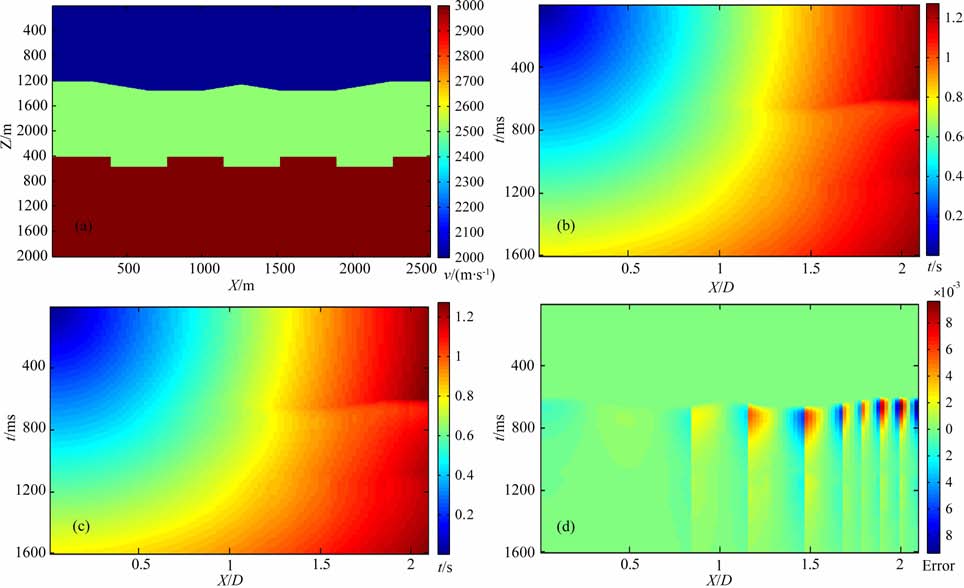
3 模型验证为了体现两种方法在走时计算上的一致性以及大炮检距对走时残差的影响,将两者的走时表做如下对比.建立一个如图 1a 所示的模型,纵向深度2000m, 最大勘探深度是1200 m, 最大偏移距为2500m, 最小偏移距为0m, 震源位于原点处.首先,用模拟退火法求出在不同范围内二阶方法最佳逼近六阶方法的转换系数m;不同区间最优逼近的m值及对应的误差值如表 2 所示.之后,利用优化后的Chebyshev二阶多项式计算基于上述模型的走时表(图 1c),并与六阶弯曲射线走时表(图 1b)做对比,结果示于图 1d.
|
图 1 两种方法的走时图及时差百分比图 (a)层速度-深度模型;(b)六阶走时公式计算的走时图;(c)优化二阶Chebyshev走时公式计算的走时图;(d)两者时差百分比图 Fig. 1 Traveling-time chart of two methods and the time difference graph (a)Interval velocity-depth model; (b) Traveling time chart by 6th-order travel time formula; (c)Traveling time chart by optimized 2nd-order Chebyshev formula; (d)Travel time difference percentage graph between (b)and(c) |
从表 2可以看出,在大炮检距((X)/D>2)范围内,常规二阶方法与六阶走时式的百分比误差随着炮检距增加不断增加,而优化以后的二阶Chebyshev多项式计算的走时与六阶走时却有良好的一致性,误差都保持在1%以内,但是随着炮检距的增加,高阶部分所占的比例逐渐加大,用二阶来逼近高阶要增加优化的次数,同时缩小优化的范围,这样才能满足两种方法的一致性要求.在实际偏移处理中,对于中小偏移距数据,偏移孔径处于正常的范围内((X)/D<1.25),此时二阶走时式可直接在全局进行优化,求取最佳m值;但如果偏移孔径较大((X)/D>1.25),要对一炮数据进行分段优化,求出每段的最优m值,之后扩展到所有炮即可.
|
|
表 2 误差对比表 Table 2 Error contratt chart |
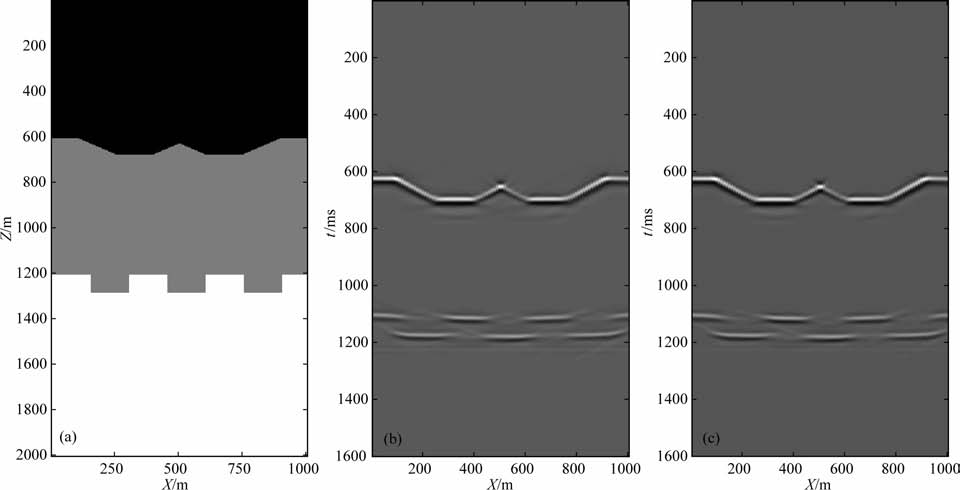
为了验证优化二阶Chebyshev 弯曲射线方法的正确性,设计了三层各向同性介质和VTI介质模型.图 2是一各向同性介质,三层纵波速度分别是2000m/s、2500m/s、3000m/s, 第一个是中间凸起的杯状界面,第二个界面是一个锯齿状界面,如图2a所示.震源使用的是30 HzRicker子波,采用声波方程高阶有限差分法模拟,1600 个时间采样点,时间采样间隔1ms, 炮间距20m, 道间距10m, 201个检波点双边接受,共61 炮.偏移孔径为1800,全局优化以后的转换系数m=1746,采用优化二阶Chebyshev弯曲射线方法和六阶对称走时方法偏移以后的结果如图 2b和图 2c所示.从图 2可以看出,均匀介质中两种方法具有相当的成像精度.但走时计算上,优化二阶Chebyshev偏移方法要比六阶对称走时方法节省50%的运算时间.
|
图 2 速度模型以及两种方法的成像对比 (a)局部速度模型;(b)六阶弯曲射线KPSTM 成像结果;(c)优化二阶Chebyshev弯曲射线KPSTM 成像结果. Fig. 2 Velocity model and the contrast of two methods (a) Partial velocity model; (b)Migrated section by 6th-order bend-ray KPSTM;(c)Migrated section by optimized 2nd-order Chebyshev bend-ray KPSTM. |
对于VTI介质,同样构建一个三层模型,如图2a示,三层介质垂向方向纵波速度Vp0 依次是2000m/s, 2500m/s和3000m/s, 三层的各向异性参数ε(i),δ(i)分别为:0.15,0.0417;0.25,0.0357;0.35,0.1071,相应的非椭圆各向异性参数η(i)分别为:0.1,0.2,0.2.最大深度2000 m.震源参数与观测系统设计和上一模型一致,由于Hake四阶走时式的局部不稳定性,在偏移中走时计算的异常区用四阶分式结果来代替,且参数优化的目标函数不考虑这些异常区域,在此基础下,偏移孔径选为800m, 优化后的转换系数m=1059,两种方法的偏移结果如图 3(b, c)所示.可以看出,对于VTI介质,两种方法都能比较准确地成像,同时优化二阶Chebyshev偏移方法相对四阶方法减少了33%走时计算时间.

|
图 3 VTI介质垂向速度模型以及两种方法的成像对比 (a)局部速度模型;(b)四阶弯曲射线KPSTM 成像剖面;(c)优化二阶Chebyshev弯曲射线KPSTM 成像结果. Fig. 3 Vertical velocity model of VTI media and the contrast of two methods (a) Partial velocity model; (b) Migrated section by 4th-order bend-ray KPSTM;(c)Migrated section by optimized 2nd-order bend-ray KPSTM. |
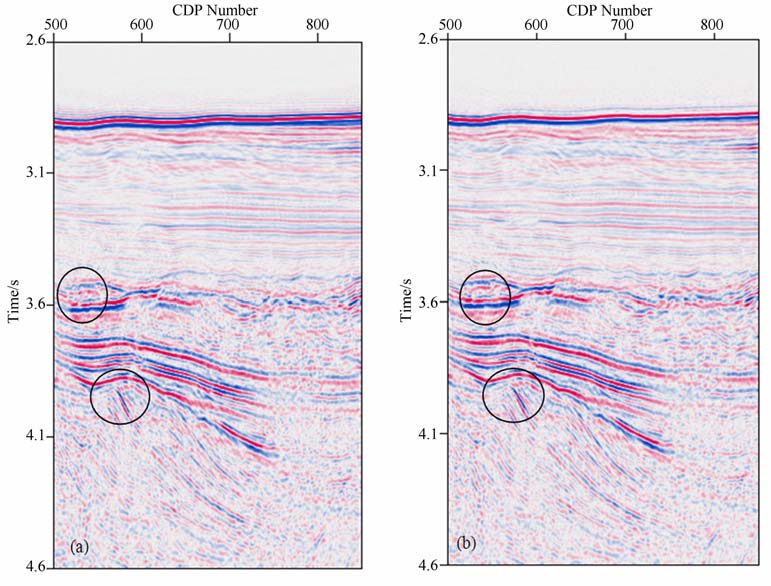
我们采用某工区实际地震资料进行测试,数据共96000道,400炮,炮间距25 m, 道间距12.5 m, 采样间隔2ms, 记录时间7s, 分别对其进行六阶弯曲射线Kirchhoff 叠前时间偏移和优化二阶Chebyshev叠前时间偏移,偏移孔径按照经验公式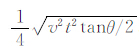
|
图 4 两种方法的成像对比图 (a)六阶弯曲射线KPSTM 处理结果;(b)优化Chebyshev二阶KPSTM 处理结果. Fig. 4 Imaging contrast graph between two methods (a) The profile processed by 6th-order bend-ray KPSTM;(b) The profil eacquired by optimized 2nd-order Chebyshev KPSTM. |
本文利用Chebyshev多项式实现了对高阶弯曲射线Kirchhoff叠前时间偏移的保精度降阶约简,减少了其走时计算量.优化以后的二阶Chebyshev走时公式计算的走时表不仅在大炮检距范围内可以与原高阶走时式最优逼近,而且对均匀介质、VTI介质和实际资料的偏移结果也具有与高阶方法相当的精度.相应的转换系数m是方法的关键,处理时可以视观测系统和偏移孔径来分段优化或全局优化之,以使误差最小.
同时,从理论上和模型实验上证实了Chebyshev正交多项式在解决多项式保精度约简问题上的有效性,不仅可以用于文中的弯曲射线Kirchhoff偏移,也可以推广到其他基于高阶多项式计算的方法.
附录A Chebyshev 对多项式做项数约简的数学依据
Chebyshev对多项式做项数约简的依据有二.
依据一:
设Fn(x)表示所有最高阶次系数为1的n次多项式,则利用Chebyshev 正交多项性的极值性,可以得到:在x∈ [-1,1]上,
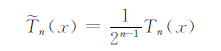
|
(A1) |
与零的偏差最小,且其偏差为1/2n-1,即对于任何p(x)∈Fn(x),有
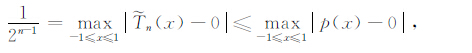
|
(A2) |
此结论可以用反证法证明之.正是这种最小偏差使得切比雪夫多项式在尽量保持精度的前提下进行多项式项数约简.尤其对于高阶项,1/2n-1 可以近似为零,所以
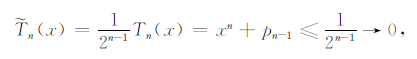
|
(A3) |
所以,可以利用文中推导进行高阶走时计算式的项数约简.
依据二[24]:首先用切比雪夫正交多项式来表示出xn,通式如下:

|
(A4) |
当n为偶数时,

|
(A5) |
将函数f(x),x∈ [-1,+1],在x= 0 处做Taylor展开:
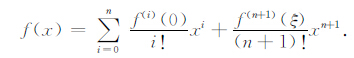
|
(A6) |
先设n为奇数,将(A4)和(A5)两式带入(A6)中,略去高阶误差,整理后得:
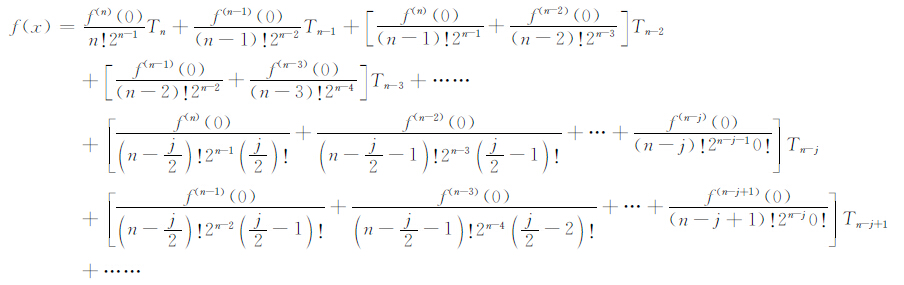
|
令n-j=m,进一步整理得:
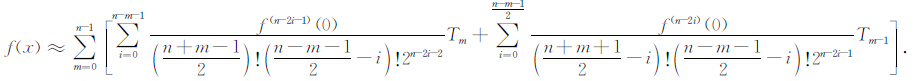
|
(A7) |
从(A7)式中可以看出,Tm的系数随m值的增大而变小,故我们可以略去次数高的Tm,同样,当n为偶数时,也可以得到类似的结果.所以,我们可以看出,利用Chebyshev项式可以使多项式的次数降低,以较低的阶次获得Taylor高阶展开的精度.
综上可以看出Chebyshev 正交多项式适合做多项式的约简.
| [1] | 罗银河, 刘江平, 董桥梁, 等. Kirchhoff弯曲射线叠前时间偏移及应用. 天然气工业 , 2005, 25(8): 35–37. Luo Y H, Liu J P, Dong Q L, et al. Kirchhoff curved-ray prestack time migration and its application. Natural Gas Industry (in Chinese) , 2005, 25(8): 35-37. |
| [2] | Schneider W A. Integral formulation for migration in two and three dimensions. Geophysics , 1978, 43(1): 49-76. DOI:10.1190/1.1440828 |
| [3] | Berryhill J R. Wave-equation datuming. Geophysics , 1979, 44(8): 1329-1333. DOI:10.1190/1.1441010 |
| [4] | Berkhout A J. Seismic Migration -Imaging of Acoustic Energy by Wavefield Extrapolation. Amsterdam: Elsevier Science Publishing, 1980 . |
| [5] | Taner M T, Koehler F. Velocity spectra-digital computer derivation and applications of velocity function. Geophysics , 1969, 34(6): 859-881. DOI:10.1190/1.1440058 |
| [6] | 刘洋. 反射波分式展开时距方程及其精度分析. 石油物探 , 2003, 12(4): 441–447. Liu Y. Fraction expansion time-distance equation of reflection wave and its accuracy analysis. Geophysical Prospecting for Petroleum (in Chinese) , 2003, 12(4): 441-447. |
| [7] | Hake H, Helbig H, Mesday C S. Three-term Taylor series fort2-x2-curves of P-and S-waves over layered transversely isotropic ground. Geophysical Prospecting , 1984, 32(5): 828-850. DOI:10.1111/gpr.1984.32.issue-5 |
| [8] | Tsvankin I, Thomsen L. Nonhyperbolic reflection moveout in anisotropic media. Geophysics , 1994, 59(8): 1290-1304. DOI:10.1190/1.1443686 |
| [9] | Alkhalifah T, Tsvankin I. Velocity analysis for transversely isotropic media. Geophysics , 1995, 60(5): 1550-1566. DOI:10.1190/1.1443888 |
| [10] | Sun C W, Wang H W, Martinez R D. Optimized 6th order NMO correction for long-offset seismic data. 72ndAnnual International Meeting, SEG, Expanded Abstracts, 2002 |
| [11] | Sun C, Martinez R D. 3D Kirchhoff PS-wave prestack time migration forV(z) and VTI media. 73rd Annual International Meeting, SEG, Expanded Abstracts, 2003. 957-960 |
| [12] | 刘洪, 王秀闽, 曾锐, 等. 单程波算子积分解的象征表示. 地球物理学进展 , 2007, 22(2): 463–471. Liu H, Wang X M, Zeng R, et al. Symbol description to integral solution of one-way wave operator. Progress in Geophysics (in Chinese) , 2007, 22(2): 463-471. |
| [13] | 刘洪, 袁江华, 陈景波, 等. 大步长波场深度延拓的理论. 地球物理学报 , 2006, 49(6): 1779–1793. Liu H, Yuan J H, Chen J B, et al. Theory of large step wavefield depth extrapolation. Chinese J. Geophys. (in Chinese) , 2006, 49(6): 1779-1793. |
| [14] | 张廉萍, 刘洪. 适于Kirchhoff叠前深度偏移的地震走时李代数积分算法. 地球物理学报 , 2010, 53(8): 1893–1901. Zhang L P, Liu H. Lie algebra integral algorithm of travel-time calculation for pre-stack Kirchhoff depth migration. Chinese J. Geophys. (in Chinese) , 2010, 53(8): 1893-1901. |
| [15] | 刘国峰, 刘洪, 王秀闽, 等. Kirchhoff积分时间偏移的两种走时计算及并行算法. 地球物理学进展 , 2009, 24(1): 131–136. Liu G F, Liu H, Wang X M, et al. Two kinds of traveling time computation and parallel computing methods of Kirchhoff migration. Progress in Geophysics (in Chinese) , 2009, 24(1): 131-136. |
| [16] | Heigl W M. Computing gaussian derivative waveforms of any order. Geophysics , 2007, 72(4): H39-H42. DOI:10.1190/1.2716624 |
| [17] | Zhang J H, Wang W M, Wang S Q, et al. Optimized Chebyshev Fourier migration: A wide-angle dual-domain method for media with strong velocity contrasts. Geophysics , 2010, 75(2): S23-S34. DOI:10.1190/1.3350861 |
| [18] | 井涌泉. 叠前时间偏移: 各向异性、多次波衰减及应用 . 北京: 中国科学院地质与地球物理研究所, 2009 Jing Y Q. Pre-stack time migration: anisotropy、demultiple and application (in Chinese). Beijing: Institute of Geology and Geophysics, CAS, 2009 http://cn.bing.com/academic/profile?id=2417368916&encoded=0&v=paper_preview&mkt=zh-cn |
| [19] | Thomsen L. Weak elastic anisotropy. Geophysics , 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [20] | 马振华, 等. 现代应用数学手册. 北京: 清华大学出版社, 2005 . Ma Z H. Modern Applied Mathematics Manual (in Chinese). Beijing: Tsinghua University Press, 2005 . |
| [21] | 邹振, 刘洪, 刘红伟. Kirchhoff叠前时间偏移角度道集. 地球物理学报 , 2010, 53(5): 1207–1214. Zou Z, Liu H, Liu H W. Common-angle gathers based on Kirchhoff pre-stack time migration. Chinese J. Geophys. (in Chinese) , 2010, 53(5): 1207-1214. |
| [22] | Zhang Y, Gray S, Yong J. Exact and approximate weights for Kirchhoff migration. 70th Annual International Meeting, SEG, Expanded Abstracts, 2000. 1039-1039 |
| [23] | Lee S, King D, Lin S. Efficient true-amplitude weights in Kirchhoff time migration. 74th Annual International Meeting, SEG, Expanded Abstracts, 2004. 1089-1092 http://www.oalib.com/references/18989708 |
| [24] | 赵国清, 李书波, 刘英菊. 利用切比雪夫多项式降低近似式项数. 哈尔滨科学技术大学学报 , 1983(1): 62–69. Zhao G Q, Li S B, Liu Y J. Decrease number of terms of polynomial by Chebyshev polynomial. Journal of Harbin University of Science and Technology (in Chinese) , 1983(1): 62-69. |
 2011, Vol. 54
2011, Vol. 54