2. 武汉大学测绘遥感信息工程国家重点实验室, 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University. Wuhan 430079, China
GPS技术的出现不仅从根本上解决了物理大地测量的研究目的之一---地球几何形状的确定,也使更具明确物理内涵的扰动重力的直接获取成为现实,提出了所谓GPS 重力边值问题:即以地球自然表明为已知边界,以其上的扰动重力为边界条件,确定(似)大地水准面及外部重力场[1].GPS重力边值问题本质上是非线性固定边值问题,早在GPS技术被广泛应用之前,Koch、Bjerhammar、Graferend等大地测量学者就已对此问题进行了大量研究[2].GPS技术出现后,为充分发挥GPS 大地高的优势,Moritz最先提出了GPS重力边值问题的概念,并从Molodensky收缩法角度直接给出了该问题的解[3].在此基础上,李斐等[2, 4]给出了GPS 重力边值问题更详尽的数学定义,求得该问题的一阶逼近解,并应用于局部似大地水准面的计算,达到了较好的精度效果.于锦海等[5]则推导出GPS 重力边值问题在O(T2)精度下椭球界面边值问题的积分解.吴晓平等[6]也对此问题进行了讨论,指出了利用扰动重力的优点.唐元义[7]利用自然边界元法对GPS重力边值问题进行数值求解.
Bjerhammer方法是为了解算Molodensky 问题而由瑞典学者Bjerhammer于1964 年提出的一种解析延拓理论.其数学本质是以正则调和函数的Runge-Krarup定理为基础,借助于Poisson核函数的再生性,将问题变为球外部边值问题[8, 9].1987年Bjerhammer[10]进一步将它发展为在虚拟球上以有限个重力场异常脉冲求解外部重力场的确定性离散方法,给出了简洁易算的封闭公式,并指出Bjerhammer方法解的稳定性与虚拟场元分布、虚拟球半径大小密切相关.本文将Bjerhammer方法应用于GPS重力边值问题的求解,并针对具体计算中虚拟场元的分布和求解、虚拟球半径的确定及奇异积分等问题进行研究.最后通过具体算例来验证算法的可行性.
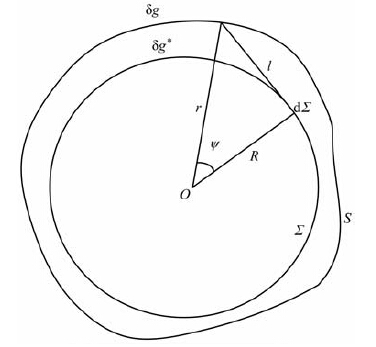
2 基本原理如图 1所示,S表示地球表面,Σ 表示Bjerhammar虚拟球面,R为Bjerhammar球半径,δg和δg分别代表地面上和球面上的扰动重力.按照Bjerhammar理论,δg和δg 之间可通过Poisson积分建立如下关系:
|
图 1 Bjerhammar方法示意图 Fig. 1 Illustration of Bjerhammar method |

|
(1) |
在求得虚拟扰动重力δg* 后,可按Hotine公式来计算地球表面及其外部的扰动位:

|
(2) |
式中,H(r,ψ)为Hotine函数:
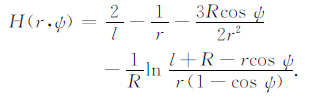
|
(3) |
根据Bruns公式,可按下式计算高程异常:
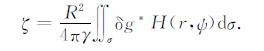
|
(4) |
在将Bjerhammer方法应用于具体实践计算时,虚拟场元的分布和求解、虚拟球半径的确定及奇异积分等是必须解决的问题.
3.1 虚拟场元的分布和求解虚拟场元的分布和求解主要有两种方法:一种是迭代算法,以观测数据点在Bjerhammer球面上的对应点为虚拟场元的分布点,通过迭代来计算虚拟场元;另一种是离散化算法,即在计算区对应的球面域按等经纬度间隔格网化,将积分方程离散化,然后计算虚拟场元的格网数据.在本文中,我们采用第一种方法的虚拟场元分布,而利用离散化算法来计算虚拟场元.将积分方程式(1)离散化为一个线性方程组:

|
(5) |
式中,i(i=1,2,…,n)是地面离散扰动重力点号,k(k=1,2,…,n)是待求虚拟场元δgk*的点号,ΔSk为该虚拟场元所代表球面区域面积.因为没有划分网格,也就没有办法确定ΔSk的大小.考虑到式(4)可离散为
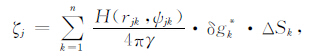
|
(6) |
则可将δg$\dot{k}$ΔSk视作一个整体进行求解,然后代入上式中计算区域内任意一点的高程异常.
3.2 Bjerhammer球半径的确定Bjerhammer曾指出解的稳定性随t(t=R/r)值的增大而增强.但因为观测数据本身是离散的,也就意味着并不是虚拟球离地球自然表面越近越好,否则会带来另外一个问题,即每个虚拟场元更多受到局部高频信号的影响,从而降低对整个局部重力场逼近的效果.因而如何最优选择虚拟球半径,将在很大程度上决定应用Bjerhammer方法进行局部重力场逼近的效果.我们认为虚拟球半径大小与观测数据的空间分布密度密切相关,即观测数据越密,虚拟球应该离地球自然表面越近,观测数据越稀,虚拟球则应离地球自然表面越远.因此,本文提出通过(7)式来确定虚拟球半径:
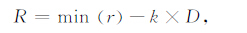
|
(7) |
式中,k为比例因子,D为观测数据相邻点间的平均距离.通过(7)式,在虚拟球半径和观测数据密度间建立起关系,并将虚拟球半径的确定问题转化为比例因子k的确定.下面在平面近似下给出k的近似值.
在Bjerhammer理论下,可将地面重力场元观测数据看成球面虚拟重力场元在某种函数映射下的响应.对单个虚拟扰动重力场元而言,其在地球表面产生的响应可描述为
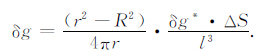
|
(8) |
在平面近似下,令h=r-R,l2 =h2 +s2,其中h为地面点离虚拟球面的距离,s为地面点离虚拟场元的水平距离,则式(8)可近似为

|
(9) |
由(9)式可知,当虚拟场元的大小和离地面的深度一定时,该虚拟场元在地面点的响应大小只与该点离虚拟场元的水平距离s有关.设两相邻点间水平距离为D,虚拟场元离地面点距离h为kD,则任一虚拟场元在其对应地面点产生的响应值为

|
(10) |
在两相邻点中间产生的响应值为
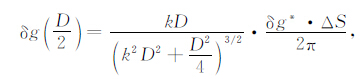
|
(11) |
对于重力场信号而言,可认为最相邻点间强线性相关,即认为两相邻虚拟场元中间点的响应值大小为两虚拟场元对应地面点响应值的平均值.则将式(11)除以式(10)可得
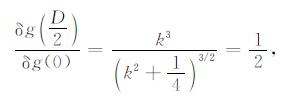
|
(12) |
根据(12)式可求得比例因子k近似值为0.65,本文中的计算主要采用这个近似值.
3.3 奇异积分处理当球心角距很小时,Hotine公式将出现奇异情况.为避免奇异积分,在内区采用近似计算公式[8]:
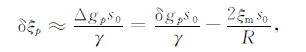
|
(13) |
式中,s0 表示计算点P为中心小球冠的半径,δgp为计算点P的残余扰动重力,ξm 为计算点模型高程异常.
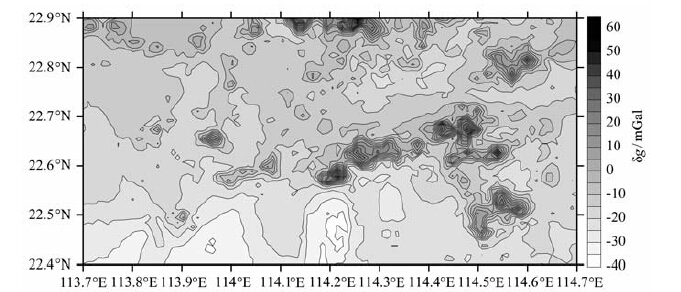
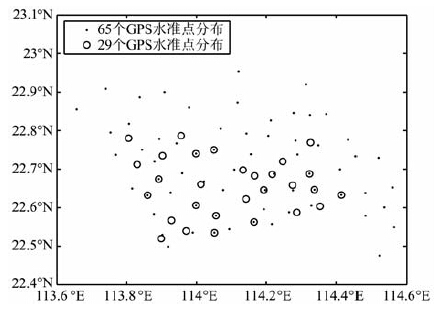
4 实际应用 4.1 数据及其处理我们收集到某地区4870 个GPS/重力点观测数据(空间分辨率约为1km)和94个高精度GPS/水准点数据.其中GPS大地高最大值为960.34m,最小值为-29.10m,平均值为51.19 m,图 2 为该地区GPS大地高模型图.在计算过程中,采用了“移去-恢复"技术,首先根据GPS/重力数据计算出各点扰动重力(利用WGS84 椭球参数),扰动重力最大值为59.20mGal,最小值为-34.44 mGal,平均值为-13.02mGal,图 3为该地区扰动重力等值线图.再以EIGEN-4C 全球重力场模型为参考重力场模型计算剩余扰动重力和模型高程异常,然后采用本文提出的计算方法确定了本地区的GPS 重力似大地水准面.为了评价本文计算方法的合理性,人为地将外业采集的GPS 重力观测数据密度分别降低为1.5km(实际利用1314 个GPS 重力点)、2km(实际利用814个GPS重力点)、3km(实际利用390个GPS重力点)和5km(实际利用157 个GPS 重力点),并利用65个高精度GPS 水准数据(空间分布见图 4)对GPS 重力高程异常进行了外部检核,比较分析比例因子k对计算结果的影响.另外,我们用这65个高精度GPS 水准数据对GPS 重力高程异常进行系统差拟合改正,然后用另外29 个GPS 水准点(空间分布见图 4)对拟合后的GPS重力高程异常进行了精度评定.
|
图 2 该地区GPS大地高模型图 Fig. 2 GPS geodetic height model |
|
图 3 该地区扰动重力等值线图 Fig. 3 Contour map of gravity disturbance |
|
图 4 GPS水准点分布图 Fig. 4 The distribution of GPS/level in gpoints |
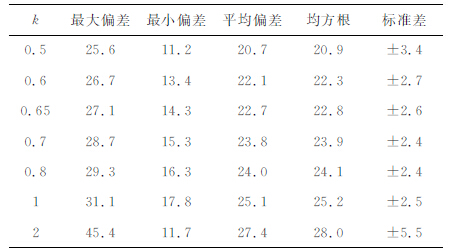
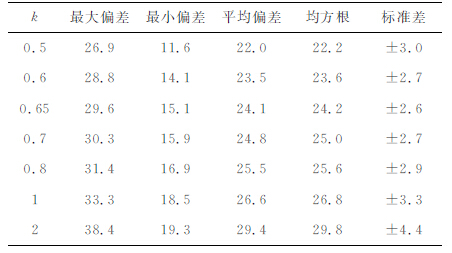
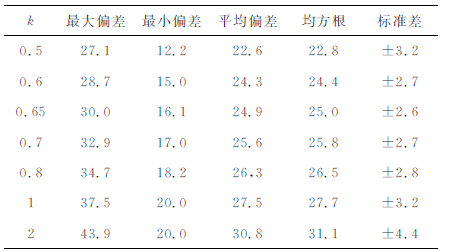
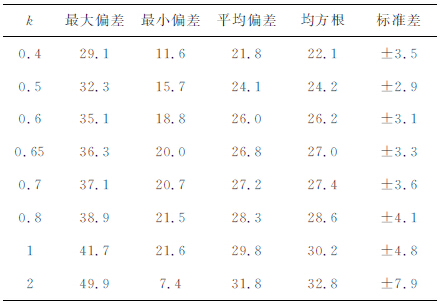
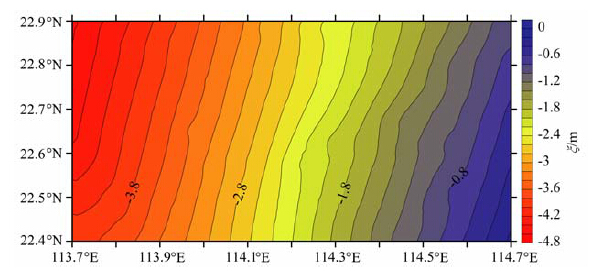
首先采用本文的计算方法利用4870个GPS重力点计算了该地区的高程异常.图 5 为该地区的高程异常等值线图,从该图可以看出,该区域似大地水准面变化较为平缓.表 1 为依不同比例因子k所计算的GPS重力高程异常和65 个高精度GPS 水准点差值的统计结果.从表中可以看出,利用本文方法所计算的GPS 重力高程异常取得了较好的结果,GPS水准点检核精度可达±2.4cm,说明两者之间主要是系统性偏差.同文献[11, 12]中结果比较可以发现,本文方法不仅精度更高,系统性偏差也明显更小.表 2是通过二次多项式拟合将GPS重力似大地水准面“贴"近GPS 水准似大地水准面后,用另外29个GPS水准点进行检核的统计结果,其精度为±1.4cm,最大偏差为2.2cm,最小偏差为-3.0cm,这比文献[11]采用三次多项式拟合后的统计结果略好,与文献[12]中经过两次拟合后得得到的结果精度一致.表 3-6 分别是将GPS 重力数据密度降低为1.5km(实际利用1314个GPS重力点)、2km(实际利用814 个GPS 重力点)、3km(实际利用390个GPS重力点)和5km(实际利用157个GPS重力点)后依不同比例因子k所计算的高程异常与65个高精度GPS 水准点差值的统计结果.从这几个表中及表 1的结果可以看出,GPS重力高程异常计算结果精度与k的大小(或者说虚拟球半径大小)密切相关.正如前文所指出,比例因子k存在一个最优值.本文通过假设近似计算出的比例因子k=0.65并不是最优值,这是因为地球重力场信号本身是多尺度的,并不严格满足我们的假设.尽管如此,从表中结果也可看出用k=0.65 作为近似值代入计算对精度影响较小,这说明我们的假设是合理的,而且这个近似值也有助于我们寻找虚拟球半径的最优值.
|
|
表 1 GPS重力(4870点)高程异常与GPS/水准(65点)高程异常差值统计结果(单位:cm) Table 1 Accuracy statistics of GPS/gravity(4870 points) height anomaly with 65 GPS/leveling points (Unit: cm) |
|
|
表 2 拟合后GPS重力高程异常与GPS/水准高程异常差值的统计结果(单位:cm) Table 2 Accuracy statistics of GPS/gravity height anomaly after fitting (Unit: cm) |
|
|
表 3 GPS重力(1314点)高程异常与GPS/水准(65点)高程异常差值统计结果(单位:cm) Table 3 Accuracy statistics of GPS/gravity( 1314 points) height anomaly with 65 GPS/leveling points (Unit: cm) |
|
|
表 4 GPS重力(814点)高程异常与GPS/水准(65点)高程异常差值统计结果(单位:cm) Table 4 Accuracy statistics of GPS/gravity(814 points) height anomaly with 65 GPS/leveling points (Unit: cm) |
|
|
表 5 GPS重力(390点)高程异常与GPS/水准(65点)高程异常差值统计结果(单位:cm) Table 5 Accuracy statistics of GPS/gravity(390 points) height anomaly with 65 GPS/leveling points (Unit: cm) |
|
|
表 6 GPS重力(157点)高程异常与GPS/水准(65点)高程异常差值统计结果(单位:cm) Table 6 Accuracy statistics of GPS/gravity(157 points) height anomaly with 65 GPS/leveling points (Unit: cm) |
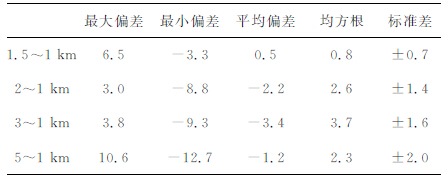
我们也将低分辨率GPS 重力数据计算的高程异常同利用4870个GPS重力点数据计算的高程异常进行了比较,分析GPS重力数据密度对确定似大地水准面精度的影响.图 6 和表 7 分别是不同分辨率GPS重力数据所计算高程异常间差值的等值线图和统计结果.从该图和表中的信息可以看出,GPS重力数据分辨率越低,其计算的高程异常与原始数据计算的高程异常差值就越大.其中ζ1×1 -ζ1.5×1.5标准差为±0.7cm,说明两者计算结果相差不大,可认为精度相当.对比图 2可发现,图 6中差值较大的地区一般是地形起伏较大的地区,由此也可得出一些与文献[13]相一致的结论,本文不再赘述.
|
|
表 7 不同分辨率GPS重力数据所计算高程异常差值统计结果(单位:cm) Table 7 Statictics of height anomaly difference between different GPS/gravity points(Unit:cm) |
|
图 5 某地区GPS重力高程异常(4870点)等值线图 Fig. 5 Contour map of GPS/gravity height anomaly(4870 gavity points) |

|
图 6 不同分辨率GPS重力数据计算高程异常差值等值线图(a)ζ1×1 -ζ1.5×1.5 等值线图;(b)ζ1×1 -ζ2×2 等值线图;(c)ζ1×1 -ζ3×3 等值线图;(d)ζ1×1 -ζ5×5 等值线图. Fig. 6 Contour map of height anomaly difference between different GPS/gravity points |
本文将Bjerhammar方法应用于GPS重力似大地水准面的确定,并针对计算中虚拟场元的分布和求解、虚拟球半径的确定及奇异积分等问题提出具体的解决办法.从本文的实例计算结果可以得出如下一些结论:
(1) 通过本文方法计算的GPS重力似大地水准面,以高精度GPS 水准点进行外部检核,其标准差为±2.4cm.经二次多项式拟合将GPS重力似大地水准面“贴"近GPS水准似大地水准面后,其外部检核精度可达到±1.4cm.这说明了Bjerhammar方法应用于GPS重力边值问题求解的合理性及本文计算方法的可行性和可靠性.
(2) 利用Bjerhammer方法进行局部重力场逼近的效果与虚拟球半径的大小密切相关,本文在虚拟球半径和GPS重力数据密度之间建立起关系,将虚拟球半径大小的确定转换为比例因子k的求解,并通过假设近似推导出k的近似值.通过比较分析不同分辨率GPS重力数据下,比例因子k对计算结果的影响,可发现尽管这个近似值不是最优值,但其对重力场逼近效果影响不是很大.当然如何最优确定比例因子k仍值得进一步研究.
(3) 降低GPS重力数据分辨率会对局部重力场逼近效果产生影响,在地势较为平坦地区,精度影响较小,而在地形起伏比较大的地区,精度影响较大.这说明野外数据采集时根据地形合理优化设计,将能起到节约成本和提高逼近精度的效果.
| [1] | 李斐, 陈武, 岳建利. GPS在物理大地测量中的应用及GPS边值问题. 测绘学报 , 2003, 32(3): 198–203. Li F, Chen W, Yue J L. Physical geodesy with GPS. Acta Geodaetica et Cartographica Sinica (in Chiese) (in Chinese) , 2003, 32(3): 198-203. |
| [2] | 李斐, 陈武, 岳建利. GPS/重力边值问题的求解及应用. 地球物理学报 , 2003, 46(5): 595–599. Li F, Chen W, Yue J L. On solution and application of GPS/gravity boundary value problem. Chinese J. Geophys. (in Chinese) , 2003, 46(5): 595-599. |
| [3] | Moritz H. Molodensky's theory and GPS. In: Moritz H, Yurkina M I, eds. M. S. Molodensky: in memoriam. Graze, 2000 |
| [4] | 李斐, 岳建利, 张利明. 应用GPS/重力数据确定(似)大地水准面. 地球物理学报 , 2005, 48(2): 294–298. Li F, Yue J L, Zhang L M. Determination of geoid by GPS/gravity data. Chinese J. Geophys. (in Chinese) , 2005, 48(2): 294-298. |
| [5] | 于锦海, 张传定. GPS-重力边值问题. 中国科学(D辑) , 2003, 33(10): 988–996. Yu J H, Zhang C D. GPS-gravity boundary value problem. Science in China (Series D) (in Chinese) (in Chinese) , 2003, 33(10): 988-996. |
| [6] | 吴晓平, 李珊珊, 张传定. 扰动重力边值问题与实际数据处理的研究. 武汉大学学报(信息科学版) , 2003, 28(Special): 73–78. Wu X P, Li S S, Zhang C D. Problem of the boundary value of disturbing gravity and practical data processing. Geomatics and Informaton Science of Wuhan University (in Chinese) (in Chinese) , 2003, 28(Special): 73-78. |
| [7] | 唐元义. GPS-边值问题的自然边界元数值解法. 武汉理工大学学报(交通科学与工程版) , 2007, 31(2): 266–269. Tang Y Y. Numerical solution of GPS-boundary value problem based on the natural boundary element method. Journal of Wuhan University of Technology (Transportation Science & Enginering) (in Chinese) (in Chinese) , 2007, 31(2): 266-269. |
| [8] | 管泽霖, 管铮, 黄谟涛, 等. 局部重力场逼近理论和方法. 北京: 测绘出版社, 1997 . |
| [9] | Bjerhammar A. A new theory of geodetic gravity. Trans. Roy. Inst. Tech., No. 243, 1964 |
| [10] | Bjerhammar A. Discrete physical geodesy. Rep. No 380, Dept. of Geodetic Science and Surveying. Columbus: The Ohio State University, 1987 |
| [11] | 张利明. GPS/重力边值问题及其应用研究 . 武汉: 中国科学院测量与地球物理研究所, 2007 Zhang L M. GPS/gravity boundary value problem and its application (in Chinese). Wuhan: Institute of Geodesy and Geophysics, CAS, 2007 |
| [12] | 宁津生, 罗志才, 杨沾吉, 等. 深圳市1 km高分辨率厘米级高精度大地水准面的确定. 测绘学报 , 2003, 32(2): 102–107. Ning J S, Luo Z C, Yang Z J, et al. Determination of Shenzhen geoid with 1 km resolution and centimeter accuracy. Acta Geodaetica et Cartographica Sinica (in Chinese) (in Chinese) , 2003, 32(2): 102-107. |
| [13] | 张利明, 李斐, 陈武. 重力数据分辨率对GPS/重力边值问题的影响研究. 武汉大学学报(信息科学版) , 2007, 32(6): 523–526. Zhang L M, Li F, Chen W. Influence of gravity disturbance resolution on GPS/gravity boundary value problom. Geomatics and Informaton Science of Wuhan University (in Chinese) (in Chinese) , 2007, 32(6): 523-526. |
 2011, Vol. 54
2011, Vol. 54