声波测量为了解地下储层岩性、流体性质和井周地层性质等提供了非常有用的信息.声波测井是用来评价储集层油气存在和指导油田安全生产等的主要测量手段之一[1~6].例如,在岩石力学分析中,声波资料能够提供孔隙压力、岩石强度、地层侵入、地应力方位和大小等信息[5].在岩石物理分析中,声波资料能够用来评价地层岩性、孔隙度和识别孔隙流体类型[6].近年来,为节省钻井架占用时间、实时判断钻井效率和风险管理,随钻测井技术得到快速发展[7].实时的随钻声波测量能够为井壁稳定性分析、最佳钻井、孔隙压力预测和地震标定等提供及时的数据[8].
随钻测井在非常恶劣的环境(扭曲、撞击和震动等)下工作,随钻声波测量装置必须安装在高强度的厚壁钻铤上,为沿着钻铤传播的声波提供了良好的波导.这种波称钻铤模式仪器直达波,它对拟测的地层信号形成极大干扰.因此,随钻声波测井仪器的隔声体设计至关重要.随钻单极子声源激发的钻铤模式波幅度往往大于地层纵波的幅度,且相干性极强,必须经过压制处理才能测量到地层纵波(Tangand Cheng[1],2004).比较幸运的是,钻铤模式波在频域上存在一个阻带(大约有2~3kHz的带宽),这个阻带存在的频率范围大约是在10~20kHz, 具体频率位置由钻铤尺寸所决定(Sinhaand Plonaet al[9, 10].,1992;Rama Raoand Vandiver[11]1997; Tangand Cheng[1],2004).回顾电缆声波测井仪器的发展历史,仪器直达波均是通过在发射声源和接收器之间的壳体上加工狭缝和刻槽等手段来消除的.随钻声波测井隔声体设计也可以利用在钻铤上周期性地切割凹槽来有效地衰减钻铤波或拓宽钻铤波的阻带.目前,针对声波测井三维问题的理论研究主要是利用有限元和有限差分等数值模拟方法[12~22].闫向宏等[23]利用二维有限元模拟研究了刻槽尺寸和结构对钻铤波传播规律的影响.杨勇等[24]利用有限差分模拟了三种周期性凹槽结构的随钻声波测井隔声体的隔声效果,并分别计算了不同结构隔声体在井孔中的响应特征.王华等[25]利用有限差分系统研究了随钻多极子波的响应特征,提出了用信号处理的手段消除钻铤波的干扰.以上研究工作均未给出实验室和现场资料的验证结果.Leggett等[26]和Tang等[27]曾报道过一种周期刻槽式隔声体设计可以获得40 dB 的钻铤波衰减.Tang[28]等和Kinoshita[29]等分别报道了贝克休斯和斯伦贝谢公司设计的新型随钻声波隔声体的现场测试效果.上述公司的新型随钻声波测井隔声体是在大量有限差分数值模拟和实验测试研究基础上设计的,与原有隔声体相比钻铤模式波基本被衰减掉,地层纵波和斯通利波波形质量都非常好.
本文用三维有限差分程序数值模拟了刻槽前、后随钻声波测井钻铤模式波波形.给出了钻铤波固有阻带分布规律与钻铤尺寸的关系和钻铤波衰减频段与刻槽宽度、深度的关系.设计了一种随钻声波测井隔声体结构,通过数值模拟和现场实验井中隔声体测试结果验证了该隔声体结构有效地消除了钻铤直达波的干扰,能够测量到高质量地层纵波的波形和时差.
2 三维有限差分方法本文采用直角坐标系下三维非均匀交错网格有限差分[12~22]程序模拟随钻声波测井响应.考虑到井孔和钻铤的圆周边界我们采用更精细的空间步长,空间步长(Δx,Δy,Δz)选择满足:
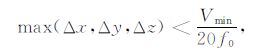
|
(1) |
其中,Vmin 是介质中最小声速,f0 为声源的中心频率.
对于采样空间四阶交错网格差分,时间二阶差分的情况,时间步长Δt满足的稳定条件:
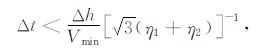
|
(2) |
其中,Δh是Δx、Δy、Δz中的最小网格步长,η1 =9/8,η2 =-1/24差分算子系数.
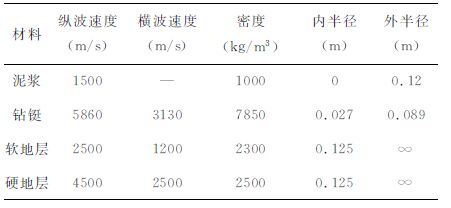
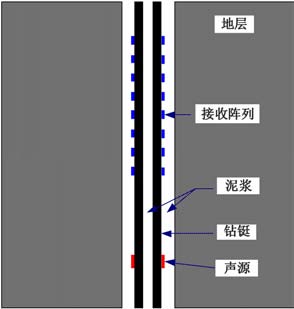
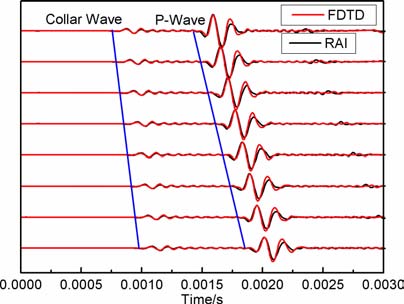
为了验证三维有限差分程序,计算了轴对称情况下的随钻声波测井全波波形,并与实轴积分法结果对比,模型示意图如图 1所示,在紧靠钻铤的应力节点上加载点声源,通过控制点声源的相位来实现多极子声源.计算中地层、钻铤和泥浆参数由表 1给出.模型尺寸为2m×2m×6m, 空间步长0.0025m, 时间步长1×10-7s.图 2给出了利用有限差分和实轴积分模拟的软地层随钻单极子声波波形,声源为主频8kHz的Ricker子波,源距3.3 m, 接收间距0.15m, 图中红线为有限差分计算结果,黑线为实轴积分计算结果.图中可见,对钻铤模式波和地层纵波来说,有限差分的计算结果和实轴积分结果基本吻合.地层纵波和后续波均略有偏差,但可以验证数值模拟方法的正确性,作为考察随钻声波测井钻铤波传播规律,精度满足要求.
|
|
表 1 地层、钻铤、泥浆参数和尺寸 Table 1 Formation collar mud parameter and size |
|
图 1 随钻声波测井理论模型 Fig. 1 LWD acoustic theory model |
|
图 2 均勻地层模型三维有限差分(红线)和实轴积分(黑线)计算波形对比 Fig. 2 Waveform comparisons for 3D FDTD (red lines) and RAI (black lines) methods tn isotropic formation model |
随钻声波测井仪器为了消除沿钻铤传播的直达波对地层波测量的干扰,通常在发射声源和接收器之间的钻铤上刻槽,即随钻声波测井的隔声体.本文模拟了随钻声波测井隔声体刻槽前、后钻铤模式波的波形响应特征对比.钻铤内径0.08m, 外径0.174m, 声速参数见表 1,为考察钻铤模式波井外地层用泥浆代替.在钻铤外壁周期刻环形槽,槽深d1=0.015m, 槽宽L1=0.1 m, 槽间距L2=0.1 m, 槽个数N=10.图 3(a)和(b)分别给出了钻铤刻槽前、后钻铤模式波时域波形和对应的频谱图.图中黑线给出发射和接收换能器之间钻铤未刻槽情况的钻铤模式波波形和频谱,红线是刻槽后钻铤波的波形和频谱.可看出未刻槽的钻铤波幅度较大,刻槽后的钻铤波幅度与未刻槽相比明显降低.从频谱图中可看出刻槽前钻铤波在13kHz频率附近存在一个频带较窄(12.5~14.5kHz)的振幅很小的阻带,这个阻带为该尺寸钻铤的固有阻带.通过对钻铤刻槽使钻铤模式波幅度明显降低,同时将钻铤波阻带变宽(12.3~16.8kHz),即该刻槽结构基本实现12~17kHz频率范围内的钻铤波完全衰减,其中最大衰减频率为15.7kHz.

|
图 3 钻铤刻槽前、后钻铤模式波波形和频谱 Fig. 3 The waveforms and spectrums of collar mode wave with grooves or without |
杨勇等[24]理论研究表明,随钻声波测井隔声体使某一中心频率附近钻铤波达到最佳衰减效果的刻槽结构是槽宽和槽间距约等于该频率处波长的1/4,即满足以下关系:
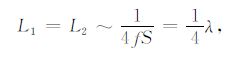
|
(3) |
其中,L1 槽的轴向长度;L2 两个槽之间的距离;f预定的中心频率;S钻铤纵波时差;λ 为波长.本文数值模拟时钻铤纵波速度为5860m/s, 上述刻槽结构的槽宽L1 和槽间距L2 为最大衰减频率处波长的0.268倍,本文结果与文献[24]中的结论一致.
因此,从刻槽后的钻铤模式波的频谱中可以看出,随钻声波测井隔声体设计的关键在于了解给定尺寸钻铤的固有阻带的中心频率和带宽,通过改变刻槽结构来拓宽该阻带,达到仪器设计要求.
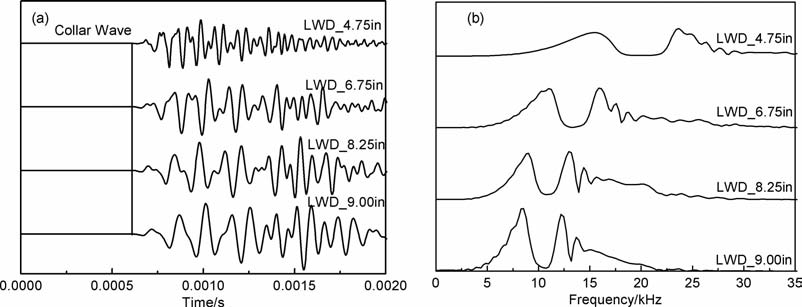
3.1 固有阻带的中心频率、宽度与钻铤尺寸的关系图 4(a, b)分别给出了实际生产中使用的四种不同规格尺寸钻铤(外径4.75in, 6.75in, 8.25in 和9in钻铤,1in=2.54cm, 下同)的钻铤模式波的波形和对应的频谱.从频谱图可看出,不同尺寸钻铤的钻铤波均明显存在一个阻带,且随着钻铤外径变小阻带的中心频率升高,阻带宽度增加.
|
图 4 不同尺寸钻铤的钻铤波波形和对应的频谱 Fig. 4 The waveforms and its spectrum of collar mode wave of different collar sizes |
图 5(a, b)分别给出钻铤模式波固有阻带中心频率和阻带宽度与钻铤尺寸的关系.图 5a横坐标是钻铤内径和外径之和(d1+d2),单位英寸,纵坐标是钻铤模式波固有阻带的中心频率fc, 图中方块为固有阻带的中心频率,图中实线为固有阻带中心频率的拟合曲线.图 5b横坐标是钻铤内径和外径之和,单位英寸,纵坐标是钻铤模式波固有阻带的宽度Δf,图中方块为固有阻带的宽度,实线为拟合曲线.

|
图 5 钻铤模式波固有阻带的中心频率和宽度与钻铤尺寸的关系 Fig. 5 The relationship between the center frequency and band width of the colkr mode wave inherent stopband and the collar sizes |
从图中可看出,四种常用尺寸钻铤的拟合结果很好,清楚地反映出外径4.75in、6.75in、8.25in 和9in四种常用尺寸钻铤的钻铤模式波固有阻带的中心频率fc 和宽度Δf与钻铤内、外径或壁厚的关系,具体关系为:
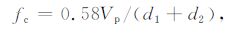
|
(4) |

|
(5) |
其中Vp-钻铤纵波速度,单位为m/s;d1 -钻铤内径,单位为英寸;d2 -钻铤外径,单位为英寸;d1 +d2 -实际上反映钻铤的壁厚.
3.2 钻铤波衰减幅度与刻槽深度的关系图 6a给出了不同刻槽深度隔声体的钻铤波波形.图中黑线为未刻槽的钻铤波波形,蓝线为刻槽深度0.015m 的钻铤波波形,红线为刻槽深度0.02m的钻铤波波形.对比三种情况可看出,刻槽深度增加使钻铤波幅度减小,同时使残余钻铤波的延迟时间增加.图 6b给出了对应的频谱曲线.对比刻槽深、浅的两种情况的频谱发现,刻槽深度增加可使钻铤波阻带频率范围略有加宽.因此,在满足钻铤强度的前提下,适当增加刻槽深度可提高随钻声波测井隔声体的隔声效果.
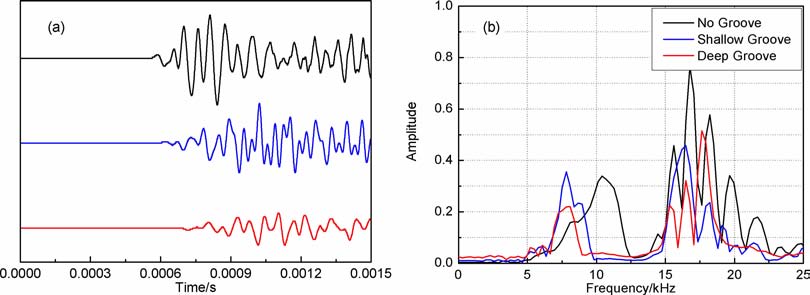
|
图 6 不同刻槽深度钻铤模式波的时域波形和对应频谱图 Fig. 6 The waveforms and spectrums of collar mode wave with different groove depth |
图 7给出了钻铤外壁周期刻槽和内壁周期刻槽的钻铤波频谱对比.图中黑线为未刻槽的钻铤波频d1=0.015m, 槽宽L1=0.1m, 槽间距L2=0.1m, 槽个数N=10)的钻铤波频谱.从图中可看出,同样的刻槽尺寸下,在钻铤外壁周期刻槽主要衰减较高频率成分的二阶钻铤模式波,而钻铤内壁周期刻槽主要衰减低频成分的一阶钻铤模式波.因此,在实际随钻声波测井隔声体设计时,可考虑在钻铤内、外壁同时周期刻槽到达最佳隔声效果.
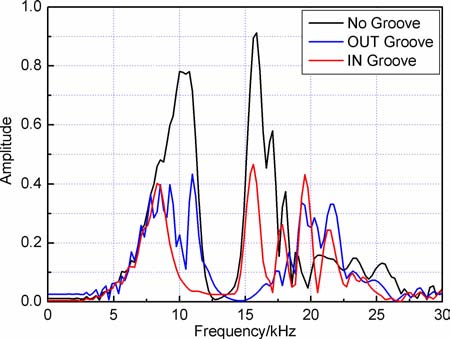
|
图 7 钻铤内、外壁刻槽钻铤波频谱对比 Fig. 7 The spectrums of collar mode wave with in groove and out groove |
随钻测井在非常恶劣的环境(扭曲、撞击和震动等)下工作,仪器的主体结构必须具有很高的机械强度.随钻声波测井刻槽式隔声体是力学薄弱环节,在实际仪器设计时可以考虑在钻铤周向360°铣一系列槽孔来代替周向环形通槽来增加仪器强度,但对隔声效果会有所影响.
图 8a给出了周向间隔15°铣一系列45°槽的有限差分网格图,轴向相邻两个槽交错排列,如图上、下所示.图 8b给出了数值模拟的两种刻槽结构钻铤波对比图,作为对比上图给出隔声体近端未刻槽接收的波形,中间图为经过周向刻环形槽后的钻铤波波形,下图为经过轴向交错排列周向45°铣槽后的钻铤波波形.对比两种刻槽结构的钻铤波可看出,周向45°铣槽隔声体对钻铤波的衰减要比周向环形槽隔声体小,但是在幅度上差别并不大.因此,在满足钻铤机械强度和隔声效果的前提下,实际随钻声波测井隔声体设计可以利用较深的交错排列铣槽代替周向环槽结构.
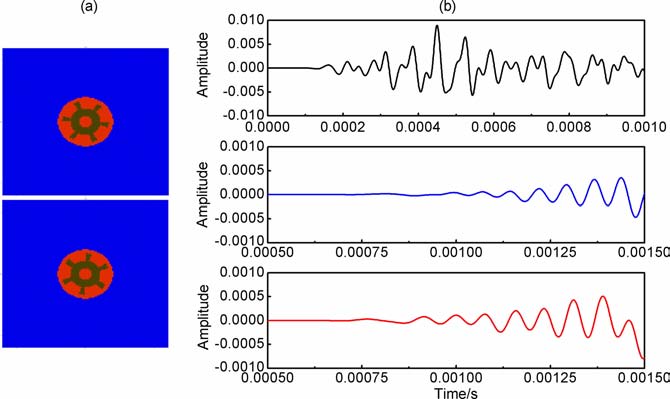
|
图 8 周向环形通槽与周向45°铣槽的钻铤波波形对比 Fig. 8 The comparison of colar wave from circle grooves and grooves with 45 degrees interval |
基于上述钻铤模式波传播规律与刻槽结构关系的理论研究,本文设计了一种钻铤规格8.25in随钻声波测井隔声体,如图 9 所示.钻铤外径8.25in, 隔声体部分水眼内径4in.刻槽的隔声体部分长度2.2m, 发射声源和接收换能器安装在钻铤外壁的0.01m 深度的凹槽内,钻铤两端安装发射和接收电子线路部分的内径5.5in.隔声体部分主要包含三组刻槽结构,一组刻槽为钻铤外壁轴向360°车通槽,槽宽0.03 m, 槽深0.02 m, 槽间距0.155m, 共10个;另一组为钻铤外壁相差30°交错排列的45°铣槽,如8a所示结构,槽宽0.025m, 槽深0.03m, 槽间距0.155 m;第一和二组槽的间距为0.09 m;第三组为钻铤内壁轴向360°车通槽,如图中隔声体内壁,槽宽0.01m, 槽深0.015m, 槽间距0.155m.

|
图 9 随钻声波测井隔声体结构示意图 Fig. 9 The schematic diagram of LWD acoustic isolator |
图 10分别给出了三维有限差分数值模拟的隔声体在刻槽前、后的阵列时域波形、频谱及其计算的相对声衰减曲线,数值模拟时选用主频11kHz的宽带Ricker子波声源函数.图 10a给出隔声体刻槽前、后的波形,源距3.05 m, 接收间距0.2 m, 黑线为刻槽前的波形,红线刻槽后的波形,可看出声波经过刻槽的隔声体部分幅度明显衰减;图 10b给出了对应的频谱.从未刻槽的钻铤波频谱可看出,外径8.25in的标准钻铤的钻铤波固有阻带的中心频率在10kHz左右,带宽约2kHz;刻槽后的新型隔声体的钻铤波阻带频率范围拓宽到7.5~15kHz.图 10c给出了刻槽后的钻铤波相对于未刻槽情况的相对声衰减曲线,横坐标为频率,纵坐标为相对声衰减.可看出在阻带频率范围内的相对声衰减约-10dB,计算公式参考文献[30],在固有阻带中心频率10kHz频率附近声衰减值增大是因为在该频段刻槽前后的钻铤波幅度本身很小导致的.该尺寸钻铤的内径变化(水眼部分内径4in, 电路部分内径5.5in)导致的钻铤波衰减约-10dB,因此,本文设计的新型隔声体在7.5~15kHz频率范围内的声衰减在-20dB以上.

|
图 10 新型8.25in随钻声波测井隔声体数值模拟波形、频谱和相对声衰减曲线 Fig. 10 The simulation waveforms, its spectrum and relative acoustic attenuation curve by new 8.25 in LWD acoustic isolator |
根据刻槽前、后钻铤波的首波到达时间可以计算得到,隔声效果差时一阶模式钻铤波对地层纵波速度为4500m/s的地层干扰较大,隔声体效果好时二阶模式钻铤波对地层纵波速度为2570 m/s的地层干扰较大.本文选取两种典型的软、硬地层模拟井孔中的响应波形,地层、井孔参数如表 1所示.
根据刻槽后隔声体的频谱和衰减曲线,本文数值模拟时选用主频11kHz, 频带7.0kHz~15kHz的高斯声源函数,该声源的频率落在隔声体最佳衰减的阻带范围内.图 11给出数值模拟的声源函数和对应的频谱曲线,图中黑线为声源时域波形,蓝线为对应的声源频谱曲线.
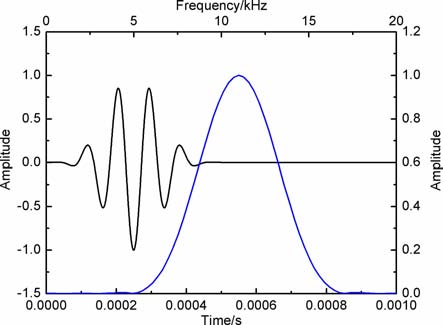
|
图 11 随钻声波测井井孔响应模拟的声源波形和频谱 Fig. 11 LWD acoustic simulation source waveform and spectrum |
图 12给出了本文隔声体在软地层井孔中单极子声源的模拟波形和对应的时差- 时间相关分析图.图 12a给出了模拟的阵列波形,从波形中可看出,该隔声体的随钻声波测井测量的全波列中只有幅度较大的地层纵波,钻铤波幅度非常小.波形幅度放大50倍后,如图下部的波形,可看到残余的钻铤波,地层波信号与干扰的钻铤波信号的信噪比非常高.图 12b给出了对理论模拟波形的时差-时间相关分析图,图中横坐标为时间,纵坐标为时差(速度的倒数),颜色代表相关系数.可看出在时差-时间相关系数图上存在两个极大值,分别对应钻铤波时差和地层纵波时差,即钻铤波的速度为4976 m/s, 地层纵波速度为2490m/s.用本文设计隔声体的随钻声波测井在软地层测量的地层纵波速度与理论值非常接近.
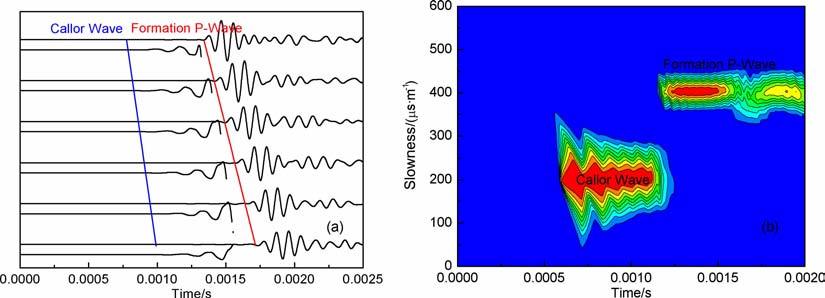
|
图 12 软地层理论模拟波形和时差一时间相关分析图 Fig. 12 Theoretical simulation waveforms in soft formation and Slowness-Time Coherence analysis |
图 13给出了本文隔声体在硬地层井孔中单极子声源的模拟波形和对应的时差-时间相关分析图.图 13a给出了模拟的阵列波形,从波形中可看出,硬地层中测量的全波列中幅度最大的是地层横波,与之相比地层纵波幅度非常弱.波形幅度放大12.5倍后,如图中下部的波形,可以看到清晰的地层纵波波形,残余的钻铤波幅度非常小,有效的地层波纵波信号与干扰的钻铤波信号的信噪比也很高.图 13b给出了对理论模拟波形的时差-时间相关分析图.可看出在时差-时间相关系数图上存在两个明显的极大值,分别对应地层横波时差和地层纵波时差,即地层纵波的速度为4018m/s, 地层横波速度为2472m/s.从图中也可看出在纵波相关系数极大值附近也存在钻铤波的相关系数极大值,但相关系数较小.用本文设计隔声体的随钻声波测井在硬地层测量的地层纵波速度和地层横波速度与理论值非常接近.
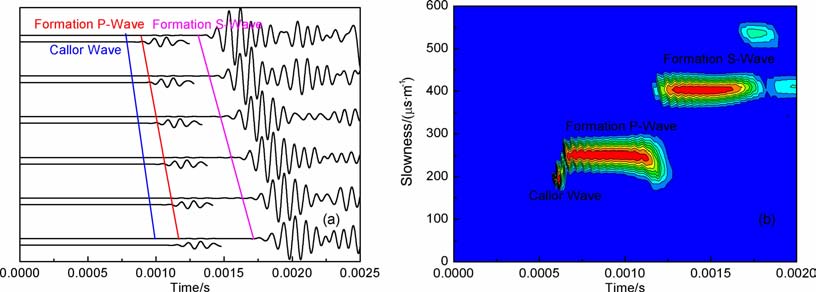
|
图 13 硬地层理论模拟波形和时差一时间相关分析图 Fig. 13 Theoretical simulation waveforms in fast formation and Slowness-Time Coherence analysis |
因此,本文在理论研究的基础上设计的随钻声波测井隔声体在典型软、硬地层均能测量到高质量的地层纵波.对比两种地层情况发现,随钻声波测量在软地层测量的全波列中地层纵波幅度最大,地层纵波与钻铤波的信噪比高;硬地层中测量的全波列地层横波幅度非常大,实际应用时要注意地层横波对纵波的干扰.
4.3 现场实验井的隔声效果测试基于本文隔声体结构的随钻声波测井仪器样机在某油田实验井中进行了隔声效果现场测试,测试井段为2000~2100m, 该井段地层纵波速度5000m/s左右,属于硬地层.实验过程中是用电缆吊着随钻声波实验样机在目的层进行测试,发射声源采用主频13kHz的3个周期正弦波激励,随着电缆匀速缓慢上提,等时间间隔存储测量的全波列.图 14 给出了随钻声波测井仪器样机在实验井中的现场测试结果.图中第1道给出了测量的随钻单极子声波变密度波形和地层纵波到时曲线;第2 道给出对应的时差相关系数图;第3 道给出测量的地层纵波时差曲线.从测量的变密度波形和相关系数图中可看出,本文设计的随钻声波测井隔声体在硬地层实验井中,没有钻井噪声且仪器居中的情况下有效地消除了钻铤直达波的干扰,测量到了高质量的地层纵波波形和时差.

|
图 14 随钻声波测井仪器样机在实验井中的现场测试结果 Fig. 14 Field experiment hole test results of LWD acoustic logging tool |
本文利用三维有限差分程序模拟了钻铤刻槽前、后的随钻声波测井钻铤模式波响应特征,分析了钻铤模式波的衰减规律,在此基础上设计了随钻声波测井隔声体结构,并得到现场实验井测试数据的验证,从中得出以下认识与结论:
(1) 均匀钻铤的钻铤模式波存在一个频带较窄的固有阻带,通过钻铤刻槽可拓宽该阻带的频率范围.
(2) 钻铤波固有阻带的中心频率随着钻铤尺寸(钻铤内、外径之和)增加按非线性规律降低,固有阻带的频带宽度随着钻铤尺寸增加按非线性规律减小.
(3) 随钻声波测井隔声体使某一中心频率附近钻铤波达到最佳衰减效果的刻槽结构是槽宽和槽间距约等于该频率处波长的1/4.
(4) 钻铤刻槽深度增加使钻铤波幅度减小、延迟时间增加,同时可使钻铤波阻带频率范围略有加宽.在满足钻铤强度的前提下,适当增加刻槽深度可提高随钻声波测井隔声体的隔声效果.
(5) 数值模拟研究和现场实验井测试结果表明,利用本文设计的隔声体开发的随钻声波测井仪器样机有效地消除了钻铤波直达波干扰,能够测量到高质量的地层纵波波形和时差.
致谢感谢两位匿名审稿专家提出的宝贵意见和建设性建议.
| [1] | 唐晓明, 郑传汉. 定量测井声学. 北京: 石油工业出版社, 2004 . Tang X M, Zheng C H. Quantitative acoustic well logging (in Chinese). Beijing: Petroleum Industry Press, 2004 . |
| [2] | 江玉龙, 王祝文, 伍东. 阵列声波处理技术的研究与应用. 地球物理学进展 , 2009, 24(1): 246–253. Jiang Y L, Wang Z W, Wu D. Research and applications of high resolution array acoustic processing techniques. Progress in Geophysics (in Chinese) , 2009, 24(1): 246-253. |
| [3] | 李铭, 李艳华, 楚泽涵. 声频谱测井方法研究进展. 地球物理学进展 , 2003, 18(2): 229–233. Li M, Li Y H, Chu Z H. Research evolution of acoustic spectrum logging methods. Progress in Geophysics (in Chinese) , 2003, 18(2): 229-233. |
| [4] | 张碧星, 王克协. 各向异性介质地层中多极源声波测井的现状与发展. 地球物理学进展 , 1998, 13(2): 1–14. Zhang B X, Wang K X. Status quo and development of the acoustic multipole logging in anisotropic formation. Progress in Geophysics (in Chinese) , 1998, 13(2): 1-14. |
| [5] | 高坤, 陶果, 马勇. 多极子阵列声波测井资料在塔河油田酸压设计施工中的应用. 地球物理学进展 , 2006, 21(4): 1227–1231. Gao K, Tao G, Ma Y. Application of multipole array sonic logging to acid hydralic fracuring. Progress in Geophysics (in Chinese) , 2006, 21(4): 1227-1231. |
| [6] | Joyce B, Patterson D, Leggett J, et al. Introduction of a new omni-directional acoustic system for improved real-time LWD sonic logging-tool design and field test results. SPWLA 42th Annual Logging Symposium, 2001, paper SS |
| [7] | 张辛耘, 郭彦军, 王敬农. 随钻测井的昨天、今天和明天. 测井技术 , 2006, 30(6): 487–492. Zhang X Y, Guo Y J, Wang J N. The logging while drilling: past, present and future. Well Logging Technology (in Chinese) , 2006, 30(6): 487-492. |
| [8] | Alford J, Goobie R B, Sayers C M, et al. A sound approach to drilling. Oilfield Review , 2006(4): 68-78. |
| [9] | Sinha B K, Plona T J, Kostek S, et al. Axisymmetric wave propagation in fluid-loaded cylindrical shells: I-Theory. J. Acoust. Soc. Am. , 1992, 92(2): 1132-1143. DOI:10.1121/1.404040 |
| [10] | Plona T J, Sinha B K, Kostek S, et al. Axisymmetric wave propagation in fluid-loaded cylindrical shells: II-Theory versus experiment. J. Acoust. Soc. Am. , 1992, 92(2): 1144-1155. DOI:10.1121/1.404041 |
| [11] | Rama Rao V N, Vandiver J K. Acoustics of fluid-filled boreholes with pipe: Guided propagation and radiation. J. Acoust. Soc. Am. , 1999, 105(6): 3057-3066. DOI:10.1121/1.424635 |
| [12] | Liu Q H, Daube F, Randall C, et al. A three-dimensional finite-difference simulation of sonic logging. J. Acoust. Soc. Am. , 1996, 100(1): 72-79. DOI:10.1121/1.415869 |
| [13] | Cheng N Y, Cheng C H, Toksoz M N. Borehole wave propagation in three dimensions. J. Acoust. Soc. Am. , 1995, 97(6): 3483-3493. DOI:10.1121/1.412996 |
| [14] | Wang T, Tang X M. Finite-difference modeling of elastic wave propagation: A nonsplitting perfectly matched layer approach. Geophysics , 2003, 68(5): 1749-1755. DOI:10.1190/1.1620648 |
| [15] | 杨慧珠, 张友生, 陶果. 井眼条件下弹性波传播问题的三维有限差分数值模拟. 地球物理学进展 , 2003, 18(2): 348–352. Yang H Z, Zhang Y S, Tao G. Three dimensional finite difference numerical simulation of elastic wave propagation under borehole conditions. Progress in Geophysics (in Chinese) , 2003, 18(2): 348-352. |
| [16] | 林伟军, 王秀明, 张海澜. 倾斜地层中的井孔声场研究. 地球物理学报 , 2006, 49(1): 284–294. Lin W J, Wang X M, Zhang H L. Acoustic wave propagetion in a borehole penetrating an inclined layered formation. Chinese J. Geophys. (in Chinese) , 2006, 49(1): 284-294. |
| [17] | 何峰江, 陶果, 王锡莉. 贴井壁声波测井仪的有限差分模拟研究. 地球物理学报 , 2006, 49(3): 923–928. He F J, Tao G, Wang X L. Finite difference modeling of the acoustic field by sidewall logging devices. Chinese J. Geophys. (in Chinese) , 2006, 49(3): 923-928. |
| [18] | 王秀明, 张海澜, 王东. 利用高阶交错网格有限差分法模拟地震波在非均匀孔隙介质中的传播. 地球物理学报 , 2003, 46(6): 842–849. Wang X M, Zhang H L, Wang D. Modelling of seismic wave propagetion in heterogeneous poroelastic media using a high-order staggered finite-difference-method. Chinese J. Geophys. (in Chinese) , 2003, 46(6): 842-849. |
| [19] | 赵海波, 王秀明, 王东, 等. 完全匹配层吸收边界在孔隙介质弹性波模拟中的应用. 地球物理学报 , 2007, 50(2): 581–591. Zhao H B, Wang X M, Wang D, et al. Applications of the boundary absorption using a perfectly matched layer for elastic wave simulation in poroelastic media. Chinese J. Geophys. (in Chinese) , 2007, 50(2): 581-591. |
| [20] | 乔文孝, 车小花, 鞠晓东, 等. 声波测井相控圆弧阵及其辐射指向性. 地球物理学报 , 2008, 51(3): 939–946. Qiao W X, Che X H, Ju X D, et al. Acoustic logging phased arc array and its radiation directivity. Chinese J. Geophys. (in Chinese) , 2008, 51(3): 939-946. |
| [21] | He X, Hu H S, Guan W. Fast and slow flexural waves in a deviated borehole in homogeneous and layered anisotropic formations. Geophys. J. Int. , 2010, 181(1): 417-426. DOI:10.1111/gji.2010.181.issue-1 |
| [22] | 宋若龙, 刘金霞, 姚桂锦, 等. 非轴对称套管井中声场的并行有限差分模拟. 地球物理学报 , 2010, 53(11): 2767–2775. Song R L, Liu J X, Yao G J, et al. Parallel finite difference modeling of acoustic fields in nonaxisymmetric cased hole. Chinese J. Geophys. (in Chinese) , 2010, 53(11): 2767-2775. |
| [23] | 闫向宏, 苏远大, 孙建孟, 等. 周期性轴对称凹槽结构隔声特性数值模拟. 计算物理 , 2010, 27(6): 869–876. Yan X H, Su Y D, Sun J M, et al. Acoustic Characteristics of Axisymmetric Periodic Groove Structures. Chinese Journal of Computational Physics (in Chinese) , 2010, 27(6): 869-876. |
| [24] | 杨勇, 车小花, 李俊, 等. 基于时域有限差分法的随钻声波测井仪隔声体隔声效果的数值模拟. 中国石油大学学报 (自然科学版) , 2009, 33(3): 66–70. Yang Y, Che X H, Li J, et al. Sound isolation numercial simulation on isolator of logging while drilling sonic tool using finite difference time-domain method. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese) , 2009, 33(3): 66-70. |
| [25] | 王华, 陶果, 王兵, 等. 多极子随钻声波测井波场模拟与采集模式分析. 地球物理学报 , 2009, 52(9): 2402–2409. Wang H, Tao G, Wang B, et al. Wave field simulation and data acquisition scheme analysis for LWD acoustic tool. Chinese J. Geophys. (in Chinese) , 2009, 52(9): 2402-2409. |
| [26] | Leggett J V III, Dubinsky V, Petterson D, et al. Field test results demonstrating improved real-time data quality in an advanced LWD acoustic system. SPE Annual Conference and Exhibition, 2001, paper 71732 |
| [27] | Tang X M, Dubinsky V, Harrison C W, et al. Logging-While-Drilling shear and compressional measurements: case histories. SPWLA 44th Annual Logging Symposium Transactions, 2003, paper II |
| [28] | Tang X M, Lilly D, Petpisit K. Analysis of LWD acoustic data validates its accuracy. SPWLA 48th Annual Logging Symposium Transactions, 2007, paper B |
| [29] | Kinoshita T, Dumont A, Hori H, et al. LWD sonic tool design for high-quality logs. 80th Ann. Internat. Mtg., Soc. Explor. Geophys., Expanded Abstracts, 2010. 513~516 |
| [30] | 乔文孝, 陈雪莲, 杜光升, 等. 隔声体性能评价的方法研究. 测井技术 , 2002, 26(2): 104–106. Qiao W W, Chen X L, Du G S, et al. On Performance Evaluation of a Sound Isolator. Well Logging Technology (in Chinese) , 2002, 26(2): 104-106. |
 2011, Vol. 54
2011, Vol. 54