2. 中国科学院研究生院,北京 100049
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China
复杂地表条件地区地震资料的采集和处理效果在很大程度上取决于地形起伏、地面地质风化、地表岩性变化和表层地质结构的复杂程度.其中,地形起伏和表层地质结构导致严重的静校正问题,同时还引起强散射噪音,常常干涉并掩盖来自深层的有效地震反射信号,严重降低地震资料的信噪比;地面地质风化和非均匀地表岩性变化波散化近地表散射波和深部反射信号,波形破碎带严重,半随机半相干的近地表散射噪音弥漫整个剖面.因此,精确模拟复杂近地表条件下地震波场特征和传播的规律对复杂地区地震资料采集、处理和解释具有重要的理论价值和实际意义.
对勘探地震而言,复杂近地表主要由两种介质构成.第一种是边界介质,包括起伏地形和表层地质结构,往往具有很强的速度反差,导致强边界散射(反射),形成炮集上的主要能量分布;第二种是体积介质,包括地表下的非均匀低降速带介质和近地表结构内部的非均匀介质,形成体散射(反射)波,干涉和波散化边界反射波,导致波形破碎和衰减.精确模拟这两种介质构成对地震波传播的影响是本文的研究内容.复杂近地表地震波传播数值模拟常用的有限差分法、伪谱法和有限元法[1],将边界散射和体散射融为一体进行模拟.有限差分法和伪谱法中自由表面需要过于精细的网格化处理[2].自由表面坐标变换的伪谱法模拟[3, 4]和有限差分法模拟[5]稳定性受到地形起伏程度的制约.有限元方法可以通过复杂的几何关系和任意大小的单元对起伏自由边界做灵活的处理[6].另外,上述常用模拟方法的共同特点是通过网格化隐式地使用边界连续条件,对不规则界面上波的反射/透射进行全数值模拟时难以达到足够高的精度,也难以分离来自不同类型介质的波场.
精确描述起伏地形、显式应用边界连续条件的起伏地表数值模拟方法得到了广泛的研究,包括离散波数边界积分方程法[7, 8]、边界积分方程广义反射/透射矩阵方法[9, 10]、直接边界元地震模拟方法[11, 12]、间接边界元地震模拟方法[13, 14].这些边界离散方法在几何上精确描述起伏地形和近地表构造的不规则边界,能够精确模拟复杂近地表中的边界介质;显式应用近地表地层界面的连续边界条件,实现半解析的地震波数值模拟;分区处理近地表复杂结构,可分别模拟来自复杂近地表不同部位的波.但这些只对近地表结构边界进行离散的方法不能模拟体积介质,即地表下的非均匀低降速带和近地表结构内部非均匀介质.边界元、有限差分和有限元混合方法[15]可以模拟复杂近地表边界+体积介质模型,但存在三种方法之间的数值衔接问题.
本文将复杂近地表中边界介质与体积介质分离,分别模拟地震波在复杂近地表中传播的边界散射和体散射,这需要考虑复杂近地表中边界-体积之间的相互耦合作用.Fu等[16]提出了一种求解Lipmann- Schwinger波动积分方程的体积元数值方法,可以精确模拟非均匀体积介质产生的强散射波.通过将边界积分方程与Lipmann-Schwinger体积分方程相结合,本文研究一种模拟复杂近地表地震波传播的边界元-体积元波动方程数值模拟方法.其中,导致强边界散射(反射)的起伏地形和表层地质结构等边界介质用边界元地震模拟方法;而产生体散射(反射)波的地表下非均匀低降速带介质和近地表结构内部的非均匀介质用体积元法模拟.在边界元-体积元数值模拟方法中,与体积分有关的散射项采用了高精度的高斯积分数值计算方法,确保对随机强非均匀体介质散射的地震模拟精度.这种方法除了具有上述边界元地震模拟方法的优点外,还能够模拟带起伏地表的分区非均匀地质结构,有效模拟复杂地表下非均匀介质对地震波场的体散射.通过几种不同复杂地表模型的数值模拟计算,本文研究了复杂近地表条件对地震波传播的影响.
2 方法原理与基本方程广义Lipmann-Schwinger积分方程由边界波动积分方程与Lipmann-Schwinger体积分方程两部分构成,描述地震波在分区非均匀介质(一种具有不规则边界、内部为随机非均匀介质的多层结构)中的传播.该方程的解由源波场、边界散射波场和体散射波场三项构成.图 1所示为起伏地形及近地表非均质低降速层,该散射介质模型Ω 由起伏的自由表面Γ0、不规则的底界面Γ1 和人工截断边界Γ∞ 形成闭合区域,即Γ=Γ0+Γ1+Γ∞ ,背景速度为v0,内部速度异常分布为v(r).假设震源位于r0 处,震源项在频率域可表示为:
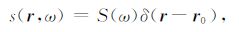
|
(1) |
式中S(ω)为震源谱,δ(r-r0)为脉冲函数.

|
图 1 起伏地形及其下非均质低降速层构成的散射介质模型 Fig. 1 Geometry of a scattering medium in the homogeneous free space |
该散射介质中地震波的传播满足如下的Helmholtz稳态标量波动方程:
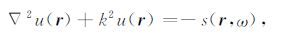
|
(2) |
式中k=ω/v(r)为波数.地震波场u(r)可表示为入射波场u0(r)、边界散射u1s(r)和体积散射u2s(r)三项之和,即
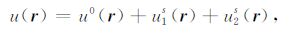
|
(3) |
其中第一项u0(r)为背景介质中的入射波场,考虑点源激发,则u0(r)可表示为
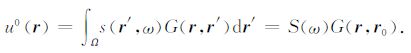
|
(4) |
第二项u1s(r)为起伏地形及近地表结构中的不规则边界贡献的边界散射波场,满足如下均匀背景介质中的边界积分方程:
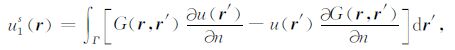
|
(5) |
式中,∂/∂n为边界法向导数.第三项u2s(r)为非均质低降速层产生的体散射波场,满足如下的Lipmann- Schwinger体积分方程:
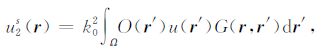
|
(6) |
式中k0 =ω/v0 为背景波数,O(r′)=v02/v2(r′)-1为速度扰动,O(r′)=0时则退化成均匀背景介质.G(r,r′)为背景介质中的格林函数,对于二维介质,G(r,r′)=iH0(1) (k0|r-r′|)/4,其中H0(1) 为汉克尔函数;对于三维介质,G(r,r′)=eik0|r-r′|/(4π|r-r′|).
将式(4)~(6)代入方程(3),即可得到广义 Lipmann-Schwinger积分方程:
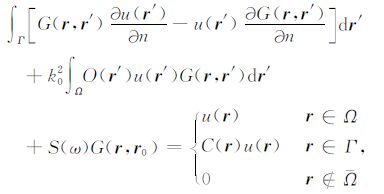
|
(7) |
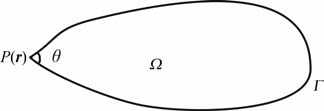
式中Ω=Ω +Γ,C(r)=$\frac{\theta }{2\pi }$,θ为角点P(r)对区域Ω 的张角(如图 2所示).
|
图 2 角点P(r)及对应的张角 Fig. 2 Angular point P(r) and its angle |
广义Lippmann-Schwinger 积分方程(7)是边界元-体积元地震模拟方法的核心方程,属于第二类 Fredholm 积分方程.根据Fredholm 积分方程理论,数学上可以证明,在Neumann 和Dirichlet边界条件下,上式对于内边值问题(r′,r0 ∈Ω),其解存在,且惟一.由于格林函数在r→r′ 时出现奇异积分,虽然数学上该奇异点为可去奇点[16],但为了确保数值计算的稳定性,需要进行奇异积分处理,可采用格林函数的离散波数展开[7]或奇异积分在奇异点展开的解析处理方法[12].广义Lippmann-Schwinger 积分方程自然满足无穷远处边界条件,即位移场,由于基本解为Hankel函数或eikr/r的形式,而在无穷远处趋于0.对于模型两端的人工截断,可采用无限元法处理人工截断边界的吸收问题[17].
3 积分方程的数值离散广义Lippmann-Schwinger 积分方程中,震源项u0(r)为已知,由计算频率和源点r0 确定,u1s(r)和u2s(r)分别为散射体边界和内部各点上的未知量.积分方程离散常用的方法为配置法,以二维问题为例,首先把边界Γ 划分为L个互不重叠的线性单元Γe(e=1,2,…,L),域Ω 剖分为M个三角形或四边形单元Ωe(e=1,2,…,M).假定边界加上内部共有N个节点,并统一节点号.对于各个变量(r,u,∂u/∂n)在单元内任意点的值,利用插值型函数Φ ,可以近似地表示成相邻节点I1 至I2 的线性和,例如位移函数可表示为:
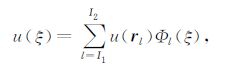
|
(8) |
式中ξ 为一个单元的局部坐标.这样,方程(7)中的各项积分可写为:
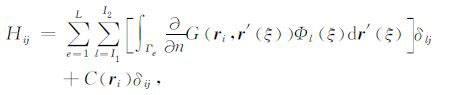
|
(9) |
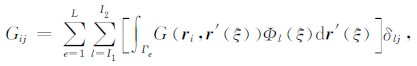
|
(10) |

|
(11) |
其中,δlj和δij为Kronecker脉冲函数.上述离散单元积分可利用高精度的高斯积分数值算法计算.方程(7)可改写为算子的形式:
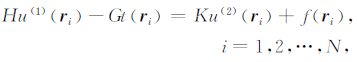
|
(12) |
其中,u(1) 为边界Γ 上的地震响应,t为u(1) 的法向导数,u(2) 为Ω 域内的地震响应,f为入射波场,H、G为边界积分算子,K为体积分算子.
对于如图 1所示表层含有非均匀介质的复杂近地表结构,设Γ0 的离散点数为N0,不规则底界面Γ1 的离散点数为N1,非均质区域Γ 内的离散点数为NP.对于自由边界Γ0 上的离散点,由自由边界条件可知t(r)=0.设定地层边界Γ1 上面介质的密度为ρ0,速度为v0,下面介质的密度为ρ1,速度为v1.根据边界连续条件,边界Γ1 上面与下面的位移、应力连续,即u+ (r)=u- (r),μ1u+ (r)= -μ0u- (r).其中μ0 =ρ0v02,μ1 =ρ1v12.利用方程(12),对所有节点建立联立方程组,得到如下总体矩阵方程组:

|
(13) |
式中左边的各个子矩阵分别为利用公式(9)、(10)、(11)计算得到的边界Γ0 上的各个离散点和边界Γ1上的各个离散点以及非均质区域内的各个散射点的相互作用积分算子矩阵;式中右边的各个子向量分别为利用公式(4)计算得到的点源激发对边界和边界Γ1 上的各个离散点以及非均质区域内的各个散射点的作用产生的震源项向量.
例如H00为利用公式(9)计算得到的边界Γ0 上的各个离散点对其上的其他离散点的相互作用积分算子矩阵,即
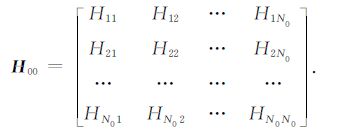
|
(14) |
F0 为利用公式(4)计算得到的点源激发入射到边界Γ0 上的各个离散点作用而产生的震源项向量,即

|
(15) |
求解公式(13)的总体系数矩阵,就可以得到公式(13)左边未知数向量对应的边界和内部各点的波场值.对于多层结构的复杂近地表结构,需要对各层计算的系数矩阵H,G,K按照应力和位移边界连续条件进行总体系数矩阵组装,最后求解总体系数矩阵方程,得到所有层边界和内部各点的波场值.
方程(13)包含了穿过整个模型的地震波的信息.对方程(13)进行求解,回代入公式(7)就可求得任一接收点处的地震响应波场值,这个值是在频率域给出的.设接收点的个数为NR,则接收点单个频率的波场值向量UR 可由下面的公式给出:
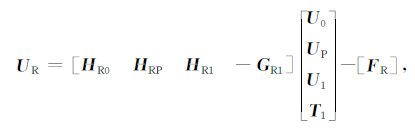
|
(16) |
式中HR0、HRP、HR1、GR1 分别为利用公式(9)、(10)、(11)计算得到的各个接收点与自由边界Γ0 上的各个离散点和边界Γ1 上的各个离散点以及非均质区域内的各个散射点的相互作用积分算子矩阵.公式(16)中去掉[FR]项就可以得到没有直达波的波场.通过对接收点的不同频率的波场值进行逆FFT 变换,即可得到所要的合成地震记录.
利用边界-体积分波动方程进行复杂地表地震数值模拟的具体步骤为:
(1) 针对具体模型,建立包含震源项的边界-体积分方程.
(2) 选用不同的离散单元与形函数,对边界积分方程进行边界元离散,用配置法对体积分方程进行离散.
(3) 对由(2)式得到的单元系数矩阵组装成总体系数矩阵.
(4) 求解总体系数矩阵并回代入对应的边界-体积分方程,得到频率域的波场值.
(5) 对不同频率的波场值进行逆FFT,变换到时间域,得到接收点处的合成地震记录.
在实际的计算过程中,由于地震勘探中震源位于近地表且仅需要计算自由表面的地震响应,根据这些特点,采用由深至浅逐层进行式(13)中的系数矩阵H、G和K的数值计算、组装和消元,消去两个相邻子域公共边界上的耦合数据,如此计算直到地表层,得到最后的矩阵方程,其维数仅由地表层的节点数确定.此矩阵隐含着穿过整个模型的地震波的信息.将此矩阵与地表多测线多震源相结合,可计算出地表任意处的观测波场.为提高算法的效率,我们采用了改进的分块高斯消去法来求解矩阵方程.在整个计算过程中,全局系数矩阵需要的最大内存限于最大一个子域的总节点数.这样既节省了内存又缩短了计算时间.
4 数值解与解析解的对比分析本文对如图 3所示的半圆峡谷和沉积谷地两个半空间模型进行了数值解与解析解的比较.由于这两个模型形态在自然界中的普遍性,常常被作为两个经典例子来研究局部地形和不规则近地表结构对地震波传播的影响.两个模型的半径均为a,半空间背景介质的SH-波速度为β,密度为ρ,由于模型的对称性,其SH-波入射的解析解[18, 19]可表示为Bessel函数的线性和.模型两端(x=±a)90°的拐角点是测试各种地震数值模拟方法和算法精度的最佳靶点.

|
图 3 半圆峡谷模型(a)和均匀沉积谷模型(b)及SH 波入射示意图 Fig. 3 Geometry of semicircular canyon topography model (a) and semicircular valley with homogeneous medium model (b) with incident SH waves |
定义无量纲化频率η 为半圆峡谷或沉积谷直径与入射波长的比值,即
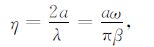
|
(17) |
式中,λ 为入射波波长.在半径a不变的情况下,η越小,表示入射波的频率越小,反之亦然.
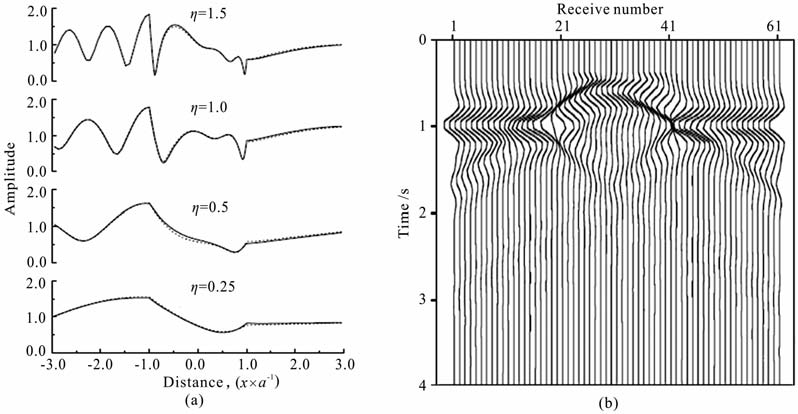
图 4为半圆峡谷模型的地震响应,图 4a为60° SH-波入射地表各点对不同η 值的振幅响应.可见地形的突变会引起地震波响应的巨大变化,数值解(虚线)与解析解(实线)之间吻合很好,微小的误差源于半圆弧的单元逼近误差.图 4b为SH-波垂直入射地表各点的地震合成记录,震源为Ricker 子波,计算频率为0~4Hz, 可见半圆地形两端垂直拐角处波场的强烈干涉作用.
|
图 4 半圆峡谷模型的地震响应 (a)SH 波45°入射地表各点对不同η 值的振幅响应(实线为解析解,虚线为数值解);(b)SH-波垂直入射地表各点的地震合成记录. Fig. 4 The seismic responses of the semicircular canyon topography model (a) The amplitude response for various n with 45° incident harmonic plane wave(solid lines denote the exact solutions and the dots denote numeric results) ; (b) Synthetic seismograms with 0° incident harmonic plane wave. |
在均匀沉积谷模型中,假定谷内介质SH-波速度β和密度为ρ 满足:ρ/ρ=1.5和β/β=2,图 5a为 SH-波垂直入射地表各点对不同η 值的振幅响应,数值解(虚线)与解析解(实线)基本一致,说明方法的正确性.图 5b为SH-波垂直入射地表各点的地震合成记录,震源为Ricker子波,计算频率为0~4Hz, 半圆谷底的反射和两端垂直拐角点散射波清晰可见.

|
图 5 SH-波垂直入射均匀沉积谷模型的地震响应 (a)地表各点对不同η 值的振幅响应(实线为解析解,虚线为数值解);(b)地表各点的地震合成记录. Fig. 5 The seismic responses of the semicircular valley model with 0° incident harmonic plane wave (a) The amplitude response for various n (solid lines denote the exact solutions and the dots denote numeric results) ; (b)Synthetic seismograms. |
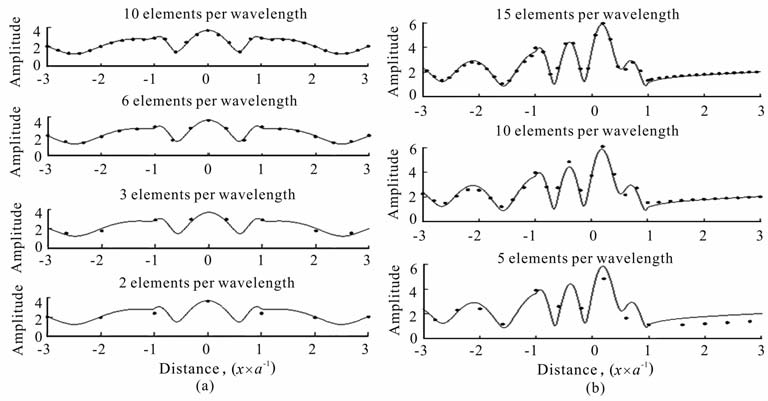
离散单元的尺寸大小是影响数值模拟精度和效率的主要因素,下面以沉积谷模型为例分析离散单元长度的选择.采用不同离散单元长度对均匀沉积谷模型进行数值模拟,取η = 1 时地表各点的地震振幅响应曲线如图 6a所示,实线为解析解,虚线为数值解.可见,在SH-波垂直入射情况下,每个波长用两个离散单元的结果与解析解在半圆的垂直拐角处稍有偏差,用三个离散单元就能达到很好吻合.增大入射角度,地面地震波振幅响应变化剧烈,图 6b模拟结果表明每个波长需要用五个离散单元才能达到与解析解较好的吻合.时间域的合成地震记录对离散单元长度的变化相对于上述频率域的振幅响应而言显示不敏感,因此,合成地震记录对离散单元尺寸的要求要弱些,通过大量的地震数值模拟表明,每个波长用三个离散单元基本上能满足实际需要.
|
图 6 SH-波入射沉积谷模型(垂直入射(a),60°入射(b))对不同离散单元长度进行数值模拟得到的η =1时地表各点的地震振幅响应(实线为解析解,虚线为数值解) Fig. 6 The seismic responses of the semicircular valley model (0° incident SH wave (a) and 60° incident SH wave(b) with the dimensionless frequencies η=1 for various sampling rates (the solid lines denote the exact solutions and the dots denote numeric results) |
我们用边界元-体积元法模拟沉积谷中填充随机非均匀介质的地震响应频率响应.图 7 为非均匀沉积谷模型,谷内随机非均匀介质由三个参数确定: SH-波平均速度β、平均密度ρ 和速度扰动量δ.

|
图 7 半空间随机非均质沉积谷模型 Fig. 7 The semicircular valley with random heterogeneous medium model in the half-space with incident SH wave |
对大部分近地表而言,地表下低降速带的速度扰动量变化一般为5%~15%之间.例如,对谷内平均速度β=3000m/s进行δ=10% 的扰动,实际谷内随机速度分布在2700~3300m/s之间.假定谷内介质平均速度β和平均密度为ρ 满足:ρ/ρ=1.5和β/β=2,取速度扰动量δ 为0%、5%、10%和15%,对随机非均质沉积谷模型进行数值模拟,图 8a为 SH-波垂直入射地表各点对η =1 时振幅响应.可见,对于δ>10%后,谷内随机非均匀体积介质对地面地震响应产生较大的影响,波场振幅扰动非常强烈,特别是在半圆两端垂直拐角点的散射波场变化剧烈.图 8b为取δ=10%时,SH-波垂直入射地表各点对不同η 值的振幅响应,可见,谷内随机非均匀体介质对高频地震响应产生更大的影响.

|
图 8 SH-波入射随机非均质沉积谷模型地表各点的地震振幅响应曲线 固定η =1对谷内速度扰动量δ 取不同值时的数值模拟结果(a)和固定δ=10%对不同η 值的数值模拟结果(b). Fig. 8 The seismic responses of the semicircular valley with random heterogeneous medium model (a) The amplitude response with η=1 for various velocity perturbation 8;(b) The amplitude response with 8=10% for various velocity perturbation η |
上述频率域地震振幅响应的对比研究表明,本文的方法对近地表带自由表面的复杂结构进行地震波传播模拟具有很高的模拟精度,对含有地层尖灭、断层、陡峭拐角等复杂地质构造具有很好的适应能力.下面我们用边界元-体积元地震数值模拟方法来模拟地震波在复杂近地表中的传播.
5 数值算例对于实际地震勘探来讲,震源一般放置在自由界面下10~30m, 检波器在自由界面下十几厘米至几十厘米,炮检距一般为30 m~3km.这样的地震数据采集观测设置导致了起伏地表的影响很大程度上与震源和检波器附近的地表几何形状、近地表结构和低降速带介质的非均质性密切相关,特别是近地表散射体尺度与地震主波长相当时会引起较强的散射.
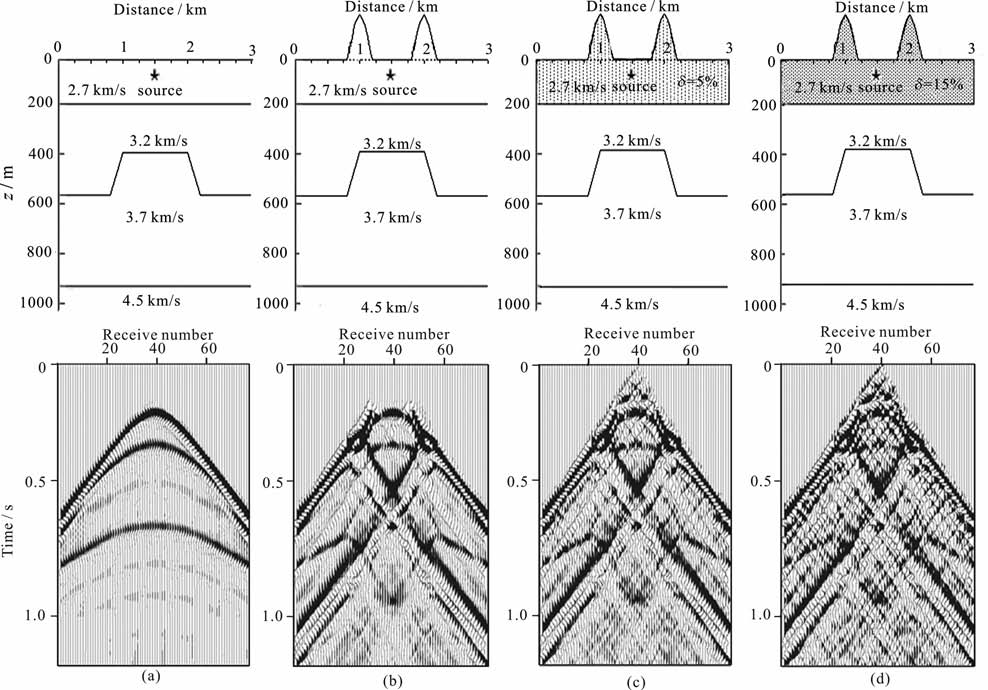
我们首先对简单的、起伏程度不同的复杂近地表模型进行数值模拟,以便直观了解复杂近地表对地震响应的影响模式和影响程度,如图 9所示.地震模拟计算采用Ricker子波,频率范围0~40 Hz, 震源位于自由界面以下20m.为了直观展示起伏地表的散射影响,模拟计算时滤除了直达波.由图可见,平地表合成记录地震反射规则清晰,两个山包形状的地表起伏引起很强的散射波分布,特别是山根下波场干涉严重,但地表散射和地层反射波都具有较好的相干性.相比之下,当近地表层介质为随机非均匀时,非均匀体介质产生的漫散射及其对边界波的干涉使整个记录波散化,波前破碎.增加近地表层随机非均匀介质的速度扰动到δ=15% 时,相干散射波场进一步随机化,变为半随机半相干的散射噪音,弥漫整个剖面,干涉和掩盖地层反射波.
|
图 9 不同复杂程度近地表模型及其对应的地表合成地震炮集记录 (a)平地表匀均介质近地表模型及其地表合成地震炮集记录;(b)起伏地表模型及其地表合成地震炮集记录;(c)起伏地表弱非均质(δ=5%)近地表层模型及其地表合成地震炮集记录;(d)起伏地表强非均质(δ=15%)近地表层模型及其地表合成地震炮集记录. Fig. 9 The models of different complex near surface and the synthetic seismograms for these model (a) The homogeneous near-surface mdoel with flat topography and its synthetic seismograms; (b) The homogeneous near-surface model with rough topography and its synthetic seismograms; (c) The weak heterogeneous near-surface model (δ=5%) with rough topography and its synthetic seismograms; (d) The strong heterogeneous near-surface model(δ= 15%) with rough topography and its synthetic seismograms. |
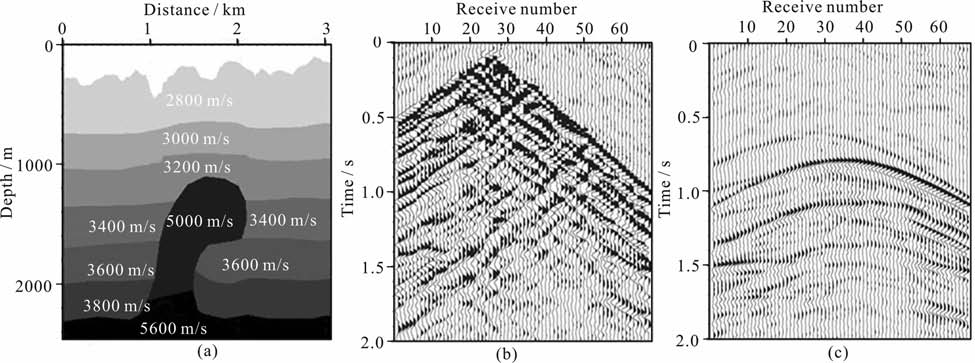
图 10a为一个包含复杂地表的盐丘模型,速度分布如图所示.模拟该模型的主要目的是对来自盐丘的强反射能量与复杂地表强散射能量进行比较.震源位于水平距离1350m, 自由表面下25m 处,数值模拟得到的自由表面接收合成地震记录如图 10b所示.由图可见,地表强散射噪音能量很大,弥漫整个剖面,具有一定的相干性,干涉和淹没来自地表下各地层和盐丘的反射信号.图 10c为把起伏地表变平进行数值模拟得到的合成记录,来自盐丘的强反射在此炮集上很突出.由此可见,剧烈的起伏地表是降低地震资料品质的主要原因之一.
|
图 10 复杂地表与平地表盐丘模型地震模拟比较 (a)复杂地表盐丘模型;(b)起伏自由表面接收合成的反射地震记录;(c)平地表合成的反射地震记录. Fig. 10 Synthetic seismograms for rugged free surface (a) Satt model with rough topography;(b) The reflection synthetic seismograms with rough topography;(c) The reflection synthetic seismograms with flat topography. |
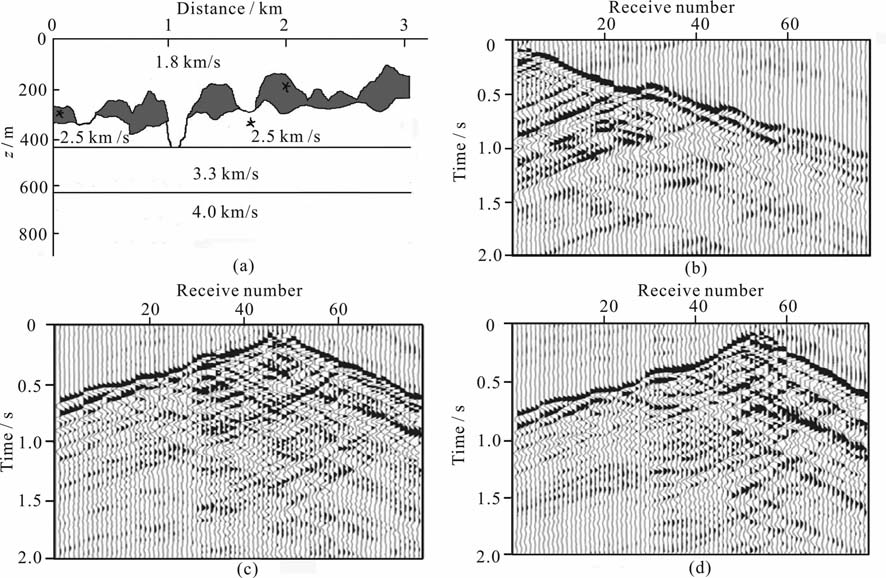
图 11是针对中国西部某地区起伏地表模型进行地震数值模拟得到的合成地震炮集记录.本区地表起伏剧烈、高差近400 m, 低降速带横向变化较大,对地震采集数据品质造成严重影响,主要表现为采集的地震资料信噪比低.地震模拟计算采用 Ricker子波,频率范围0~40 Hz, 3 个震源位置如图所示,位于自由表面以下25m, 图 11(b~d)为自由表面接收合成的3个炮集记录.由图可见,近地表散射分布受地表起伏和低降速带横向变化的影响,形成很强的、延续至中深层的散射噪音环境,破坏来自地下深部的反射.另外,崎岖地表和相关的近地表低速异常带为来自地下深部的反射波提供一个再次散射的平台,进一步增强剖面上中深层的散射噪声.
|
图 11 崎岖地表低降速带复杂近地表模型地震模拟 (a)复杂近地表模型;(b)左边放炮地表接收合成炮集;(c)中间放炮地表接收合成炮集;(d)右边放炮地表接收合成炮集. Fig. 11 Synthetic seismograms for complex near surface model with rugged free surface and low subweathered zone (a) The complex near surface model;(b) The synthetic seismograms with the source on the left;(c) The synthetic seismograms with the source at the center;(d) The synthetic seismograms with the source on the right. |
复杂近地表边界元-体积元地震模拟方法将边界积分方程与Lipmann-Schwinger体积分方程相结合,边界元法模拟起伏地形和表层地质结构边界对地震波传播的影响,体积元法模拟起伏地表下非均质低降速层对地震波的体散射影响.该方法的主要优点为几何上精确描述含崎岖地表在内的近地表结构中各种不规则界面,实现精确模拟复杂近地表对地震波传播的边界散射;显式应用近地表地层界面的连续边界条件,实施半解析-半数值的地震模拟;有效模拟复杂地表下随机非均匀介质对地震波场的体散射,实现边界散射与体散射的有机结合;可以分别模拟来自近地表不同地质体的反射(散射)波,实现直观表达地质元素与地震波场构成的相互关系.
利用边界元-体积元地震模拟方法对复杂近地表模型进行的地震数值模拟结果表明,起伏地表和低降速带的横向变化是影响地震资料品质的主要原因,主要表现为复杂近地表引起下伏构造反射走时畸变;崎岖自由表面散射形成很强的相干性散射噪音,干涉并掩盖来自下伏地层的反射波;低降速带随机非均匀介质引起的体散射波散化整个波场,形成很强的半随机半相干近地表散射噪音环境,严重降低采集地震资料的信噪比.
| [1] | 牟永光, 裴正林. 三维复杂介质地震数值模拟. 北京: 石油工业出版社, 2005 . Mou Y G, Pei Z L. Seismic Numerical Modeling for 3D Complex Media (in Chinese). Beijing: Petroleum Industry Press, 2005 . |
| [2] | Komatitsch D, Coutel F, Mora P. Tensorial formulation of the wave equation for modeling curved interfaces. Geophys. J. Internat. , 1996, 127(1): 156-168. DOI:10.1111/gji.1996.127.issue-1 |
| [3] | Carcione J M, Wang J P. A Chebyshev collocation method for the elastodynamic equation in generalized coordinates. Comput. Fluid Dynamics J. , 1993, 2(3): 269-290. |
| [4] | Tessmer E, Kosloff D. 3-D elastic modeling with surface topography by a Chebychev spectral method. Geophysics , 1994, 59(3): 464-473. DOI:10.1190/1.1443608 |
| [5] | Hestholm S O, Ruud B O. 2D finite-difference elastic wave modeling including surface topography. Geophysical Prospecting , 1994, 42(5): 371-390. DOI:10.1111/gpr.1994.42.issue-5 |
| [6] | Marfurt K J. Accuracy of finite-difference and finite-element modeling of the scale and elastic wave equations. Geophysics , 1984, 49(5): 533-549. DOI:10.1190/1.1441689 |
| [7] | Bouchon M, Campillo M, Gaffet S. A boundary integral equation-discrete wavenumber representation method to study wave propagation in multilayered media having irregular interfaces. Geophysics , 1989, 54(9): 1134-1140. DOI:10.1190/1.1442748 |
| [8] | Bouchon M, Schultz C A, Toksz M N. Effect of three dimensional topography on seismic motion. J. Geophys. Res. , 1996, 101(B3): 5835-5846. DOI:10.1029/95JB02629 |
| [9] | Chen X F. Seismogram synthesis for multi-layered media with irregular interfaces by global generalized reflection/transmission matrices method. I. Theory of two-dimensional SH case. Bull. Seism. Soc. Am. , 199, 80(6): 1696-1724. |
| [10] | Chen X F. Seismogram synthesis for multi-layered media with irregular interfaces by the global generalized reflection/transmission matrices method. Bull. Seism. Soc. Am. , 1995, 85(4): 1094-1106. |
| [11] | Bakamjian B. Boundary integrals: An efficient method for modeling seismic wave propagation in 3-D. 62th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 1992. 1232~1235 |
| [12] | 符力耘, 牟永光. 弹性波边界元法正演模拟. 地球物理学报 , 1994, 37(4): 521–529. Fu L Y, Mou Y G. Boundary element method for elastic wave forward modeling. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1994, 37(4): 521-529. |
| [13] | Sánchez-Sesma F J, Campillo M. Diffraction of P, SV and Rayleigh waves by topographic features: a boundary integral formulation. Bull. Seism. Soc. Am. , 1991, 81(6): 2234-2253. |
| [14] | Sánchez-Sesma F J, Campillo M. Topographic effects for incident P, SV and Rayleigh waves. Tectonophysics , 1993, 218(1-3): 113-125. DOI:10.1016/0040-1951(93)90263-J |
| [15] | Moczo P, Bystricky E, Kristek J, et al. Hybrid modeling of P-SV seismic motion at inhomogeneous viscoelastic topographic structures. Bull. Seis. Soc. Am. , 1997, 87(5): 1305-1323. |
| [16] | Fu L Y, Mu Y G, Yang H J. Forward problem of nonlinear Fredholm integral equation in reference medium via velocity- weighted wavefield function. Geophysics , 1997, 62(2): 650-656. DOI:10.1190/1.1444173 |
| [17] | Fu L Y, Wu R S. Infinite boundary element absorbing boundary for wave propagation simulations. Geophysics , 2000, 65(2): 625-637. |
| [18] | Trifunac M D. Surface motion of a semi-cylindrical alluvial valley for incident plane SH waves. Bull. Seism. Soc. Am. , 1971, 61(5): 1755-1770. |
| [19] | Trifunac M D. Scattering of plane SH waves by a semi-cylindrical canyon. Earthquake Engineering and Structural Dynamics , 1973, 1(3): 267-281. |
 2011, Vol. 54
2011, Vol. 54

